This work brings algebraic pandiagonal striped and semi-striped magic squares of orders 4 to 12 for the reduced entries. The even orders are striped magic squares and odd orders are semi-striped magic squares. By reduced or less entries, we understand that instead of normal n^2 entries of a magic square order n, we are using less number of entries. Moreover, in these situations the entries are no more sequential numbers. These entries are non-sequential positive and negative numbers. Sometimes, we call these kind of magic squares as self-made. It means that these are complete in themselves. Just put the values of the entries and choose the magic sum, we get a magic square. In some cases, there may be decimal or fractional values of the entries depending on the types of magic squares. By striped magic square we understand that it is composed of equal width strips of order 2. The change in only in the lengths of the magic rectangles. There are three types of magic squares studied here. For simplicity we call them as cyclic-type, flat-type and corner-type. This type of work is not known before in the literature of magic square. It is brought for the first time here. For the study on sequential entries magic squares i.e., the idea of double-digit bordered magic squares for sequential number entries is studied by the author. This work is for non-sequential entries. Moreover, in this work the magic rectangles are considered as cyclic, flat or corner-types. In case of odd orders, except the magic square of orders 3 or 5, all others are magic rectangles of width 2. The change is always in length of magic rectangles. These kind of magic squares we call as semi-striped. For similar kind of work for different orders in different styles and designs, the readers are suggested to see author’s work
This work is online available at the following link:
Inder J. Taneja, Algebraic Pandiagonal Striped and Semi-Striped Magic Squares of Orders 4 to 12, Zenodo, January 12, 2026, pp. 1-52, https://doi.org/10.5281/zenodo.18221904.
Algebraic Pandiagonal Striped Magic Squares of Even Orders
Below are algebraic pandiagonal striped magic squares of even orders, i.e., of orders 4, 6, 8, 10 and 12. These are followed by examples for each orders.
Striped Pandiagonal Magic Square of Order 4
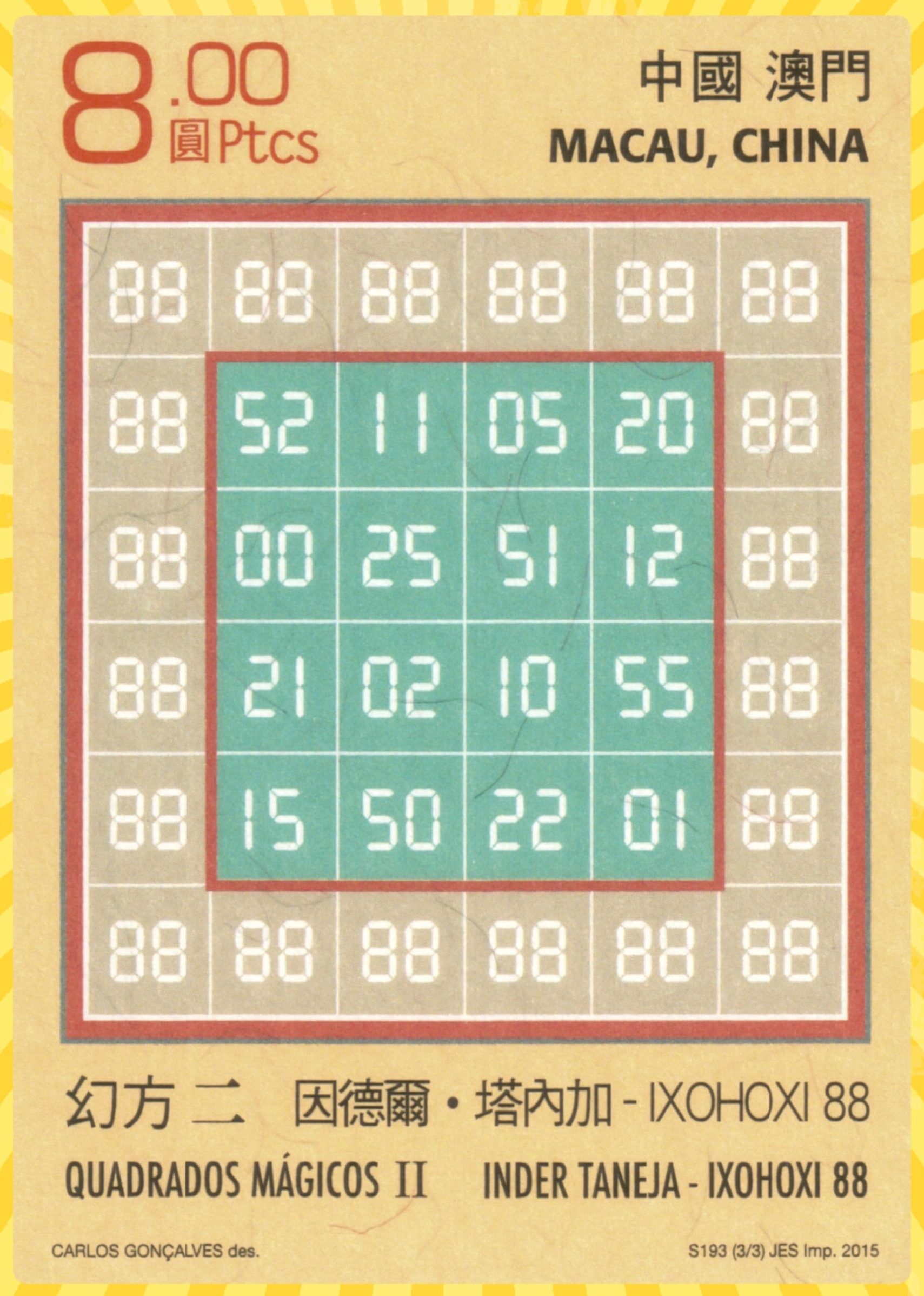
Result 1. Striped Magic Square of Order 4
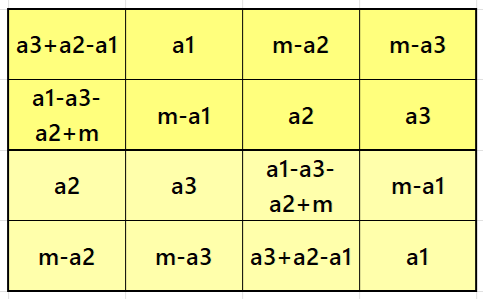
Example 1.
See below an example of a striped pandiagonal magic square of order 4 based on above result
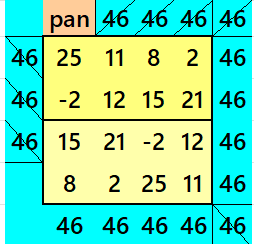
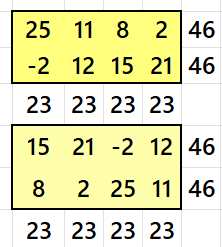
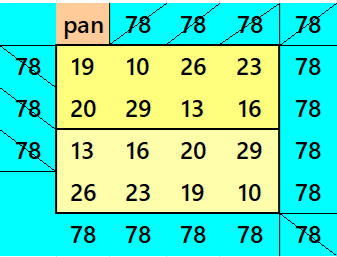
Below are sums of strips:
Striped Pandiagonal Magic Squares of Order 6
Result 2. Striped Pandiagonal Magic Square of Order 6
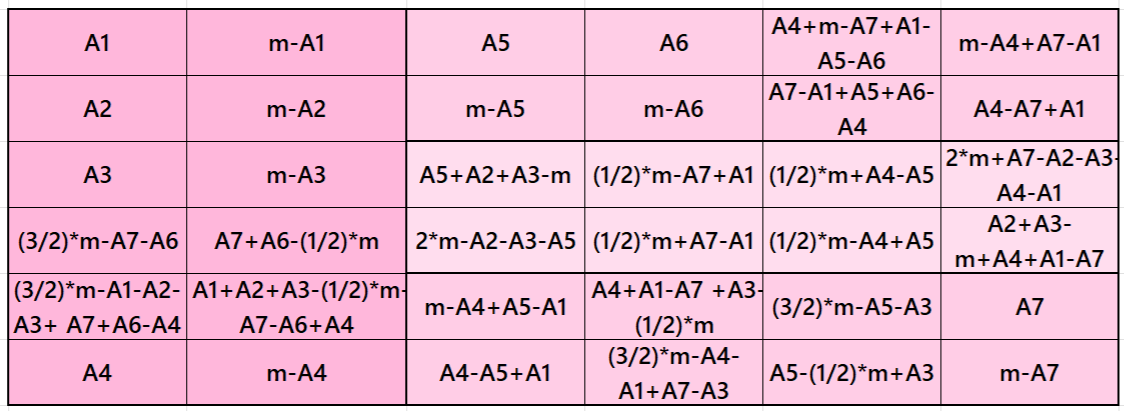
Example 2.
See below an example of a striped pandiagonal magic square of order 6 based on the Result 1.
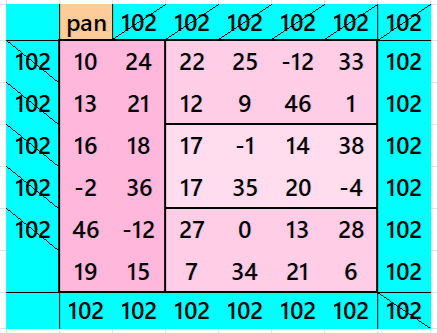
Below are sums of strips:
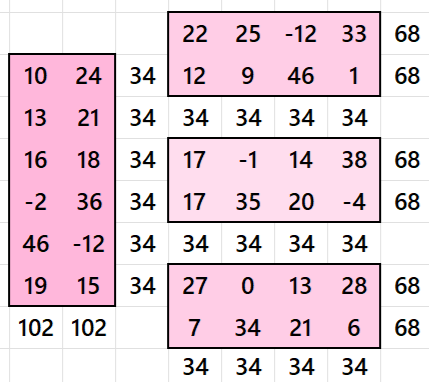
Result 3. Striped Pandiagonal Magic Square of Order 6

Example 3.
See below an example of a striped pandiagonal magic square of order 6 based on the Result 2
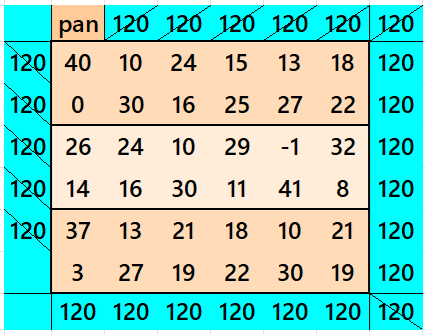
Below are sums of strips:
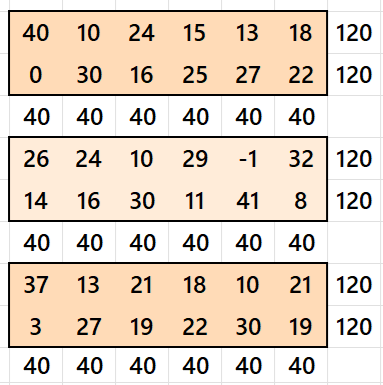
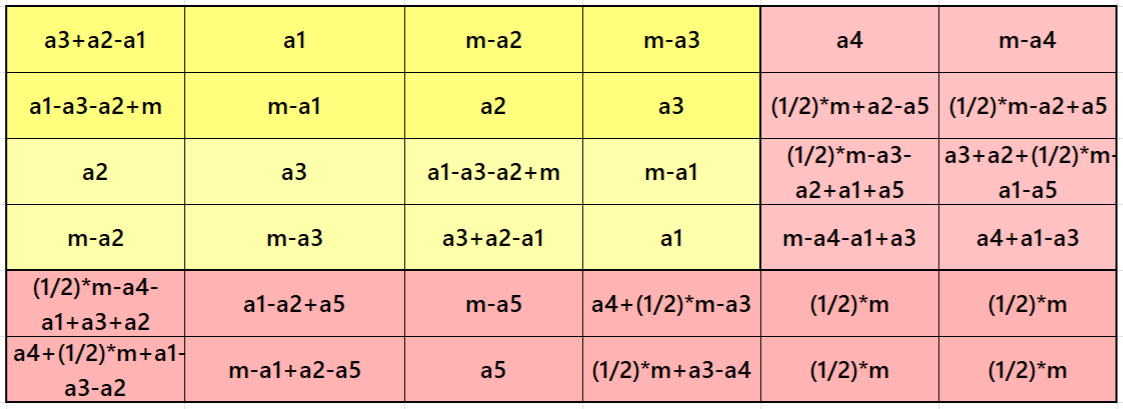
Result 4. Striped Pandiagonal Magic Square of Order 6
Example 4.
See below an example of a striped pandiagonal magic square of order 6 based on the Result 4
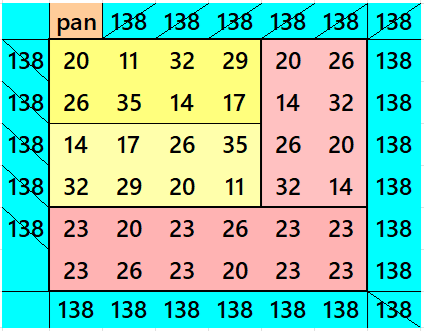
Below is pandiagonal magic square of order 4 appearing in upper-left corner.
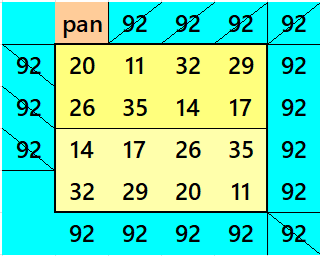
Striped Pandiagonal Magic Squares of Order 10
Result 5. Striped Pandiagonal Magic Square of Order 10
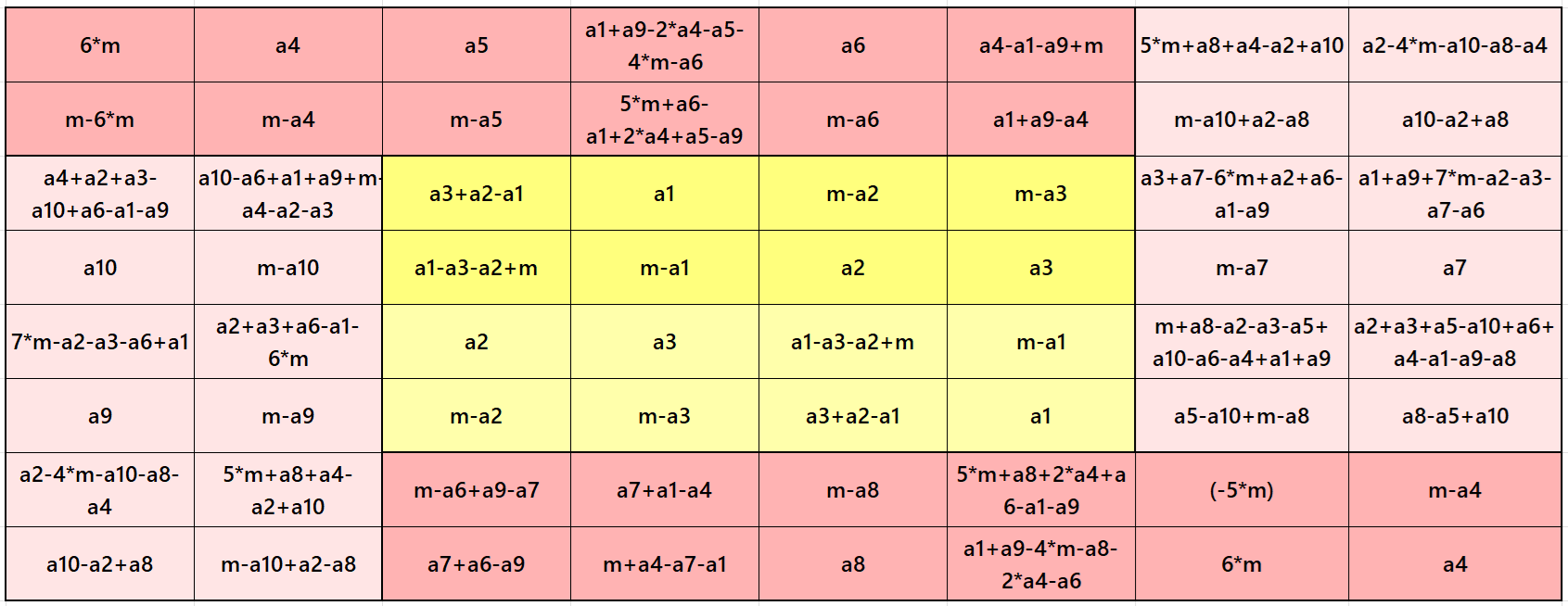
Example 5.
See below an example of a striped pandiagonal magic square of order 8 based on the Result 5.
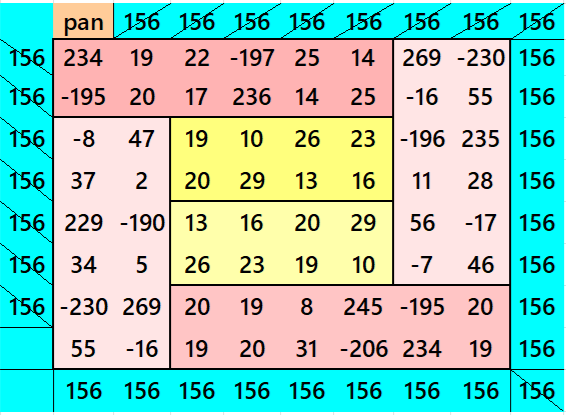
Below is a pandiagonal magic square of order 4 appearing in the middle.
Result 6. Striped Pandiagonal Magic Square of Order 8
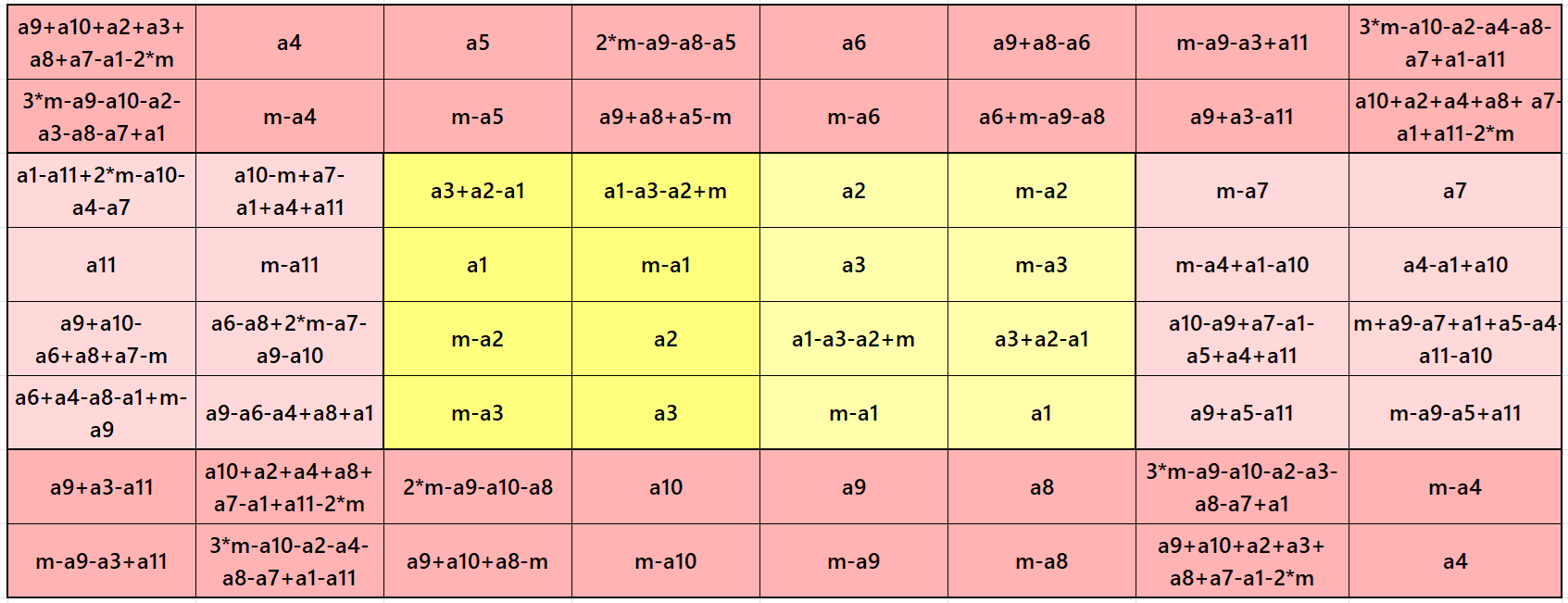
Example 6.
See below an example of a striped pandiagonal magic square of order 8 based on the Result 6
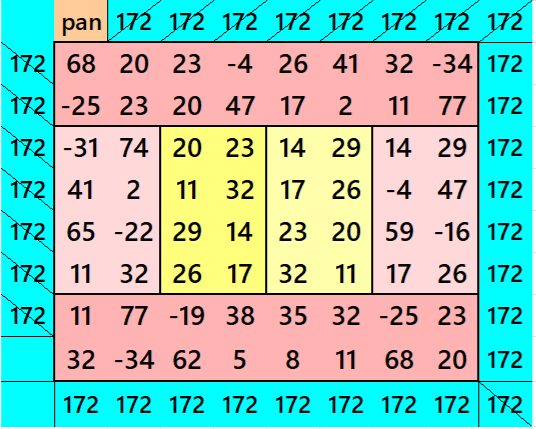
Below is a pandiagonal magic square of order 4 appearing in the middle.
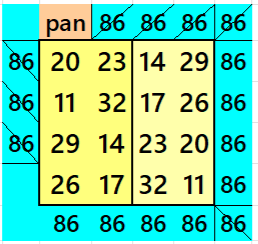
Result 7. Striped Pandiagonal Magic Square of Order 8
Example 7.
See below an example of a striped pandiagonal magic square of order 8 based on the Result 7
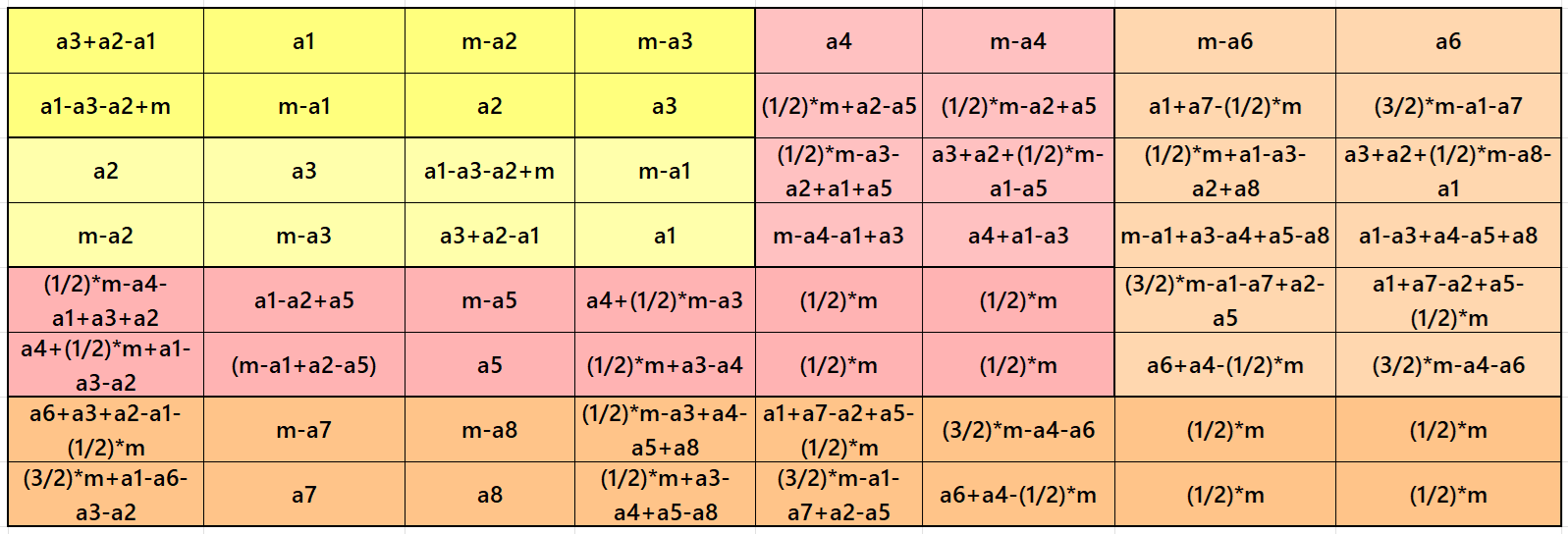
Below are pandiagonal magic squares of orders 6 and 4 appearing in the upper-left corner.
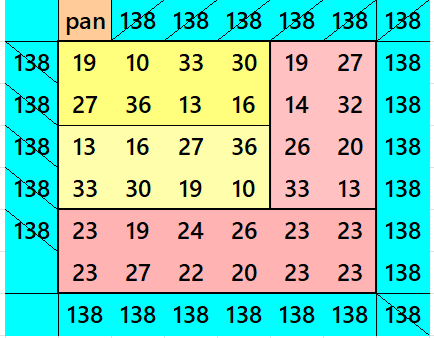
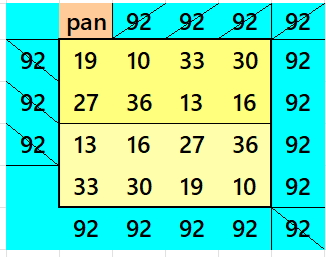
Striped Pandiagonal Magic Squares of Order 10
Result 8. Striped Pandiagonal Magic Square of Order 10
Example 8.
See below an example of a striped pandiagonal magic square of order 10 based on the Result 8.
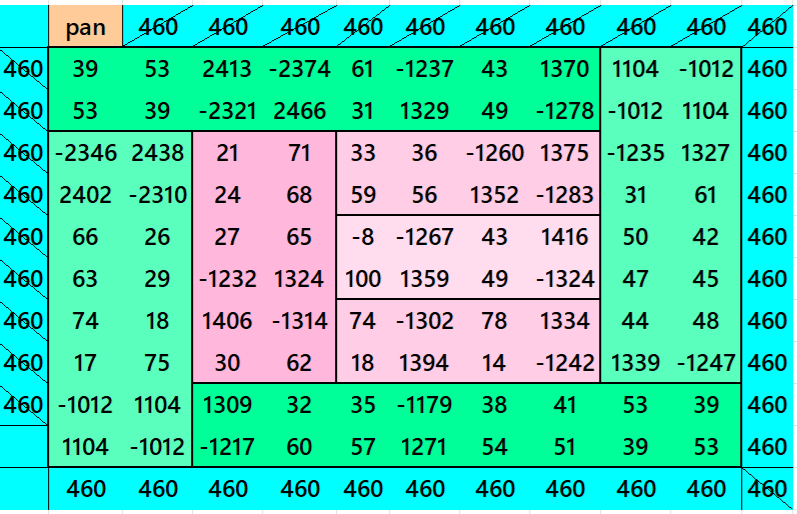
Below is a pandiagonal magic square of order 6 appearing in the middle. The sum of strips is also given
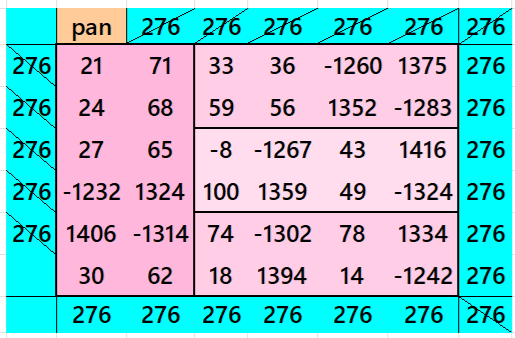
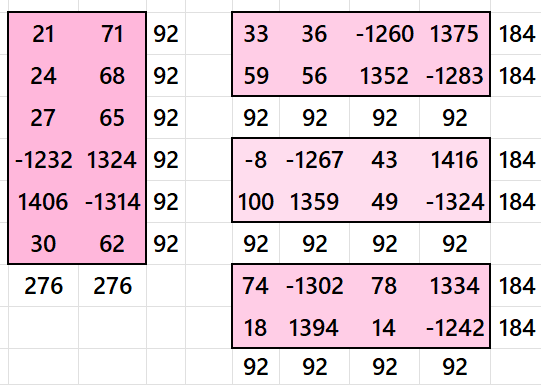
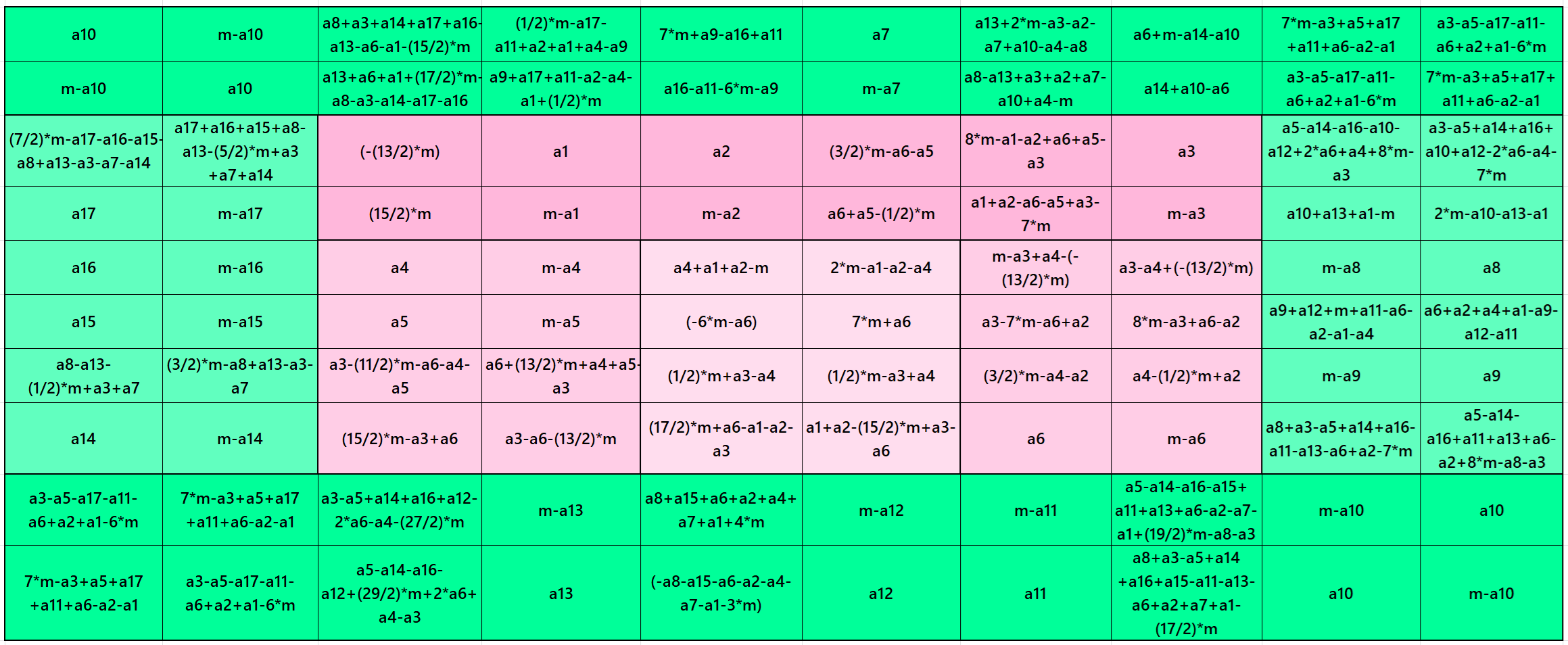
Result 9. Striped Pandiagonal Magic Square of Order 10
Example 9.
See below an example of a striped pandiagonal magic square of order 10 based on the Result 9
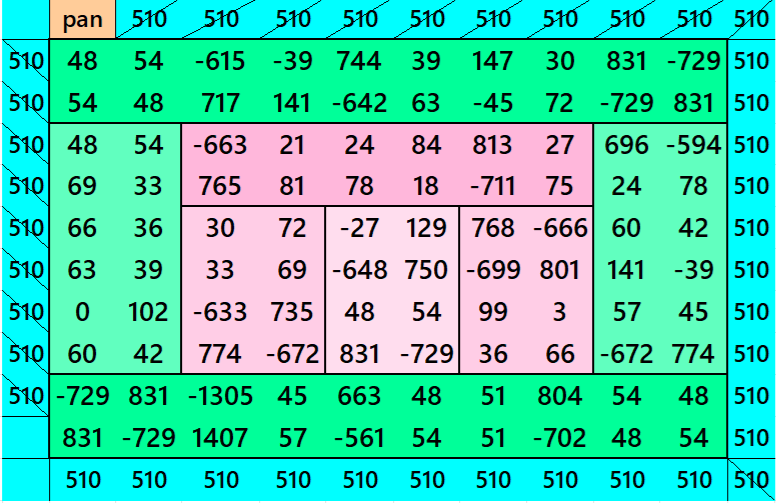
Below is a pandiagonal magic square of order 6 appearing in the middle. The sum of strips is also given
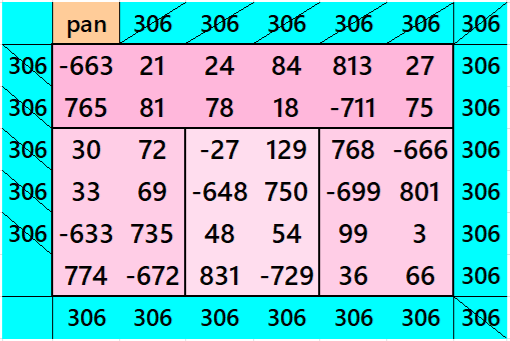
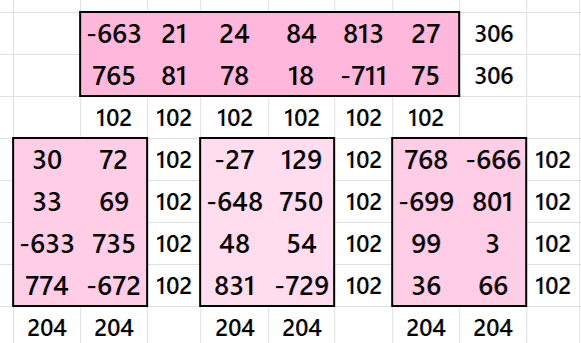
Result 10. Striped Pandiagonal Magic Square of Order 10
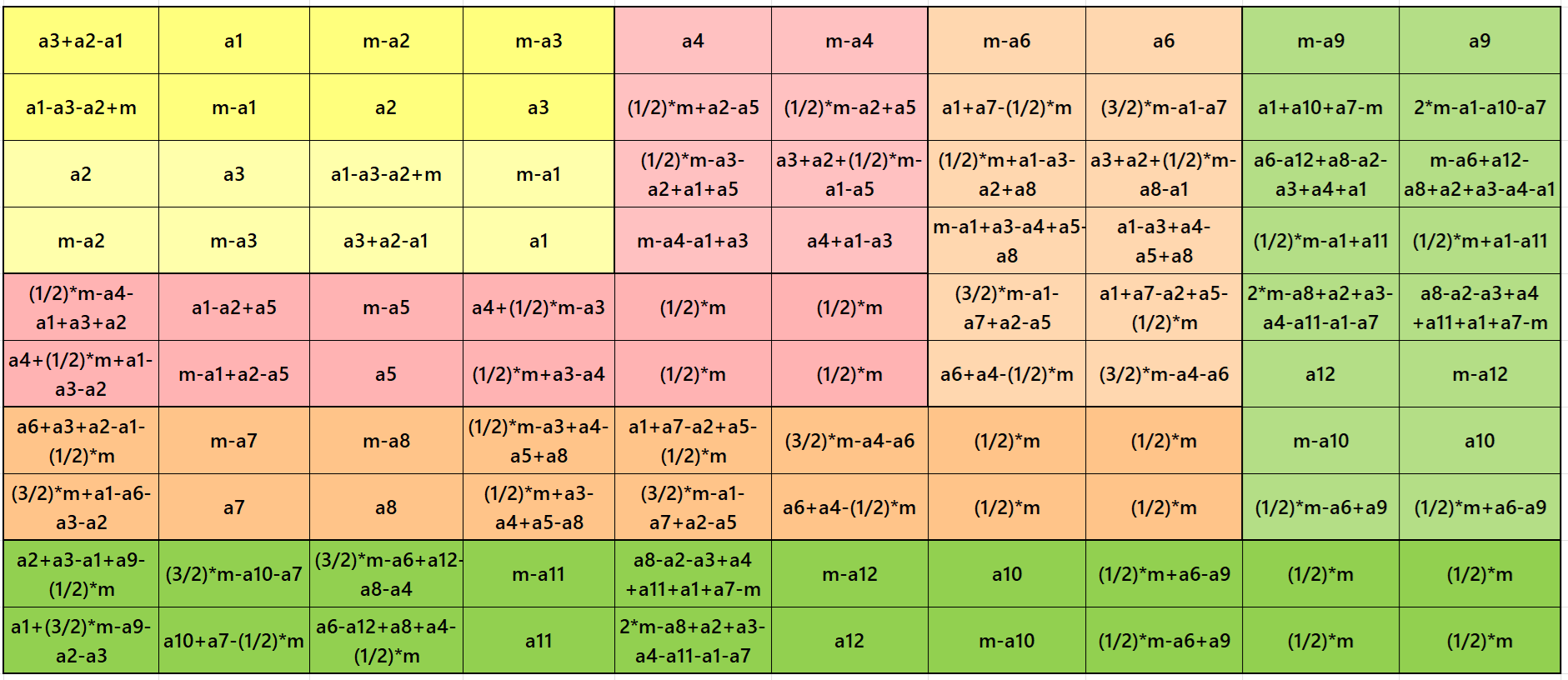
Example 10.
See below an example of a striped pandiagonal magic square of order 10 based on the Result 10
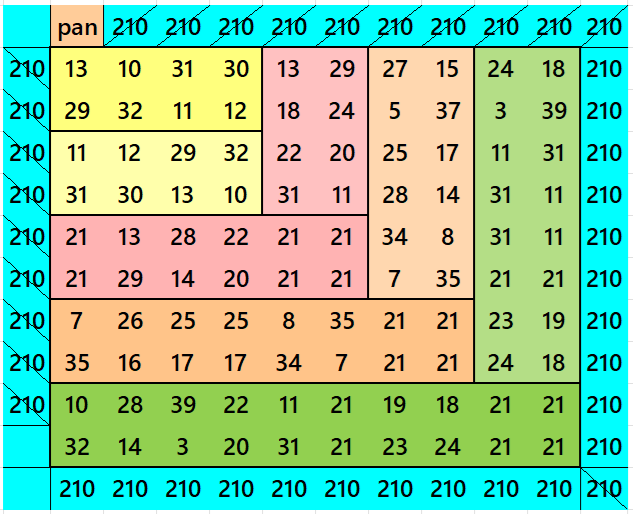
Below are pandiagonal magic squares of orders 8, 6 and 4 appearing in the upper-left corner.
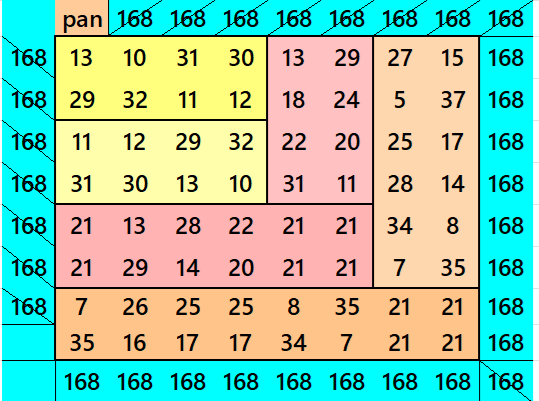
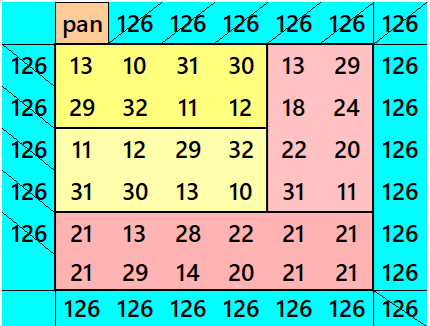
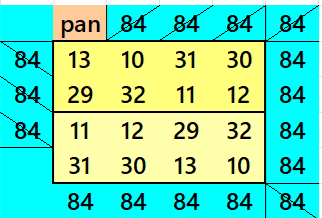
Striped Pandiagonal Magic Squares of Order 12
Result 11. Striped Pandiagonal Magic Square of Order 12
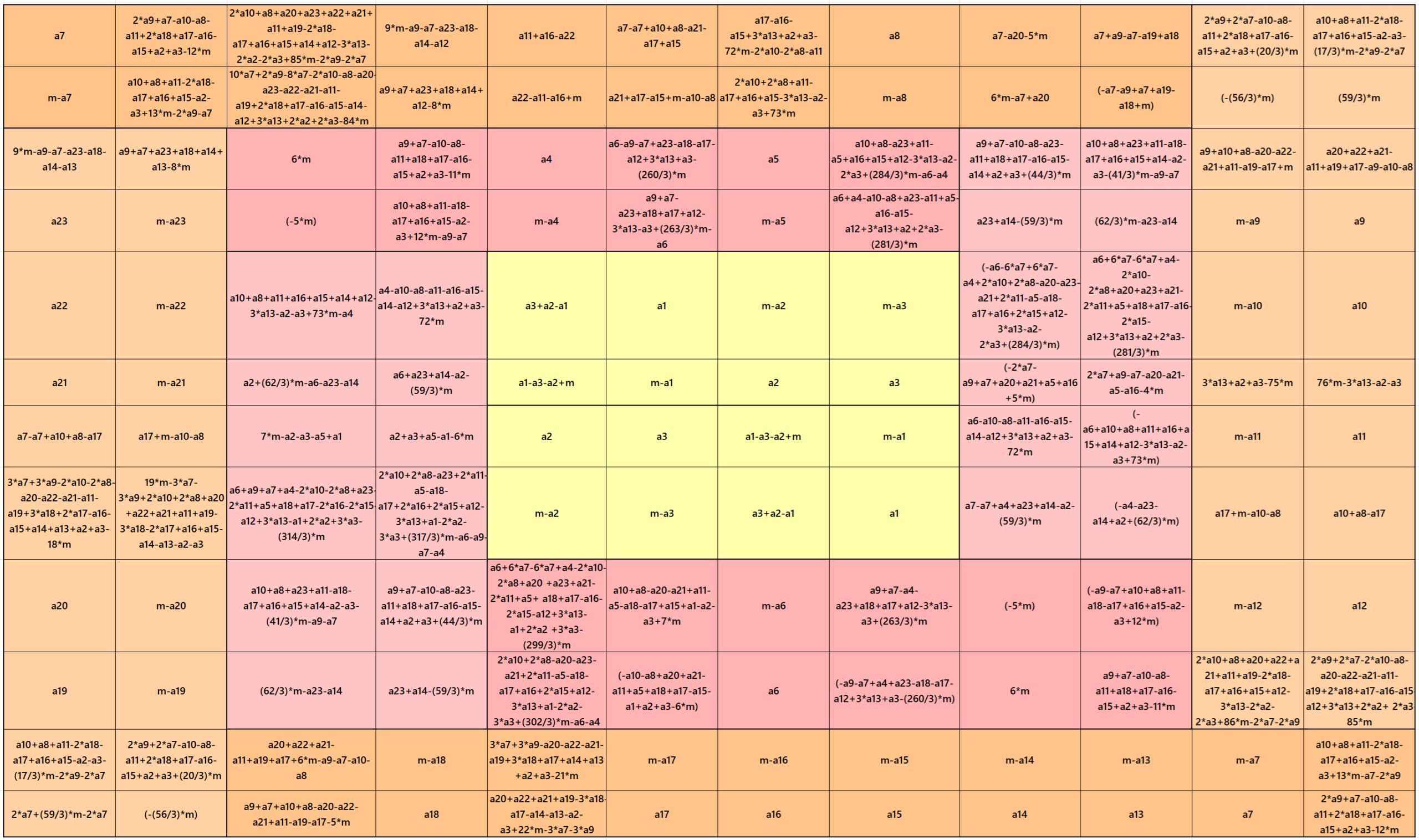
Example 11.
See below an example of a striped pandiagonal magic square of order 12 based on the Result 11.
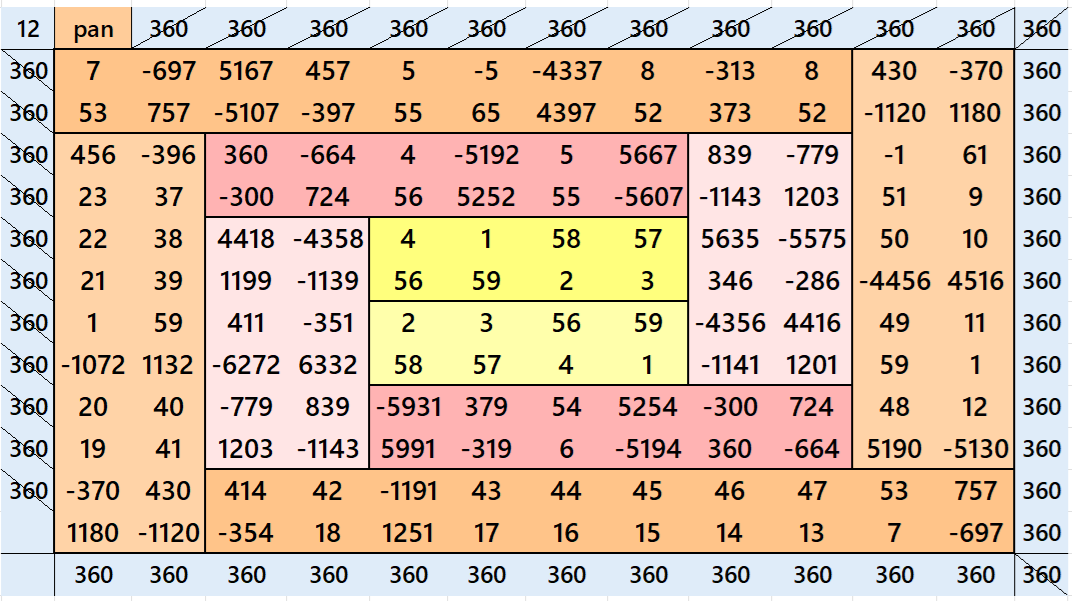
Below are pandiagonal magic squares of orders 8 and 4 appearing in the middle.
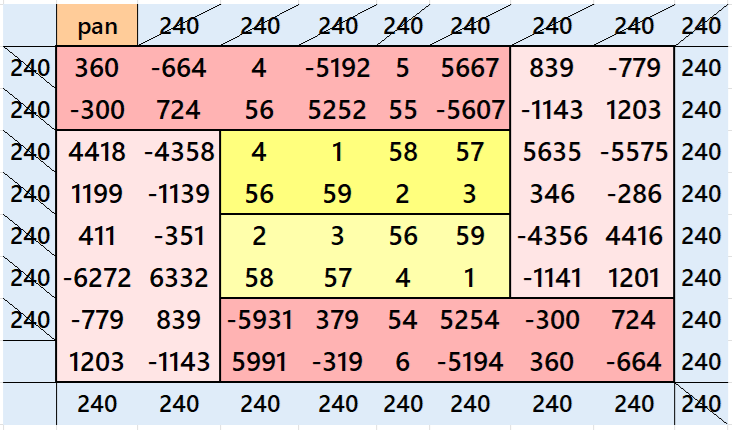
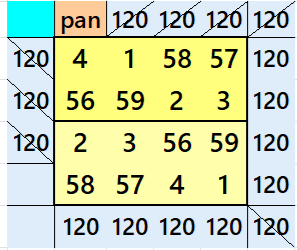
Result 12. Striped Pandiagonal Magic Square of Order 12
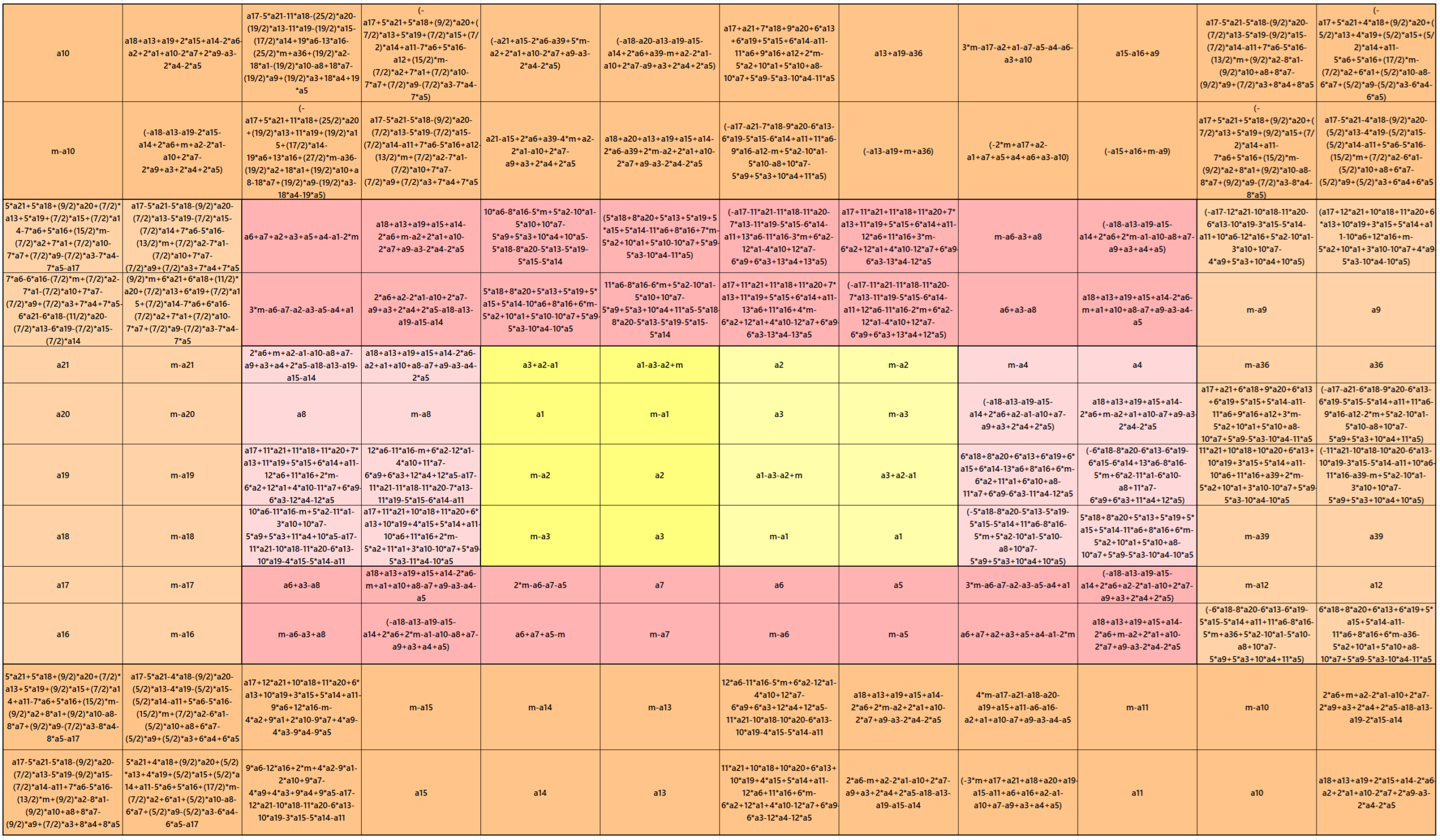
Example 12.
See below an example of a striped pandiagonal magic square of order 12 based on the Result 12
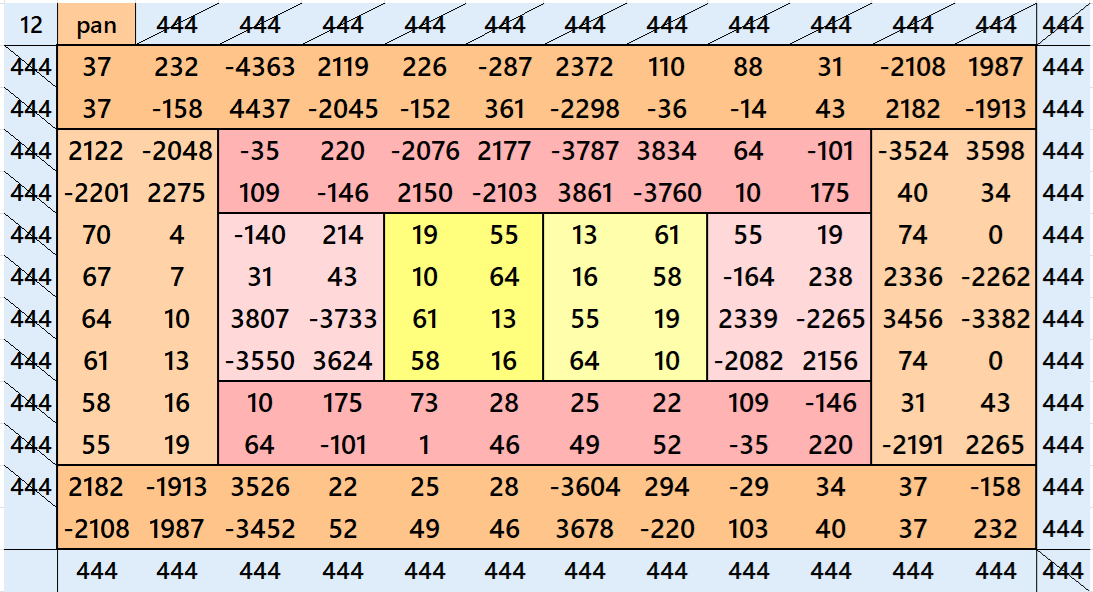
Below are pandiagonal magic square of order 8 and 4 appearing in the middle.
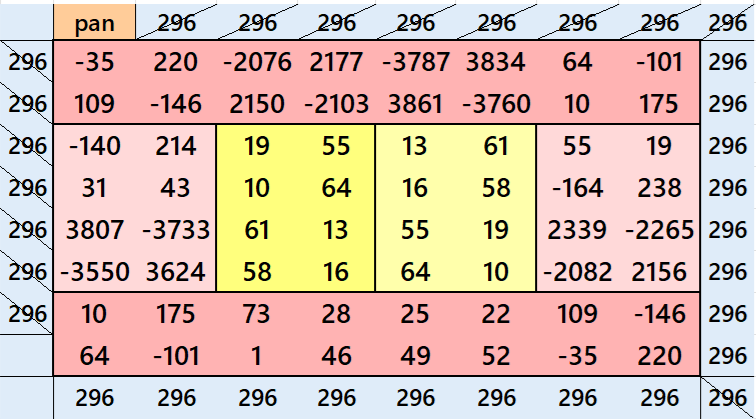
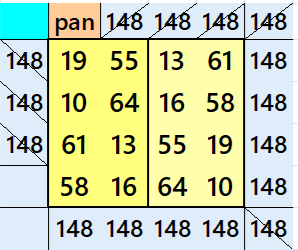
Result 13. Striped Pandiagonal Magic Square of Order 12
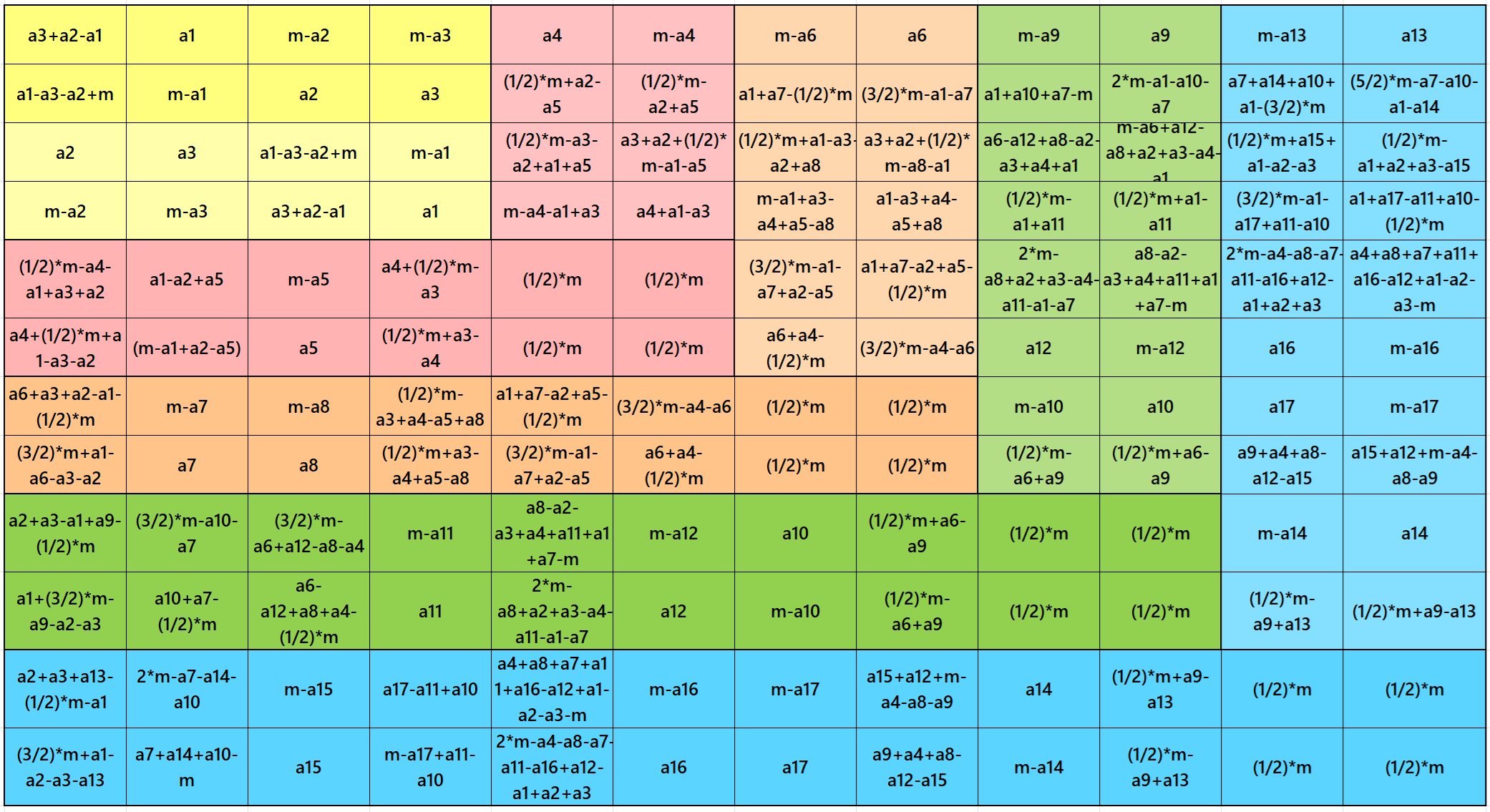
Example 13.
See below an example of a striped pandiagonal magic square of order 11 based on the Result 13

Below are pandiagonal magic squares of orders 10, 8, 6 and 4 appearing in the upper-left corner.
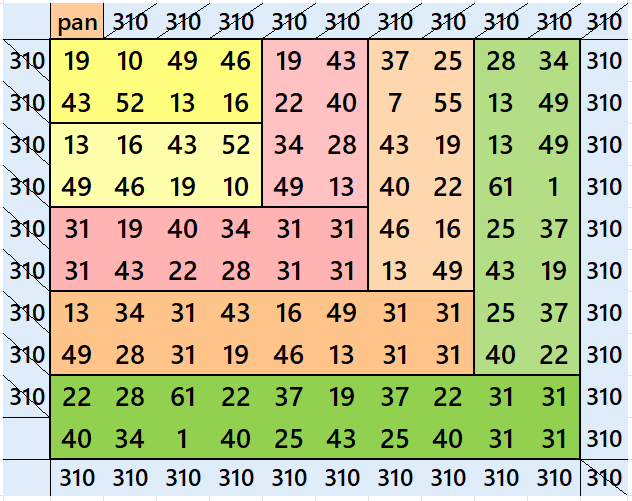
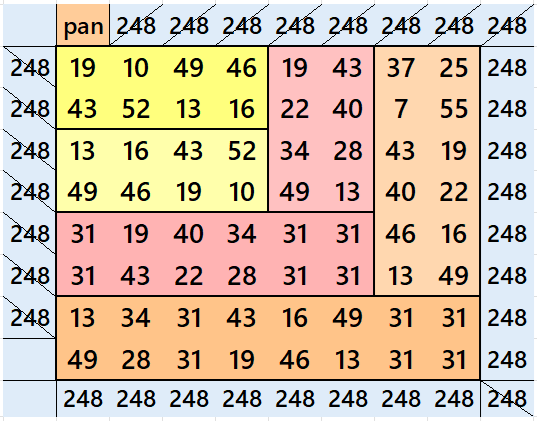
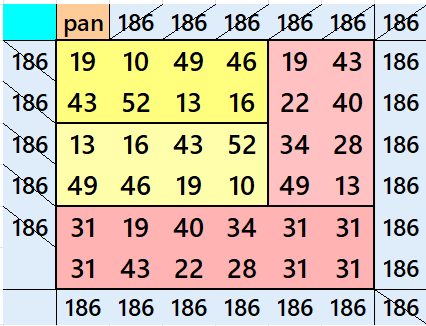
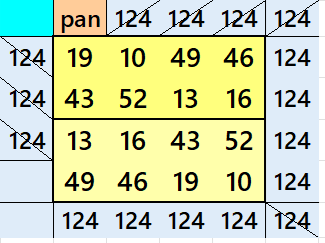
Algebraic Pandiagonal Semi-Striped Magic Squares of Odd Orders
Below are algebraic pandiagonal semi-striped magic squares of odd orders, i.e., of orders 5, 7, 9 and 11. These are followed by examples for each orders. We call them as semi-striped because there is either magic square of order 3 or 5, that don’t satisfy the property of strip. Strip we understand as a magic rectangle with width 2.
Semi-Striped Pandiagonal Magic Square of Order 5
Result 14. Semi-Striped Pandiagonal Magic Square of Order 5
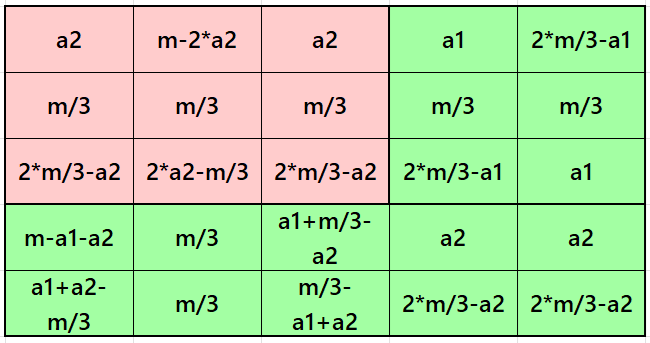
Example 14.
See below an example of a semi-striped pandiagonal magic square of order 5 based on the Result 14
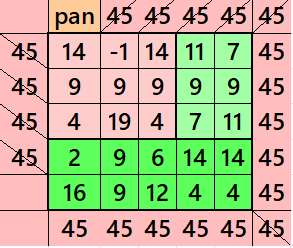
Below is a magic squares of order 3 appearing in the upper-left corner.
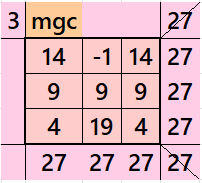
Semi-Striped Pandiagonal Magic Square of Order 7
Result 15. Semi-Striped Pandiagonal Magic Square of Order 7
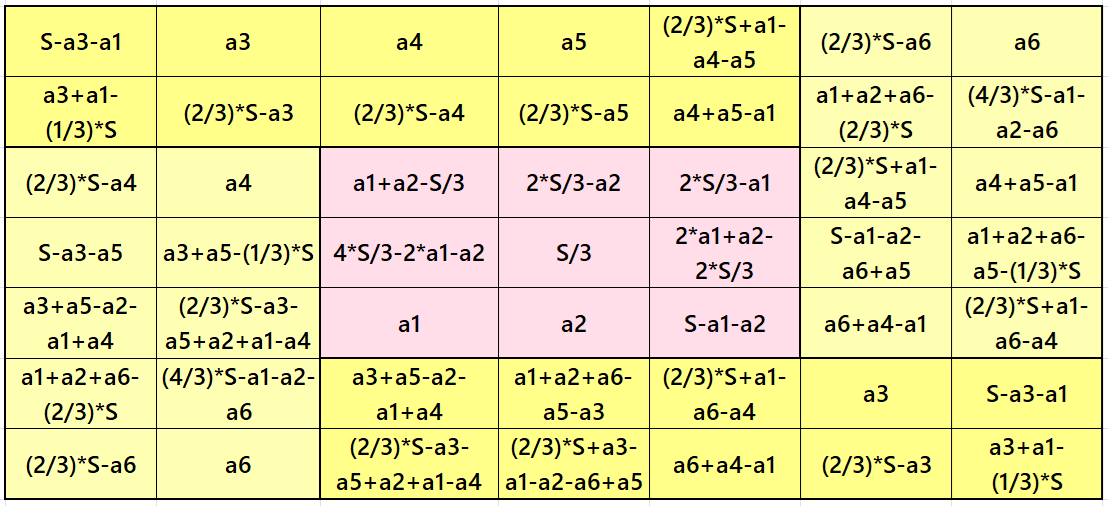
Example 15.
See below an example of a semi-striped pandiagonal magic square of order 7 based on the Result 15
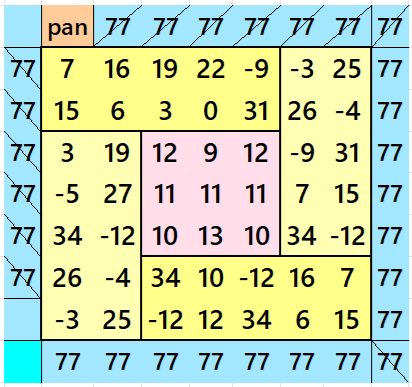
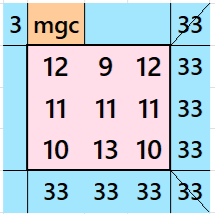
Below is a magic squares of order 3 appearing in the middle of above magic square;
Result 16. Semi-Striped Pandiagonal Magic Square of Order 7
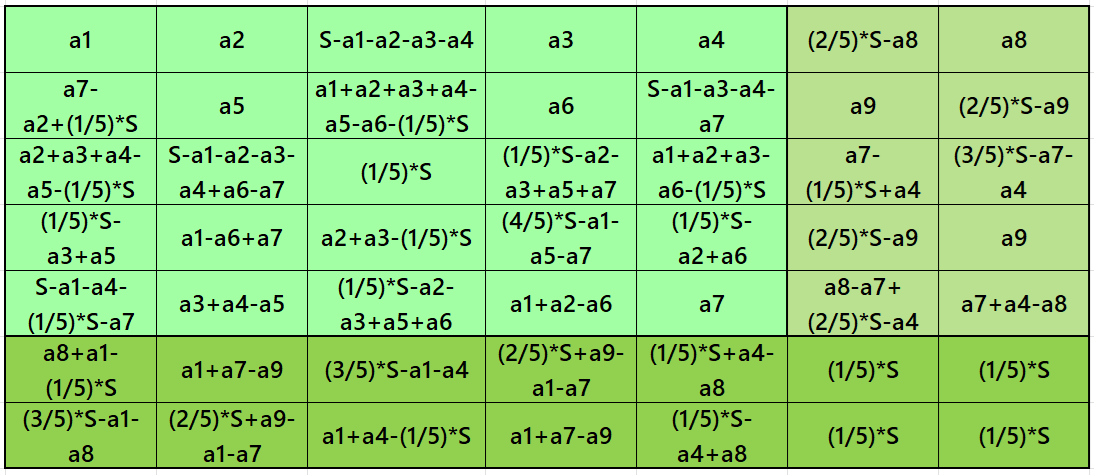
Example 16.
See below an example of a semi-striped pandiagonal magic square of order 7 based on the Result 16
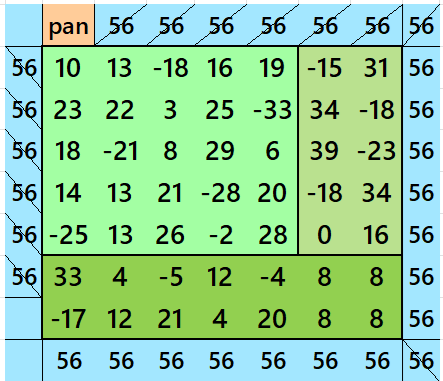
Below is a pandiagonal magic squares of order 5 appearing in the upper-left corner.
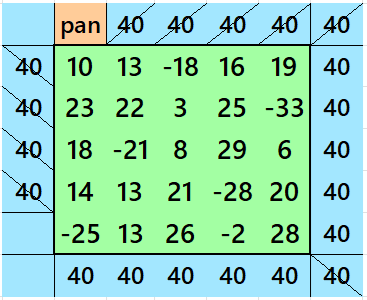
Semi-Striped Pandiagonal Magic Square of Order 9
Result 17. Semi-Striped Pandiagonal Magic Square of Order 9
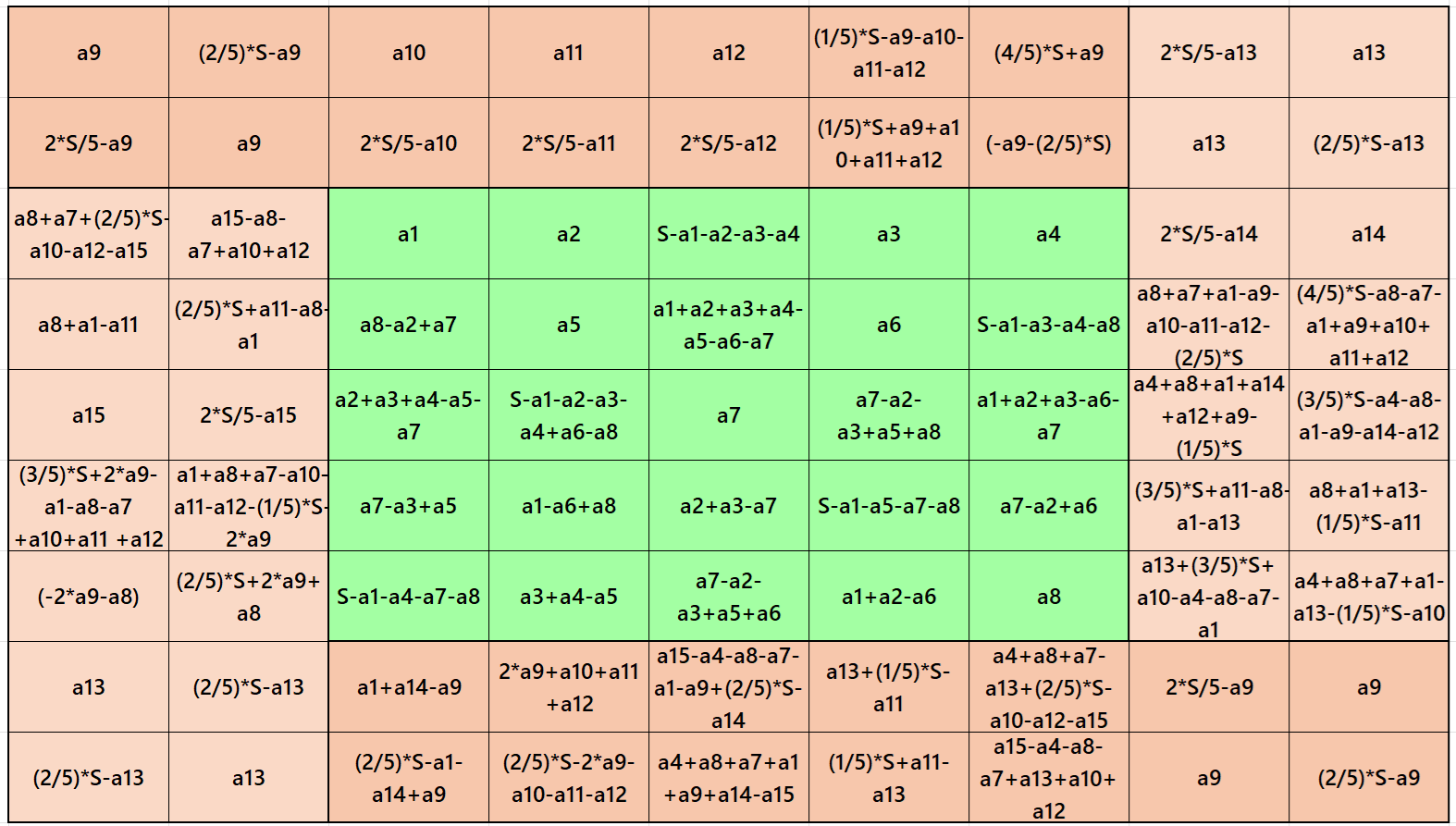
Example 17.
See below an example of a semi-striped pandiagonal magic square of order 9 based on the Result 17
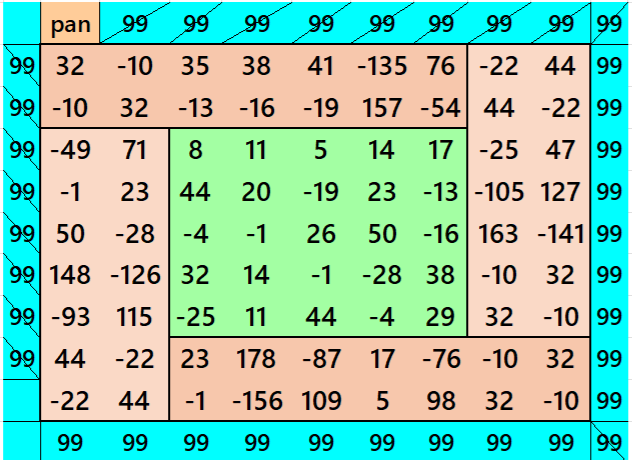
Below is a pandiagonal magic squares of order 5 appearing in the middle of the above magic square.
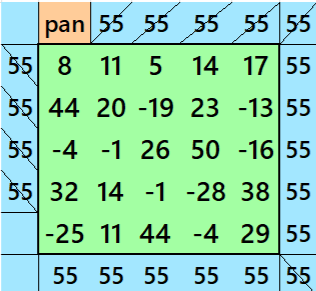
Result 18. Semi-Striped Pandiagonal Magic Square of Order 9
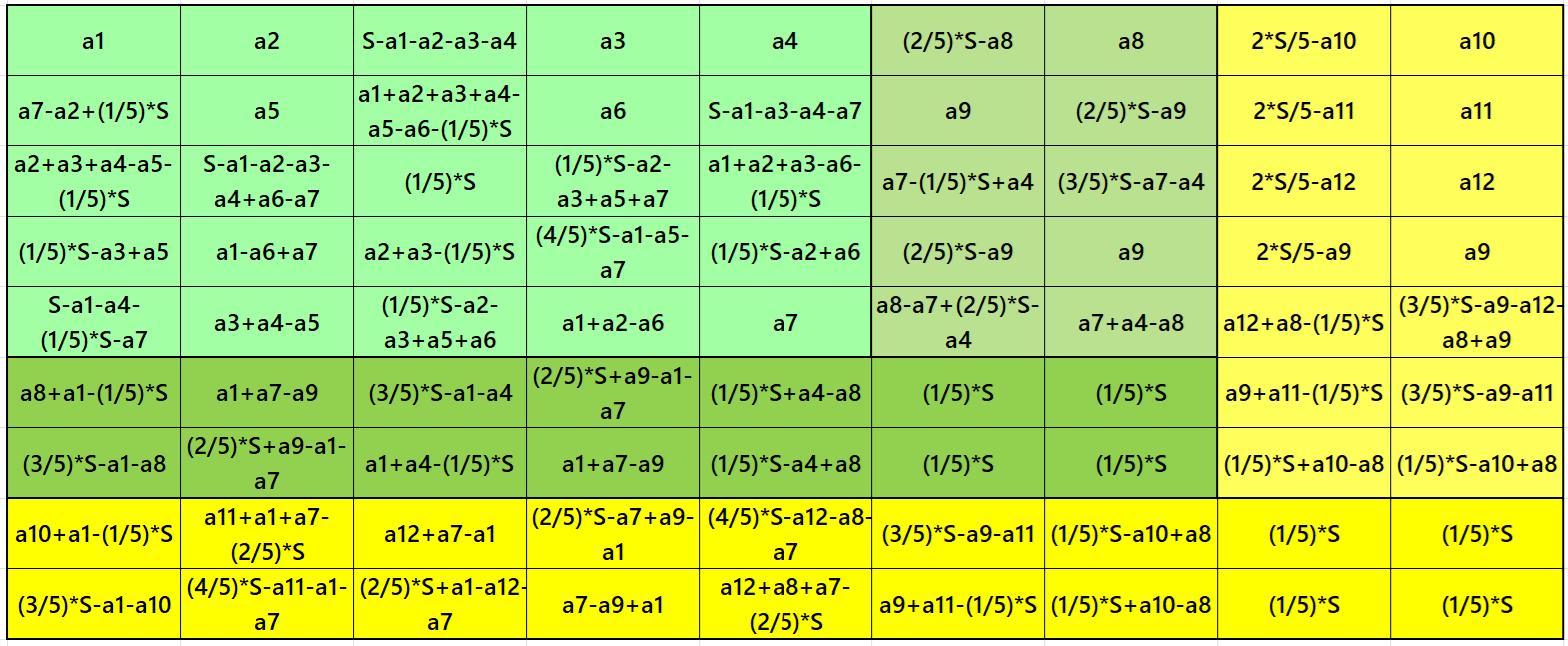
Example 18.
See below an example of a semi-striped pandiagonal magic square of order 9 based on the Result 18
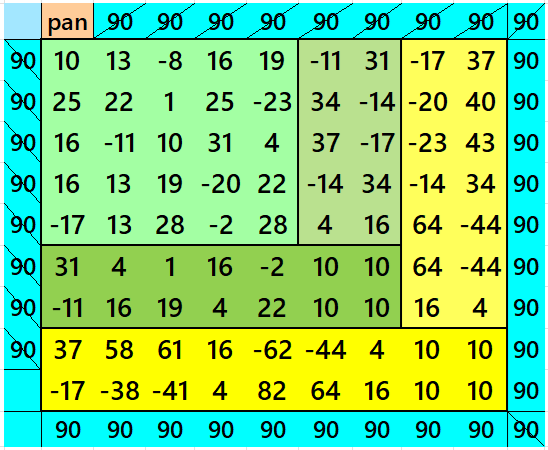
Below is are pandiagonal magic squares of orders 7 and 5 appearing in the upper-left corner.
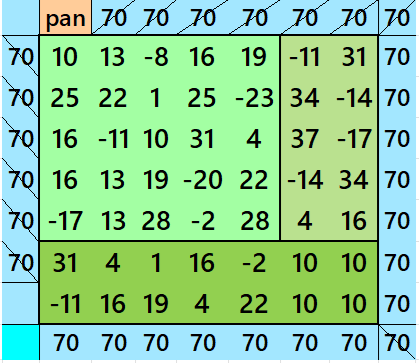
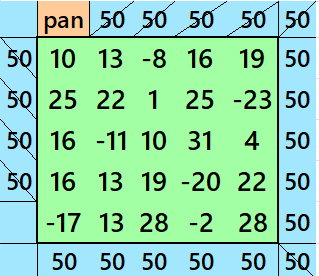
Semi-Striped Pandiagonal Magic Square of Order 11
Result 19. Semi-Striped Pandiagonal Magic Square of Order 11
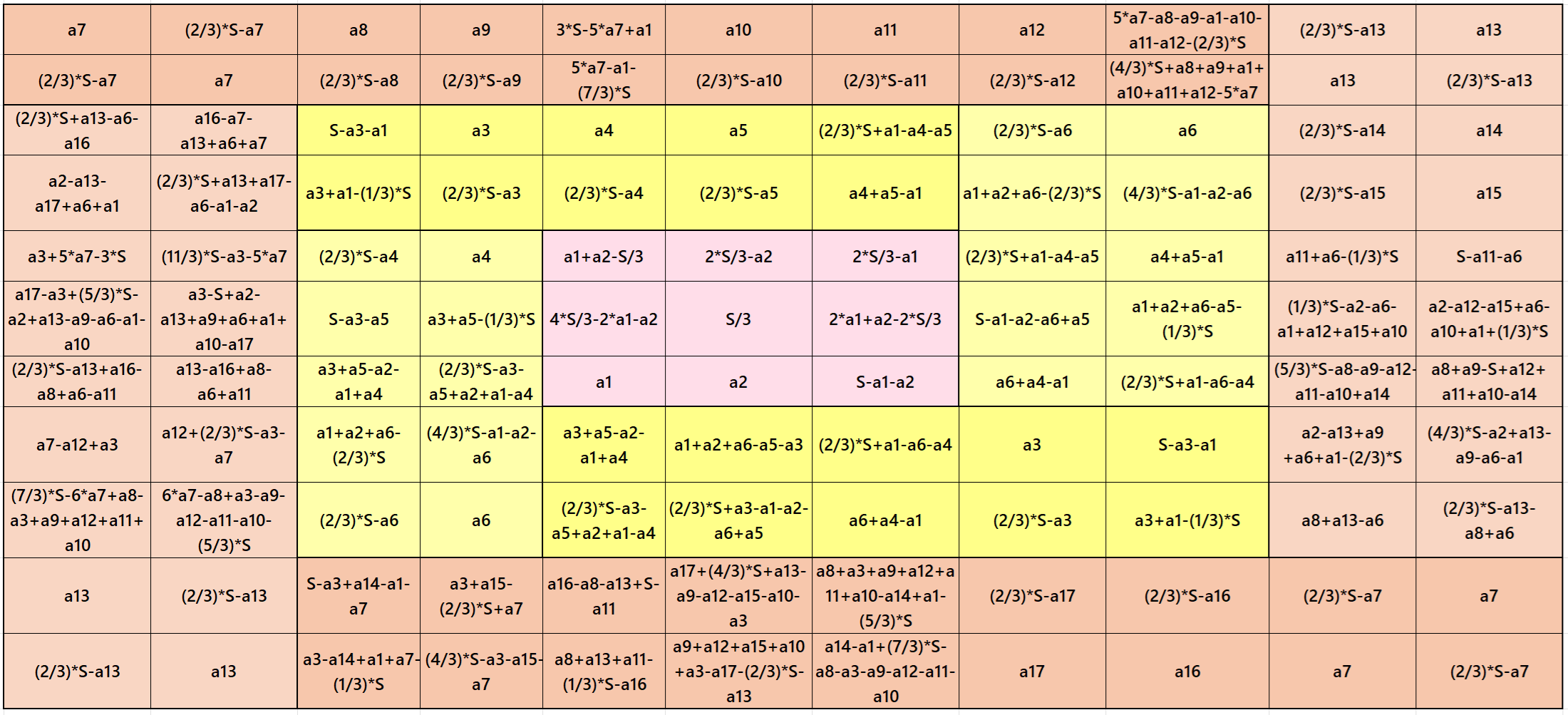
Example 19.
See below an example of a semi-striped pandiagonal magic square of order 7 based on the Result 15
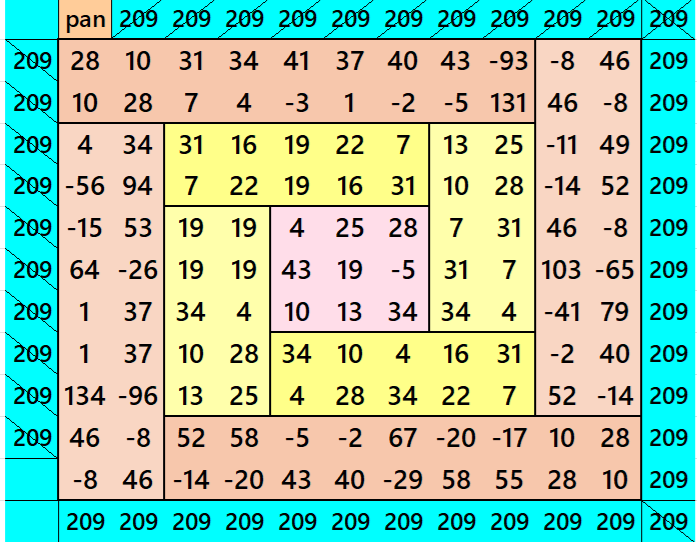
Below is are magic squares of order 7 and 3 appearing in the middle. The magic square of order 7 is pandiagonal.
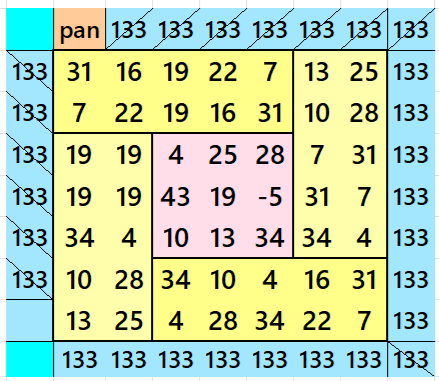
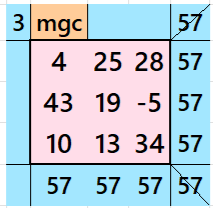
Result 20. Semi-Striped Pandiagonal Magic Square of Order 11
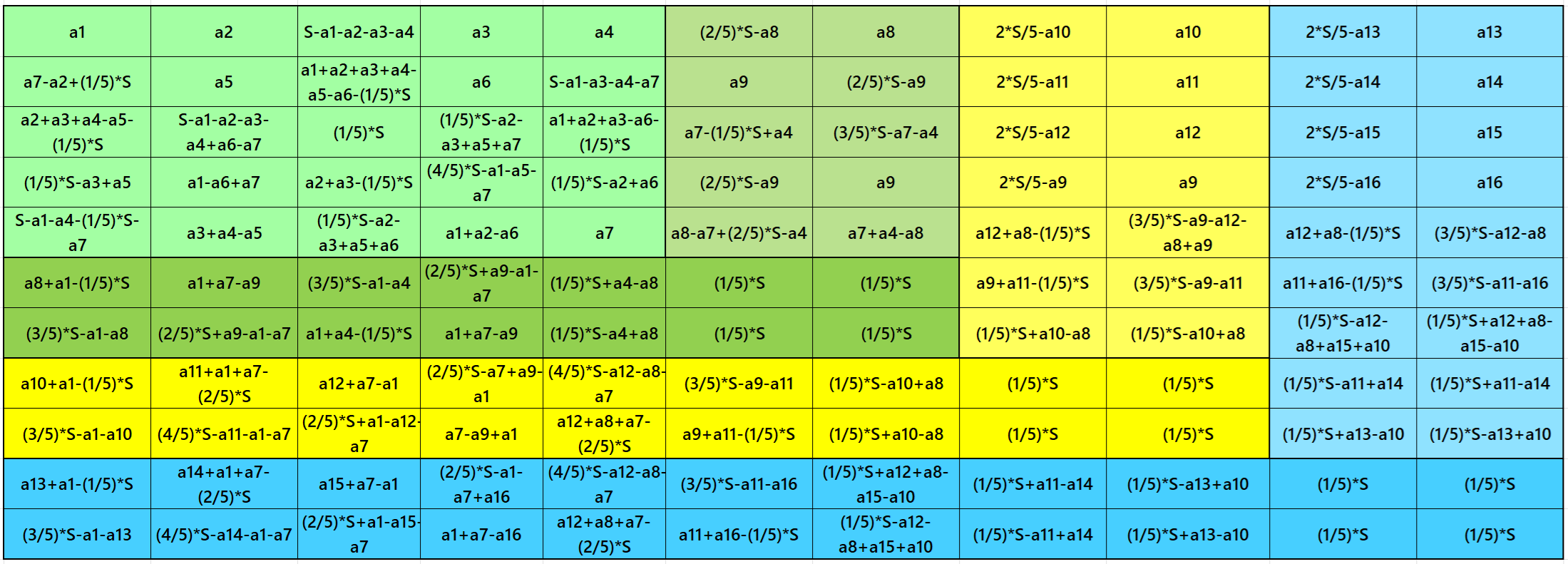
Example 20.
See below an example of a semi-striped pandiagonal magic square of order 11 based on the Result 20
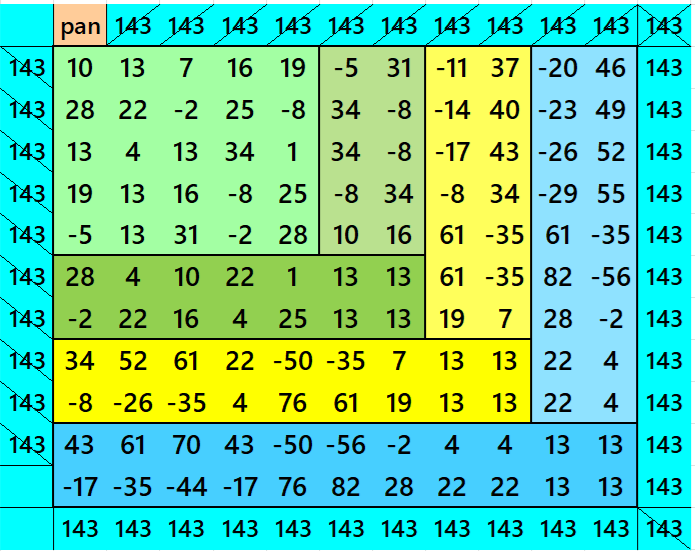
Below are pandiagonal magic squares of orders 9, 7 and 5 appearing in the upper-left corner.
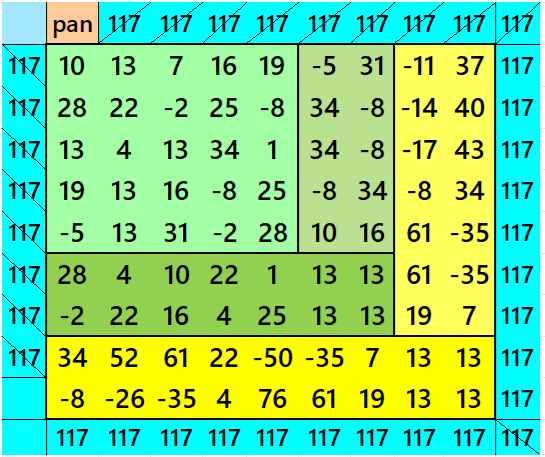
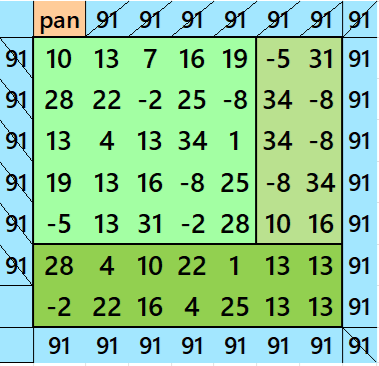
References
Part 1: Day and Dates of the Year – 2025 in Terms of Magic Squares
- Inder J. Taneja, Magic Squares of Orders 3 to 7 in Representing Dates and Days of the Year 2025, Zenodo, May 04, 2025, pp. 1-474, https://doi.org/10.5281/zenodo.15338142.
- Site Link: Magic Squares of Orders 3 to 7 Representing Dates and Days of the Year 2025 (new site)
- Site Link: Magic Squares of Orders 3 to 7 Representing Dates and Days of the Year 2025 (old site)
- Inder J. Taneja, Magic Squares of Order 8 Representing Days and Dates of the Year 2025, Zenodo, May 04, 2025, pp. 1-134, https://doi.org/10.5281/zenodo.15338246.
- Site Link: Magic Squares of Order 8 Representing Days and Dates of the Year 2025 (new site)
- Site Link: Magic Squares of Order 8 Representing Days and Dates of the Year 2025 (old site)
- Inder J. Taneja, Magic Squares of Order 9 Representing Days and Dates of the Year 2025, Zenodo, May 09, 2025, pp. 1-132, https://doi.org/10.5281/zenodo.15375349.
- Site Link: Magic Squares of Order 9 Representing Days and Dates of the Year 2025 (new site)
- Site Link: Magic Squares of Order 9 Representing Days and Dates of the Year 2025 (old site)
- Inder J. Taneja, Magic Squares of Order 10 Representing Days and Dates of the Year 2025, Zenodo, May 21, 2025, pp. 1-59, https://doi.org/10.5281/zenodo.15481738.
- Inder J. Taneja, Magic Squares of Order 12 Representing Days and Dates of the Year 2025 Zenodo, June 10, 2025, pp. 1-43, https://doi.org/10.5281/zenodo.15631884.
Part 2: Reduced Entries Agebraic Magic Squares
- Inder J. Taneja, Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Orders 3 to 7, Zenodo, September 29, 2025, pp. 1-59, https://doi.org/10.5281/zenodo.17219769.
- Site Link: Reduced Entries Algebraic Magic Squares of Orders 3, 5, 7 and 9 (new site)
- Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (new site)
- Site Link: Reduced Entries Algebraic Magic Squares of Orders 3, 5, 7 and 9 (old site)
- Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (old site)
- Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 8, Zenodo, September 23, 2025, pp. 1-65, https://doi.org/10.5281/zenodo.17186001.
- Site Link: Reduced Entries Algebraic Magic Squares of Orders 4, 6, 8 and 10 (new site)
- Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (new site)
- Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (old site)
- Inder J. Taneja, Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9, Zenodo, August 27, 2025, pp. 1-92, https://doi.org/10.5281/zenodo.16955571.
- Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9 (new site)
- Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9 (old site)
- Inder J. Taneja. Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 10, Zenodo, September 18, 2025, pp. 1-112, https://doi.org/10.5281/zenodo.17149185
- Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 10 (new site)
- Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 10 (old site)
- Inder J. Taneja, Self-Made Algebraic Magic Squares of Order 11, Zenodo, October 12, 2025, pp. 1-58, https://doi.org/10.5281/zenodo.17330815 .
- Site Link: Self-Made Algebraic Magic Squares of Order 11 (new site)
- Site Link: Self-Made Algebraic Magic Squares of Order 11 (old site)
- Inder J. Taneja, Self-Made Algebraic Semi-Magic Squares of Order 11, Zenodo, October 12, 2025, pp. 1-77, https://doi.org/10.5281/zenodo.17330822.
- Site Link: Self-Made Algebraic Semi-Magic Squares of Order 11 (new site)
- Site Link: Self-Made Algebraic Semi-Magic Squares of Order 11 (old site)
- Inder J. Taneja, Reduced Entries Algebraic Magic and PanMagic Squares of Order 12, Zenodo, July 23, 2025, pp. 1-74, https://doi.org/10.5281/zenodo.16370556.
- Site Link: Reduced Entries Algebraic Magic and Panmagic Squares of Order 12 (new site)
- Site Link: Reduced Entries Algebraic Magic and Panmagic Squares of Order 12 (old site)
- Inder J. Taneja, Reduced Entries Algebraic Semi-Magic Squares of Order 12, Zenodo, July 23, 2025, pp. 1-60, https://doi.org/10.5281/zenodo.15692014.
- Site Link: Reduced Entries Algebraic Semi-Magic Squares of Order 12 (old site)
- Site Link: Reduced Entries Algebraic Semi-Magic Squares of Order 12 (old site)
Part 3: Agebraic Magic Squares: Double-Digits, Cyclic, Flat, Cornered, Striped and Semi-Striped
- Inder J. Taneja, Double-Digit Cyclic-Type Bordered Reduced Entries Algebraic Magic Squares of Orders 7 to 20, Zenodo, November 21, 2025, pp.1-37, https://doi.org/10.5281/zenodo.17675032.
- Inder J. Taneja, Algebraic Cyclic, Flat and Cornered Striped Magic Squares for Even Orders from 4 to 20, Zenodo, December 02, 2025, pp. 1-58, https://doi.org/10.5281/zenodo.17793845.
- Algebraic Double-Digit and Cornered Magic Squares of Odd Orders from 5 to 19, Zenodo, December 08, 2025, pp. 1-46, https://doi.org/10.5281/zenodo.17859037.
- Inder J. Taneja, Algebraic Pandiagonal Striped and Semi-Striped Magic Squares of Orders 4 to 12, Zenodo, January 12, 2026, pp. 1-52, https://doi.org/10.5281/zenodo.18221904.