This work brings algebraic magic and semi-magic squares of orders 3, 5, 7 and 9 for reduced entries. By reduced or less entries, we understand that instead of normal n2 entries of a magic square order n, we are using less numbers. Moreover, in these situations the entries are no more sequential numbers. These entries are non-sequential positive and negative numbers. In some cases, these may be decimal or ractional values depending on the orders of magic squares. In this work we bring different ways of writing magic and semi-magic squares of orders 3, 5, 7 and 9. These are based on three types of magic squares, i.e., cornered, single-digit bordered and double-digit bordered magic squares, except for the magic square of orders 5 and 7. In some cases, we worked with pandiagonal magic squares of orders 5 and 7 for reduced entries. It is not necessary, but we worked with magic rectangles with equal widths and lengths. of the same category within a magic square. Previously, the author brought similar kind of work for the orders 3 to 12 specially for the for the dates and days of the year 2025, where the dates are few entries and days are the sums of magic squares. For this kind of work refer the first of the reference list given below. This work we work is revised and enlarged version of previous works.
For more details see the link given below:
Inder J. Taneja – Reduced Entries Algebraic Magic and Semi-Magic Squares of Orders 3, 5, 7 and 9, Zenodo, July 01, 2025, pp. 1-65, https://doi.org/10.5281/zenodo.15783321.
Summary of the work is given below in terms of magic orders
Reduced Entries Algebraic Magic Squares of Order 3
Result 1: Magic Square of Order 3
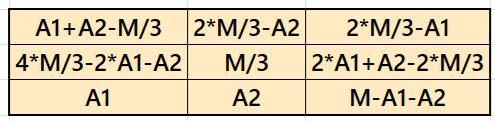
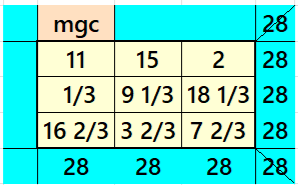
It is magic square of order 3. To avoid decimal entries we need magic sum M multiple of 3. It can given seen in F. Gaspalou’ s webs-site http://www.gaspalou.fr/magic-squares/. See two examples below

Result 2: Semi-Magic Square of Order 3
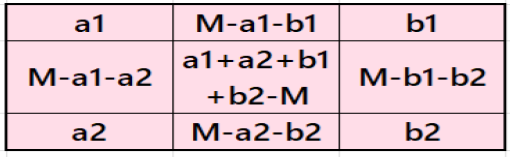
It is semi-magic square of order 3. Above two magic squares shall be used in construction of pandiagonal magic squares of orders 6, 9 and 12.
Reduced Entries Algebraic Magic Squares of Order 5
Below are few results giving algebraic magic squares of order 5.
Result 1: Cornered Magic Square
It is cornered magic square of order 5, where there is a magic square of order 3 at the upper-left corner. The magic rectangles of orders 2×3 are of equal width and length. In order to get magic square without decimal entries, we must consider magic sum of magic square of order 3 as multiple of 3. See below two examples with even and odd magic sums:

Result 2: Pandiagonal Magic Square
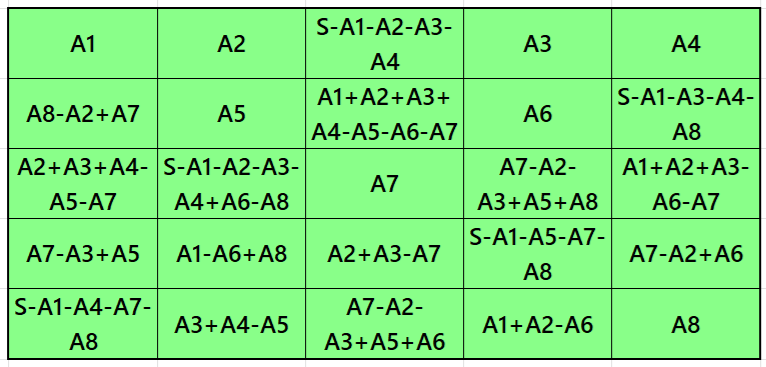
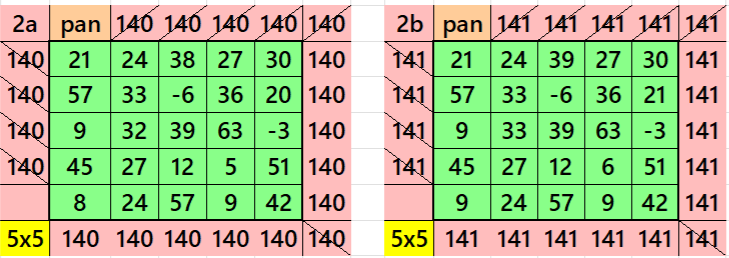
It is an algebraic pandiagonal magic square of order 5. It uses only few entries to bring magic squares of order 5. It can given seen in F. Gaspalou’ s webs-site http://www.gaspalou.fr/magic-squares/. See below wo examples with even and odd magic sums:
Result 3: Single-Digit Semi-Magic Square
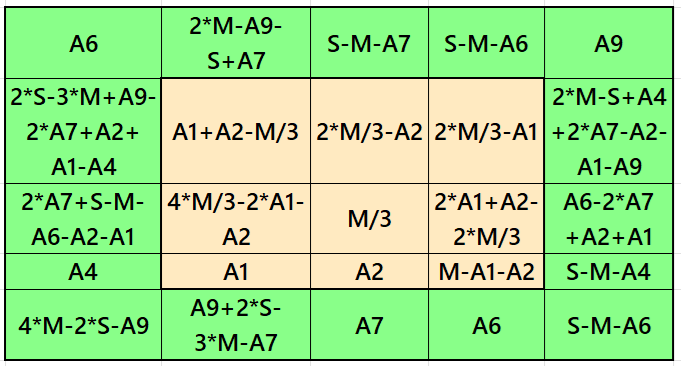
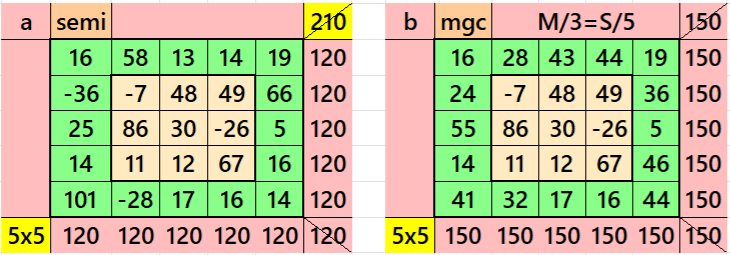
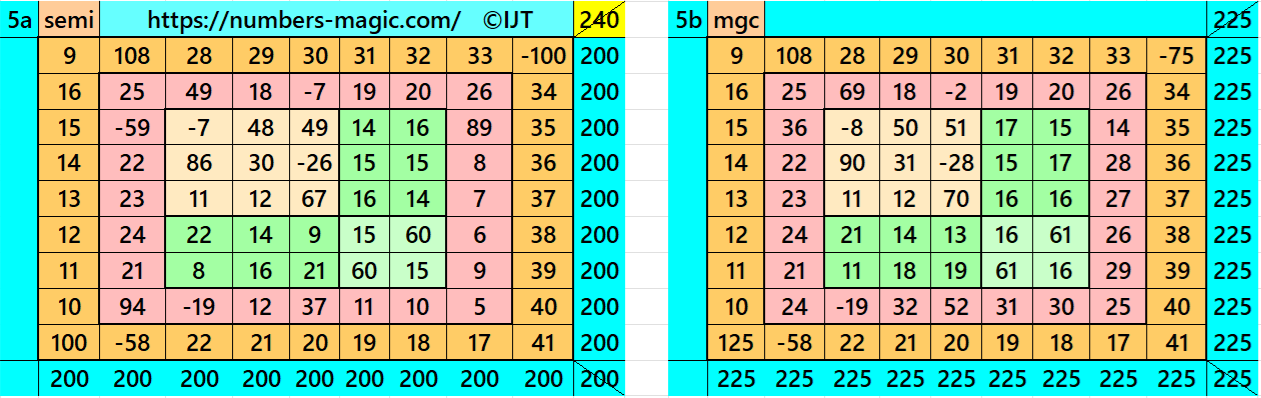
It is single-digit bordered semi-magic square of order 5 embedded with a magic square of order 3. It is semi-magic square only at one diagonal. If we apply the condition M = 3*S/5 then it becomes magic square, where M and S are the magic sums of the magic squares of order 3 and 5, respectively. See below two examples.
Reduced Entries Algebraic Magic Squares of Order 7
Below are few results giving algebraic magic squares of order 7.
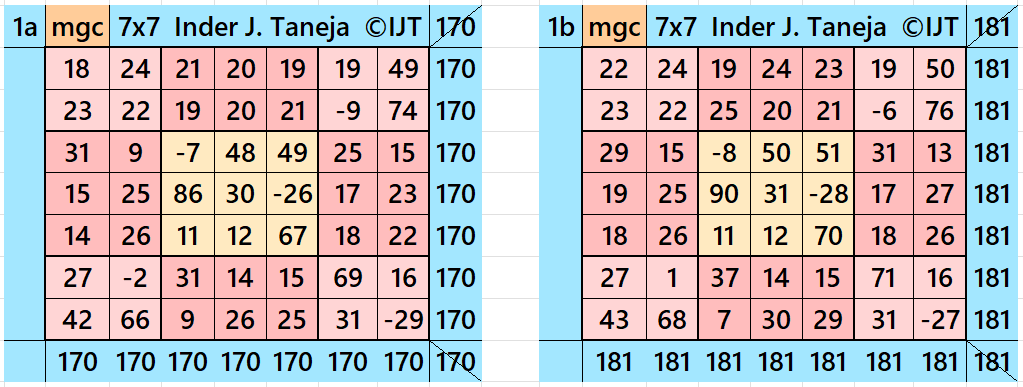
Result 1: Double-Digits Bordered Magic Square
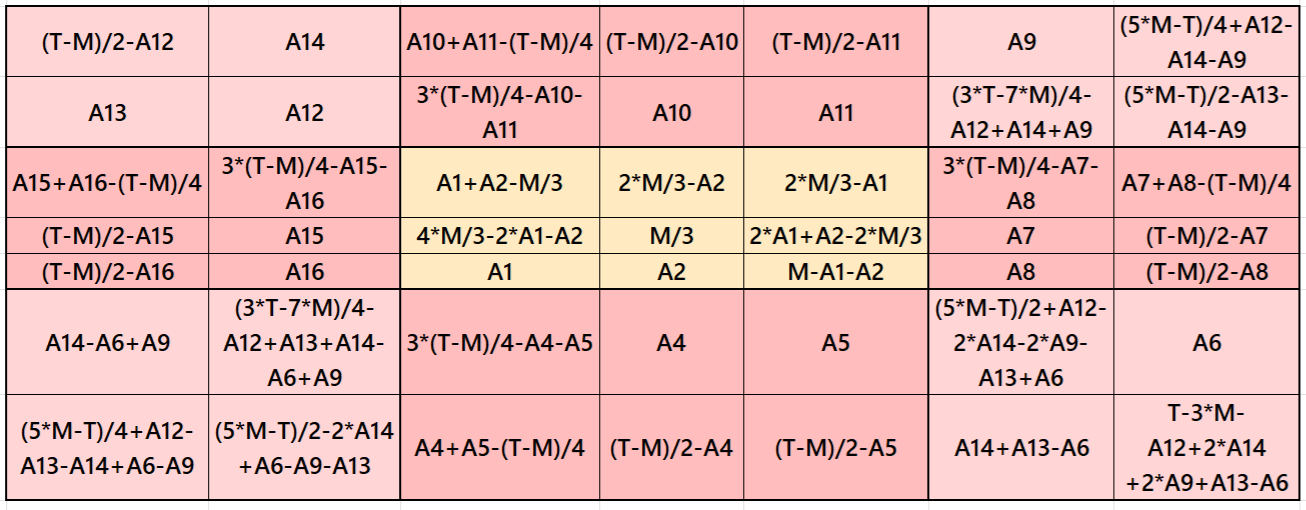
It is double-digit bordered magic square of order 7 embedded with magic square of order 3. The four magic rectangles of order 2×3 are of equal sums, i.e., equal width and equal length. The magic square of order 3 is with decimal entries. To get the result without decimal entries, we must consider magic sum for order 3 as multiple of 3. The letters M and T are magic sums of magic squares of orders 3 and 7 respectively. See below two examples with even and odd magic sums:
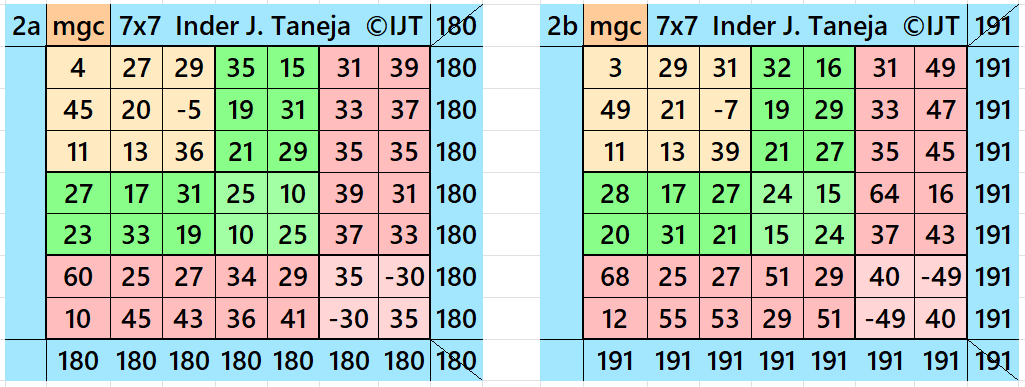
Result 2: Cornered Magic Square
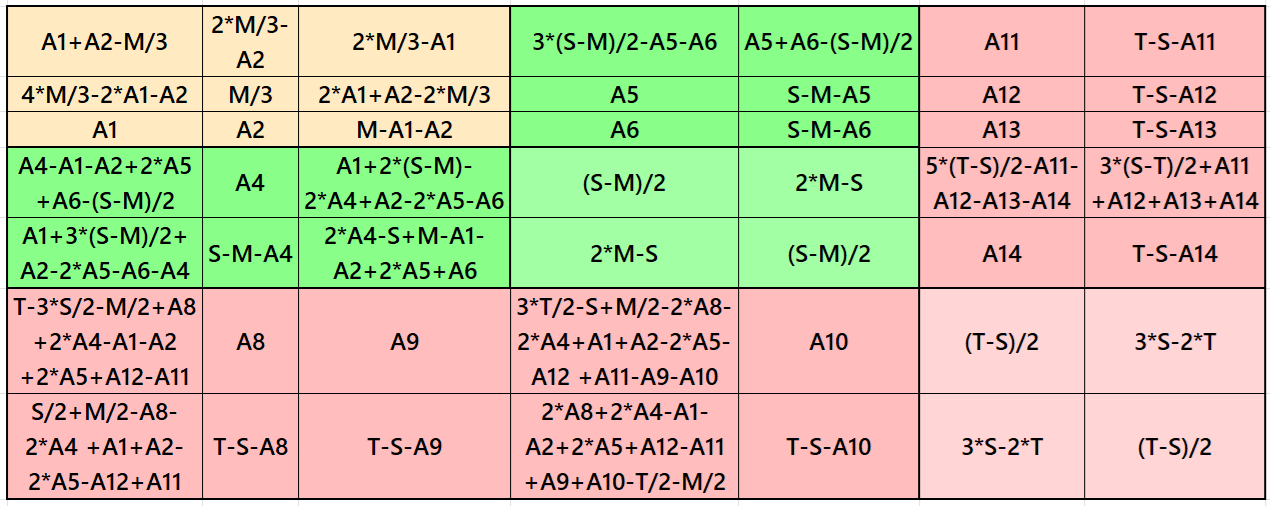
It is cornered magic square of order 7, where there are magic square of orders 3 and 5 at the upper-left corner. The magic rectangles of orders 2×3 and 2×5 are of equal width and length in each case. The magic square of order 3 is with decimal entries. To get the result without decimal entries, we must consider magic sum for order 3 as multiple of 3. The letters M, S and T are magic sums of magic squares of orders 3, 5 and 7 respectively. See below two examples with even and odd magic sums:
Result 3: Cornered Magic Square
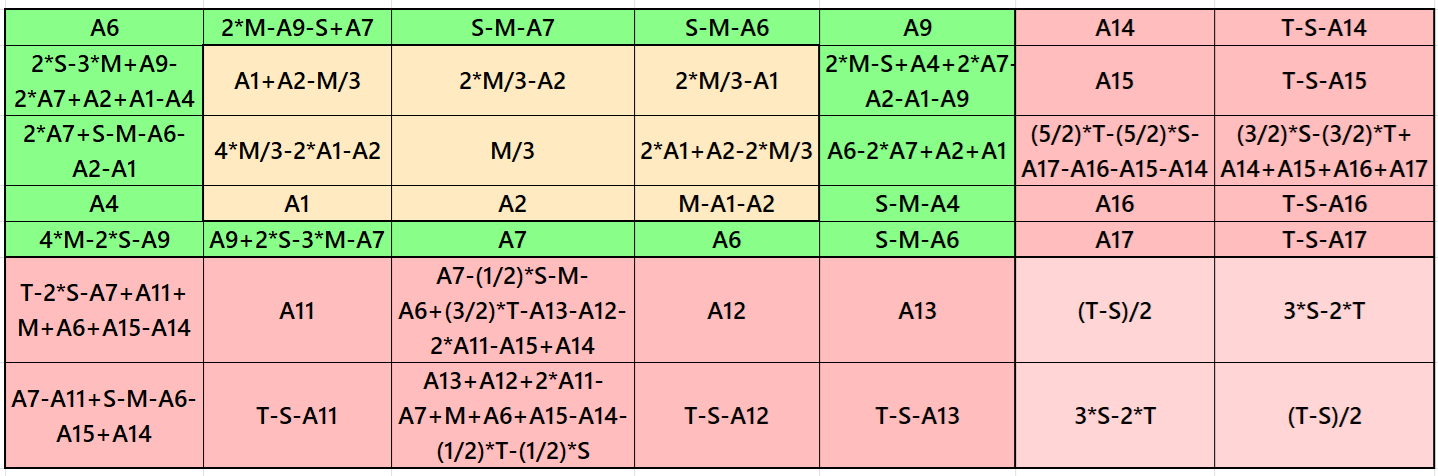
It is cornered magic square of order 7, where there is a single-digit bordered magic square of order 5 at the upper-left corner embedded with magic square of order 3. The two magic rectangles of orders 2×5 are of equal width and length. In order to get magic square without decimal entries, we must consider magic sum of magic square of order 3 as multiple of 3. The letters M, S and T are magic sums of magic squares of orders 3, 5 and 7 respectively. Alternatively, we can replace here the magic square of order 3 by semi-magic square of order 3. See below two examples with even and odd magic sums:

Result 4: Cornered Magic Square
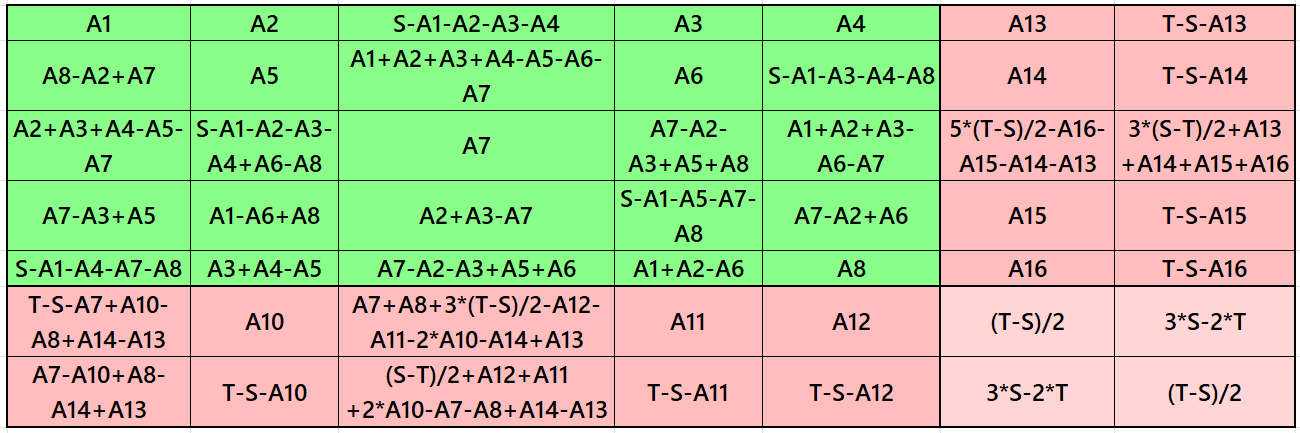
It is cornered magic square of order 7, where there is a magic square of order 5 at the upper-left corner. The two magic rectangles of orders 2×5 are of equal width and length. Moreover, the magic square of order 5 is pandiagonal. The letters S and T are magic sums of magic squares of of orders 5 and 7 respectively. See below two examples with even and odd magic sums:
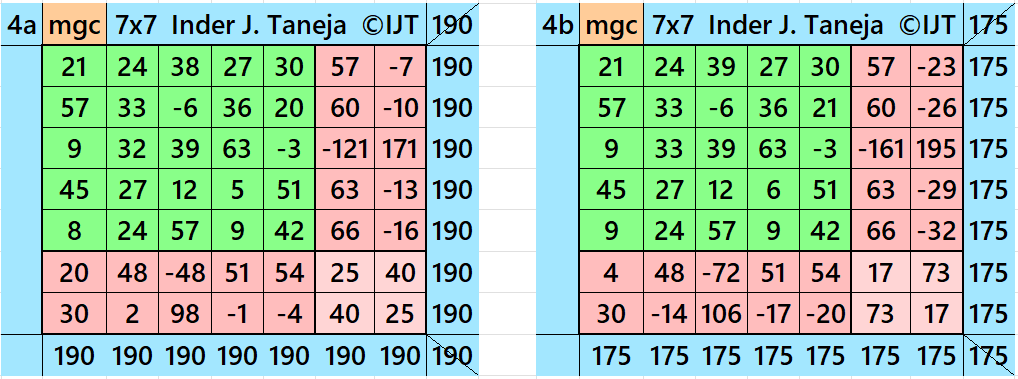
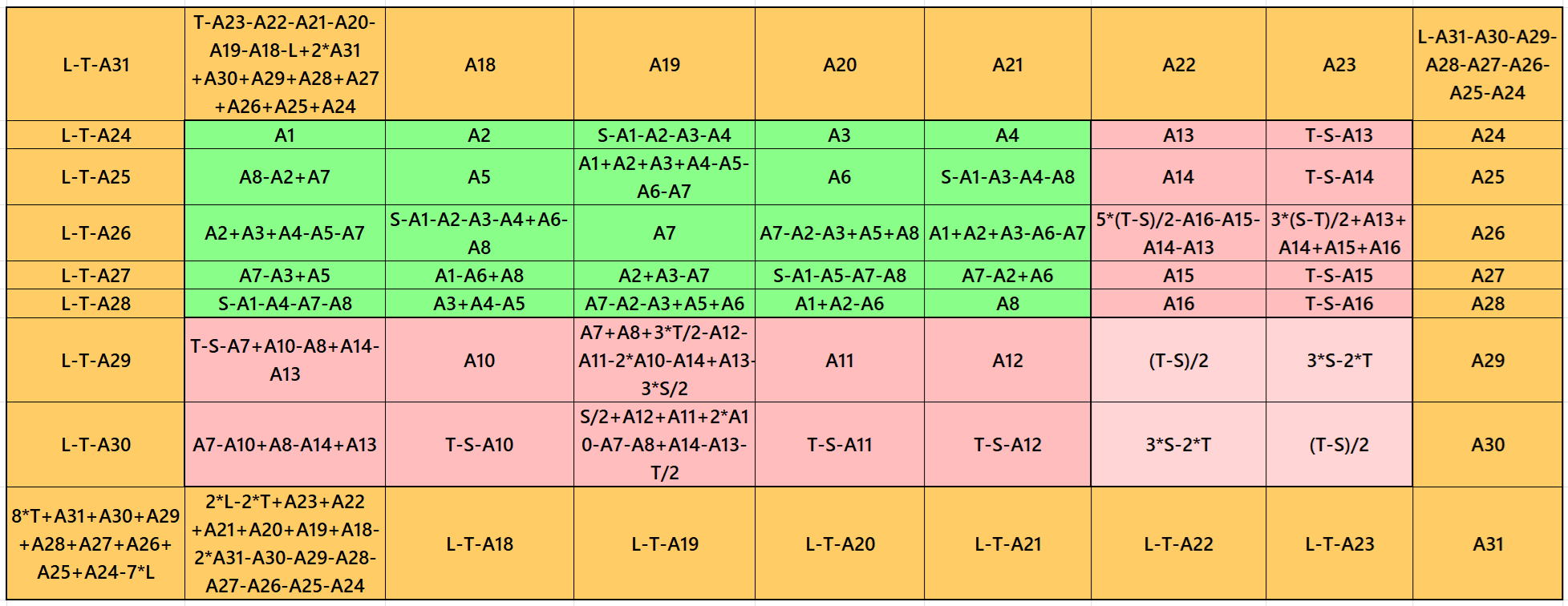
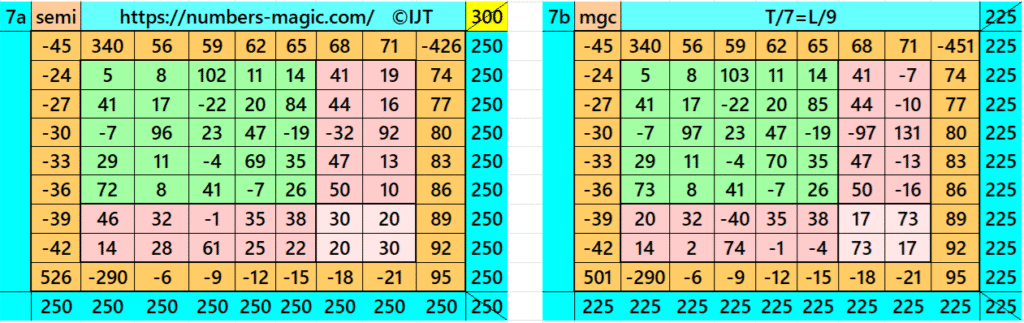
Result 5:Pandiagonal Magic Square
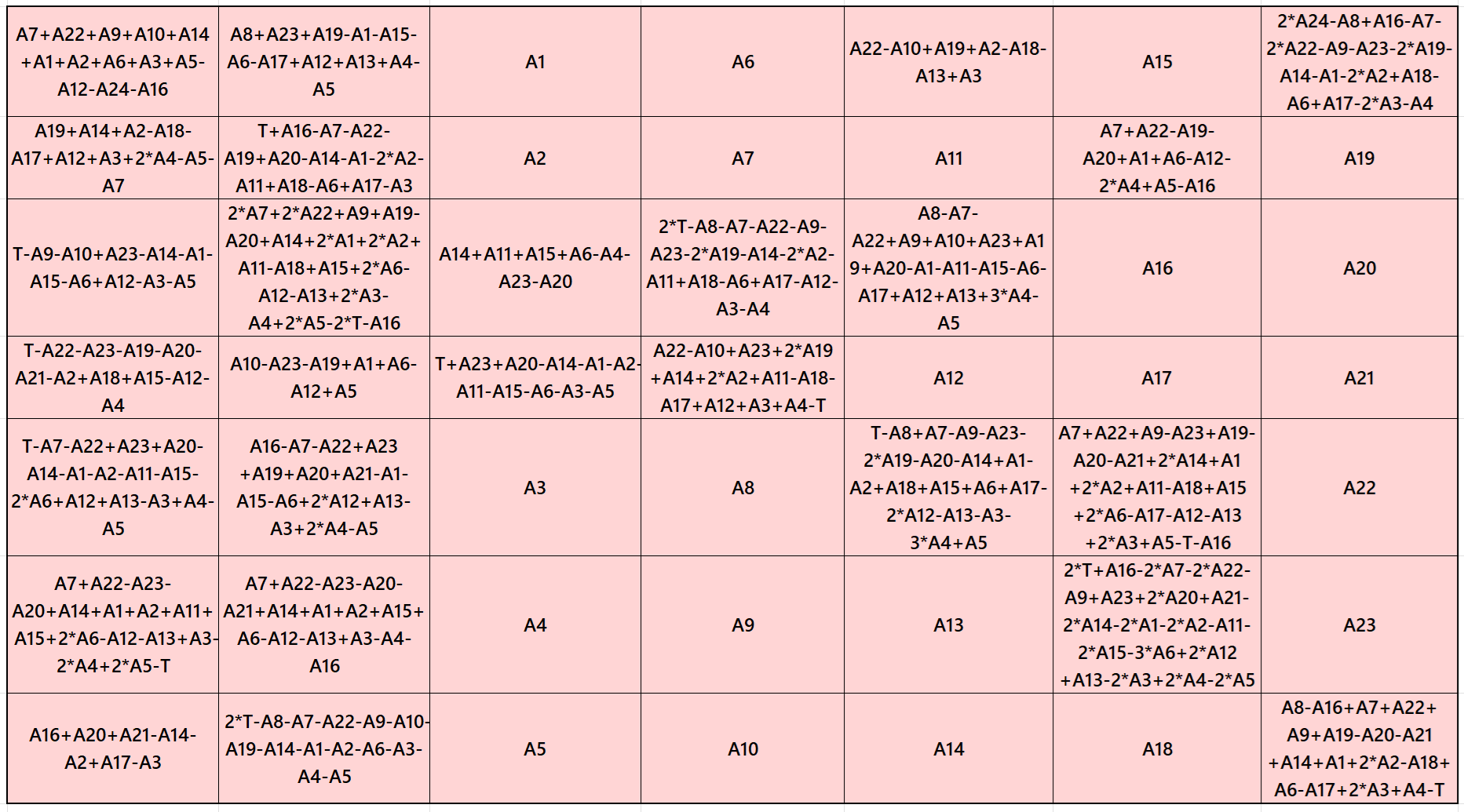
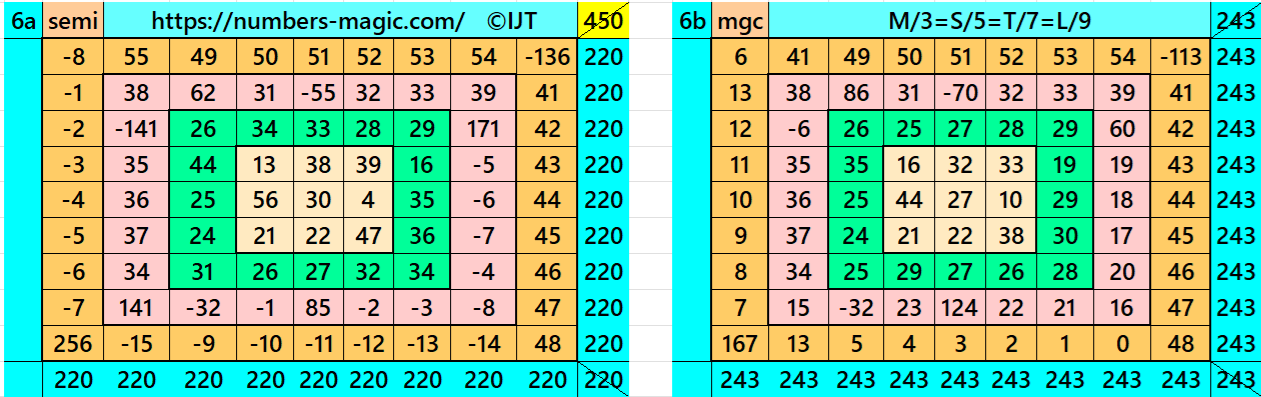
It is a pandiagonal magic square of order 7. It uses only 23 entries instead of 49. It is presented here for the first time in the history. See below two examples with even and odd magic sums
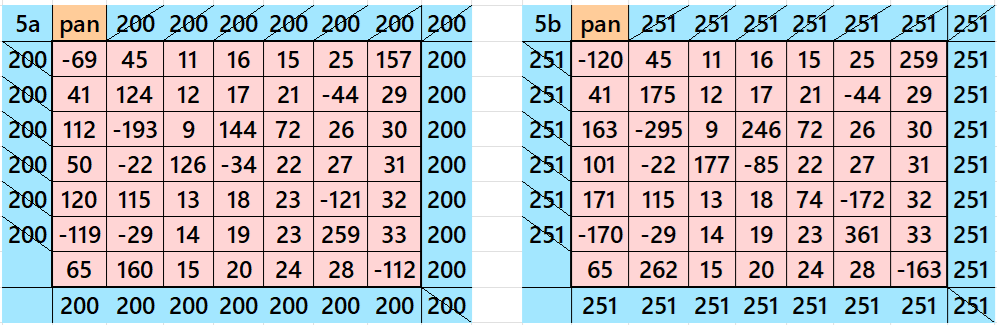
Result 6: Single-Digit Bordered Semi-Magic Square
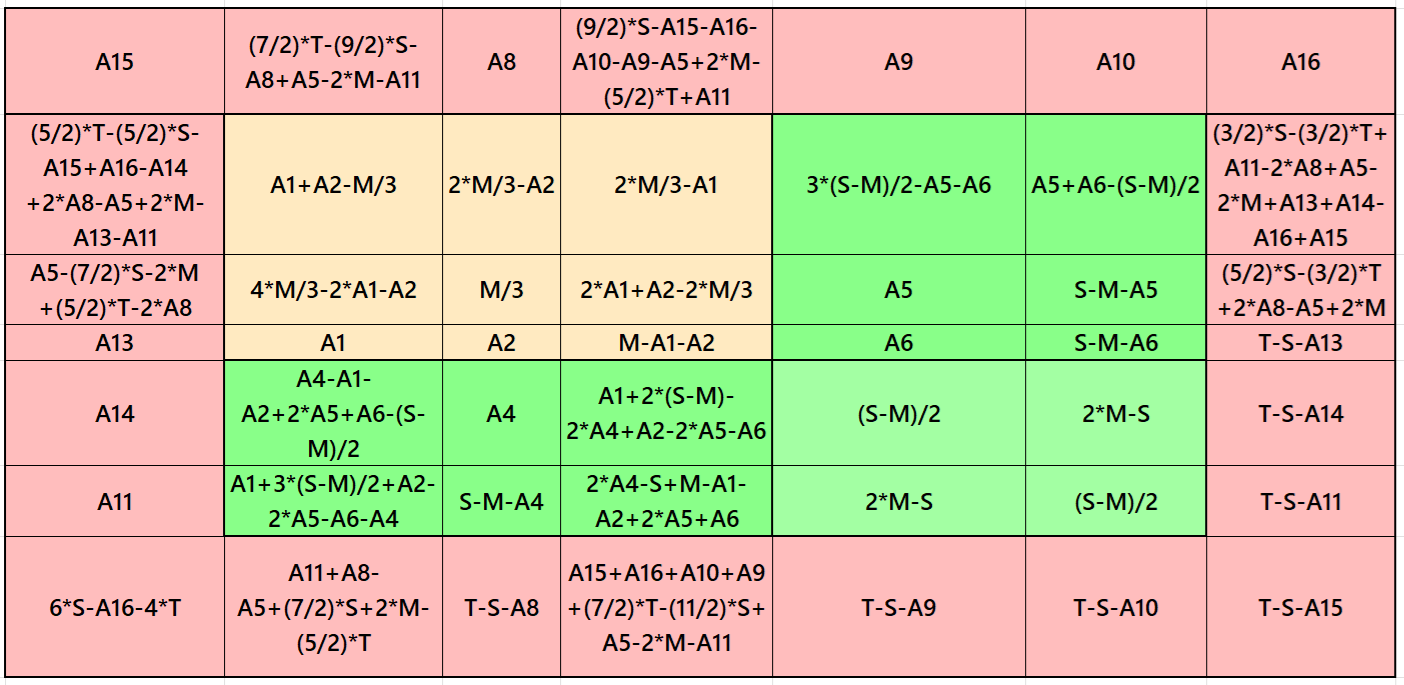
It is single-digit bordered semi-magic square of order 7 embedded with a cornered magic square of order 5. It contains magic square of order 3 at upper-left corner. The magic rectangles of order 2×3 are of equal width and length. In order to get magic square without decimal entries, we must consider magic sum of magic square of order 3 as multiple of 3. Moreover, in order to get a magic square of order 7, we must have the condition T = 7*S/5. The letters M, S and T are magic sums of magic squares of of orders 3, 5 and 7 respectively. See below two examples with semi-magic and magic sums:
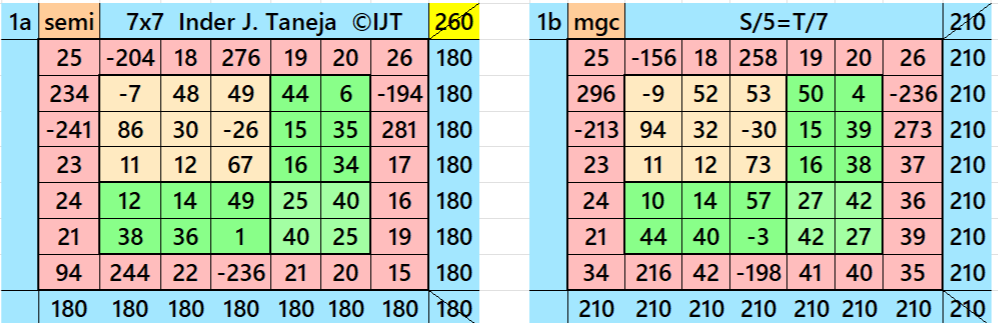
Result 7: Single-Digit Bordered Semi-Magic Square
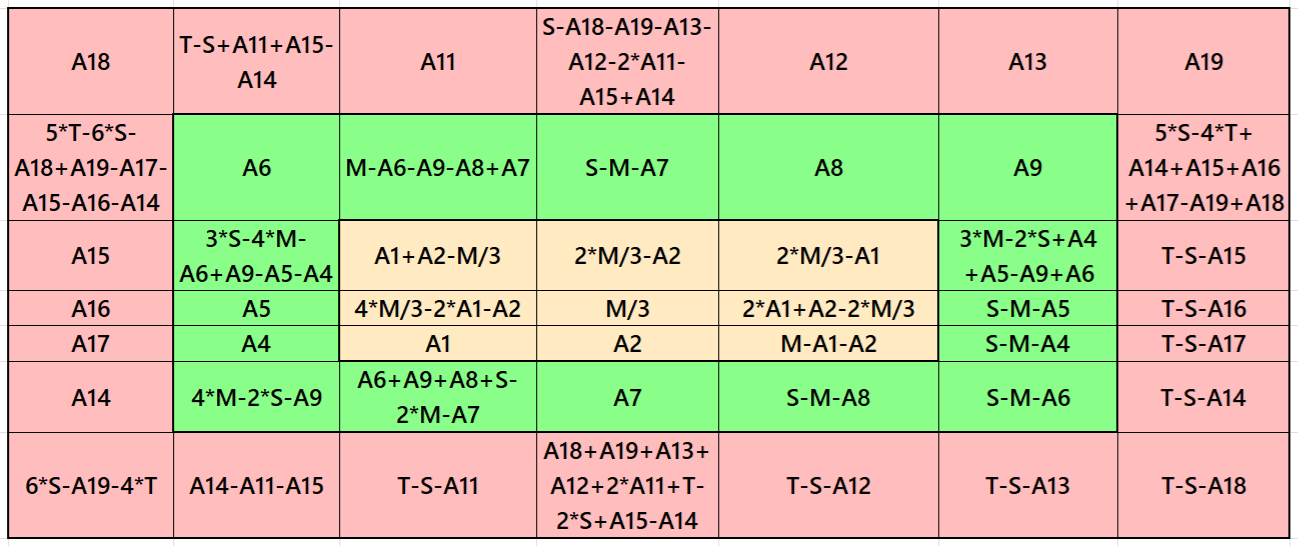
It is single-digit bordered semi-magic square of order 7 embedded with magic squares of orders 5 and 3. In order to get magic square without decimal entries, we must consider magic sum of magic square of order 3 as multiple of 3. Moreover, in order to get a magic square of order 7, we must have two conditions T=7*S/5 and S=5*M/3. The letters M, S and T are magic sums of magic squares of of orders 3, 5 and 7 respectively. See below two examples with semi-magic and magic sums:
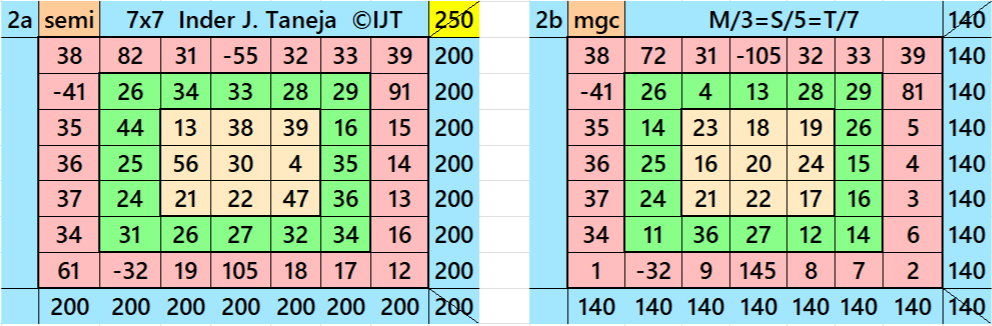
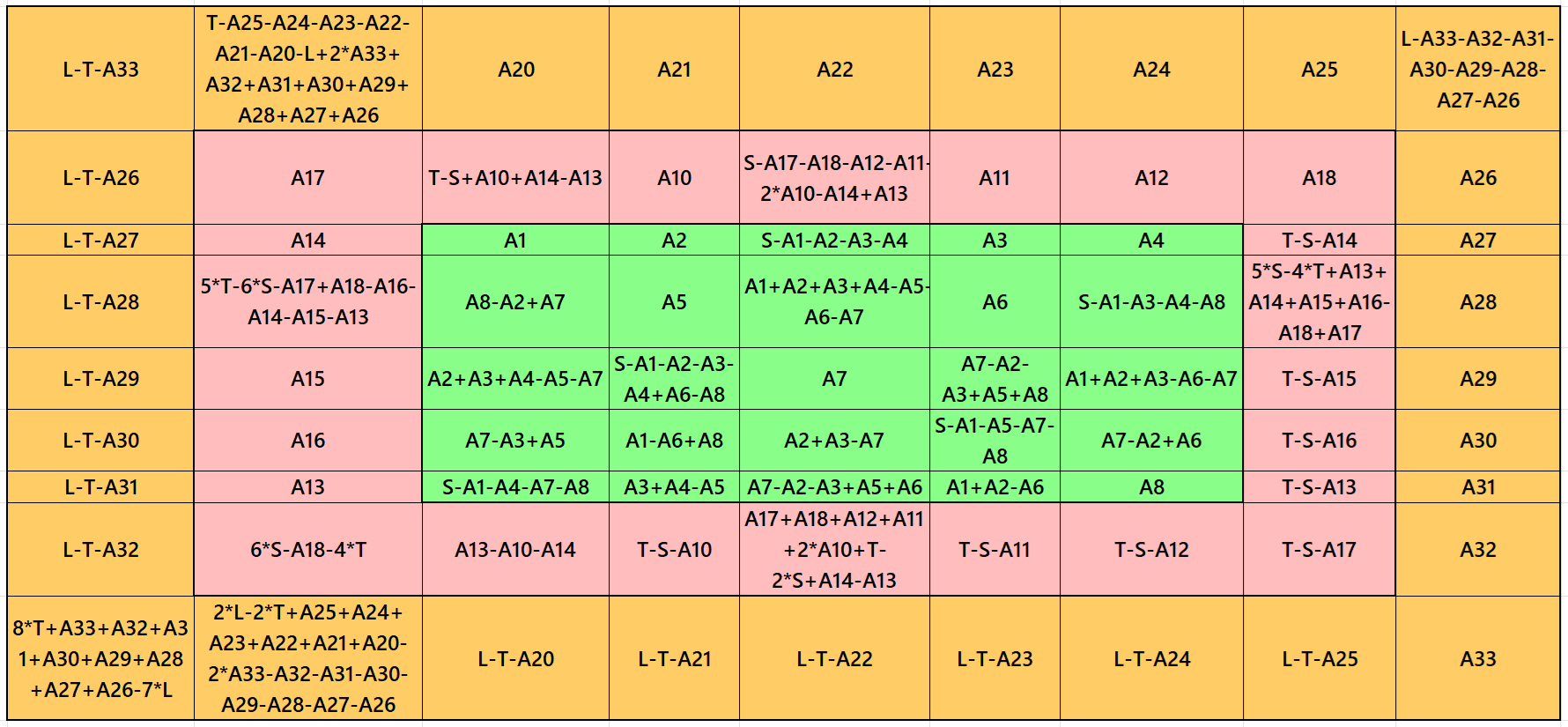
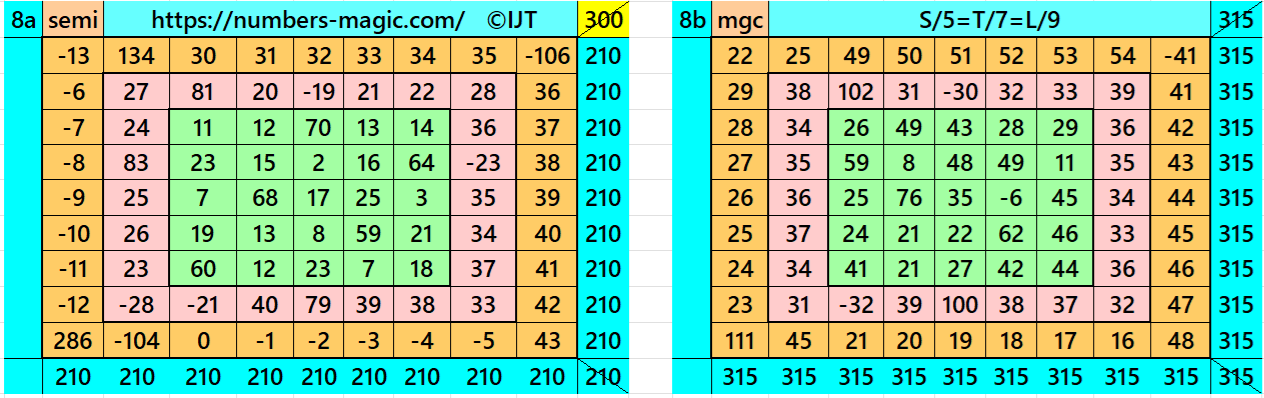
Result 8: Single-Digit Bordered Semi-Magic Square
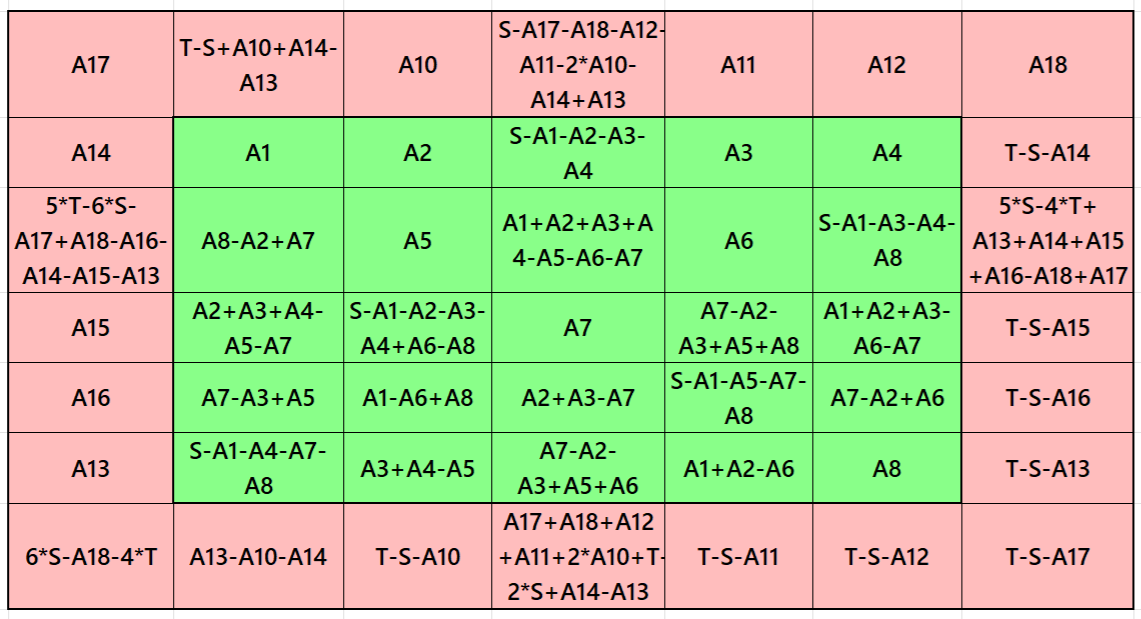
It is single-digit bordered magic square of order 7, where there is a pandiagonal magic square of order 5 in the middle. Moreover, in order to get a magic square of order 7, we must have the condition T=(7/5)*S. The letters S and T are magic sums of magic squares of orders 5 and 7 respectively. See below two examples with semi-magic and magic sums:
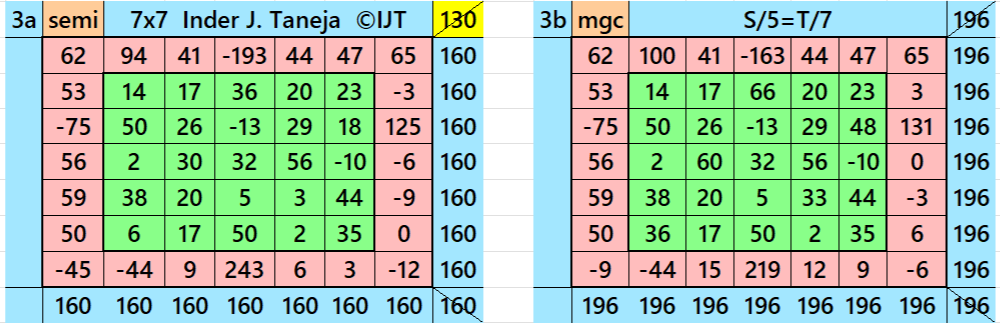
Reduced Entries Algebraic Magic Squares of Order 9
Part 1: With Magic Square of Order 3
Result 1: Double-Digit Bordered Magic Square
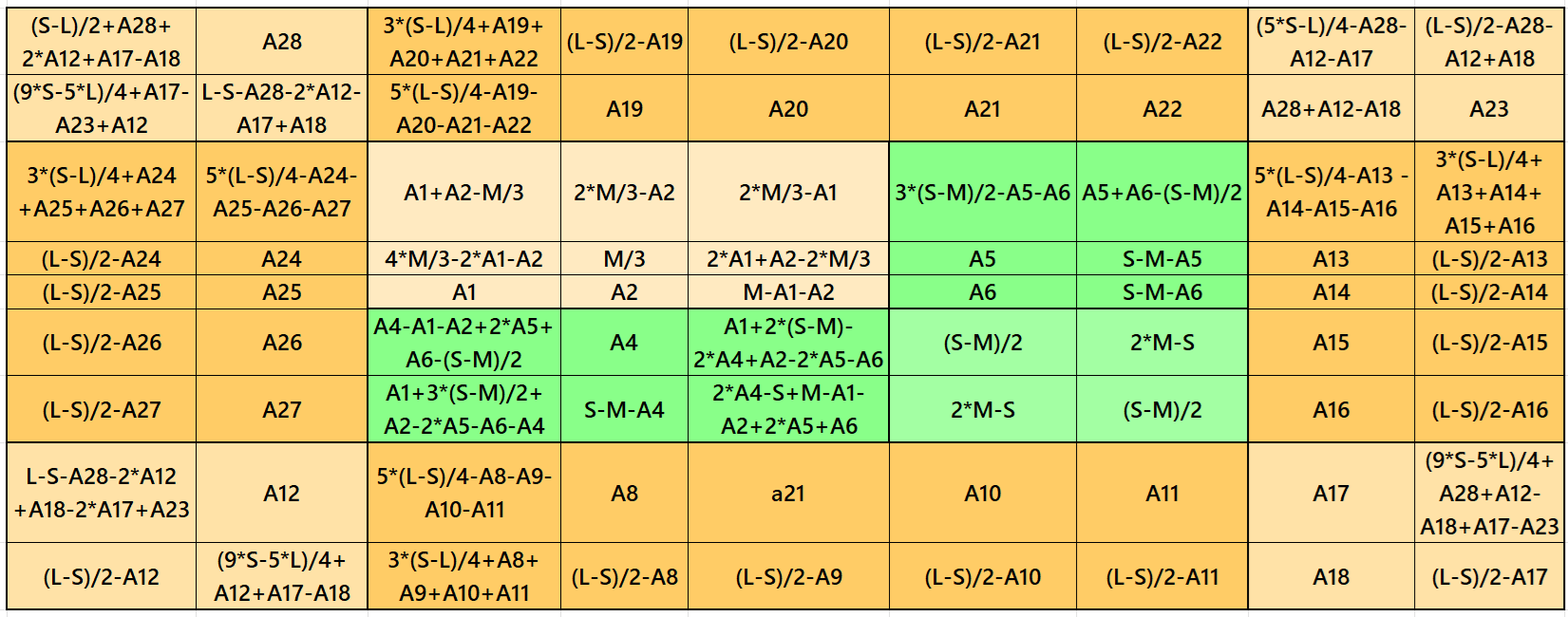
It is double-digit bordered magic square of order 9 embedded with cornered magic square of order 5 containing magic square of order 3 at upper-left corner. The four magic rectangles of order 2×5 are of equal sums, i.e., equal width and equal length. To avoid decimal entries we must have magic sum of magic square of order 3 as a multiple of 3. The letters M, S and L are magic sums of magic squares of orders 3, 5 and 9 respectively. See below two examples with even and odd magic sums:
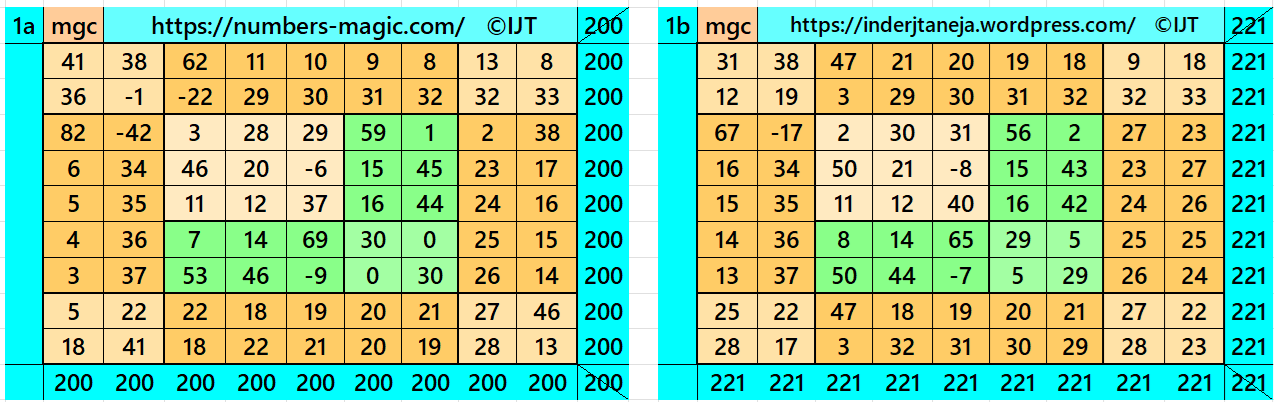
Result 2: Cornered Magic Square
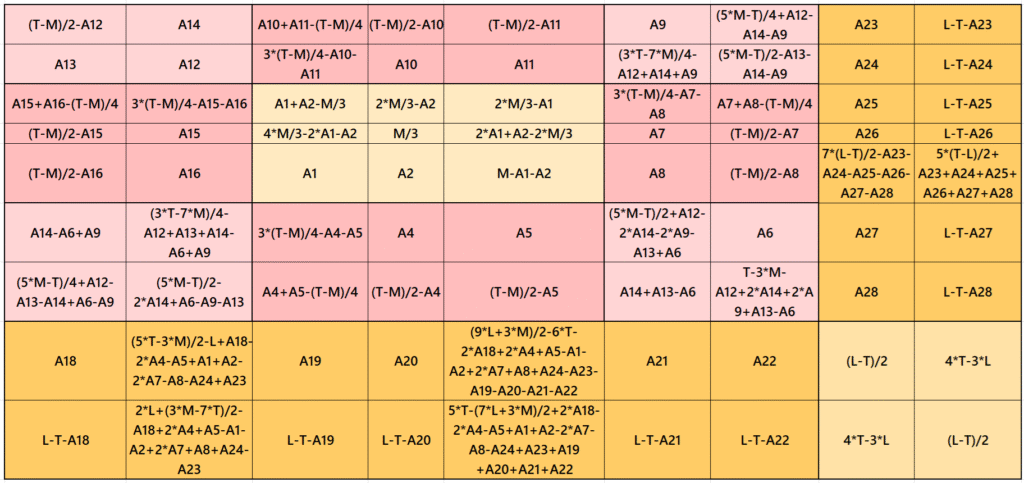
It is cornered magic square of order 9 with double-digit bordered magic square of order 7 at upper-left having a magic square of order 3 in the middle of it. The four magic rectangles of order 2×33 are of equal sums, i.e., equal width and equal length. Also, the magic rectangles of order 2×7 are of equal sums. To avoid decimal entries we must have magic sum of magic square of order 3 as a multiple of 3. To avoid it, we can consider semi-magic square of order 3. The letters M, T and L are the magic sums of magic squares of orders 3, 7 and 9 respectively. See below two examples with even and odd magic sums:
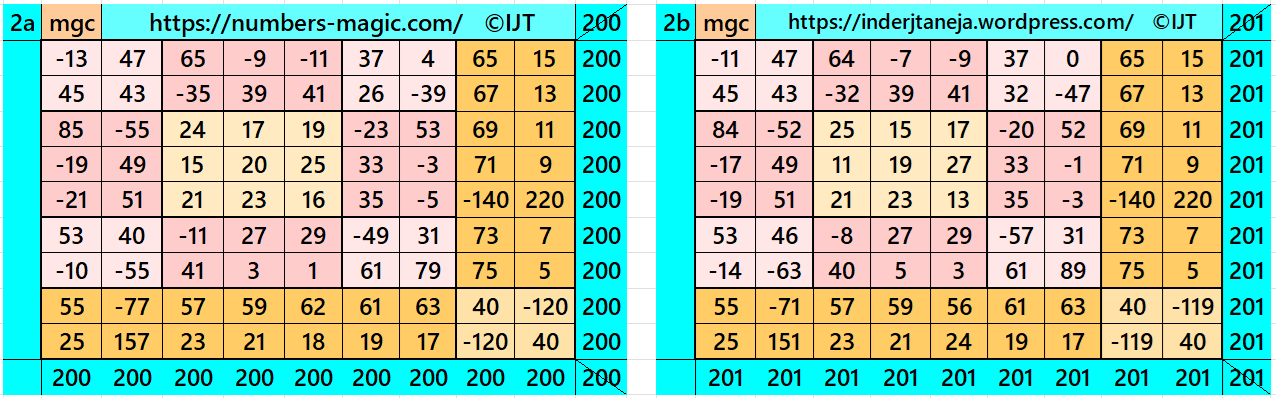
Result 3: Cornered Magic Square
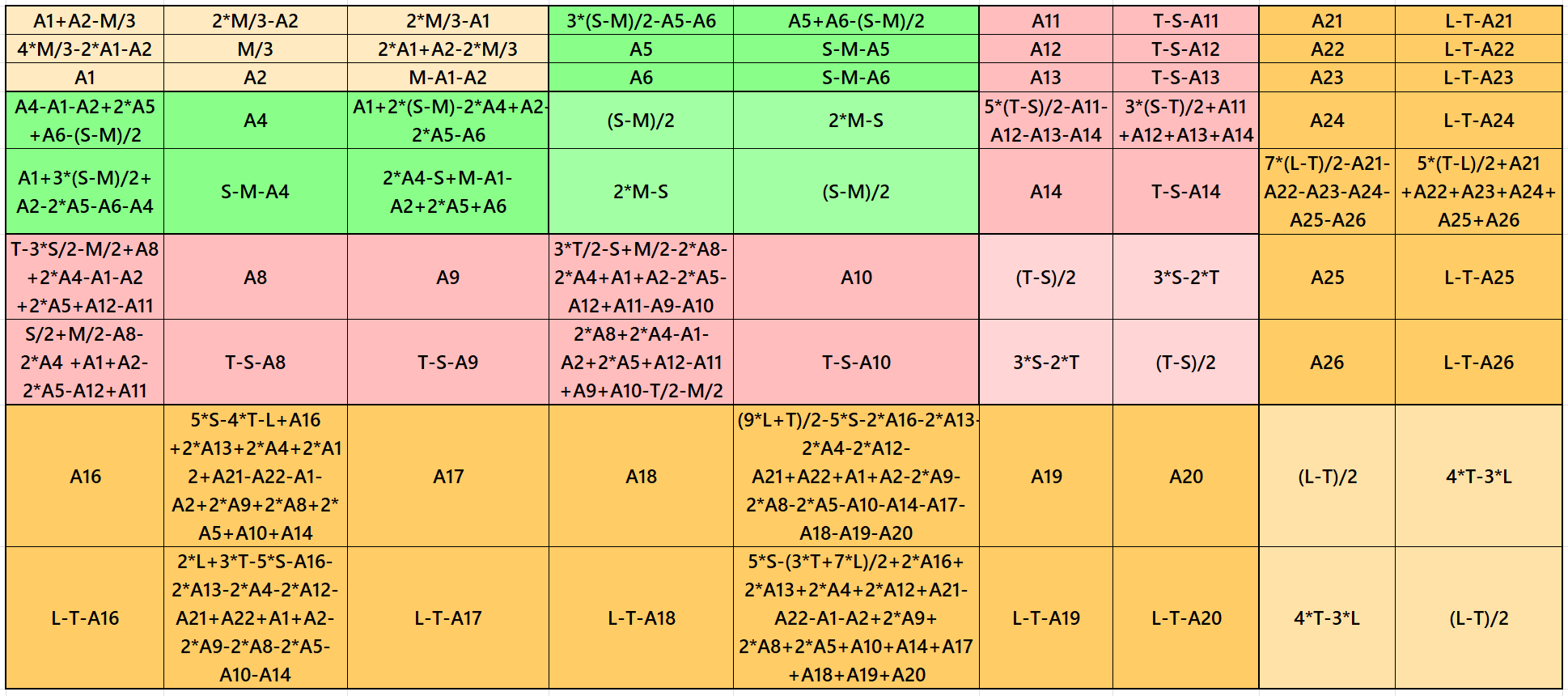
It is cornered magic square of order 9 with cornered magic square of order 7 at upper-left corner having a magic square of order 5 and 3 again at upper-left corner. Each two magic rectangles of orders 2×3, 2×5 and 2×7 are of equal sums, i.e., equal width and equal length in each case. Again, to avoid decimal entries we must have magic sum of magic square of order 3 as a multiple of 3. To avoid it, we can consider semi-magic square of order 3. The letters M, S, T and L are the magic sums of magic squares of orders 3, 5, 7 and 9 respectively. See below two examples with even and odd magic sums:
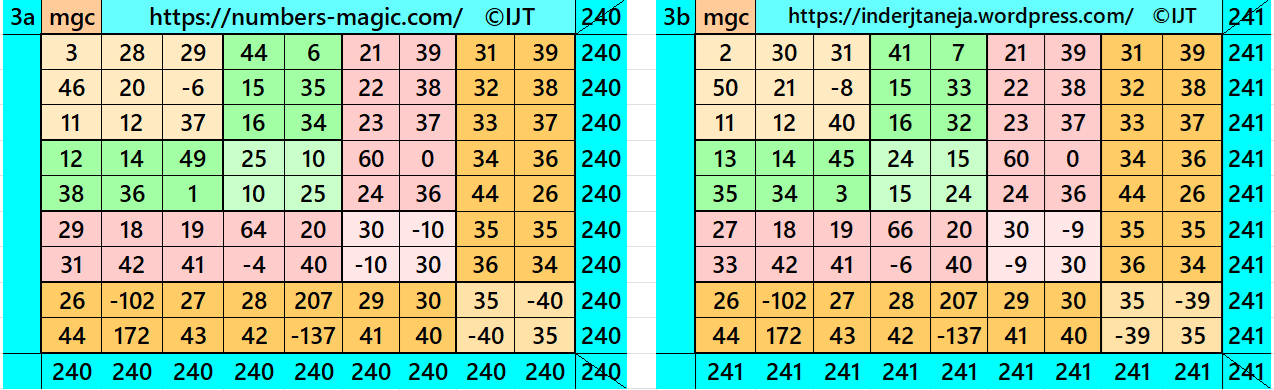
Result 4: Cornered Magic Square
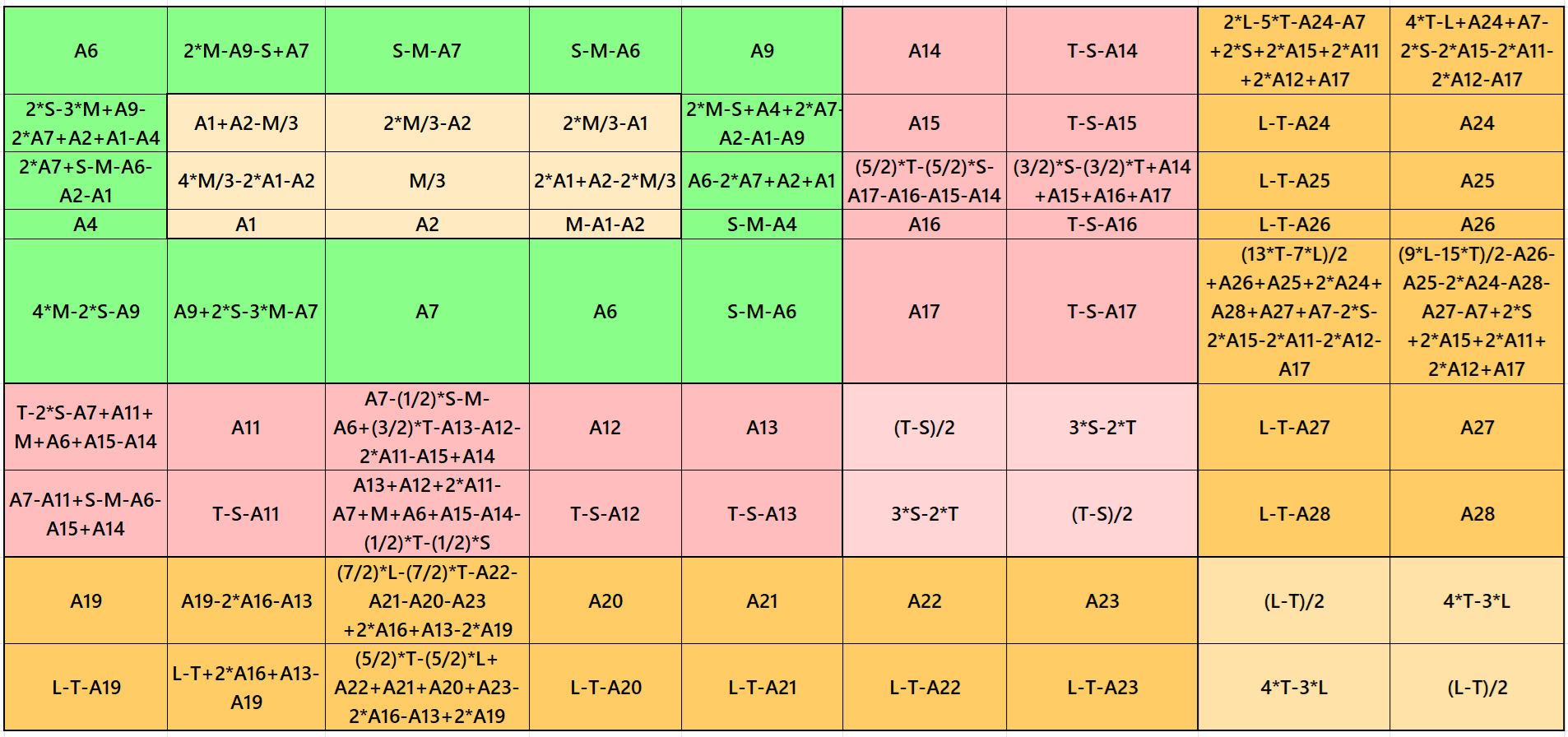
It is cornered magic square of order 9 with cornered magic square of order 7 at upper-left corner having a single-digit bordered magic square of order 5 at upper-left corner. It has magic square of order 3 in the middle. Each two magic rectangles of orders 2×5 and 2×7 are of equal sums, i.e., equal width and equal length in each case. Again, to avoid decimal entries we must have magic sum of magic square of order 3 as a multiple of 3. To avoid it, we can consider semi-magic square of order 3. The magic sum of magic square of order 5 may be semi-magic but still we have order 9 as a magic square. The letters M, S, T and L are the magic sums of magic squares of orders 3, 5, 7 and 9 respectively. See below two examples with even and odd magic sums:

Result 5: Cornered Magic Square
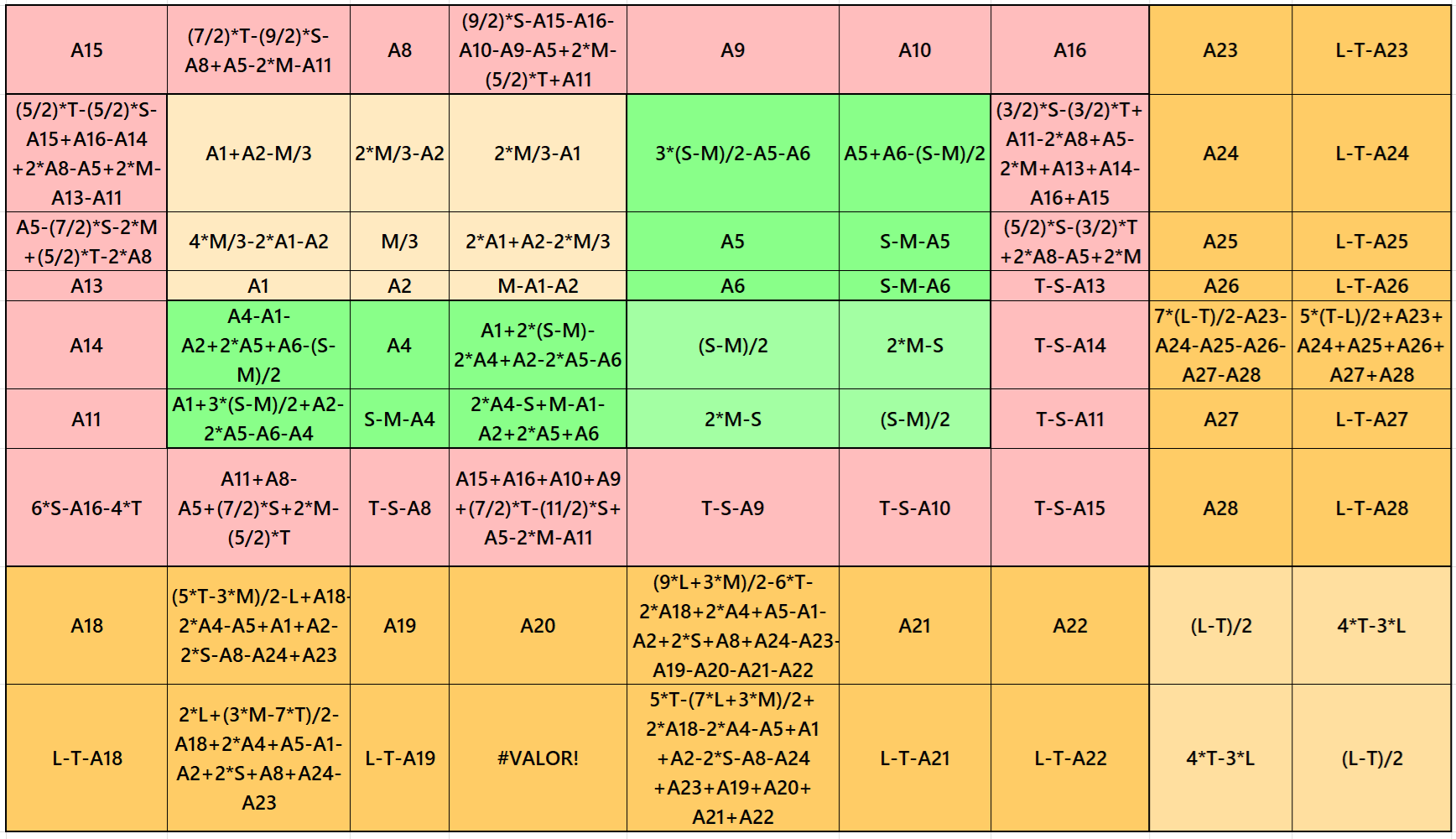
It is cornered magic square of order 9 with single-digit bordered magic square of order 7 at upper-left corner embedded with a cornered magic square of order 5. It has magic square of order 3 at the upper- left corner of it. The two magic rectangles of orders 2×7 are of equal sums, i.e., equal width and equal length. Again, to avoid decimal entries we must have magic sum of magic square of order 3 as a multiple of 3. The magic sum of magic square of order 7 may be semi-magic but still we have order 9 as a magic square. The letters M, S, T and L are the magic sums of magic squares of orders 3, 5, 7 and 9 respectively. See below two examples with even and odd magic sums:
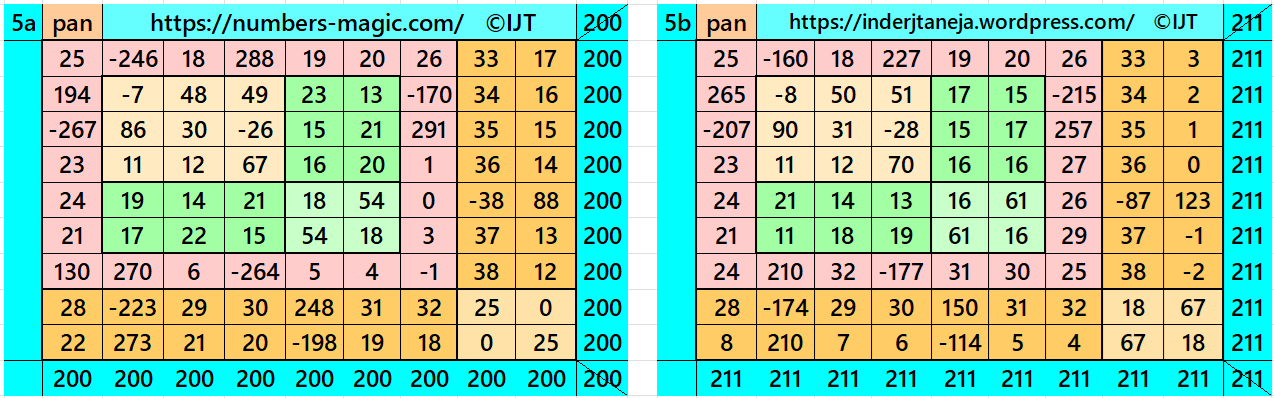
Result 6: Cornered Magic Square
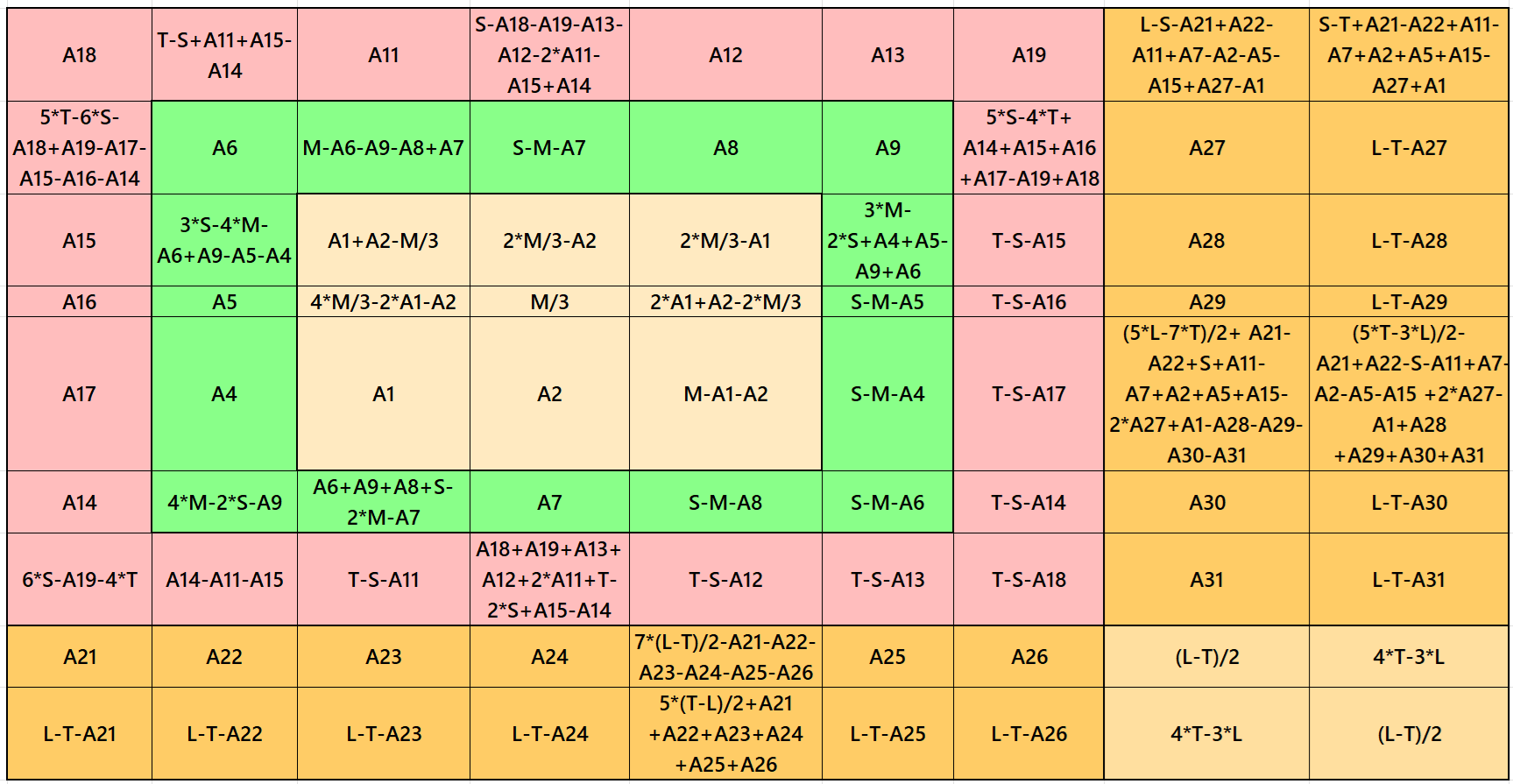
It is cornered magic square of order 9 with single-digit bordered magic square of order 7 at upper-left corner embedded with a cornered magic square of orders 5 and 3. The two magic rectangles of orders
2×7 are of equal sums, i.e., equal width and equal length. Again, to avoid decimal entries we must have magic sum of magic square of order 3 as a multiple of 3. The magic sum of magic square of order 7 may be semi-magic but still we have order 9 as a magic square. The letters M, S, T and L are the magic sums of magic squares of orders 3, 5, 7 and 9 respectively. See below two examples with even and odd magic sums:
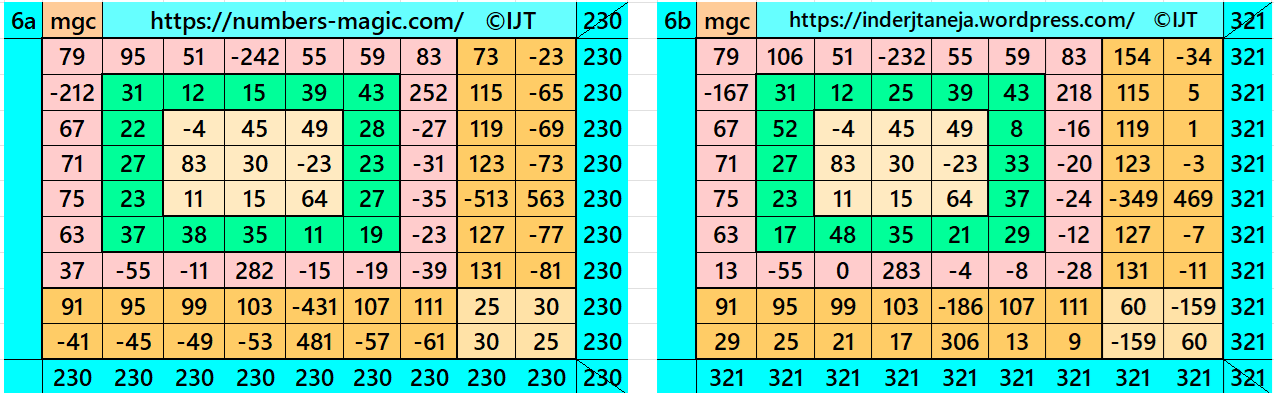
Part 2: With Pandiagonal Magic Square of Orders 5 and 7
Result 7: Double-Digit Bordered Magic Square
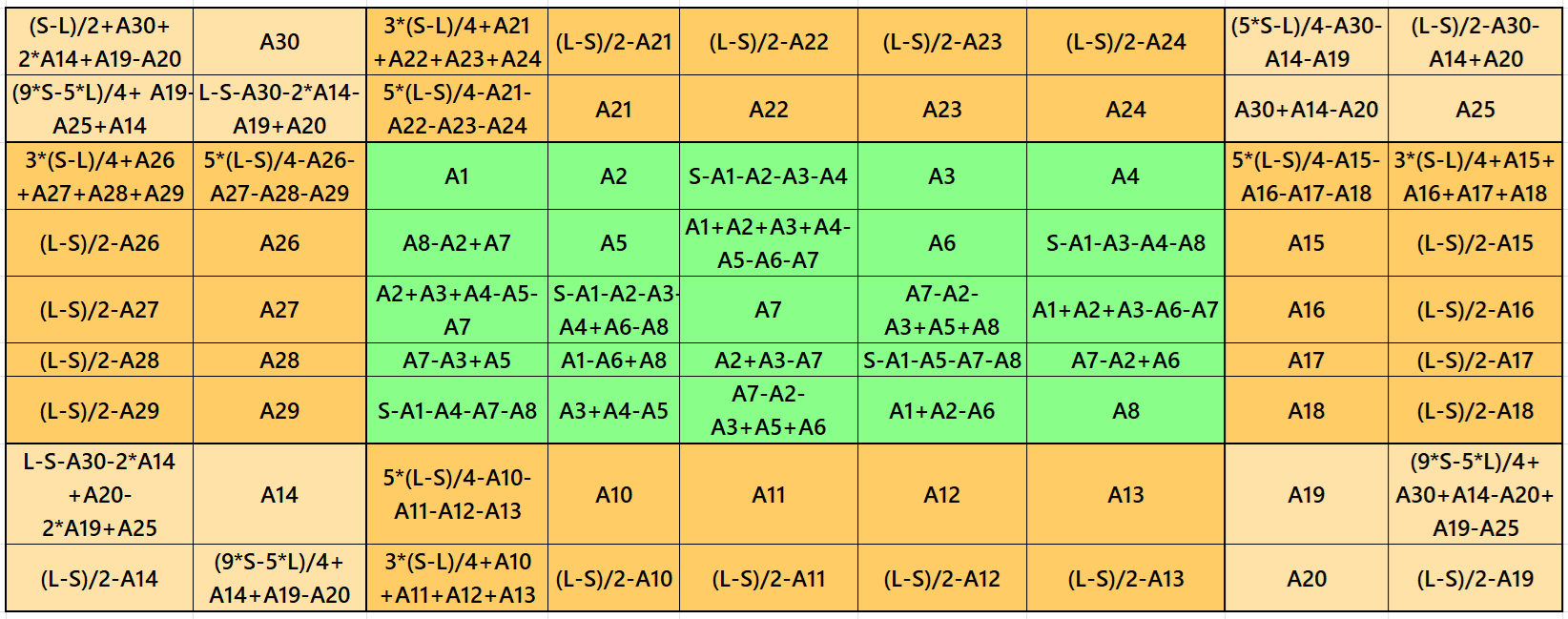
It is double-digit bordered magic square of order 9 with embedded with a pandiagonal magic square of order 5 at the middle of it. The four magic rectangles of orders 2×5 are of equal sums, i.e., equal width and equal length. The letters S and L are the magic sums of magic squares of orders 5 and 9 respectively. See below two examples with even and odd magic sums:
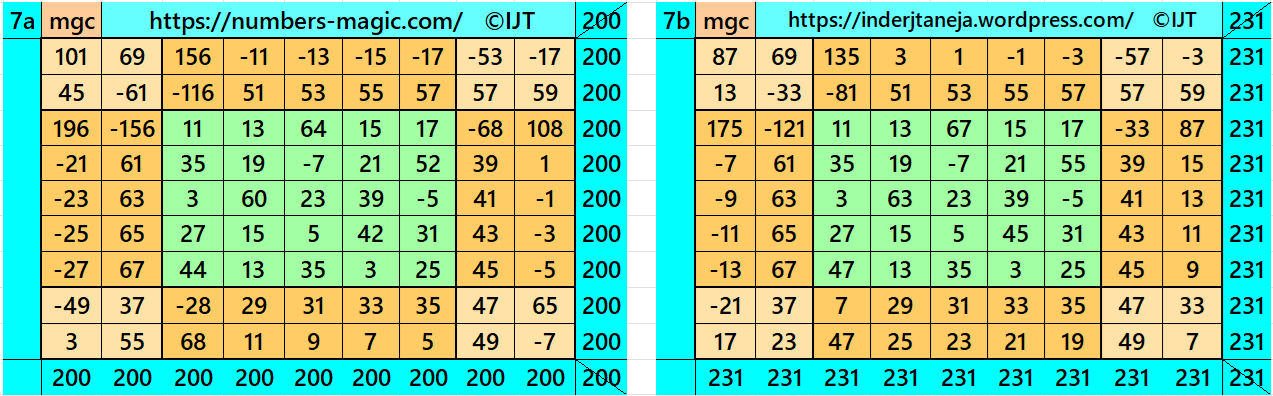
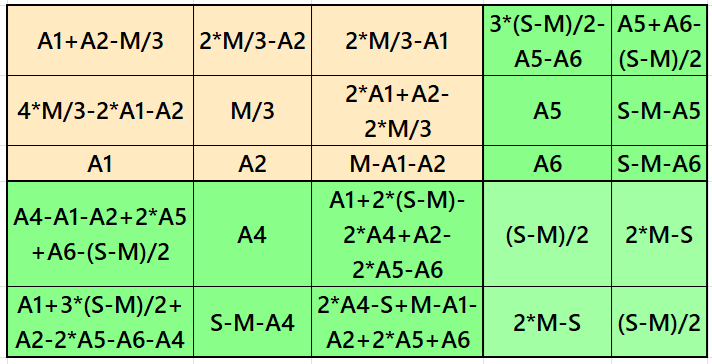
Result 8: Cornered Magic Square
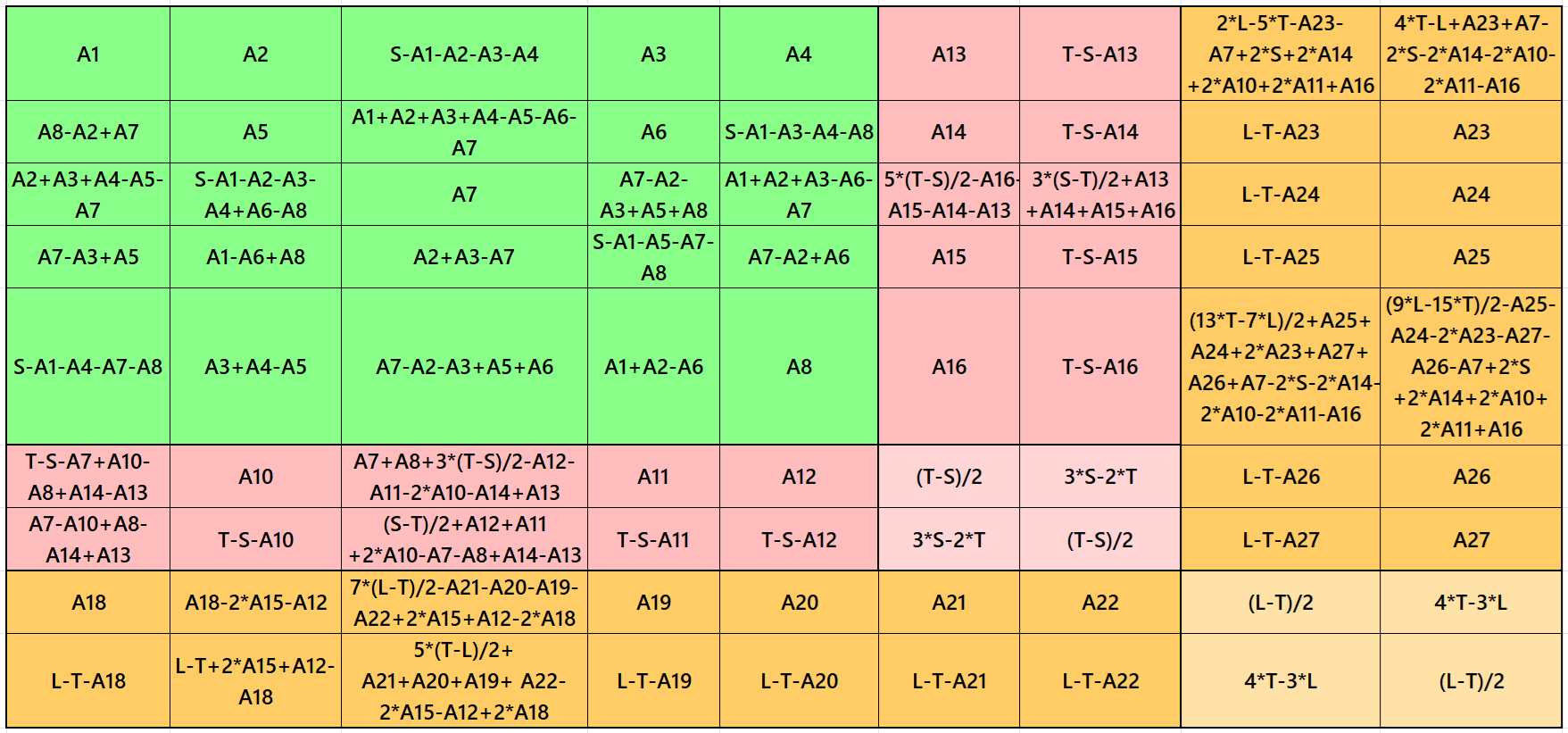
It is cornered magic square of order 9 with pandiagonal magic square of order 5 at upper-left corner. It contains magic square of order 7 also as a cornered magic square. The magic rectangles of orders 2×5 and 2×7 are of equal sums, i.e., equal width and equal length in each case. The letters S, T and L are the magic sums of magic squares of orders 5, 7 and 9 respectively. See below two examples with even and odd magic sums:
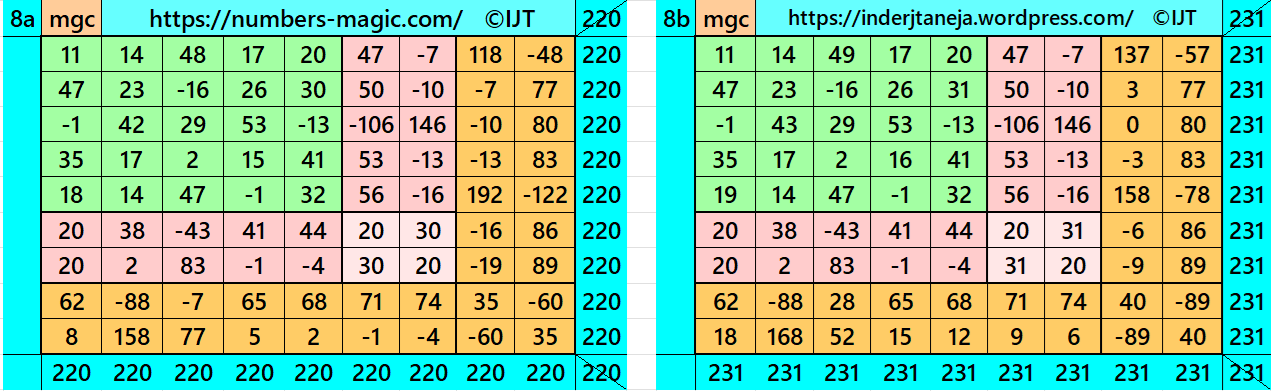
Result 9: Cornered Magic Square
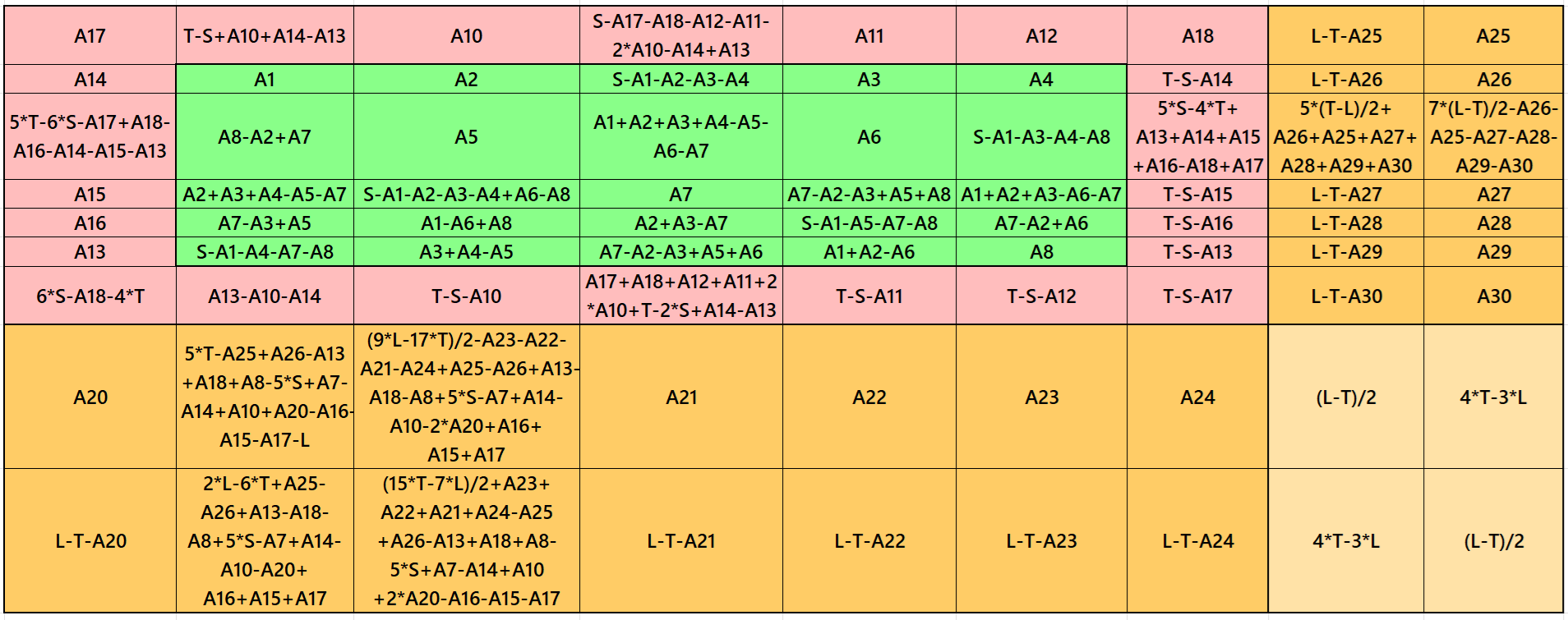
It is cornered magic square of order 9 with single-digit bordered magic square of order 7 at upper-left corner. It contains pandiagonal magic square of order 5 in the middle. The magic rectangles of order 2×7 are of equal sums, i.e., equal width and equal length. The magic sum of magic square of order 7 may be semi-magic but still we have order 9 as a magic square. The letters S, T and L are the magic sums of magic squares of orders 5, 7 and 9 respectively. See below two examples with even and odd magic sums:
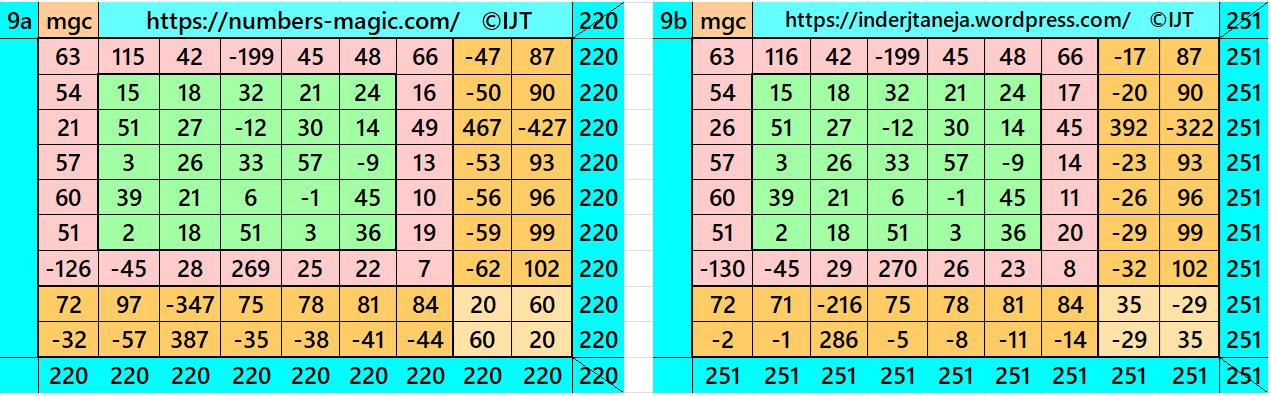
Result 10: Cornered Magic Square
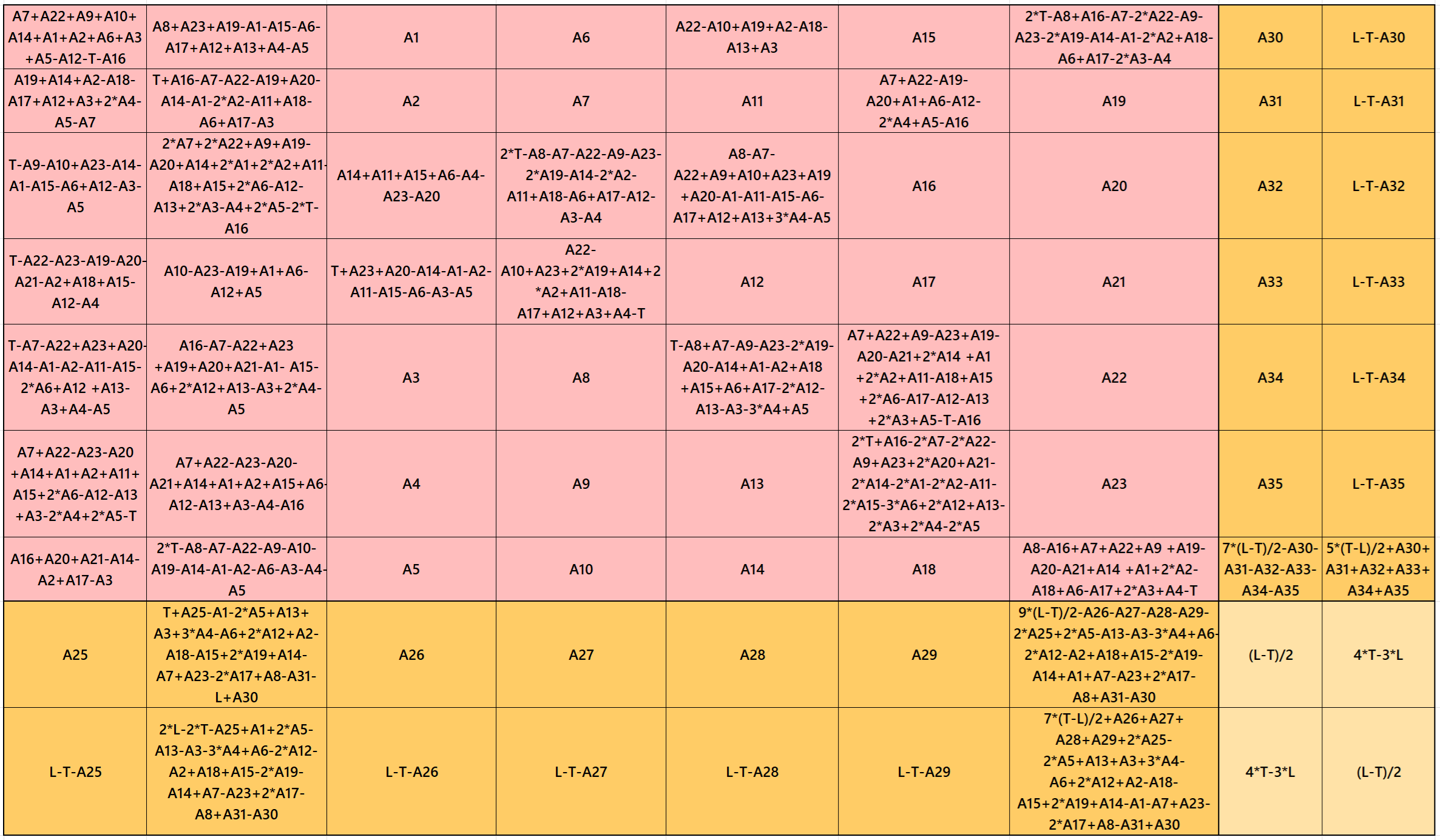
It is cornered magic square of order 9 with pandiagonal magic square of order 7 at upper-left corner. The two magic rectangles of orders 2×7 are of equal sums, i.e., equal width and equal length. The letters T and
L are the magic sums of magic squares of orders 7 and 9 respectively. See below two examples with even and odd magic sums:
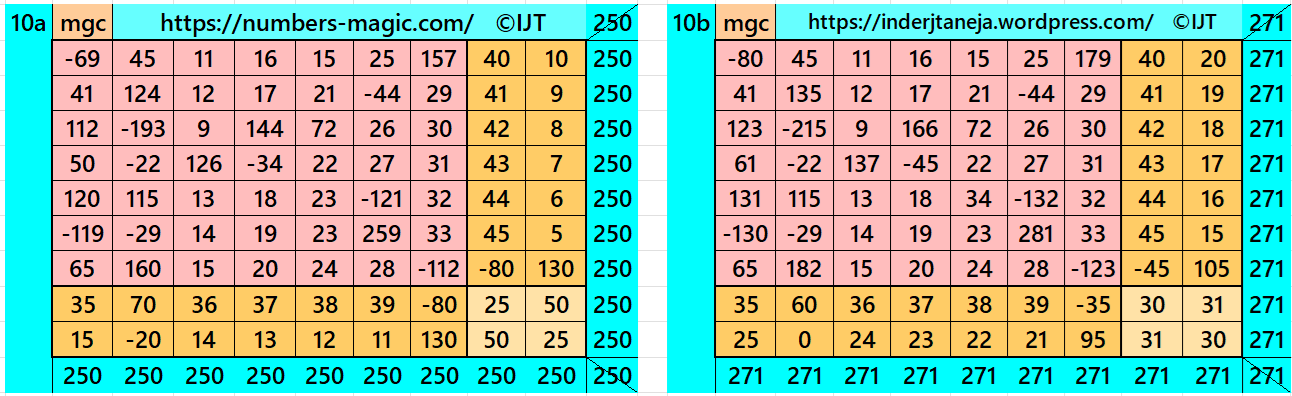
Part 3: Pandiagonal Magic Square of Order 9
Result 11: Pandiagonal Magic Square of Order 9
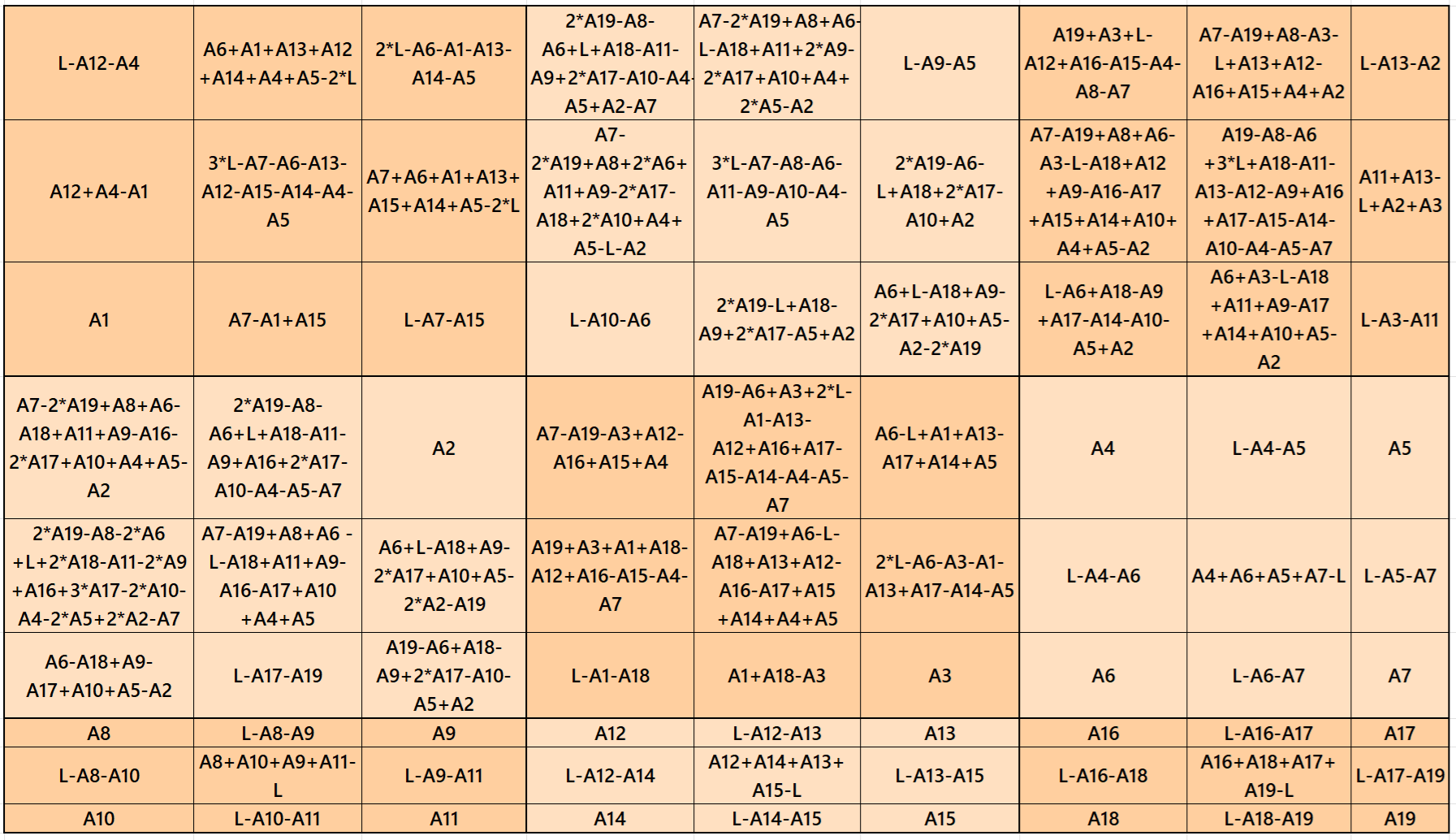
It is a pandiagonal magic square of order 9 with nine equal sums semi-magic squares of order 3. See below two examples with even and odd magic sums:
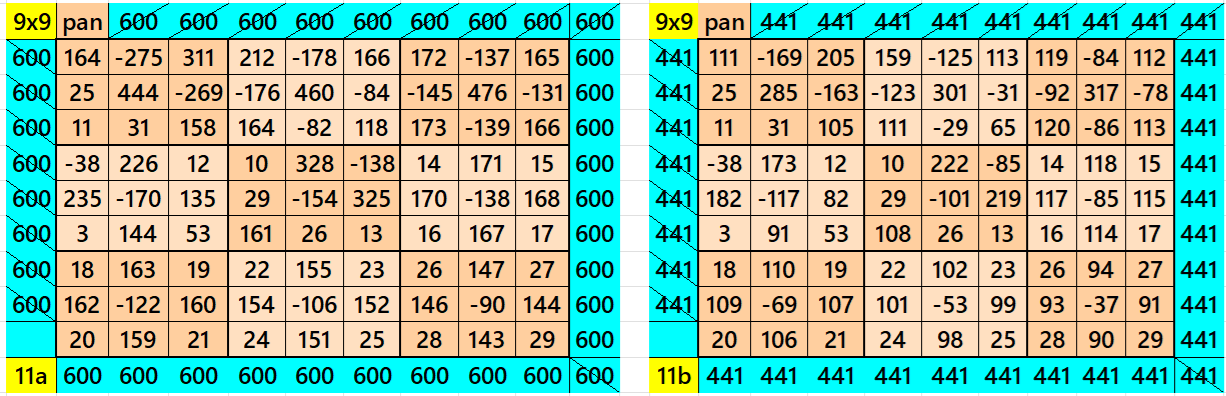
Part 4: Semi-Magic Squares of Order 9
Result 12: Double Digits Bordered Magic Square
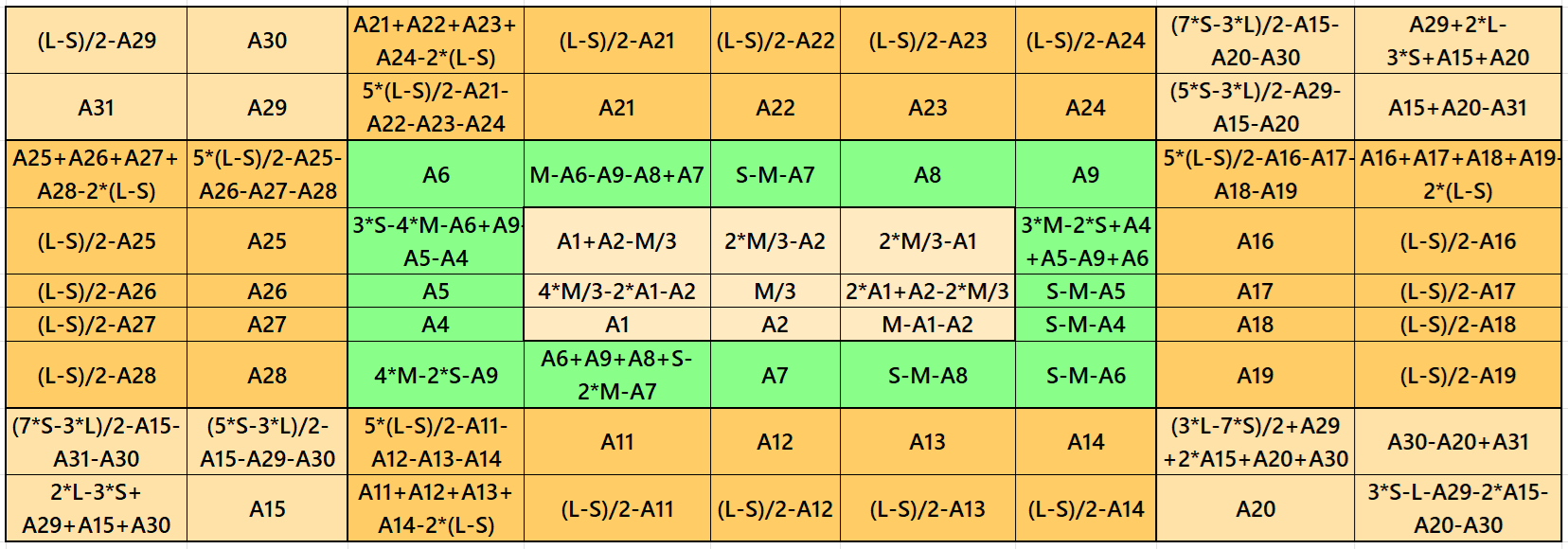
It is double-digit bordered semi-magic square of order 9 embedded with a single-digit bordered magic square of order 5. The four magic rectangles of order 2×5 are of equal sums, i.e., equal width and equal length. The magic square of order 3 is with decimal entries. To get the result without decimal entries, we must consider magic sum for order 3 as multiple of 3. It is semi-magic because of single-digit bordered magic square of order 5 in the middle. To get it a magic square of order 9, we must have a condition M=3*S/5. The letters M, S and L are magic sums of magic squares of orders 3, 5 and 9 respectively. See below two examples with semi-magic and magic sums:
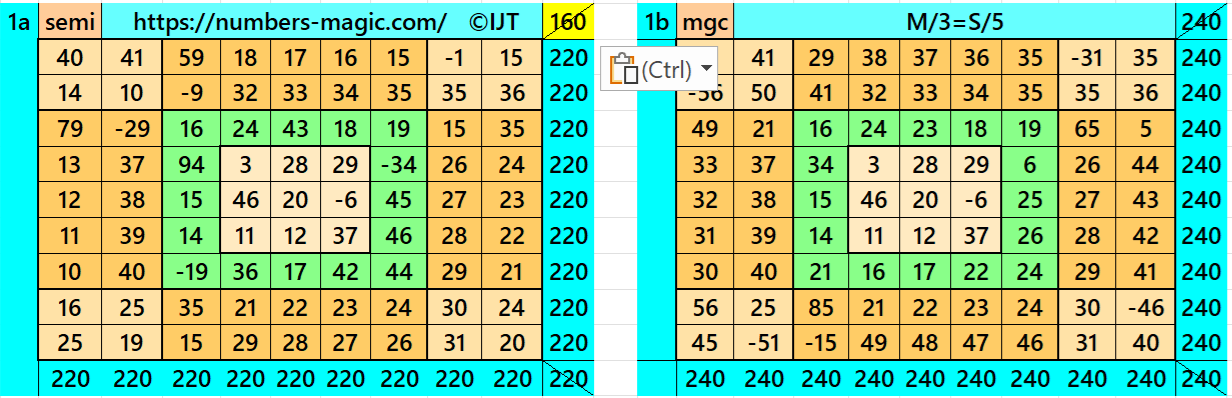
Result 13: Single-Digit Bordered Magic Square
It is single-digit bordered semi-magic square of order 9 embedded with a double-digit bordered magic square of order 7. The four magic rectangles of order 2 × 3 are of equal sums, i.e., equal width and equal length. The magic square of order 3 is with decimal entries. To get the result without decimal entries, we must consider magic sum for order 3 as multiple of 3. It is semi-magic because of single-digit bordered magic square of order 9. To get it a magic square of order 9, we must have a condition T=(7/9)*L. The letters M, T and L are magic sums of magic squares of orders 3, 7 and 9 respectively. See below two examples with semi-magic and magic sums:
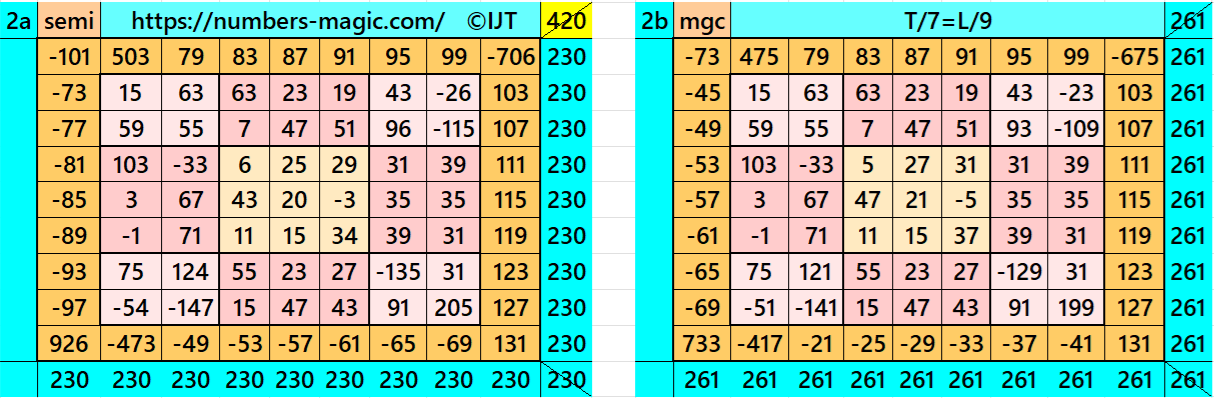
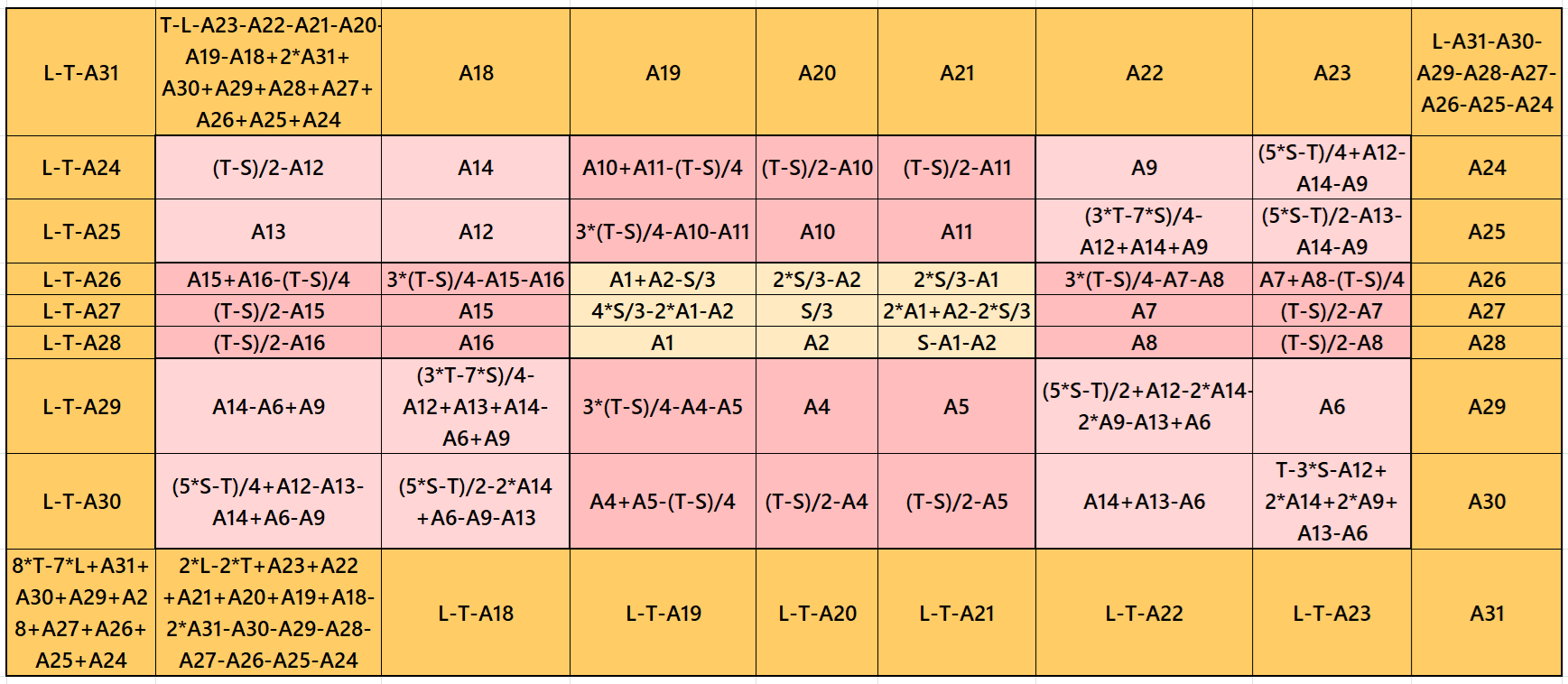
Result 14: Single-Digit Bordered Magic Square
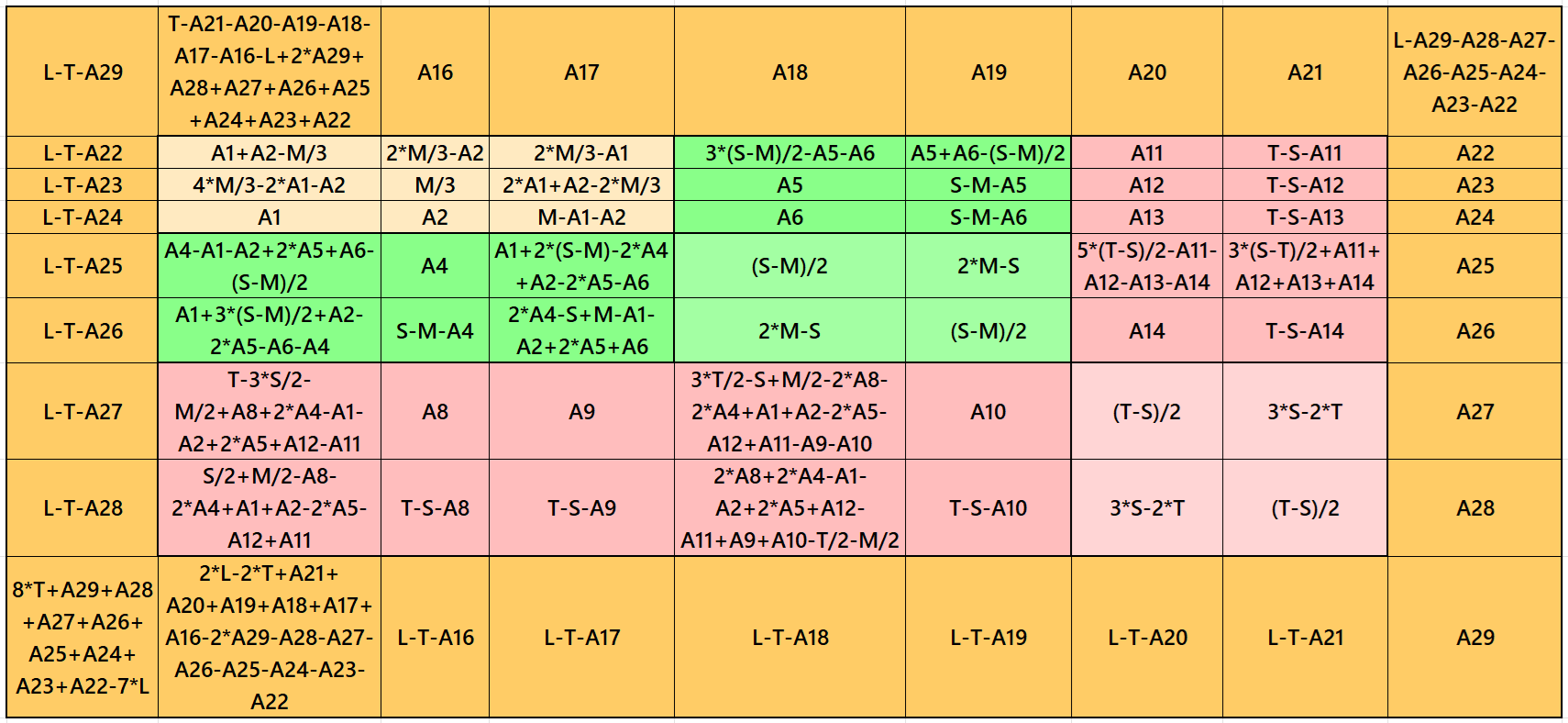
It is single-digit bordered semi-magic square of order 9 embedded with a cornered magic square of order 7. The magic rectangles of order 2×3, 2×5 and 2×7 are of equal sums, i.e., equal width and equal length in each case. The magic square of order 3 is with decimal entries. To get the result without decimal entries, we must consider magic sum for order 3 as multiple of 3. It is semi-magic because of single-digit bordered magic square of order 9. To get it a magic square of order 9, we must have a condition T=(7/9)* L. The letters M, S, T and L are magic sums of magic squares of orders 3, 5, 7 and 9 respectively. See below two examples with semi-magic and magic sums:
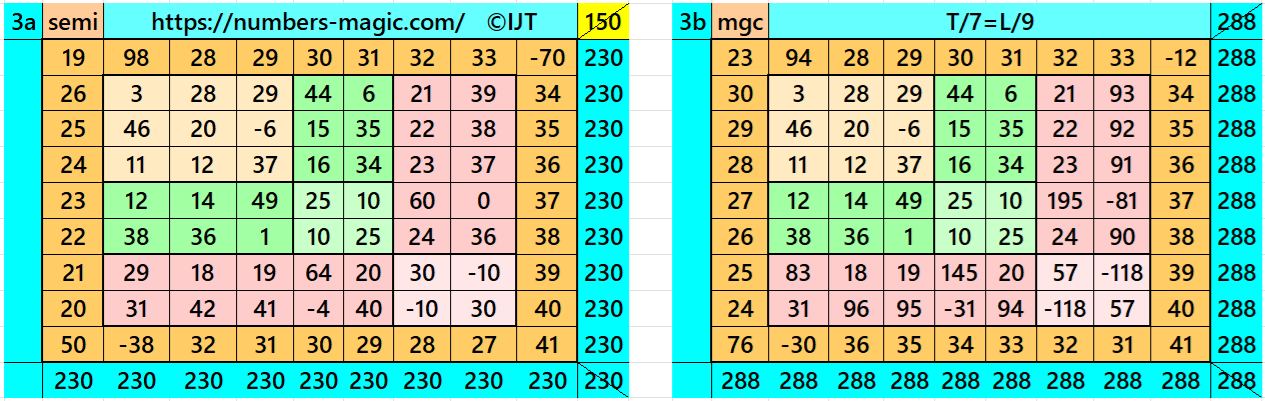
Result 15: Single-Digit Bordered Magic Square
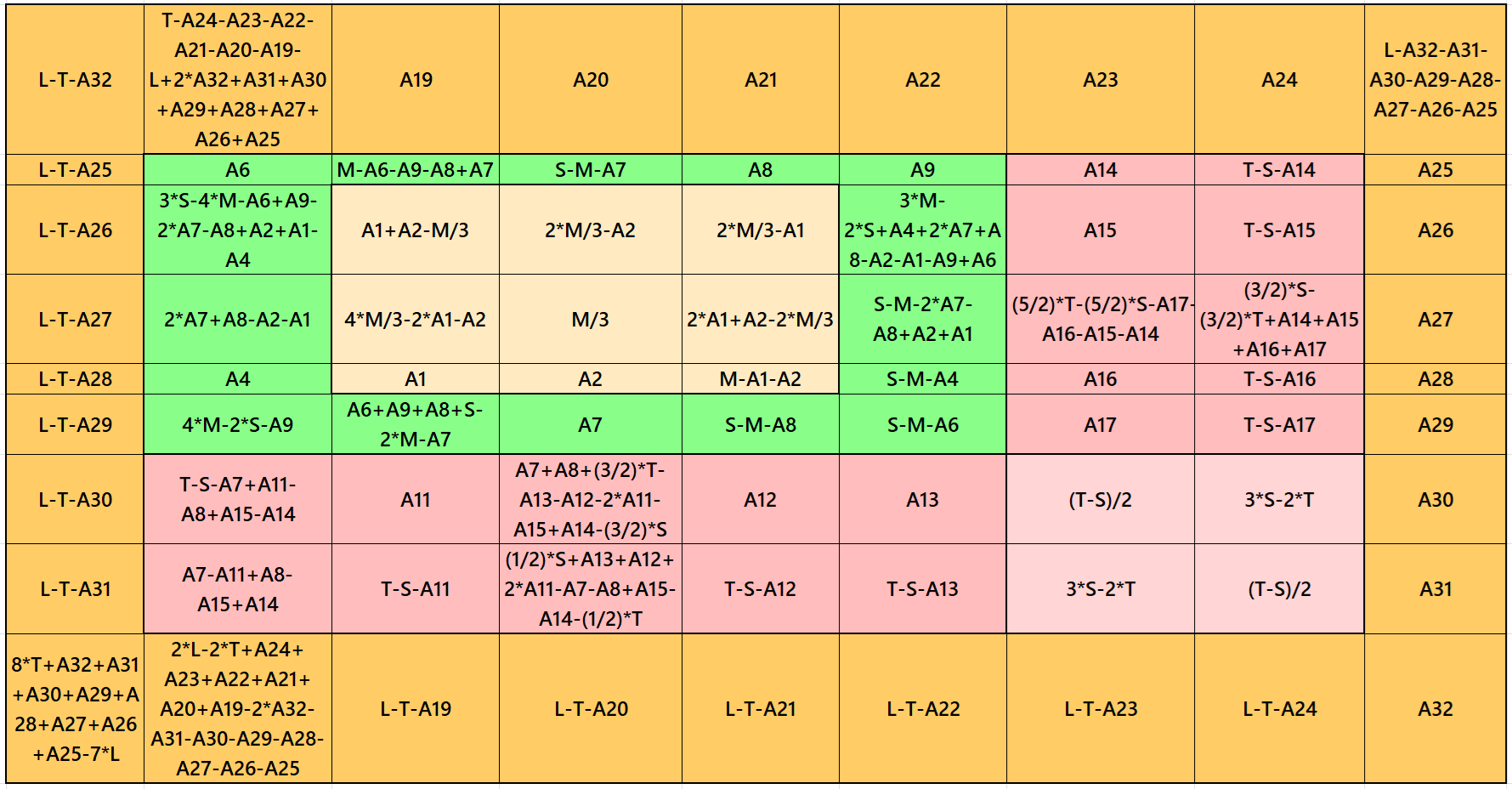
It is single-digit bordered semi-magic square of order 9 embedded with a cornered magic square of order 7. It again contains a single-digit bordered semi-magic of order 5 at the upper-left corner. The magic rectangles of order 2×5 are of equal sums, i.e., equal width and equal length. The magic square of order 3 is with decimal entries. To get the result without decimal entries, we must consider magic sum for order 3 as multiple of 3. It is semi-magic because of single-digit bordered magic square of order 9. To get it a magic square of order 9, we must have a condition T = (7/9)*L. The single-digit bordered magic square of order 5 is also semi-magic, but it don’t make any effect on the magic sum of order 9. The letters M, S, T and L are imagic sums of magic squares of orders 3, 5, 7 and 9 respectively. See below two examples with semi-magic and magic sums:
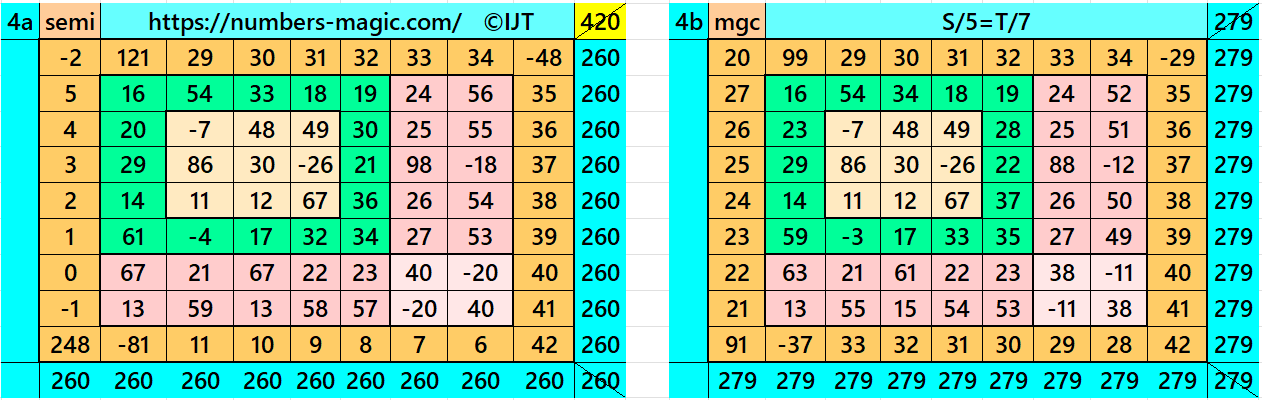
Result 16: Single-Digit Bordered Magic Square
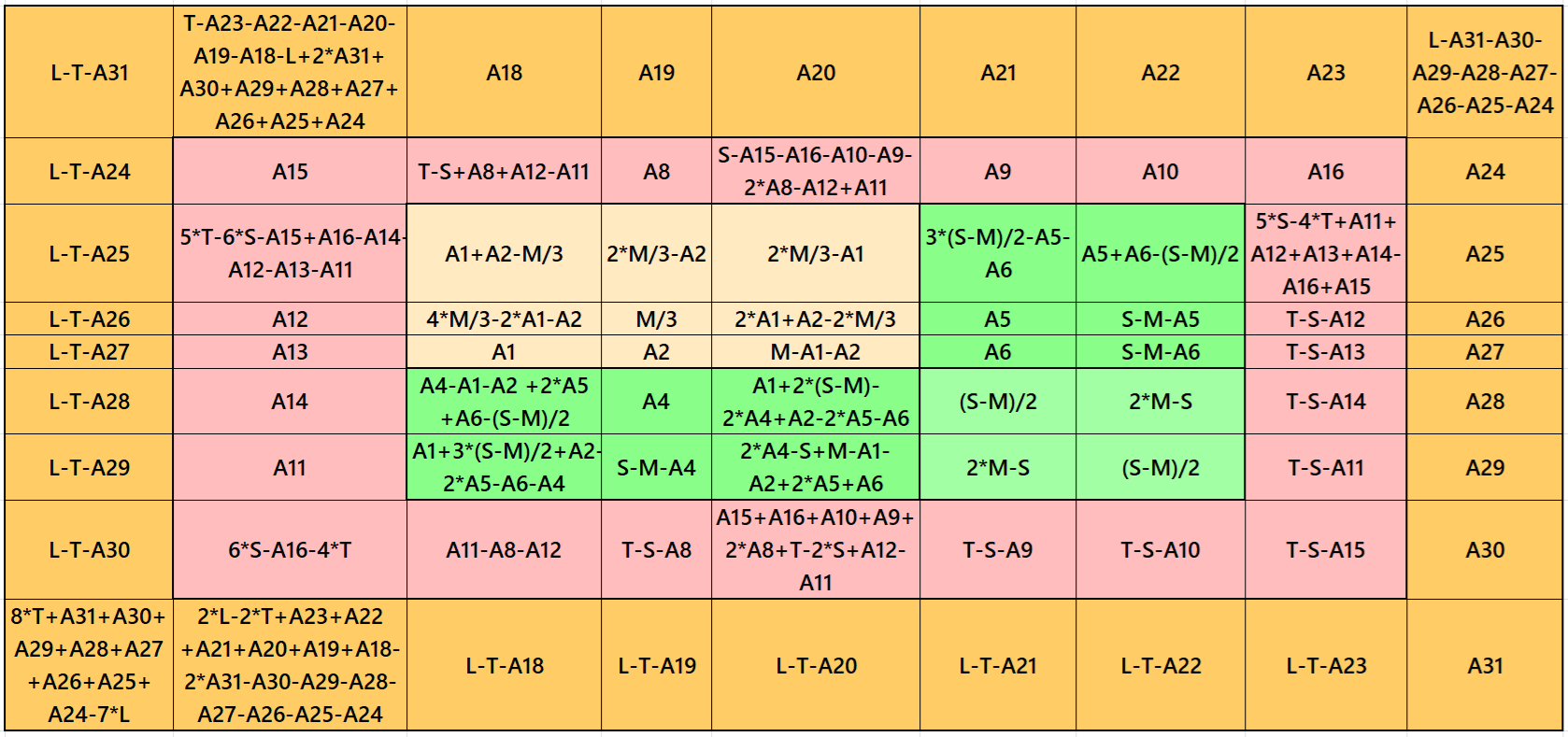
It is single-digit bordered semi-magic square of order 9 embedded with a cornered magic square of order 5. The magic rectangles of order 2×3 are of equal sums, i.e., equal width and equal length. The magic square of order 3 is with decimal entries. To get the result without decimal entries, we must consider magic sum for order 3 as multiple of 3. It is semi-magic because of single-digit bordered magic squares of orders 9 and 7. To get it a magic square of order 9, we must have two conditions T = (7/9)*L and S = (5/7)*T. The letters M, S, T and L are magic sums of magic squares of orders 3, 5, 7 and 9 respectively. See below two examples with semi-magic and magic sums:
Result 17: Single-Digit Bordered Magic Square
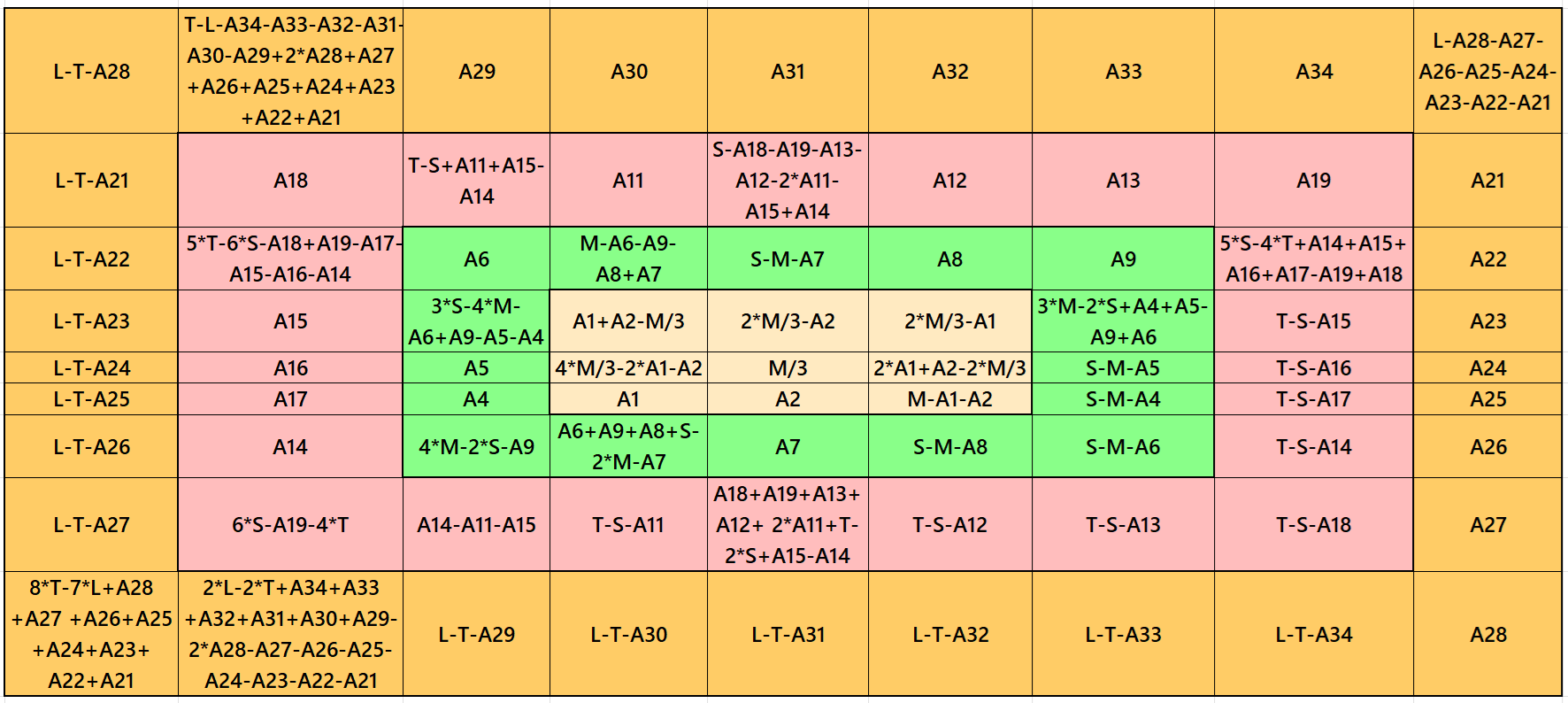
It is a single-digit bordered semi-magic square of order 9 embedded with a magic square of order 3. The magic square of order 3 is with decimal entries. To get the result without decimal entries, we must consider magic sum for order 3 as multiple of 3. It is semi-magic because of single-digit bordered magic squares of orders 9, 7 and 5. To get it a magic square of order 9, we must have three conditions T=7/9)*L, S=(5/7)*T and M=(3/5)*S. The letters M, S, T and L are magic sums of magic squares of orders 3, 5, 7 and 9 respectively. See below two examples with semi-magic and magic sums:
Result 18: Single-Digit Bordered Magic Square
It is single-digit bordered semi-magic square of order 9 embedded with a cornered magic square of order. It contains pandiagonal magic square of order 5 at the upper-left corner. It is semi-magic because of single-digit bordered magic squares of order 9. To get it a magic square of order 9, we must a condition T=(7/9)*L. The letters S, T and L are magic sums of magic squares of orders 5, 7 and 9 respectively. See below two examples with semi-magic and magic sums:
Result 19: Single-Digit Bordered Magic Square
It is single-digit bordered semi-magic square of order 9 embedded with a pandiagonal magic square of order 5. It is semi-magic because of single-digit bordered magic squares of orders 9 and 7. To get it a magic square of order 9, we must two conditions T=(7/9)*L and S=(5/7)*T. The letters S, T and L are magic sums of magic squares of orders 5, 7 and 9 respectively. See below two examples with semi-magic and magic sums:
Result 20: Single-Digit Bordered Magic Square
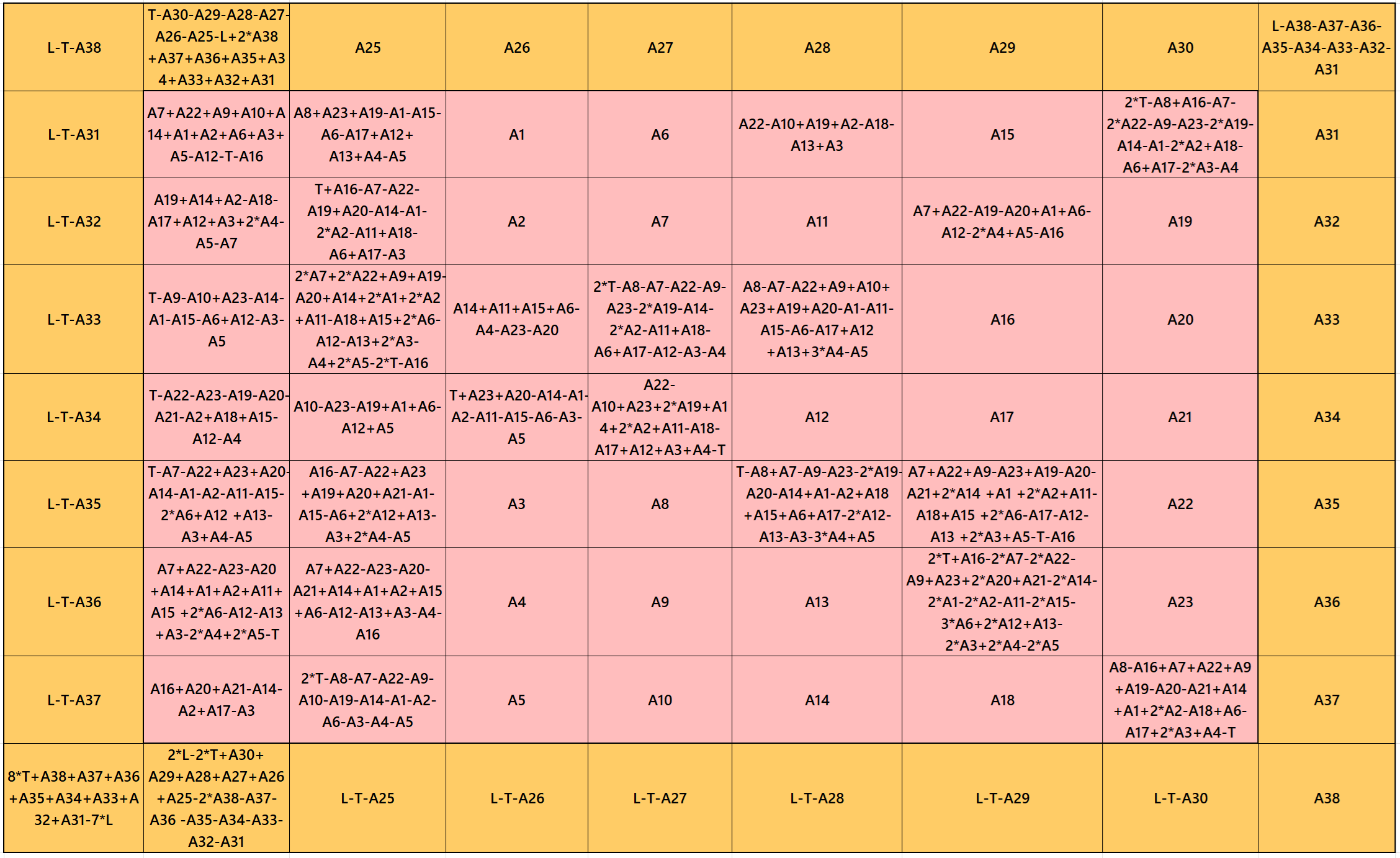
It is a single-digit bordered semi-magic magic square of order 9 embedded with a pandiagonal magic square of order 7 in the middle. To get it a magic square of order 9, we must apply a condition T=(7/9*L. The letters T and L are the magic sums of magic squares of orders 7 and 9 respectively. See below two examples with semi-magic and magic sums:
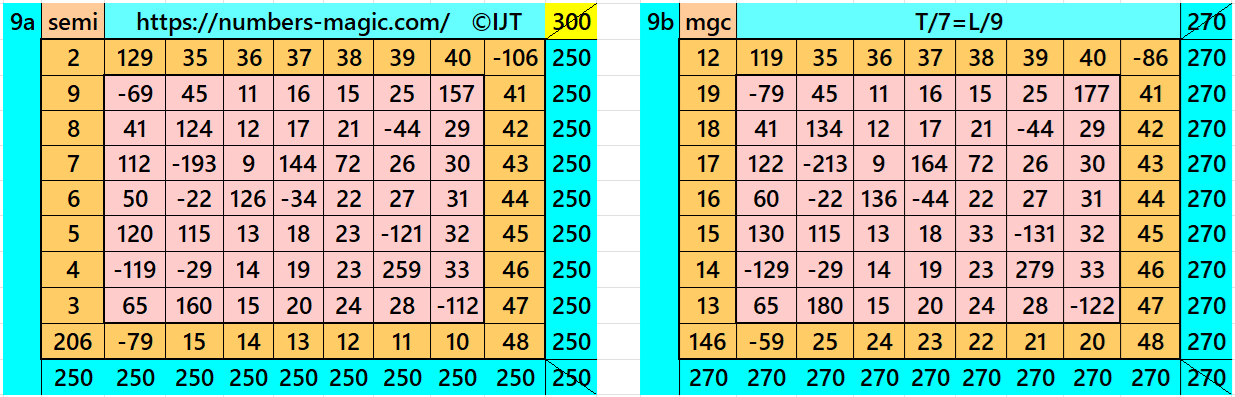
References
Part 1: Representing Days and Date
- Inder J. Taneja, Magic Squares of Orders 3 to 7 in Representing Dates and Days of the Year 2025, Zenodo, May 04, 2025, pp. 1-474, https://doi.org/10.5281/zenodo.15338142.
- Site Link: Magic Squares of Orders 3 to 7 Representing Dates and Days of the Year 2025 (new site)
- Site Link: Magic Squares of Orders 3 to 7 Representing Dates and Days of the Year 2025 (old site)
- Inder J. Taneja, Magic Squares of Order 8 Representing Days and Dates of the Year 2025, Zenodo, May 04, 2025, pp. 1-134, https://doi.org/10.5281/zenodo.15338246.
- Site Link: Magic Squares of Order 8 Representing Days and Dates of the Year 2025 (new site)
- Site Link: Magic Squares of Order 8 Representing Days and Dates of the Year 2025 (old site)
- Inder J. Taneja, Magic Squares of Order 9 Representing Days and Dates of the Year 2025, Zenodo, May 09, 2025, pp. 1-132, https://doi.org/10.5281/zenodo.15375349.
- Site Link: Magic Squares of Order 9 Representing Days and Dates of the Year 2025 (new site)
- Site Link: Magic Squares of Order 9 Representing Days and Dates of the Year 2025 (old site)
- Inder J. Taneja, Magic Squares of Order 11 Representing Days and Dates of the Year 2025, Zenodo, May 31, 2025, pp. 1-94, https://doi.org/10.5281/zenodo.15564676
- Inder J. Taneja, Magic Squares of Order 12 Representing Days and Dates of the Year 2025 Zenodo, June 10, 2025, pp. 1-43, https://doi.org/10.5281/zenodo.15631884.
Part 2: Revised with Examples
- Inder J. Taneja, Reduced Entries Magic and Semi-Magic Squares of order 12, Zenodo, June 18, 2025, pp. 1-57, https://doi.org/10.5281/zenodo.15692014.
- Inder J. Taneja, Reduced Entries Magic and Semi-Magic Squares of Orders 3, 5, 7 and 9, Zenodo, July 01, 2025, pp. 1-65, https://doi.org/10.5281/zenodo.15783321.
- Inder J. Taneja, Reduced Entries Magic and Semi-Magic Squares of Orders 4, 6, 8 and 10, Zenodo, July 05, 2025, pp. 1-85, https://doi.org/10.5281/zenodo.15814675.


[…] Site Link: Reduced Entries Algebraic Magic Squares of Orders 3, 5, 7 and 9 (new site) […]