Revised on July 12, 2023.
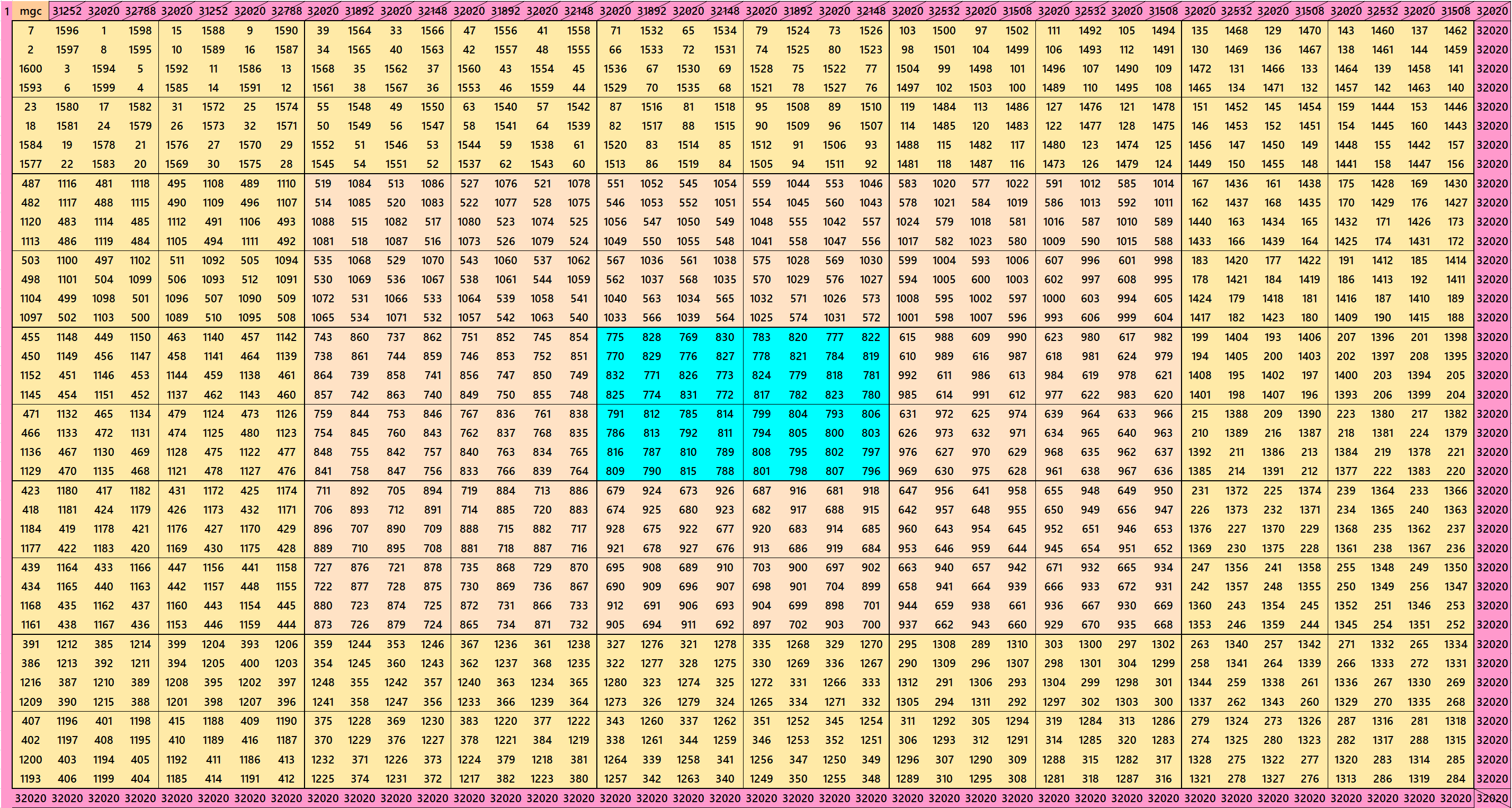
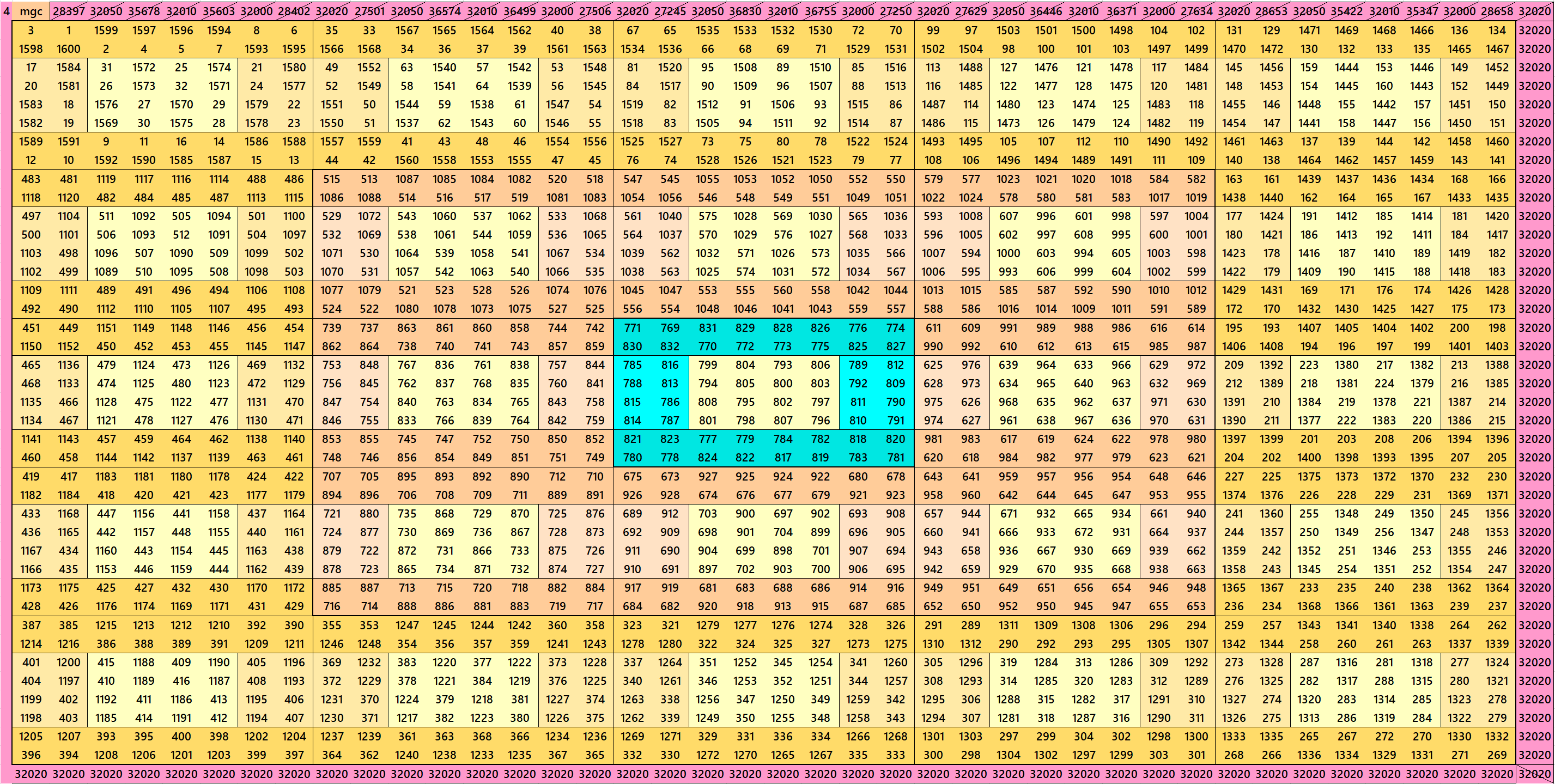
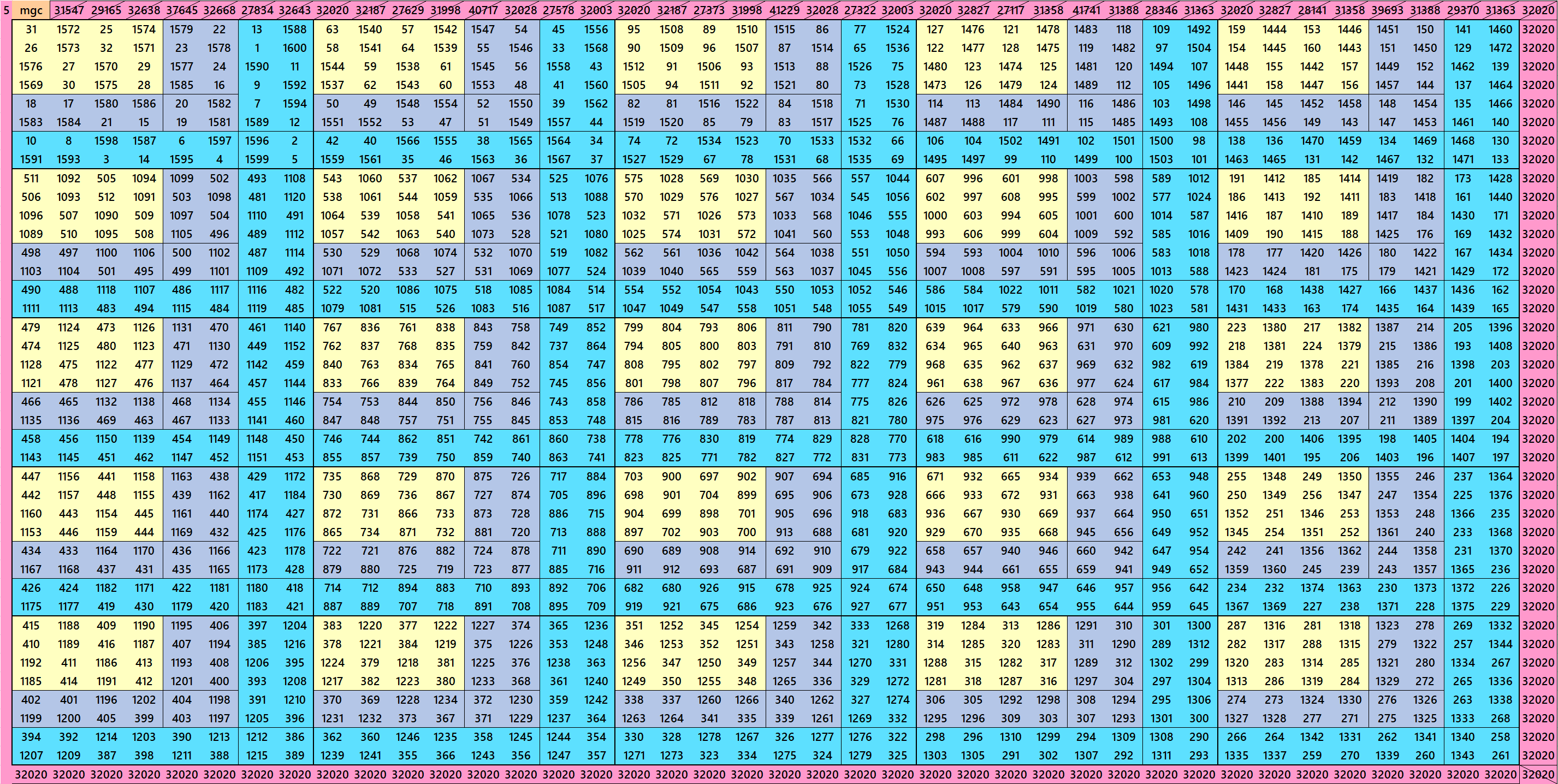
During past years author worked with block-wise, bordered and block-bordered magic squares. This work make connection between block-wise and bordered magic squares. We started with block-wise bordered magic squares of orders 120 and 112. Based on these two big magic inner order magic squares multiples of 8 are studied. By inner orders we understand that magic squares of orders 96, 88, 80, etc. Instead of working in decreasing order, we worked with increasing orders, such as, orders 8, 16, 24, etc. The construction of the block-wise bordered magic squares multiples of 8 is based on equal sum blocks of magic squares of order 8. We have taken six-type of magic squares of order 8. The advantage in studying block-wise bordered magic squares is that when we remove external border, still we are left with magic squares with sequential entries. It is the same property of bordered magic squares. The difference is that instead of numbers here we have blocks of equal sum magic squares of order 8. For multiples of orders 4 and 6 see the links below:
1. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 4.
2. Block-Wise Bordered Magic Squares Multiples of Magic and Bordered Magic Squares of Order 6.
The further multiples, such as multiples of 10, 12, 14, etc. shall be written soon. This work is up to order 120. Examples below are only up to order 40. The higher order examples can be seen in Excel file attached at the end of this work.
Magic Squares of order 8

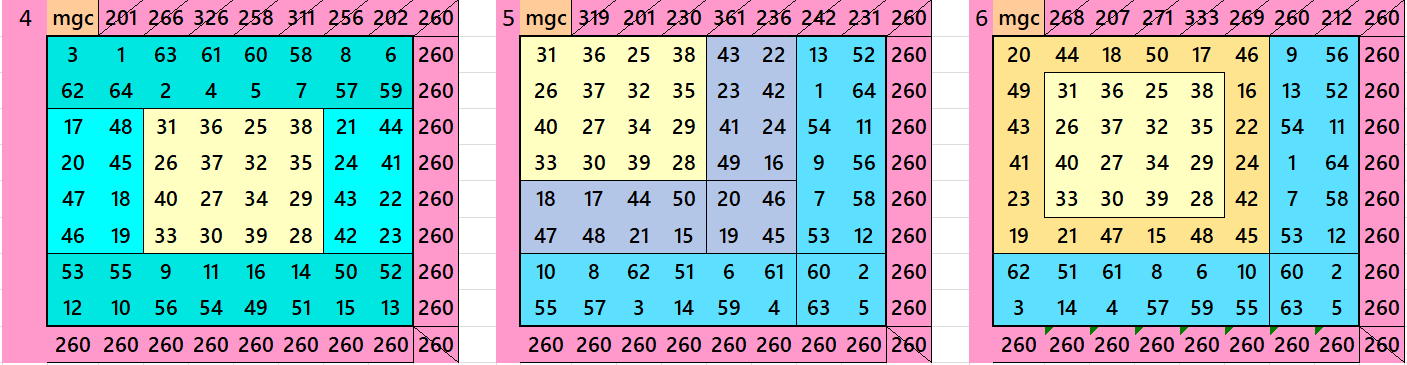
Magic Squares of order 16

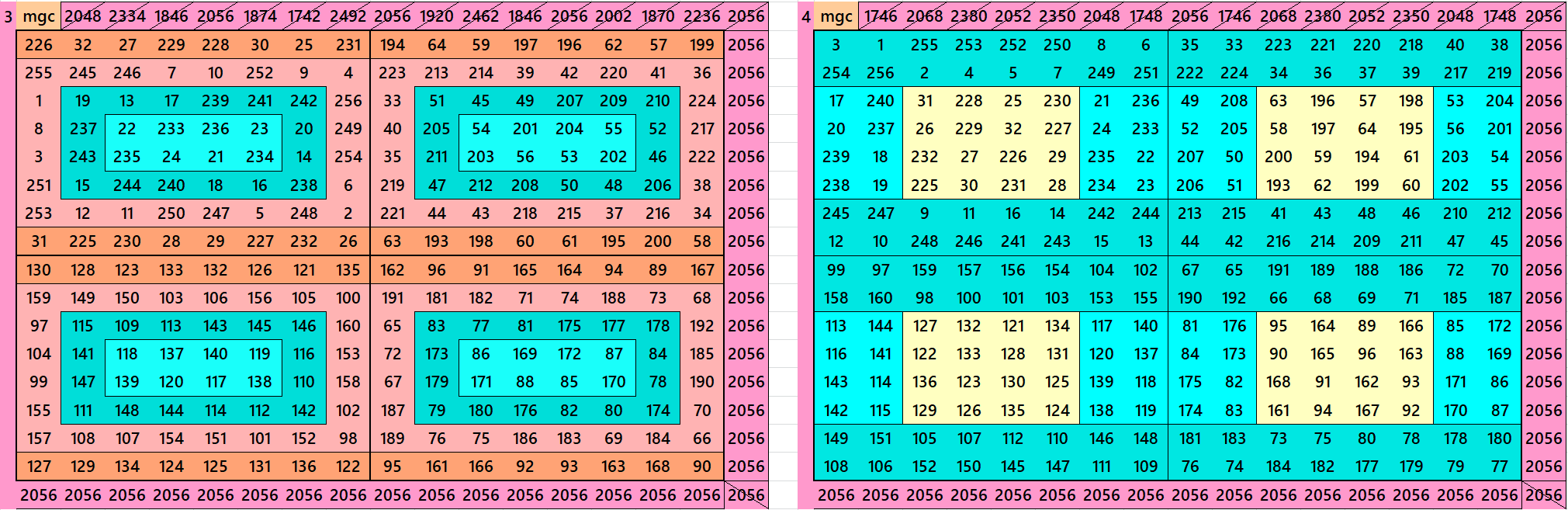

Magic Squares of order 24




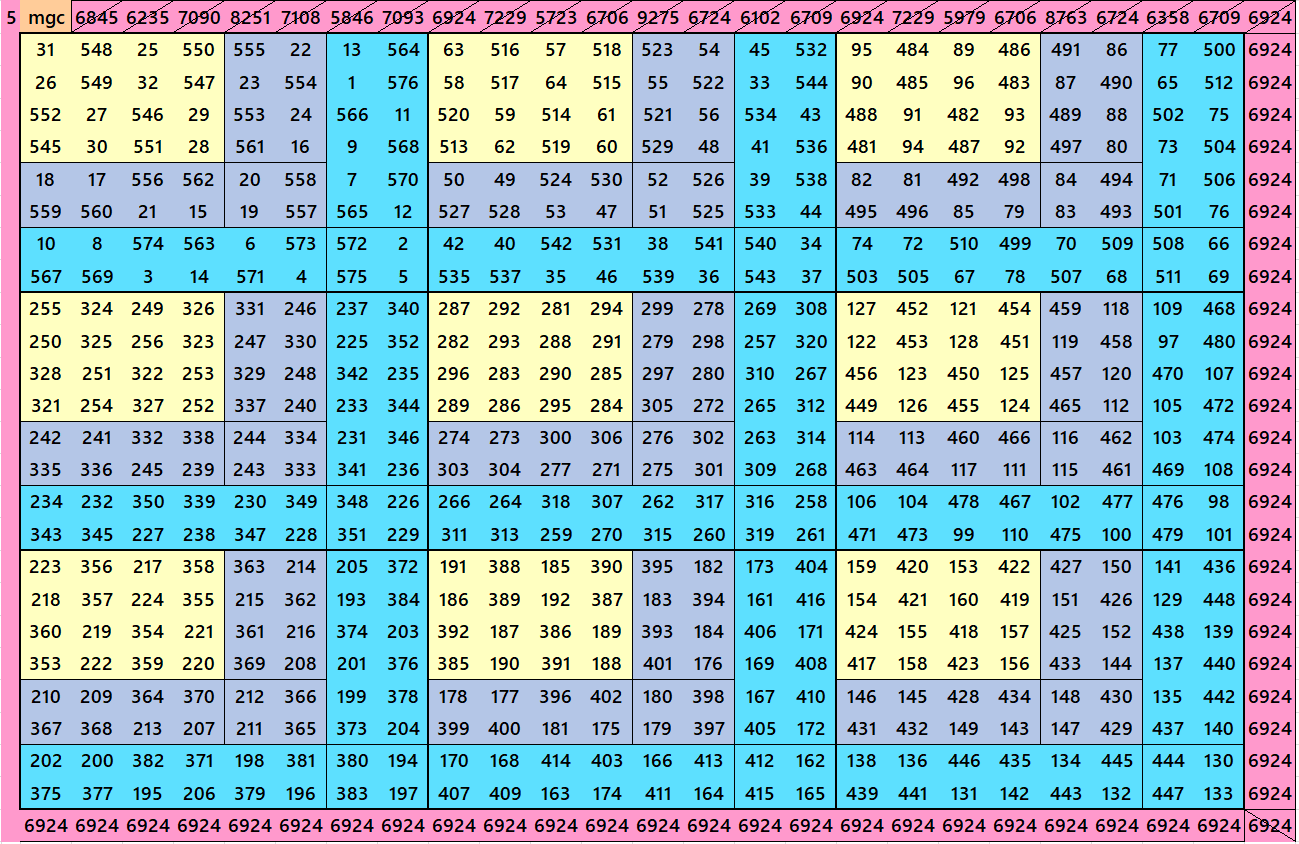
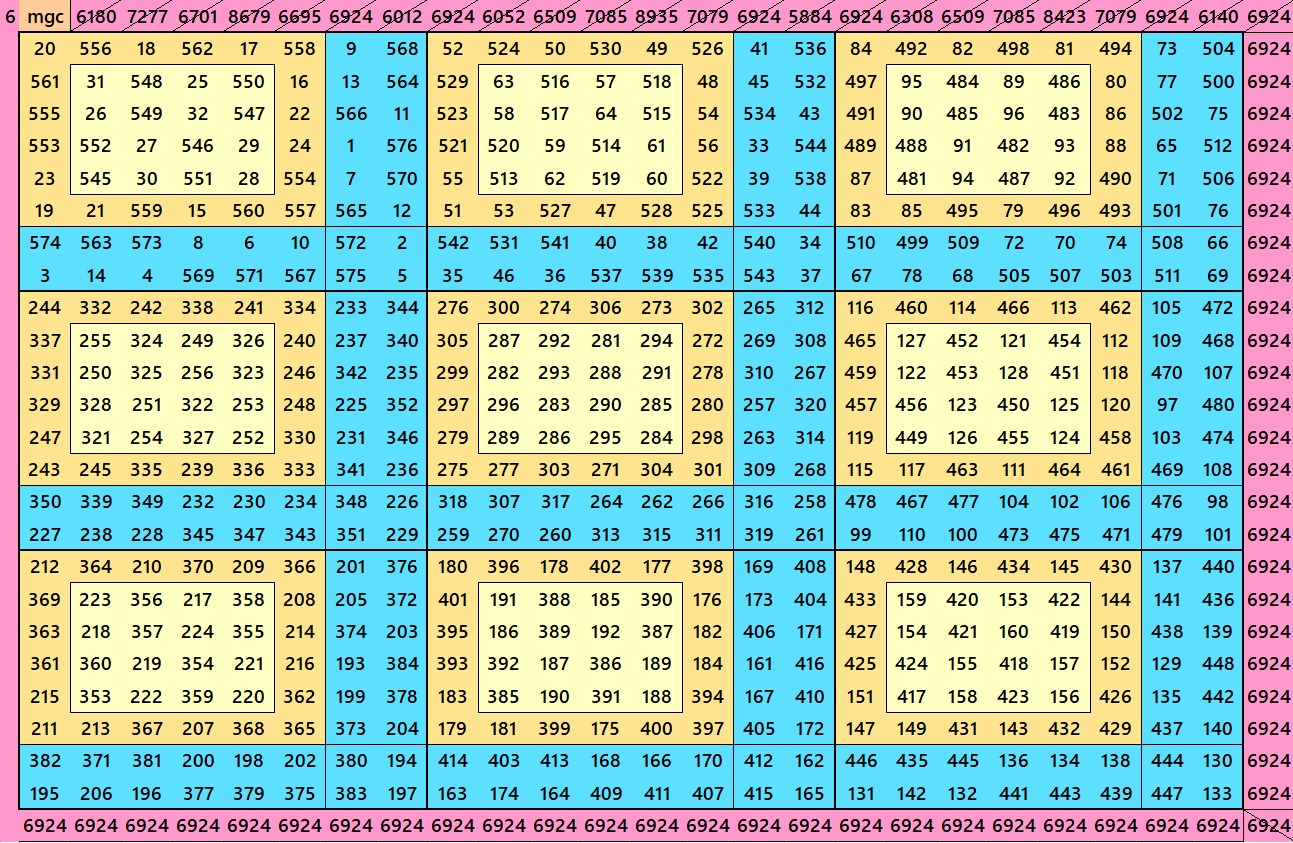
Magic Squares of order 32
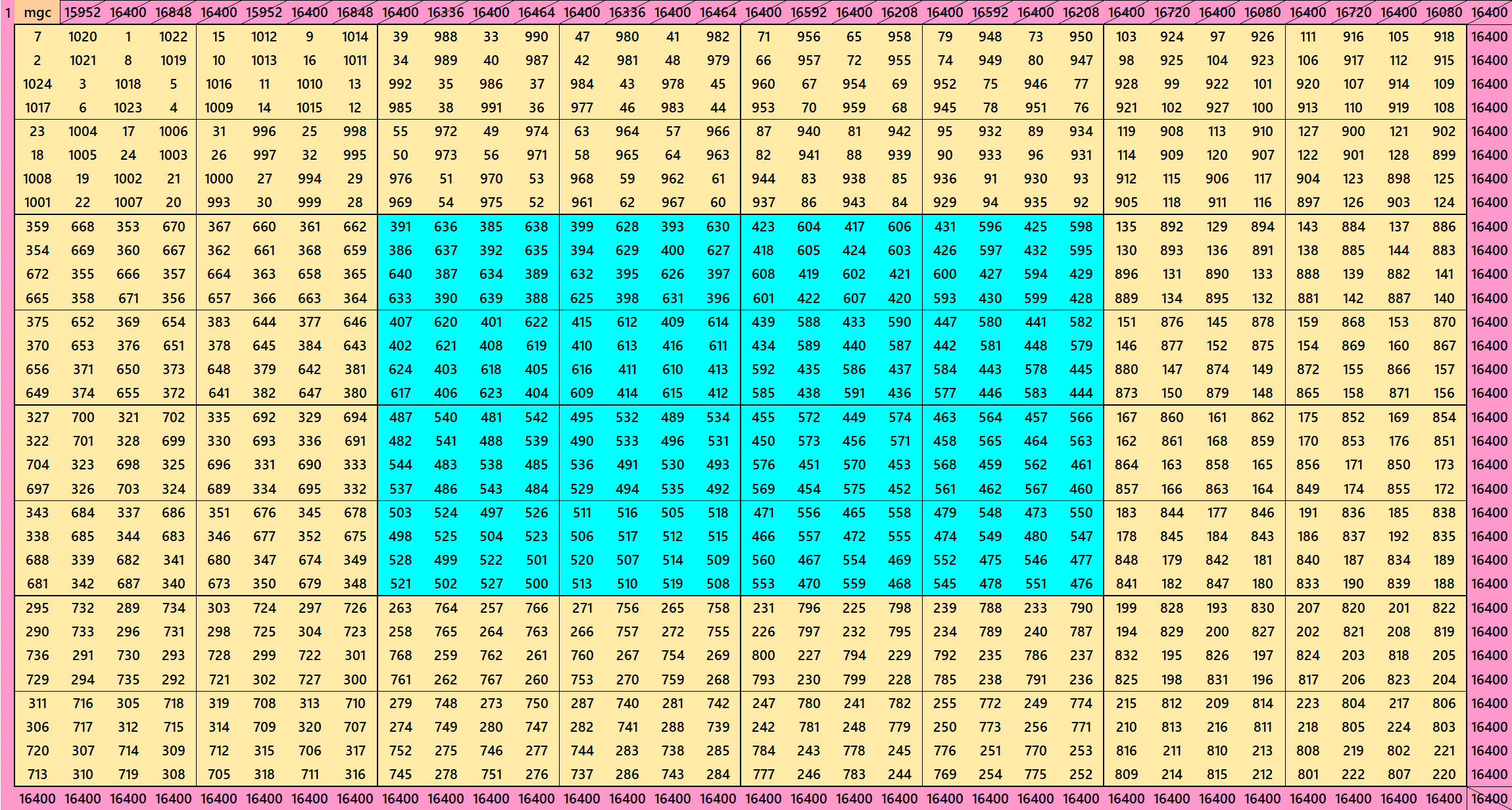
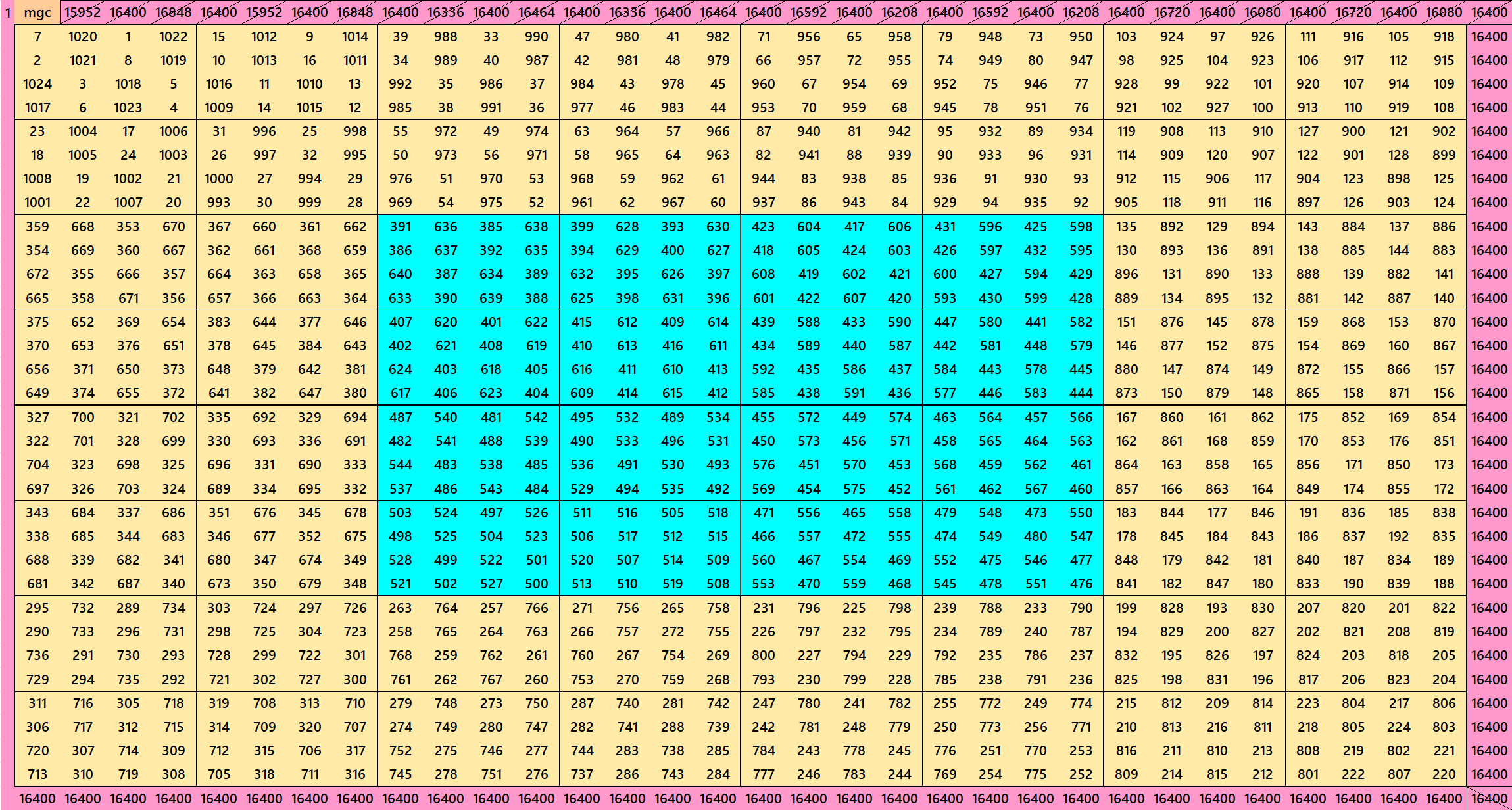

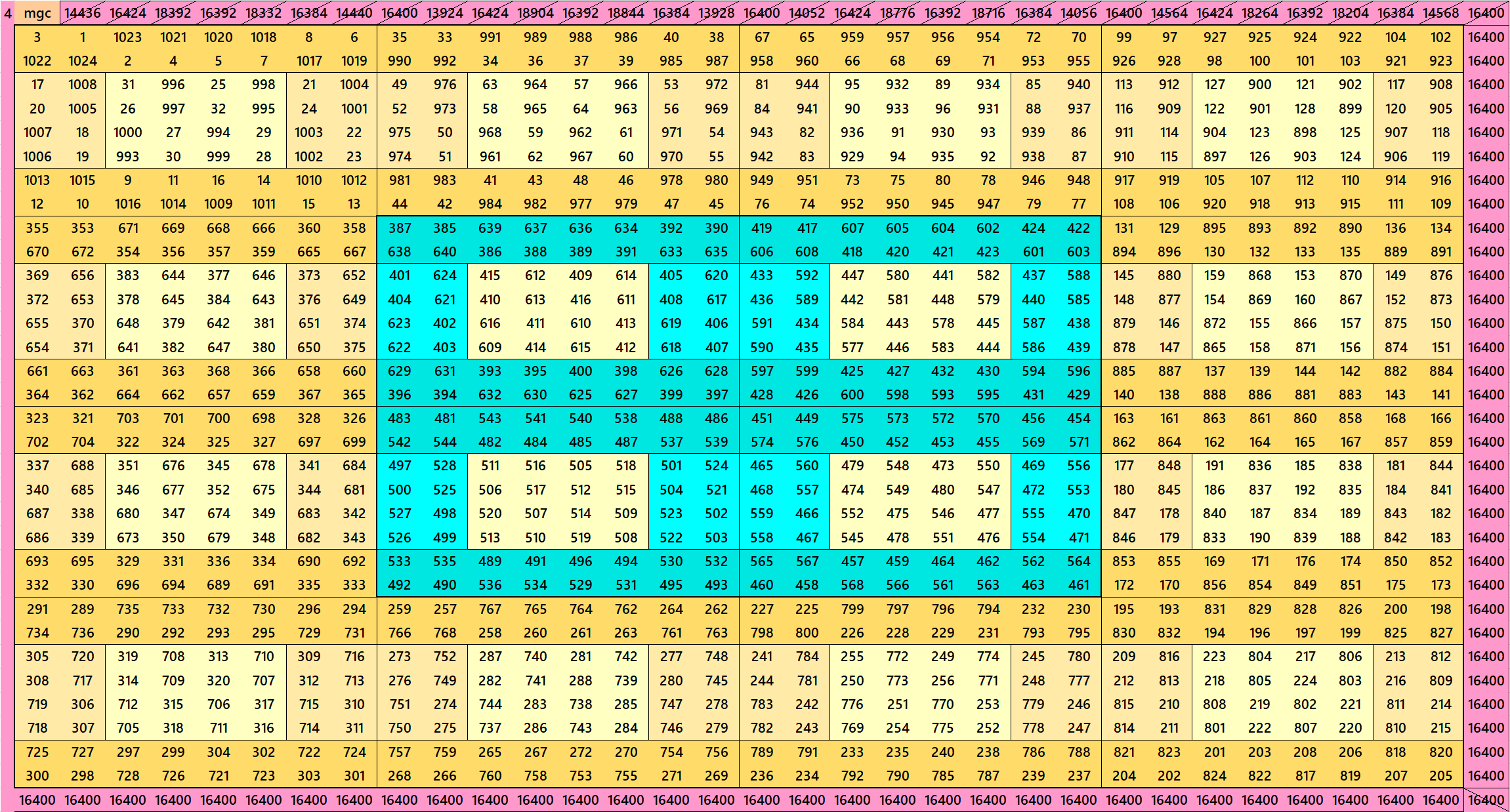
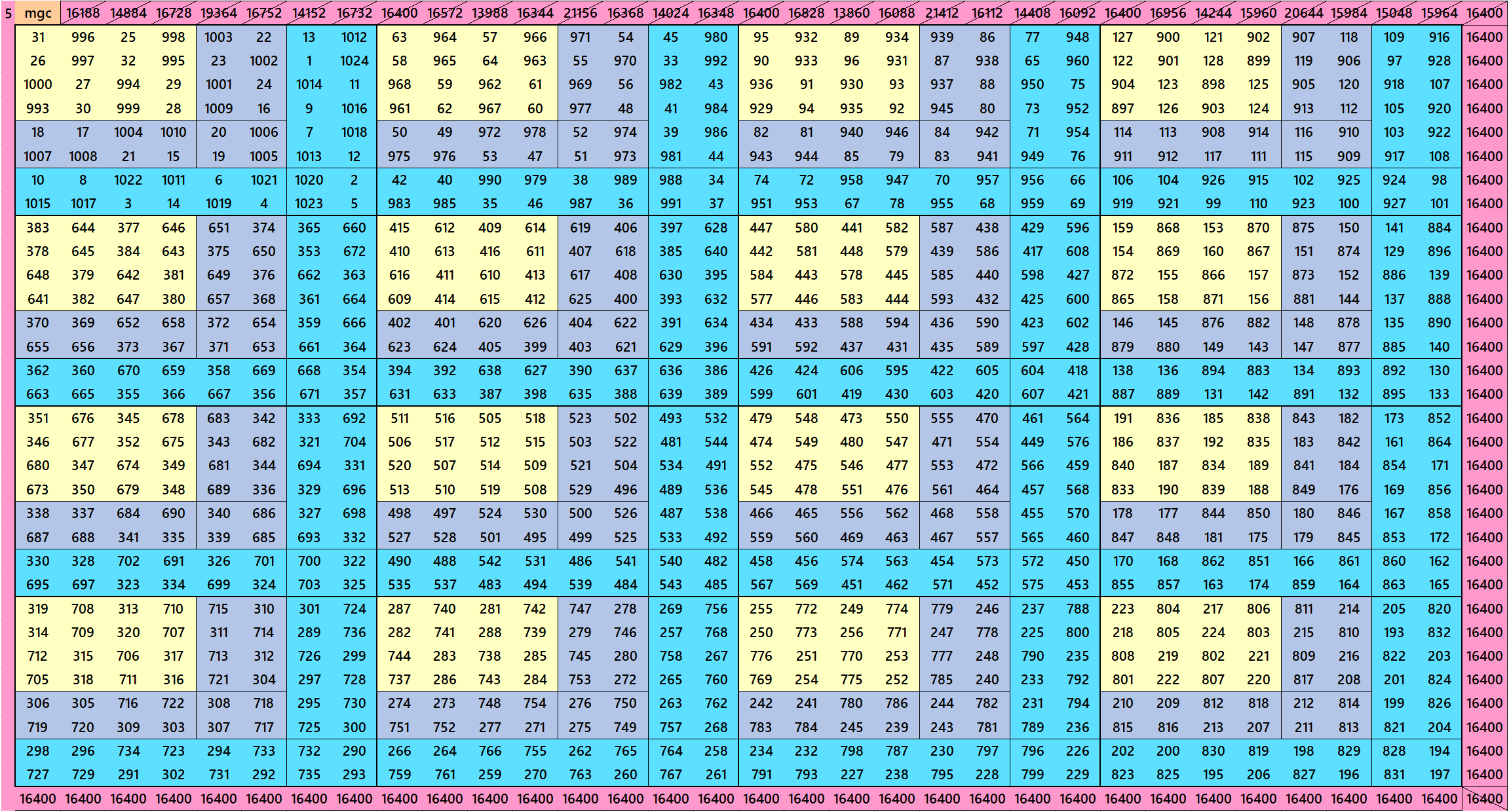

Magic Squares of order 40



Excel file for Download
The excel file below for download contains bordered magic square with blocks of magic squares of order 8. In each case, there are six examples. Total work is from orders 8 to 120.
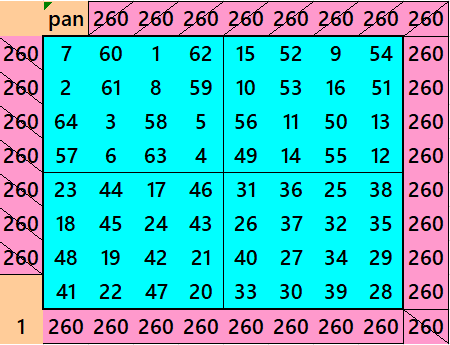
Pandiagonal Magic Squares Multiples of Order 8
Below are pandiagonal magic squares from orders 8 to 120. These are made from pandiagonal magic square formed by four pandigonal magic squares of order 4. Further orders are of equal sums of either order 4 or order 8.
Pandiagonal Magic Square of Order 8
Pandiagonal Magic Square of Order 16
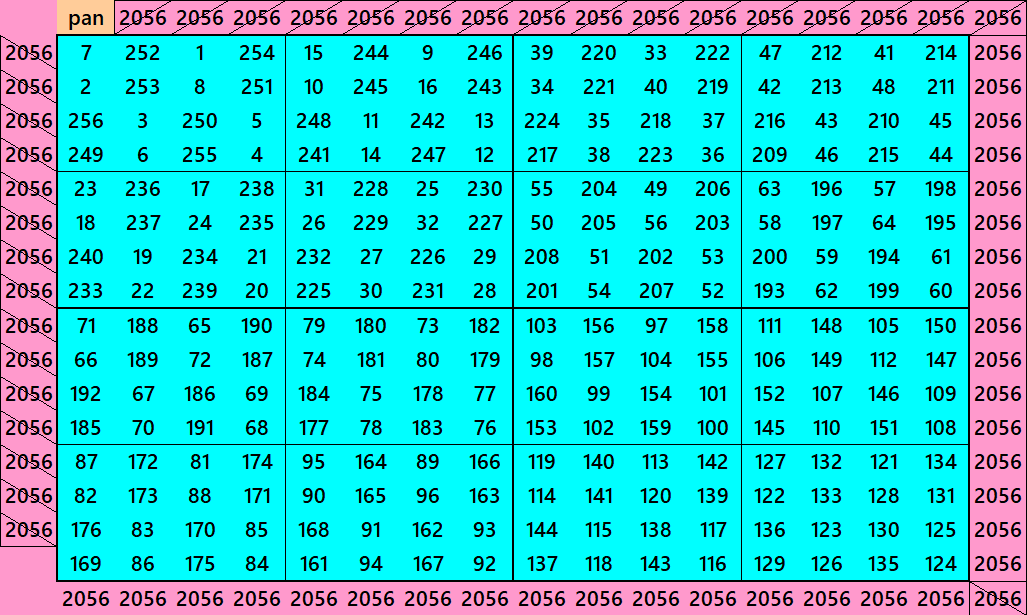
Pandiagonal Magic Square of Order 24
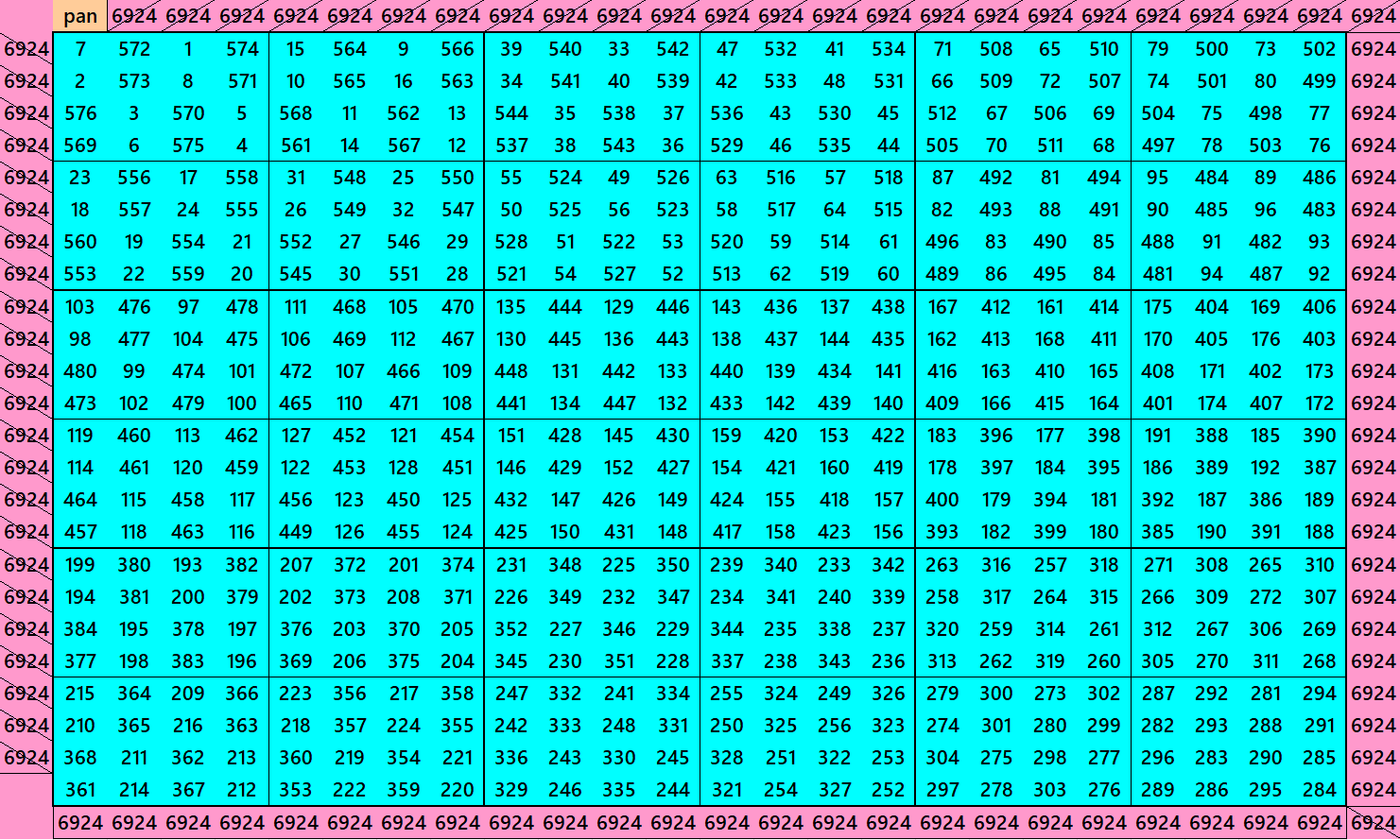
Pandiagonal Magic Square of Order 32
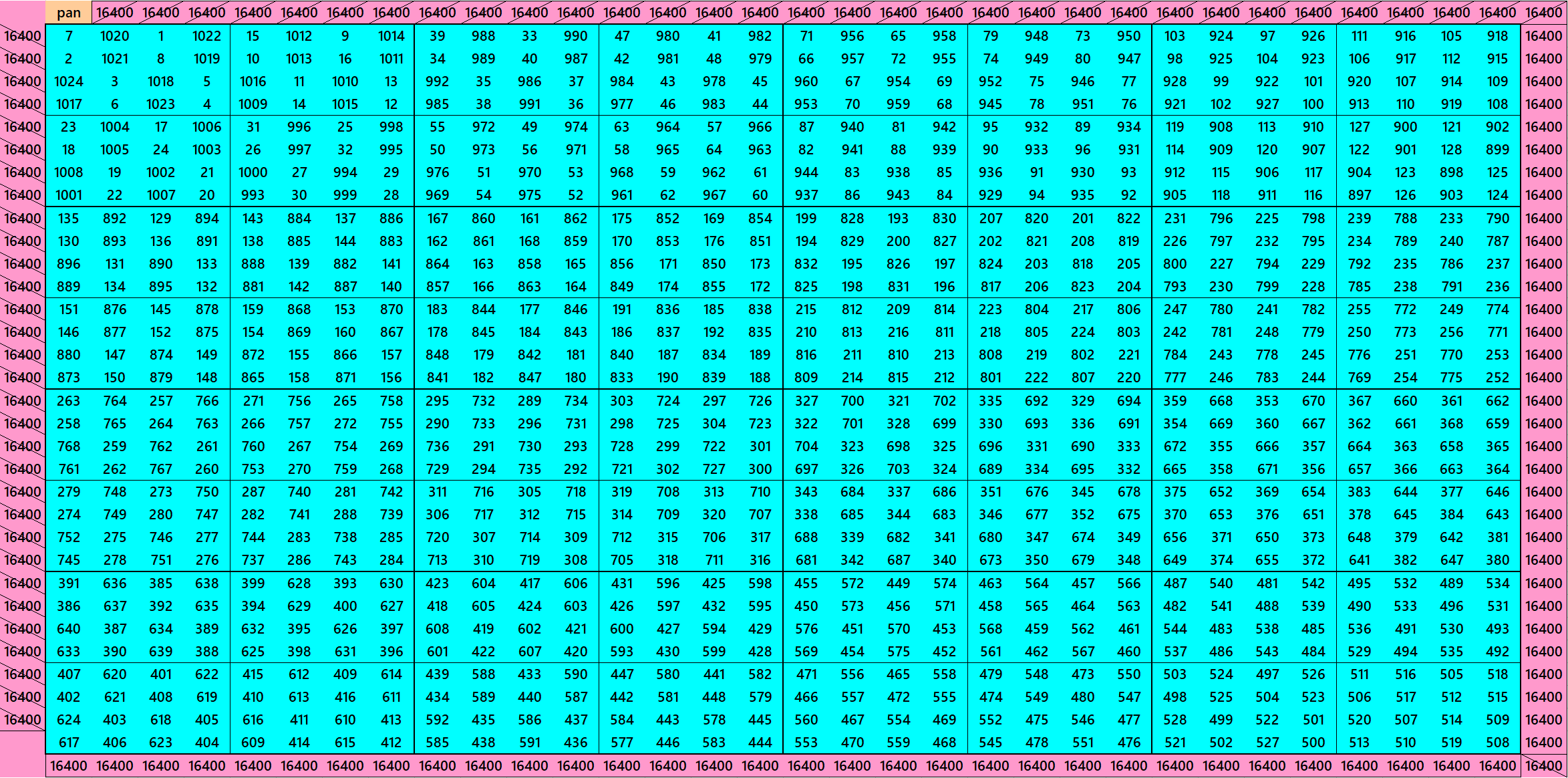
Pandiagonal Magic Square of Order 40

Excel file for Download
The excel file below for download contains pandiagonal magic squares multiples of order 8 from orders 8 to 120.

