It is well known that every magic square can be written as perfect square sum of entries. It is always possible with odd number entries starting from 1. In case of odd order magic squares we can also write with consecutive natural number entries. Still, it is unknown whether it is possible to even order magic squares. In case of odd order magic squares, still we can write them with minimum perfect square sum of entries. Based on this idea of perfect square sum of entries, we have written a magic square representing areas. It is done for the magic squares of orders 3 to 11. In all the cases, the area representations are more that one way. The whole work can be download at the following link:
- Inder J. Taneja, Creative Magic Squares: Area Representations, Zenodo, June 22, pp. 1-45, 2021, http://doi.org/10.5281/zenodo.5009224
- Inder J. Taneja, Creative Magic Squares: Area Representations With Fraction Numbers Entries (Version 2), Zenodo, August 16, 2021, 1-77, https://doi.org/10.5281/zenodo.5209502
See below examples:
Magic Squares of Order 3:
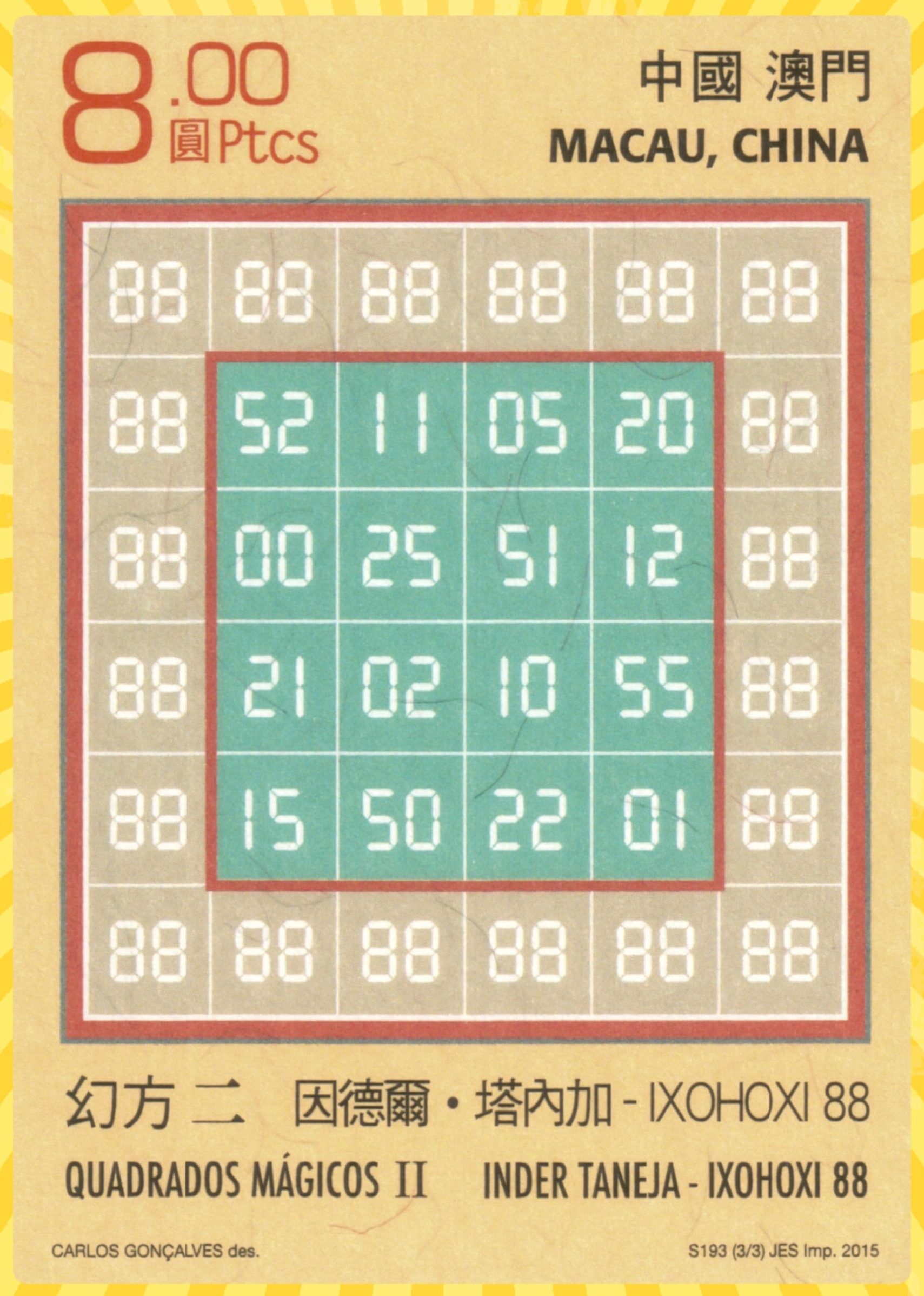
Magic Squares of Order 4:
Magic Squares of Order 4: Fraction Numbers Entries
Magic Squares of Order 5

Magic Squares of Order 6
Magic Squares of Order 6: Fraction Numbers Entries
Magic Squares of Order 7
Magic Squares of Order 8
Magic Squares of Order 8: Fraction Numbers Entries
Magic Squares of Order 9
Magic Squares of Order 10
Magic Squares of Order 10: Fraction Numbers Entries
Magic Squares of Order 11
More detailed number representations of each magic square are given in the following work for download:
- Inder J. Taneja, Creative Magic Squares: Area Representations, Zenodo, June 22, pp. 1-45, 2021, http://doi.org/10.5281/zenodo.5009224