Algebraic Cyclic, Flat and Cornered Striped Magic Squares of Even Orders from 4 to 20

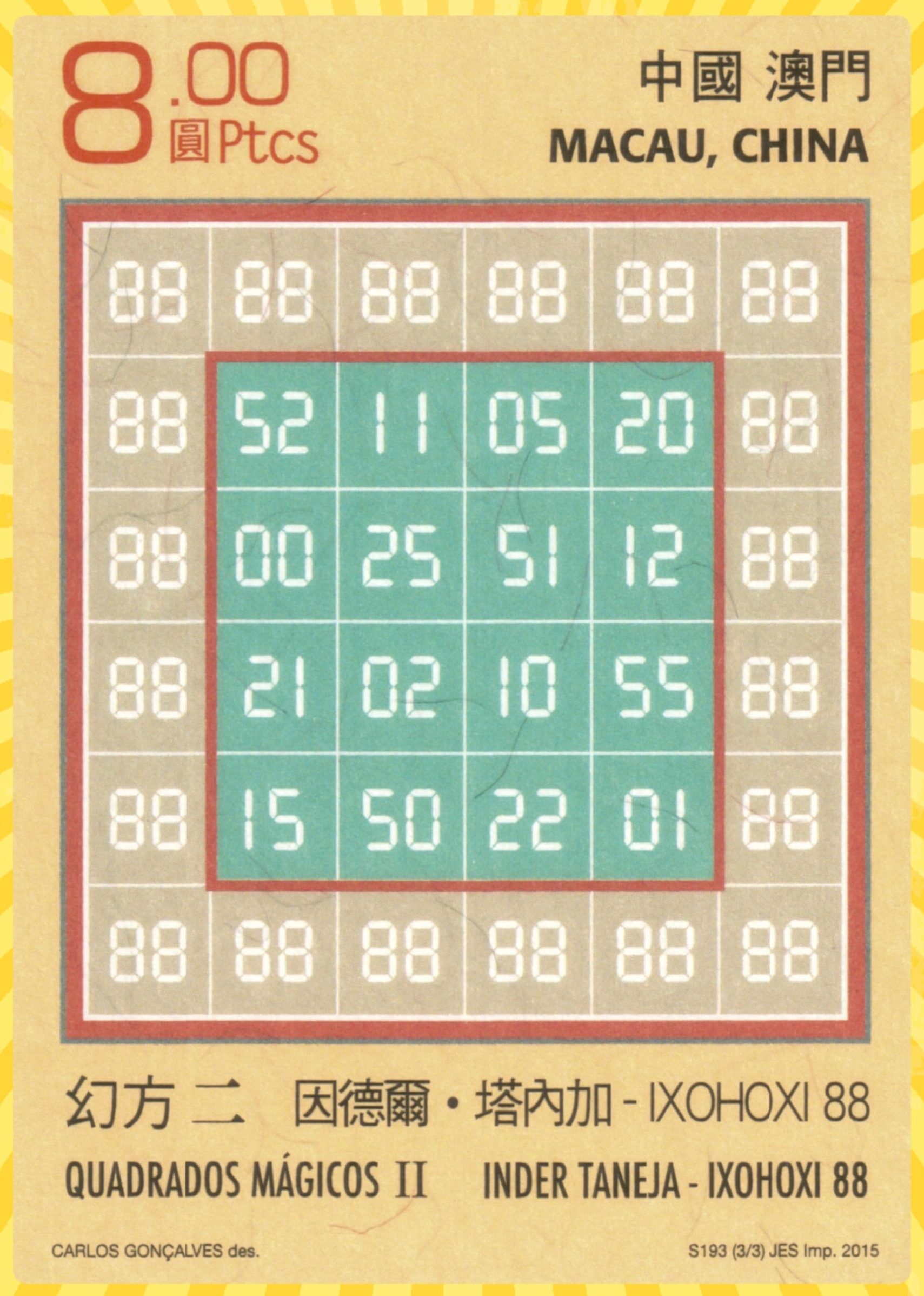
This work brings double-digit or double-layer strped algebraic magic squares of even orders 4 to 20 for reduced entries. The study striped magic squares of cyclic, Flat and Corner types. Sometimes, these types of magic squares, we call as self-made, beacause they are complete in themselves. Just choose the entries and magic sum, we always get a magic square. Whole the work is based on magic rectangles of equal width i.e., 2 and the change is always in the length. These kind of magic squares we call as striped magic squares. The idea of striped magic squares for sequential entries is already studied by the author in the following work.

We know that magic sum of a magic square of order n having 1 to n² number of entries is given by

S_nxn:= n*(1+n²)/2

In this work the entries are written as vaiables and their combinations. Instead of squential entries, we have non-sequential entries. These can be positive, negative or decimal numbers.

Whole work is also available at the following link:

Inder J. Taneja, Algebraic Cyclic, Flat and Cornered Striped Magic Squares for Even Orders from 4 to 20, Zenodo, December 02, 2025, pp. 1-58, https://doi.org/10.5281/zenodo.17793845.

Below are few examples of magic squares of even orders 4 to 20

Algebraic Striped Magic Squares of Order 4

Result 1: Striped Magic Square of Order 4

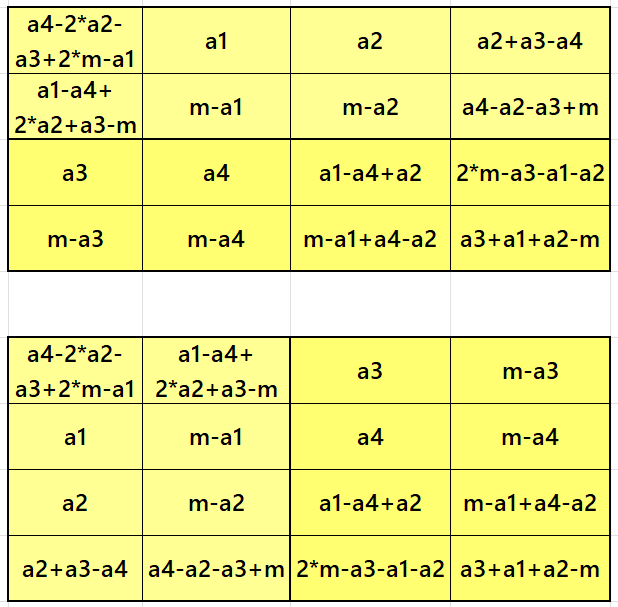
Above there are two ways of representing algebraic stripled magic square of order 4 where the strips are either in a horizonal way or in a veritical way. In both the situations, the result is always a magic square. Here we use on 4 entries instead of 16, where m is the width of the magic rectangle. See below some examples:

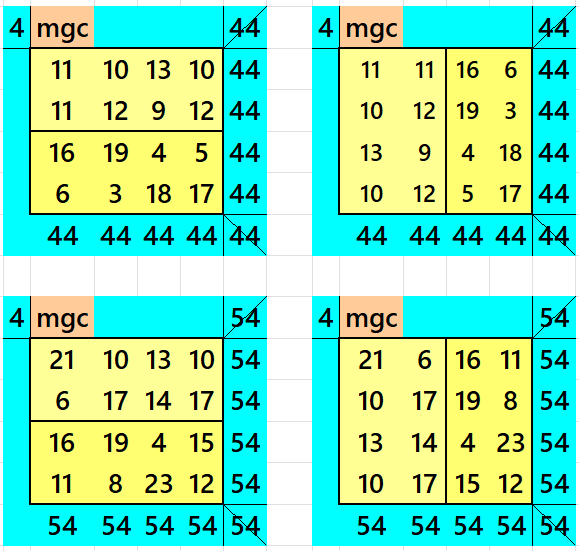
In the first case, the magic sum is S_4×4 := 44, m := 22.
In the second case, the magic sum is S_4×4 := 54, m := 27.

Algebraic Striped Magic Squares of Order 6

Result 2: Striped Magic Square of Order 6: First Type

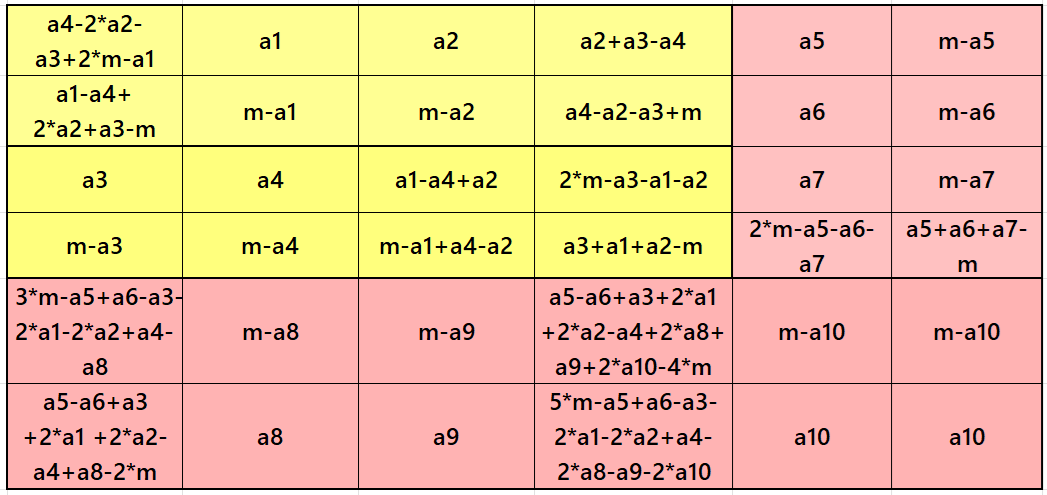
It is an algebraic cornered-type striped magic square of order 6, where there is a magic square of order 4 at the upper-left corner formed by two equal sums strips of order 2×4. The letter m represents the width of each strip. The lengths are of different order. The magic sum of order 6 is S_6×6:=3*m, where m is the width of the magic rectangles. Whole the magic square of order 6 is formed by 3 strips of order 2×4 and one strip of order 2×6. See below few examples:

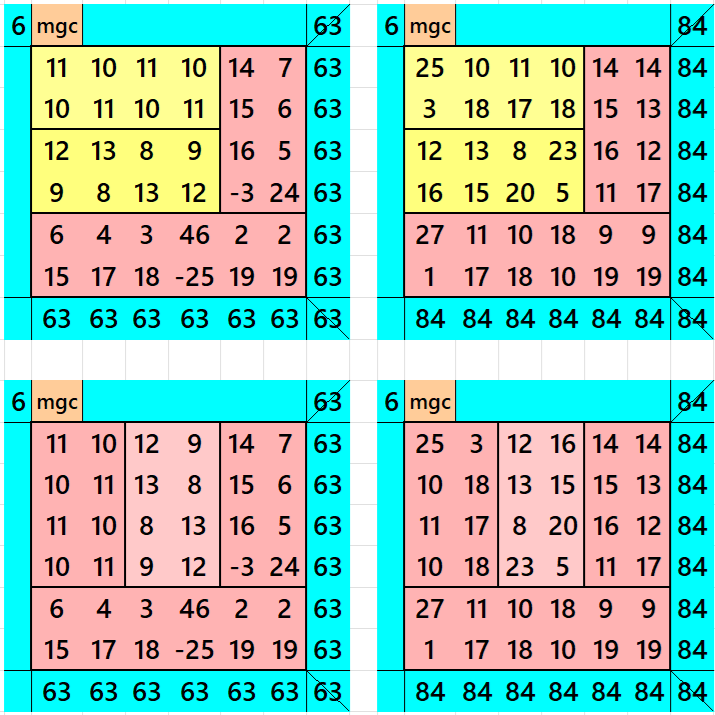
Above there are two ways of writing the algebraic striped magic square of order 6. The first way is of corner-type while the second one normal type. In both the cases the magic sums are:
First case:
First Example: S_6×6 := 63, S_4×4 := 42 and m := 21.
Second Example: S_6×6 := 84, S_4×4 := 56 and m := 28.
Second case:
First Example: S_6×6 := 63, S_4×4 := 42 and m := 21.
Second Example: S_6×6 := 84, S_4×4 := 56 and m := 28.

Result 3: Striped Magic Square of Order 6: Second Type

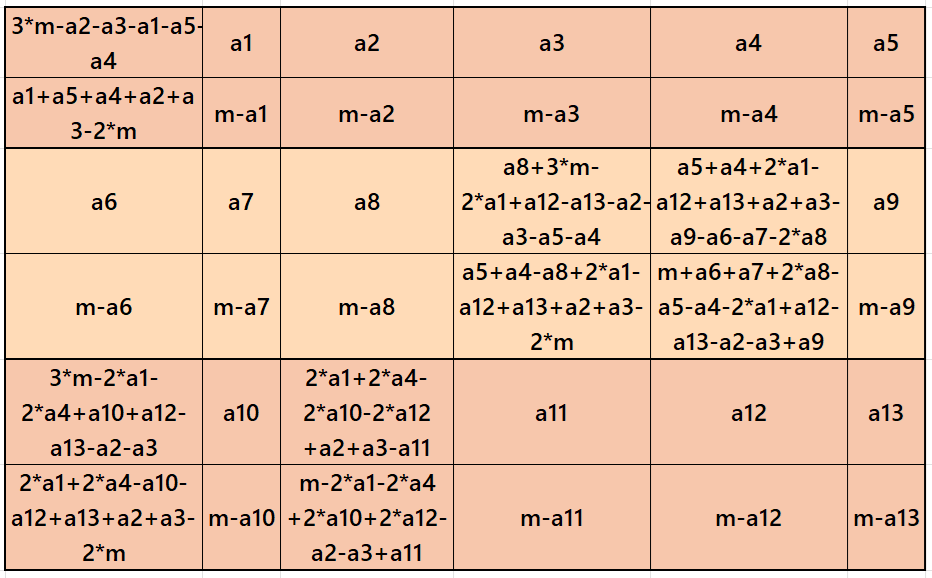
The magic square of order 6 is composed of three equal sums magic rectangles of order 2×6, where m is the width of the magic sum of magic rectange, and the magic sum of order 6 is given as S_3×3:=3*m. See below few examples:

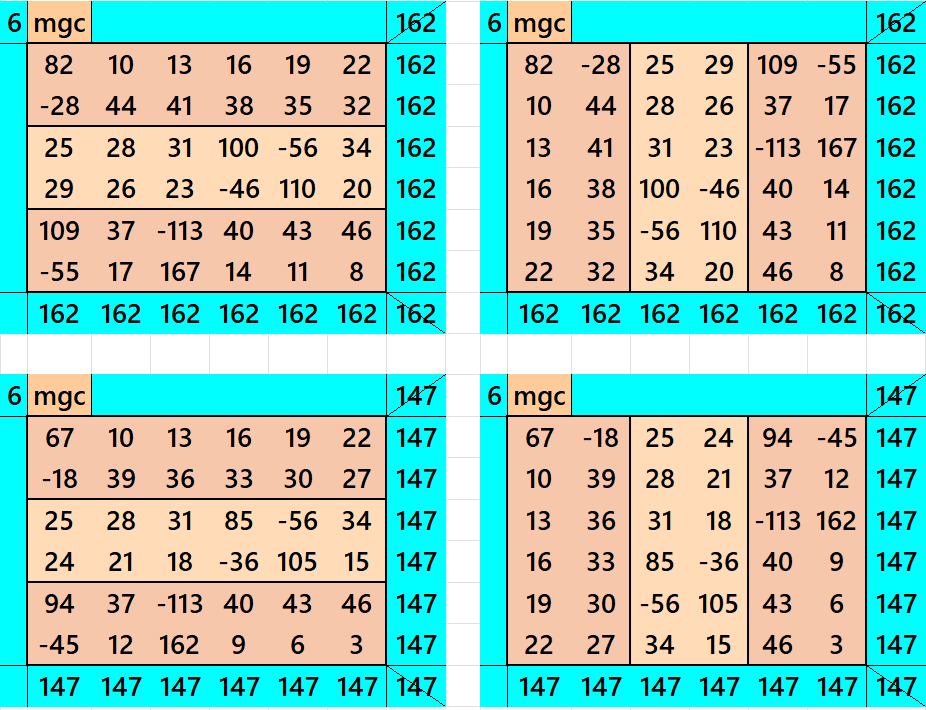
Above two examples are written two different forms. On is horzontally and another is veriically. But both are having the same entries. The magic sums in both the cases are:
First Example: S_6×6 := 162, MR_2×6 := 54×162 and m :=54.
Second Example: S_6×6 := 147, MR_2×6 := 49×147 and m :=49.

Algebraic Striped Magic Squares of Order 8

Below are three types of striped algebraic magic squares of order 8.

Result 4: Algebraic Striped Magic Squares of Order 8

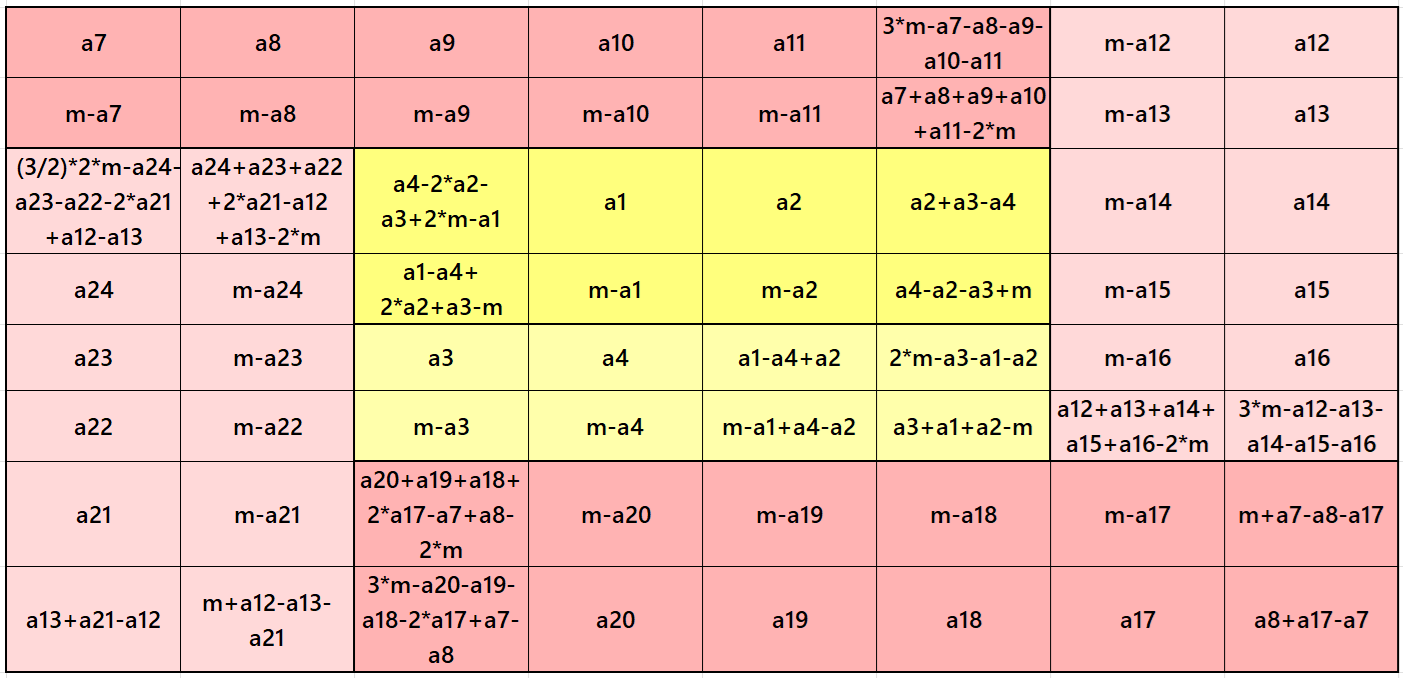
It is magic square of order 8 composed of four equal sums magic rectangles of orders 2×6 and embedded with a magic square of order 4. It is again composed of two equal sums magic rectangles of order 2×4. Since it is composed of all the strips of equal width, we can call is a algebraic striped magic square of order 8. Moreover, the external four strips are of equal sums, we can name is as a algebraic cyclic striped magic square of order 8. In this case the magic sums are S_4×4:=2*m and S_8×8:=4*m, where m is the width of the strip See below few examples:

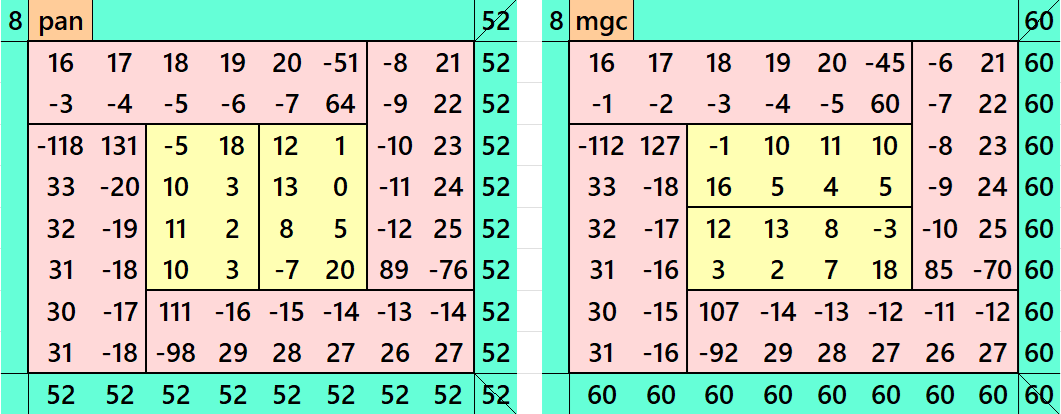
In the first example the magic sums are S_4X4 :=26, S_8×8 :=52 and m = 13.
In the second example the magic sums are S_4X4 :=30, S_8×8 :=60 and m=15.

Result 5: Algebraic Striped Magic Squares of Order 8

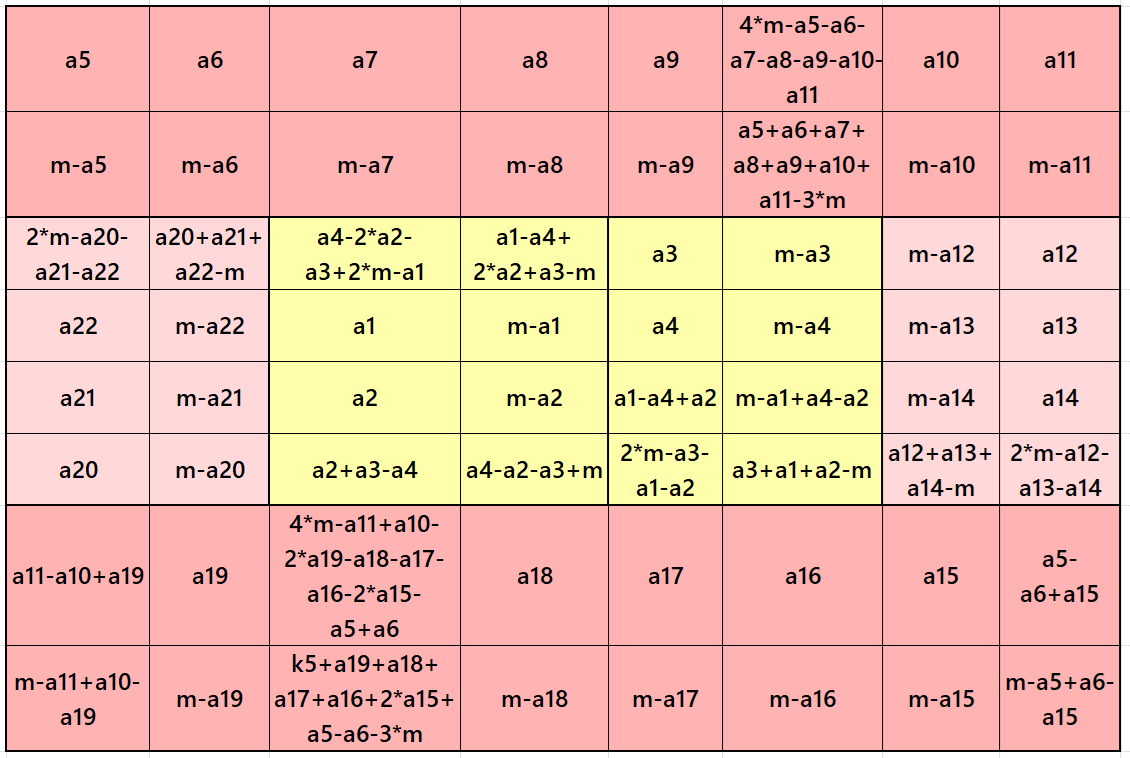
It is magic square of order 8 composed of two equal sums magic rectangles of orders 2×8 and two equal sums magic rectangles of orders 2×4 embedded with a magic square of order 4. It is again composed of two equal sums magic rectangles of order 2×4. Since it is composed of all the strips of equal width, we can call it as an algebraic striped magic square of order 8. Moreover, the external four strips are of different sizes, we can name this kind of magic square as an algebraic flat striped magic square of order 8. In this case the magic sums are S_4×4:=2*m and S_8×8:=4*m, where m is the width of the strip. See below two examples:

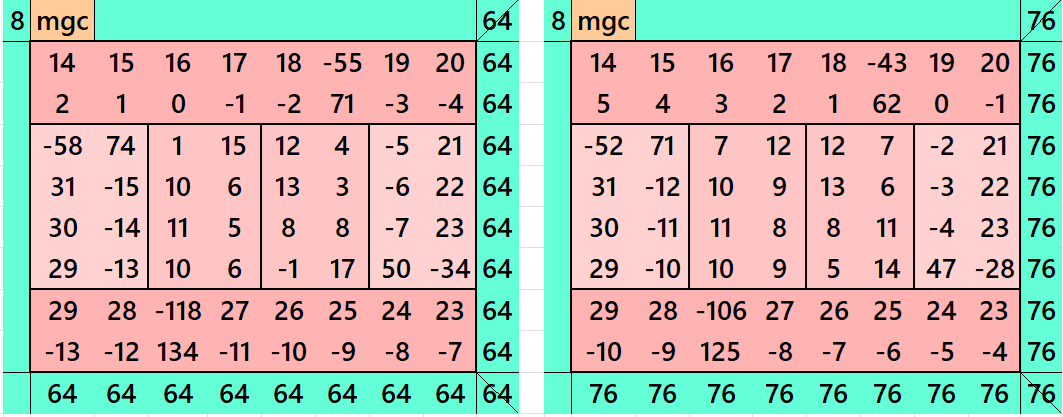
In the first example the magic sums are S_4X4 :=32, S_8×8 :=64 and m = 16.
In the second example the magic sums are S_4X4 :=38, S_8×8 :=76 and m=19.

Result 6: Algebraic Striped Magic Square of Order 8

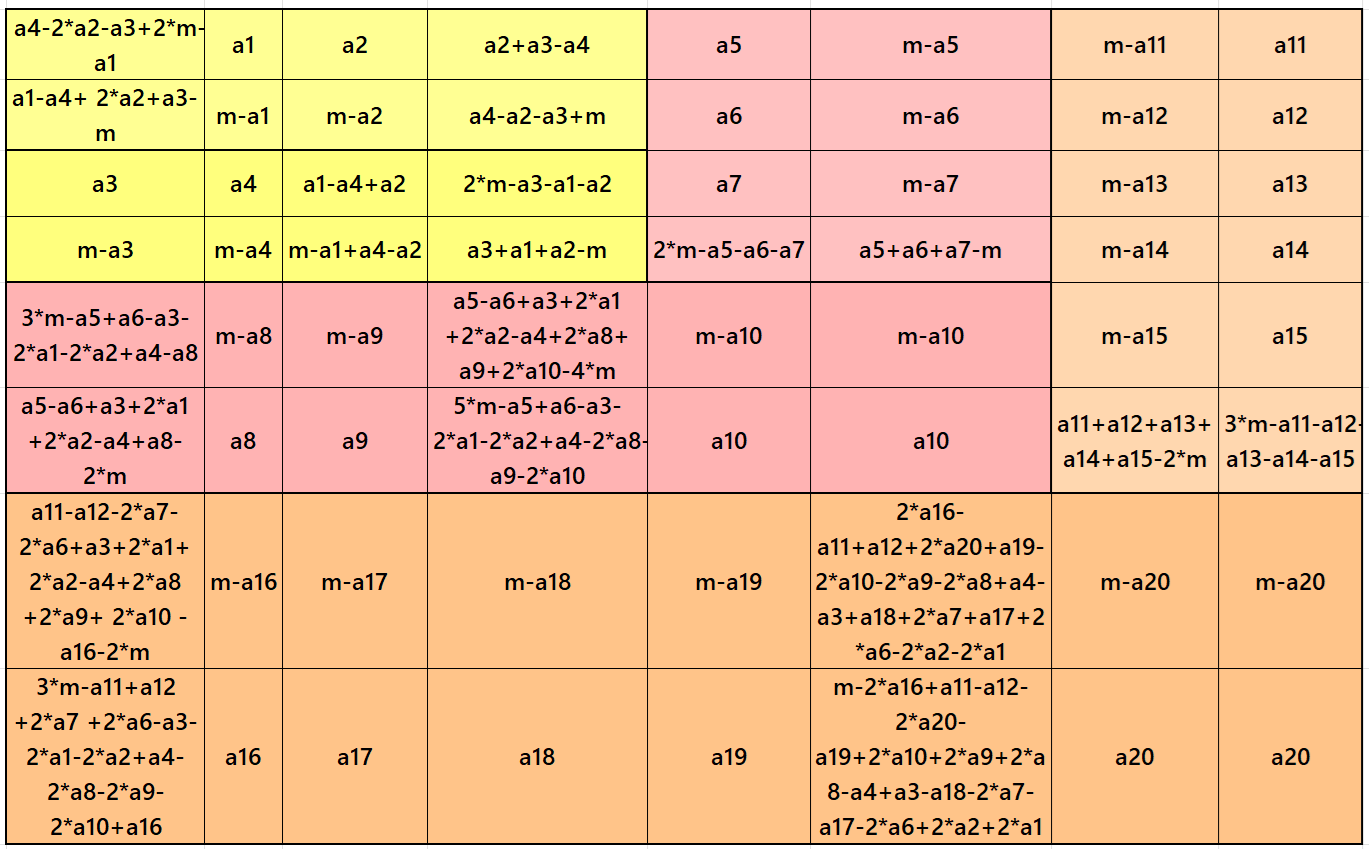
It is an algebraic cornered striped magic square of order 8, where the magic squares of order 4 and 6 are at the upper-left corner. In this case the magic sums are S_4×4:=2*m, S_6×6:=3*m, and S_8×8:=4*m, where m is the width of the strip. See below two examples:

In the first example the magic sums are S_4X4 :=62, S_6×6 :=93, S_8×8 :=124 and m:=31.
In the second example the magic sums are S_4X4 :=76, S_6×6 :=114, S_8×8 :=154 and m:=38.

Algebraic Striped Magic Squares of Order 10

Below are three types of algebraic striped magic squares of order 10.

Result 7: Algebraic Striped Magic Square of Order 10

It is an algebraic cyclic striped magic square of order 10 composed of four equal sums magic rectangles of orders 2×8 embedded with a magic square of order 6. It is again composed of three equal sums magic rectangles of order 2×6. In this case the magic sums are S_6×6:=3*m and S_10×10:=5*m, where m is the width of the strip See below few examples:

In the first example the magic sums are S_6×6 :=303, S_10×10 :=505 and m:=101.
In the second example the magic sums are S_6×6 :=348, S_10×10 :=580 and m:=116.

In the first example the magic sums are S_6×6 := 273, S_10×10 :=455 and m:=91.
In the second example the magic sums are S_6×6 :=354, S_10×10 :=590 and m:=118.

Result 8: Algebraic Striped Magic Squares of Order 10

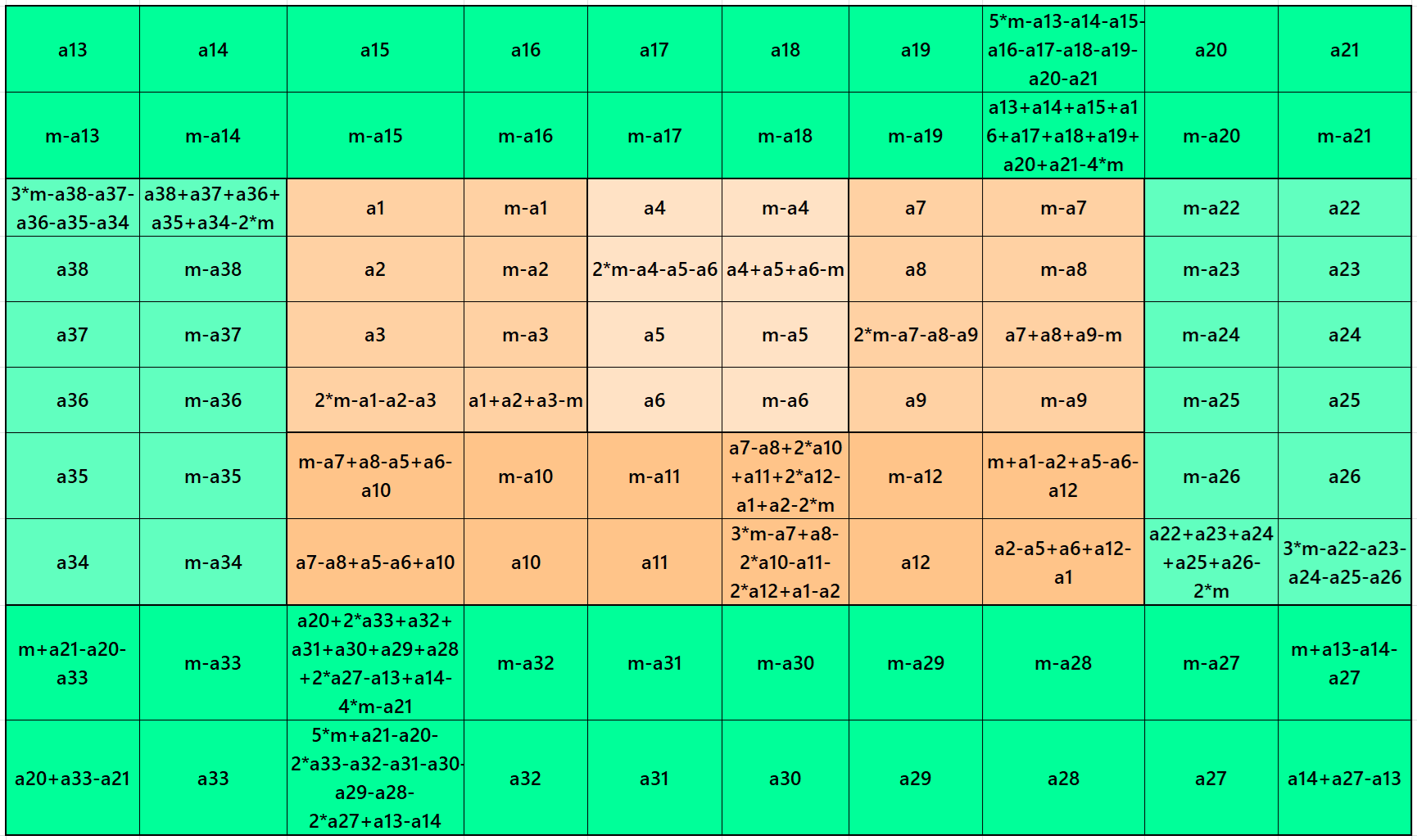
It is an algebraic flat striped magic square of order 10 composed of two equal sums magic rectangles of orders 2×10 and two magic rectangles of order 2×6 embedded with a magic square of order 6. It is again composed of three equal sums magic rectangles of order 2×4 and one magic rectangle of order 2×6. In this case the magic sums are S_6×6:=3*m and S_10×10:=5*m, where m is the width of the strip See below two examples:

In the first example the magic sums are S_6×6 := 273, S_10×10 :=455 and m:=91.
In the second example the magic sums are S_6×6 :=348, S_10×10 :=580 and m:=116.

n the first example the magic sums are S_6×6 := 273, S_10×10 :=455 and m:=91.
In the second example the magic sums are S_6×6 :=348, S_10×10 :=580 and m:=116.

In the first example the magic sums are S_6×6 := 246, S_10×10 :=410 and m:=82.
In the second example the magic sums are S_6×6 :=357, S_10×10 :=595 and m:=119.

Result 9: Algebraic Striped Magic Squares of Order 10

It is an algebraic cornered striped magic square of order 10, where the magic squares of order 4, 6 and 8 are at the upper-left corner. In this case the magic sums are S_4×4:=2*m, S_6×6:=3*m, S_8×8:=4*m and S_10×10:=5*m, where m is the width of the strip. See below two examples:

In the first example the magic sums are S_4×4 := 72, S_6×6 := 108, S_8×8 :=144 and S_10×10 :=180 and m:=36.
In the second example the magic sums are S_4×4 := 82, S_6×6 := 103, S_8×8 :=164 and S_10×10 :=205 and m:=82.

Algebraic Striped Magic Squares of Order 12

Below are three types of algebraic striped magic squares of order 12.

Result 10: Algebraic Striped Magic Squares of Order 12

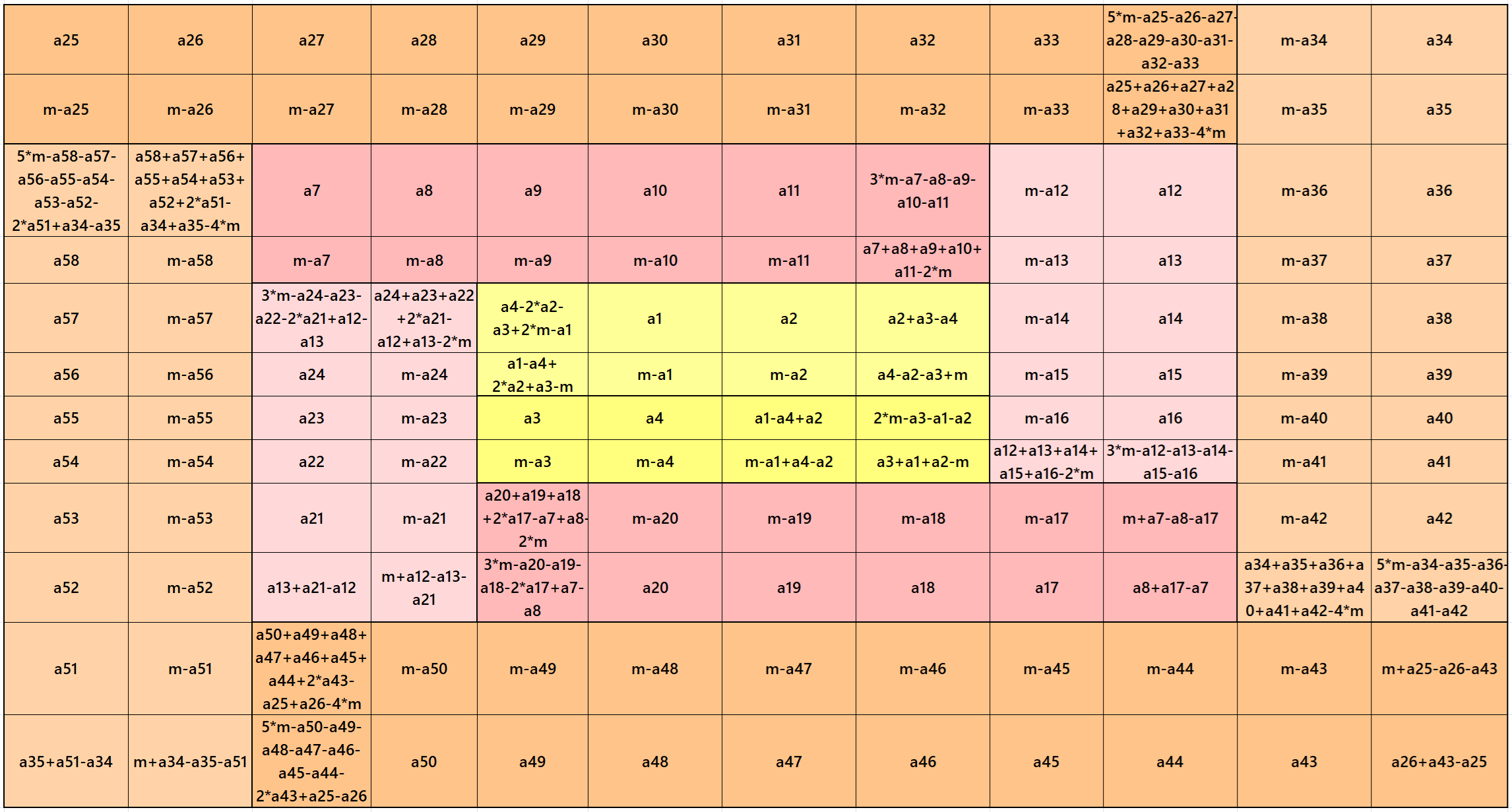
It is an algebraic cyclic striped magic square of order 12 composed of four equal sums magic rectangles of orders 2×10 embedded with a magic square of order 8 with four equal sums magic rectangles of order 2×6 having magic square of order 4 in the middle. It is again divided in two equal sum magic rectangles of order 2×4. In this case the magic sums are S_4×4:=2*m, S_8×8:=4*m and S_8×8:=12*m where m is the width of the strip or any of magic rectangle See below two examples:

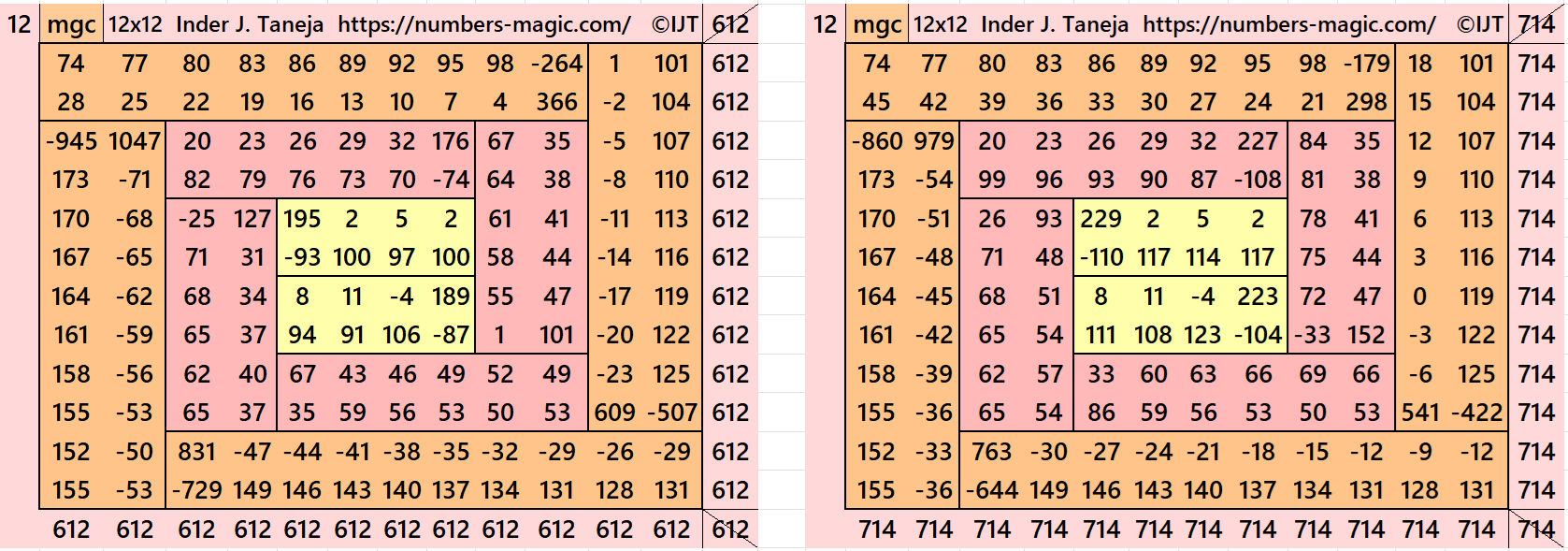
In the first example the magic sums are S_4×4 := 204, S_8×8 :=408 and S_12×12 :=612 and m:=102.
In the second example the magic sums are S_4×4 := 238, S_8×8 :=476 and S_12×12 :=714 and m:=119.

Result 11: Algebraic Striped Magic Squares of Order 12

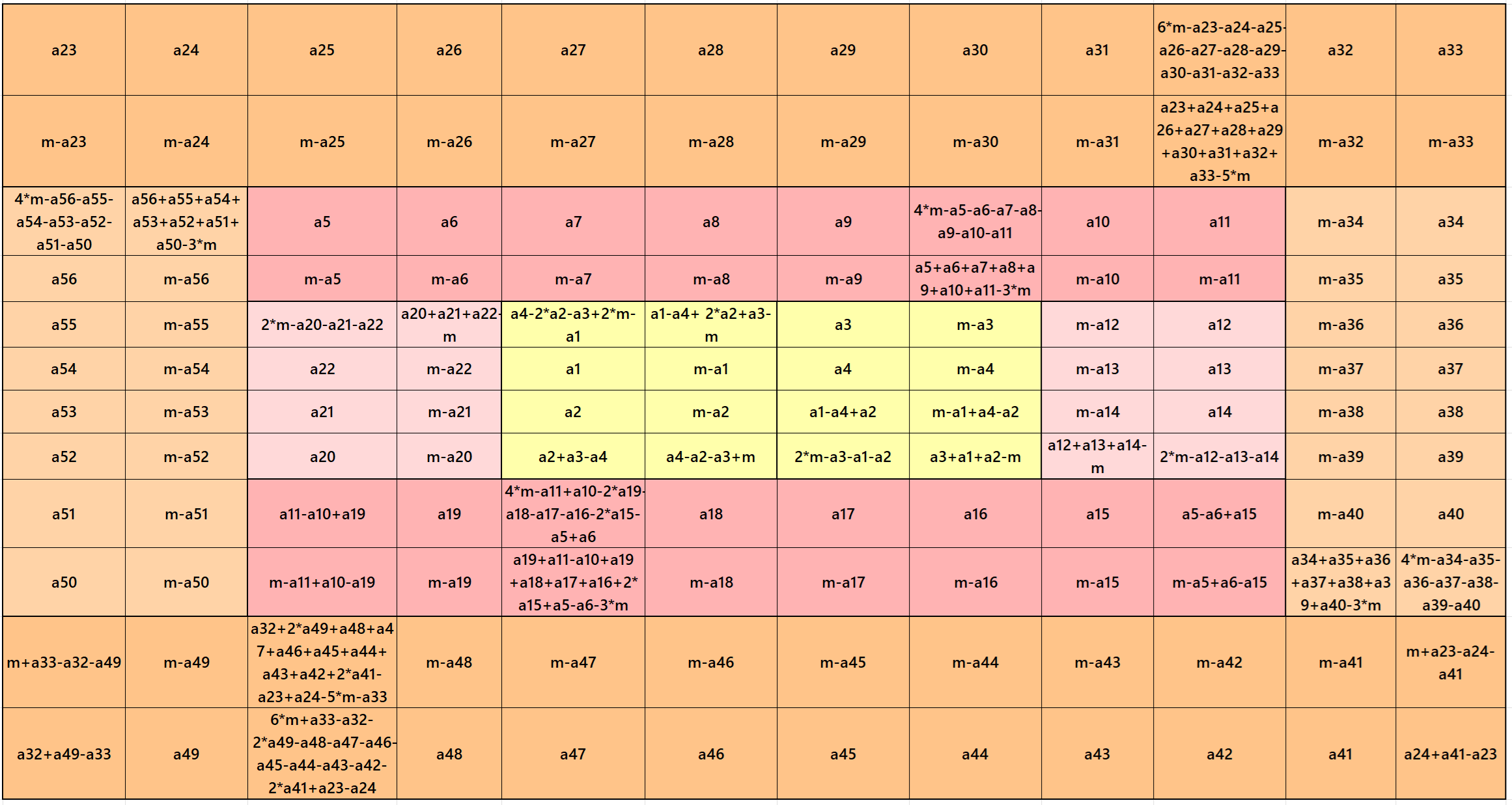
It is an algebraic flat striped magic square of order 12 composed of two equal sums magic rectangles of orders 2×12 and two magic rectangles of order 2×8 embedded with a magic square of order 8. It is again composed of two equal sums magic rectangles of orders 2×8 and two magic rectangles of order 2×4 embedded with a magic square of order 4. In this case the magic sums are S_4×4:=2*m, S_8×8:=4*m, and S_12×12:=6*m, where m is the width of the strip See below two examples:

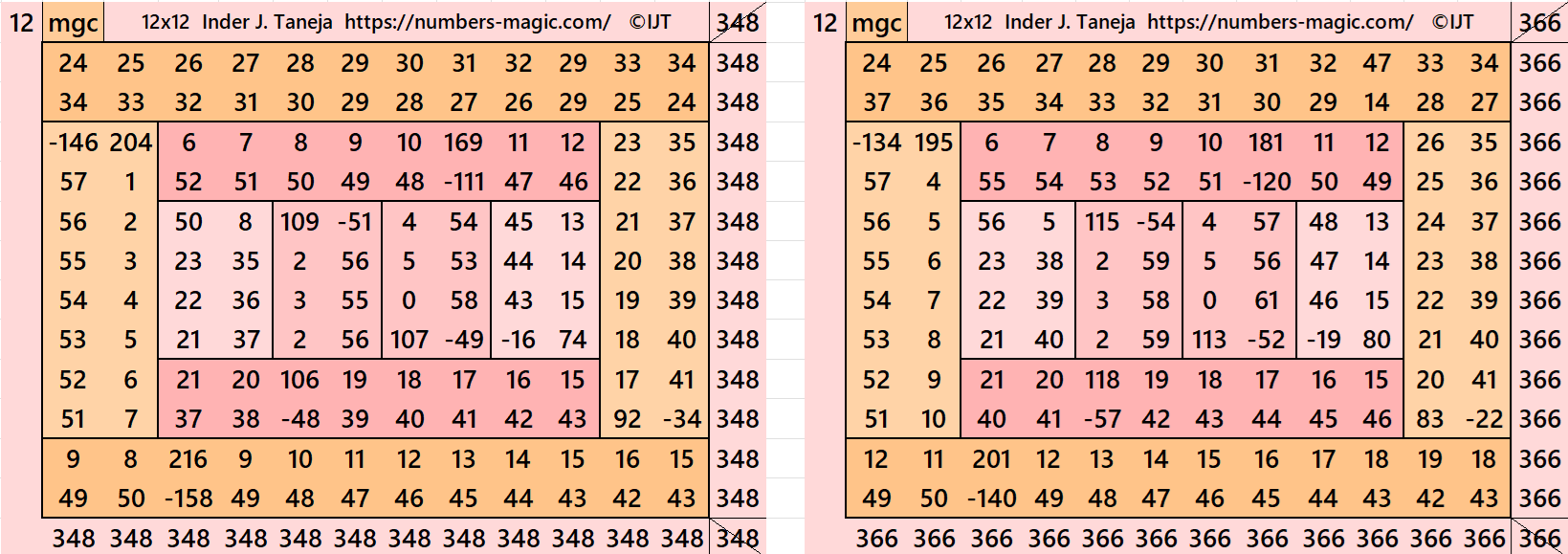
In the first example the magic sums are S_4×4 := 116, S_8×8 :=232 and S_12×12 :=348 and m:=58.
In the second example the magic sums are S_4×4 := 122, S_8×8 :=244 and S_12×12 :=366 and m:=61.

Result 12: Algebraic Striped Magic Squares of Order 12

It is an algebraic cornered striped magic square of order 12, where the magic squares of order 4, 6, 8 and 10 are at the upper-left corner. In this case the magic sums are S_4×4:=2*m, S_6×6:=3*m, S_8×8:=4*m, S_10×10:=5*m and S_12×12:=6*m, where m is the width of the strip. See below two examples:

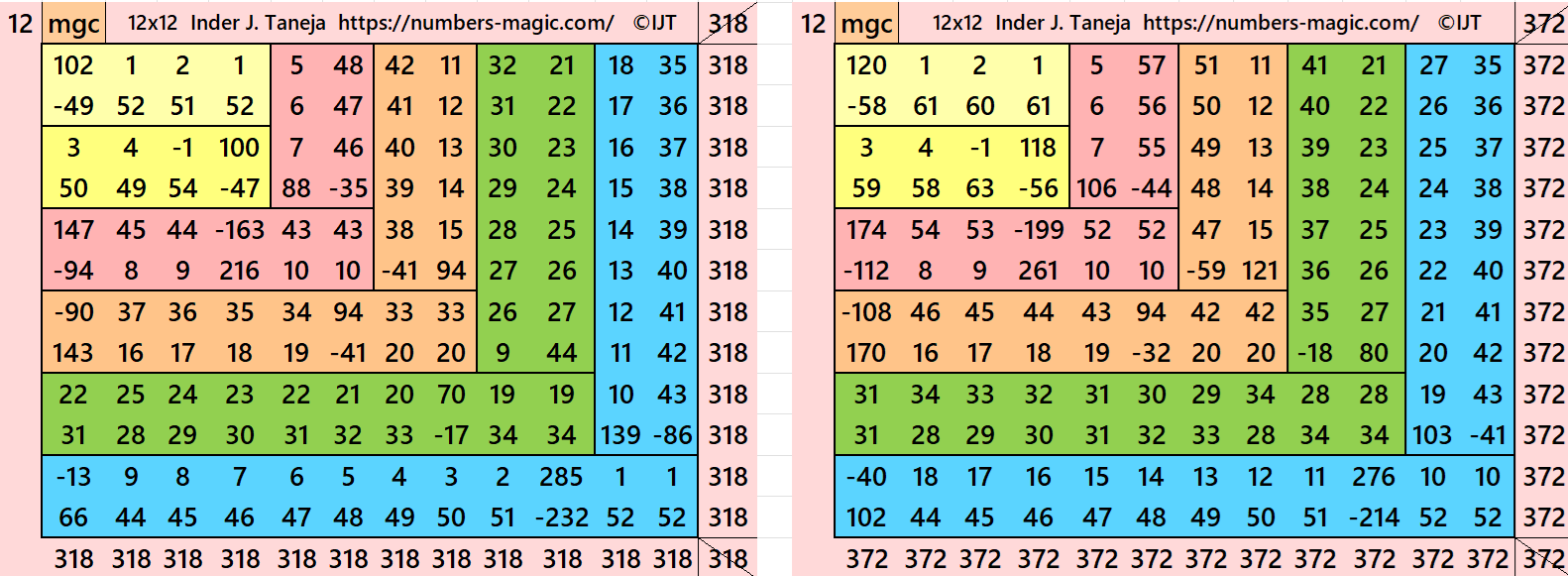
In the first example the magic sums are S_4×4 := 106, S_6×6 := 159, S_8×8 :=212, S_10×10 :=265, S_12×12 :=318 and m:=53.
In the second example the magic sums are S_4×4 := 124, S_6×6 := 186, S_8×8 :=244, S_10×10 :=310, S_12×12 :=372 and m:=62.

Algebraic Striped Magic Squares of Order 14

Below are three types of algebraic striped magic squares of order 14.

Result 13: Algebraic Striped Magic Squares of Order 14

It is an algebraic cyclic striped magic square of order 14 composed of four equal sums magic rectangles of orders 2×12 embedded with a magic square of order 10. It is again composed of four equal sums magic rectangles of orders 2×8 embedded with a magic square of order 6. It is again composed of three equal sums magic rectangles of order 2×6. In this case the magic sums are S_6×6:=3*m, S_10×10:=5*m and S_14×14:=7*m, where m is the width of the strip. See below two examples:

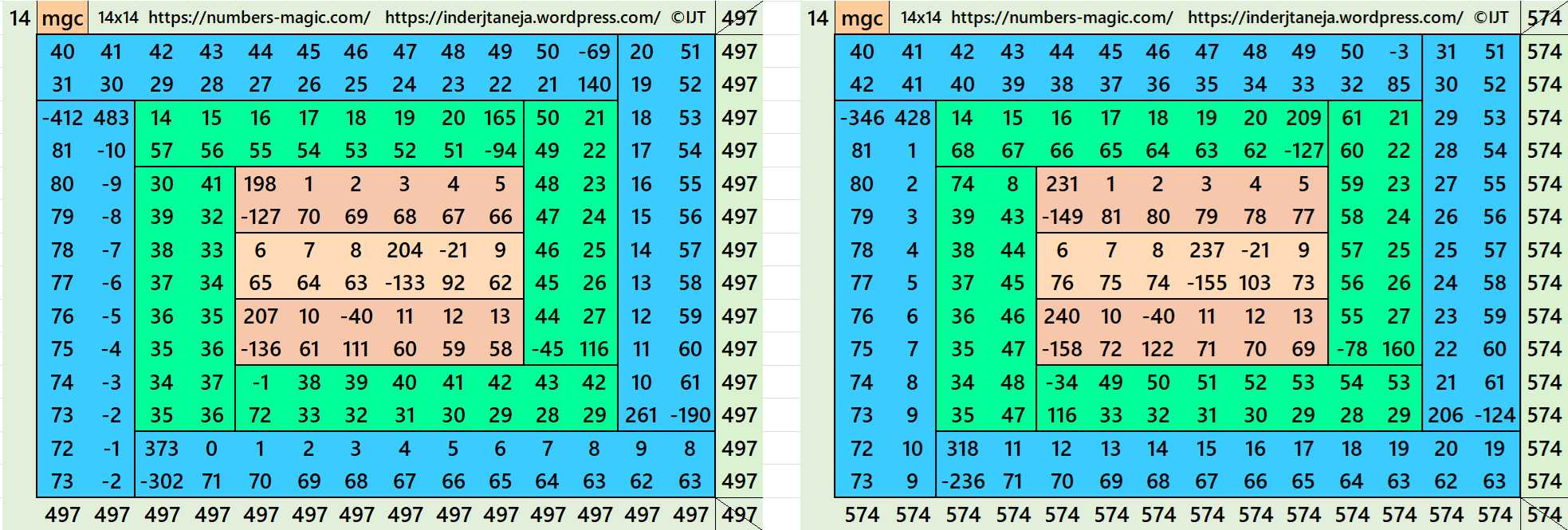
In the first example the magic sums are S_6×6 := 213, S_10×10 :=355 and S_14×14 :=497 and m:=71.
In the second example the magic sums are S_6×6 := 246, S_10×10 :=410 and S_14×14 :=574 and m:=82.

Result 14: Algebraic Striped Magic Squares of Order 14

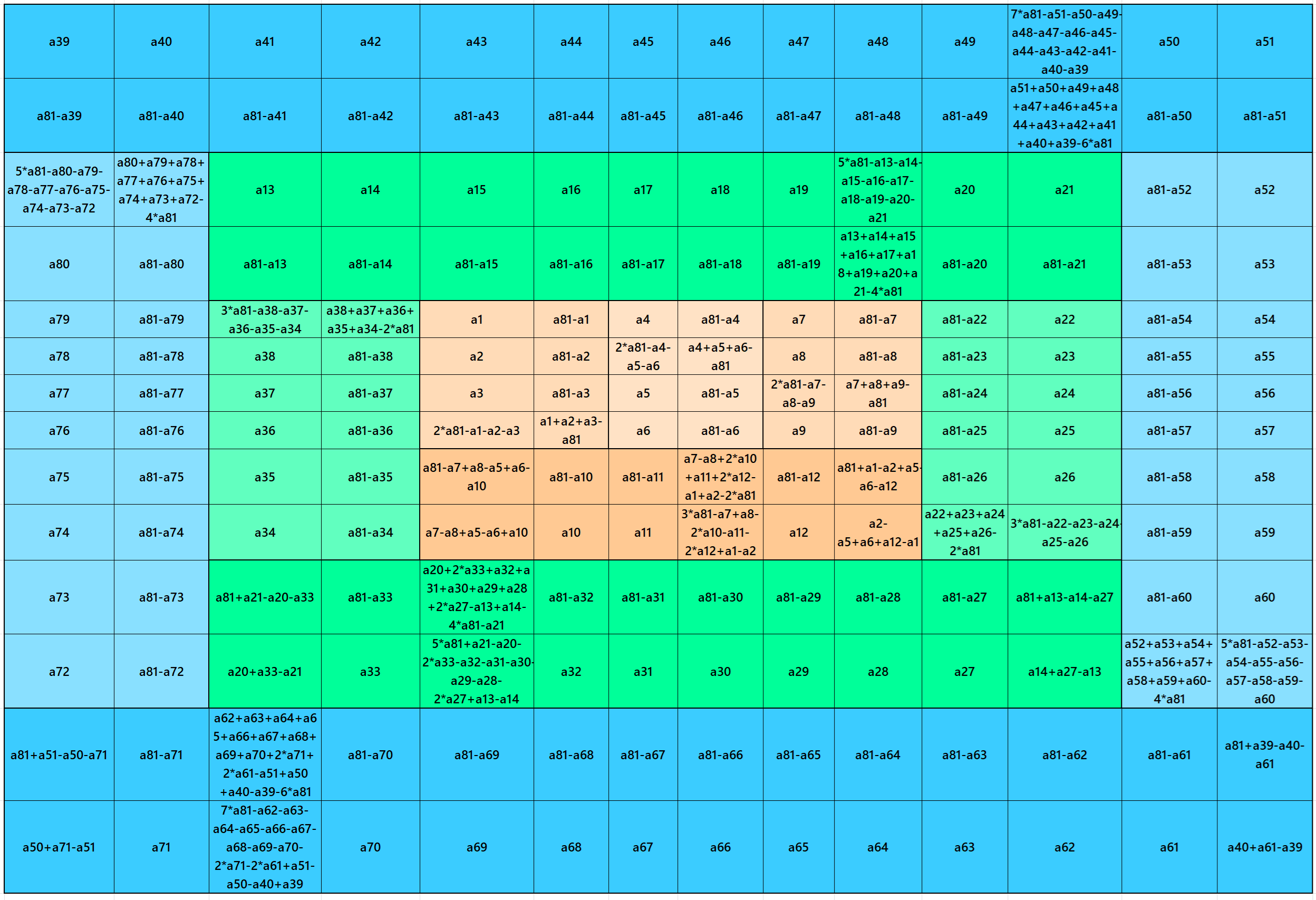
It is an algebraic flat striped magic square of order 14 composed of two equal sums magic rectangles of orders 2×14 and two magic rectangles of order 2×10 embedded with a magic square of order 10. It is again composed two equal sums magic rectangles of orders 2×10 and two magic rectangles of order 2×6 embedded with a magic square of order 6. It is again composed of three equal sums magic rectangles of order 2×4 and one magic rectangle of order 2×6. In this case the magic sums are S_6×6:=3*m and S_10×10:=5*m and S_14×14:=7*m, where m is the width of the strip See below two examples:

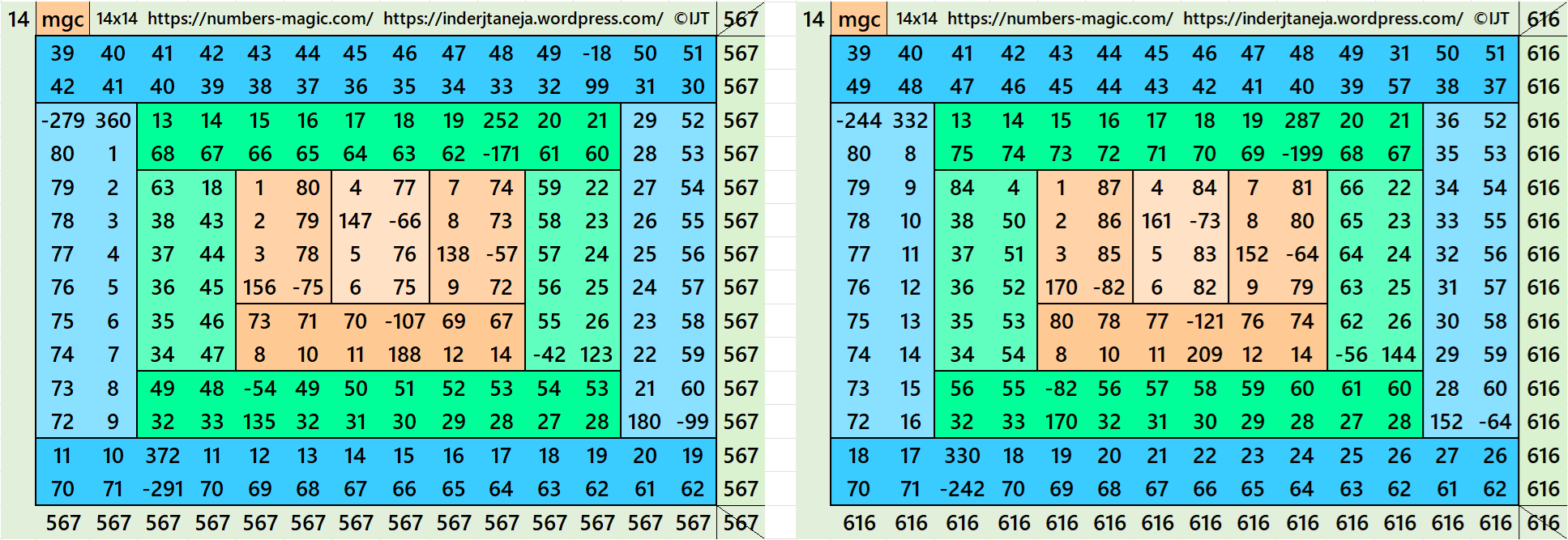
In the first example the magic sums are S_6×6 := 243, S_10×10 :=405 and S_14×14 :=567 and m:=81.
In the second example the magic sums are S_6×6 := 248, S_10×10 :=440 and S_14×14 :=574 and m:=88.

Result 15: Algebraic Striped Magic Squares of Order 14

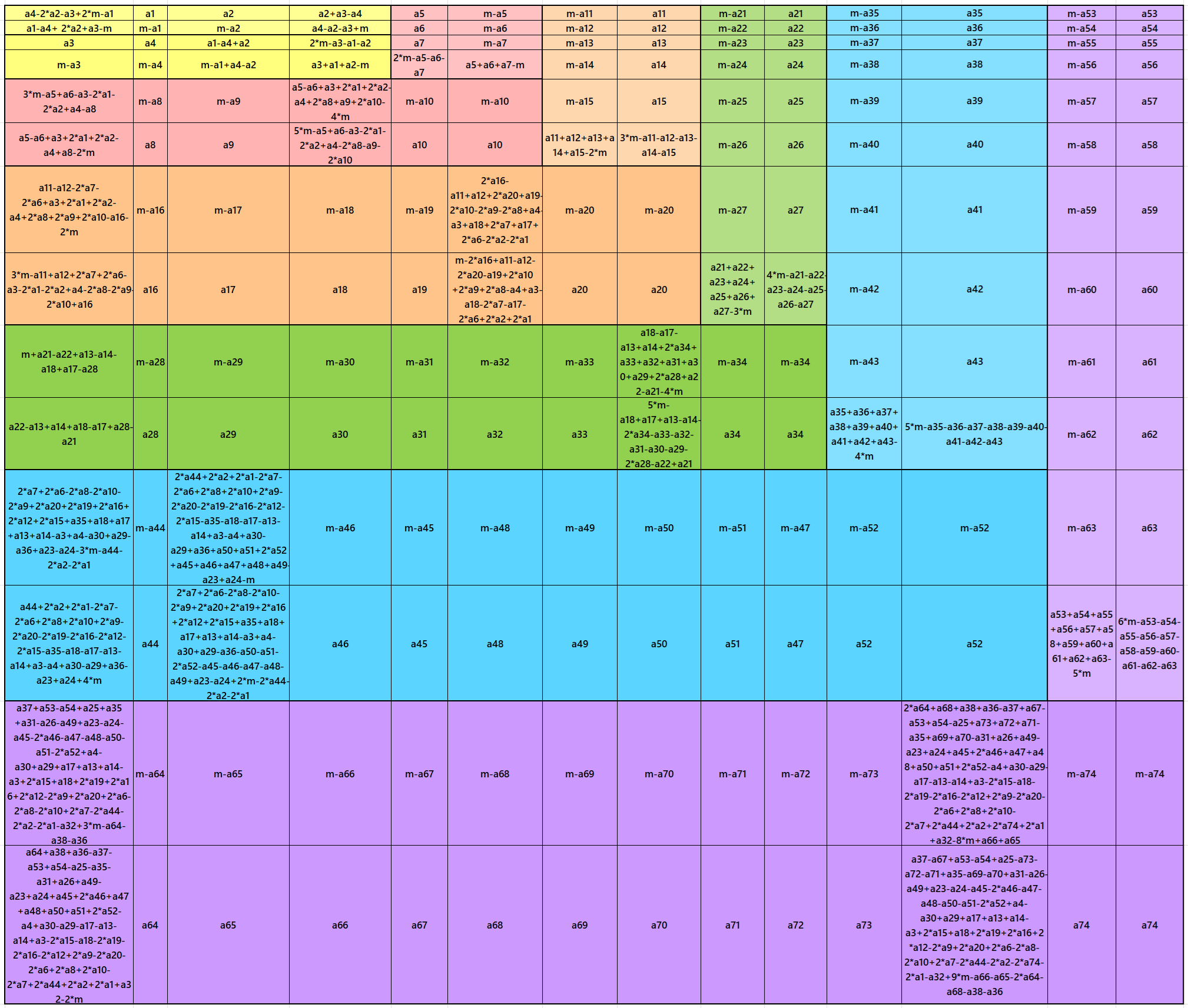
It is an algebraic striped cornered magic square of order 14, where the magic squares of order 4, 6, 8, 10 and 12 are at the upper-left corner. In this case the magic sums are S_4×4:=2*m, S_6×6:=3*m, S_8×8:=4*m S_10×10:=5*m, S_12×12:=6*m and S_14×14:=7*m,, where m is the width of the strip. See below two examples:

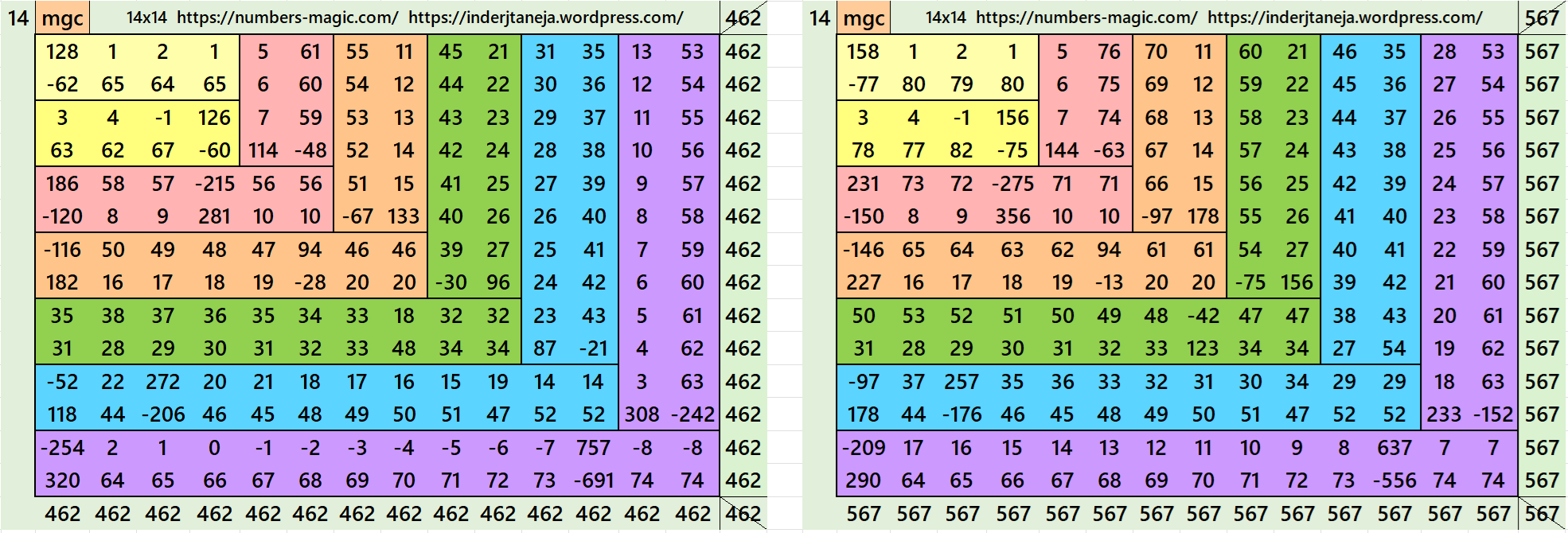
In the first example the magic sums are S_4×4 := 132, S_6×6 := 198, S_8×8 :=264, S_10×10 :=330, S_12×12 :=396, S_14×14 :=462 and m:=66.
In the second example the magic sums are S_4×4 := 162, S_6×6 := 243, S_8×8 :=244, S_10×10 :=405, S_12×12 :=486, S_14×14 :=567 and m:=81.

Algebraic Striped Magic Squares of Order 16

Below are three types of algebraic striped magic squares of order 16.

Result 16: Algebraic Striped Cyclic Magic Squares of Order 16

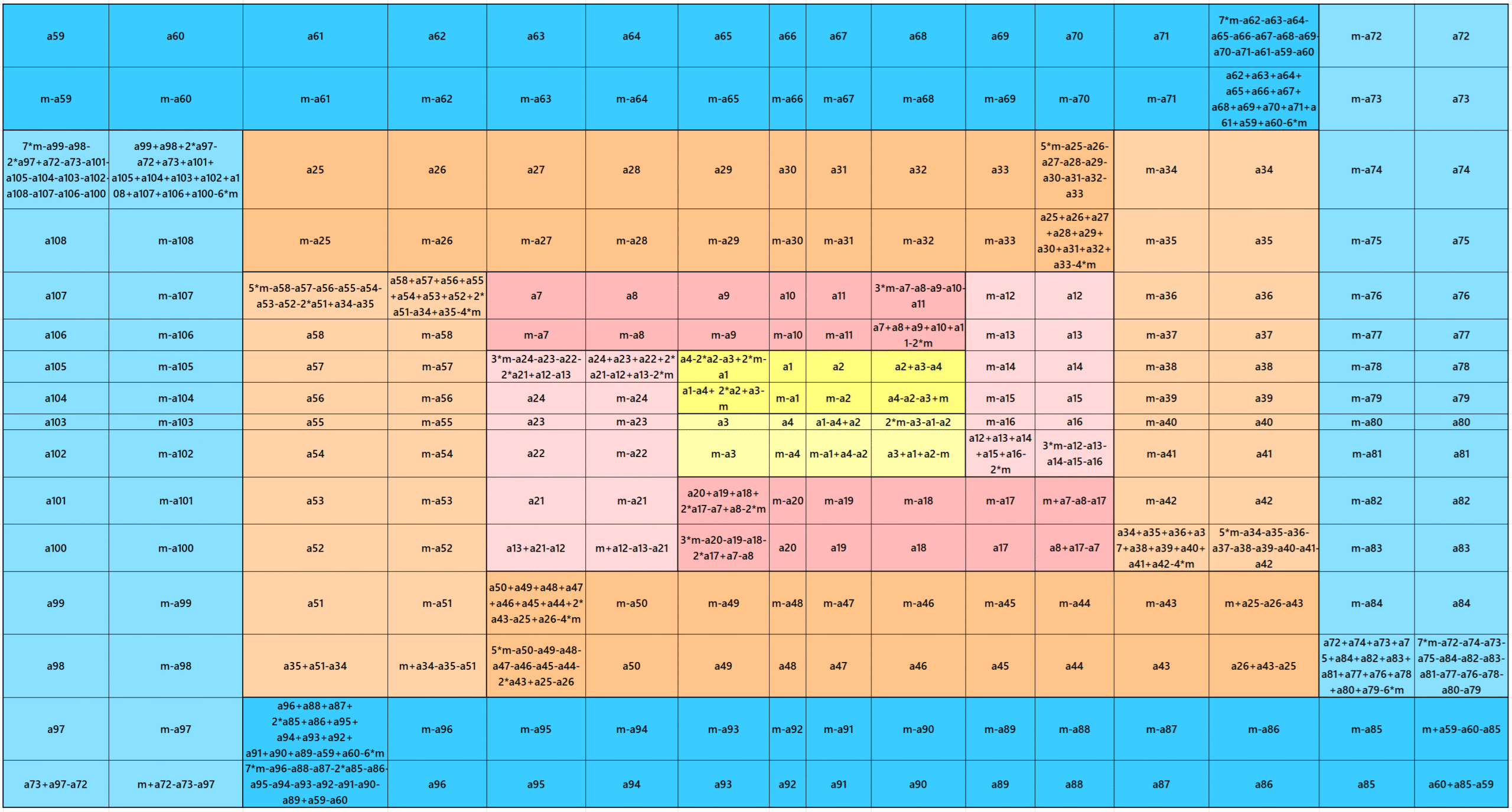
It is an algebraic cyclic striped magic square of order 16 composed of four equal sums magic rectangles of orders 2×14 embedded with a magic square of order 12. It is again composed of four equal sums magic rectangles of orders 2×10 embedded with a magic square of order 8. It is again composed of four equal sums magic rectangles of orders 2×6 embedded with a magic square of order 4. This magic square of order 4 is with equal sums two magic rectangles of order 2×4. In this case the magic sums are S_4×4:=2*m, S_8×8:=4*m, S_12×12:=6*m and S_16×16:=8*m, where m is the width of the strip. See below two examples:

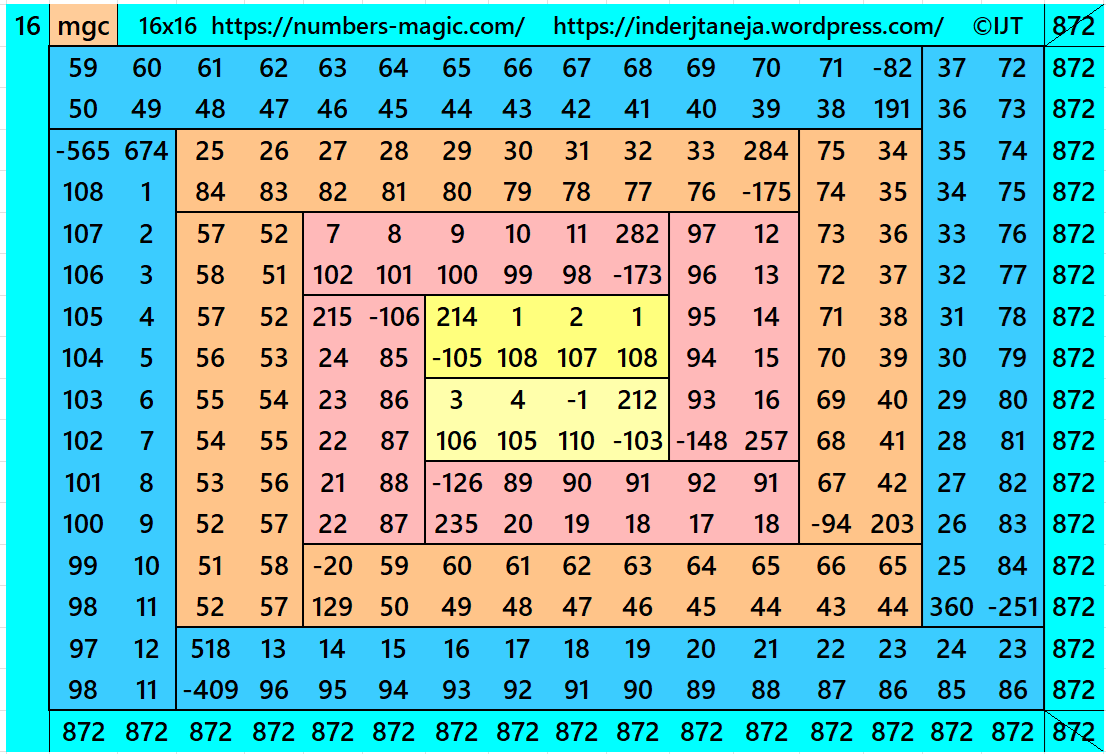
In this example the magic sums are S_4×4:=218, S_8×8:=436, S_12×12:=654, S_16×16:=872 and m:=109.

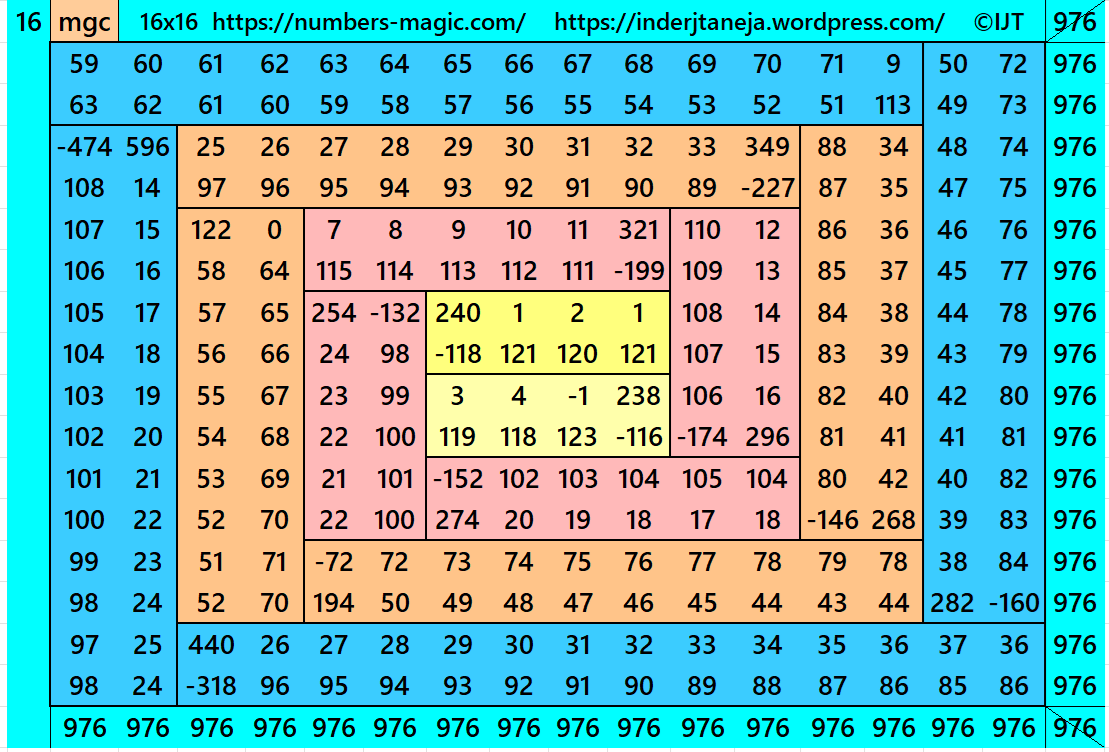
In this example the magic sums are S_4×4:=244, S_8×8:=488, S_12×12:=732, S_16×16:= 976 and m:=122

Result 17: Algebraic Striped Flat Magic Squares of Order 16

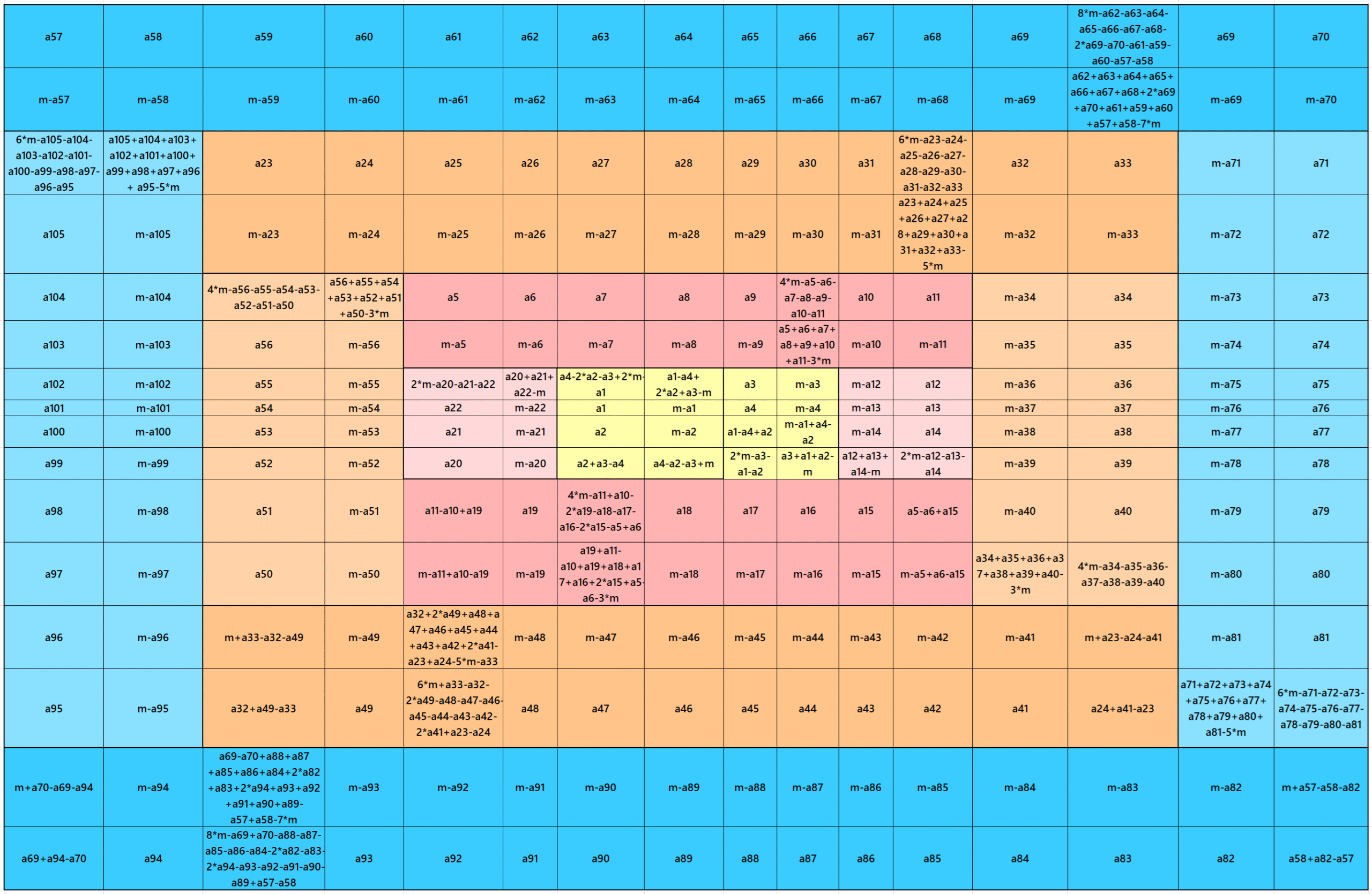
It is an algebraic flat striped magic square of order 16 composed of two equal sums magic rectangles of orders 2×16 and two magic rectangles of order 2×12 embedded with a magic square of order 12. It is again composed of two equal sums magic rectangles of orders 2×12 and two magic rectangles of order 2×8 embedded with a magic square of order 8. It is again composed of two equal sums magic rectangles of orders 2×8 and two magic rectangles of order 2×4 embedded with a magic square of order 4. It is again composed of two equal sums magic rectangles of order 2×4. In this case the magic sums are S_4×4:=2*m, S_8×8:=4*m, S_12×12:=6*m and S_16×16:=8*m, where m is the width of the strip. See below two examples:

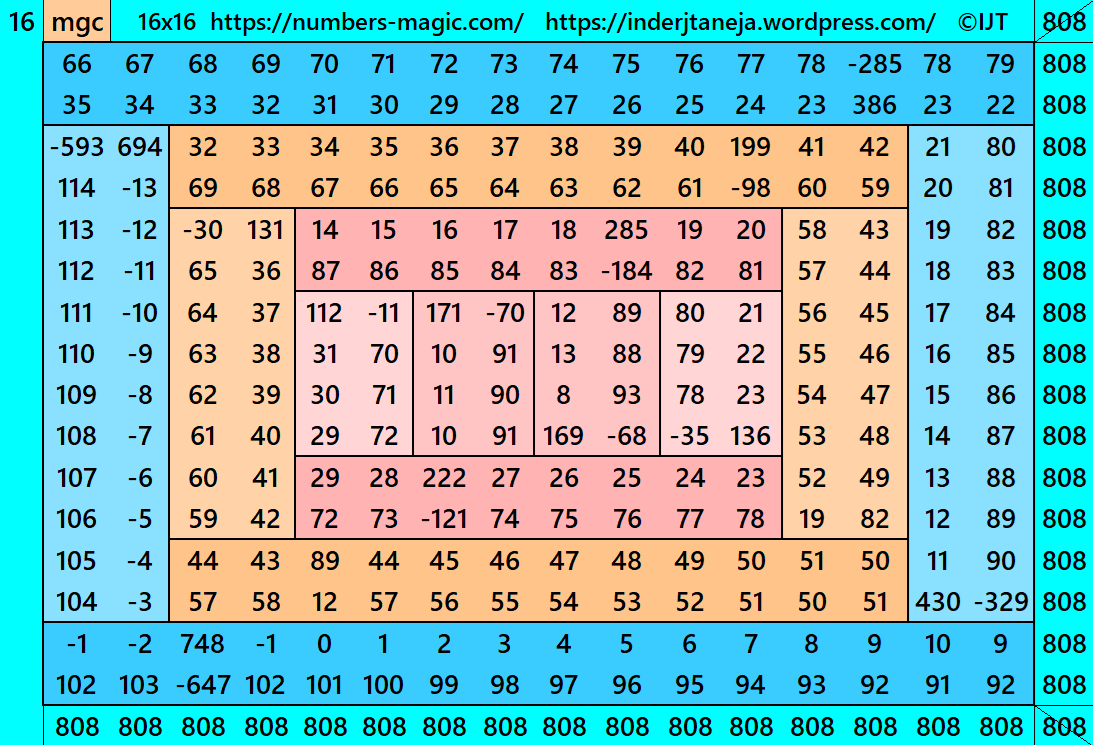
In this example the magic sums are S_4×4:=202, S_8×8:=404, S_12×12:=606, S_16×16:=808 and m:=101.

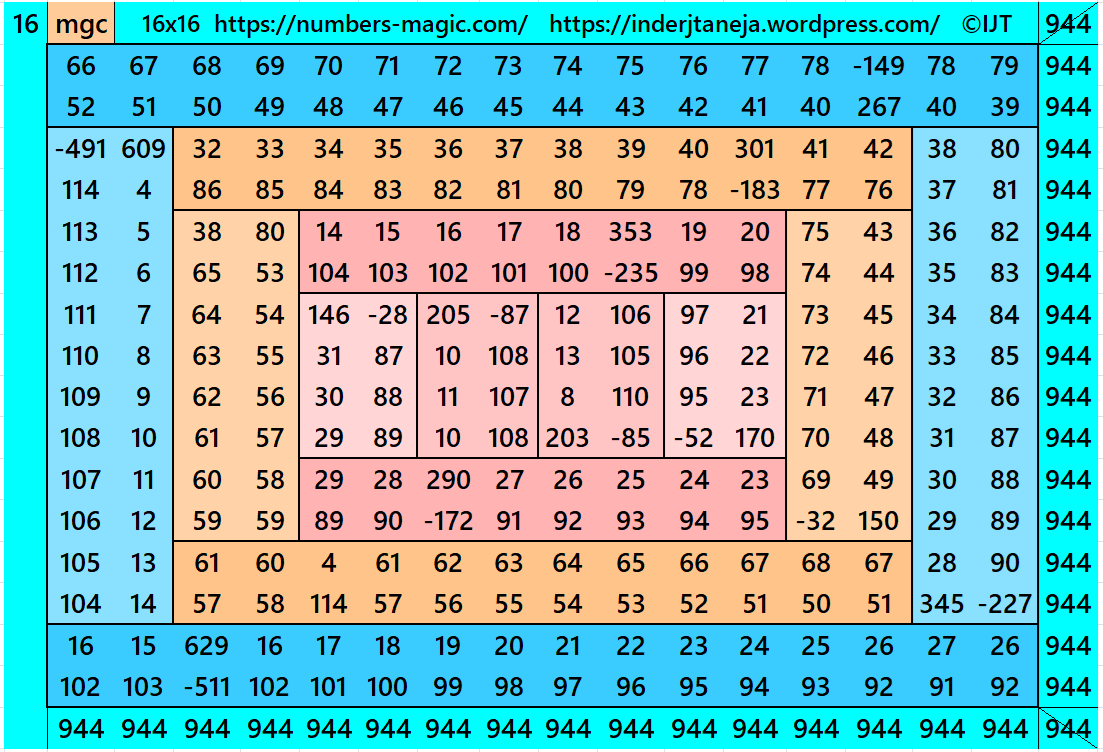
In this example the magic sums are S_4×4:=236, S_8×8:=472, S_12×12:=708, S_16×16:=944 and m:=118.

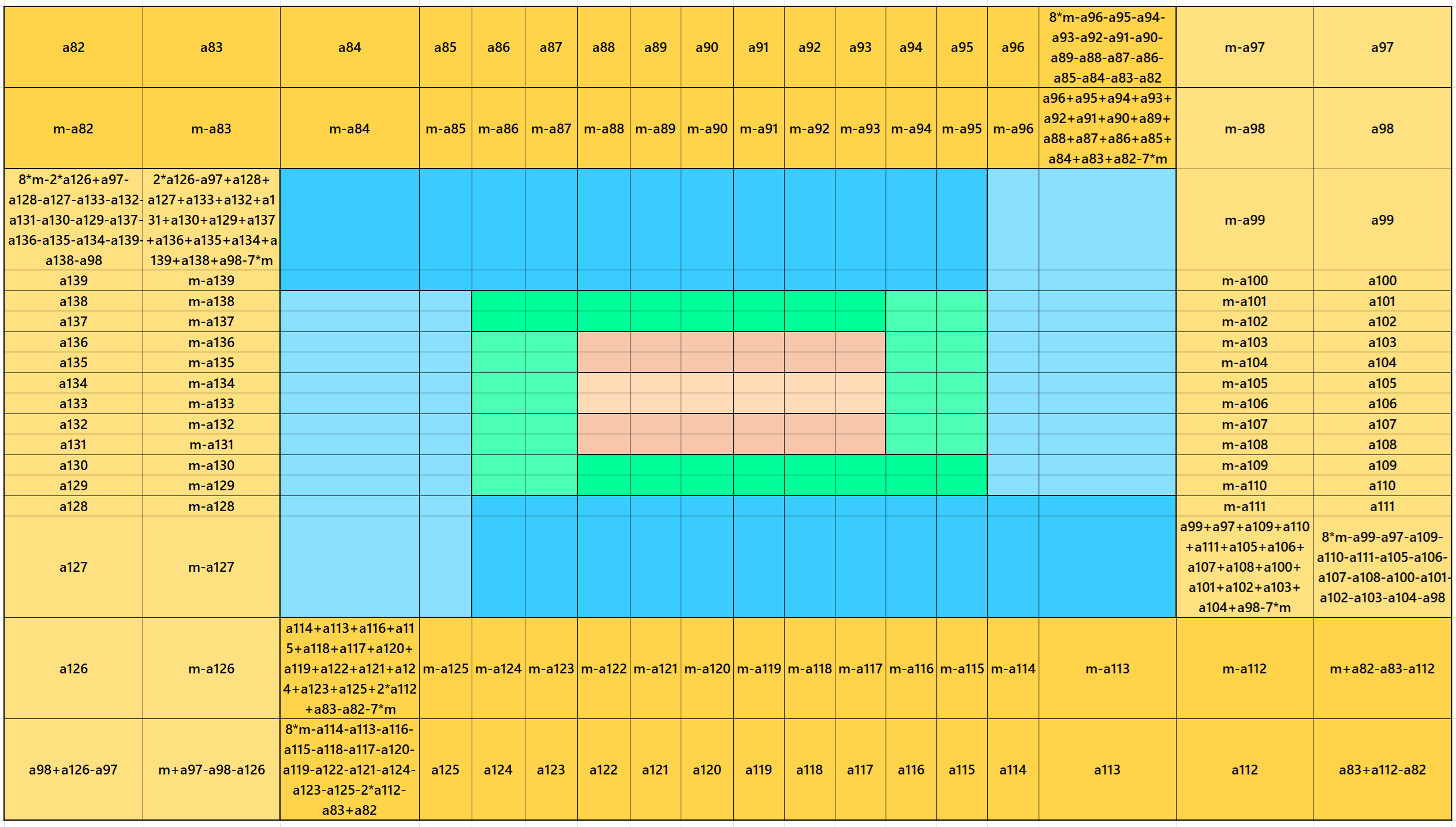
Result 18: Algebraic Striped Cornered Magic Squares of Order 16

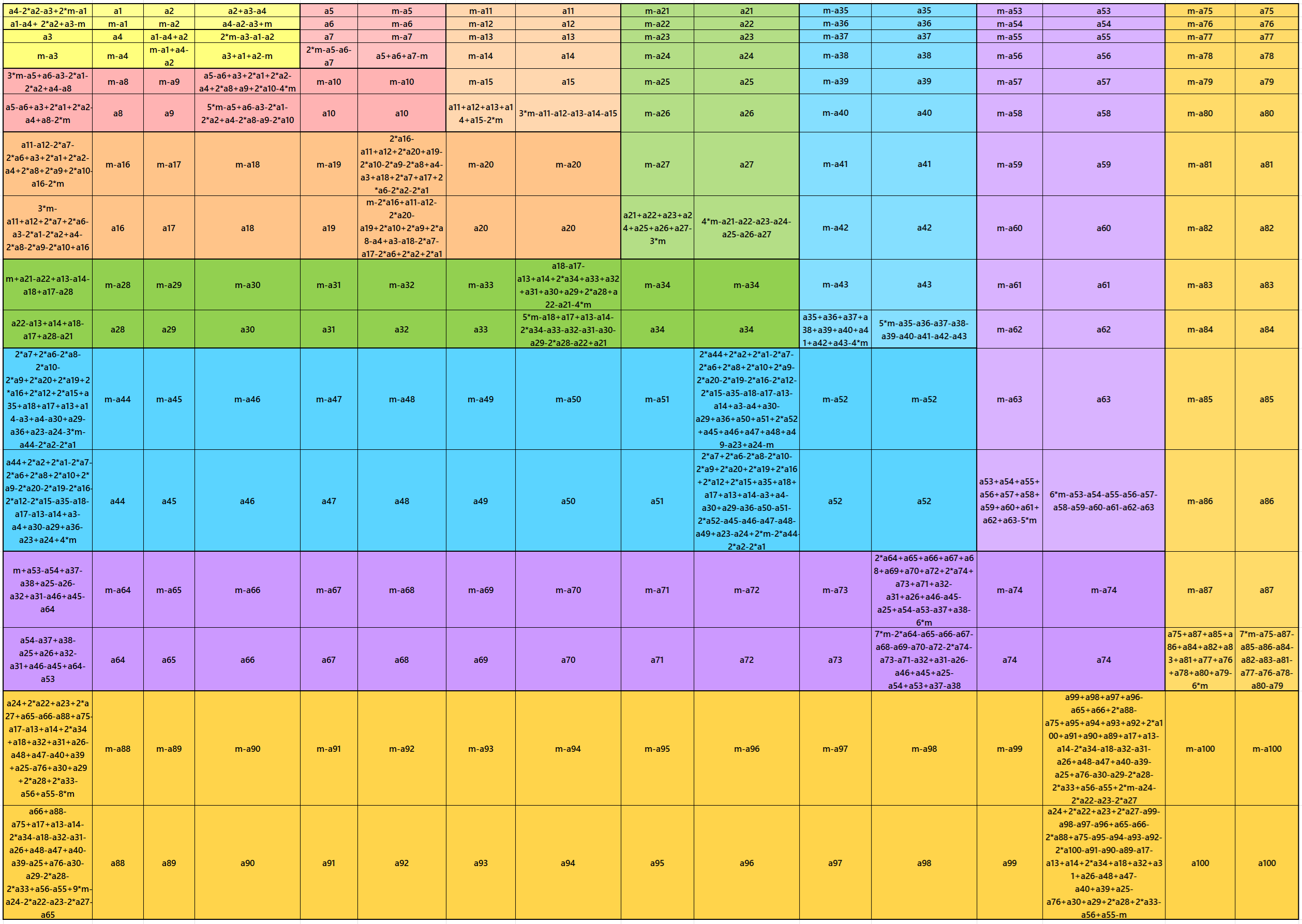
It is an algebraic striped cornered magic square of order 16, where the magic squares of order 4, 6, 8, 10, 12 and 14 are at the upper-left corner. In this case the magic sums are S_4×4:=2*m, S_6×6:=3*m, S_8×8:=4*m S_10×10:=5*m, S_12×12:=6*m, S_14×14:=7*m and S_16×16:=8*m, where m is the width of the strip. See below two examples:

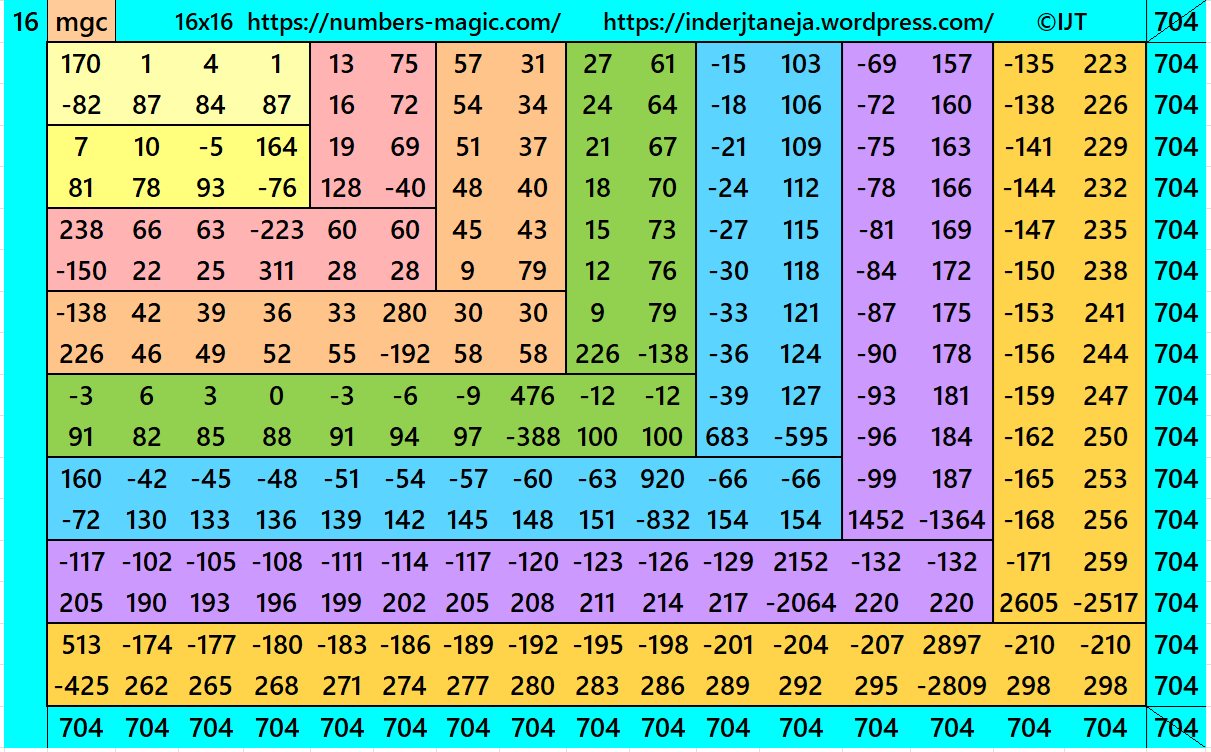
In this example magic sums are S_4×4 := 172, S_6×6 := 264, S_8×8 :=352, S_10×10 :=440, S_12×12 :=528, S_14×14 :=616, S_16×16 :=704 and m:=88.

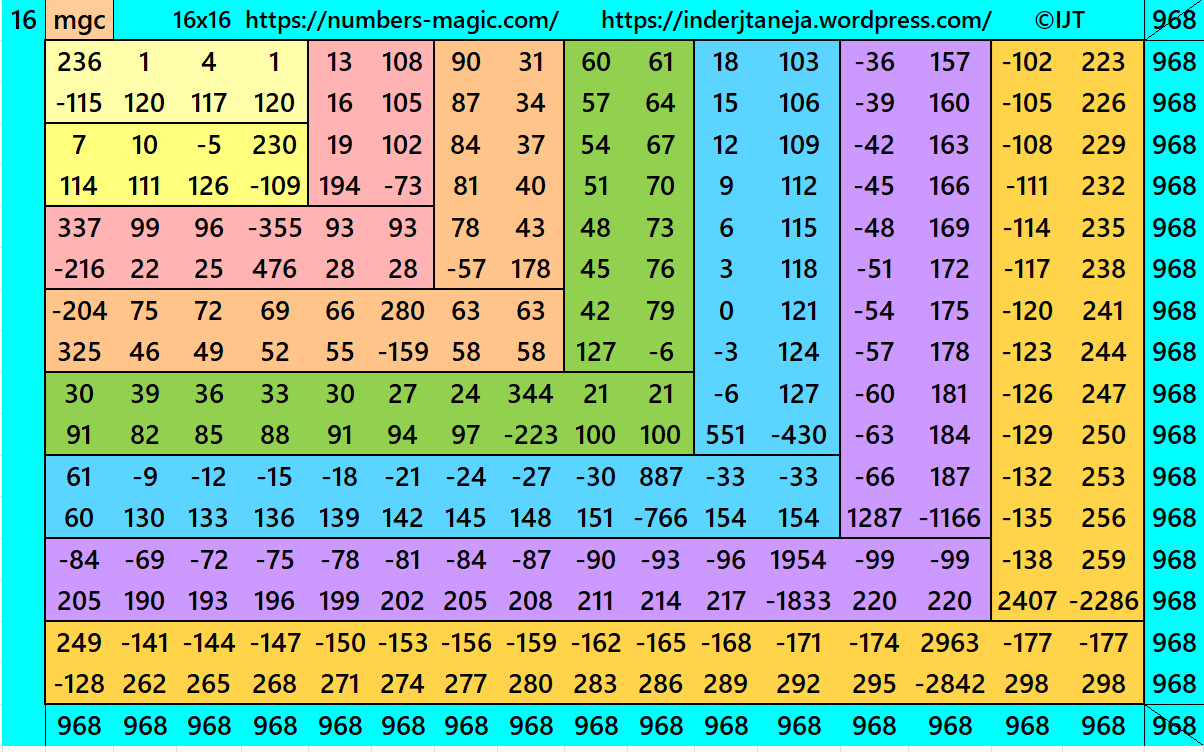
In this example the magic sums are S_4×4 := 242, S_6×6 := 363, S_8×8 :=464, S_10×10 :=585, S_12×12 :=726, S_14×14 :=847, S_16×16 :=968 and m:=121..

Algebraic Striped Magic Squares of Order 18

Below are three types of algebraic striped magic squares of order 18.

Result 19: Algebraic Striped Magic Squares of Order 18

It is an algebraic cyclic striped magic square of order 18 composed of four equal sums magic rectangles of orders 2×16 embedded with a magic square of order 14. The internal part, i.e., magic square of order 14 is as given in Result 13. In this case the magic sums are S_6×6:=3*m, S_10×10:=5*m, S_14×14:=7*m and S_18×18:=9*m, where m is the width of the strip. See below two examples:

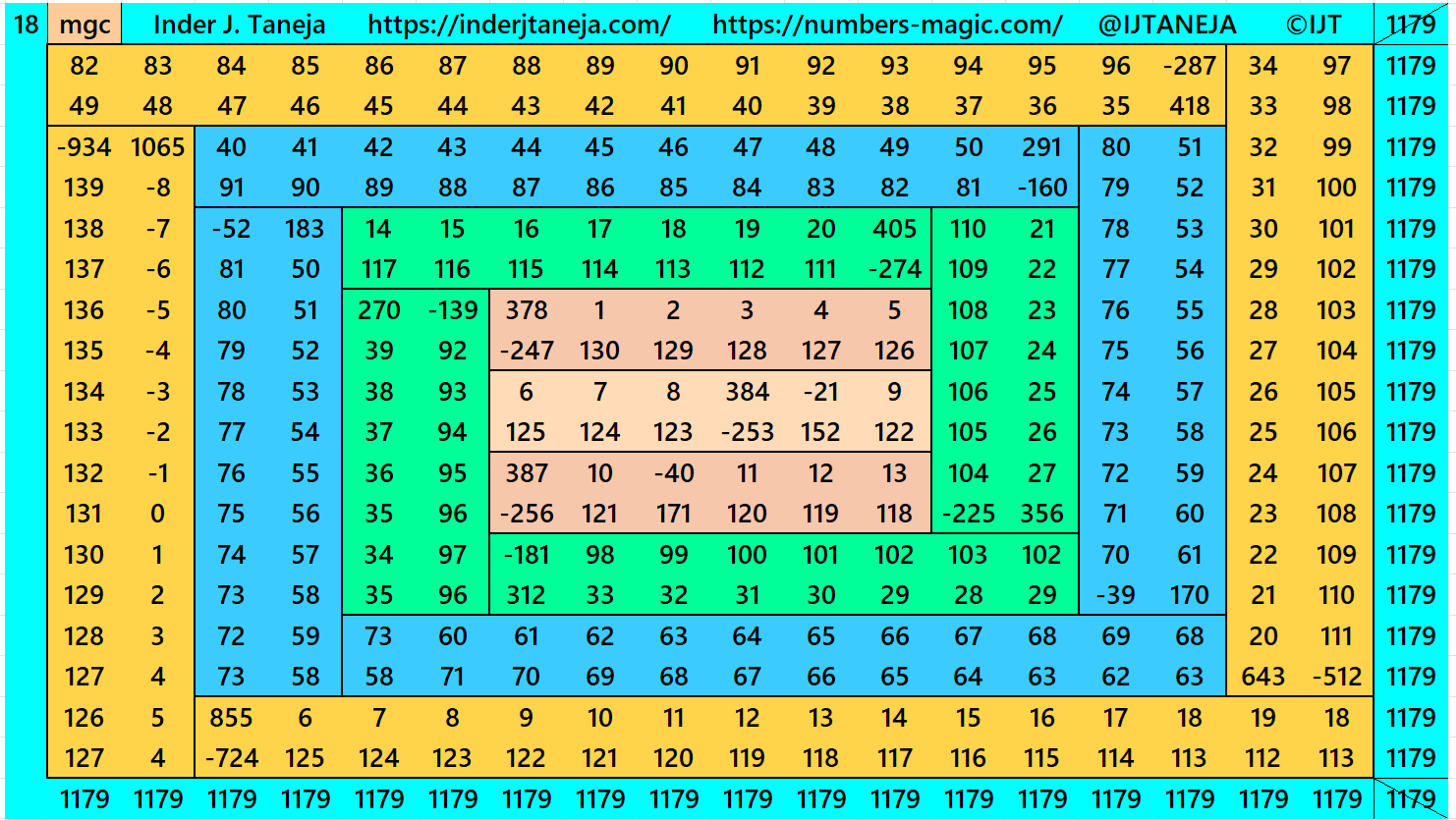
In this example the magic sums are S_6×6 := 393, S_10×10 :=655, S_14×14 :=917, S_18×18 :=1179 and m:=131.

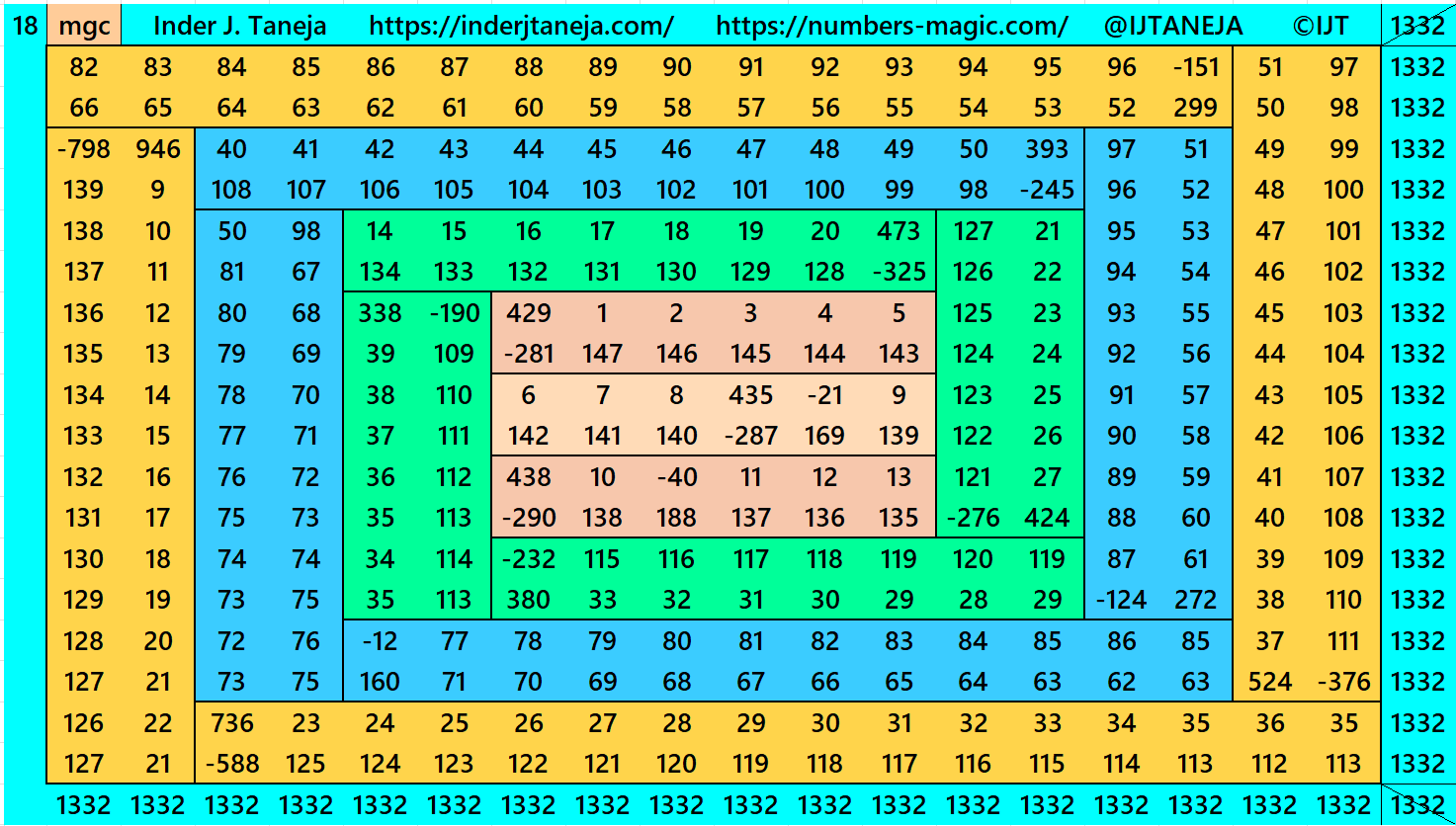
In this example the magic sums are S_6×6 := 444, S_10×10 :=740, S_14×14 :=1036, S_18×18 :=1332 and m:=148.

Result 20: Algebraic Striped Magic Squares of Order 18

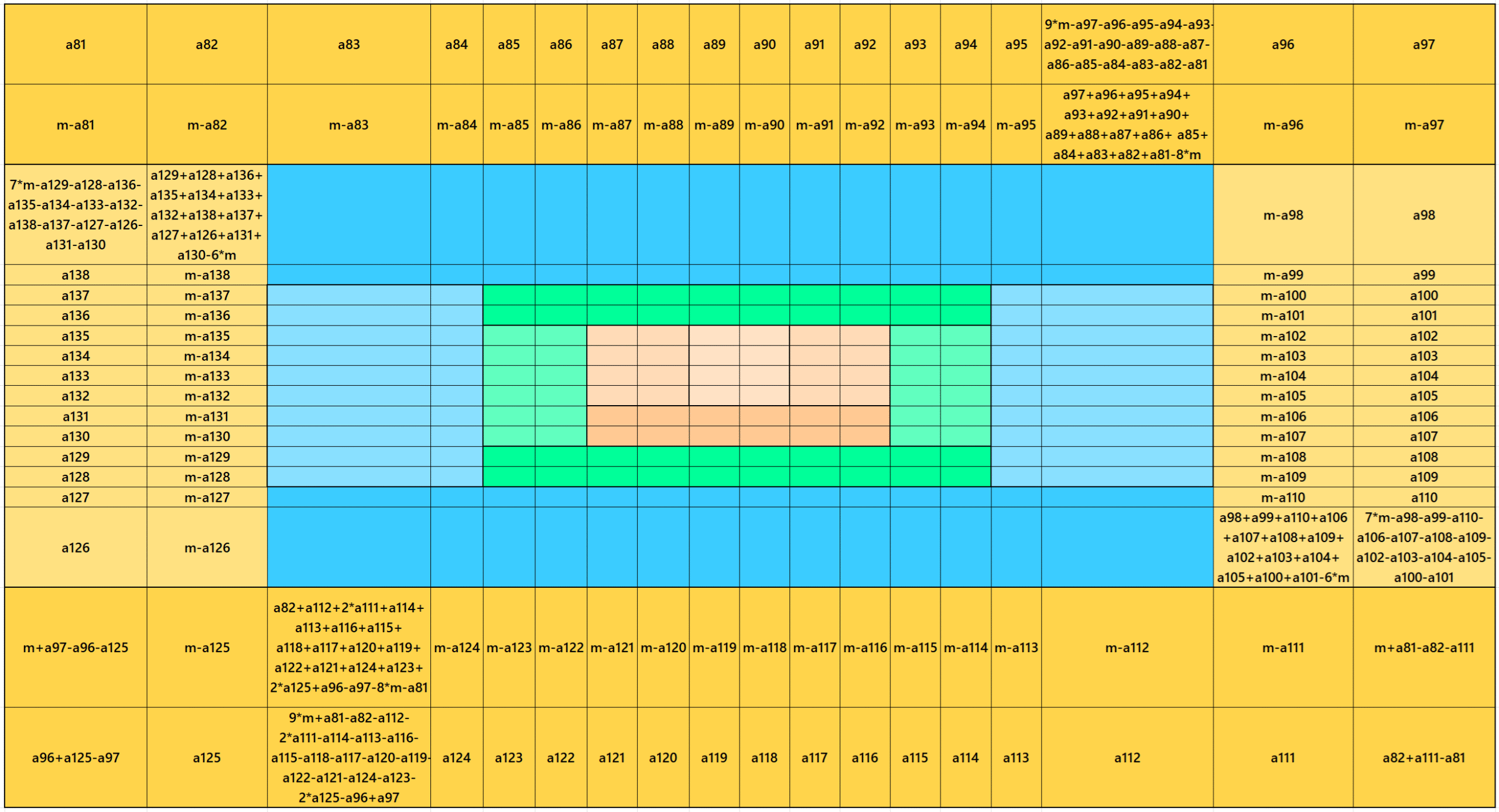
It is an algebraic flat striped magic square of order 18 composed of two equal sums magic rectangles of orders 2×18 and two magic rectangles of order 2×14 embedded with a magic square of order 14. This magic square of order 14 is exactly the same as given in the Result 14. In this case the magic sums are S_6×6 := 3*m, S_10×10 := 5*m, S_14×14 := 7*m and S_18×18 := 9*m, where m is the width of the strip. See below two examples:

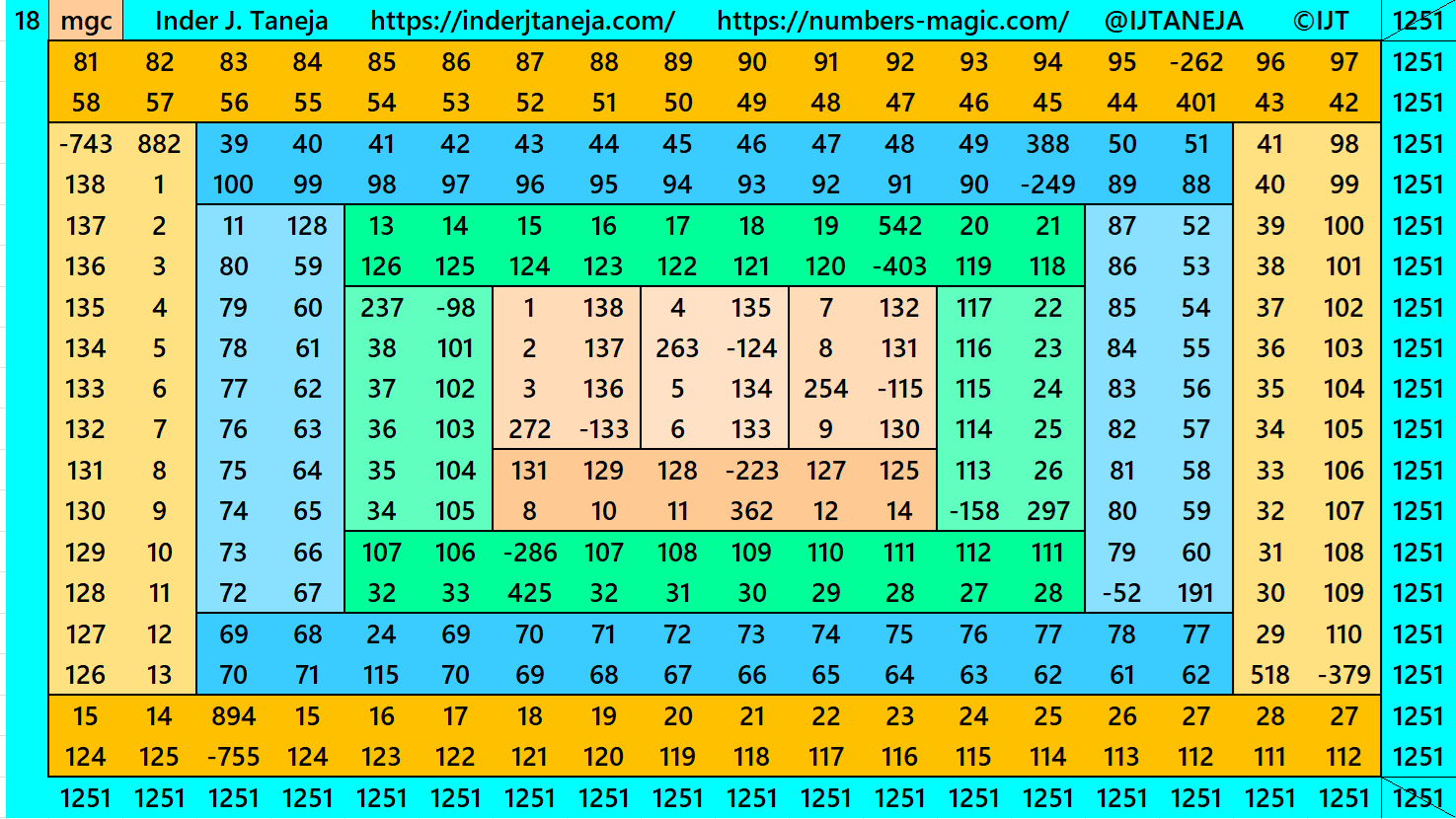
In this example the magic sums are S_6×6 := 417, S_10×10 :=695, S_14×14 :=973, S_18×18 :=1251 and m:=139.

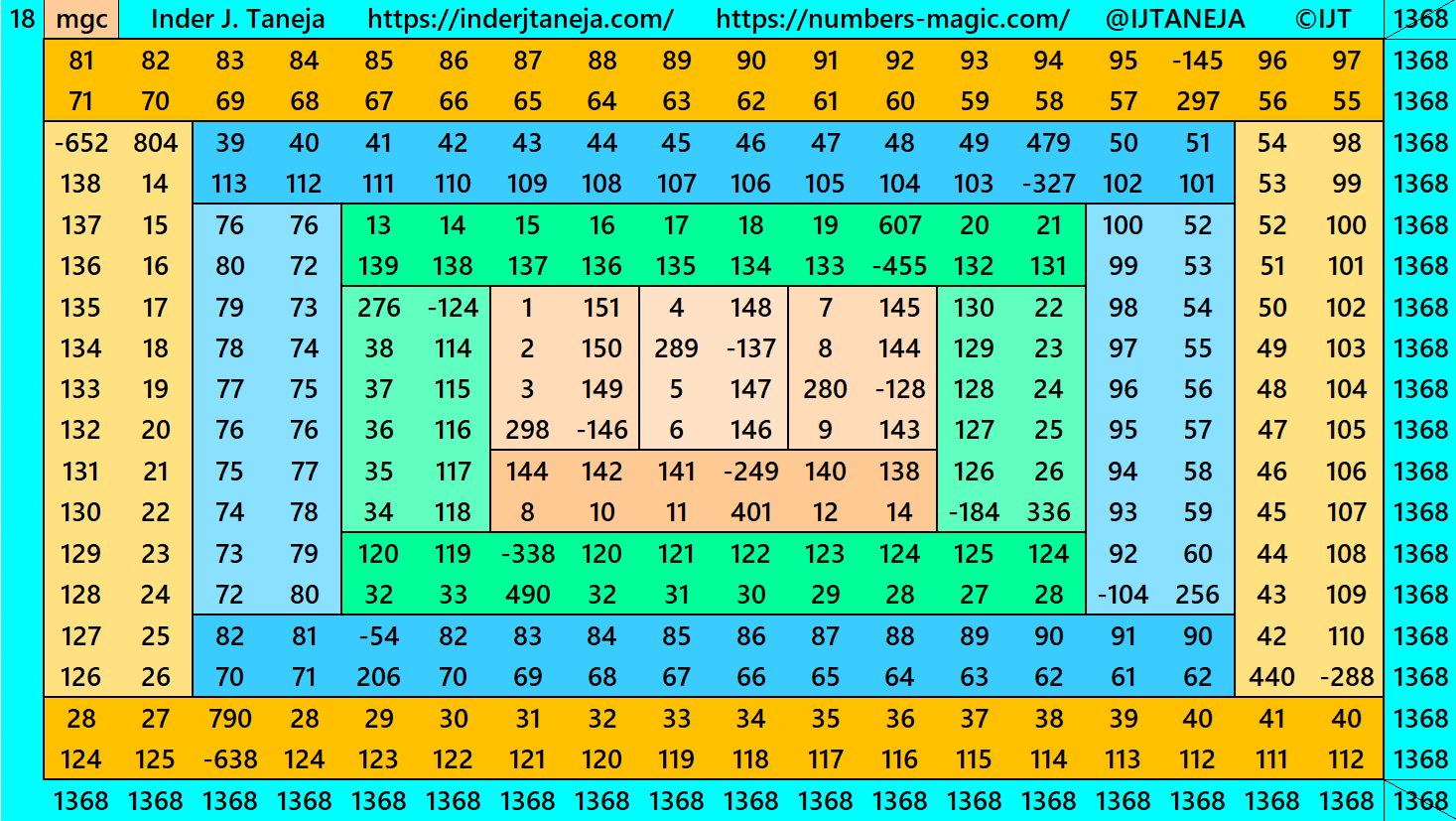
In this example the magic sums are S_6×6 := 456, S_10×10 :=760, S_14×14 :=1064, S_18×18 :=1368 and m:=152.

Result 21: Algebraic Striped Magic Squares of Order 18

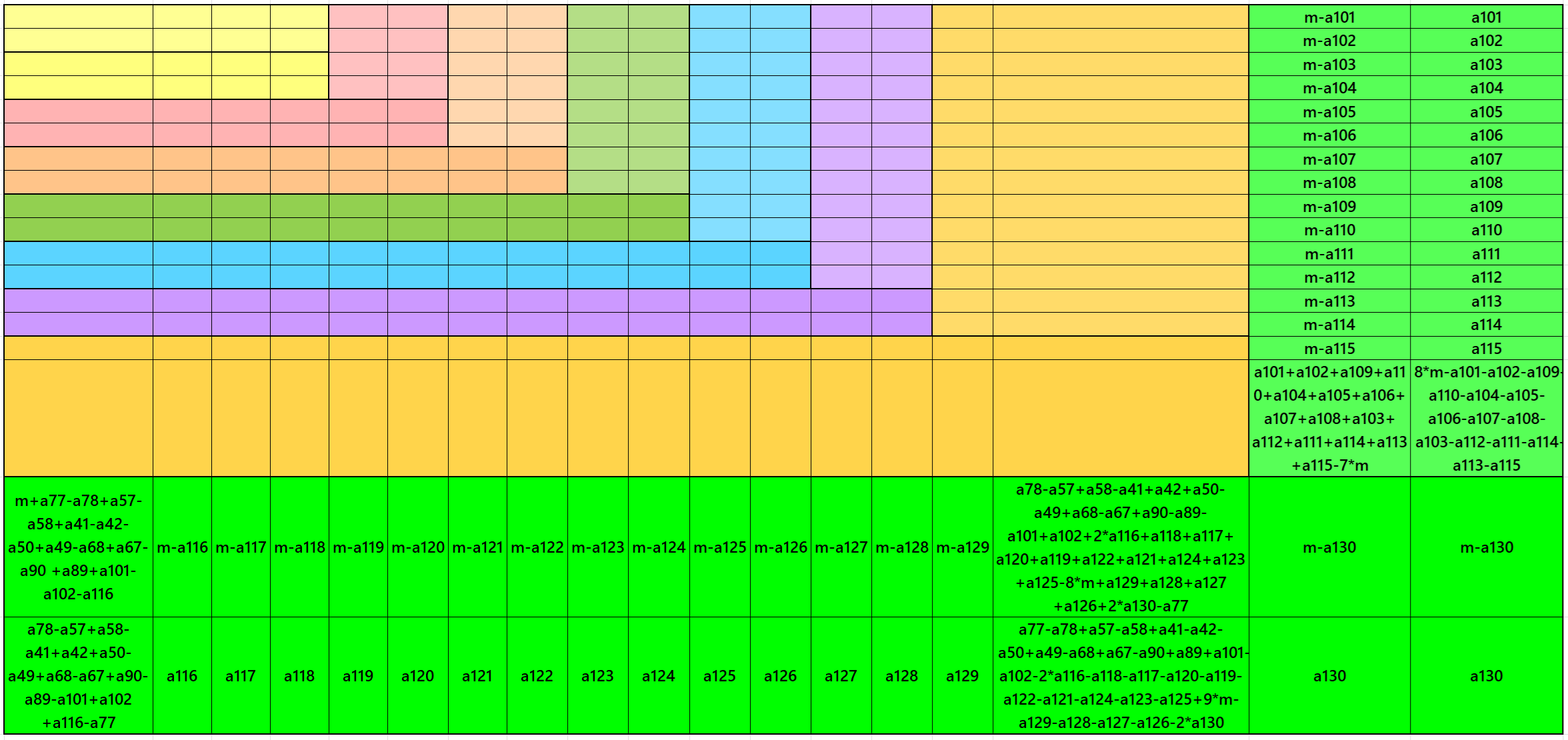
It is an algebraic striped cornered magic square of order 18, where the magic squares of order 4, 6, 8, 10, 12, 14 and 16 are at the upper-left corner. This upper-left corner is exactly the same as given in Result 18. In this case the magic sums are S_4×4:=2*m, S_6×6:=3*m, S_8×8:=4*m S_10×10:=5*m, S_12×12:=6*m, S_14×14:=7*m, S_16×16:=8*m and S_18×18:=8*m, where m is the width of the strip. See below two examples:

In this example, the magic sums are S_4×4:=262, S_6×6:=393, S_8×8:=524, S_10×10:=655, S_12×12:=786, S_14×14:=917, S_16×16:=1048, S_18×18:=1179 and m:=131.

In this example, the magic sums are S_4×4:=288, S_6×6:=432, S_8×8:=576, S_10×10:=720, S_12×12:=864, S_14×14:=1008, S_16×16:=1152, S_18×18:=1296 and m:=144.

Algebraic Striped Magic Squares of Order 20

Below are three types of algebraic striped magic squares of order 20.

Result 22: Algebraic Striped Magic Squares of Order 20

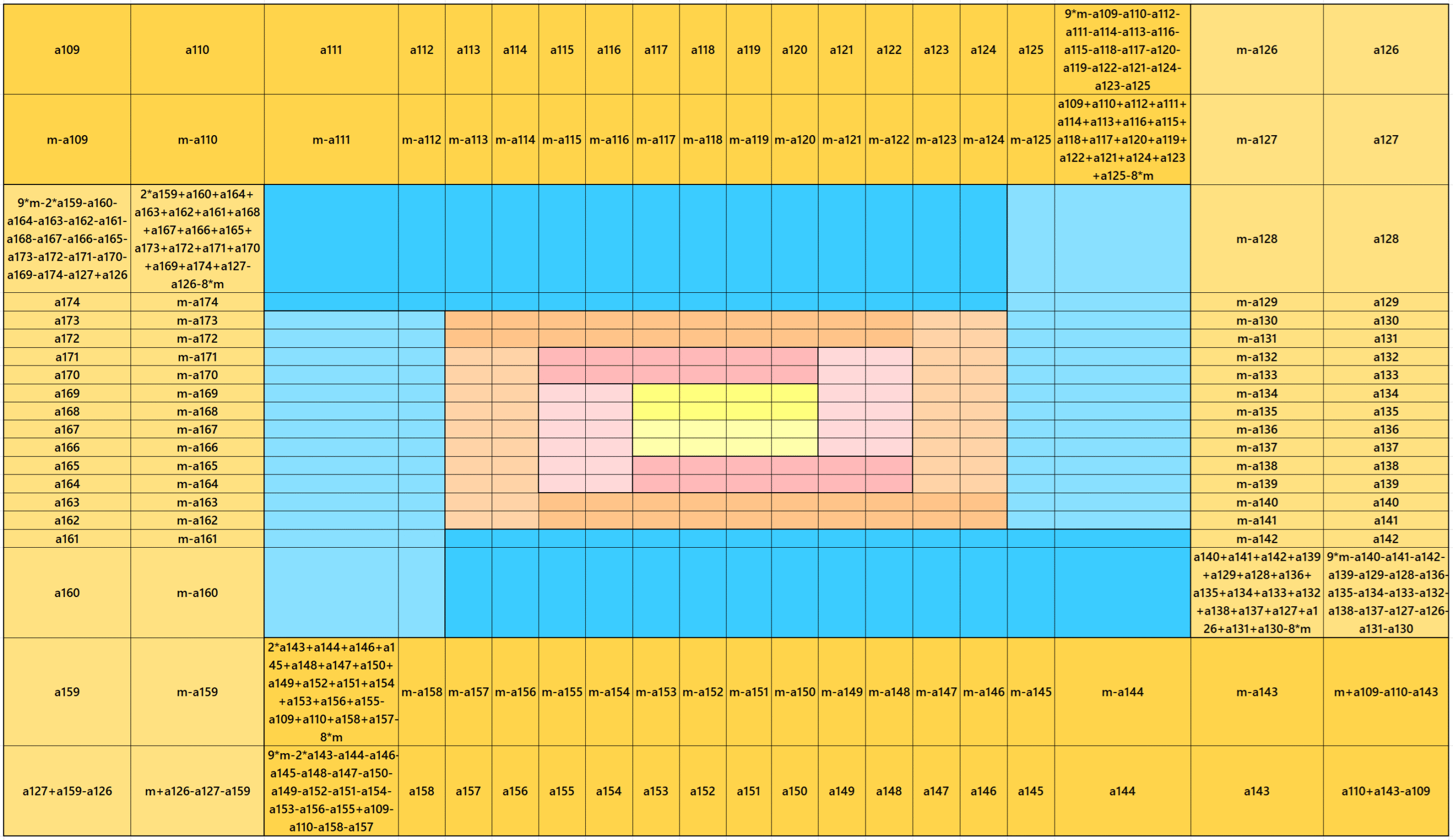
It is an algebraic cyclic striped magic square of order 20 composed of four equal sums magic rectangles of orders 2×18 embedded with a magic square of order 16. The internal part is exactly the same as given in Result 16. In this case the magic sums are S_4×4:=2*m, S_8×8:=4*m, S_12×12:=6*m, S_16×16:=8*m and S_20×20:=10*m, where m is the width of the strip. See below two examples:

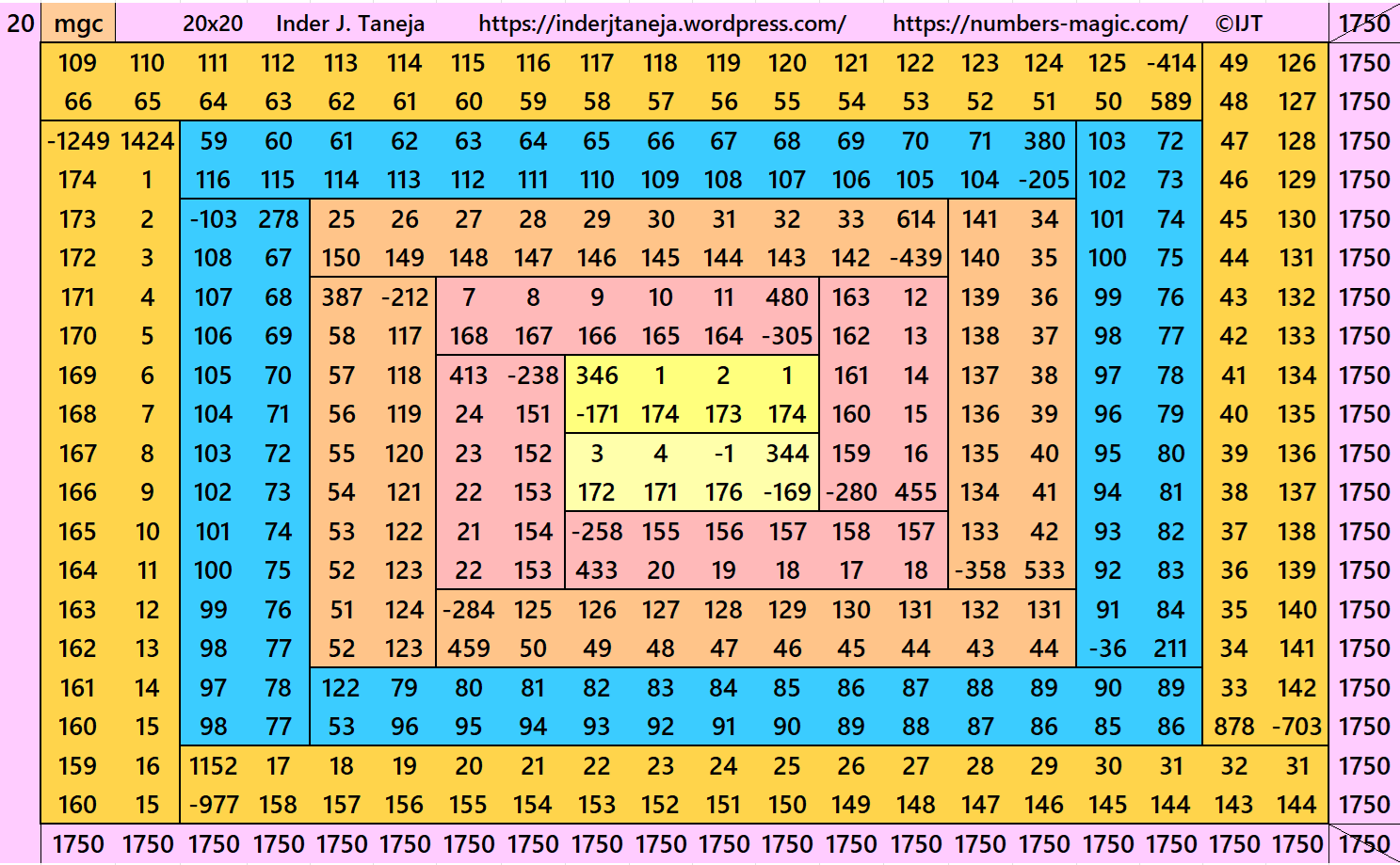
In this example, the magic sums are S_4×4:=350, S_8×8:=700, S_12×12:=1050, S_16×16:=1400 and S_20×20:=1750 and m:=175.

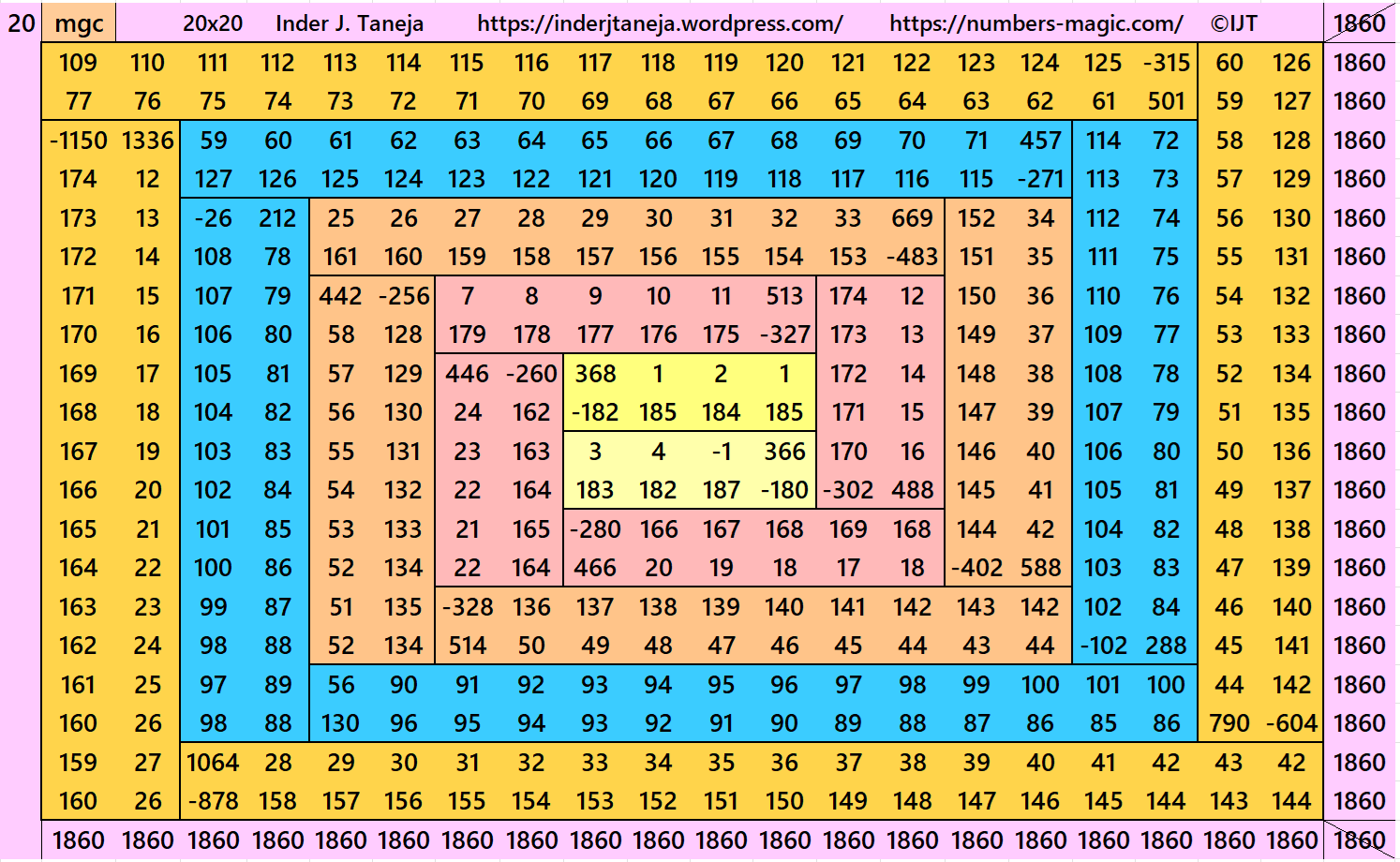
In this example, the magic sums are S_4×4:=372, S_8×8:=744, S_12×12:=1116, S_16×16:=1488 and S_20×20:=1860 and m:=186.

Result 23: Algebraic Striped Magic Squares of Order 20

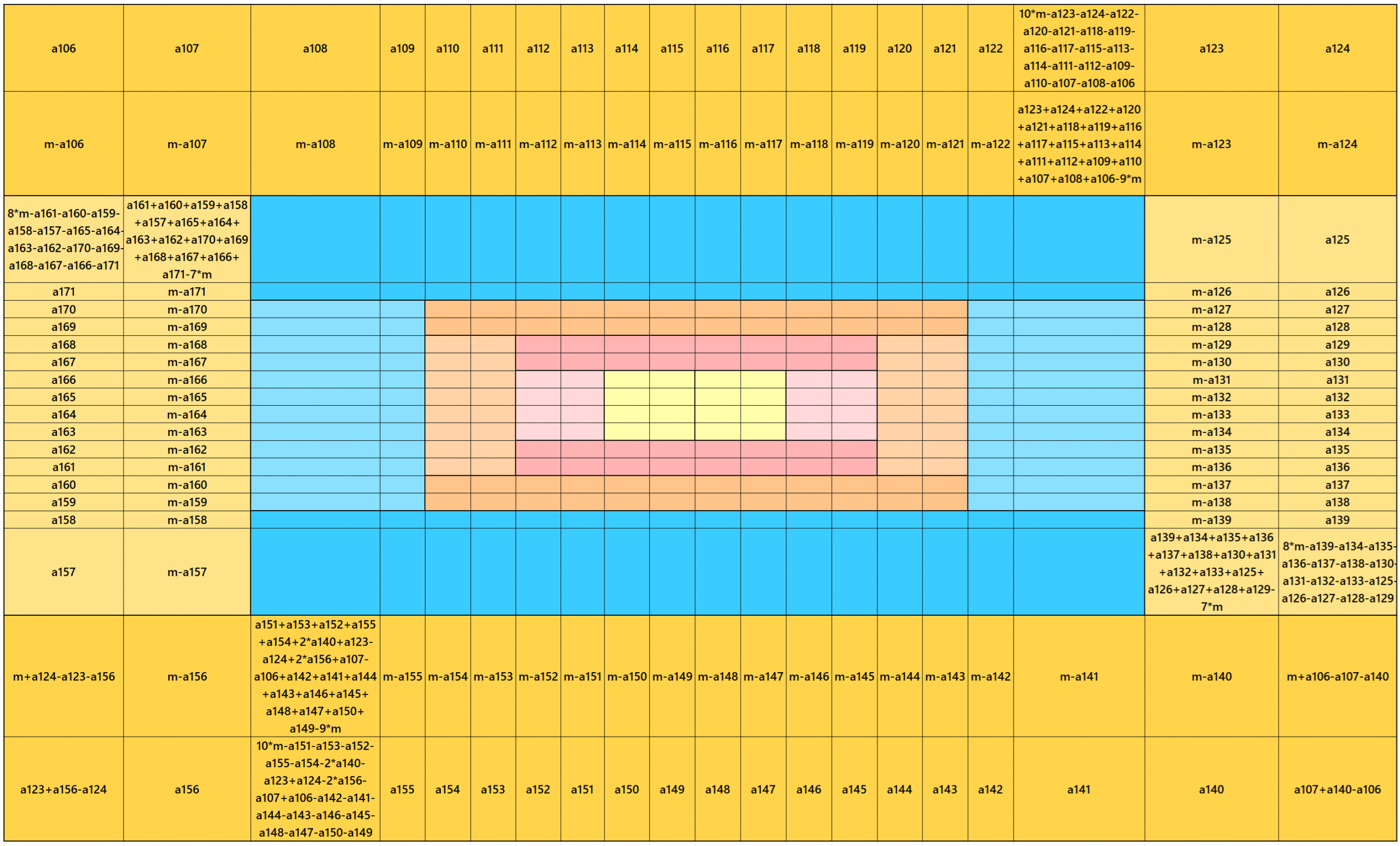
It is an algebraic flat striped magic square of order 20 composed of two equal sums magic rectangles of orders 2×20 and two magic rectangles of order 2×16 embedded with a magic square of order 16. This magic square of order 16 is exactly, the same as given in Result 17. In this case the magic sums are S_4×4:=2*m, S_8×8:=4*m, S_12×12:=6*m. S_16×16:=8*m and S_20×20:=10*m, where m is the width of the strip. See below two examples:

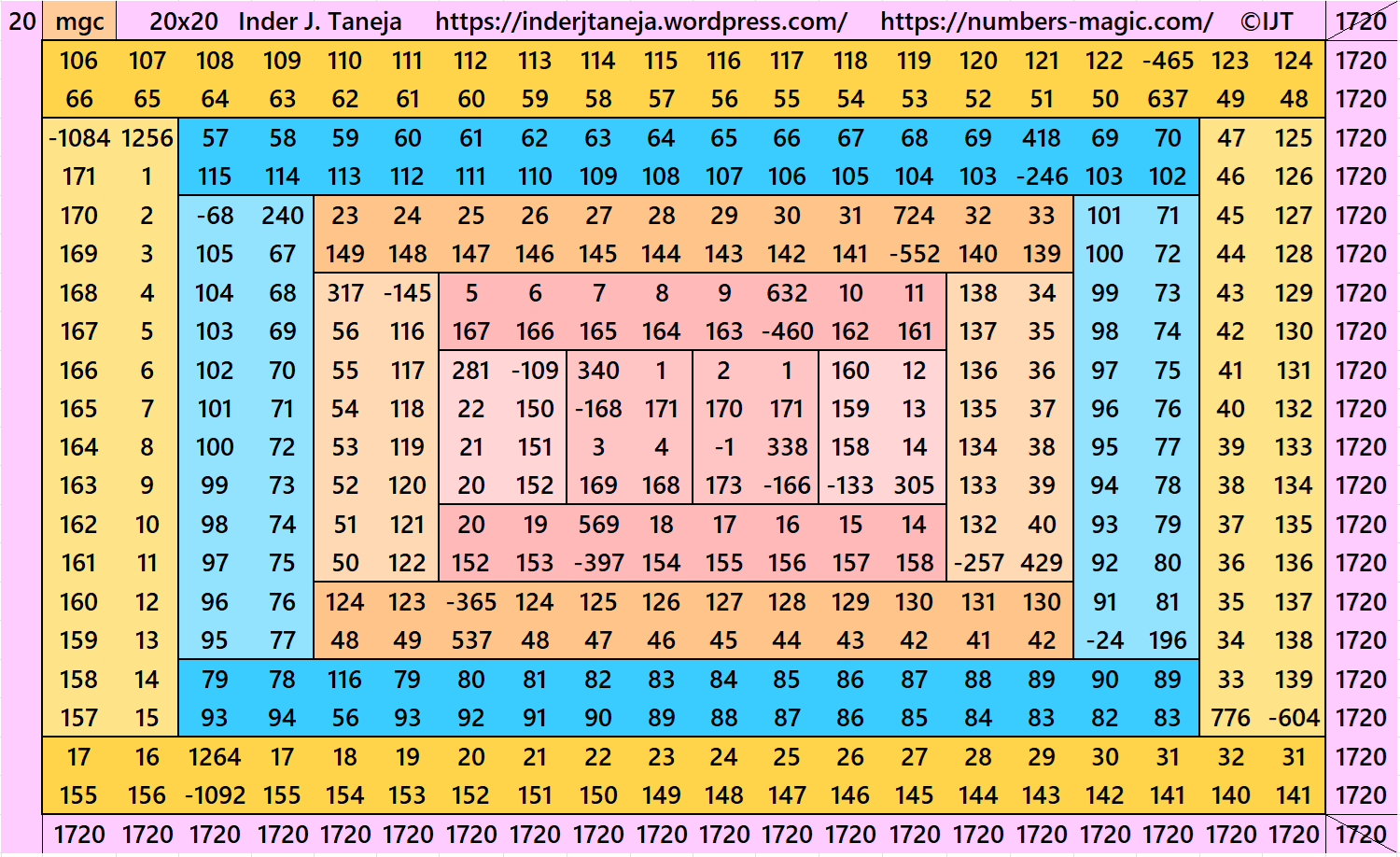
In this example, the magic sums are S_4×4:=344, S_8×8:=688, S_12×12:=1032, S_16×16:=1204 and S_20×20:=1720 and m:=172.

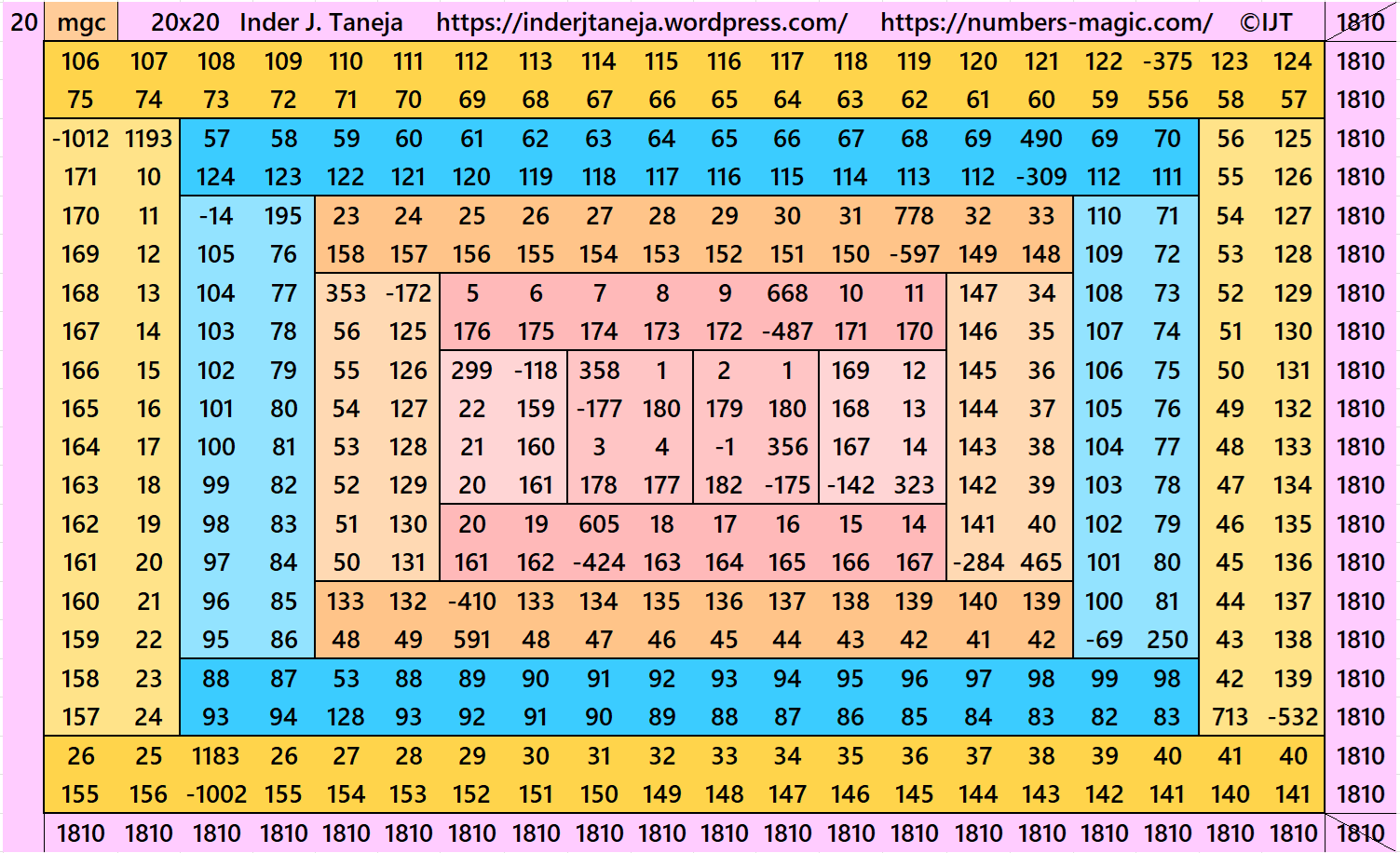
In this example, the magic sums are S_4×4:=362, S_8×8:=724, S_12×12:=1086, S_16×16:=1448 and S_20×20:=1810 and m:=181.

Result 21: Algebraic Striped Magic Squares of Order 20

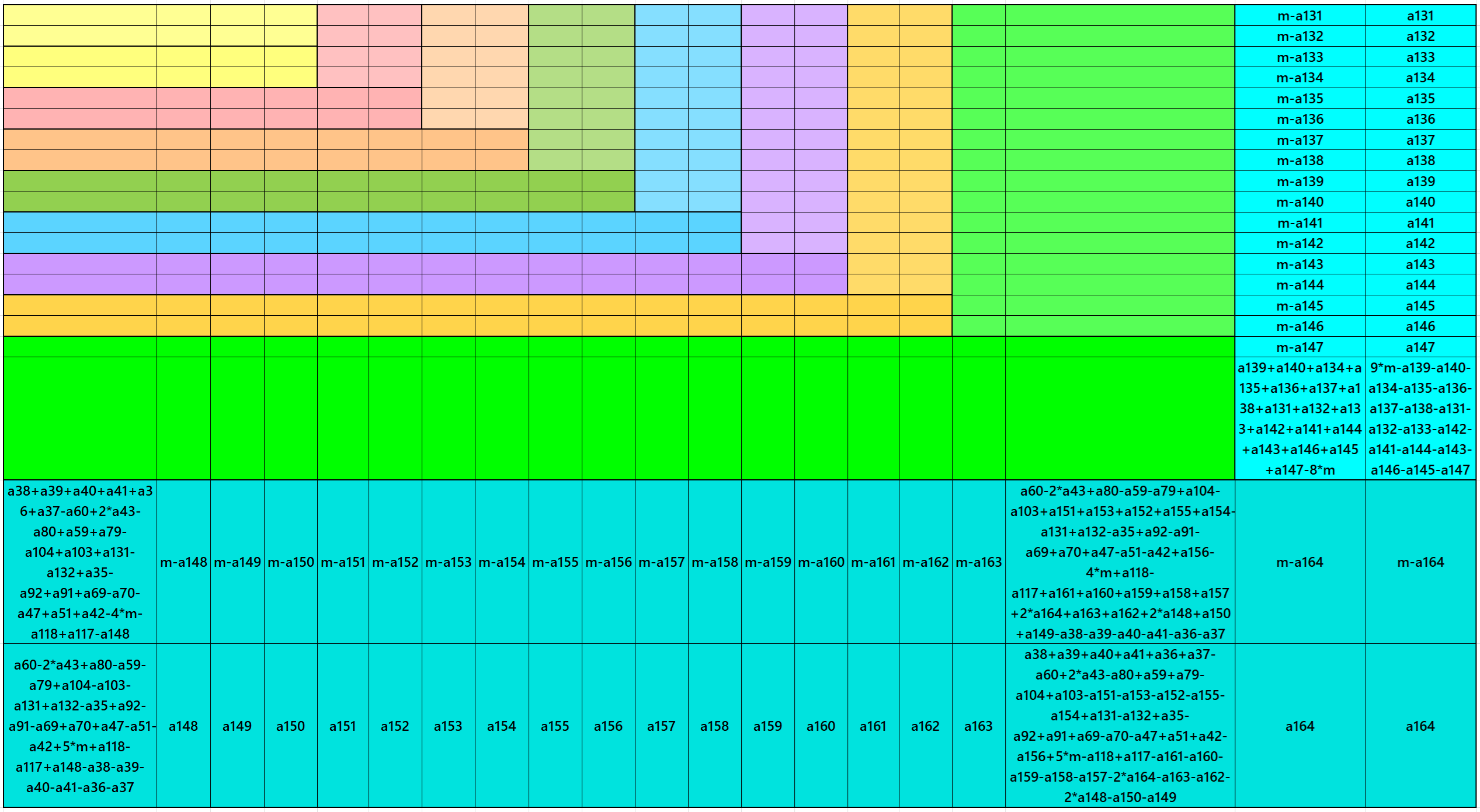
It is an algebraic striped cornered magic square of order 20, where the magic squares of order 4, 6, 8, 10, 12, 14, 16 and 18 are at the upper-left corner. This upper-left corner of magic square of order 18 is exactly the same as given in Result 21. In this case the magic sums are S_4×4:=2*m, S_6×6:=3*m, S_8×8:=4*m S_10×10:=5*m, S_12×12:=6*m, S_14×14:=7*m, S_16×16:=8*m, S_18×18:=8*m and S_20×20 := 10*m, where m is the width of the strip. See below two examples:

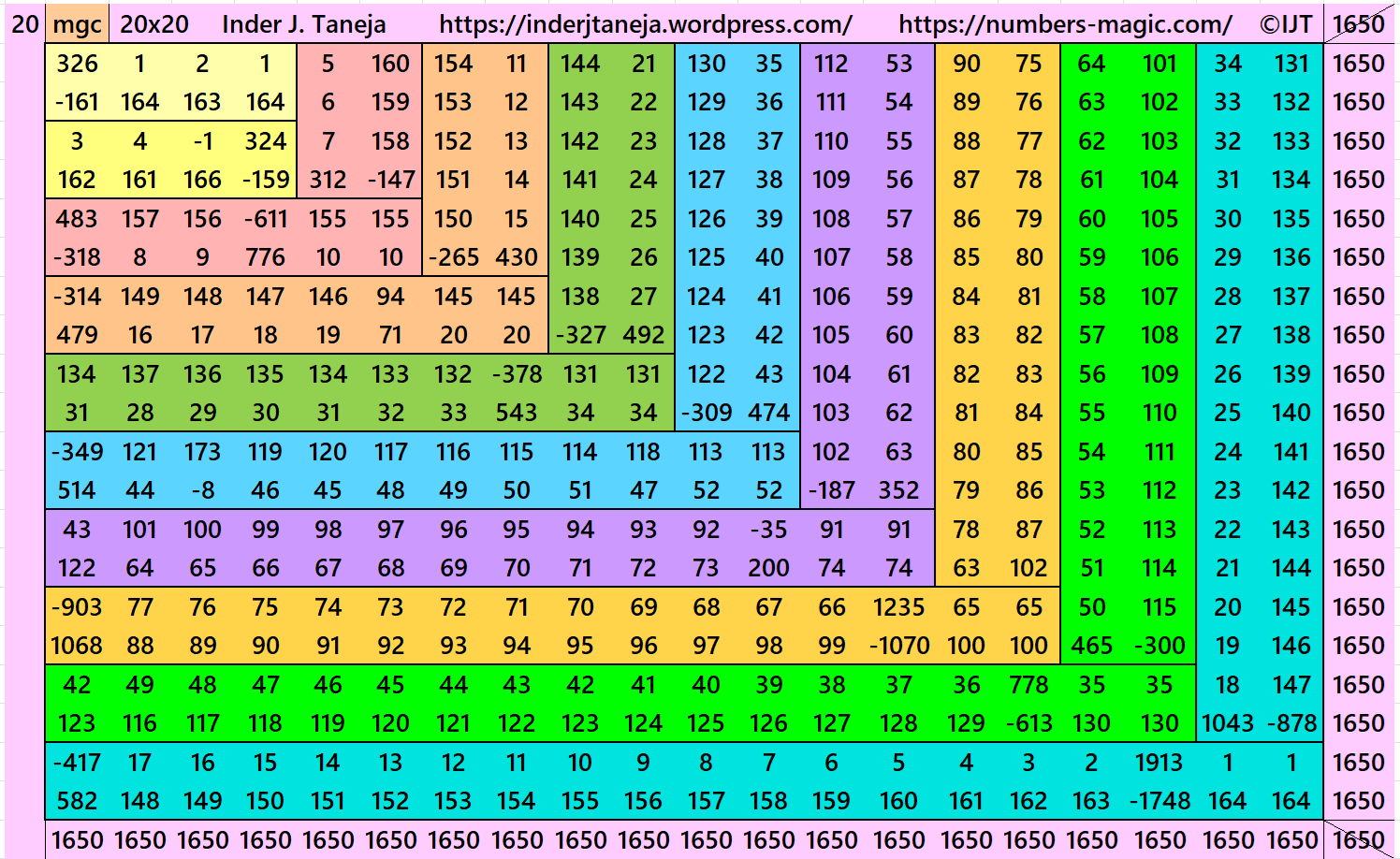
In this example, the magic sums are S_4×4:=330, S_6×6:=495, S_8×8:=660, S_10×10:=825, S_12×12:=990, S_14×14:=1155, S_16×16:=1320, S_18×18:=1485, S_20×20:=1650 and m:=165.

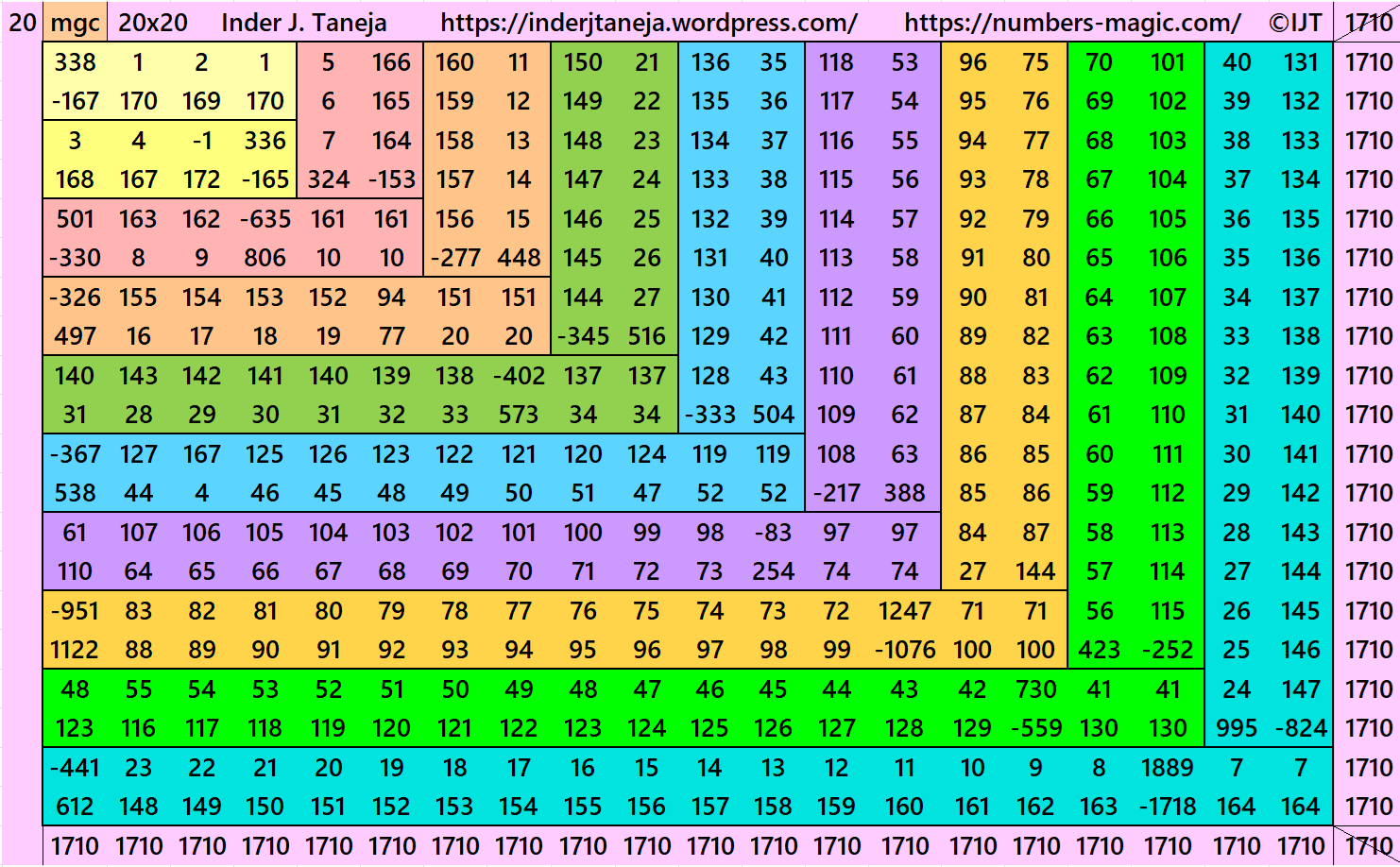
In this example, the magic sums are S_4×4:=342, S_6×6:=513, S_8×8:=684, S_10×10:=855, S_12×12:=1026, S_14×14:=1197, S_16×16:=1368, S_18×18:=1539, S_20×20:=1710 and m:=171.

References

Part 1: Representing Days and Date

1. Inder J. Taneja, Magic Squares of Orders 3 to 7 in Representing Dates and Days of the Year 2025, Zenodo, May 04, 2025, pp. 1-474, https://doi.org/10.5281/zenodo.15338142.
   • Site Link: Magic Squares of Orders 3 to 7 Representing Dates and Days of the Year 2025 (new site)
   • Site Link: Magic Squares of Orders 3 to 7 Representing Dates and Days of the Year 2025 (old site)
2. Inder J. Taneja, Magic Squares of Order 8 Representing Days and Dates of the Year 2025, Zenodo, May 04, 2025, pp. 1-134, https://doi.org/10.5281/zenodo.15338246.
   • Site Link: Magic Squares of Order 8 Representing Days and Dates of the Year 2025 (new site)
   • Site Link: Magic Squares of Order 8 Representing Days and Dates of the Year 2025 (old site)
3. Inder J. Taneja, Magic Squares of Order 9 Representing Days and Dates of the Year 2025, Zenodo, May 09, 2025, pp. 1-132, https://doi.org/10.5281/zenodo.15375349.
   • Site Link: Magic Squares of Order 9 Representing Days and Dates of the Year 2025 (new site)
   • Site Link: Magic Squares of Order 9 Representing Days and Dates of the Year 2025 (old site)
4. Inder J. Taneja, Magic Squares of Order 11 Representing Days and Dates of the Year 2025, Zenodo, May 31, 2025, pp. 1-94, https://doi.org/10.5281/zenodo.15564676
   • Site Link: Magic Squares of Order 11 Representing Dates and Days of the Year 2025 (new site)
   • Site Link: Magic Squares of Order 11 Representing Dates and Days of the Year 2025 (old site)
5. Inder J. Taneja, Magic Squares of Order 12 Representing Days and Dates of the Year 2025 Zenodo, June 10, 2025, pp. 1-43, https://doi.org/10.5281/zenodo.15631884.
   • Site Link: Magic Squares of Order 12 Representing Dates and Days of the Year 2025 – (new site)
   • Site Link: Magic Squares of Order 12 Representing Dates and Days of the Year 2025 (old site)

Part 2: Revised with Examples

1. Inder J. Taneja, Reduced Entries Magic and Semi-Magic Squares of Orders 3, 5, 7 and 9, Zenodo, July 01, 2025, pp. 1-65, https://doi.org/10.5281/zenodo.15783321.
   • Site Link: Reduced Entries Algebraic Magic Squares of Orders 3, 5, 7 and 9 (new site)
   • Site Link: Reduced Entries Algebraic Magic Squares of Orders 3, 5, 7 and 9 (old site)
2. Inder J. Taneja, Reduced Entries Magic and Semi-Magic Squares of Orders 4, 6, 8 and 10, Zenodo, July 05, 2025, pp. 1-85, https://doi.org/10.5281/zenodo.15814675.
   • Site Link: Reduced Entries Algebraic Magic Squares of Orders 4, 6, 8 and 10 (new site)
   • Site Link: Reduced Entries Algebraic Magic Squares of Orders 4, 6, 8 and 10 (olde site)
3. Inder J. Taneja, Reduced Entries Algebraic Semi-Magic Squares of Order 12, Zenodo, July 23, 2025, pp. 1-60, https://doi.org/10.5281/zenodo.15692014.
   • Site Link: Reduced Entries Algebraic Semi-Magic Squares of Order 12 (new site)
   • Site Link: Reduced Entries Algebraic Semi-Magic Squares of Order 12 (old site)
4. Inder J. Taneja – Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8, Zenodo, August 12, 2025, pp. 1-63, https://doi.org/10.5281/zenodo.16809756.
   • Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (new site)
   • Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (old site)
5. Inder J. Taneja, Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9, Zenodo, August 27, 2025, pp. 1-92, https://doi.org/10.5281/zenodo.16955571.
   • Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9 (new site).
   • Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9 (old site).
6. Inder J. Taneja, Double-Digit Cyclic-Type Bordered Reduced Entries Algebraic Magic Squares of Orders 7 to 20, Zenodo, November 21, 2025, pp. 1-37, https://doi.org/10.5281/zenodo.17675032.
   • Site Link: Double-Digit Cyclic-Type Bordered Algebraic Magic Squares of Orders 7 to 20 for Reduced Entries (New Site)
   • Site Link2: Double-Digit Cyclic-Type Bordered Algebraic Magic Squares of Orders 7 to 20 for Reduced Entries (Old Site)
7. Inder J. Taneja, Algebraic Cyclic, Flat and Cornered Striped Magic Squares for Even Orders from 4 to 20, Zenodo, December 02, 2025, pp. 1-58, https://doi.org/10.5281/zenodo.17793845.
   • Site Link1: Algebraic Cyclic, Flat and Cornered Striped Magic Squares of Even Orders from 4 to 20 (New Site).
   • Site Link2: Algebraic Cyclic, Flat and Cornered Striped Magic Squares of Even Orders from 4 to 20 (Old Site)