Double-Digit Cyclic-Type Bordered Algebraic Magic Squares of Orders 7 to 20 for Reduced Entries

This work brings double-digit or double-layer algebraic magic squares of orders 7 to 20 for reduced entries. Sometimes, these types of magic squares, we call as self-made, beacause they are complete in themselves. Just choose the entries and magic sum, we always get a magic square.

We know that magic sum of a magic square of order n having 1 to n² number of entries is given by

S_nxn:= n*(1+n²)/2

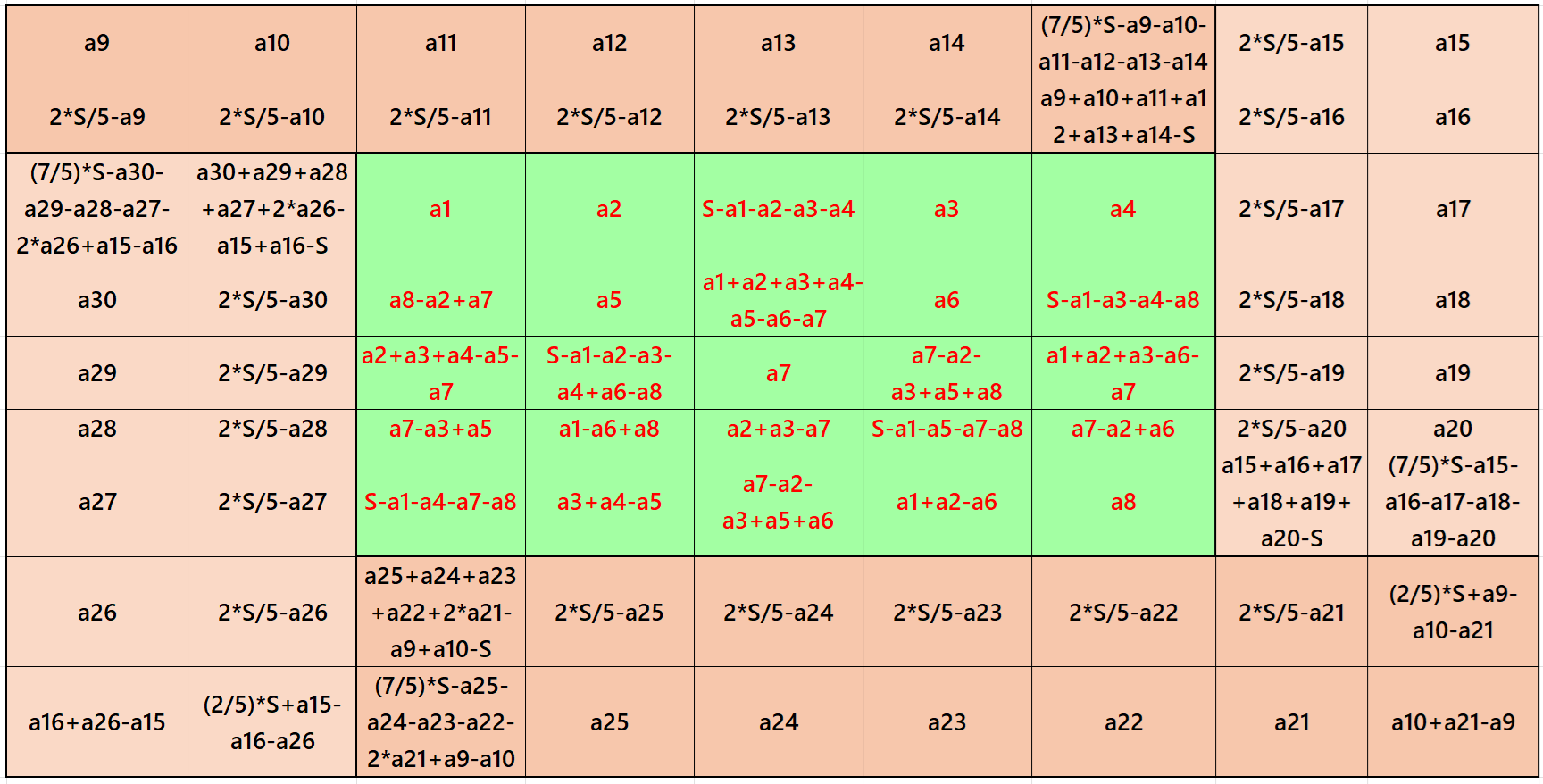
In this work the entries are written as vaiables and their combinations. The work is based on four equal sums magic rectangles in each layer or border. The width is always 2. The size of length magic rectangle depends on the orders of the magic squares. For simplicity, these types of magic squares we call as cyclic. Similar kind of study for the sequential entries can be seen at the following work.

Whole work can be downloaded at the following link:

Inder J. Taneja, Double-Digit Cyclic-Type Bordered Reduced Entries Algebraic Magic Squares of Orders 7 to 20, Zenodo, November 21, 2025, pp. 1-37, https://doi.org/10.5281/zenodo.17675032.

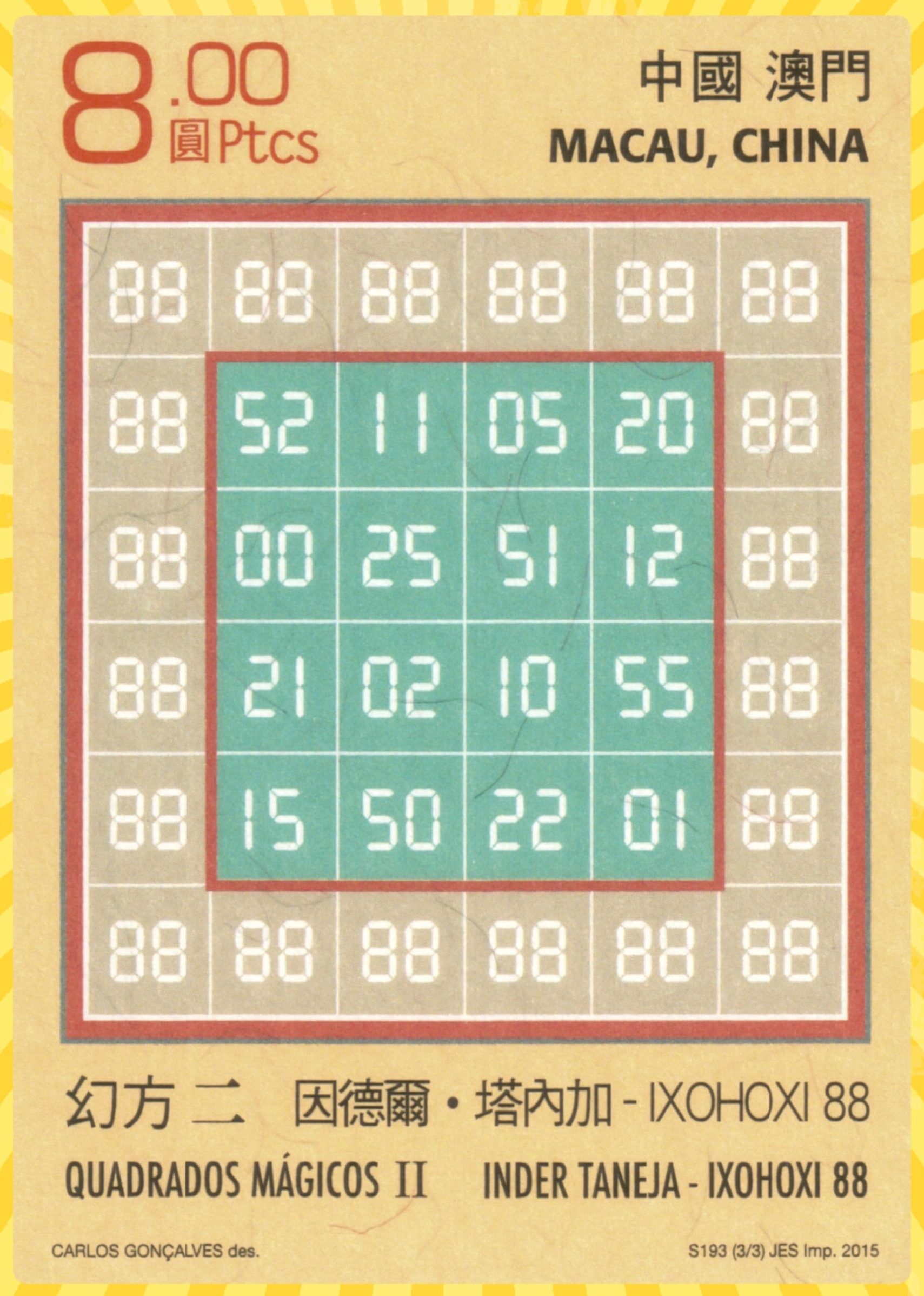
Double-Digit Bordered Algebric Magic Square of Order 7

Result 1: Double-Digit Bordered Algebric Magic Square of Order 7

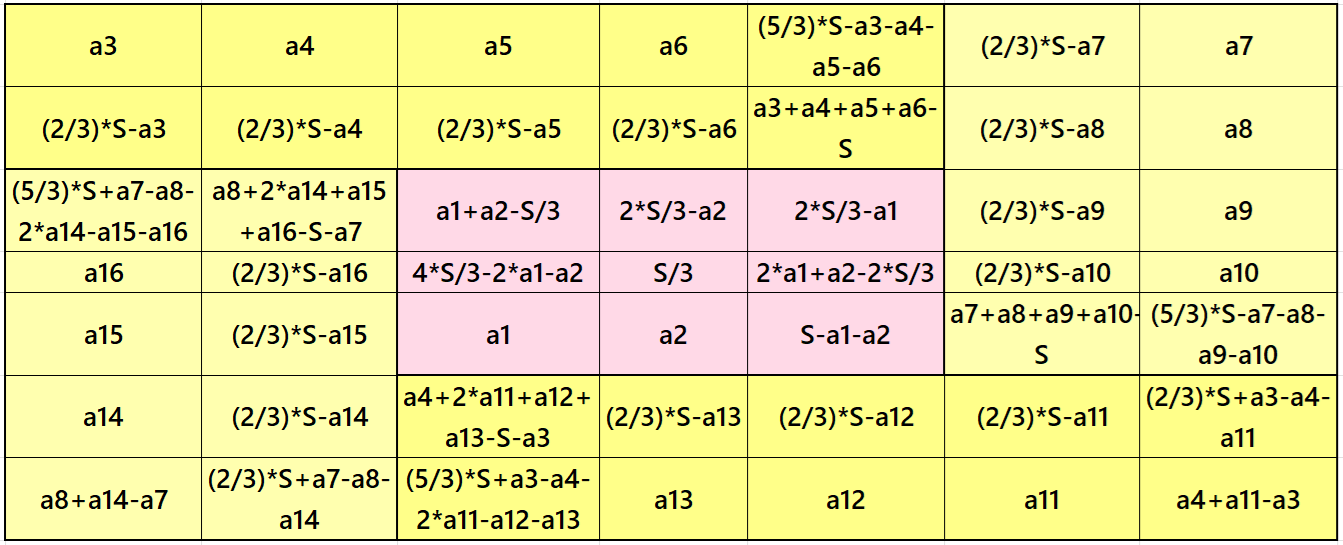
It is a composed of four equal sums magic rectangles of order 2×5 embedded with a magic square of order 3. Since the magic square of order 3 requires magic sum as multiple of 3, otherwise we have decimal entries, then the magic sum of order 7 is also multiple of 3. The magic sum of order 7 is given as S_7×7 :=7*S/3, where S is the magic sum of order 3. See below two examples:

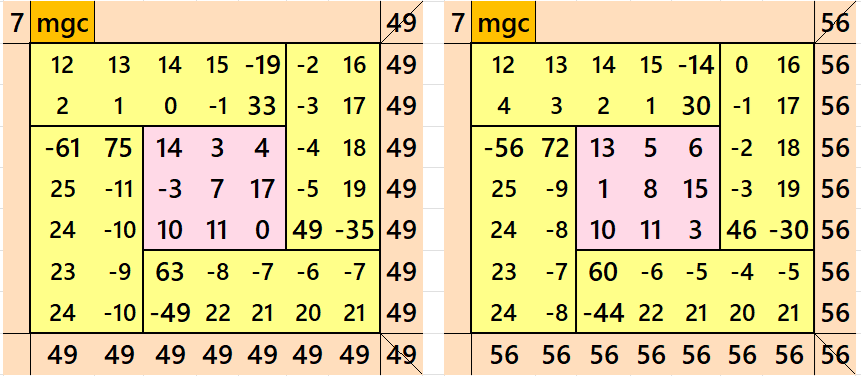
In the first example the magic sums are S_3×3 :=21 and S_7×7 :=49.
In the second example the magic sums are S_3×3 :=24 and S_7×7 :=56.

Double-Digit Bordered Algebric Magic Square of Order 8

Result 2: Double-Digit Bordered Algebric Magic Square of Order 8

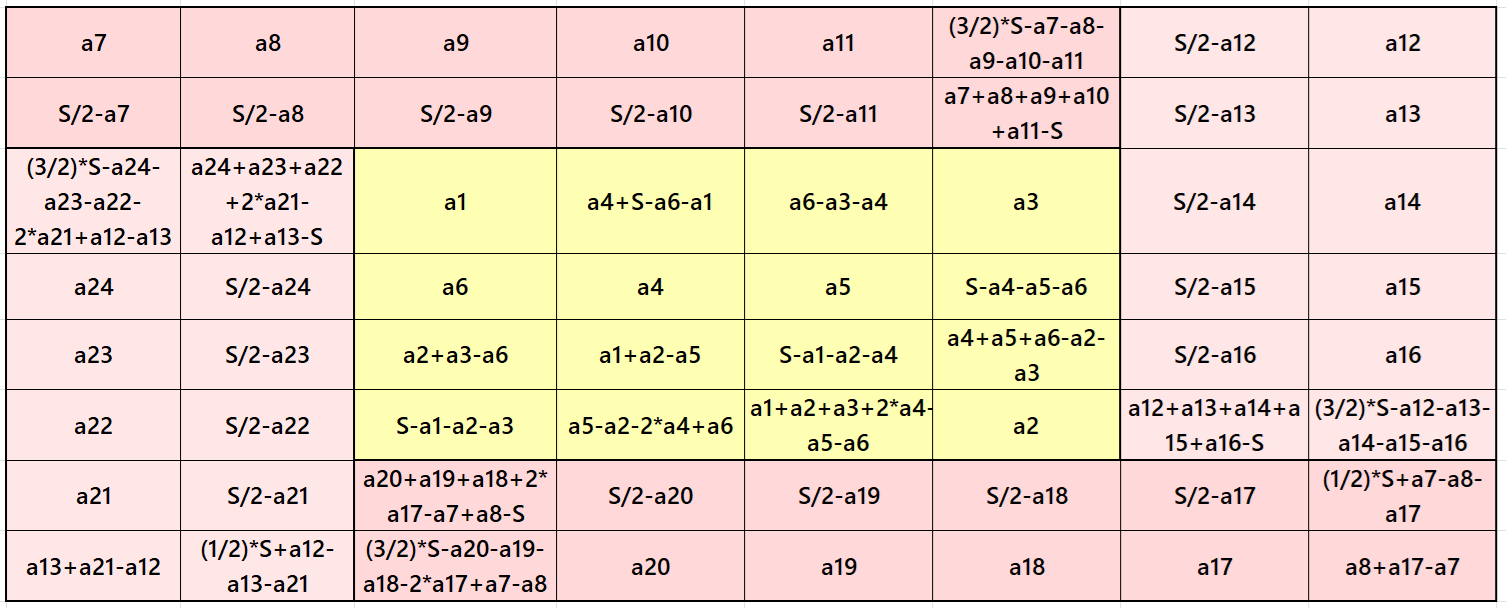
It is a composed of four equal sums magic rectangles of order 2×6 embedded with a magic square of order 4. Since the magic square of order 4 requires magic sum as multiple of 2, otherwise we have decimal entries, then the magic sum of order 8 is also multiple of 2. The magic sum of order 8 is given as S_8×8 :=2*S, where S is the magic sum of order 4. See below two examples:

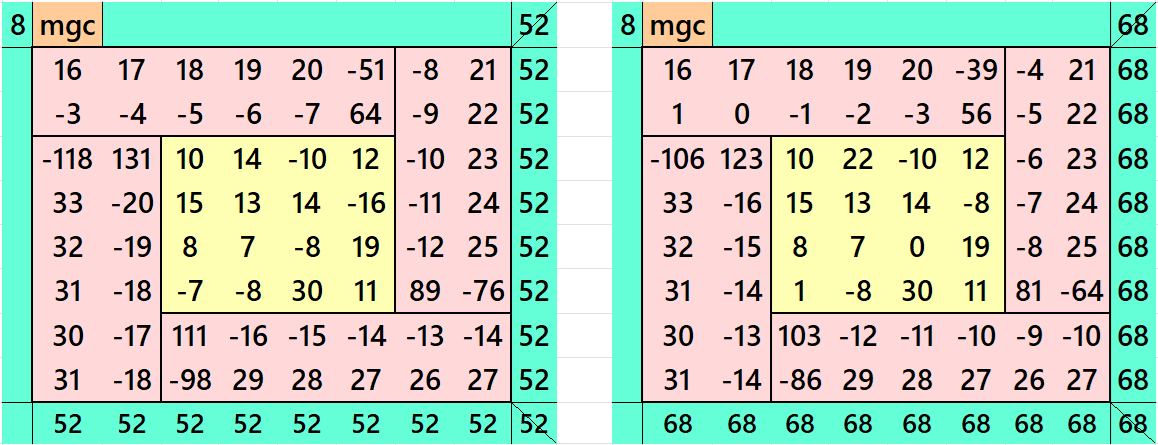
In the first example the magic sums are S_4×4 :=26 and S_8×8 :=52.
In the second example the magic sums are S_4×4 :=34 and S_8×8 :=68.

Double-Digit Bordered Algebric Magic Square of Order 9

Result 3: Double-Digit Bordered Algebric Magic Square of Order 9

It is a composed of four equal sums magic rectangles of order 2×7 embedded with a pandiagonal magic square of order 5. Here the magic sum of order 5 don’t have any condititon, but the magic sum of order 9 depends on number 5, i.e., S_9×9 :=9*S/5, where S is the magic sum of order 5. This requires the magic sum of order 5 should be multiple of 5, otherwise we may have decimal entries. See below two examples:

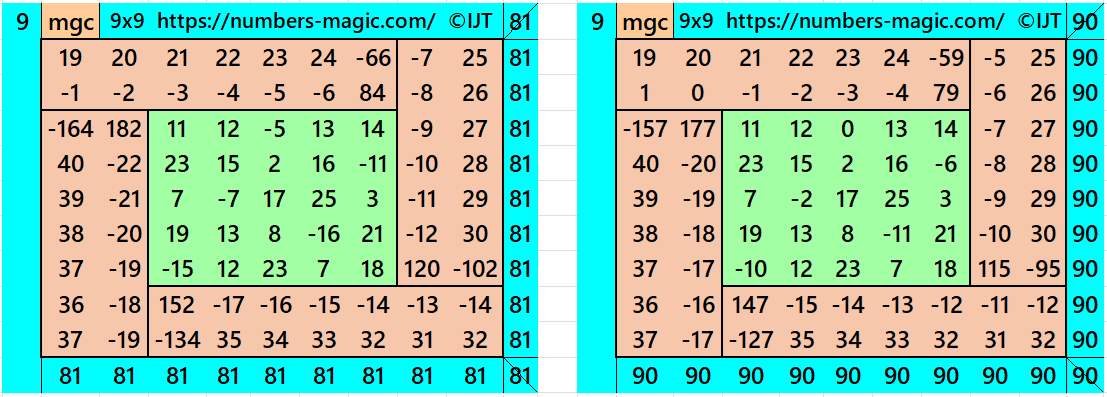
In the first example the magic sums are S_5×5 :=45 and S_9×9 :=81.
In the second example the magic sums are S_5×5 :=50 and S_9×9 :=90.

Double-Digit Bordered Algebric Magic Square of Order 10

Result 4: Double-Digit Bordered Algebric Magic Square of Order 10

It is a composed of four equal sums magic rectangles of order 2×8 embedded with a magic square of order 6. This magic square of order 6 is again composed of four equal sums magic squares of order 3. Since the magic square of order 3 requires magic sum as multiple of 3, otherwise we have decimal entries, then the magic sum of order 10 is also multiple of 3. The magic sum of order 10 is given as S_10×10 :=10*S/3, where S is the magic sum of order 3. In this case the magic sum of order 6 is given as S_6×6 :=2*S. See below two examples:

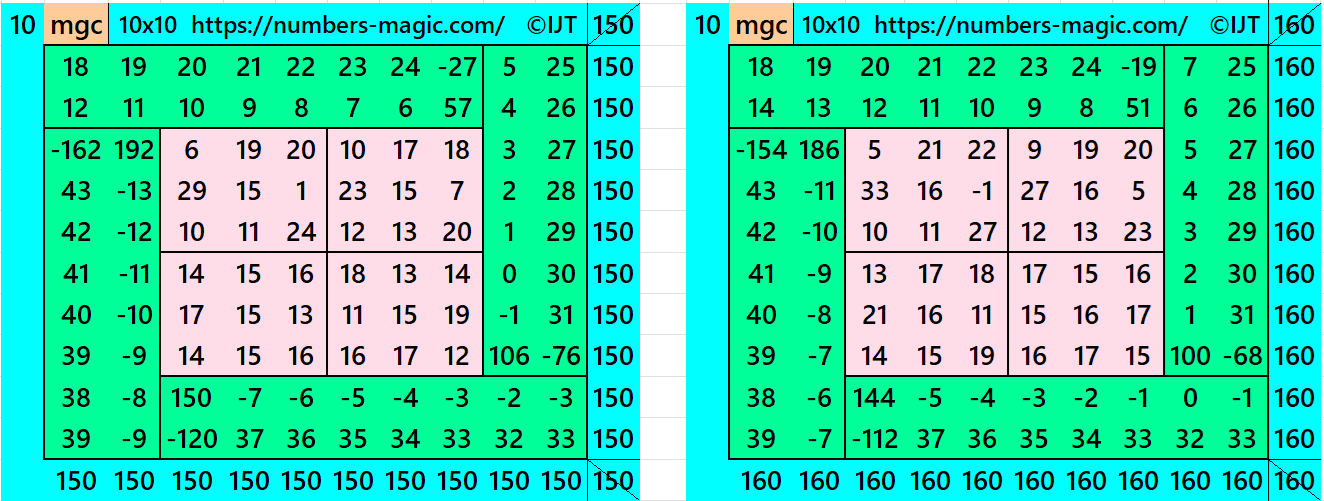
In the first example the magic sums are S_3×3 :=45, S_6×6 :=90 and S_10×10 := 150.
In the second example the magic sums are S_3×3 :=48, S_6×6 :=96 and S_10×10 := 160.

Double-Digit Bordered Algebric Magic Square of Order 11

Result 5: Double-Digit Bordered Algebric Magic Square of Order 11

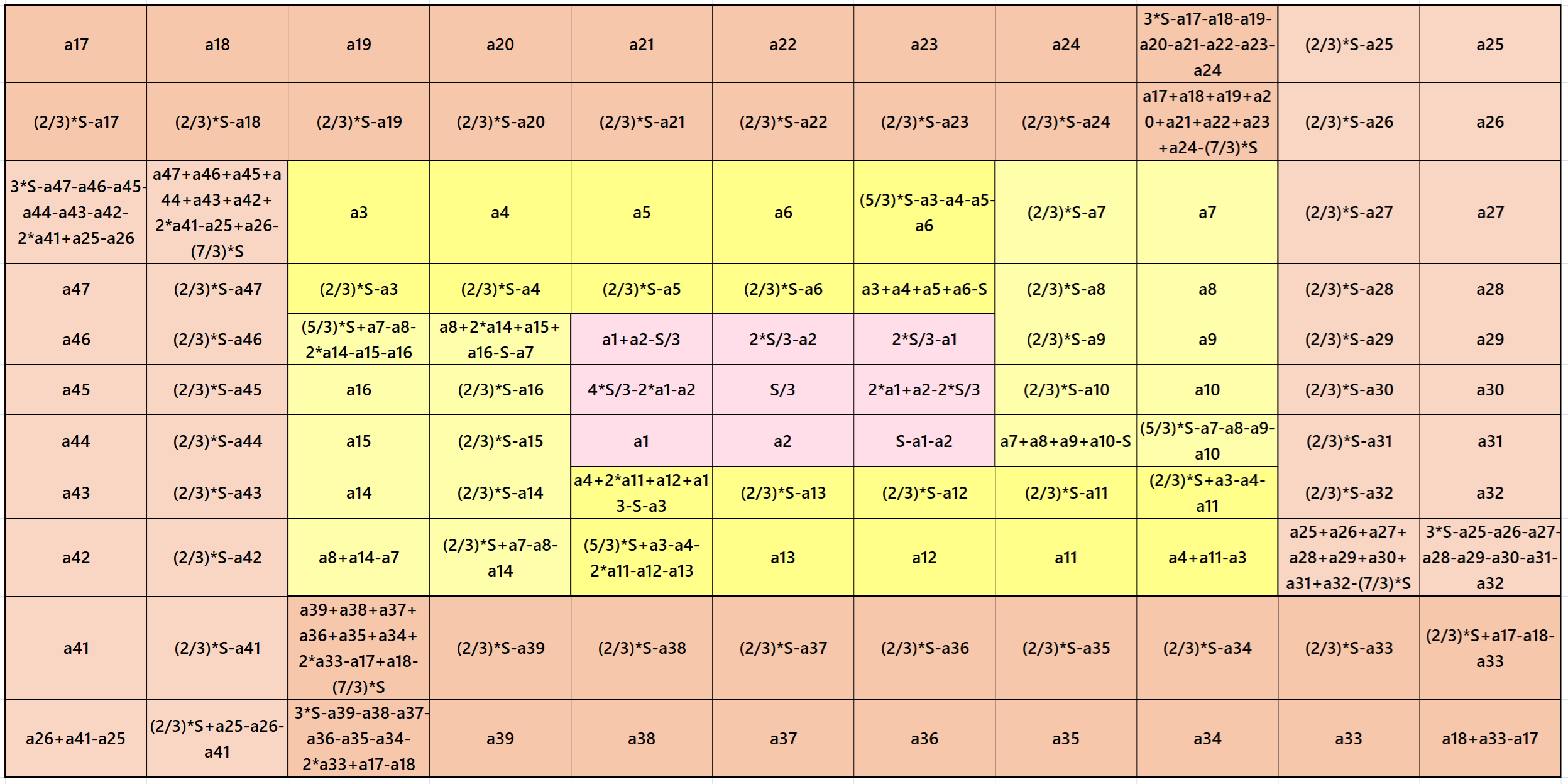
It is a composed of four equal sums magic rectangles of orders 2×5 and 2×9 (equality in each case) embedded with a magic square of order 3. Since the magic square of order 3 requires magic sum as multiple of 3, otherwise we have decimal entries, then the magic sums of orders 7 and 11 are also multiples of 3. The magic sum of orders 7 and 11 are given as S_11×11 :=7*S/3 and S_11×11 :=11*S/3, where S is the magic sum of order 3. See below two examples:

In the first example the magic sums are S_3×3 :=33, S_7×7 :=77 and S_11×11 := 121.
In the second example the magic sums are S_3×3 :=39, S_7×7 :=91 and S_11×11 := 143.

Double-Digit Bordered Algebric Magic Square of Order 12

Result 6: Double-Digit Bordered Algebric Magic Square of Order 12

It is a composed of four equal sums magic rectangles of orders 2×6 and 2×10 (equality in each case) embedded with a magic square of order 4. Since the magic square of order 4 requires magic sum as multiple of 2, otherwise we have decimal entries, then the magic sum of order 12 is also multiple of 2. The magic sum of orders 12 and 8 ares given as S_12×12 :=3*S and S_8×8 :=2*S, where S is the magic sum of order 4. See below two examples:

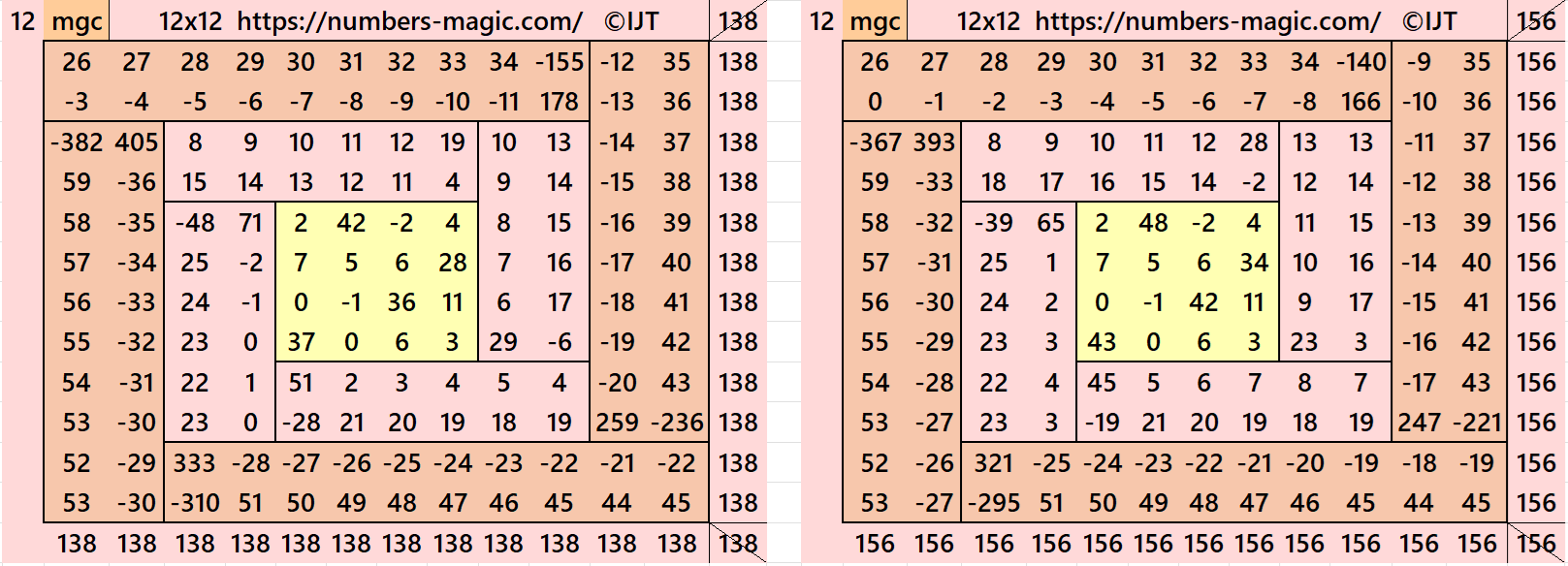
In the first example the magic sums are S_4×4 :=46, S_8×8 :=92 and S_12×12 := 138.
In the second example the magic sums are S_4×4 :=52, S_8×8 :=104 and S_12×12 := 156.

Double-Digit Bordered Algebric Magic Square of Order 13

Result 7: Double-Digit Bordered Algebric Magic Square of Order 13

It is a composed of four equal sums magic rectangles of orders 2×7 and 2×11 (equality in each case) embedded with a pandiagonal magic square of order 5. The magic square of order 5 don’t requires any condition but the magic sums of orders 13 and 9 depends on five, we mucht have these magic sums as multiples of 5 to avoid decimal entries. The magic sum of orders 13 and 9 ares given as S_13×13 :=13*S/5 and S_9×9 :=9*S/5, where S is the magic sum of order 5. See below two examples:

In the first example the magic sums are S_5×5 :=65, S_9×9 :=117 and S_13×13 := 169.
In the second example the magic sums are S_5×5 :=70, S_9×9 :=126 and S_13×13 := 182.

Double-Digit Bordered Algebric Magic Square of Order 14

Result 8: Double-Digit Bordered Algebric Magic Square of Order 14

It is a composed of four equal sums magic rectangles of orders 2×8 and 2×12 (equal in each case) embedded with a magic square of order 6. This magic square of order 6 is again composed of four equal sums magic squares of order 3. Since the magic square of order 3 requires magic sum as multiple of 3, otherwise we may have decimal entries. The magic sums of orders 10 and 14 are also multiple of 3. The magic sum of orders 10 and 14 are given as S_10×10 :=10*S/3 and S_10×10 :=14*S/3, where S is the magic sum of order 3. In this case the magic sum of order 6 is given as S_6×6 :=2*S. See below two examples:

In the first example the magic sums are S_3×3 :=66, S_6×6 :=132, S_10×10 :=220 and S_14×14 := 308.
In the second example the magic sums are S_3×3 :=75, S_6×6 :=150, S_10×10 :=250 and S_14×14 := 350.

Double-Digit Bordered Algebric Magic Square of Order 15

Result 9: Double-Digit Bordered Algebric Magic Square of Order 15

It is a composed of four equal sums magic rectangles of orders 2×5, 2×9 and 2×13 (equality in each case) embedded with a magic square of order 3. Since the magic square of order 3 requires magic sum as multiple of 3, otherwise we have decimal entries, then the magic sums of order 11 and 15 are also multiples of 3. The magic sum of orders 11 and 15 are given as S_11×11 :=11*S/3 and S_15×15 :=15*S/3=5*S, where S is the magic sum of order 3. See below two examples:

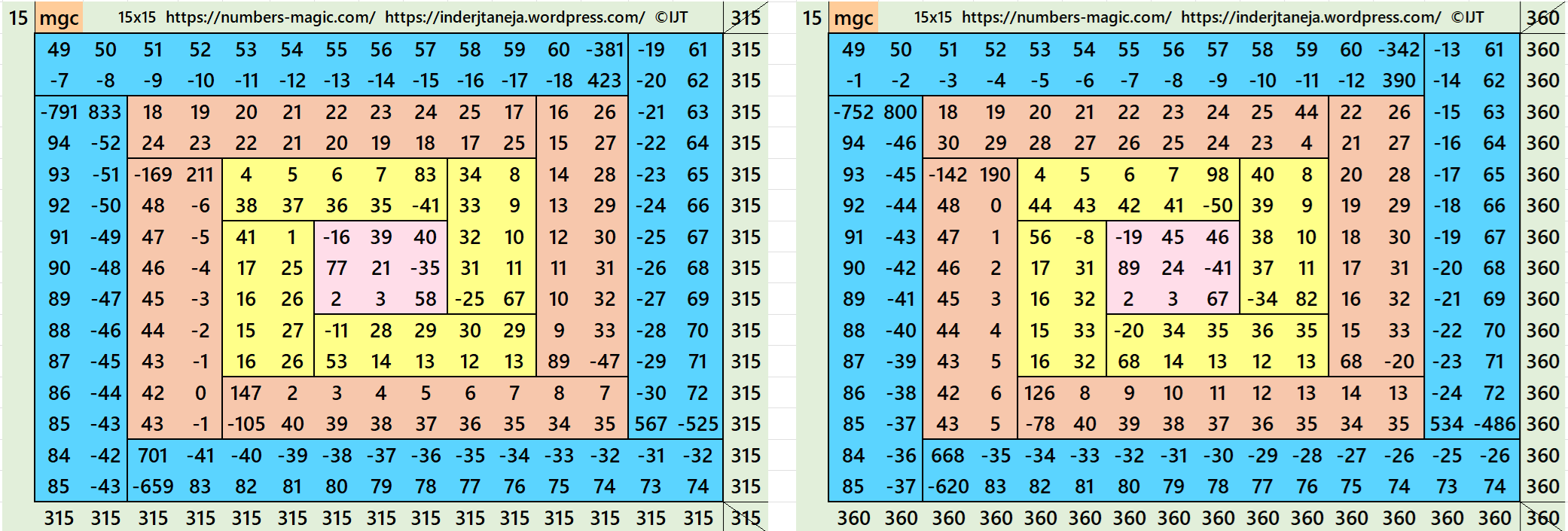
In the first example the magic sums are S_3×3 :=63, S_7×7 :=147, S_11×11 :=231 and S_15×15 := 315.
In the second example the magic sums are S_3×3 :=72, S_7×7 :=168, S_11×11 :=264 and S_15×15 := 360.

Double-Digit Bordered Algebric Magic Square of Order 16

Result 10: Double-Digit Bordered Algebric Magic Square of Order 16

It is a composed of four equal sums magic rectangles of orders 2×6, 2×10 and 2×14 (equality in each case) embedded with a magic square of order 4. Since the magic square of order 4 requires magic sum as multiple of 2, otherwise we have decimal entries, then the magic sum of orders, 8, 12 and 16 are also multiple of 2. The magic sum of orders 16, 12 and 8 ares given as S_16×16 :=4*S, S_12×12 :=3*S and S_8×8 :=2*S, where S is the magic sum of order 4. See below two examples:

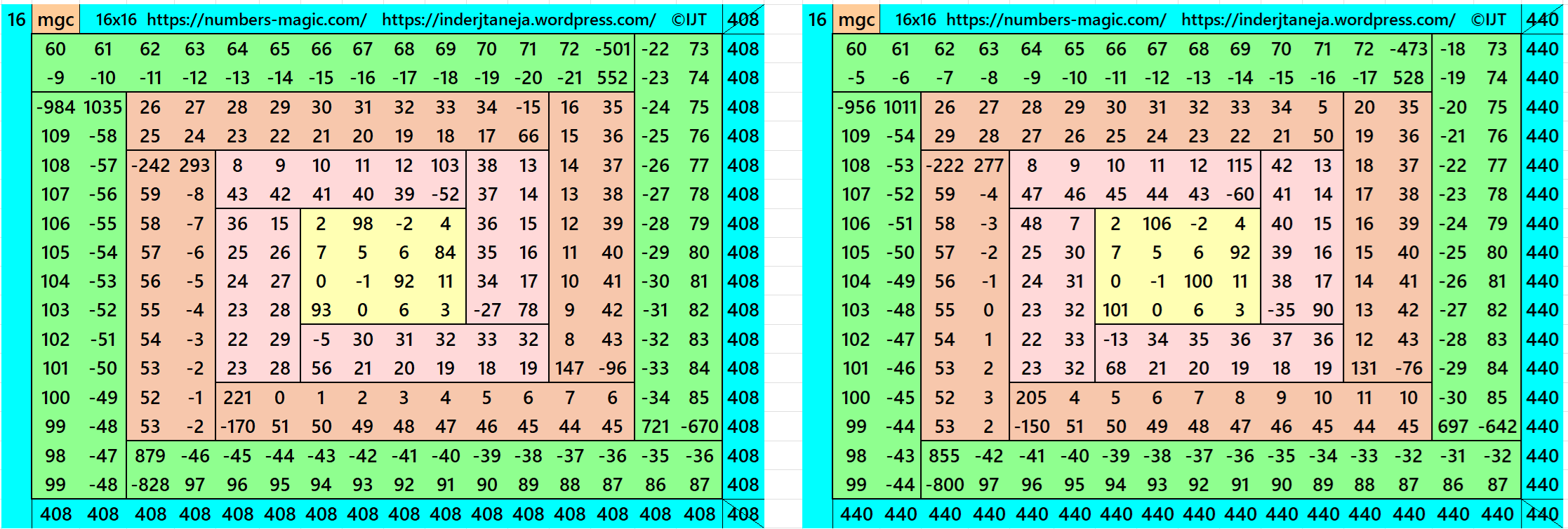
In the first example the magic sums are S_4×4 :=102, S_8×8 :=204, S_12×12 := 312 and S_16×16 := 408
In the second example the magic sums are S_4×4 :=110, S_8×8 :=220, S_12×12 := 330 and S_16×16 := 440

Double-Digit Bordered Algebric Magic Square of Order 17

Result 11: Double-Digit Bordered Algebric Magic Square of Order 17

It is a composed of four equal sums magic rectangles of orders 2×7, 2×11 and 2×15 (equality in each case) embedded with a pandiagonal magic square of order 5. The magic square of order 5 don’t requires any condition but the magic sums of orders 17, 13 and 9 depends on five. Thus, we must have these magic sums as multiples of 5 to avoid decimal entries. The magic sum of orders 17, 13 and 9 ares given as S_17×17 :=17*S/5, S_13×13 :=13*S/5 and S_9×9 :=9*S/5, where S is the magic sum of order 5. See below two examples:

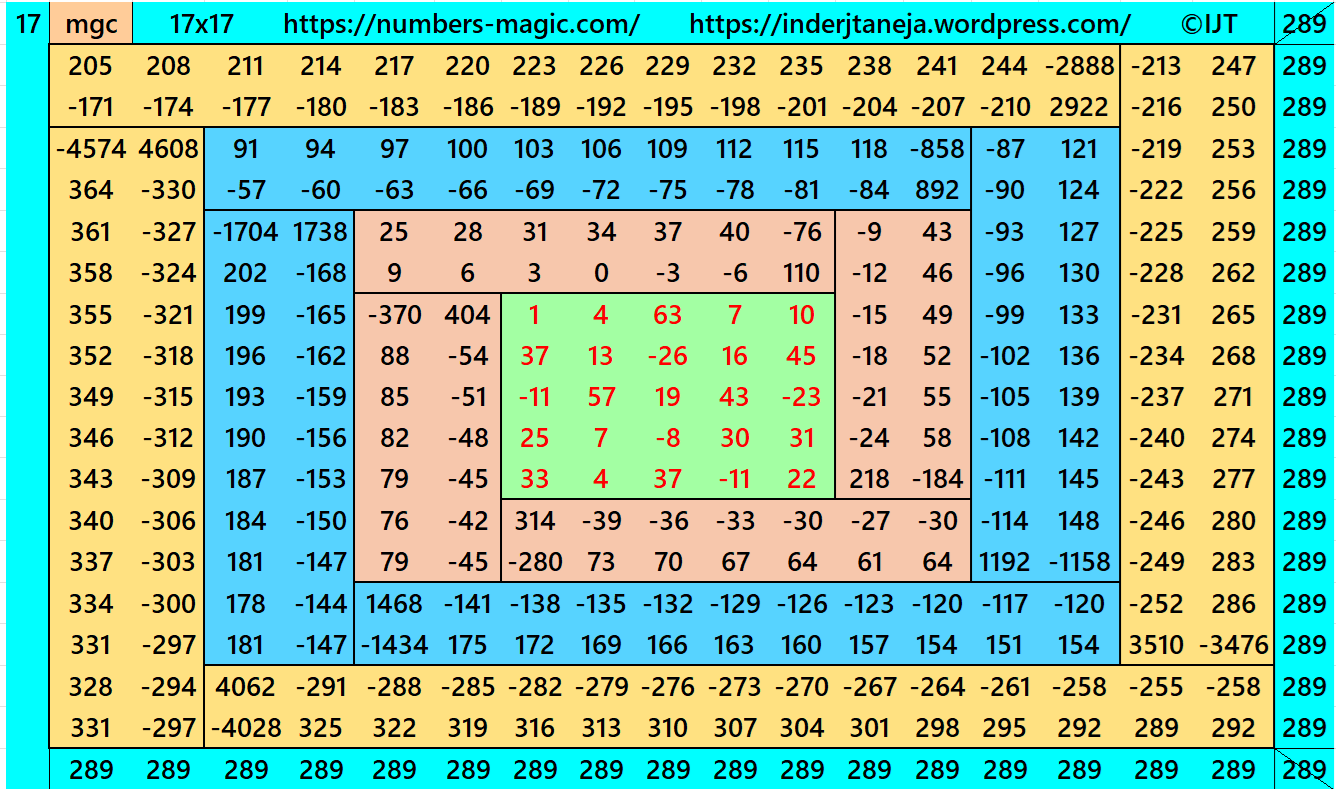
In this example the magic sums are S_5×5 :=85, S_9×9 :=153, S_13×13 :=221 and S_17×17 := 289.

In this example the magic sums are S_5×5 :=105, S_9×9 :=189, S_13×13 :=273 and S_17×17 := 357.

Double-Digit Bordered Algebric Magic Square of Order 18

Result 12: Double-Digit Bordered Algebric Magic Square of Order 18

It is a composed of four equal sums magic rectangles of orders 2×8, 2×12 and 2×16 (equal in each case) embedded with a magic square of order 6. This magic square of order 6 is again composed of four equal sums magic squares of order 3. Since the magic square of order 3 requires magic sum as multiple of 3, otherwise we may have decimal entries. The magic sums of orders 10, 14 and 18 are also multiple of 3. The magic sum of orders 10, 14 and 18 are given as S_10×10 :=10*S/3, S_14×14 :=14*S/3 and S_18×18 :=18*S/3 = 6*S, where S is the magic sum of order 3. In this case the magic sum of order 6 is given as S_6×6 :=2*S. See below two examples:

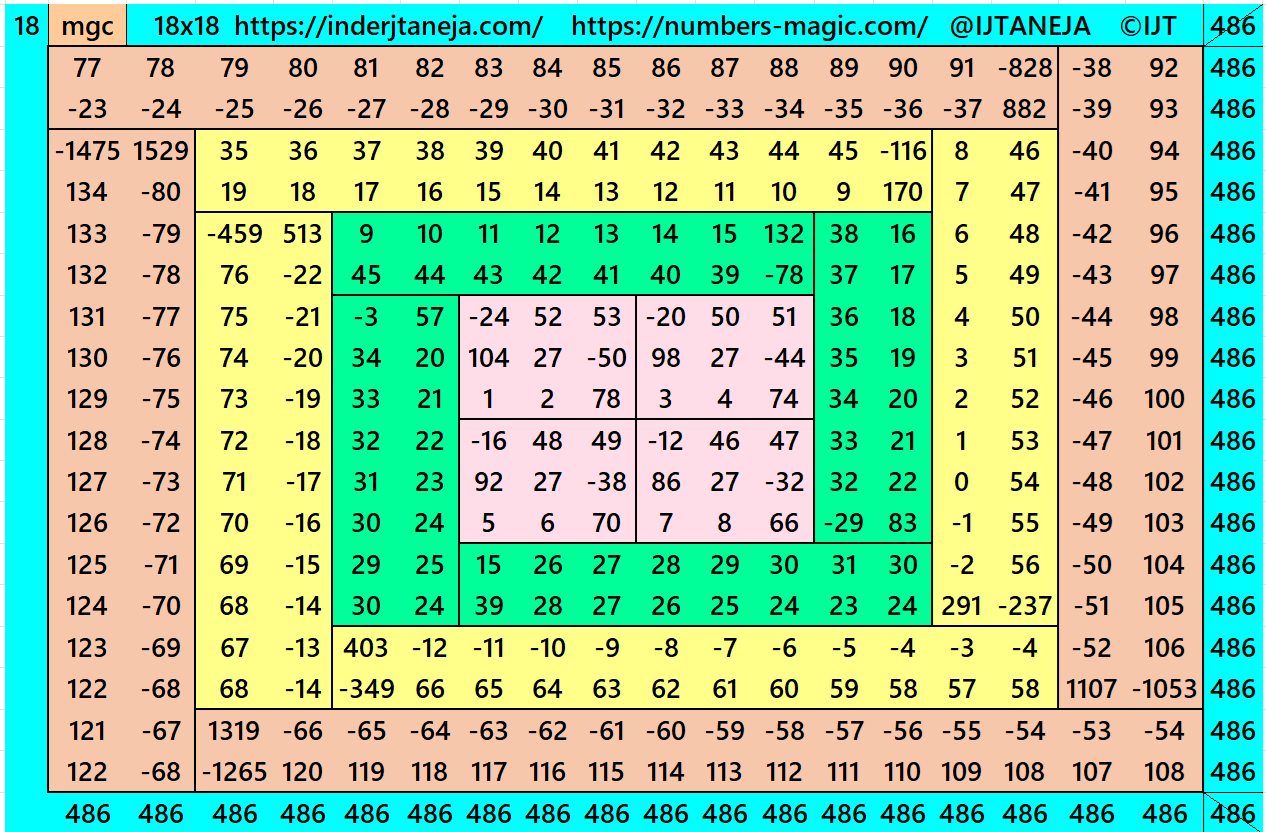
In this example the magic sums are S_3×3 :=81, S_6×6:=162, S_10×10 :=270, S_14×14 :=378 and S_18×18 := 486.

In this example the magic sums are S_3×3 :=99, S_6×6:=198, S_10×10 :=330, S_14×14 :=462 and S_18×18 := 594.

Double-Digit Bordered Algebric Magic Square of Order 19

Result 13: Double-Digit Bordered Algebric Magic Square of Order 19

It is a composed of four equal sums magic rectangles of orders 2×5, 2×9, 2×13 and 2×17 (equality in each case) embedded with a magic square of order 3. Since the magic square of order 3 requires magic sum as multiple of 3, otherwise we have decimal entries, then the magic sums of orders 7, 11, 15 and 19 are also multiples of 3. The magic sum of orders 7, 11, 15 and 19 are given as S_11×11 :=7*S/3, S_11×11 :=11*S/3, S_15×15 :=15*S/3=5*S and S_19×19 :=19*S/3 where S is the magic sum of order 3. See below two examples:

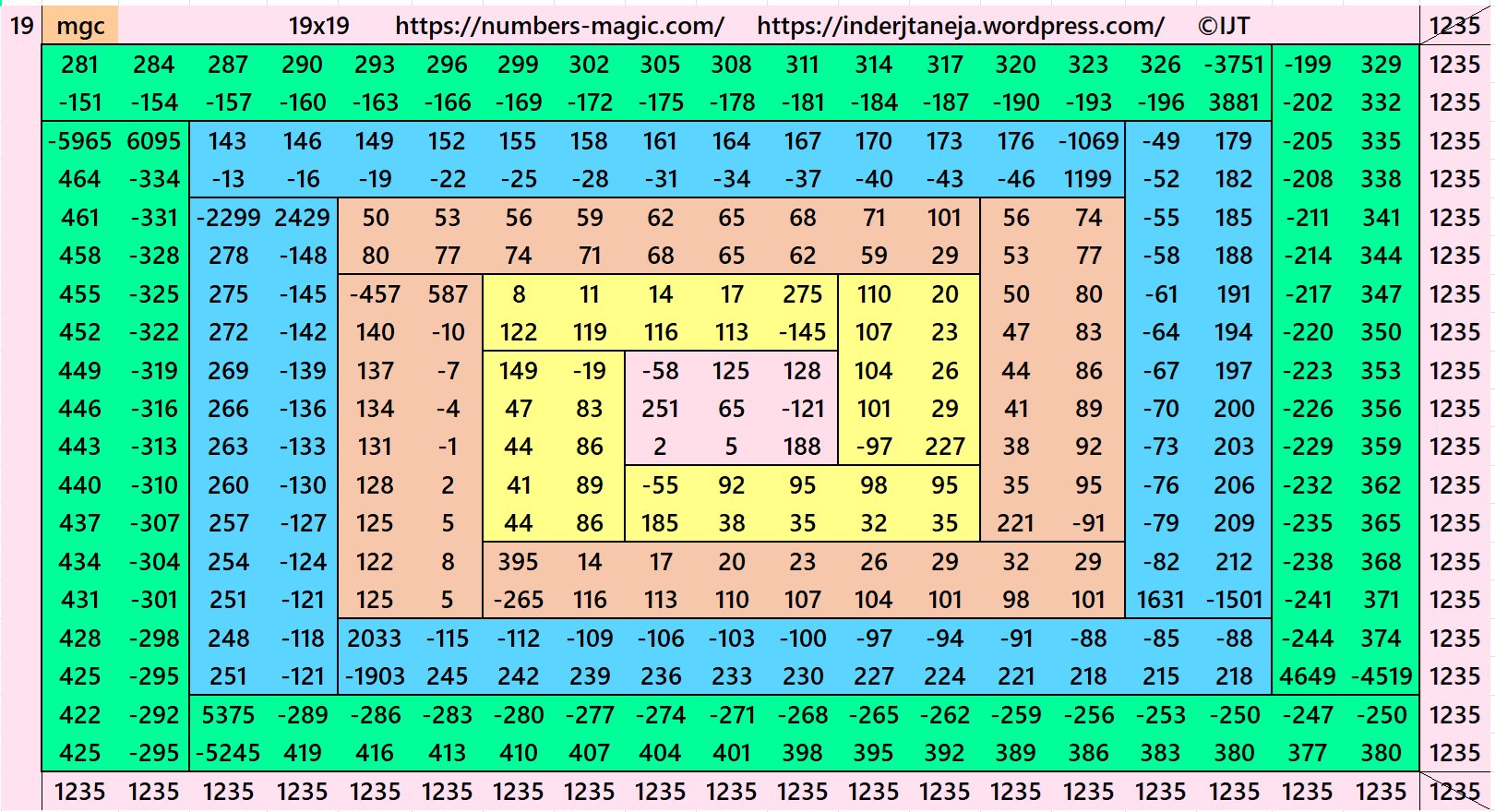
In this example the magic sums are S_3×3 :=195, S_7×7 :=455, S_11×11 :=715, S_15×15 := 975 and S_19×19 := 1235.

In this example the magic sums are S_3×3 :=198, S_7×7 :=462, S_11×11 :=726, S_15×15 := 990 and S_19×19 := 1254.

Double-Digit Bordered Algebric Magic Square of Order 20

Result 14: Double-Digit Bordered Algebric Magic Square of Order 20

It is a composed of four equal sums magic rectangles of orders 2×6, 2×10, 2×14 and 2×18 (equality in each case) embedded with a magic square of order 4. Since the magic square of order 4 requires magic sum as multiple of 2, otherwise we have decimal entries, then the magic sum of orders, 8, 12 and 16 are also multiple of 2. The magic sum of orders 20, 16, 12 and 8 ares given as S_16×16 :=5*S, S_16×16 :=4*S, S_12×12 :=3*S and S_8×8 :=2*S, where S is the magic sum of order 4. See below two examples:

In this example the magic sums are S_4×4 :=102, S_8×8 :=204, S_12×12 := 312, S_16×16 := 408 and S_20×20 := 510

In this example the magic sums are S_4×4 :=152, S_8×8 :=304, S_12×12 := 456, S_16×16 := 608 and S_20×20 := 760

References: Reduced Entries Magic Squares

Part 1: Day and Dates of the Year – 2025 in Terms of Magic Squares

• Inder J. Taneja, Magic Squares of Orders 3 to 7 in Representing Dates and Days of the Year 2025, Zenodo, May 04, 2025, pp. 1-474, https://doi.org/10.5281/zenodo.15338142.
  • Site Link: Magic Squares of Orders 3 to 7 Representing Dates and Days of the Year 2025 (new site)
  • Site Link: Magic Squares of Orders 3 to 7 Representing Dates and Days of the Year 2025 (old site)
• Inder J. Taneja, Magic Squares of Order 8 Representing Days and Dates of the Year 2025, Zenodo, May 04, 2025, pp. 1-134, https://doi.org/10.5281/zenodo.15338246.
  • Site Link: Magic Squares of Order 8 Representing Days and Dates of the Year 2025 (new site)
  • Site Link: Magic Squares of Order 8 Representing Days and Dates of the Year 2025 (old site)
• Inder J. Taneja, Magic Squares of Order 9 Representing Days and Dates of the Year 2025, Zenodo, May 09, 2025, pp. 1-132, https://doi.org/10.5281/zenodo.15375349.
  • Site Link: Magic Squares of Order 9 Representing Days and Dates of the Year 2025 (new site)
  • Site Link: Magic Squares of Order 9 Representing Days and Dates of the Year 2025 (old site)
• Inder J. Taneja, Magic Squares of Order 10 Representing Days and Dates of the Year 2025, Zenodo, May 21, 2025, pp. 1-59, https://doi.org/10.5281/zenodo.15481738.
  • Site Link: Magic Squares of Order 10 Representing Dates and Days of the Year 2025 (new site)
  • Site Link: Magic Squares of Order 10 Representing Dates and Days of the Year 2025 (old site)
• Inder J. Taneja, Magic Squares of Order 12 Representing Days and Dates of the Year 2025 Zenodo, June 10, 2025, pp. 1-43, https://doi.org/10.5281/zenodo.15631884.
  • Site Link: Magic Squares of Order 12 Representing Dates and Days of the Year 2025 (new site)
  • Site Link: Magic Squares of Order 12 Representing Dates and Days of the Year 2025 (old site).

Part 2: Reduced Entries Agebraic Magic Squares

• Inder J. Taneja, Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Orders 3 to 7, Zenodo, September 29, 2025, pp. 1-59, https://doi.org/10.5281/zenodo.17219769.
  • Site Link: Reduced Entries Algebraic Magic Squares of Orders 3, 5, 7 and 9 (new site)
  • Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (new site)
  • Site Link: Reduced Entries Algebraic Magic Squares of Orders 3, 5, 7 and 9 (old site)
  • Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (old site)
• Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 8, Zenodo, September 23, 2025, pp. 1-65, https://doi.org/10.5281/zenodo.17186001.
  • Site Link: Reduced Entries Algebraic Magic Squares of Orders 4, 6, 8 and 10 (new site)
  • Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (new site)
  • Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (old site)
• Inder J. Taneja, Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9, Zenodo, August 27, 2025, pp. 1-92, https://doi.org/10.5281/zenodo.16955571.
  • Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9 (new site)
  • Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9 (old site)
• Inder J. Taneja. Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 10, Zenodo, September 18, 2025, pp. 1-112,  https://doi.org/10.5281/zenodo.17149185
  • Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 10 (new site)
  • Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 10 (old site)
• Inder J. Taneja, Self-Made Algebraic Magic Squares of Order 11, Zenodo, October 12, 2025, pp. 1-58, https://doi.org/10.5281/zenodo.17330815 .
  • Site Link: Self-Made Algebraic Magic Squares of Order 11 (new site)
  • Site Link: Self-Made Algebraic Magic Squares of Order 11 (old site)
• Inder J. Taneja, Self-Made Algebraic Semi-Magic Squares of Order 11, Zenodo, October 12, 2025, pp. 1-77, https://doi.org/10.5281/zenodo.17330822.
  • Site Link: Self-Made Algebraic Semi-Magic Squares of Order 11 (new site)
  • Site Link: Self-Made Algebraic Semi-Magic Squares of Order 11 (old site)
• Inder J. Taneja, Reduced Entries Algebraic Magic and PanMagic Squares of Order 12, Zenodo, July 23, 2025, pp. 1-74, https://doi.org/10.5281/zenodo.16370556.
  • Site Link: Reduced Entries Algebraic Magic and Panmagic Squares of Order 12 (new site)
  • Site Link: Reduced Entries Algebraic Magic and Panmagic Squares of Order 12 (old site)
• Inder J. Taneja, Reduced Entries Algebraic Semi-Magic Squares of Order 12, Zenodo, July 23, 2025, pp. 1-60, https://doi.org/10.5281/zenodo.15692014.
  • Site Link: Reduced Entries Algebraic Semi-Magic Squares of Order 12  (old site)
  • Site Link: Reduced Entries Algebraic Semi-Magic Squares of Order 12 (old site)
• Inder J. Taneja, Double-Digit Cyclic-Type Bordered Reduced Entries Algebraic Magic Squares of Orders 7 to 20, Zenodo, November 21, 2025, pp. 1-37, https://doi.org/10.5281/zenodo.17675032.
  • Site Link1: Double-Digit Cyclic-Type Bordered Algebraic Magic Squares of Orders 7 to 20 for Reduced Entries (New Site)
  • Site Link2: Double-Digit Cyclic-Type Bordered Algebraic Magic Squares of Orders 7 to 20 for Reduced Entries (old site)

References: Double-Digit Magic Squares

• Inder J. Taneja, Two Digits Bordered Magic Squares of Orders 10, 14, 18 and 22, Zenodo, April, 30, 2023, pp. 1-43, https://doi.org/10.5281/zenodo.7880931.
• Inder J. Taneja, Two Digits Bordered Magic Squares of Orders 26 and 30, Zenodo, April, 30, 2023, pp. 1-45, https://doi.org/10.5281/zenodo.7880937.
• Inder J. Taneja, Two Digits Bordered Magic Squares of Orders 36 and 40, Zenodo, May, 04, 2023, pp. 1-41, https://doi.org/10.5281/zenodo.7896709.
• Inder J. Taneja, Two Digits Bordered Magic Squares of Orders 34 and 38, Zenodo, May 10, 2023, pp. 1-45, https://doi.org/10.5281/zenodo.7922571.
• Inder J. Taneja, Two Digits Bordered Magic Squares of Orders 28 and 32, Zenodo, April, 26, 2023, pp. 1-36, https://doi.org/10.5281/zenodo.7866981.
• Inder J. Taneja, Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24, Zenodo, April, 26, 2023, pp. 1-43, https://doi.org/10.5281/zenodo.7866956.
• Inder J. Taneja, New Concepts in Magic Squares: Double Digits Bordered Magic Squares of Orders 7 to 108, Zenodo, August 09, 2023, pp. 1-30, https://doi.org/10.5281/zenodo.8230214.