Different Types and Aspects of Magic Squares of Order 16

This work brings different types of magic squares of order 16. These includes

1. Block-Wise Pandiagonal Magic Square of Order 16.
2. Block-Wise Bimagic Square of Order 16.
3. Single-Digit Bordered Magic Squares.
4. Embedded Single Digit Magic Squares.
5. Cornered Magic Square.
6. Double-Digit Bordered Magic Squares.
7. Striped Magic Squares.
8. Different Styles of Magic Squares.
9. Four-Digits Bordered Magic Squares.
10. Latin Square Distributions
11. Palindromic Entries Magic and Bimagic Squares.
12. Perfect Square Entries Sum.
13. Pythagorean Triples Entries Type Magic Squares.
14. Upside-Down and Mirror Looking Magic and Bimagic Squares.
15. Water Reflection Magic Squares.

We can write 16:=2². It can be written as blocks of order 4. We know that magic sum of a magic square of order n having 1 to n² number of entries is given by

S_nxn:= n*(1+n²)/2

In this case we have

S_16×16:= 16*(1+16²)/2 = 2056

All the work is for the sequential entries from 1 to 256 resulting in magic sum of 2056.

Whole work can be downloaded at the following link:

Inder J. Taneja, Different Types and Aspects of Magic Squares of Order 16, Zenodo, November 06, 2025, pp. 1-66, https://doi.org/10.5281/zenodo.17543834

Below are few examples of magic squares of order 16, based on above classifications.

1. Block-Wise Magic Squares

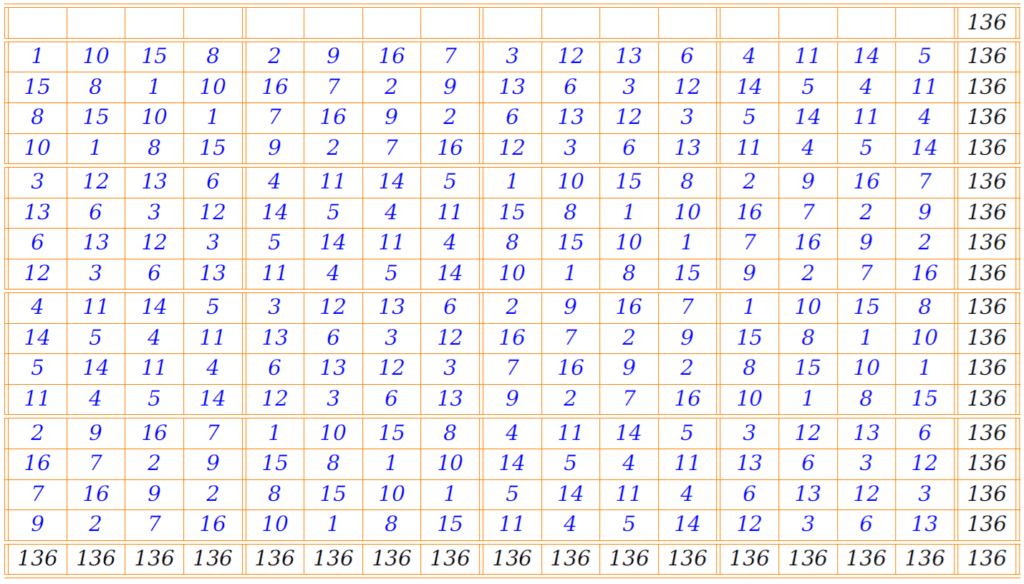
Example 1:

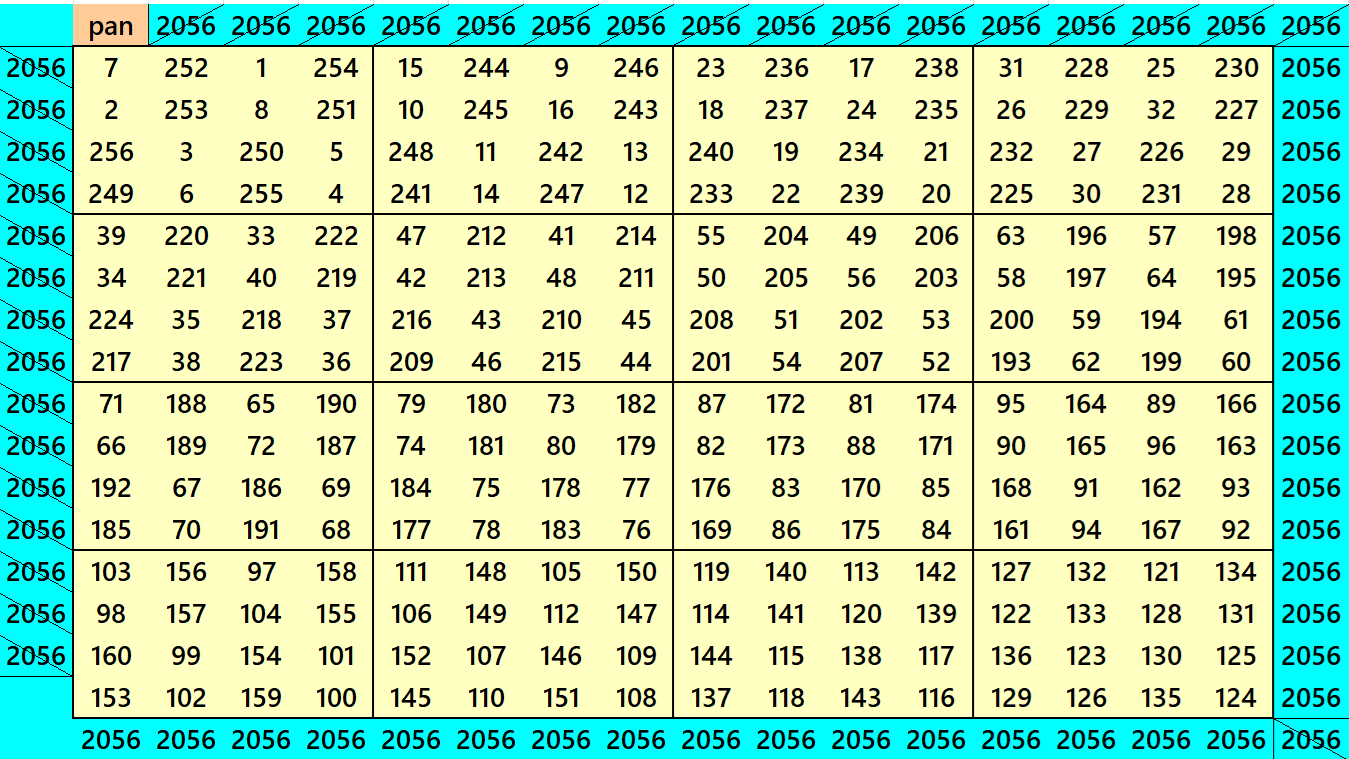
It is a block-wise pandiagonal magic square of order 16 with equal sums pandiagonal magic squares of order 4. For more study refer the following work:

Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 4

Example 2:

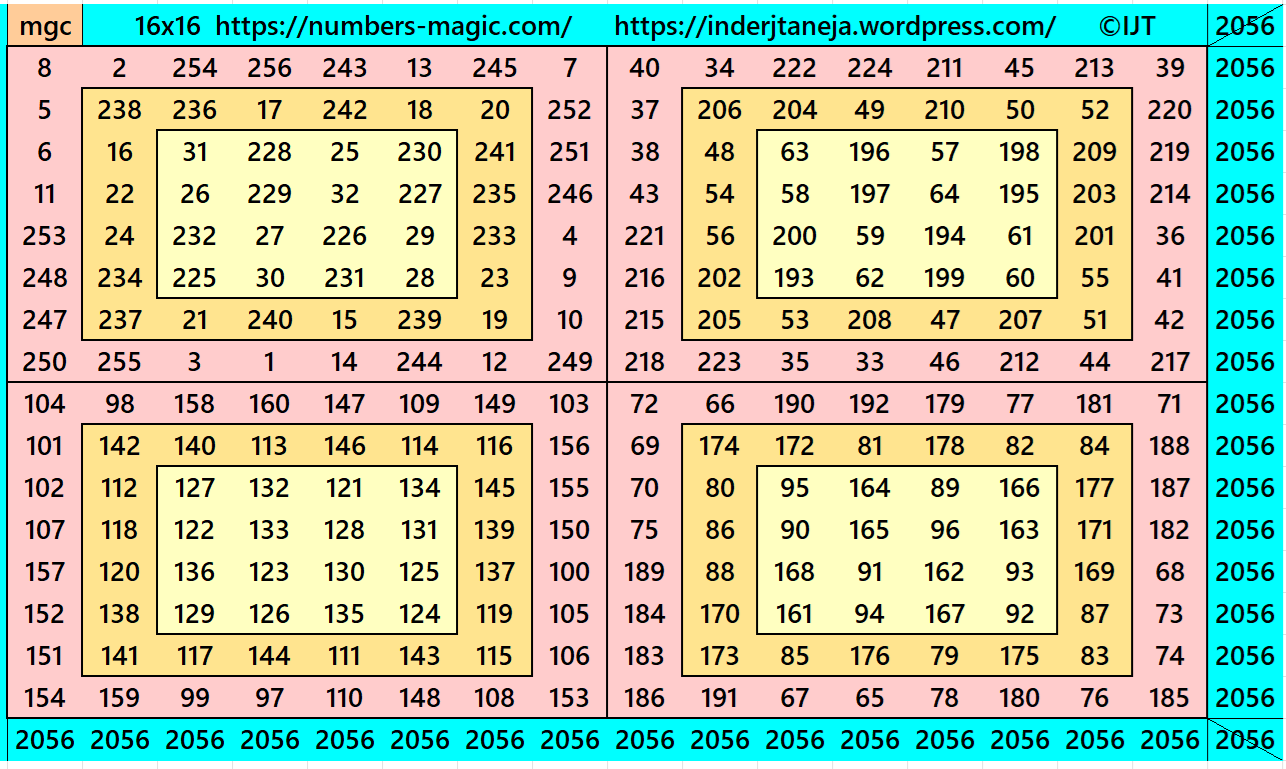
It is a block-wise magic square of order 16, where the blocks are single-digit bordered magic squares of order 8

2. Block-Wise Bimagic Square

Example 3:

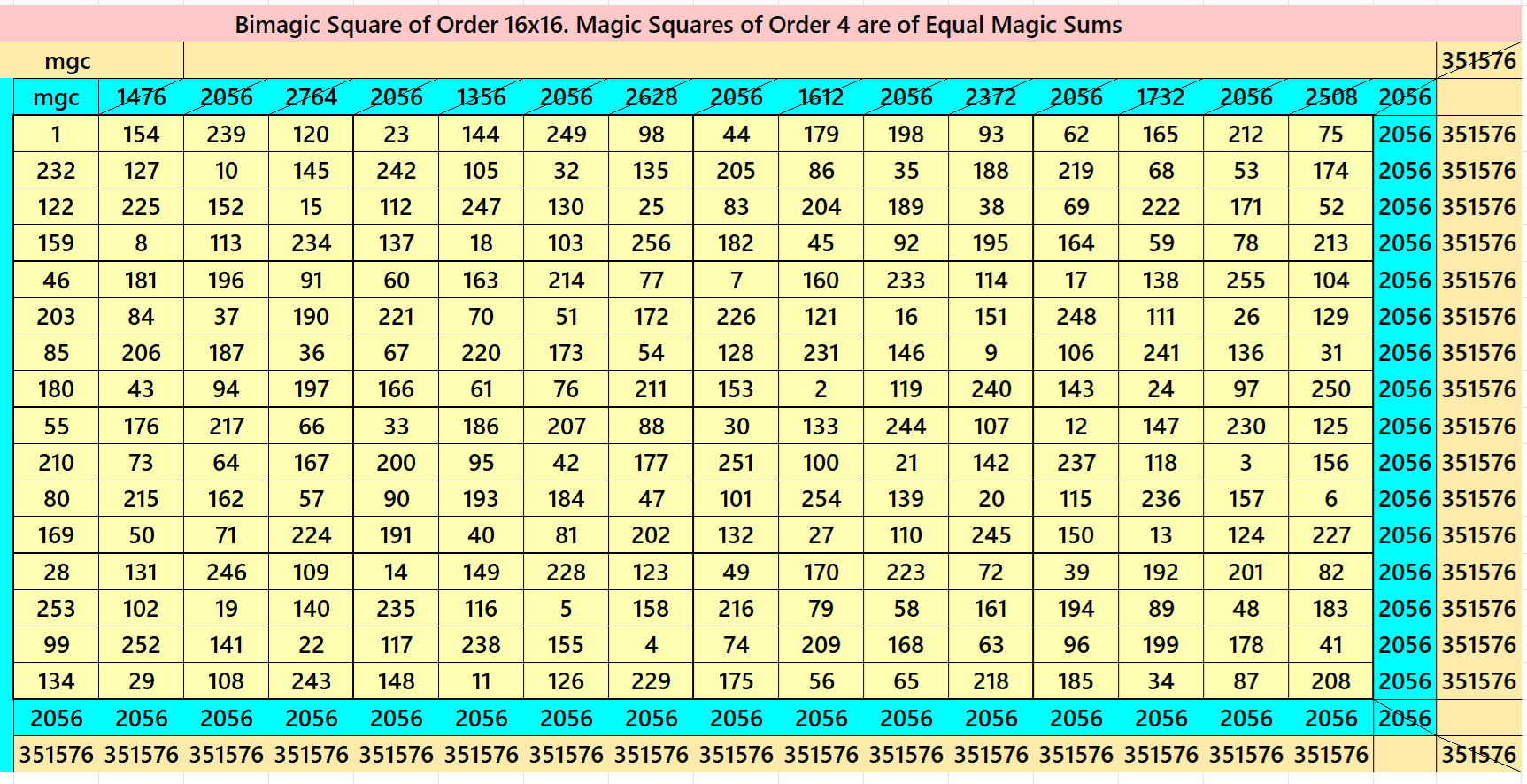
It is a bimgic square of order 16. The blocks of order 4 are equal sums magic square of order 4.

3. Single-Digit Bordered Magic Squares

Example 4:

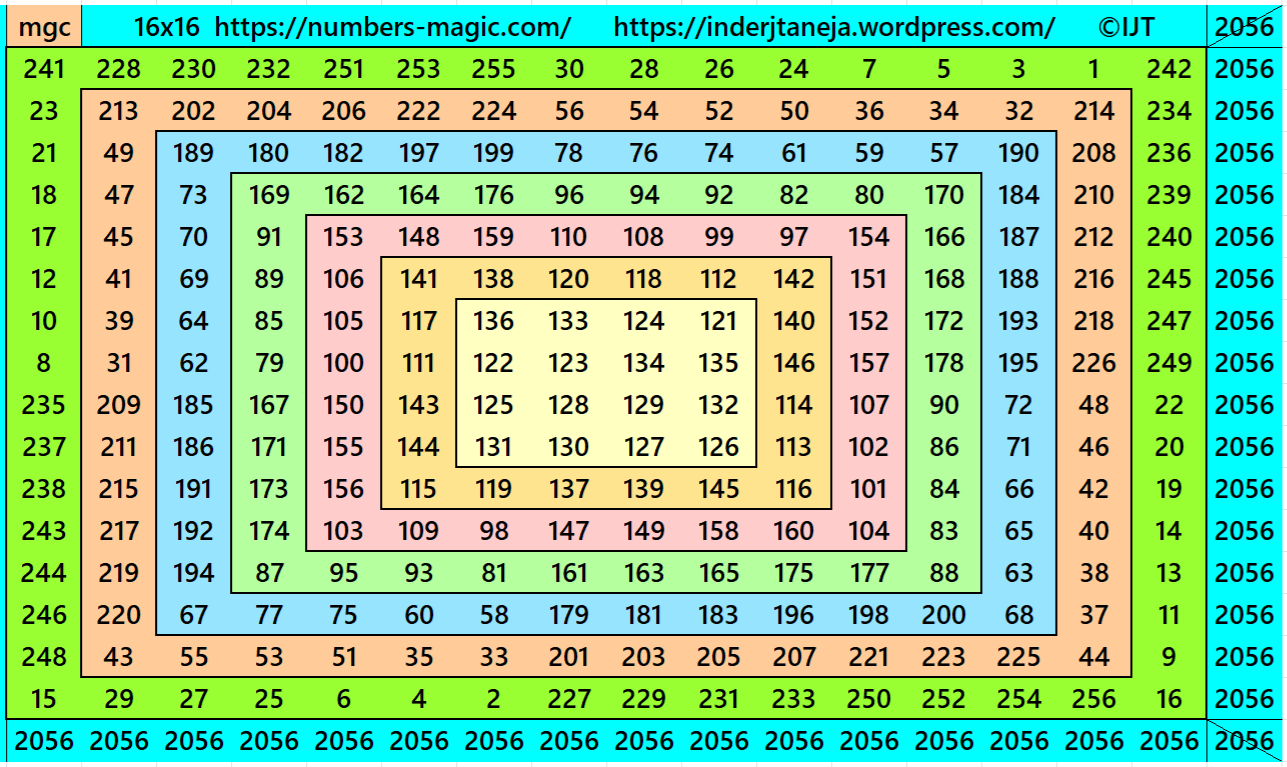
It is a single-digit bordered magic square of order 16. Removing the higher borders still we are left with magic squares of lower orders, such as of orders 14, 12, 10,… etc. The internal block is a magic square of order 4.

4. Embedded Single-Digit Bordered Magic Squares

Example 5:

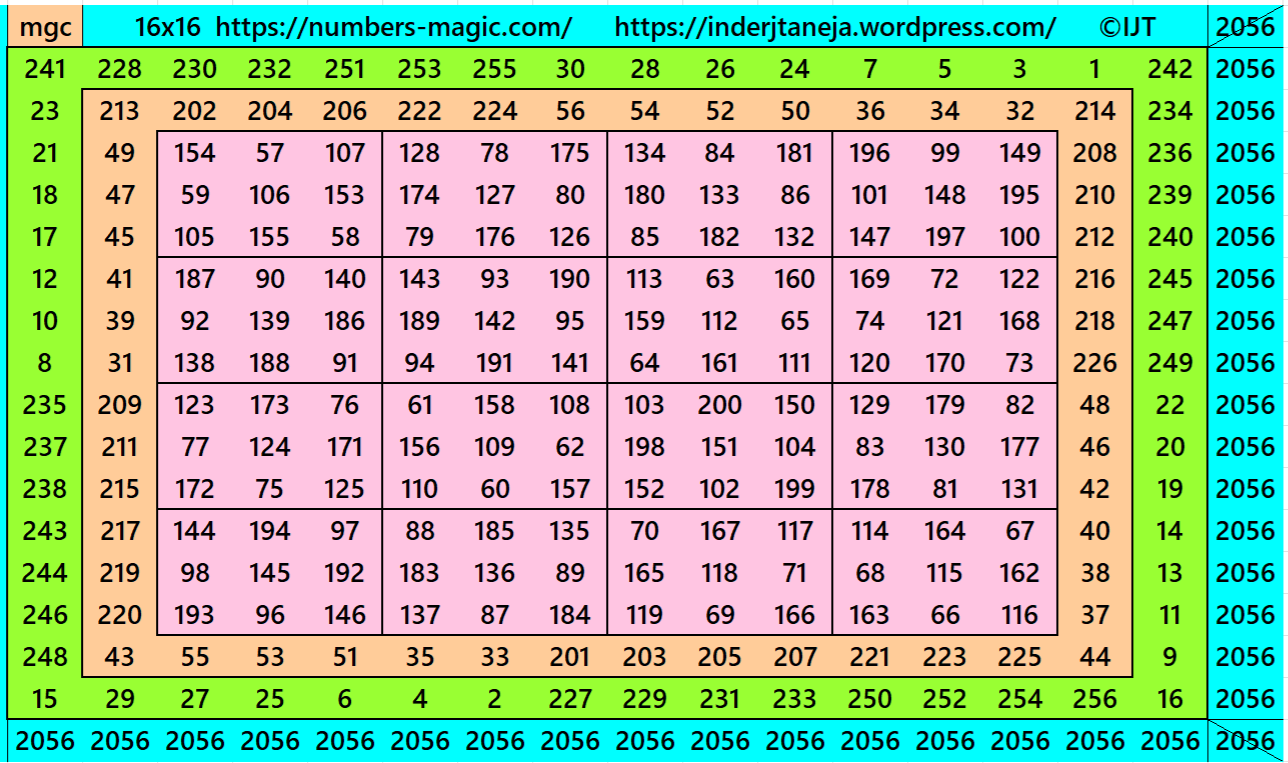
It is a single-digit bordered magic square of order 16 embedded with a magic square of order 12 formed by equal sums semi-magic squares of order 3.

Example 6:

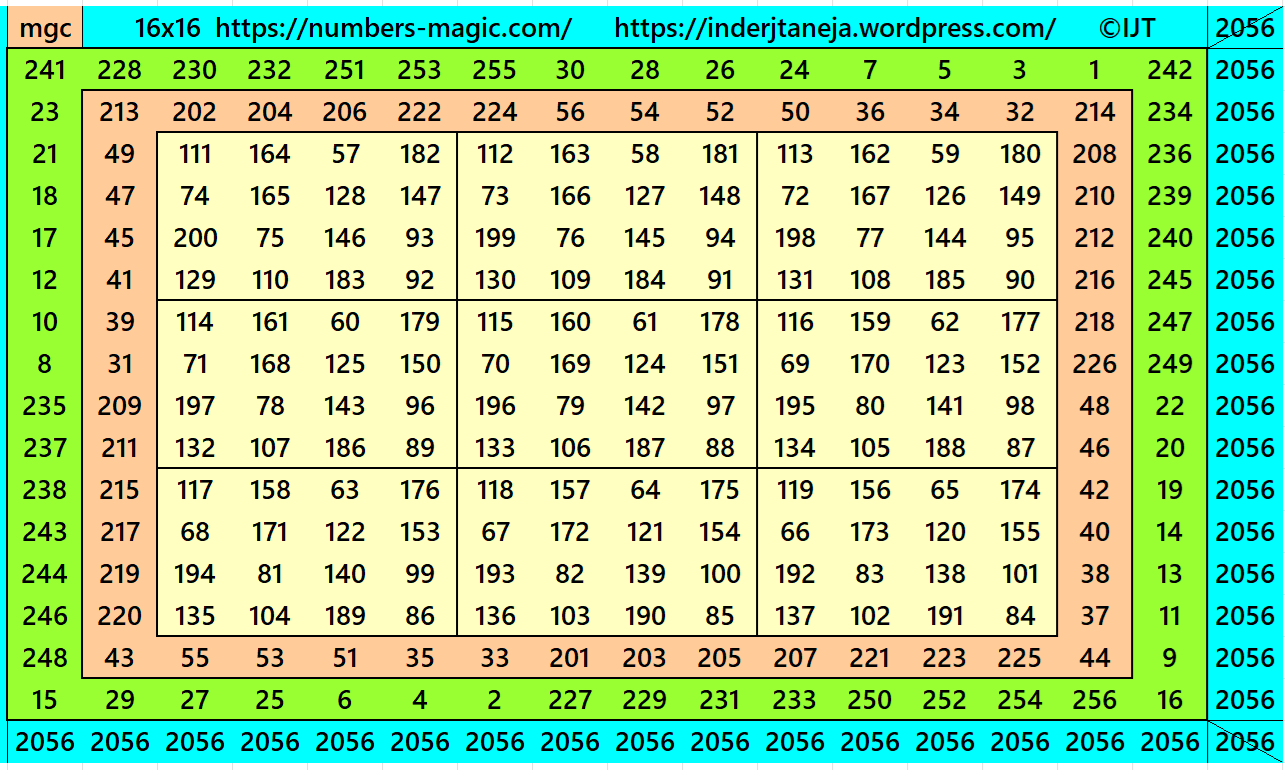
It is a single-digit bordered magic square of order 16 embedded with a magic square of order 12 formed by equal sums pandiagonal magic squares of order 4.

Example 7:

It is a single-digit bordered magic square of order 16 embedded with a magic square of order 12 formed by equal sums magic squares of order 6.

Example 8:

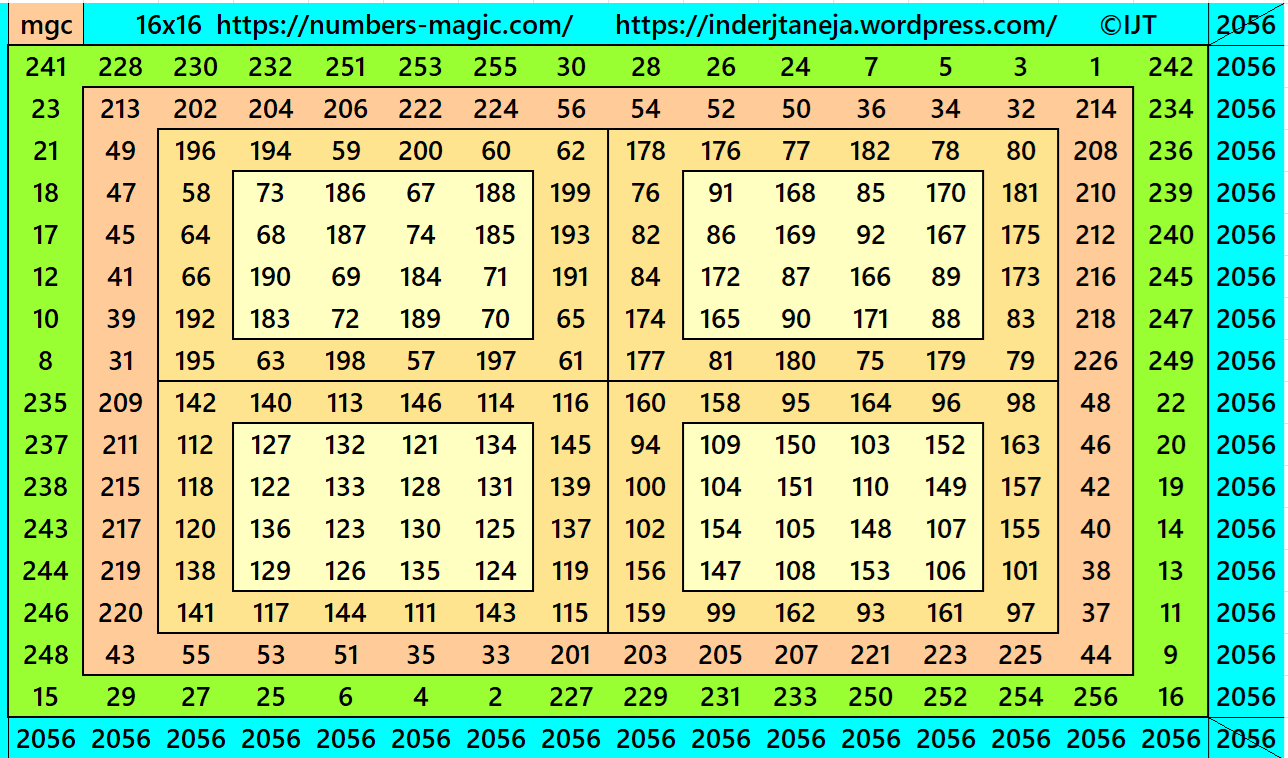
It is a single-digit bordered magic square of order 16 embedded with a magic square of order 12 fomred by four equal sums single-digit magic square of order 6

Different Types of Magic Squares: Even Number Orders From 10 to 26

5. Cornered Magic Square

Example 9:

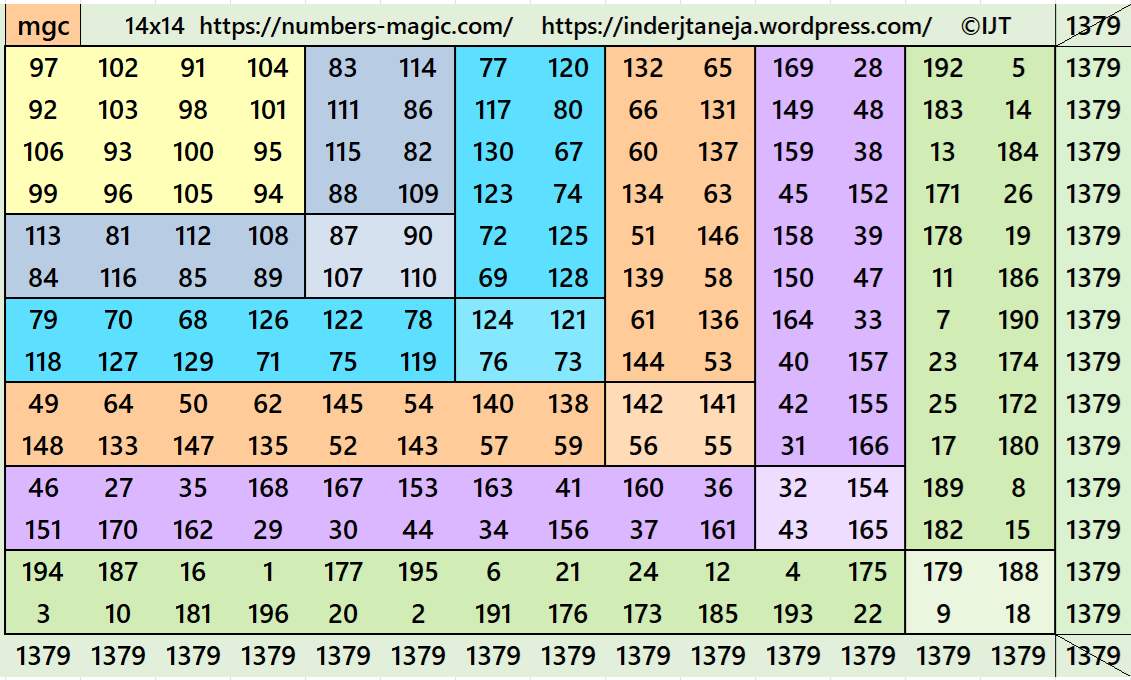
It is a cornered magic square of order 16 where upper-left to below are magic squares of orders 4, 6, 8, etc. For more details refer the following work:

1. Cornered Magic Squares in Construction of Magic Squares of Orders 16, 20, 24 and 28
2. Different Styles of Magic Squares of Order 16 Using Bordered Magic Rectangles

6. Double-Digit Bordered Magic Squares

Example 10:

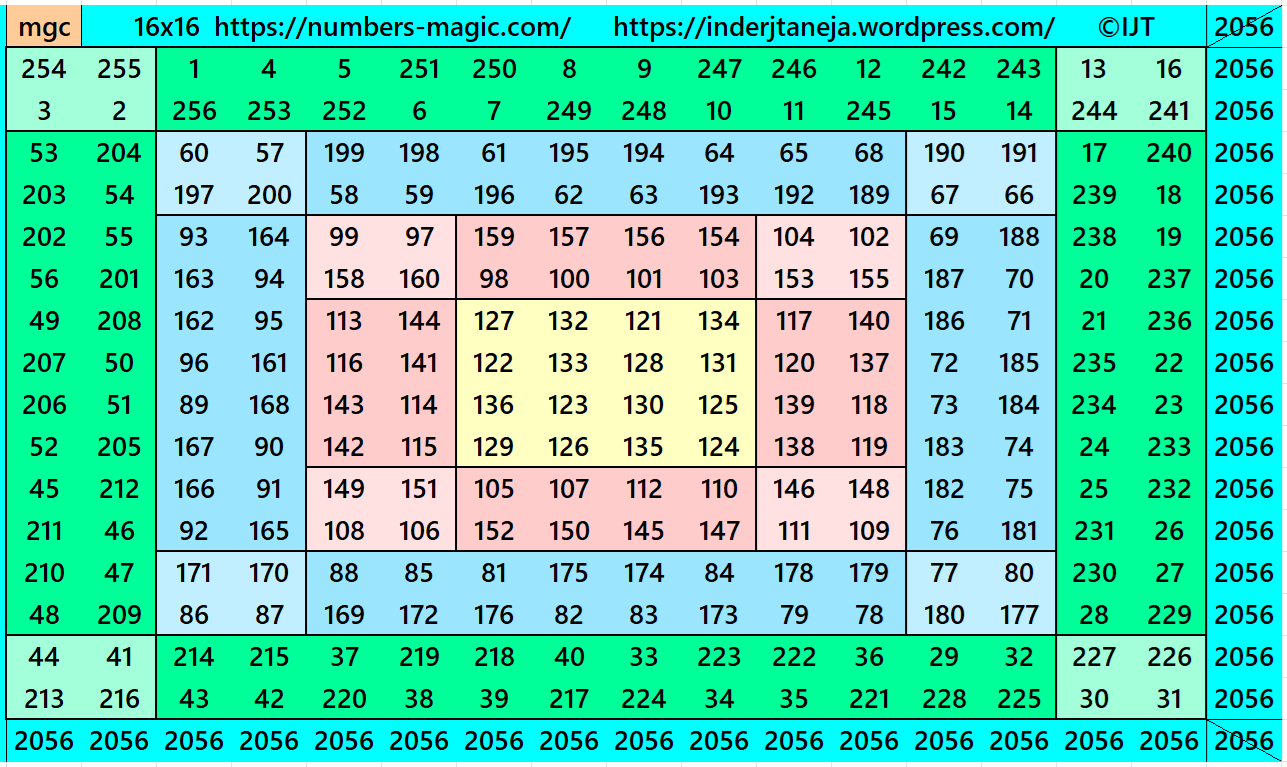
It is a double-digit bordered magic square of order 16. Removing the higher borders still we are left with magic squares of lower orders, such as of orders 12, 8 and 4. The internal block is a pandiagonal magic square of order 4.

Example 11:

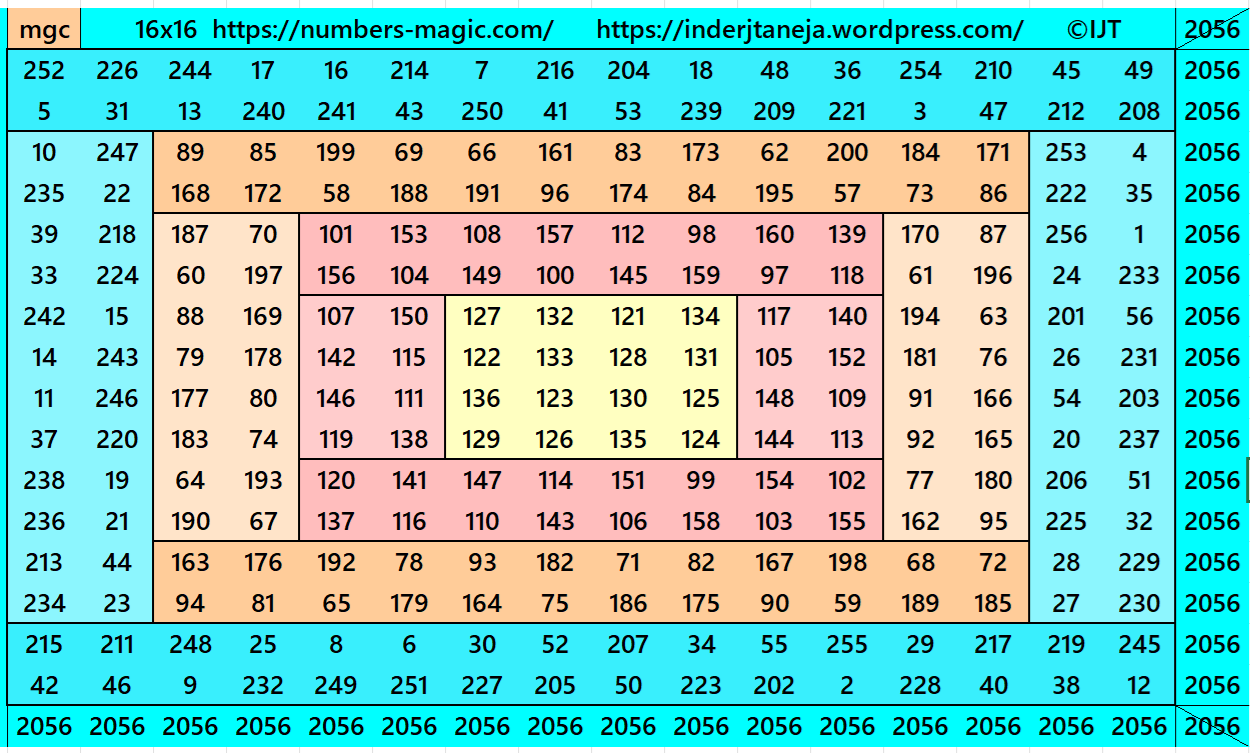
It is a also double-digit bordered magic square of order 16 written in little different way. Here we don’t have block of order 2×2 as in the previous example. Removing the higher borders still we are left with magic squares of lower orders, such as of orders 12, 8 and 4. The internal block is a pandiagonal magic square of order 4.

Example 12:

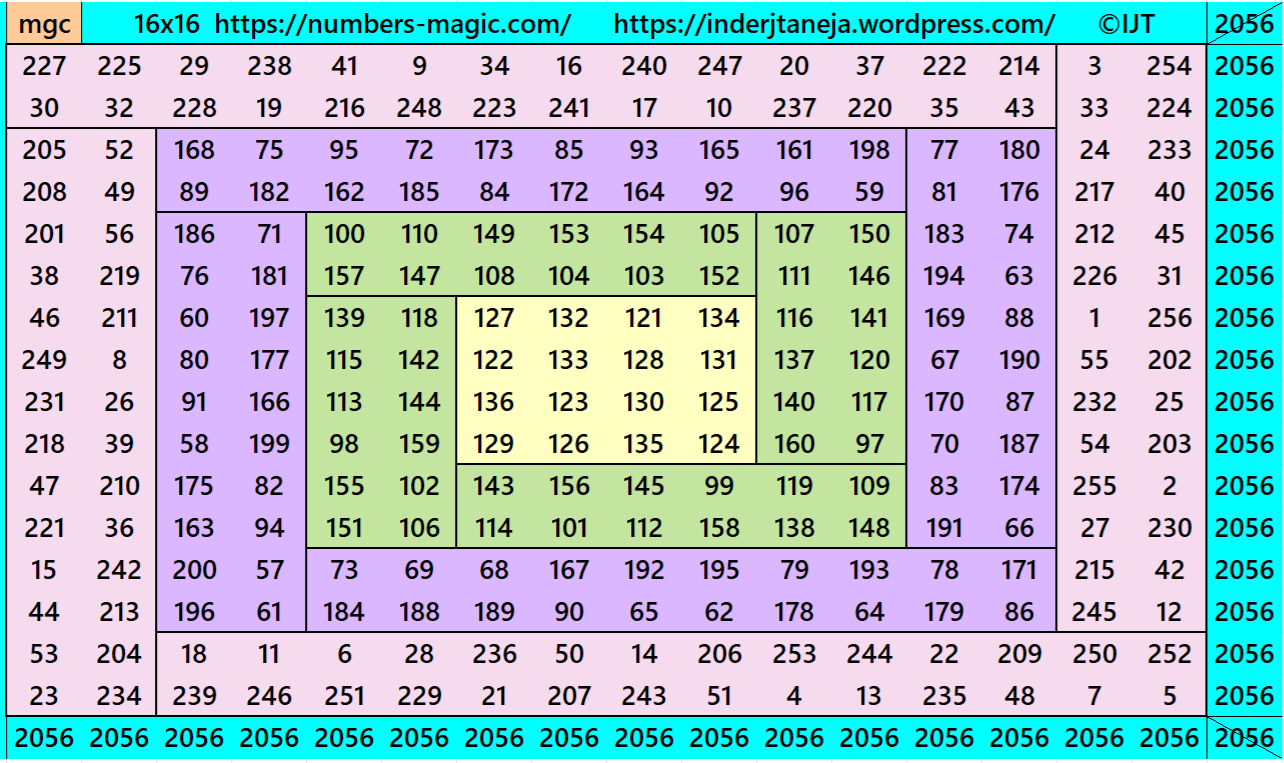
It is a also double-digit bordered magic square of order 16 written in little different way. In each blocks the magic rectangles are of equal width and length. We call these types as cyclic magic rectangles. Removing the higher borders still we are left with magic squares of lower orders, such as of orders 12, 8 and 4. The internal block is a pandiagonal magic square of order 4.

7. Striped Magic Squares of Order 16

Example 13:

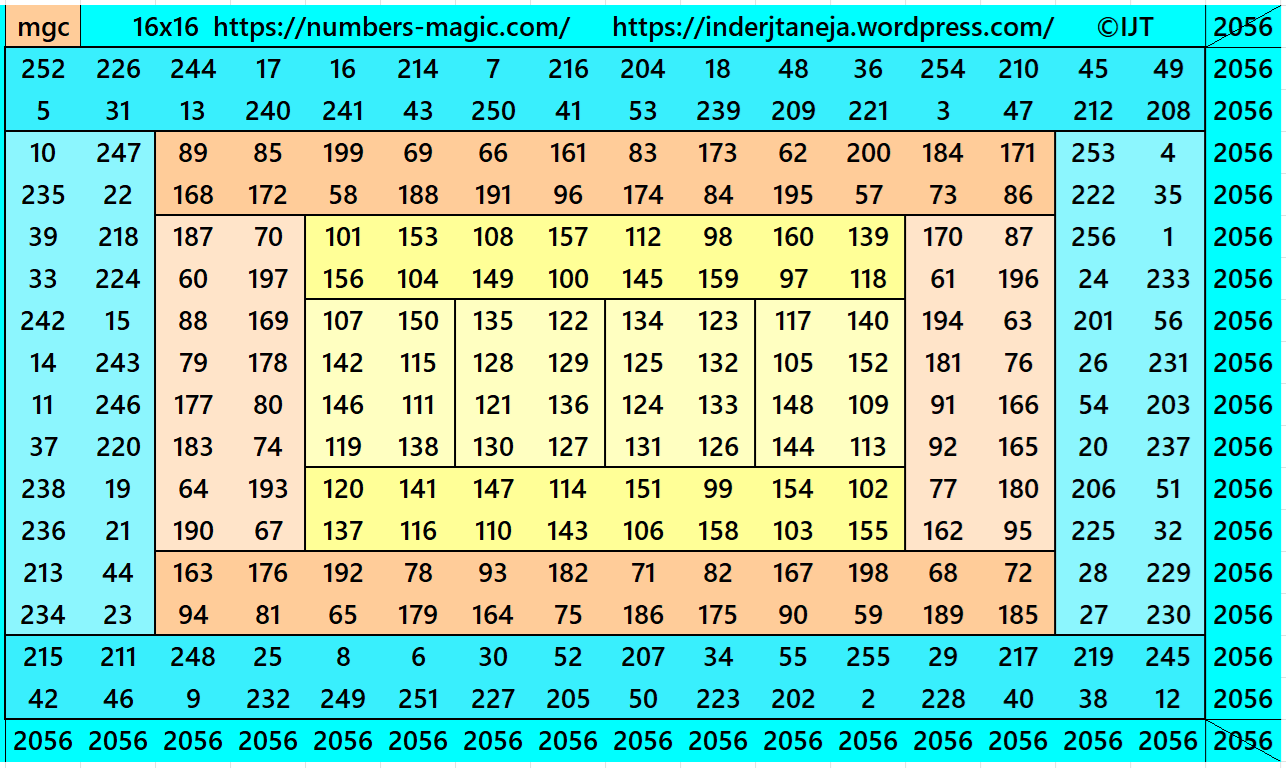
It is a also double-digit bordered magic square of order 16 formed by magic rectangle strips of equal width. The only difference is in the length of each magic rectangle. These types if magic squares we call as striped magic squares.

Example 14:

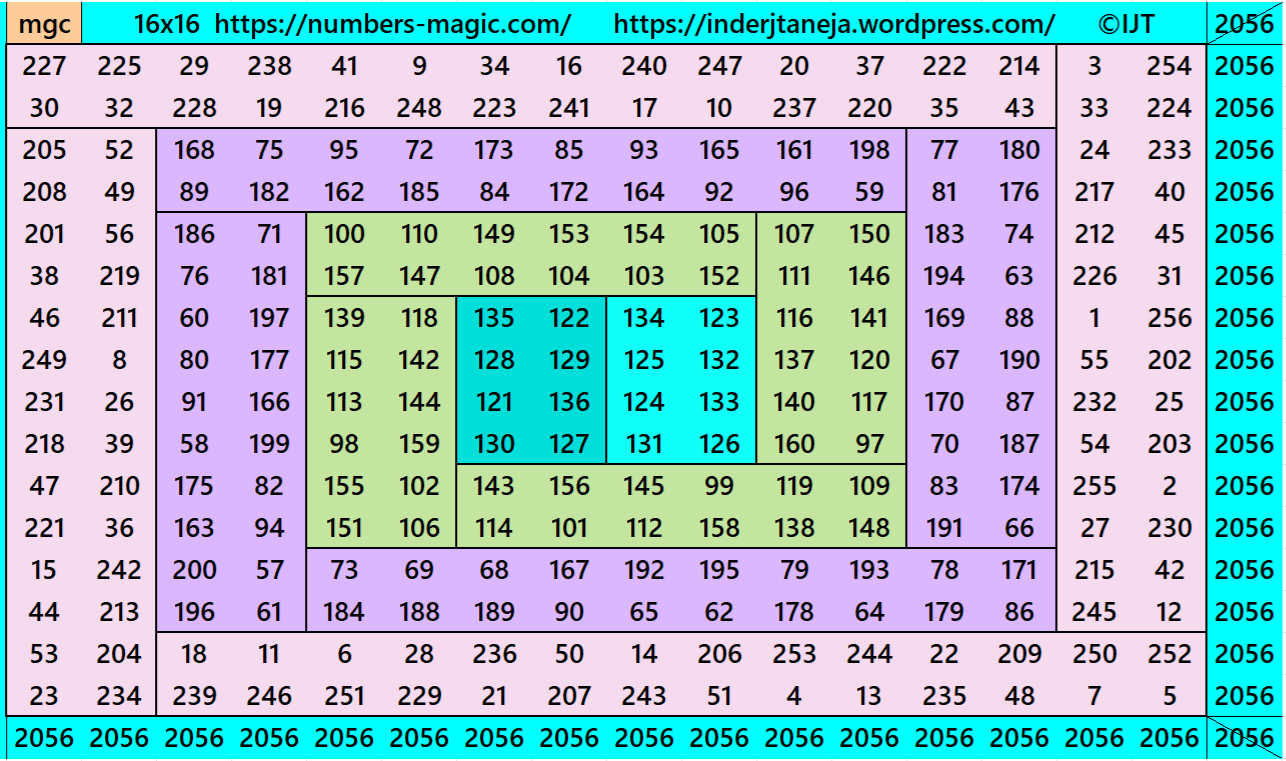
It is a also double-digit bordered magic square of order 16 formed by magic rectangle strips of equal width. The only difference is in the length of each magic rectangle. These types if magic squares we call as striped magic squares.

Example 15:

It is a also double-digit corner type magic square of order 16 formed by magic rectangle strips of equal width. The only difference is in the length of each magic rectangle. These types if magic squares we call as striped magic squares.

Example 16:

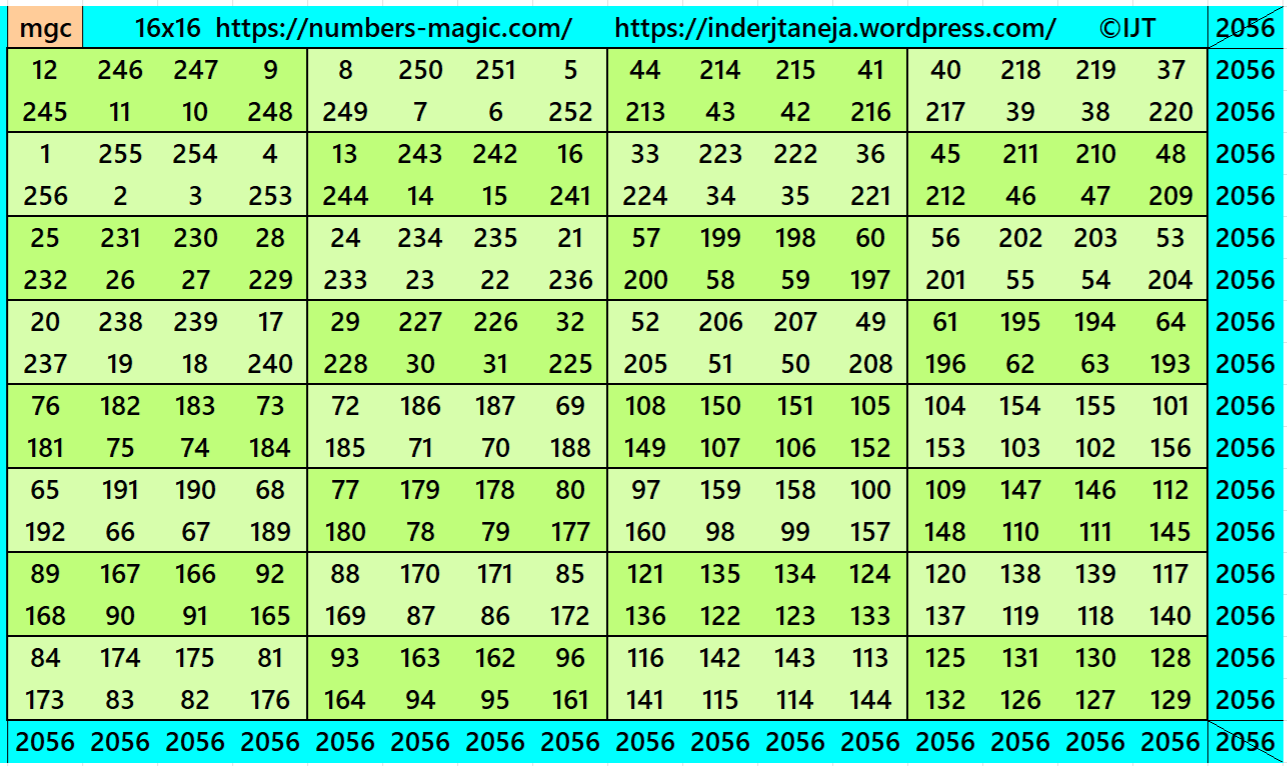
It is a also striped magic square of order 16 as it is formed by equal width and length of magic rectangles, i.e., 2×4. For more study on striped magic square of order 16 refer the author’s following work:

Striped Magic Squares of Order 16 – Revised

8. Different Styles of Magic Squares of Order 16

Example 17:

It is a magic square of order 16 formed by magic, bordered magic and bordered magic rectangles.

Example 18:

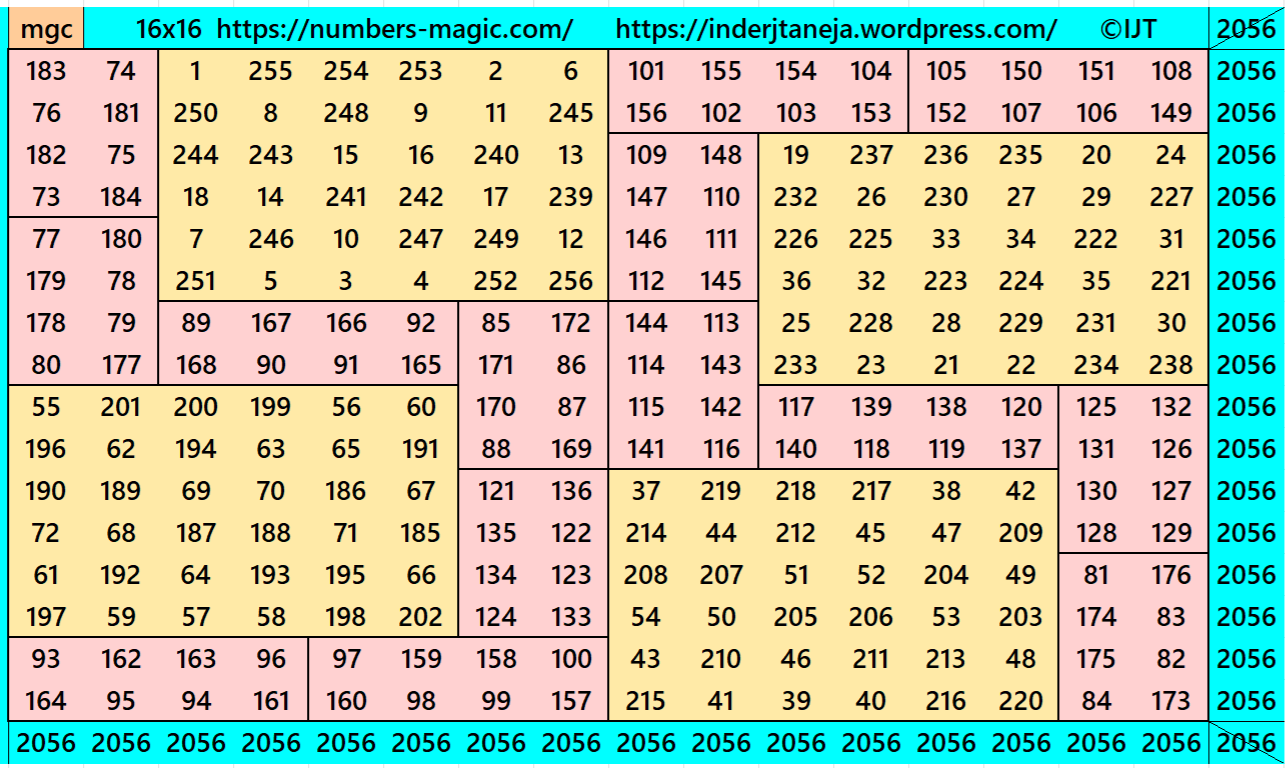
It is a magic square of order 16 formed by magic squares and magic rectangles.

Example 19:

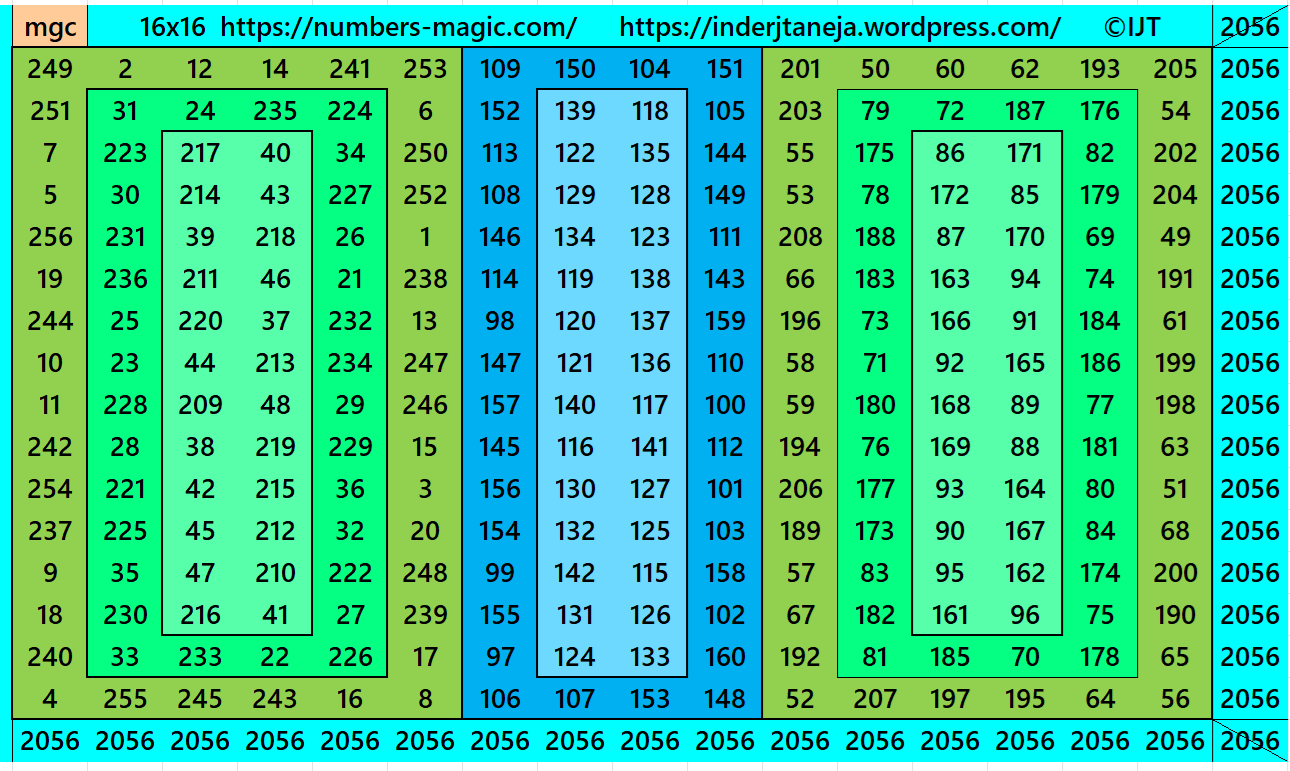
It is a magic square of order 16 formed by magic rectangles.

Example 20:

It is a magic square of order 16 formed by magic rectangles. See more details at

Bordered and Pandiagonal Magic Squares Multiples of 16

9. Four-Digits Bordered Squares of Order 16

Example 21:

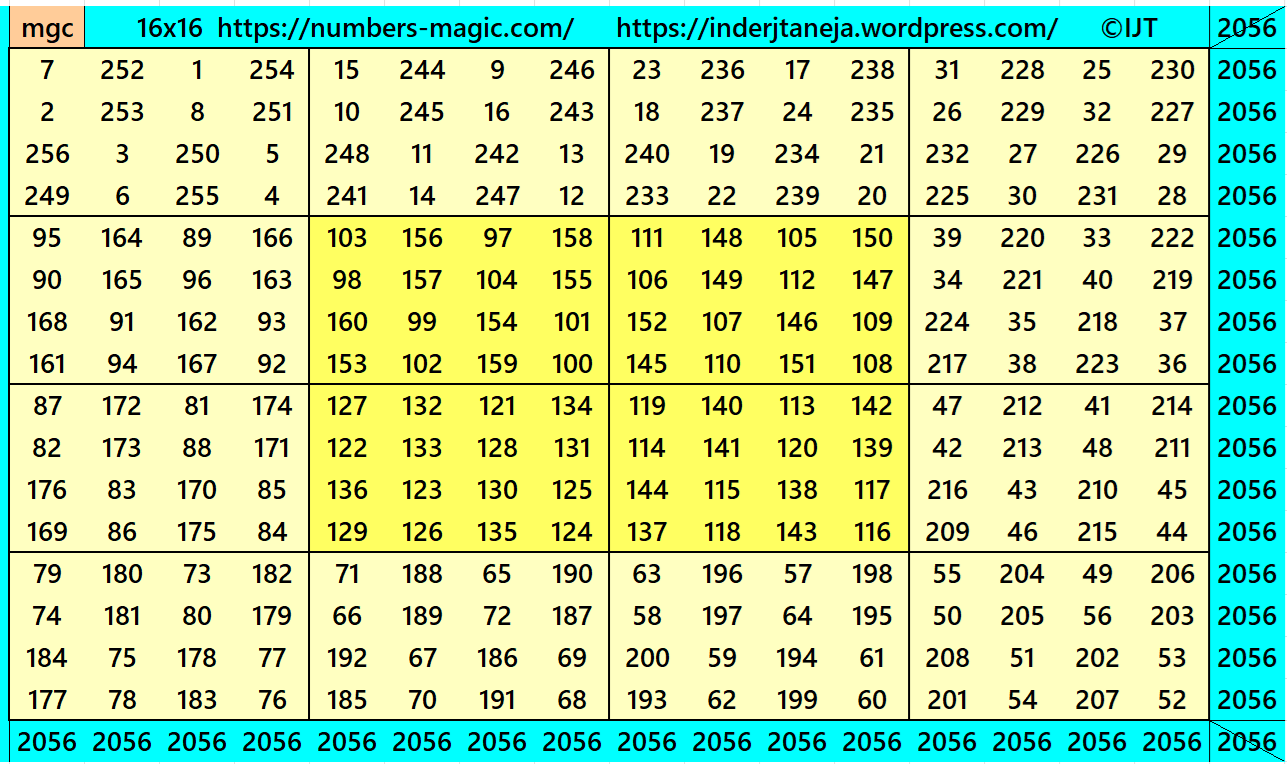
It is a four-digit bordered magic square of order 16. Four digits means border formed by magic squares of order 4. In this case case easily replace the inner part of the magic square foming magic square of order 8.

Example 22:

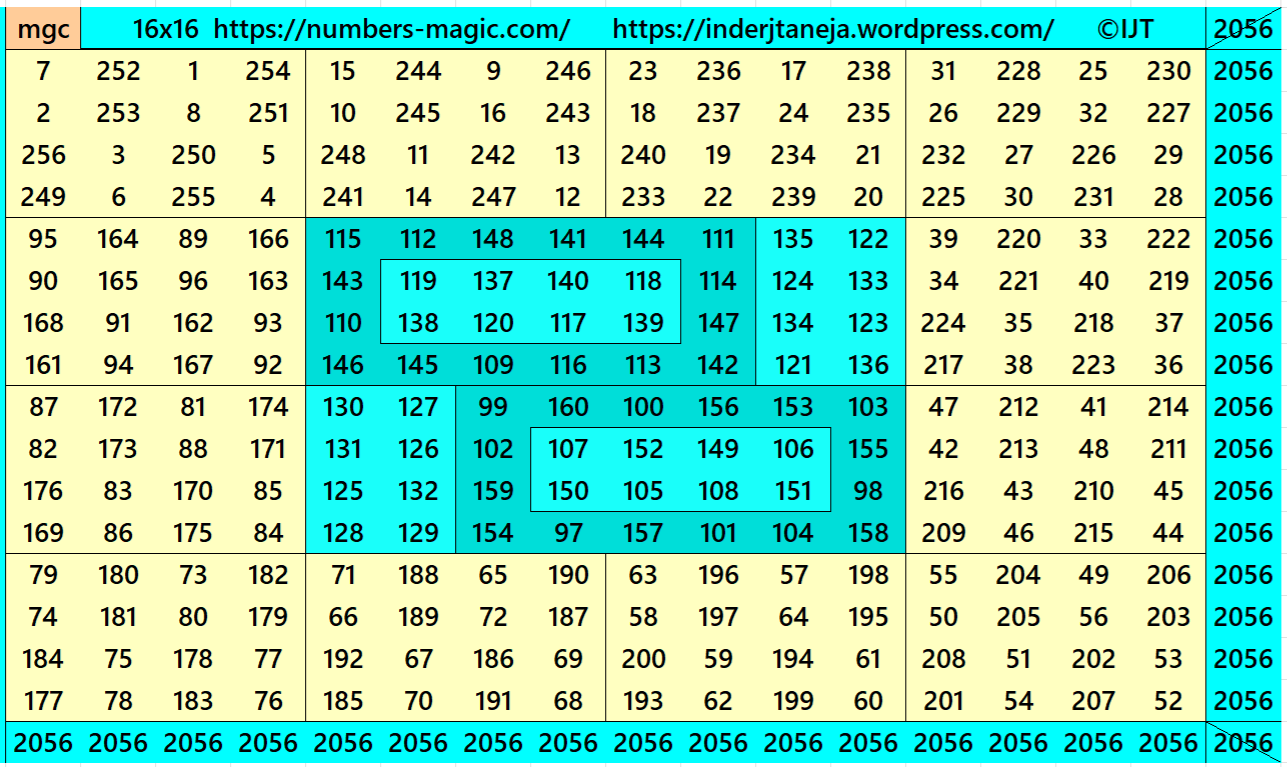
It is a four-digit bordered magic square of order 16 embedded with a magic square of order 8 formed magic bordered magic rectangles.

Example 23:

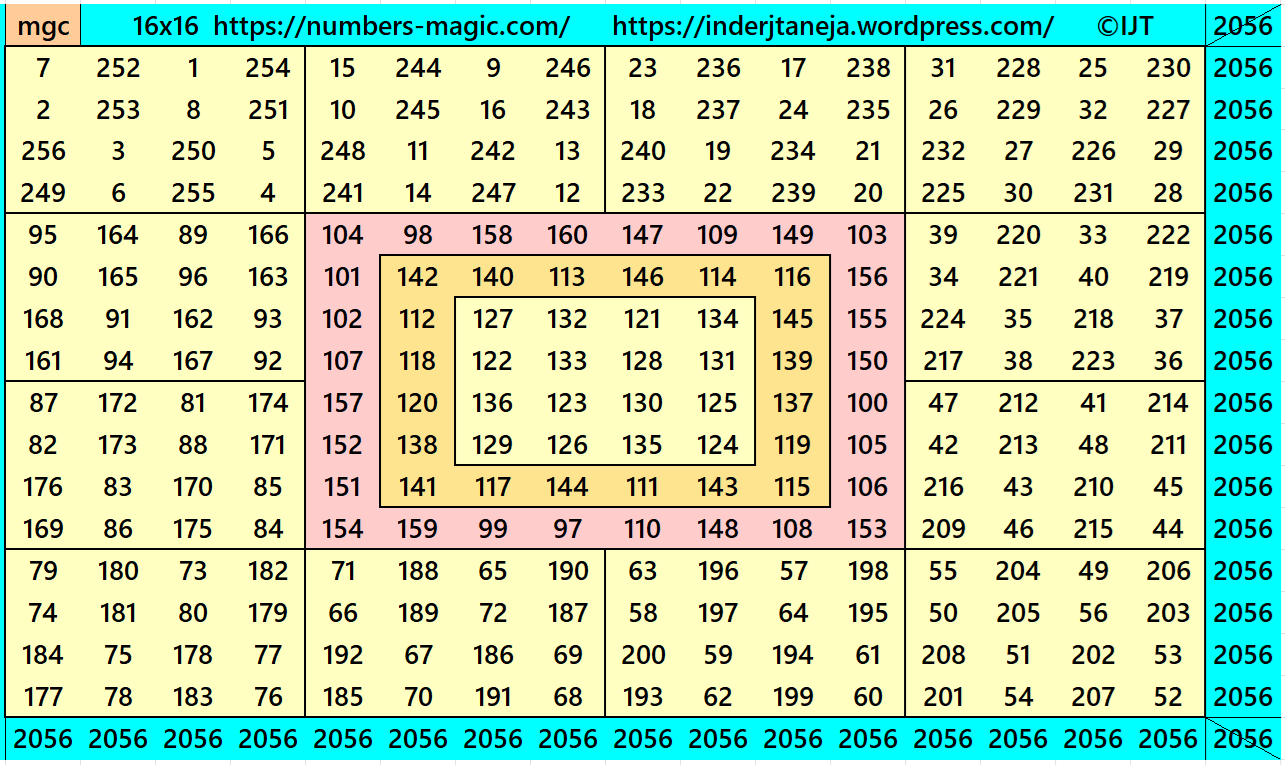
It is a four-digit bordered magic square of order 16 embedded with a single-digit bordered magic square of order 8.

Example 24:

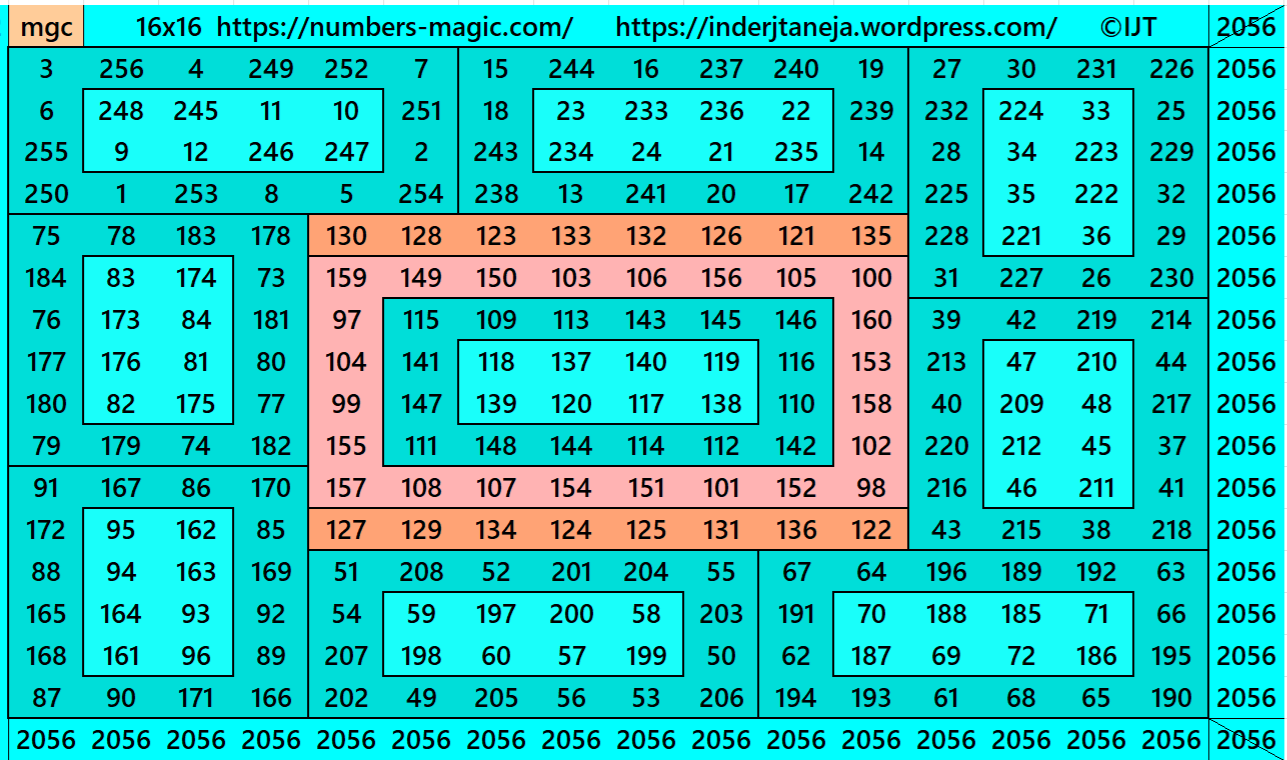
It is a four-digit bordered magic square of order 16 formed by bordered magic rectangles.

10. Latin Square Distributions

Below are Latin square distributions of Example 1.

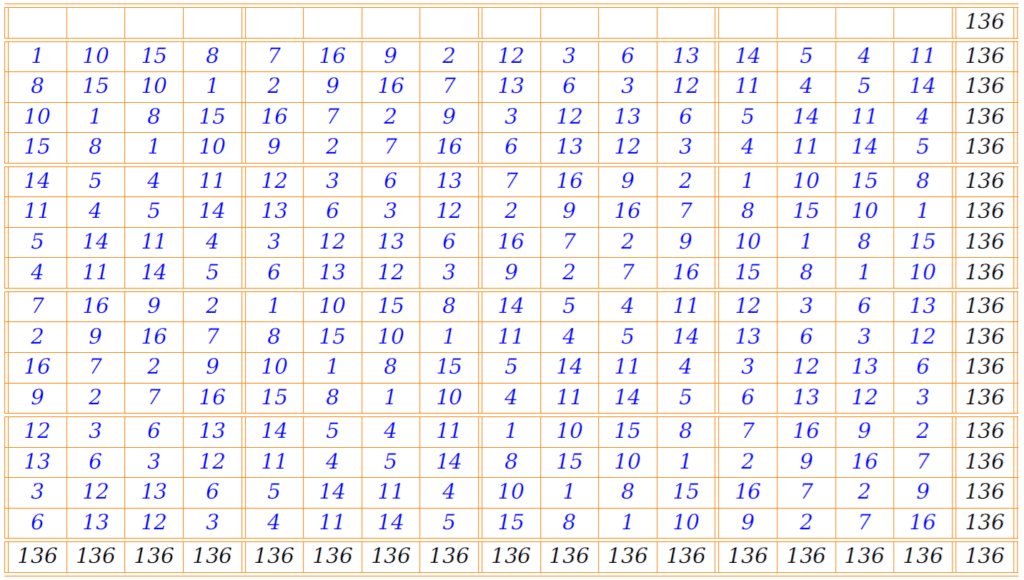
In this case, we have a pair of mutually orthogonal diagonalized Latin squares. Considering an operation 16×(A−1)+B, we get magic square of order 16 given in Example 1.

The general way writing above pair of Latin squares is as follows:

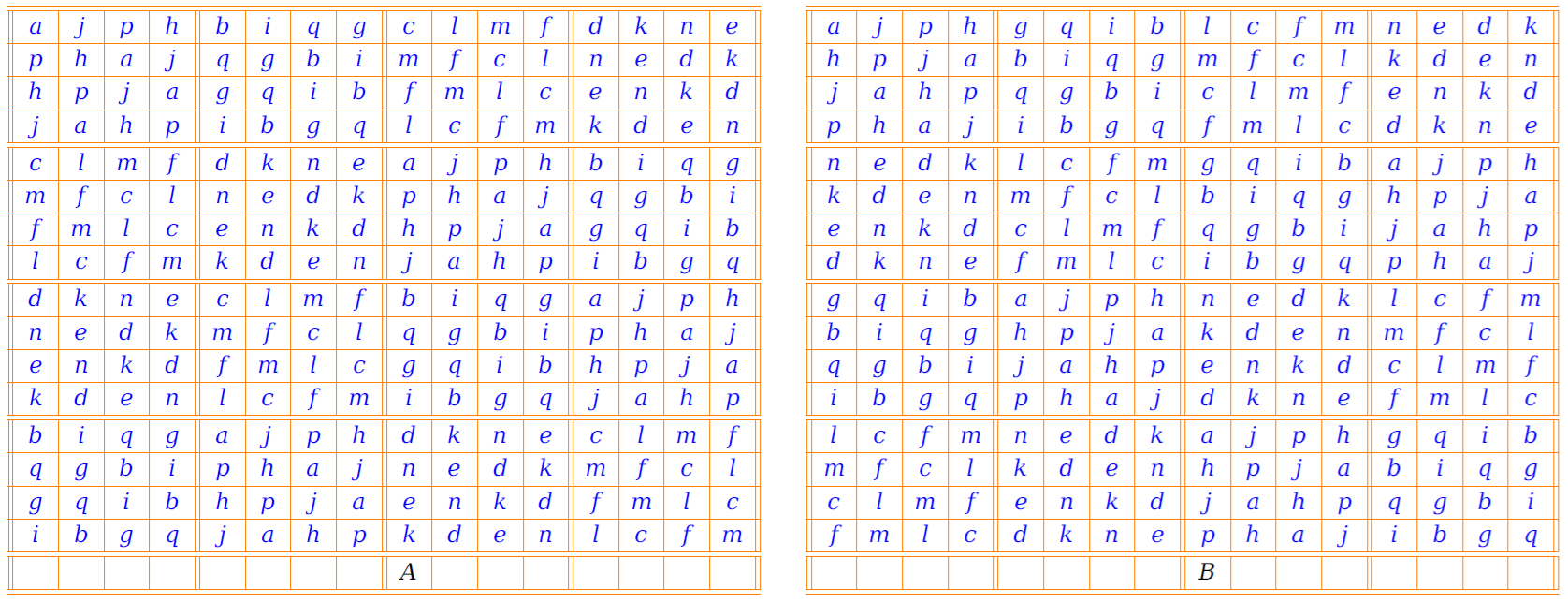
Using above structrure we can generate more magic squares of order 16 with different entries.

11. Palindromic Entries Magic and Bimagic Squares

Example 25:

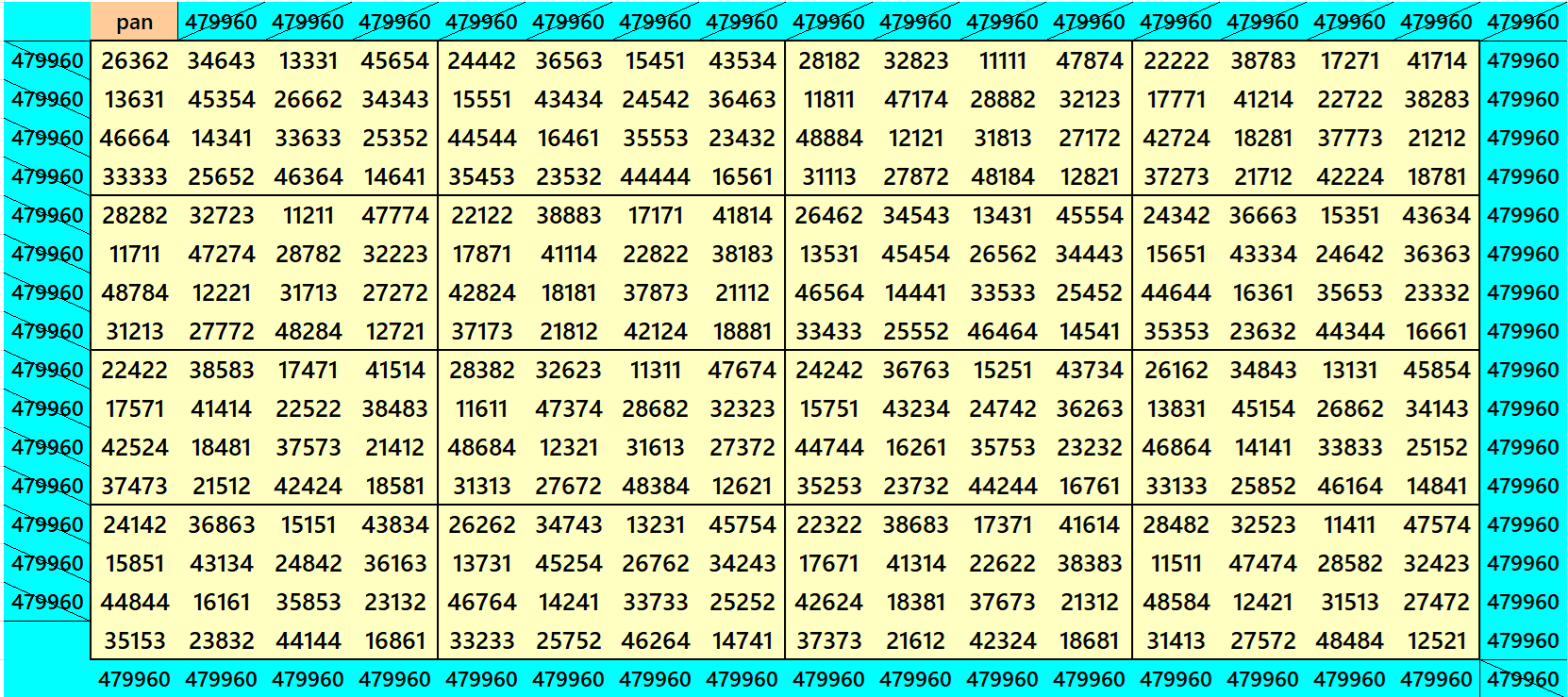
It is a pandiagonal magic square of order 16 with palindromic numbers entries. The magic squares of order 4 are also pandiagonal.

Example 26:

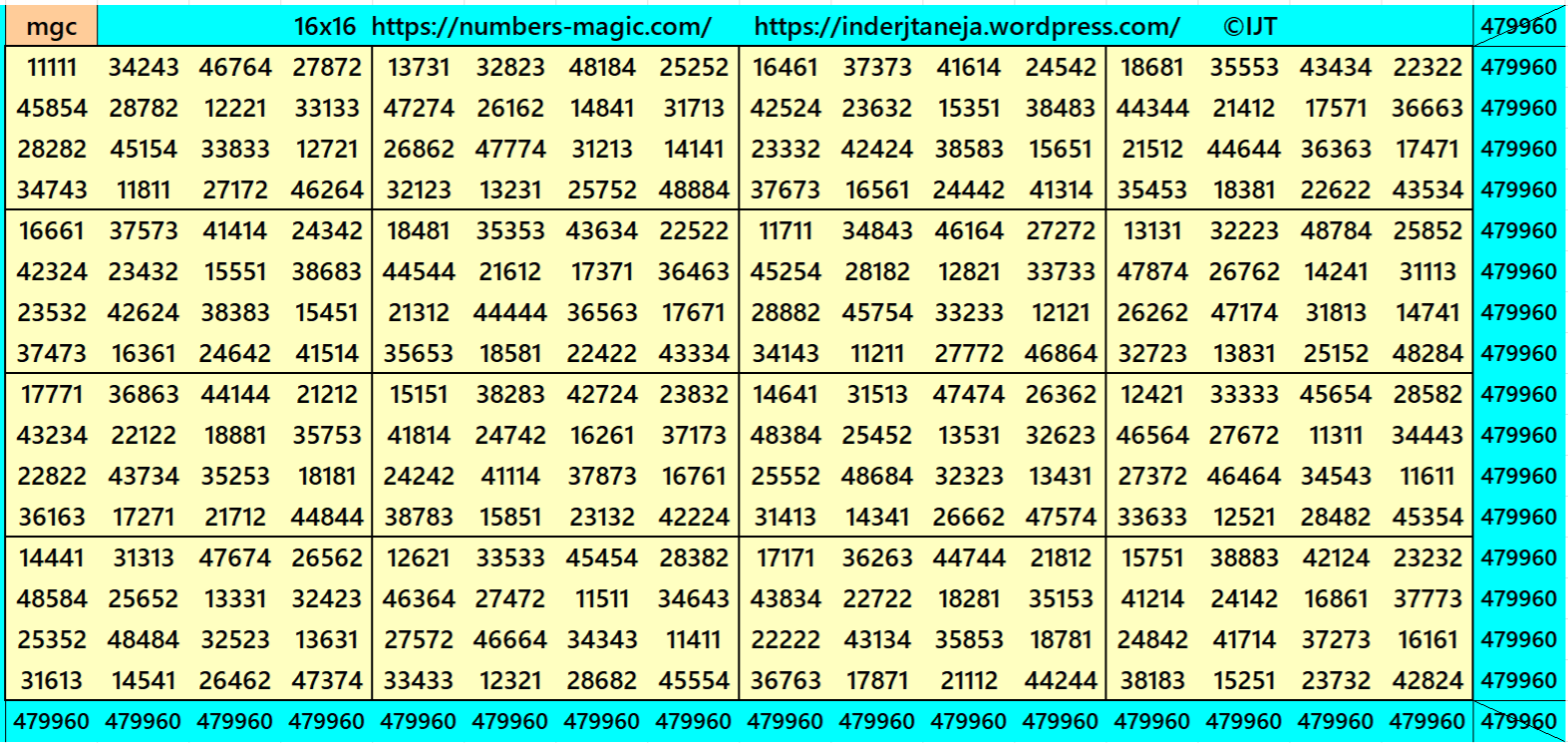
In this case, the magic and bimagic sums are S_16×16 := 479960 and Sb_16×16 := 16484528520 respectively. The blocks of order 4 are also magic squares with equal magic sums S_4×4 := 119990.

12. Perfect Square Entries Sum

Example 27:

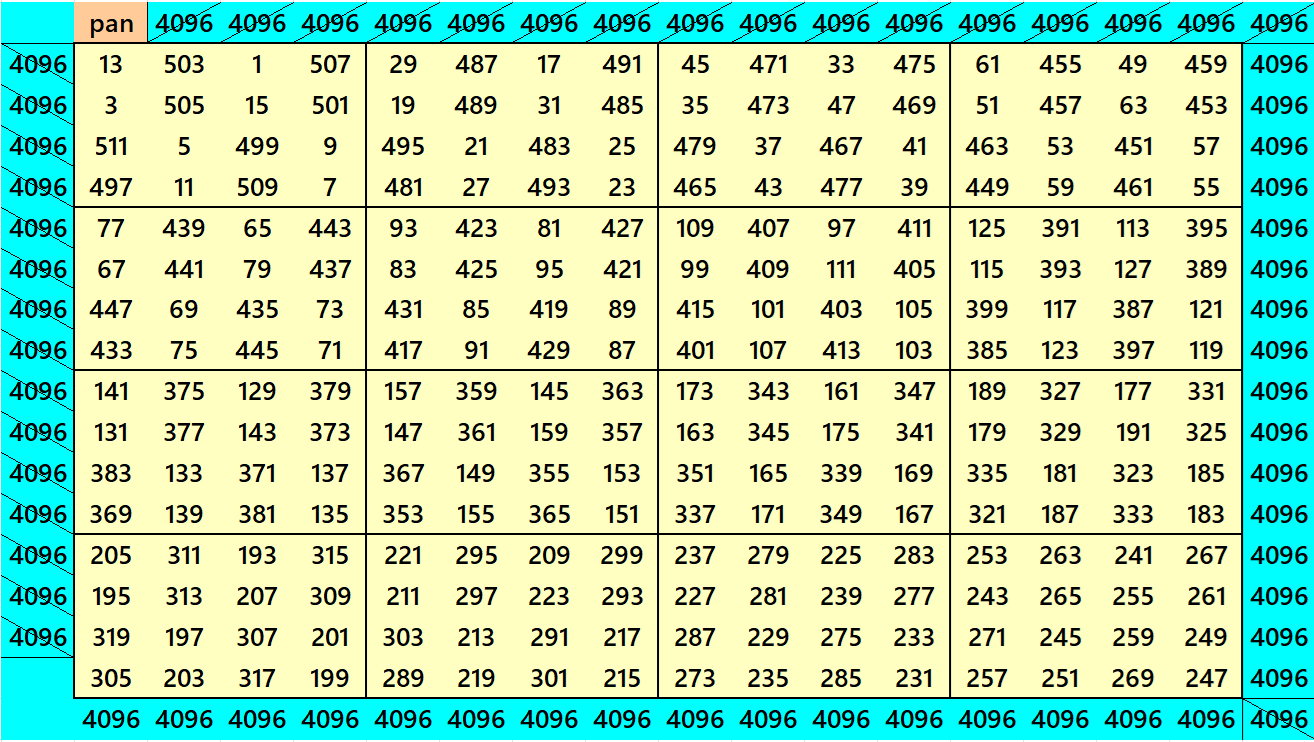
It is a block-wise pandiagonal magic square of order 16 for consecutive odd numbers entries {1, 3, 5, …, 509, 511}.

Example 28:

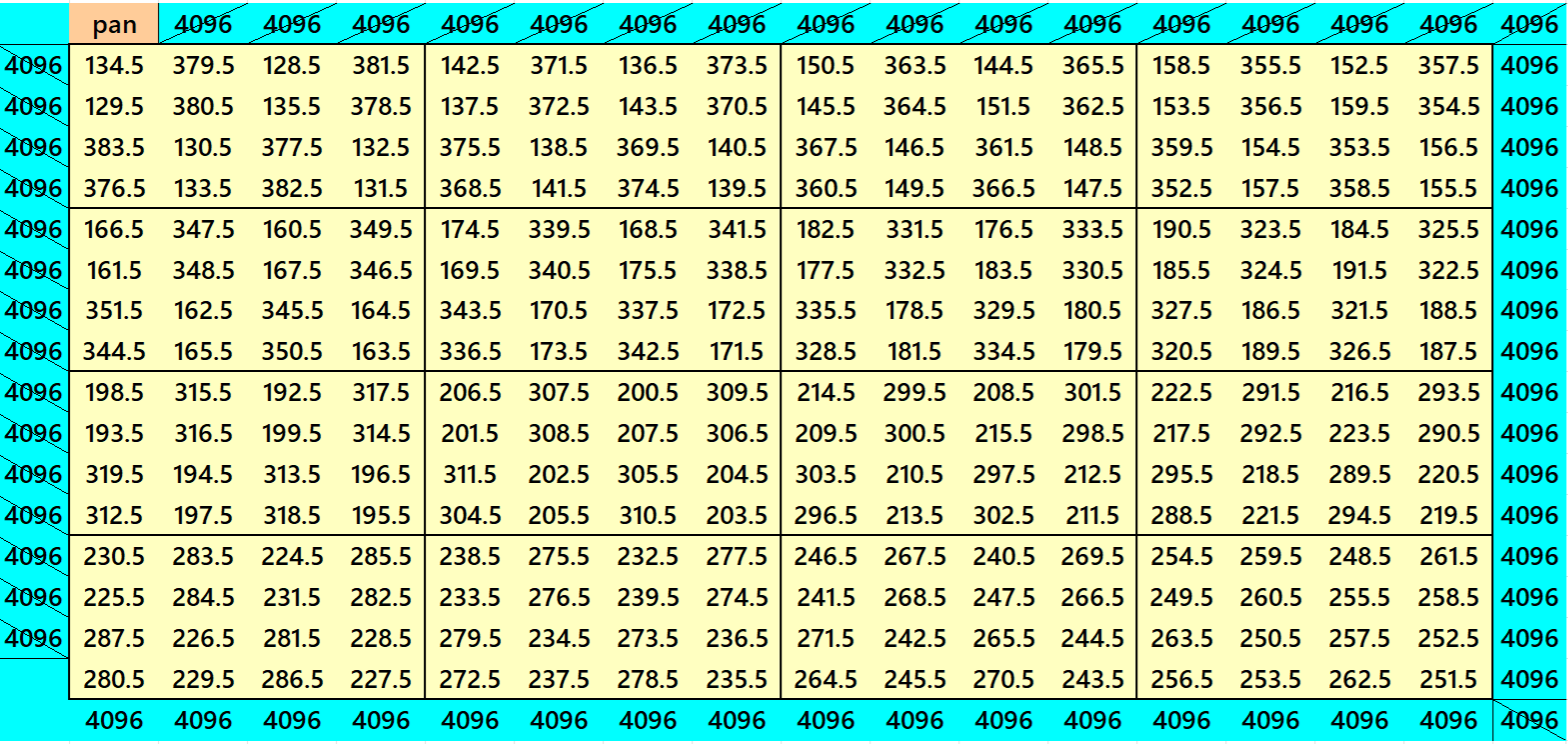
It is a block-wise pandiagonal magic square of order 16 for consecutive fraction numbers entries {257/2, 259/2, . . . , 763/2, 767/2}.

Both the Examples 27 and 28 are with equal magic sums. The blocks of order 4 are pandiagonal magic squares with equal magic sums. See the details below:

S_16×16 := 4096 = 16³, T₂₅₆ := 16*4096=65536=256²=16⁴ S_4×4 := 1024, T₁₆ := 4*1024=4096=64².

Both the Examples 27 and 28 satisfy the uniformity property, i.e., ⟨16, 16², 16³, 16⁴).

The entries sum is minimum perfect square. The blocks of order 4 are pandiagonal magic squares with equal magic sums. See below the details:
S_16×16 = 2304; T₂₅₆ := 16×2304 = 36864 and S_4×4 = 576; T₁₆ := 4×576 = 2304.

13. Pythagorean Triples Entries Type Magic Squares

Example 29:

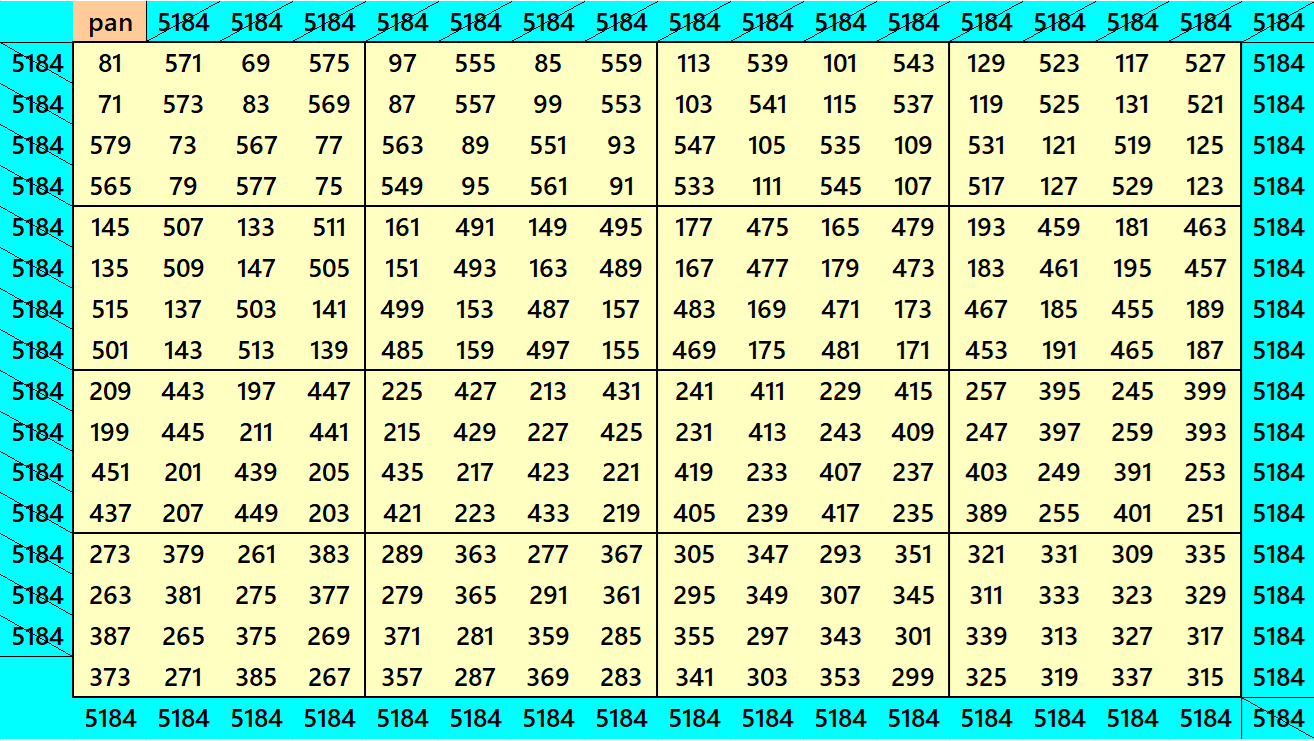
Example 30:

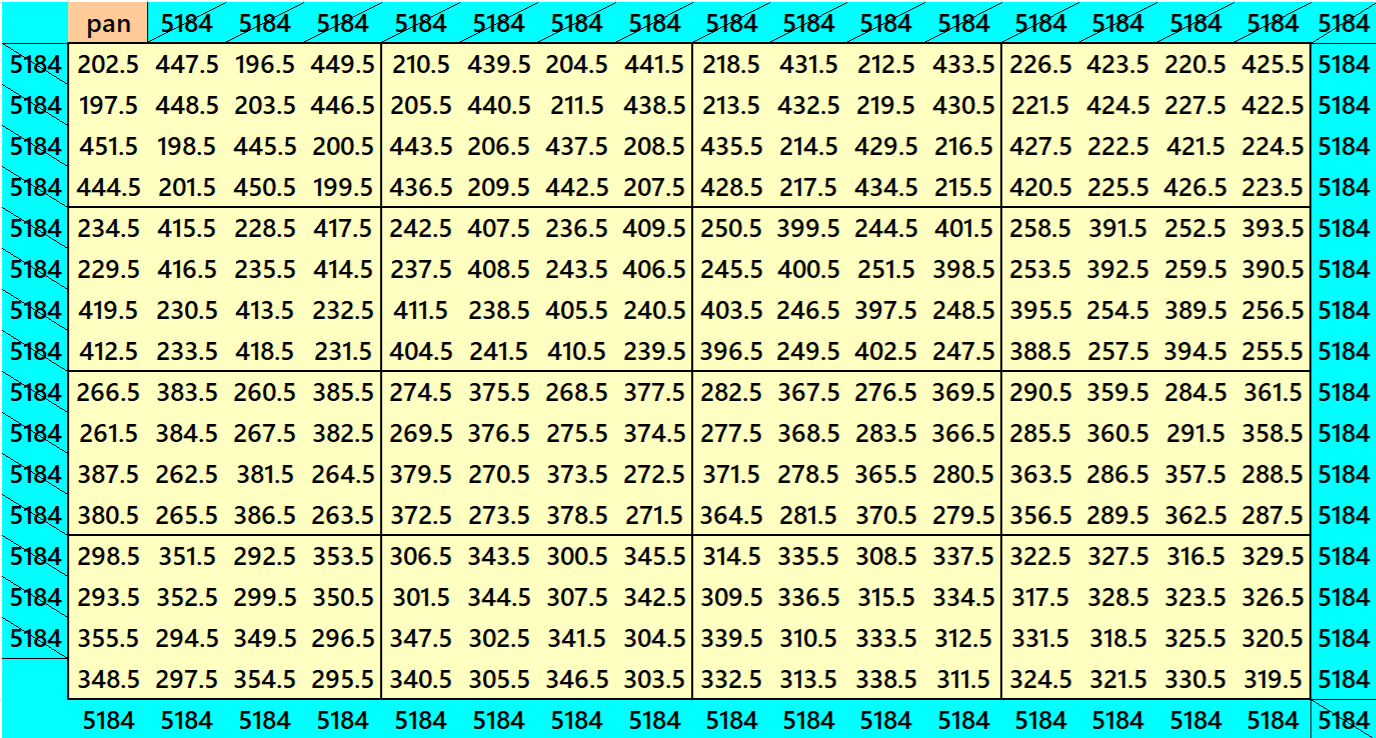
Both the Examples 29 and 30 are with equal magic sums. The blocks of order 4 are pandiagonal magic
squares with equal magic sums. See the details below:

S_16×16 = 5184; T₂₅₆ := 16×5184 = 82944 = 288²;
S_4×4 = 1296; T₁₆ := 4×1296 = 5184 = 72².

Both the Examples 29 and 30 are generated by Pythagorean triple (34, 288, 290), i.e., 34²+288² = 290²
with least possible entries resulting in perfect square entries sum.

Example 31:

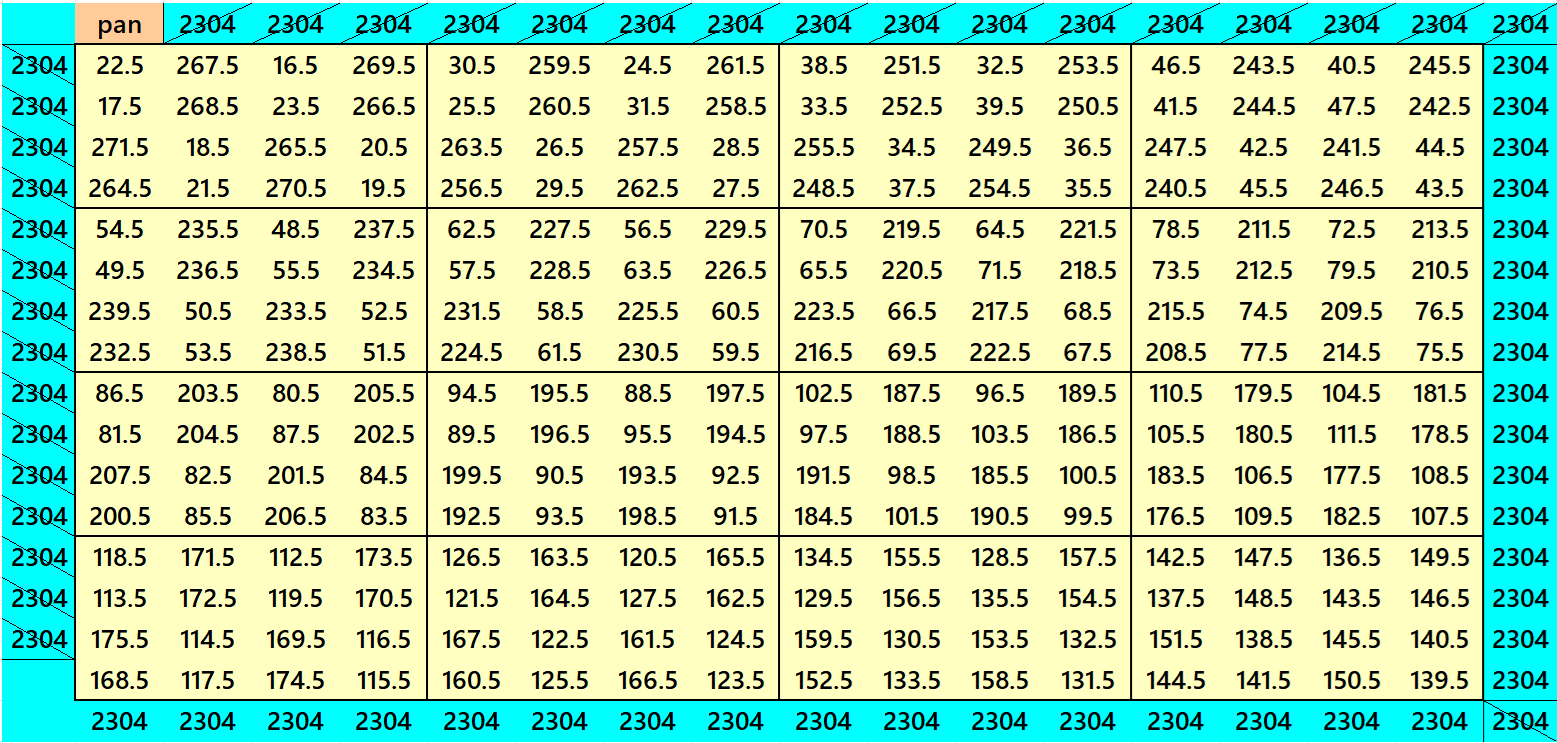
The entries sum is minimum perfect square. The blocks of order 4 are pandiagonal magic squares with
equal magic sums. See below the details:

S_16×16 = 2304; T₂₅₆ := 16×2304 = 36864 = 192²;
S_4×4 = 576; T₁₆ := 4×576 = 2304 = 48².

For more study refer the following author’s work:
Block-Wise and Block-Bordered Magic Squares Generated by Pythagorean Triples: Orders 3 to 47

14. Upside-Down and Mirror Looking Magic and Bimagic Squares

Below are some examples of magic squares of order 10 upside-down and mirror looking.

Example 32:

It is upside-down and mirror looking magic square of order 16. Here the blocks of order 4 are equal sums magic squares of order 4.

Example 33:

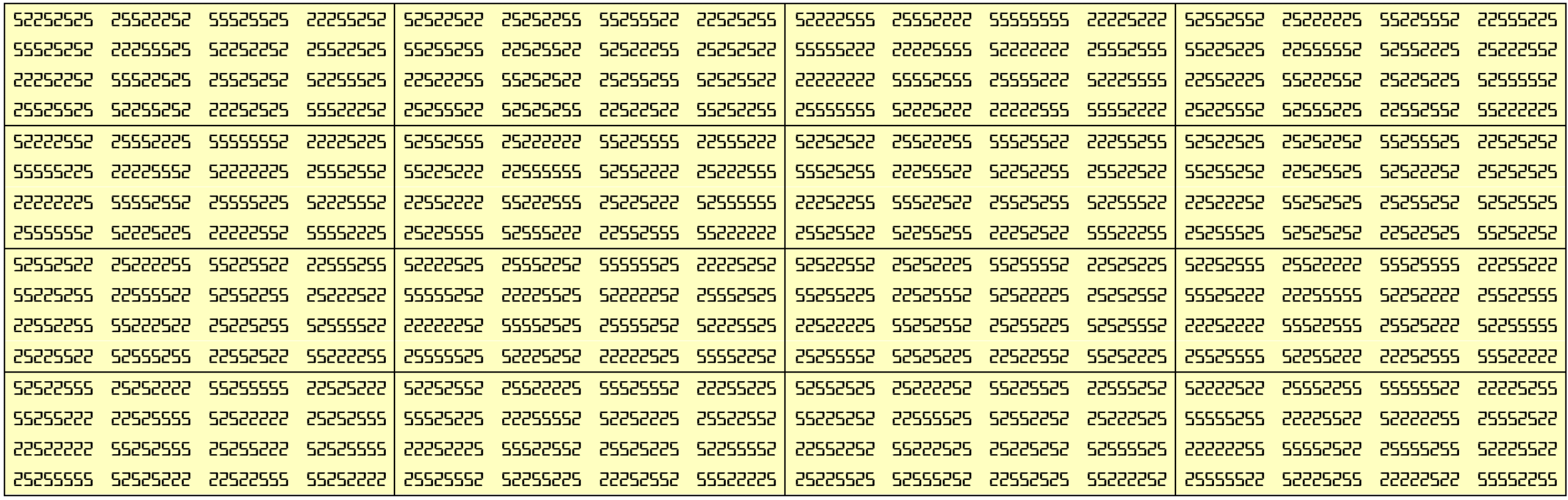
It is upside-down and mirror looking magic square of order 16. Here the blocks of order 4 are equal sums magic squares of order 4.

Example 34:

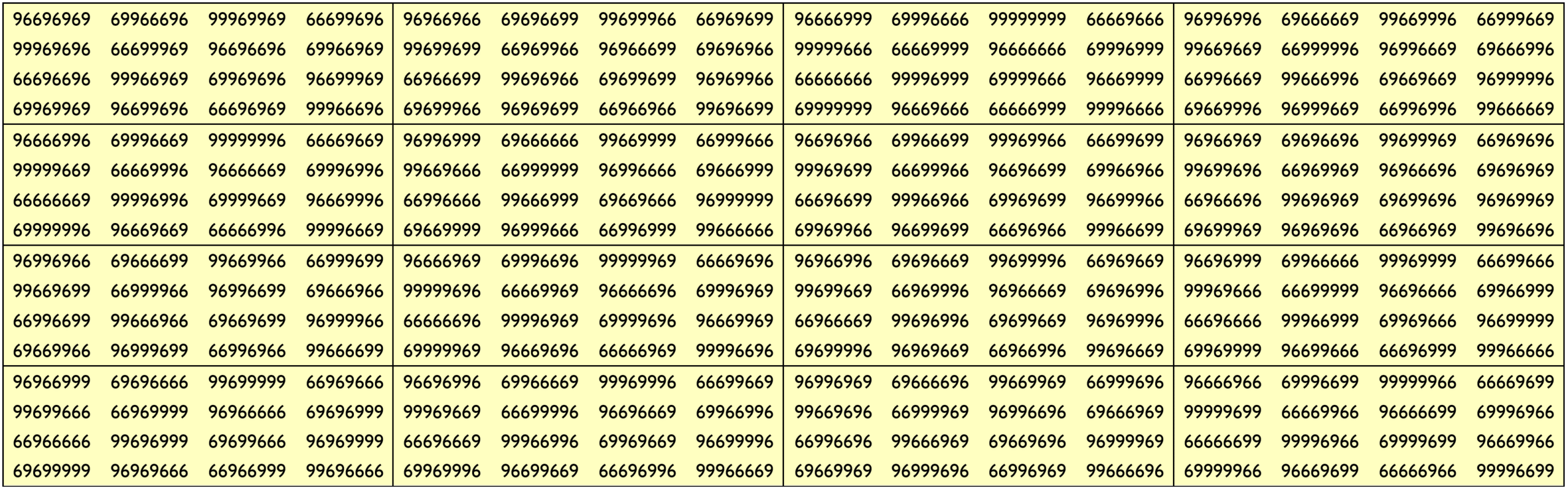
It is only upside-down magic square of order 16. Here the blocks of order 4 are equal sums magic squares of order 4.

Example 35:

It is only upside-down and mirror looking magic square of order 16 with digits (1,2,5,8). Here the blocks of order 4 are equal sums magic squares of order 4.

Example 36:

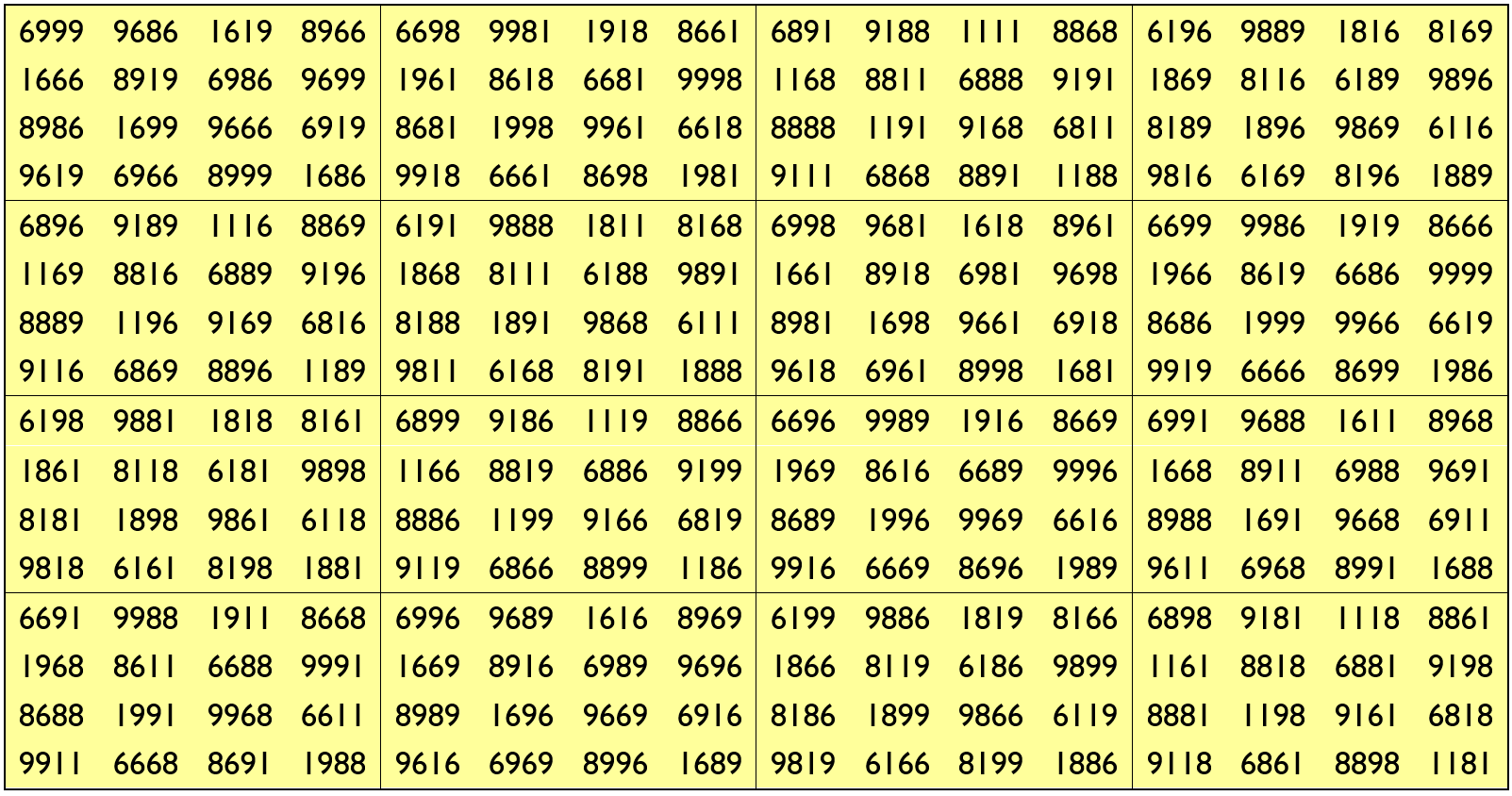
It is only upside-down magic square of order 16 with digits (1,6,8,9). Here the blocks of order 4 are equal sums magic squares of order 4.

Example 37:

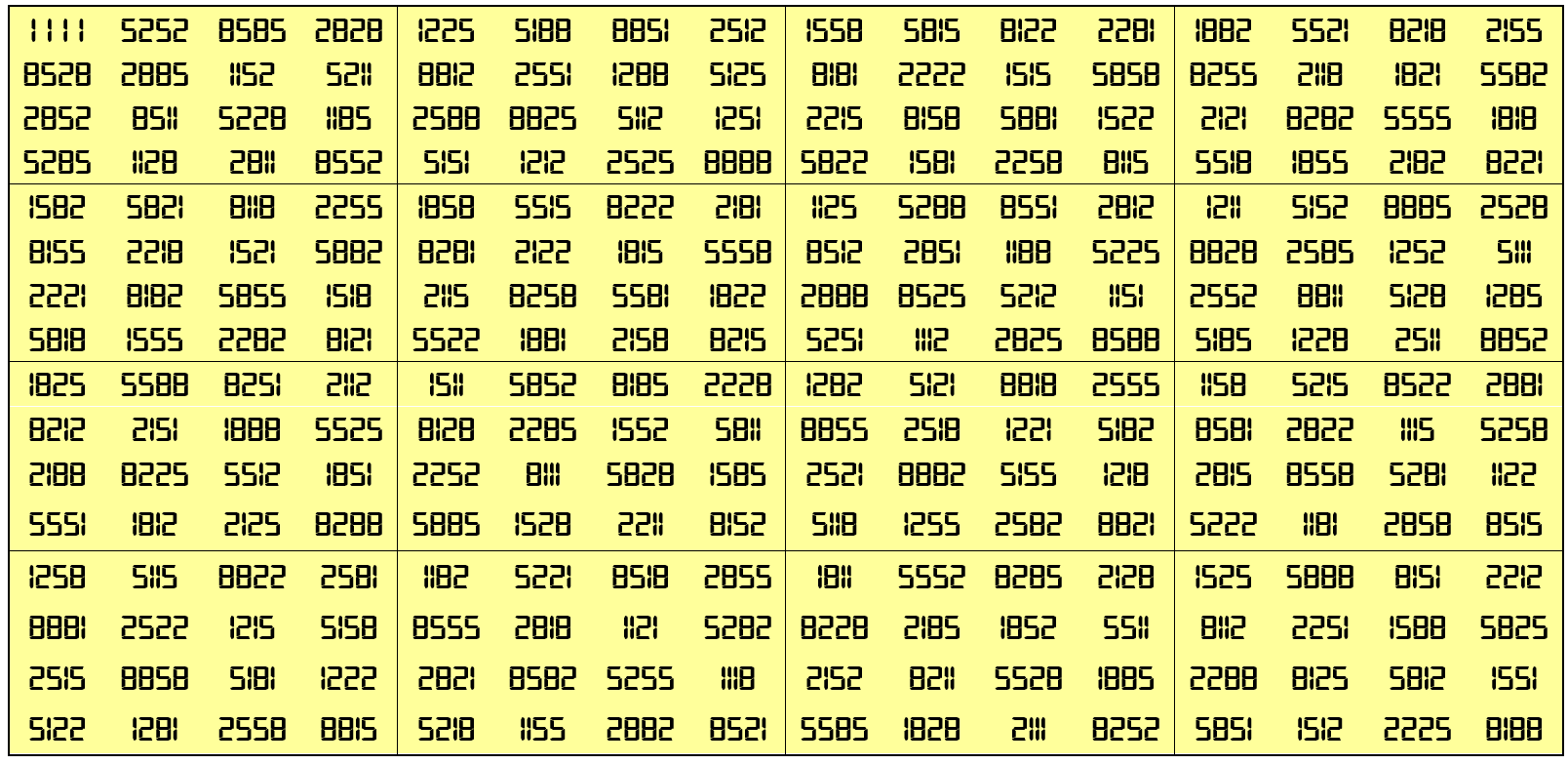
It is only upside-down and mirror looking bimagic square of order 16 with digits (1,2,5,8). Here the blocks of order 4 are equal sums magic squares of order 4.

Example 38:

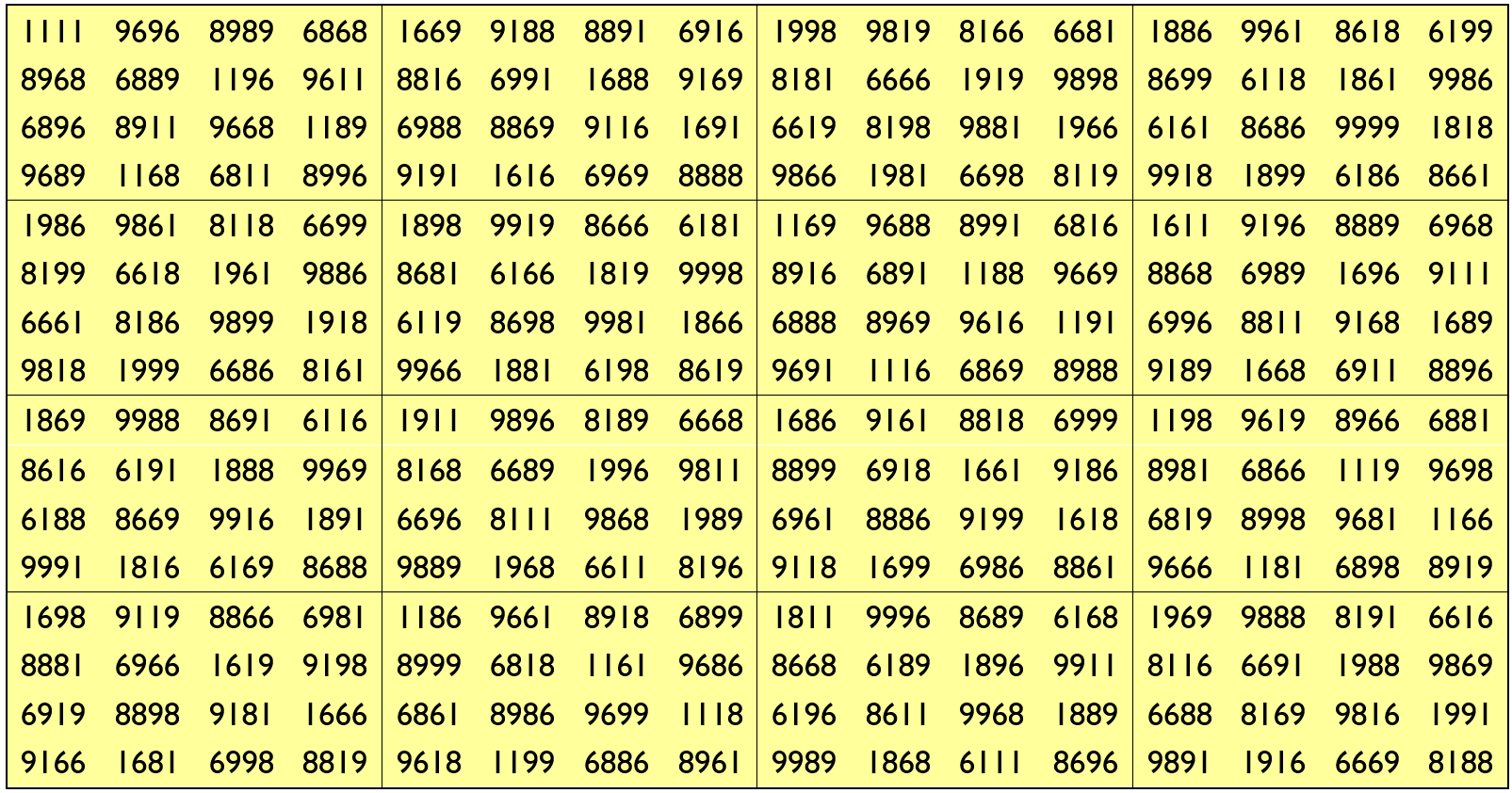
It is only upside-down bimagic square of order 16 with digits (1,6,8,9). Here the blocks of order 4 are equal sums magic squares of order 4. For more study refer the following links:

15. Water Reflection Magic Squares

Below are few examples of magic and bimagic squares of order 16. These are water reflexive magic squares. By water reflexive we understand that when we see the image of a magic square in water, it still remains a magic square. Below are few examples.

Example 39:

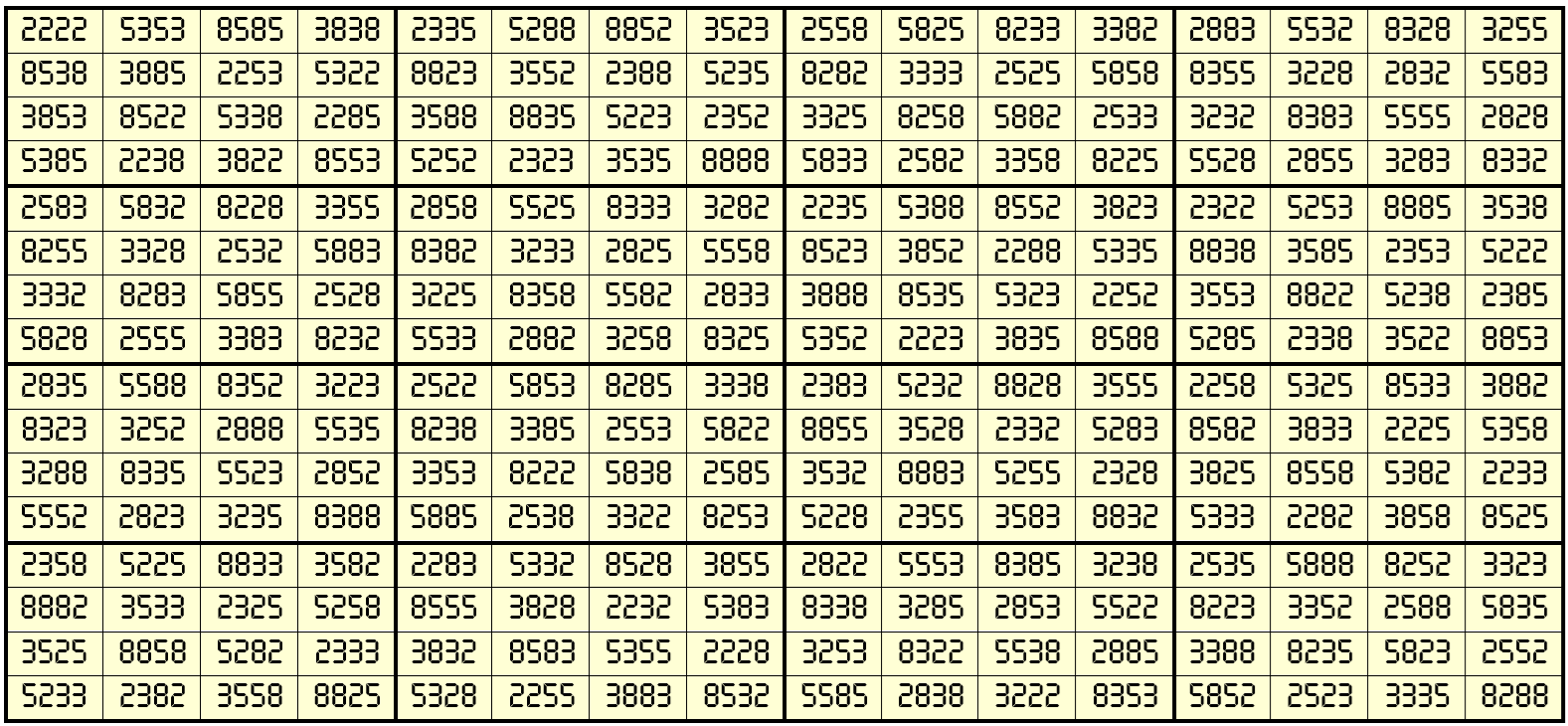
The above magic square of order 16 with digits is (2,3,5,8) is water reflexive and bimagic. The magic sums are S_16×16(2, 3, 5, 8) = 79992 and Sb_16×16(2, 3, 5, 8) = 484768488. The blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(2, 3, 5, 8) := 19998. It is warter reflexive with same magic sums.

Example 40:

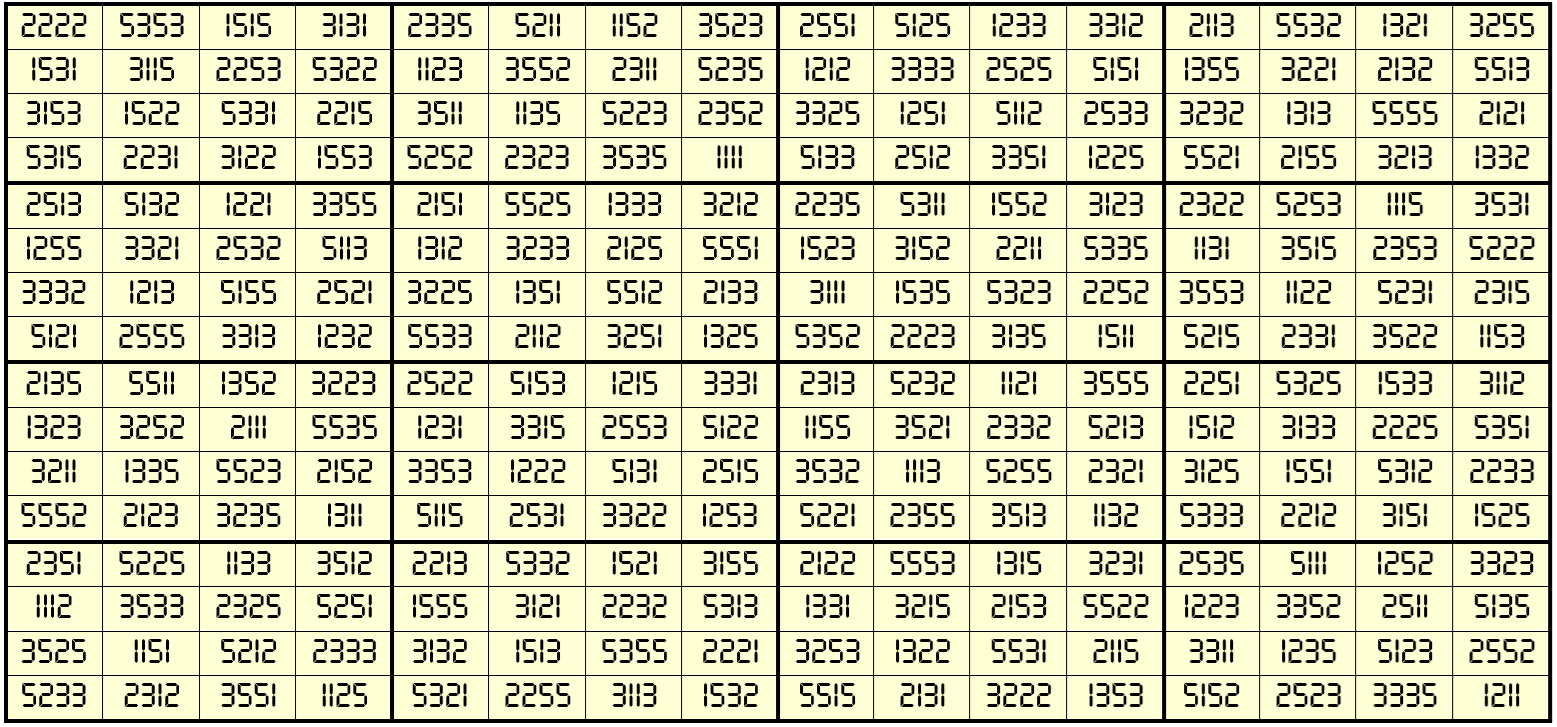
The above magic square is water reflexive with equal magic sums. The blocks of order 4 are magic squares with equal magic sums. It is bimagic. The magic sums are S_16×16(1, 2, 3, 5) := 48884 and Sb_16×16(1, 2, 3, 5) := 184706376. The blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(1, 2, 3, 5) := 12221.

Example 41:

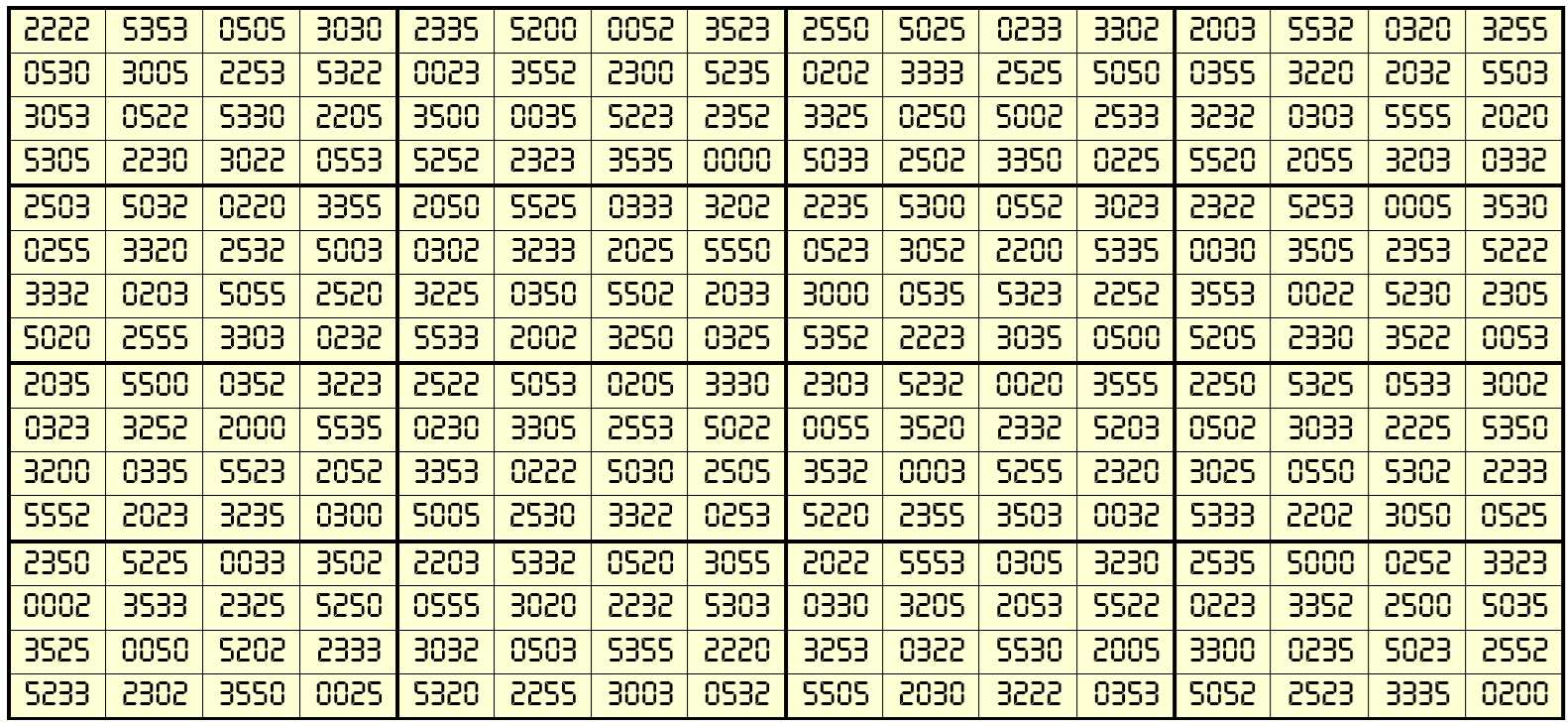
The above magic square is water reflexive with equal magic sums. The blocks of order 4 are magic squares with equal magic sums. It is bimagic. The magic sums are S_16×16(0, 2, 3, 5) := 44440 and Sb_16×16(0, 2, 3, 5) := 175957352. The blocks of order 4 are magic squares with equal magic sums, i.e., S_16×16(0, 2, 3, 5) = 11110.

Example 42:

The above magic square is water reflexive with equal magic sums. The blocks of order 4 are magic squares with equal magic sums. It is bimagic. The magic sums are S_16×16(0, 1, 3, 8) := 53328 and Sb_16×16(0, 1, 3, 8) := 331277576. The blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(0, 1, 3, 8) := 13332.

We have four bimagic squares of order 16 with 4-digits (2,3,5,8), (1,2,3,5), (0,2,3,5) and (0,1,3,8) having water reflection property with same magic and bimagic sums. The blocks of order 4 are magic squares with equal magic sums. For more study refer author’s work:

Upside-Down, Mirror Looking and Water Reflection Magic Squares: Orders 14 to 16