Algebraic Double-Digit and Cornered Magic Squares of Odd Orders from 5 to 19

This work brings double-digit or double-layer algebraic magic squares of odd orders from 5 to 19 for reduced entries. This study include three types of algebraic magic squares, i.e., cyclic-type, flat-type and corner-type. Cyclic-type and Flat-type are two different ways of writing as double-digit magic squares. Sometimes, these algebraic magic squares, we call as self-made, because they are complete in themselves. Just choose the entries and magic sum, we always get a magic square. In this work we use always magic rectangles of width 2 except in the middle or corner, where there is a magic square of order 3 or 5. The idea of double-digit and cornered magic squares for sequential entries is already studied by the authors. For details see the reference list given at the end.

We know that magic sum of a magic square of order n having 1 to n² number of entries is given by

S_nxn:= n*(1+n²)/2

By algebraic magic squares we understand that the entries are vaiables and their combinations. Thus, instead of squential entries, we have non-sequential entries. These can be positive, negative or decimal numbers.

Whole work is also available at the following link:

Inder J. Taneja, Algebraic Double-Digit and Cornered Magic Squares of Odd Orders from 5 to 19, Zenodo, December 08, 2025, pp. 1-46, https://doi.org/10.5281/zenodo.17859037.

Below are few examples of magic squares of odd orders fro 5 to 19

Algebraic Magic Square of Order 5

Result 1: Algebraic Magic Square of Order 5

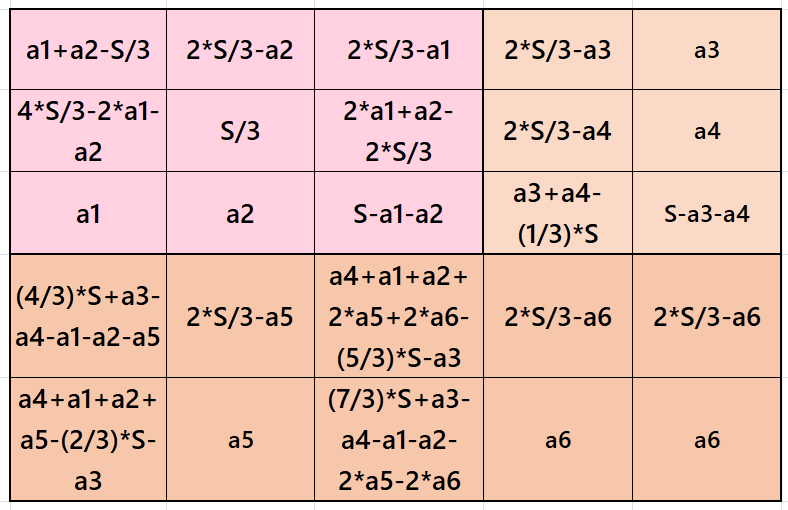
It is an algebraic cornered magic square of order 5, where there is a magic square of order 3 at the upper-left corner. There are two magic rectangles of order 2×5 and 2×3. The magic sum of order 5 is given as S_5×5 := 5*S/3, where S is the magic sum of order 3. In order to avoid decimal entries the the magic sum of order 3,i.e., S should be multiple of 3. m:=2*S/3 is the width of the magic rectangle. See below few examples:

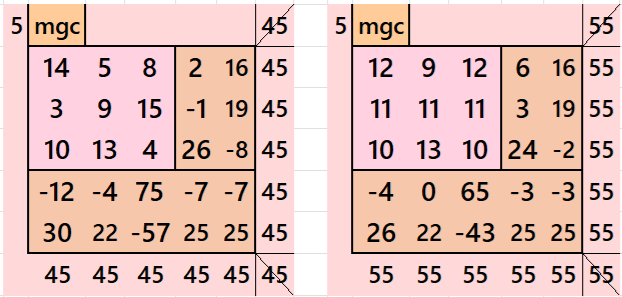
In the first example the magic sums are S_3×3 :=30, S_5×5 :=45 and m:=18.
In the second example the magic sums are S_3×3 :=33, S_5×5 :=55 and m:=22.

Algebraic Magic Squares of Order 7

Below are three types of striped algebraic magic squares of order 7.

Result 2: Algebraic Cyclic-Type Magic Square of Order 7

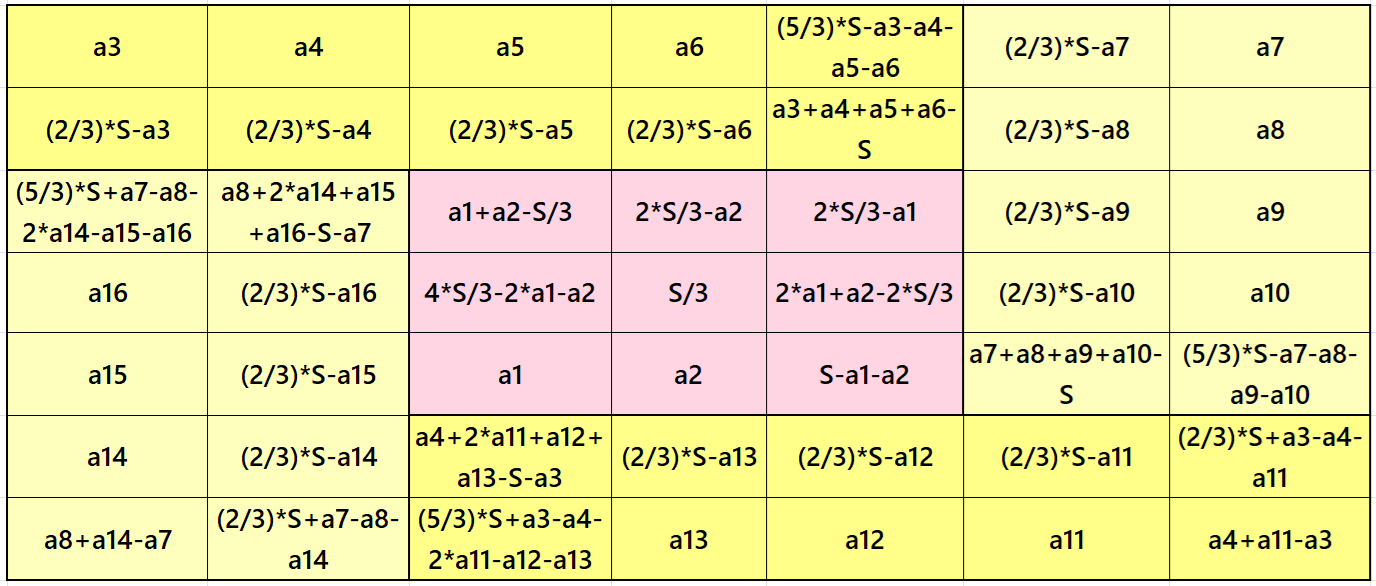
It is an algebraic magic square of order 7 composed of four equal sums magic rectangles of orders 2×5 and embedded with a magic square of order 3. Since the external four strips are of equal sums, we can name it is as an algebraic cyclic-type magic square of order 7. In this case the magic sums are S_3×3:=S and S_7×7:=7*S/3, where S is the magic sum of magic square of order 3. In order to avoid decimal entries the the magic sum of order 3 should be multiple of 3. The width of magic rectangles is given as m:=2*S/3. See below few examples:

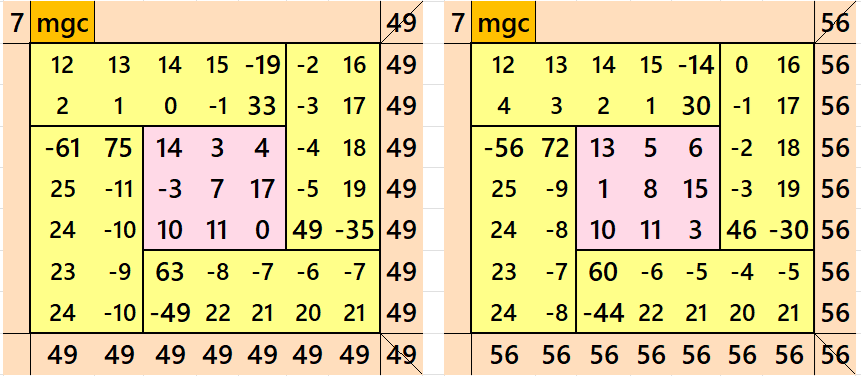
In the first example the magic sums are S_3×3 :=21, S_7×7 :=49 and m:=14.
In the second example the magic sums are S_3×3 :=24, S_7×7 :=56 and m:=16.

Result 3: Algebraic Flat-Type Magic Square of Order 7

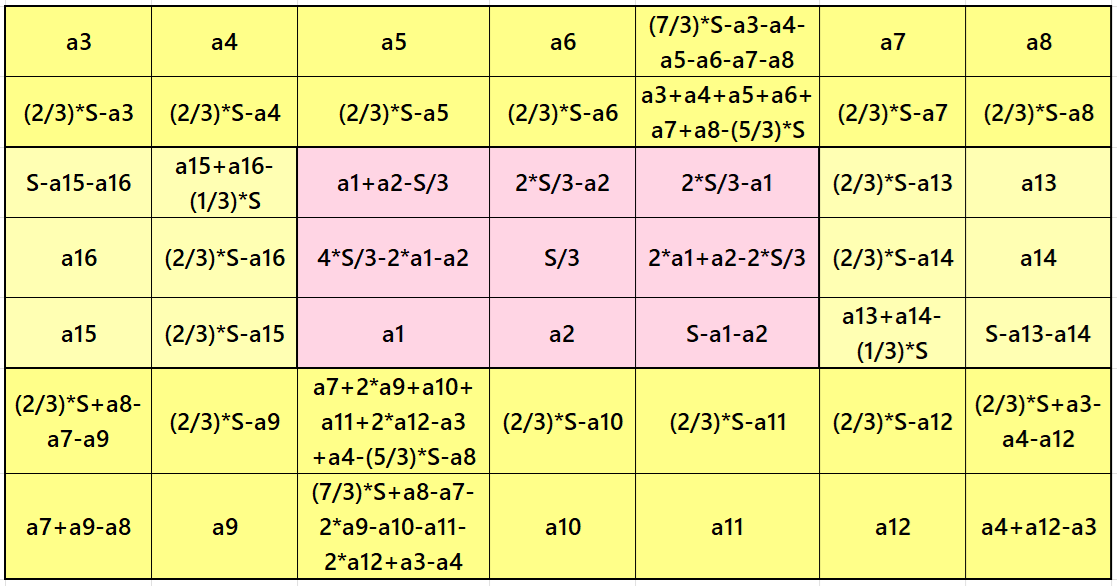
It is an algebraic magic square of order 7 composed of twor equal sums magic rectangles of orders 2×7 and two equal sum magic rectangles of order 2×3 embedded with a magic square of order 3. For simplicity, this types of magic sequares we call as flat-type. Thus we have an algebraic flat-type magic square of order 7 In this case the magic sums are S_3×3:=S and S_7×7:=7*S/3, where S is the magic sum of magic square of order 3. In order to avoid decimal entries the the magic sum of order 3 should be multiple of 3. The width of magic rectangles is given as m:=2*S/3. See below few examples:

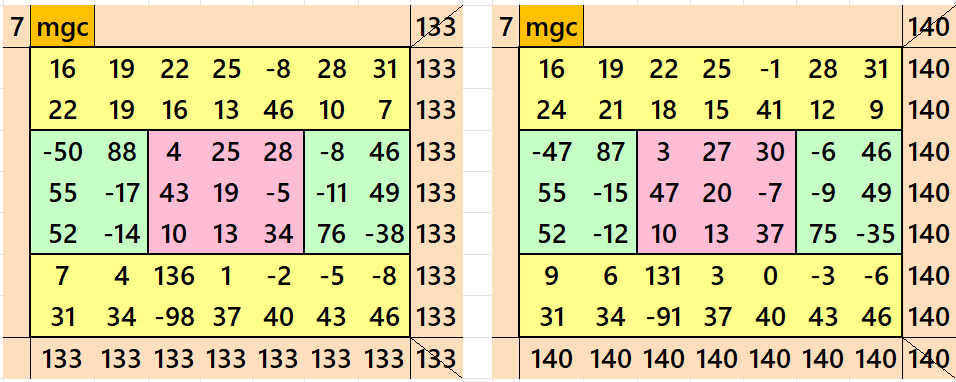
In the first example the magic sums are S_3×3 :=57, S_7×7 :=133 and m:=38.
In the second example the magic sums are S_3×3 :=60, S_7×7 :=140 and m:=40.

Result 4: Algebraic Cornered Magic Square of Order 7

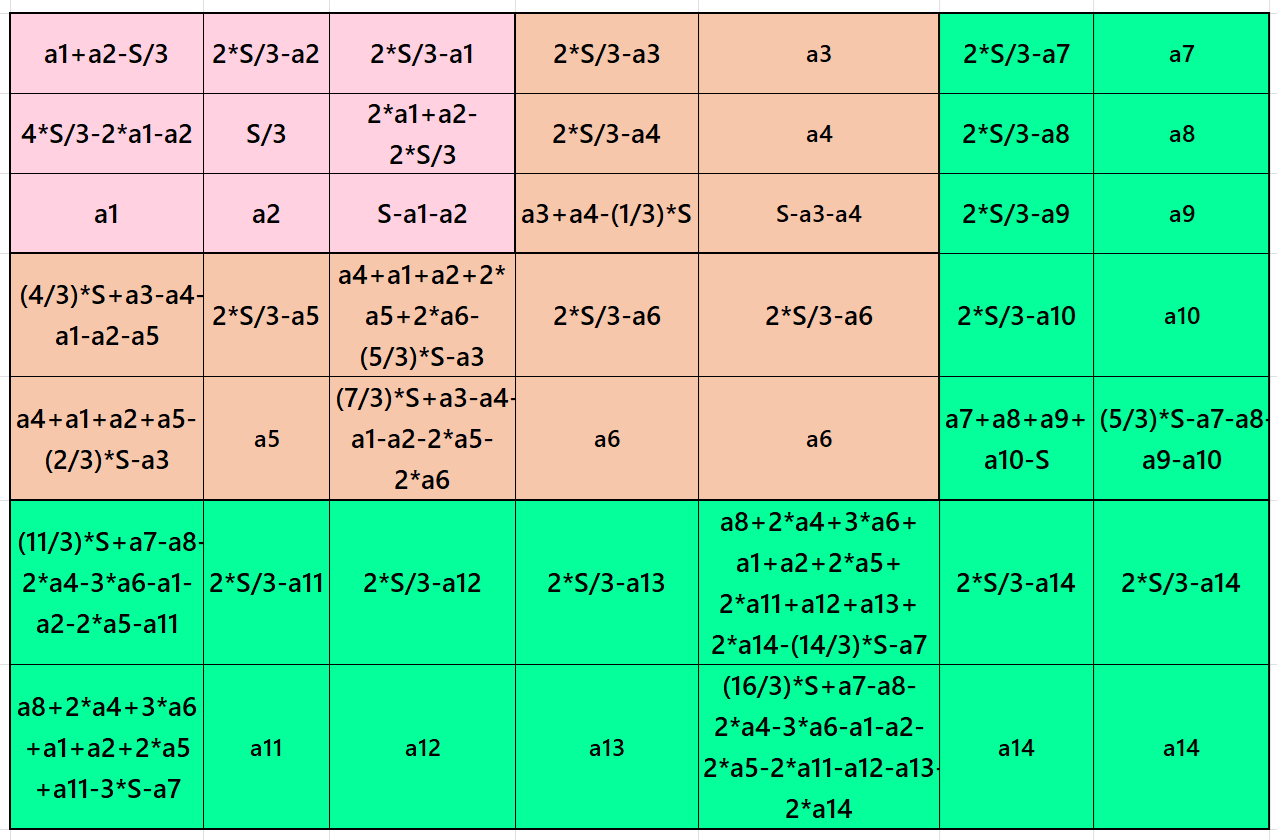
It is an algebraic cornered magic square of order 7, where the magic squares of orders 3 and 5 are at the upper-left corner. In this case the magic sums are S_3×3:= S, S_5×5:=5*S/3 and S_7×7:=7*S/3, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. The magic rectanges are of orders 2×3, 2×5 and 2×7. See below two examples:

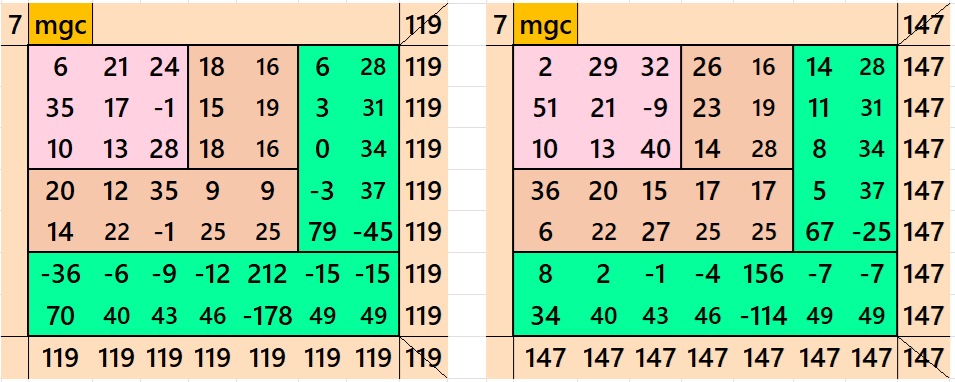
In the first example the magic sums are S_3×3 :=51, S_5×5 :=85, S_7×7 :=119 and m:=34.
In the second example the magic sums are S_3×3 :=63, S_5×5 :=105, S_7×7 :=147 and m:=42.

Algebraic Magic Squares of Order 9

Below are three types of algebraic striped magic squares of order 9.

Result 5: Algebraic Cyclic-Type Magic Square of Order 9

It is an algebraic cyclic-type magic square of order 9 composed of four equal sums magic rectangles of orders 2×7 embedded with a magic square of order 5. In this case the magic sums are S_5×5:=S and S_9×9:=9*S/5, where S is the magic sum of order 5. In this case, m:=2*S/5 is the width of magic rectangles. To avoid decimal entries the magic sums of order 5 should be multiple of 5. See below two examples:

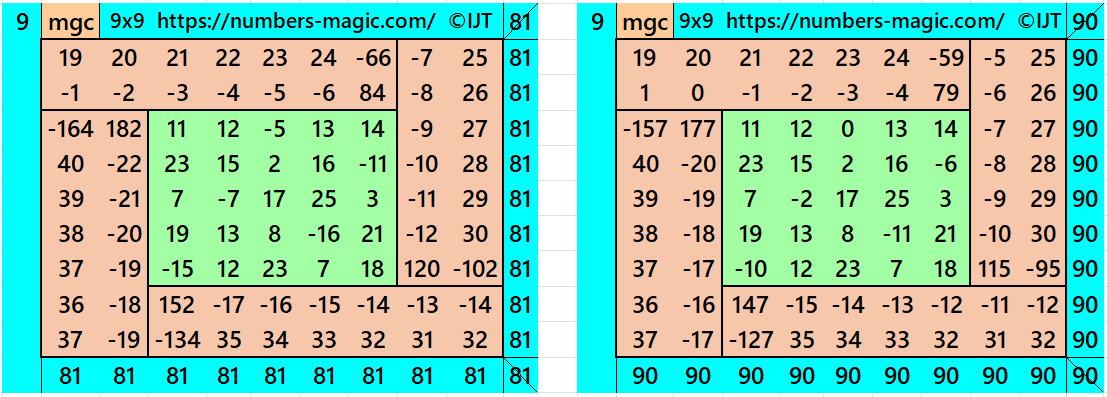
In the first example the magic sums are S_5×5 :=45, S_9×9 :=81 and m:=18.
In the second example the magic sums are S_5×5 :=50, S_9×9 :=90 and m:=20.

Result 6: Algebraic Flat-Type Magic Square of Order 9

It is an algebraic flat-type magic square of order 9 composed of two equal sums magic rectangles of order 2×9 and two equal sums magic rectangles of order 2×5 embedded with a magic square of order 5. In this case the magic sums are S_5×5:=S and S_9×9:=9*S/5, where S is the magic sum of order 5. In this case, m:=2*S/5 is the width of magic rectangles. To avoid decimal entries the magic sums of order 5 should be multiple of 5. See below two examples:

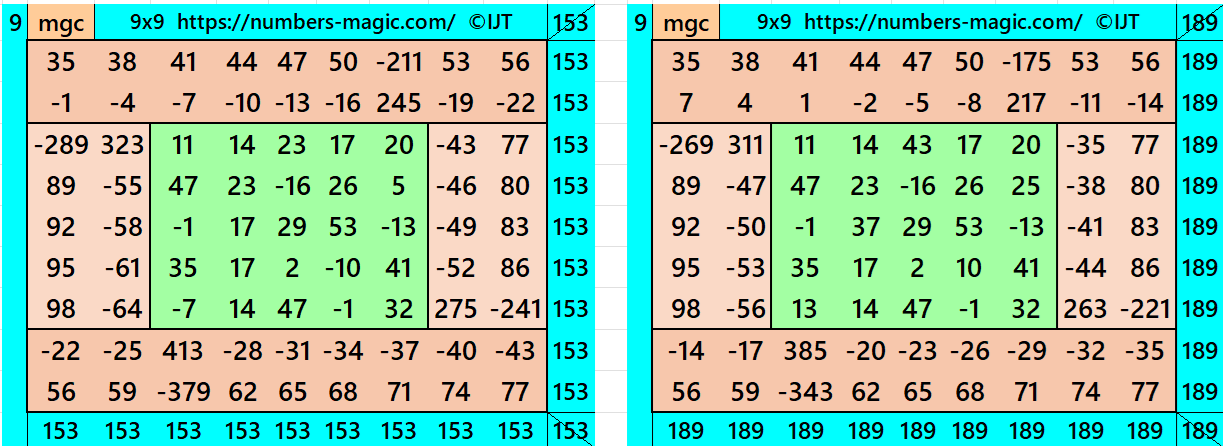
In the first example the magic sums are S_5×5 :=85, S_9×9 :=153 and m:=34.
In the second example the magic sums are S_5×5 :=105, S_9×9 :=189 and m:=42.

Result 7: Algebraic Cornered Magic Square of Order 9

It is an algebraic cornered striped magic square of order 9, where the magic squares of order 3, 5 and 7 are at the upper-left corner. The magic squares of orders 5 and 7 are also an algebraic cornered magic squares In this case the magic sums are S_3×3:=S, S_5×5:=5*S/3, S_7×7:=7*S/3 and S_9×9:=3*S, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

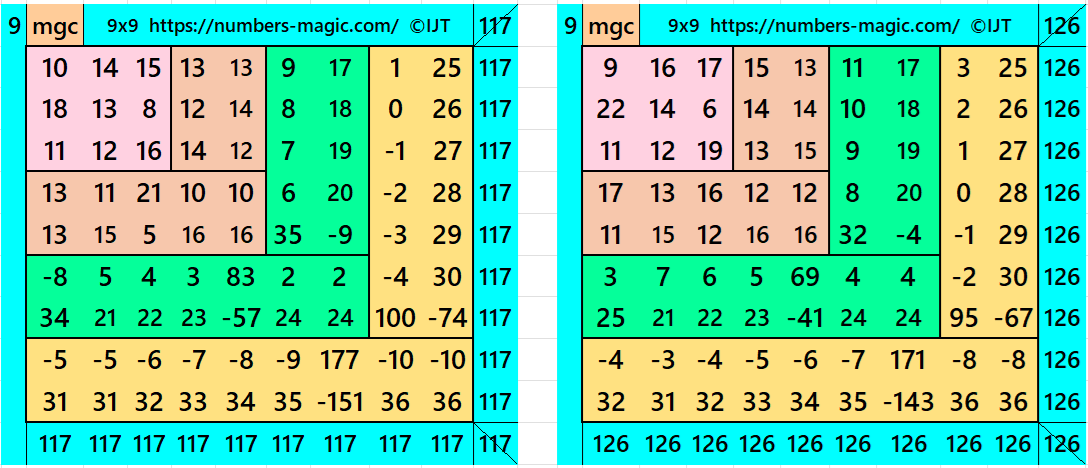
In the first example the magic sums are S_3×3 := 39, S_5×5 := 65, S_7×7:=91. S_9×9 :=117 and m:=26.
In the second example the magic sums are S_3×3 := 42, S_5×5 := 70, S_7×7:=98, S_9×9 :=126 and m:=28.

Algebraic Magic Squares of Order 11

Below are three types of algebraic striped magic squares of order 11.

Result 8: Algebraic Cyclic-Type Magic Square of Order 11

It is an algebraic cyclic-type magic square of order 11 composed of four equal sums magic rectangles of orders 2×9 embedded with a magic square of order 7. It is again composed of four equal sums magic rectangles of order 2×5 having a magic square of order 3 in the middle. In this case the magic sums are S_3×3:=S, S_7×7:=7*S/3 and S_11×11:=11*S/3, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

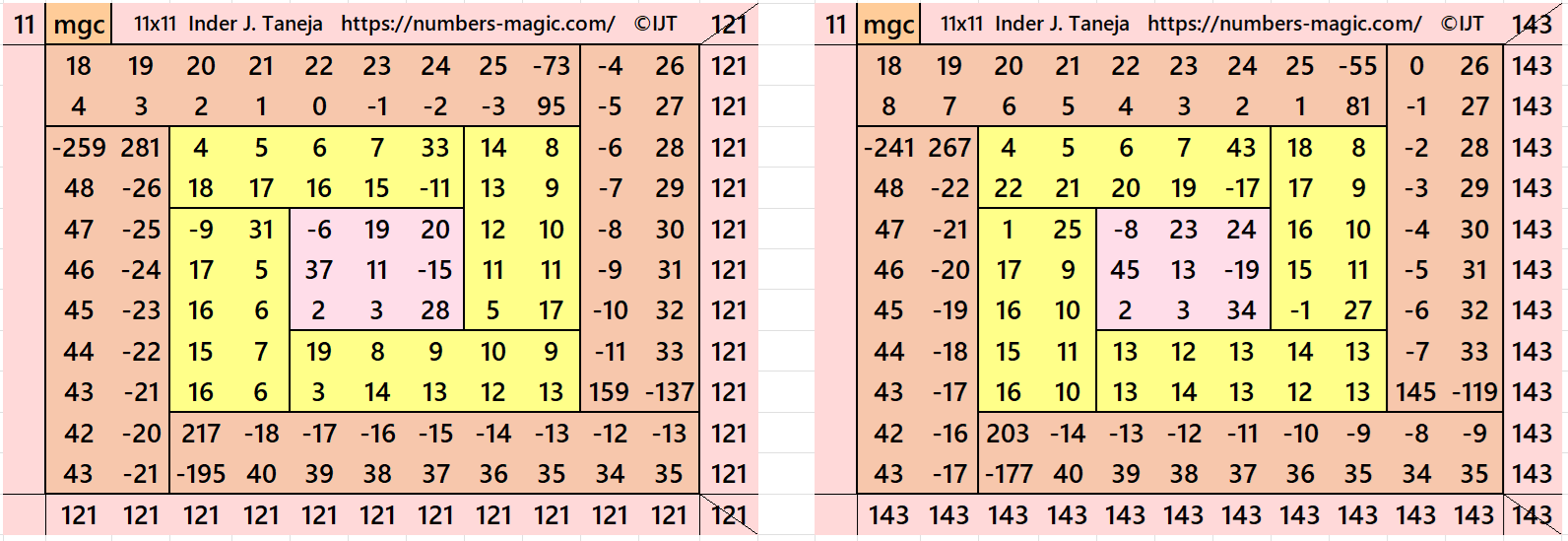
In the first example the magic sums are S_3×3 := 33, S_7×7:=77. S_11×11 :=121 and m:=22.
In the second example the magic sums are S_3×3 := 39, S_7×7:=91, S_11×11 :=143 and m:=26.

Result 9: Algebraic Flat-Type Magic Square of Order 11

It is an algebraic flat-type magic square of order 11 composed of two equal sums magic rectangles of orders 2×11 and two equal sums magic rectangles of order 2×7 embedded again with a flat-type magic square of order 7. In this case the magic sums are S_3×3:=S, S_7×7:=7*S/3 and S_11×11:=11*S/3, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

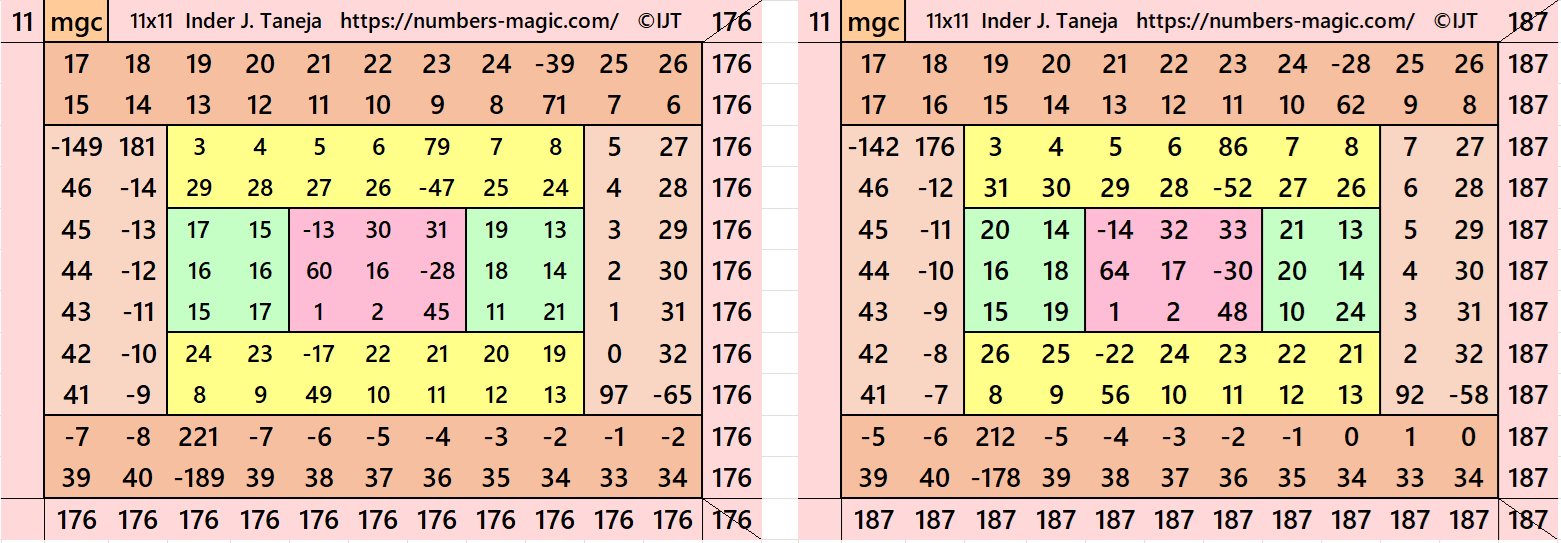
In the first example the magic sums are S_3×3 := 48, S_7×7:=112. S_11×11 :=176 and m:=32.
In the second example the magic sums are S_3×3 := 51, S_7×7:=119, S_11×11 :=187 and m:=34.

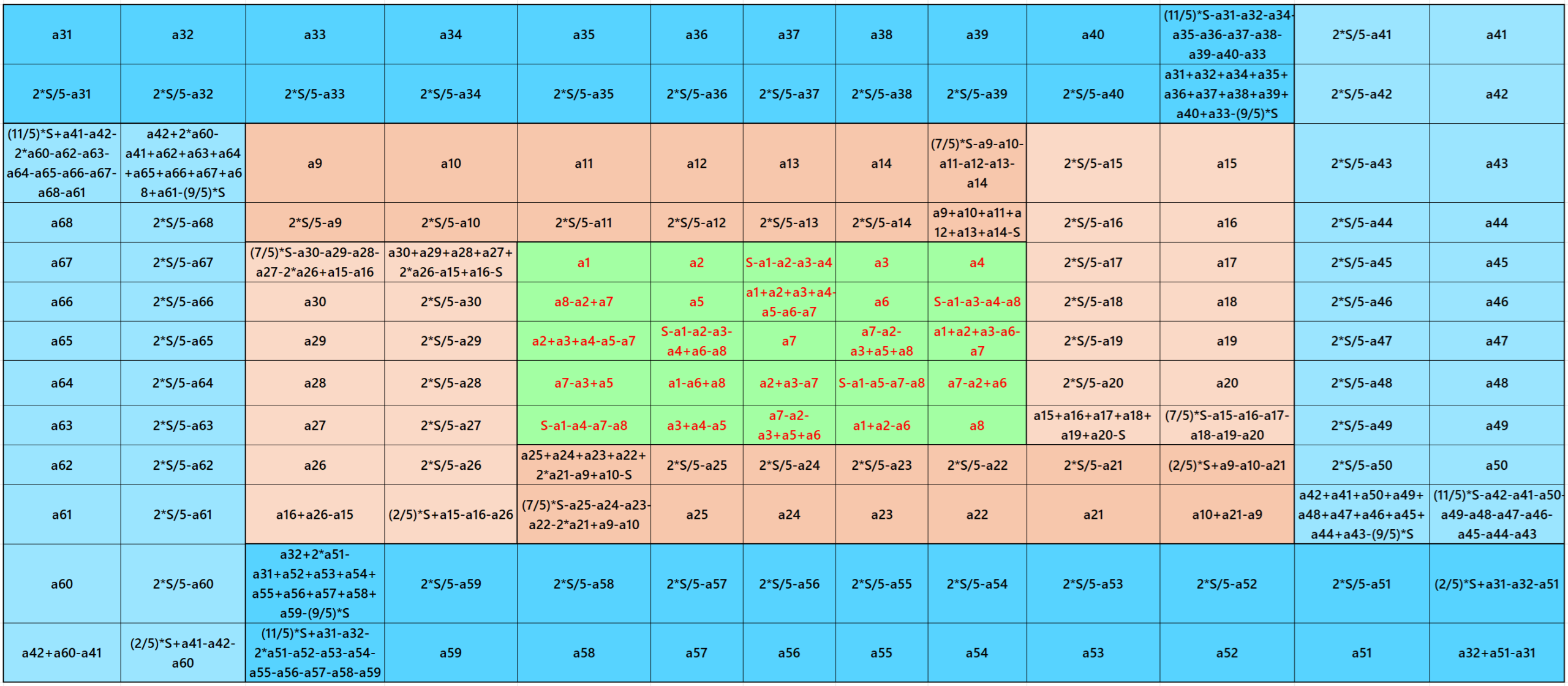
Result 10: Algebraic Cornred Magic Square of Order 11

It is an algebraic cornered striped magic square of order 11, where the magic squares of order 3, 5, 7 and 9 are at the upper-left corner. The magic squares of orders 5, 7 and 9 are also algebraic cornered magic squares In this case the magic sums are S_3×3:=S, S_5×5:=5*S/3, S_7×7:=7*S/3, S_9×9:=3*S and S_11×11:=11*S/3 where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

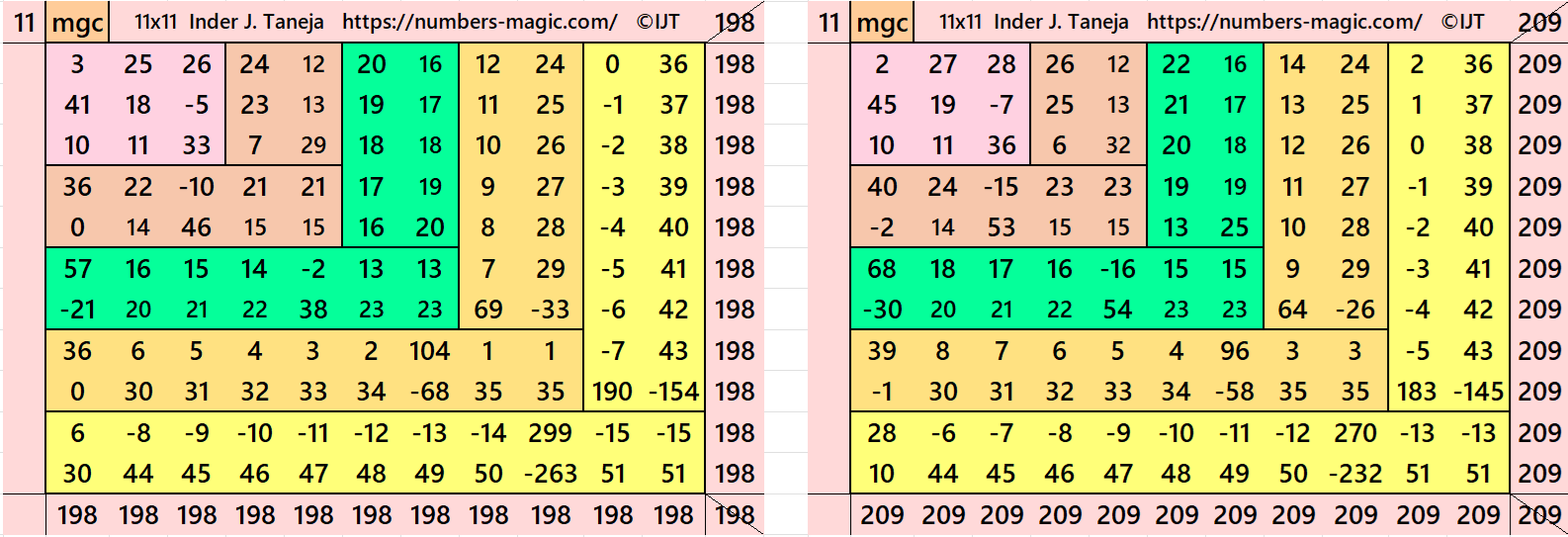
In the first example the magic sums are S_3×3:=54, S_5×5:= 90, S_7×7:=126, S_9×9:=162, S_11×11:=198 and m:=36.
In the second example the magic sums are S_3×3:=57, S_5×5:= 95 S_7×7:=133, S_9×9:=171, S_11×11:=209 and m:=38.

Algebraic Magic Squares of Order 13

Below are three types of algebraic striped magic squares of order 13.

Result 11: Algebraic Cyclic-Type Magic Square of Order 13

It is an algebraic cyclic-type magic square of order 13 composed of four equal sums magic rectangles of orders 2×11 embedded with a magic square of order 9. It is again composed of four equal sums magic rectangles of order 2×7 having a magic square of order 5 in the middle. In this case the magic sums are S_5×5:=S, S_9×9:=9*S/5 and S_13×13:=13*S/5, where S is the magic sum of order 5. In this case, m:=2*S/5 is the width of magic rectangles. To avoid decimal entries the magic sums of order 5 should be multiple of 5. See below two examples:

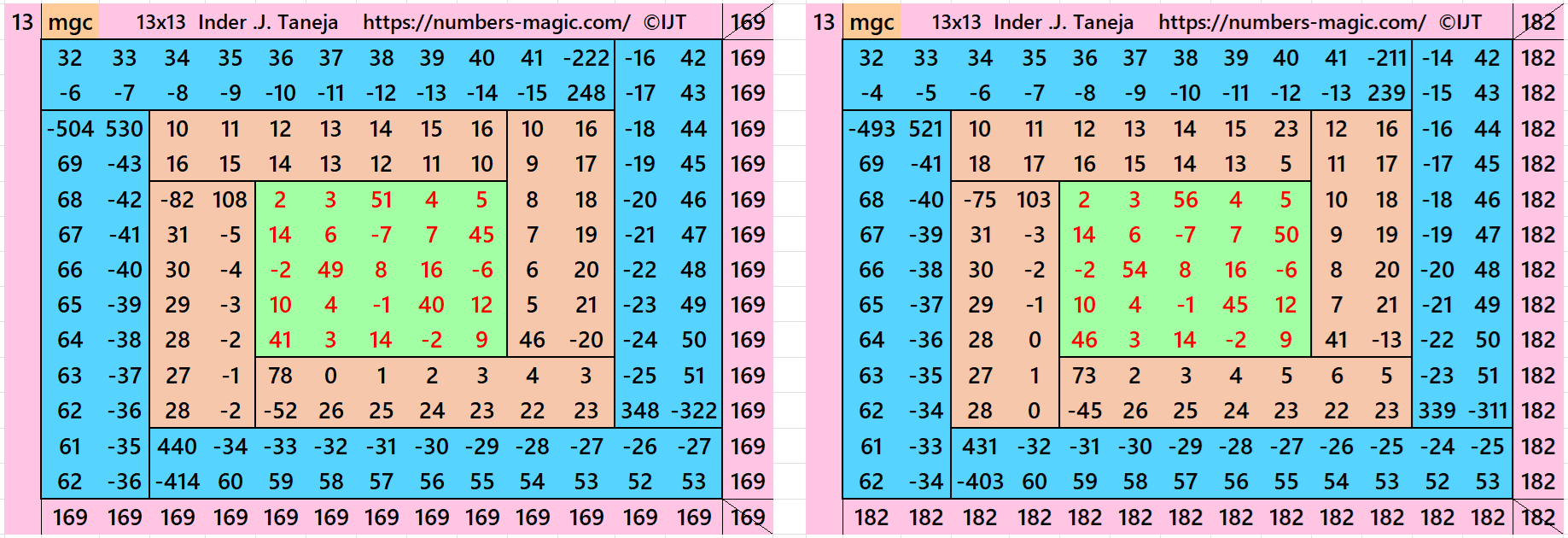
In the first example the magic sums are S_5×5:=65, S_9×9:=117, S_13×13:=169 and m:=26.
In the second example the magic sums are S_3×3 := 70, S_9×9:=126, S_13×13 :=182 and m:=28.

Result 12: Algebraic Flat-Type Magic Square of Order 13

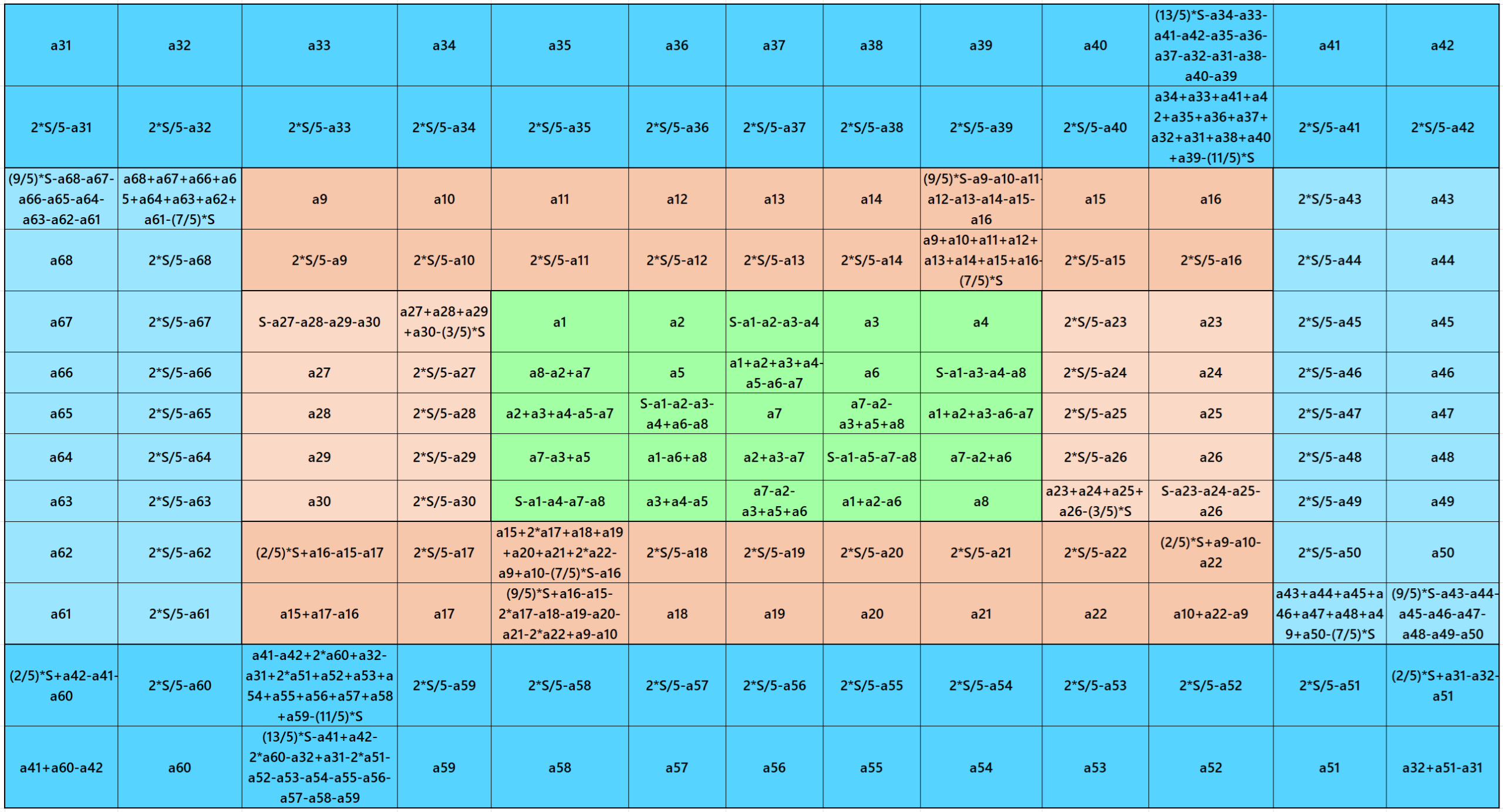
It is an algebraic flat-type magic square of order 13 composed of two equal sums magic rectangles of orders 2×13 and two equal sums magic rectangles of order 2×9 embedded again with a flat-type magic square of order 9. It is avgain a algebraic flat-type magic square of order 9 embedded with a magic square of order 5. In this case the magic sums are S_5×5:=S, S_9×9:=9*S/5 and S_13×13:=13*S/5, where S is the magic sum of order 5. In this case, m:=2*S/5 is the width of magic rectangles. To avoid decimal entries the magic sums of order 5 should be multiple of 5. See below two examples:

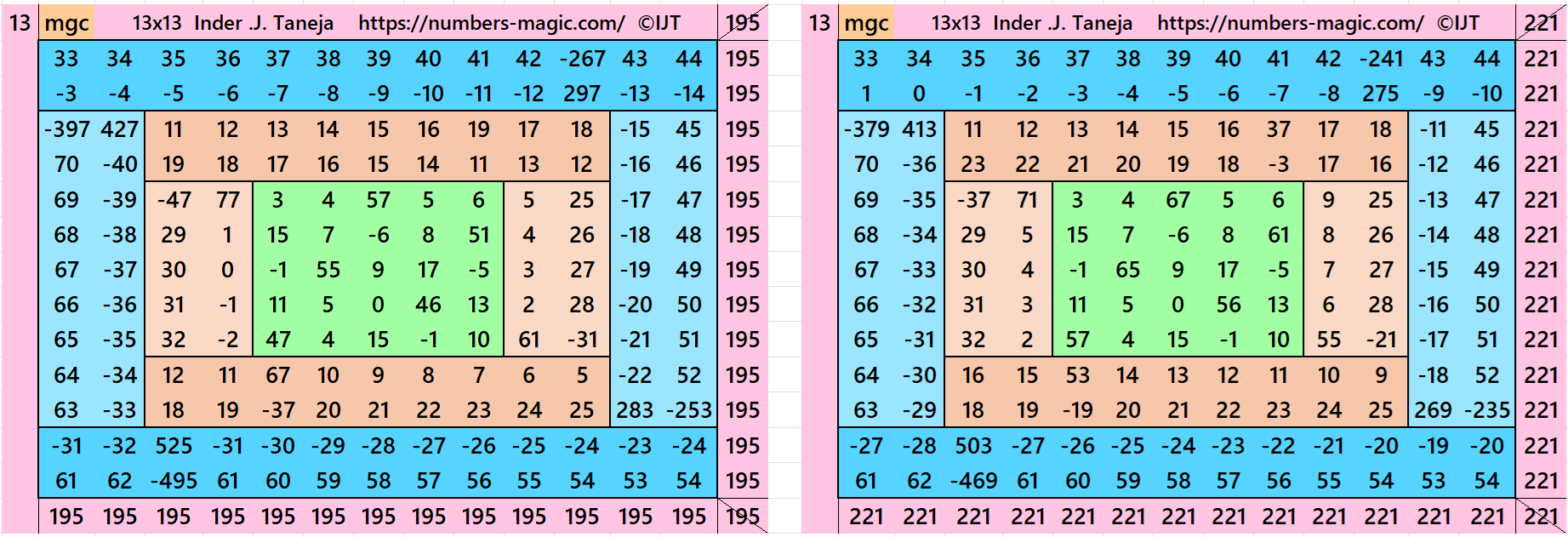
In the first example the magic sums are S_5×5:=75, S_9×9:=135, S_13×13:=195 and m:=30.
In the second example the magic sums are S_5×5 := 85, S_9×9:=153 S_13×13 :=221 and m:=34.

Result 13: Algebraic Cornered Magic Square of Order 13

It is an algebraic cornered striped magic square of order 13, where the magic squares of order 3, 5, 7, 9 and 11 are at the upper-left corner. The magic squares of orders 5, 7, 9 and 11 are also algebraic cornered magic squares In this case the magic sums are S_3×3:=S, S_5×5:=5*S/3, S_7×7:=7*S/3, S_9×9:=3*S, S_11×11:=11*S/3 and S_13×13:=13*S/3, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

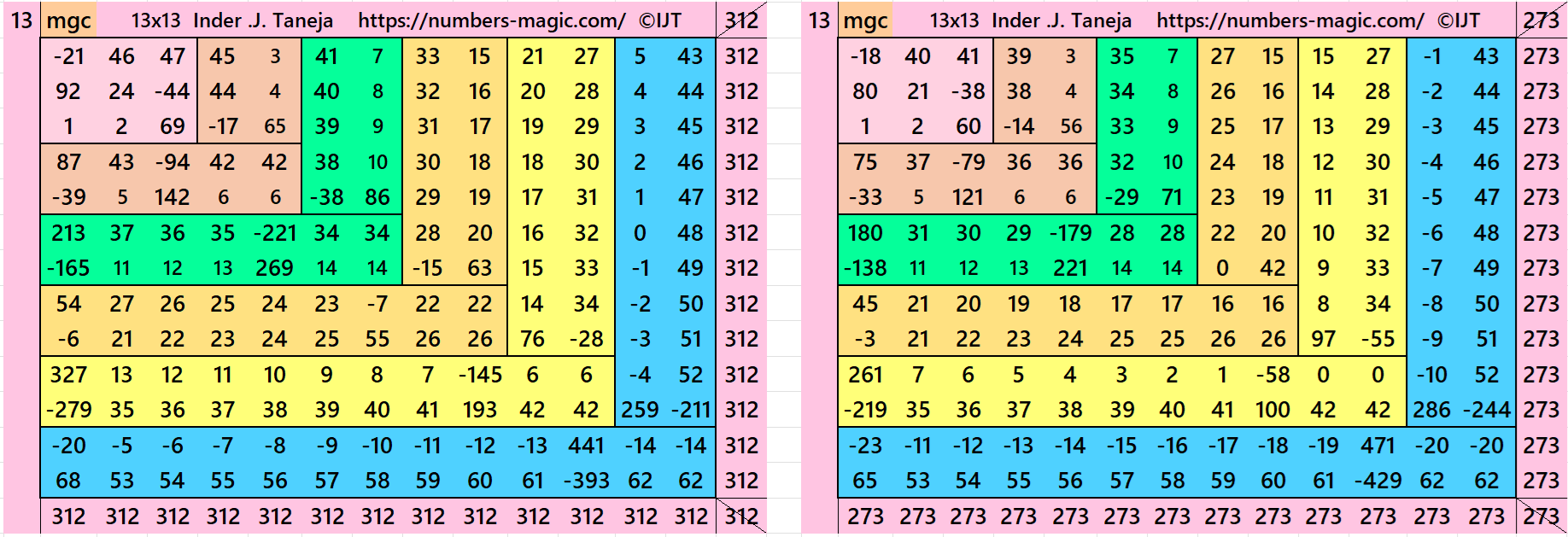
In the first example the magic sums are S_3×3:=72, S_5×5:= 120, S_7×7:=168, S_9×9:=216, S_11×11:=264, S_13×13:=312 and m:=48.
In the second example the magic sums are S_3×3:=63, S_5×5:= 105 S_7×7:=147, S_9×9:=189, S_11×11:=231, S_13×13:=273 and m:=42.

Algebraic Magic Squares of Order 15

Below are three types of algebraic striped magic squares of order 15.

Result 14: Algebraic Cyclic-Typec Magic Squares of Order 15

It is an algebraic cyclic-type magic square of order 15 composed of four equal sums magic rectangles of orders 2×13 embedded with a magic square of order 11. It is again composed of four equal sums magic rectangles of order 2×9 and so on having a magic square of order 3 in the middle. In this case the magic sums are S_3×3:=S, S_7×7:=7*S/3, S_11×11:=11*S/3 and S_15×15:=5*S, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

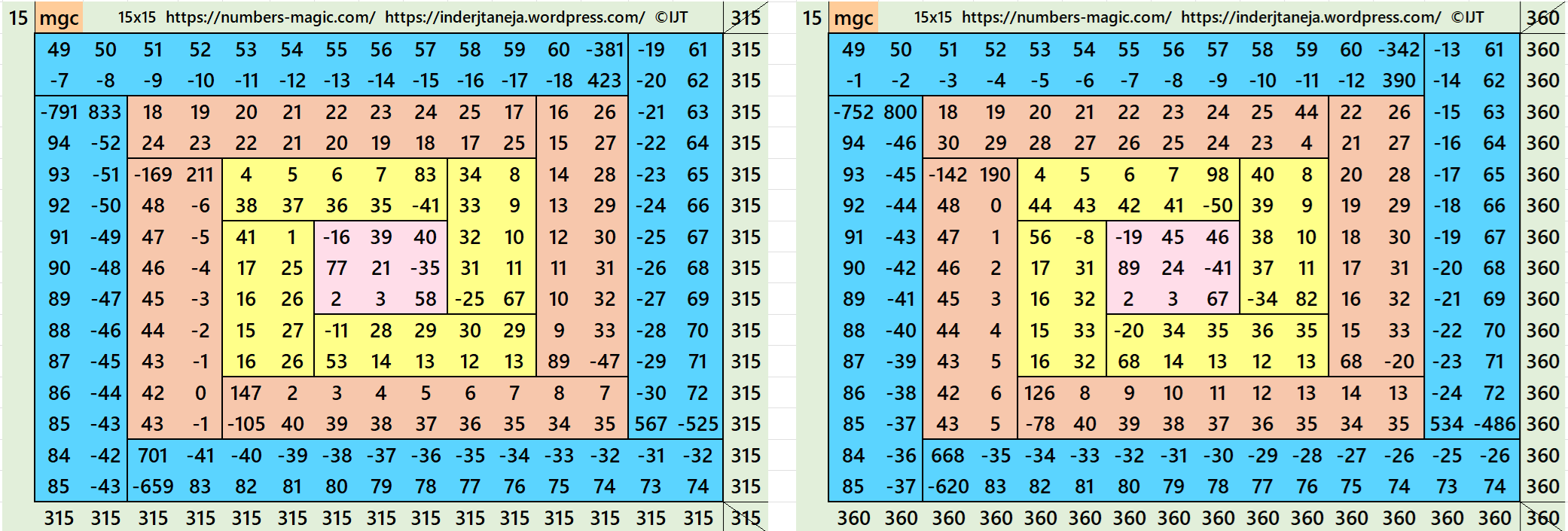
In the first example the magic sums are S_3×3 := 63, S_7×7:=147. S_11×11 :=231, S_15×15 :=315 and m:=42.
In the second example the magic sums are S_3×3 := 72, S_7×7:=168. S_11×11 :=264, S_15×15 :=360 and m:=48.

Result 15: Algebraic Flat-Type Flat Magic Square of Order 15

It is an algebraic flat-type magic square of order 15 composed of two equal sums magic rectangles of orders 2×13 and two equal sums magic rectangles of order 2×9 embedded again with a flat-type magic square of order 11 and so on. In this case the magic sums are S_3×3:=S, S_7×7:=7*S/3, S_11×11:=11*S/3 and S_15×15:=5*S, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

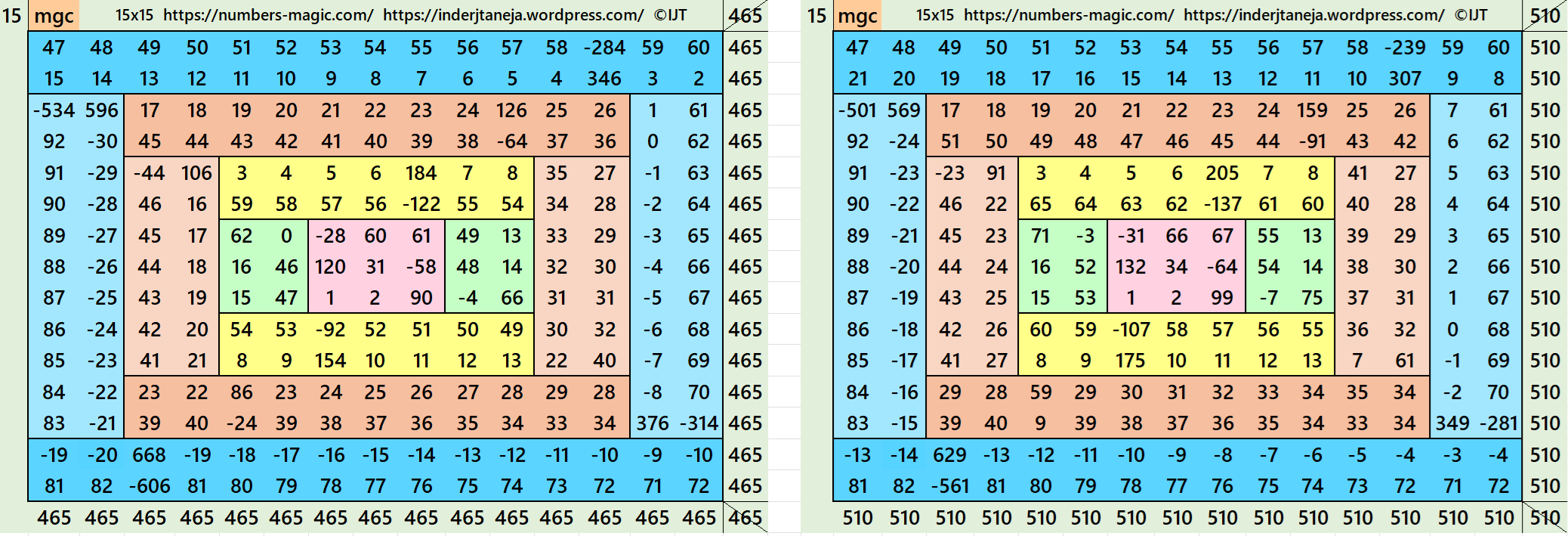
In the first example the magic sums are S_3×3 := 93, S_7×7:=217. S_11×11 :=341, S_15×15 :=465 and m:=62.
In the second example the magic sums are S_3×3 := 102, S_7×7:=238. S_11×11 :=374, S_15×15 :=510 and m:=68.

Result 16: Algebraic Cornered Magic Square of Order 15

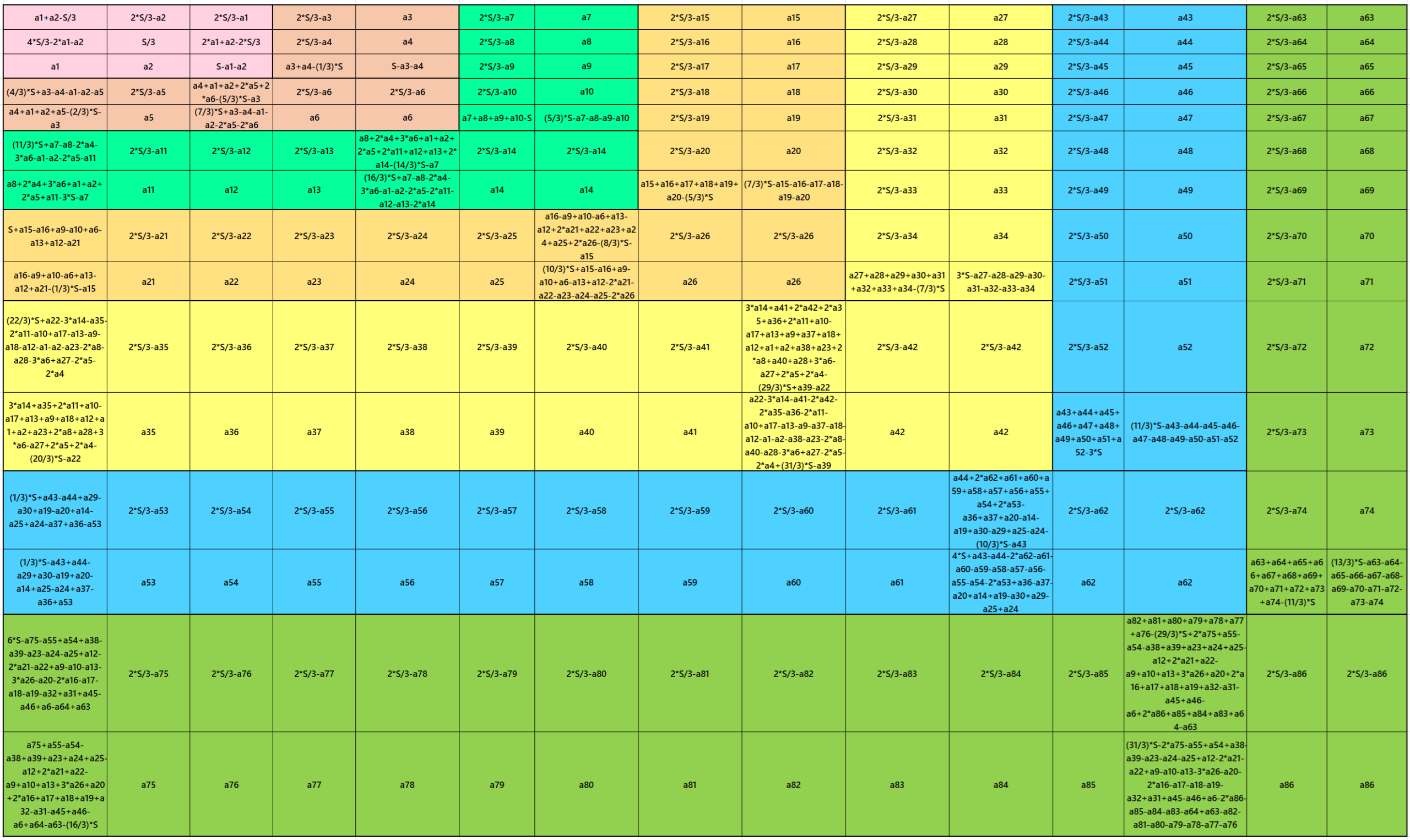
It is an algebraic cornered striped magic square of order 15, where the magic squares of order 3, 5, 7, 9, 11 and 13 are at the upper-left corner. The magic squares of orders 5, 7, 9, 11 and 13 are also algebraic cornered magic squares In this case the magic sums are S_3×3:=S, S_5×5:=5*S/3, S_7×7:=7*S/3, S_9×9:=3*S, S_11×11:=11*S/3, S_13×13:=13*S/3 and S_15×15:=5*S, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

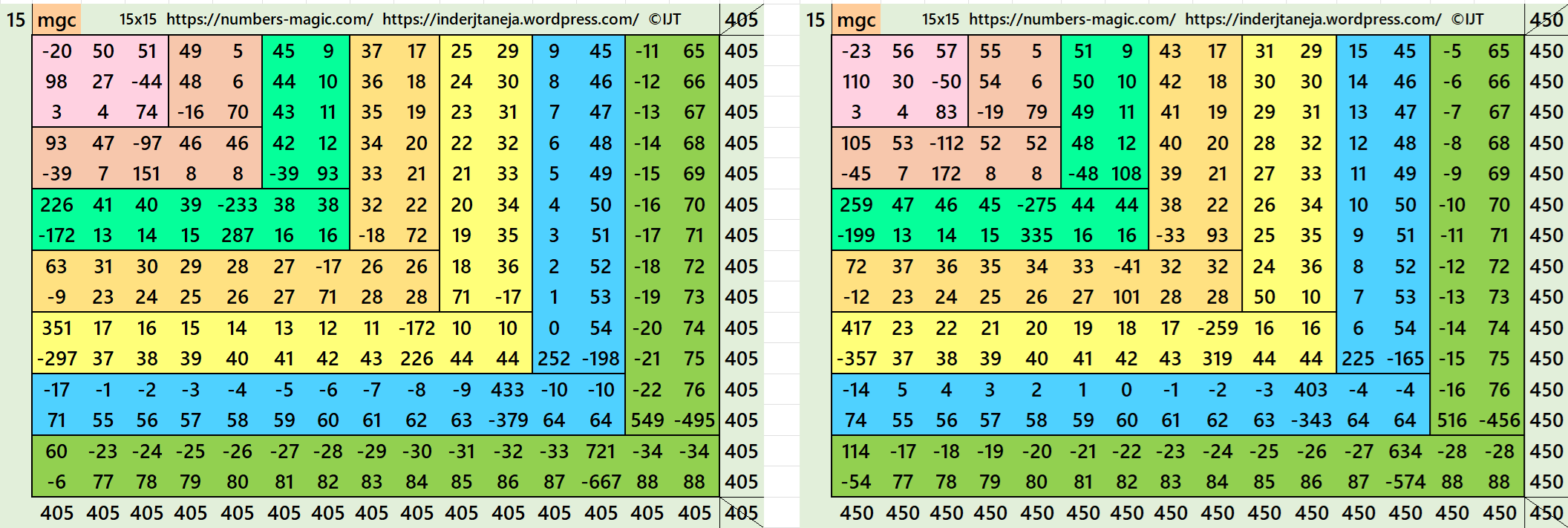
In the first example the magic sums are S_3×3:=81, S_5×5:= 135, S_7×7:=189, S_9×9:=243, S_11×11:=297, S_13×13:=351, S_15×15:=405 and m:=54.
In the second exemplem the magic sums are S_3×3:=90, S_5×5:= 150, S_7×7:=210, S_9×9:=270, S_11×11:=330, S_13×13:=390, S_15×15:=450 and m:=60.

Algebraic Magic Squares of Order 17

Below are three types of algebraic striped magic squares of order 17.

Result 17: Algebraic Cyclic-Type Magic Square of Order 17

It is an algebraic cyclic-type magic square of order 17 composed of four equal sums magic rectangles of orders 2×15 embedded with a magic square of order 13. It is again composed of four equal sums magic rectangles of order 2×11 and so on having a magic square of order 5 in the middle. In this case the magic sums are S_5×5:=S, S_9×9:=3*S, S_13×13:=13*S/3 and S_17×17:=17*S/3, where S is the magic sum of order 5. In this case, m:=2*S/5 is the width of magic rectangles. To avoid decimal entries the magic sums of order 5 should be multiple of 5. See below two examples:

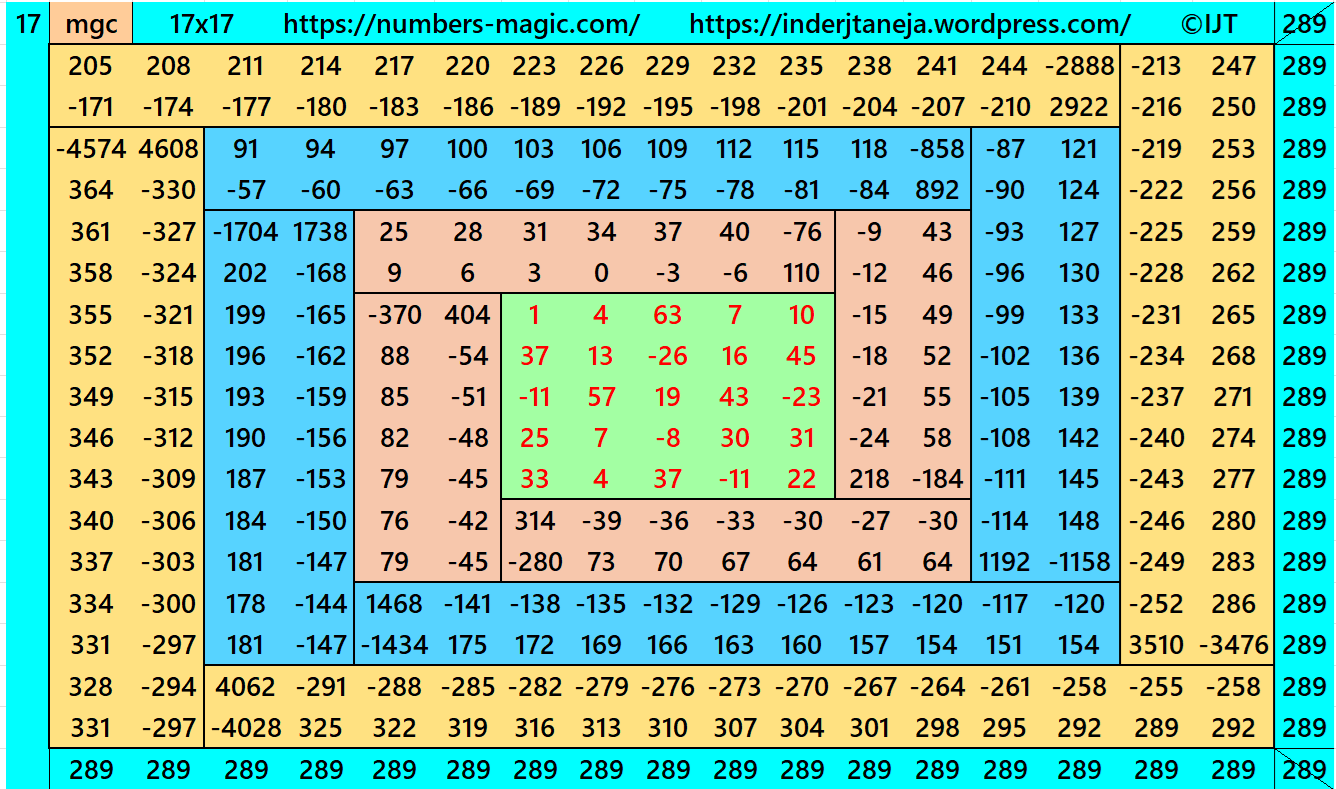
In this example the magic sums are S_5×5:=85, S_9×9:=153, S_13×13:=221, S_17×17:=289 and m:=34.

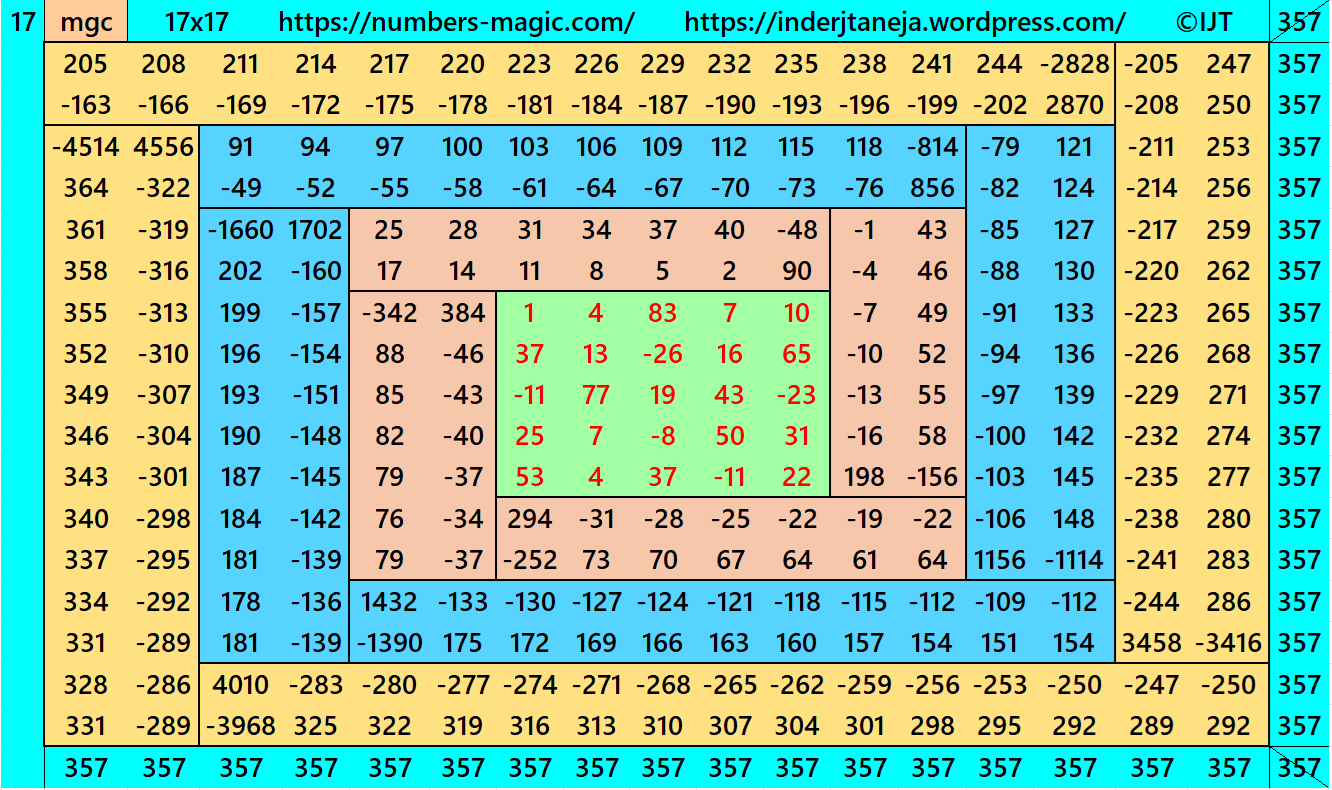
In this example the magic sums are S_5×5:=105, S_9×9:=189, S_13×13:=273, S_17×17:=357 and m:=42.

Result 18: Algebraic Flat-Type Magic Square of Order 17

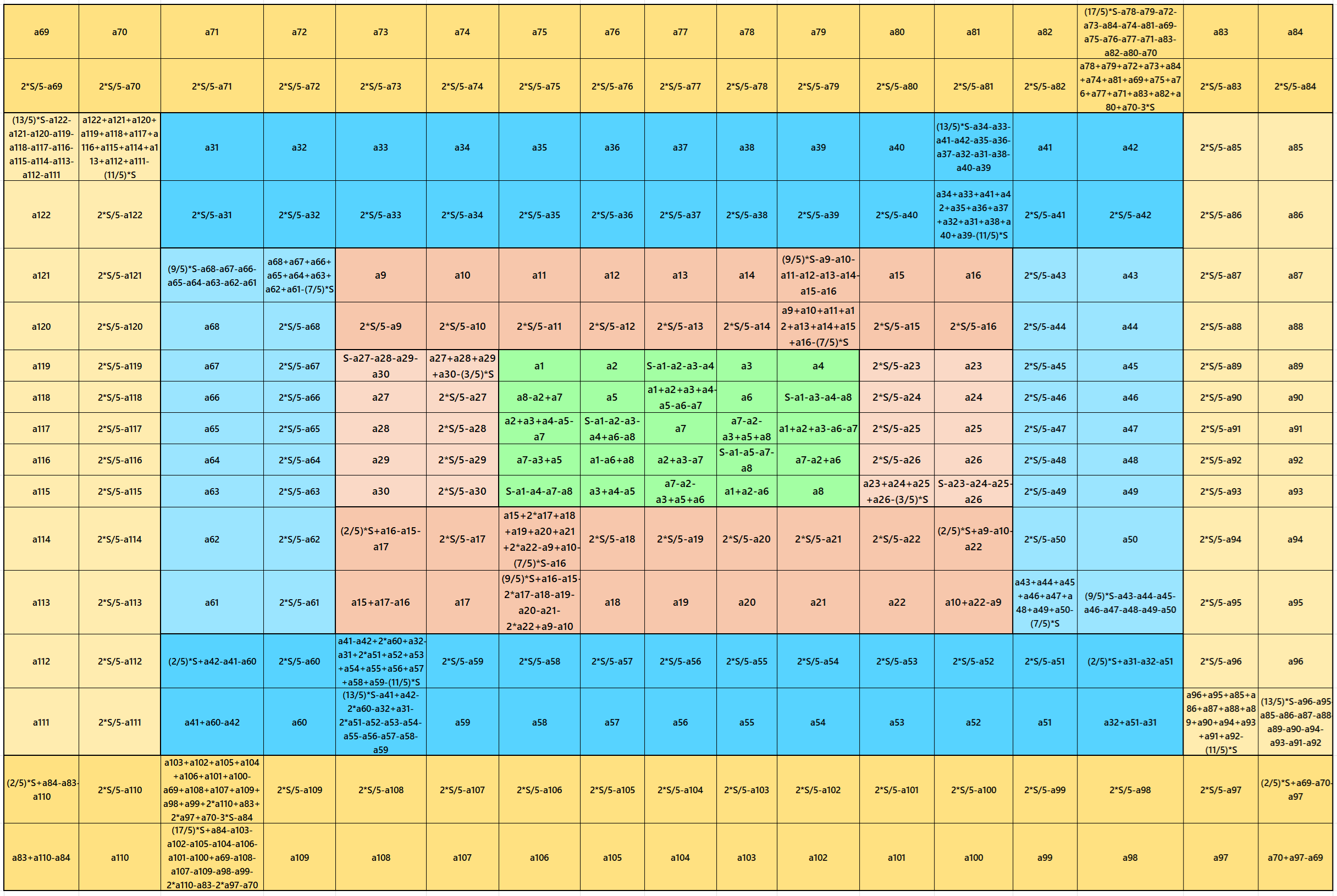
It is an algebraic flat-type magic square of order 17 composed of two equal sums magic rectangles of orders 2×17 and two equal sums magic rectangles of order 2×13 embedded again with a flat-type magic square of order 13. It is again a algebraic flat-type magic square of order 13 and so on having a magic square of order 5 in the middle. In this case the magic sums are S_5×5:=S, S_9×9:=3*S, S_13×13:=13*S/3 and S_17×17:=17*S/3, where S is the magic sum of order 5. In this case, m:=2*S/5 is the width of magic rectangles. To avoid decimal entries the magic sums of order 5 should be multiple of 5. See below two examples:

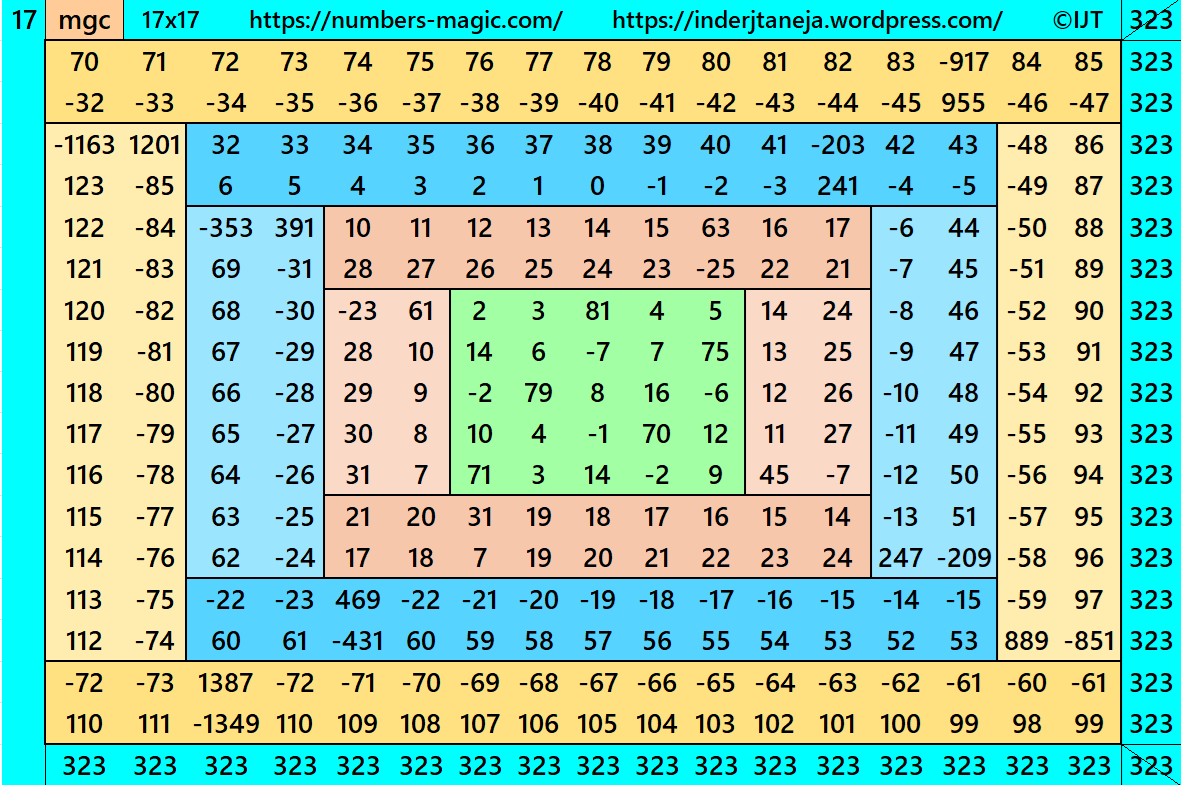
In this example the magic sums are S_5×5:=95, S_9×9:=171, S_13×13:=247, S_17×17:=323 and m:=38.

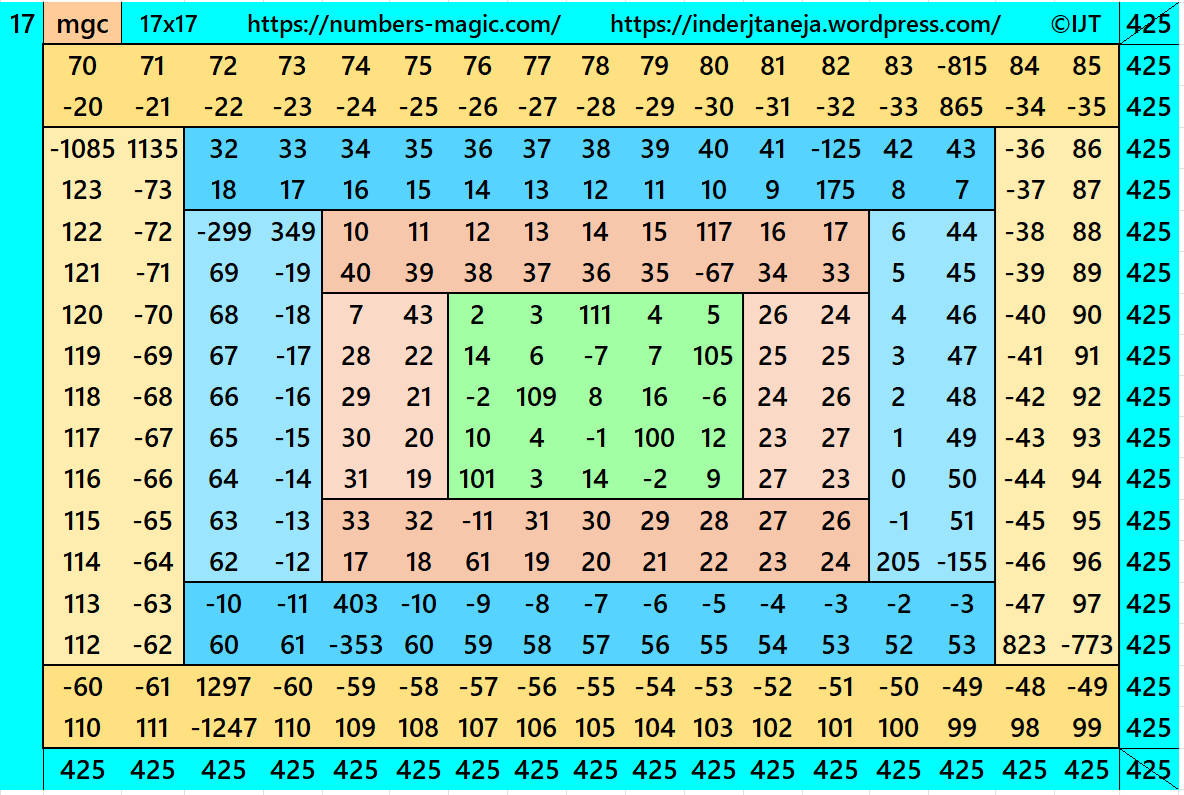
In this example the magic sums are S_5×5:=125, S_9×9:=225, S_13×13:=325, S_17×17:=425 and m:=50.

Result 19: Algebraic Cornered Magic Square of Order 17

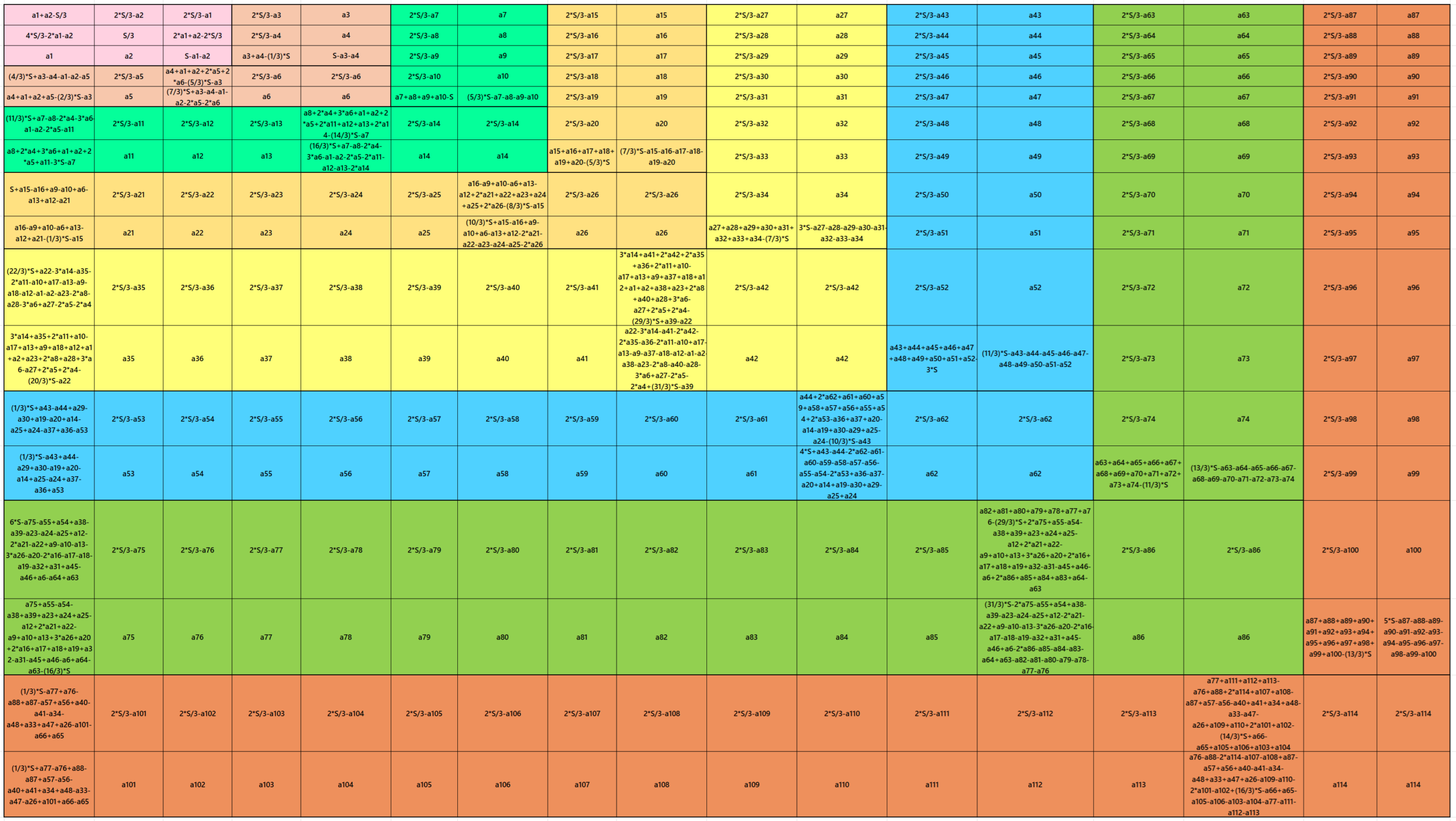
It is an algebraic cornered striped magic square of order 17, where the magic squares of order 3, 5, 7, 9, 11, 13 and 15 are at the upper-left corner. The magic squares of orders 5, 7, 9, 11, 13 and 15 are also algebraic cornered magic squares. In this case the magic sums are S_3×3:=S, S_5×5:=5*S/3, S_7×7:=7*S/3, S_9×9:=3*S, S_11×11:=11*S/3, S_13×13:=13*S/3, S_15×15:=5*S and S_17×17:=17*S/3, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

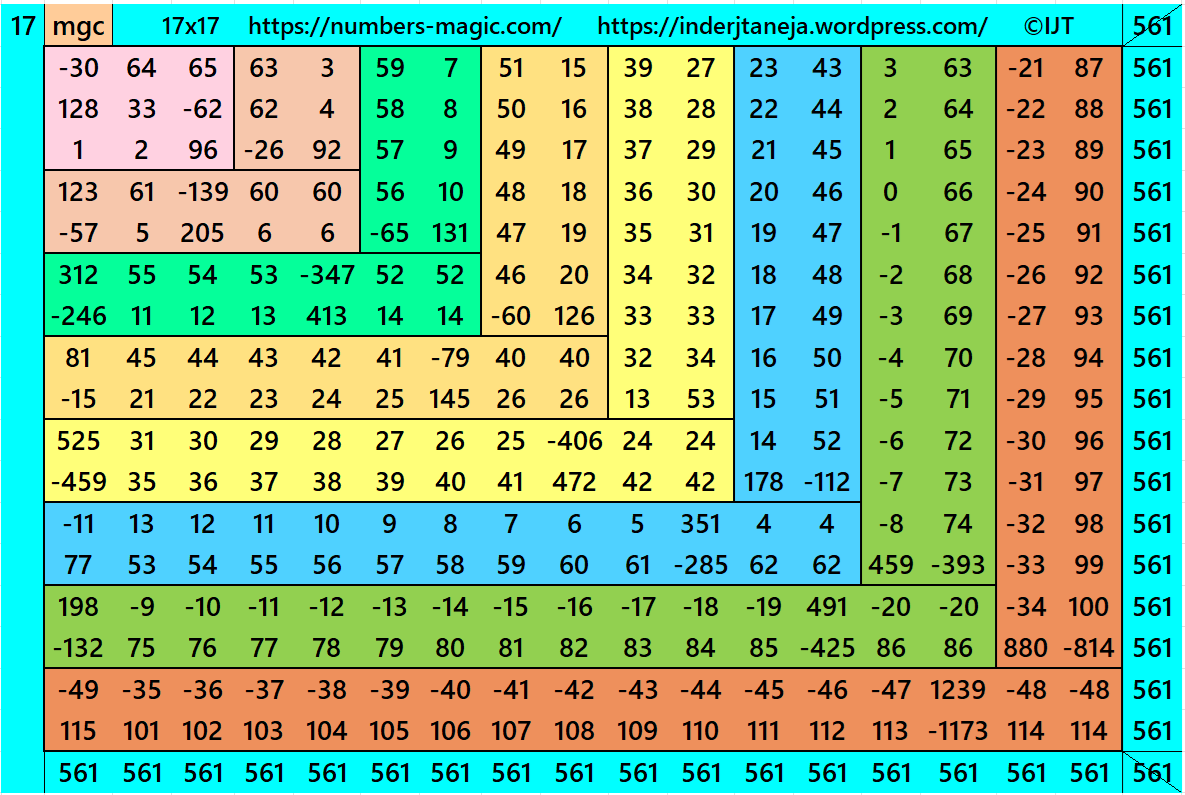
In this example the magic sums are S_3×3:=99, S_5×5:= 165, S_7×7:=231, S_9×9:=297, S_11×11:=363, S_13×13:=429, S_15×15:=495, S_17×17:=561 and m:=78.

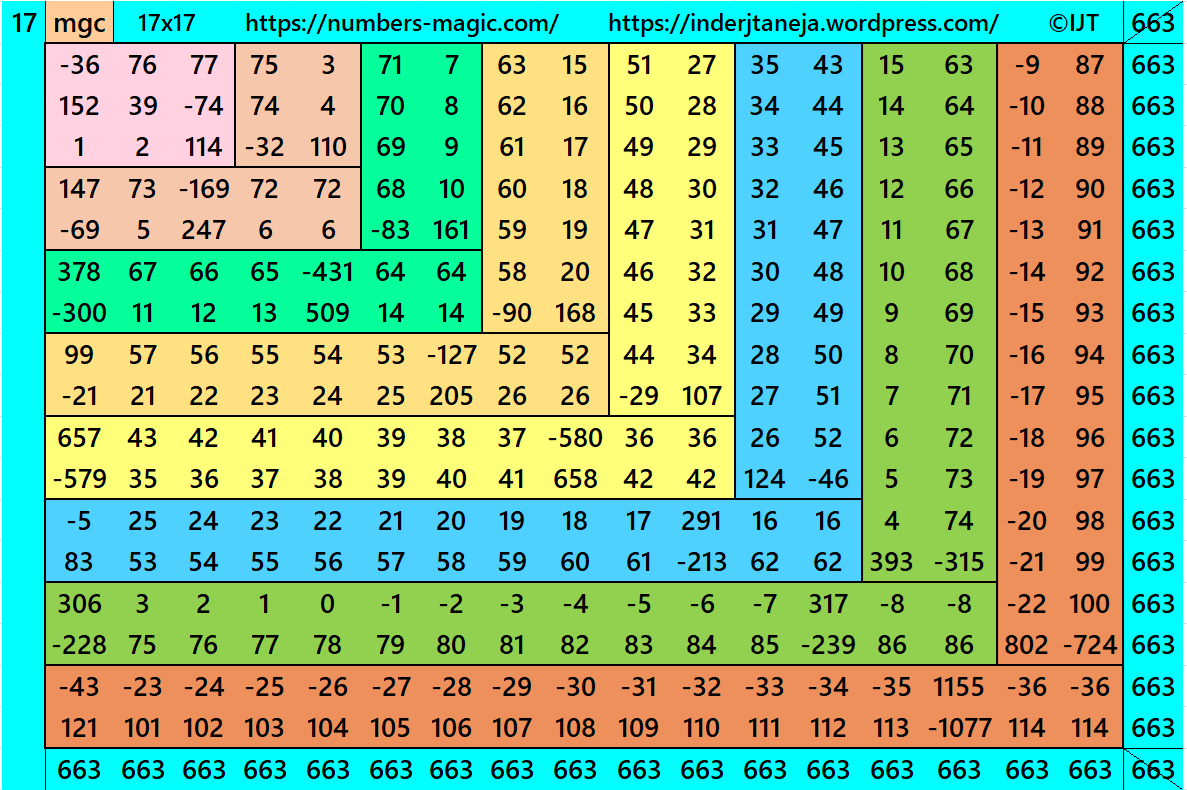
In this example the magic sums are S_3×3:=117, S_5×5:= 195, S_7×7:=273, S_9×9:=351, S_11×11:=429, S_13×13:=507, S_15×15:=585, S_17×17:=663 and m:=66.

Algebraic Magic Squares of Order 19

Below are three types of algebraic striped magic squares of order 19.

Result 20: Algebraic Cyclic-Type Magic Square of Order 19

It is an algebraic cyclic-type magic square of order 19 composed of four equal sums magic rectangles of orders 2×17 embedded with a magic square of order 15. It is again composed of four equal sums magic rectangles of order 2×13 and so on having a magic square of order 3 in the middle. In this case the magic sums are S_3×3:=S, S_7×7:=7*S/3, S_11×11:=11*S/3, S_15×15:=5*S and S_19×19:=19*S/3, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

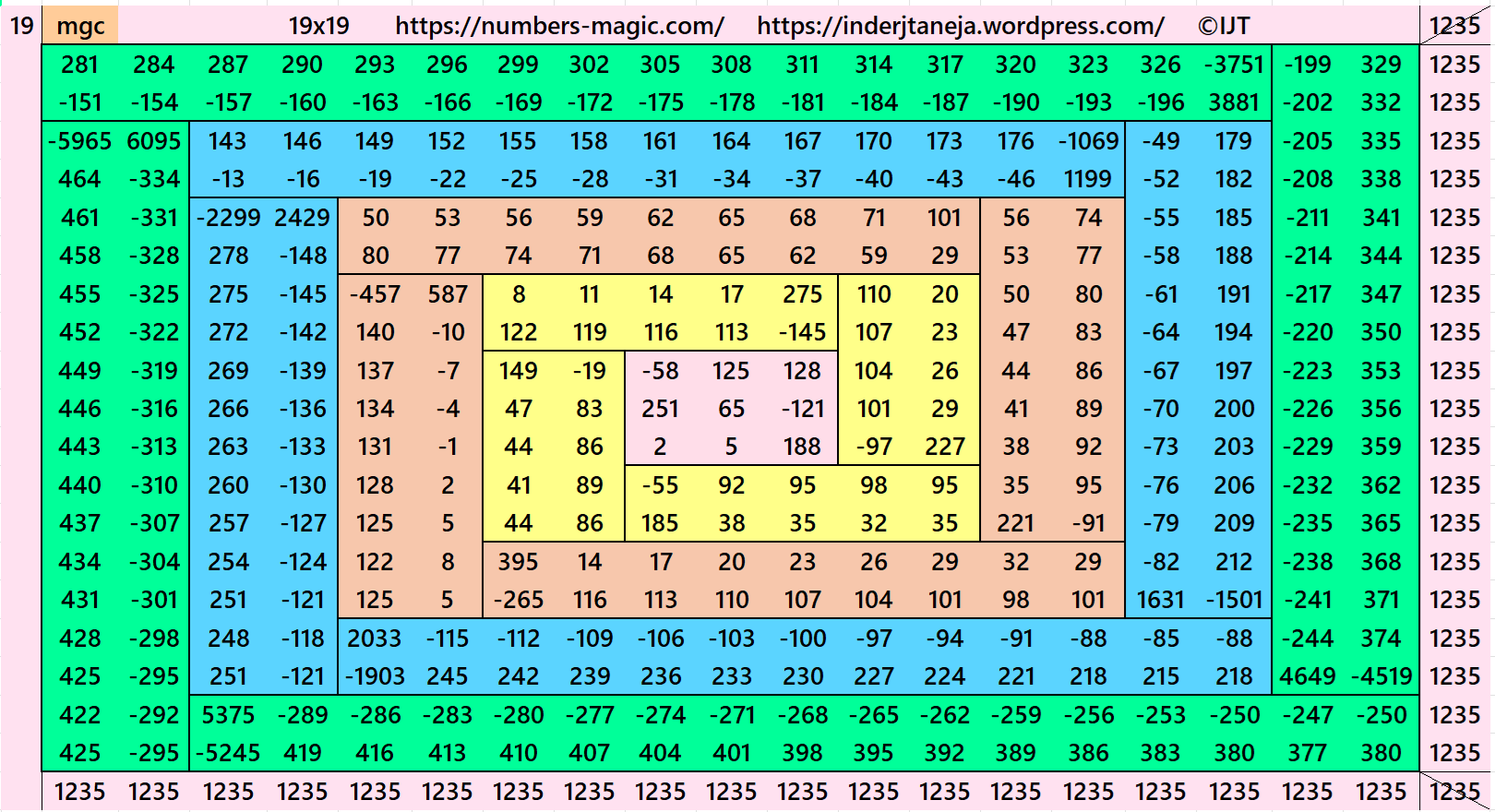
In this example the magic sums are S_3×3:=195, S_7×7:=455, S_11×11:=715, S_15×15:=975, S_19×19:=1235 and m:=130.

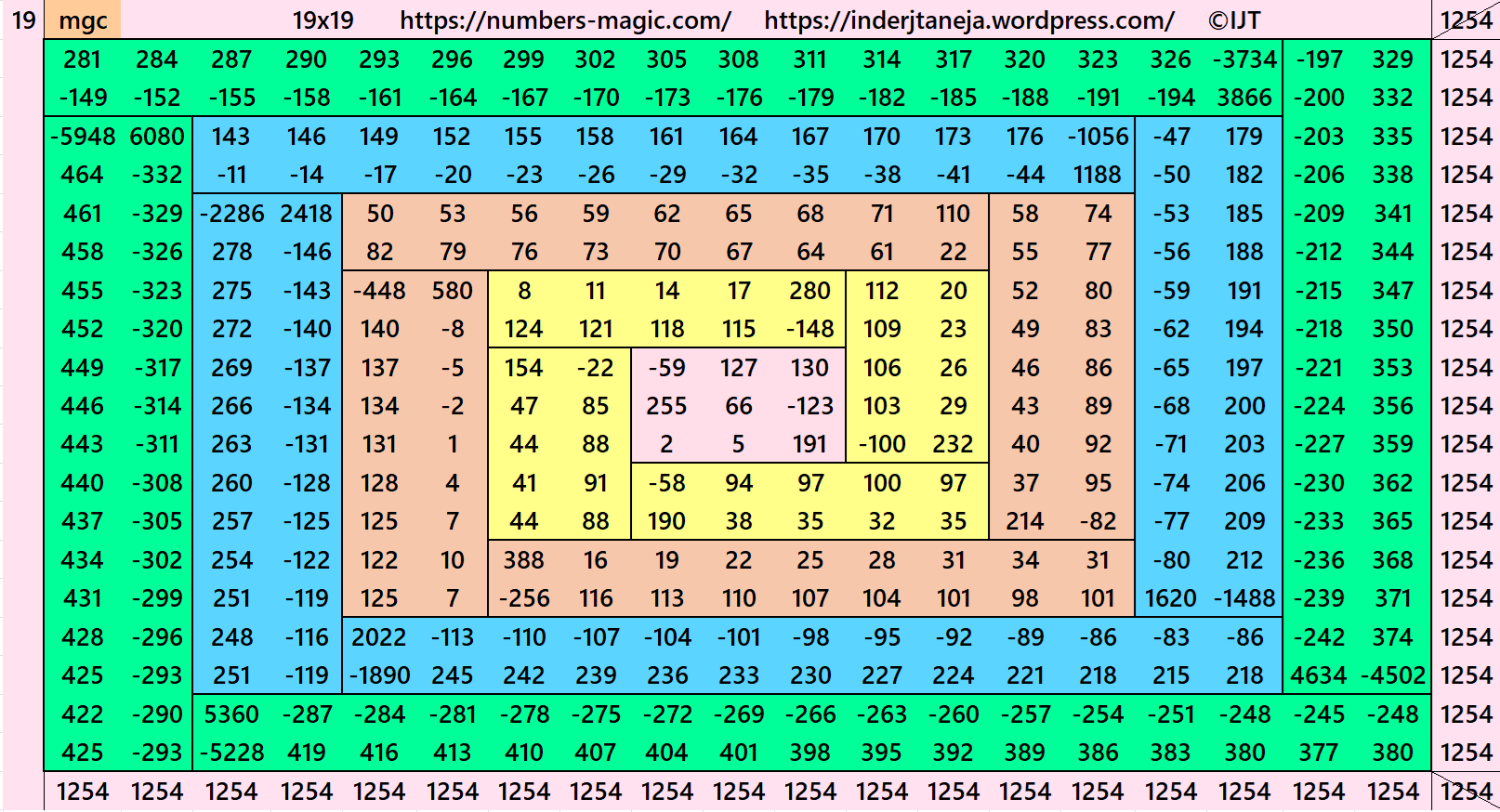
In this example the magic sums are S_3×3:=198, S_7×7:=462, S_11×11:=726, S_15×15:=990, S_19×19:=1254 and m:=132.

Result 21: Algebraic Flat-Type Magic Square of Order 19

It is an algebraic flat-type magic square of order 19 composed of two equal sums magic rectangles of orders 2×19 and two equal sums magic rectangles of order 2×15 embedded again with a flat-type magic square of order 15 and so on. In this case the magic sums are S_3×3:=S, S_7×7:=7*S/3, S_11×11:=11*S/3, S_15×15:=5*S and S_19×19:=19*S/3, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

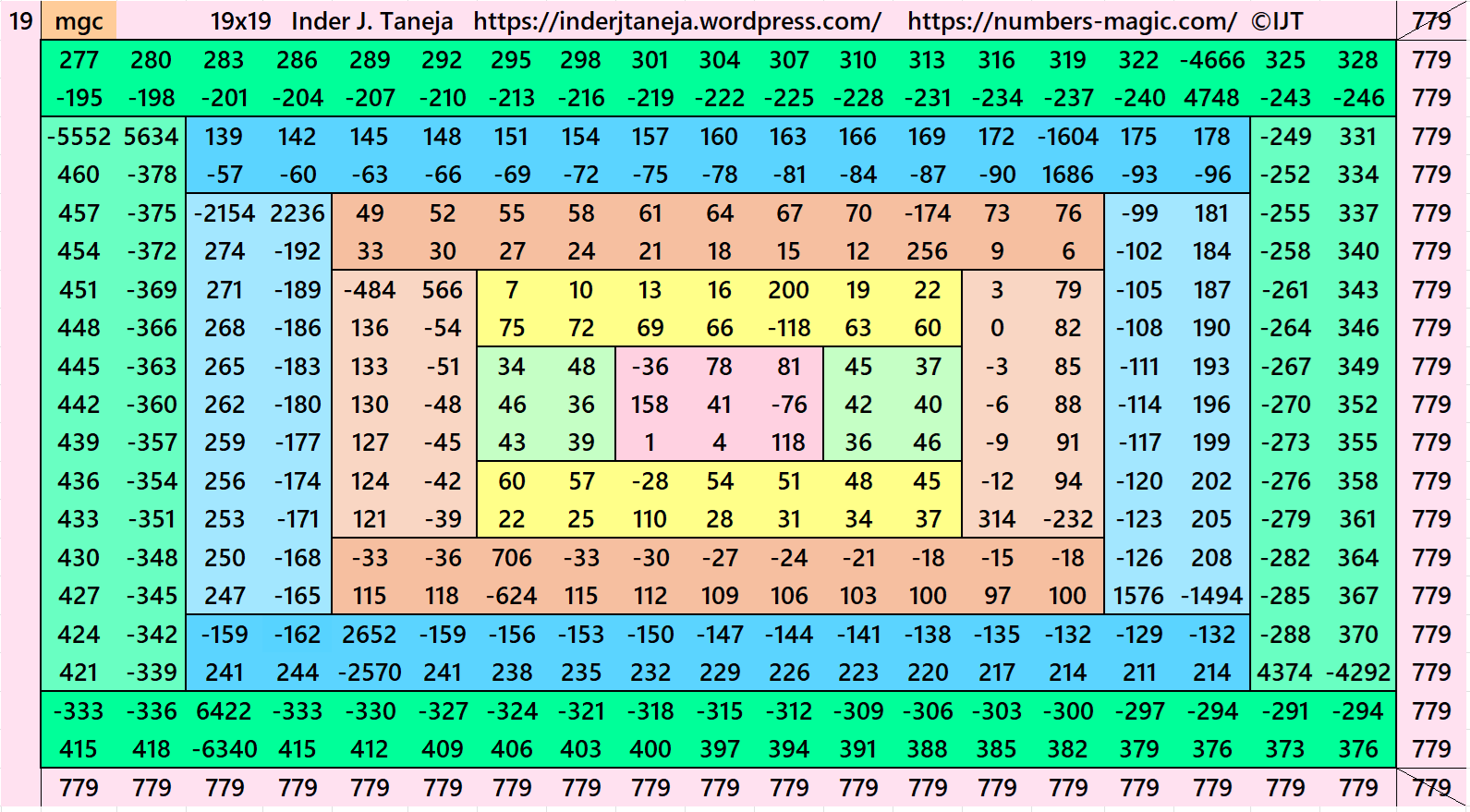
In this example the magic sums are S_3×3:=123, S_7×7:=287, S_11×11:=451, S_15×15:=615, S_19×19:=779 and m:=82.

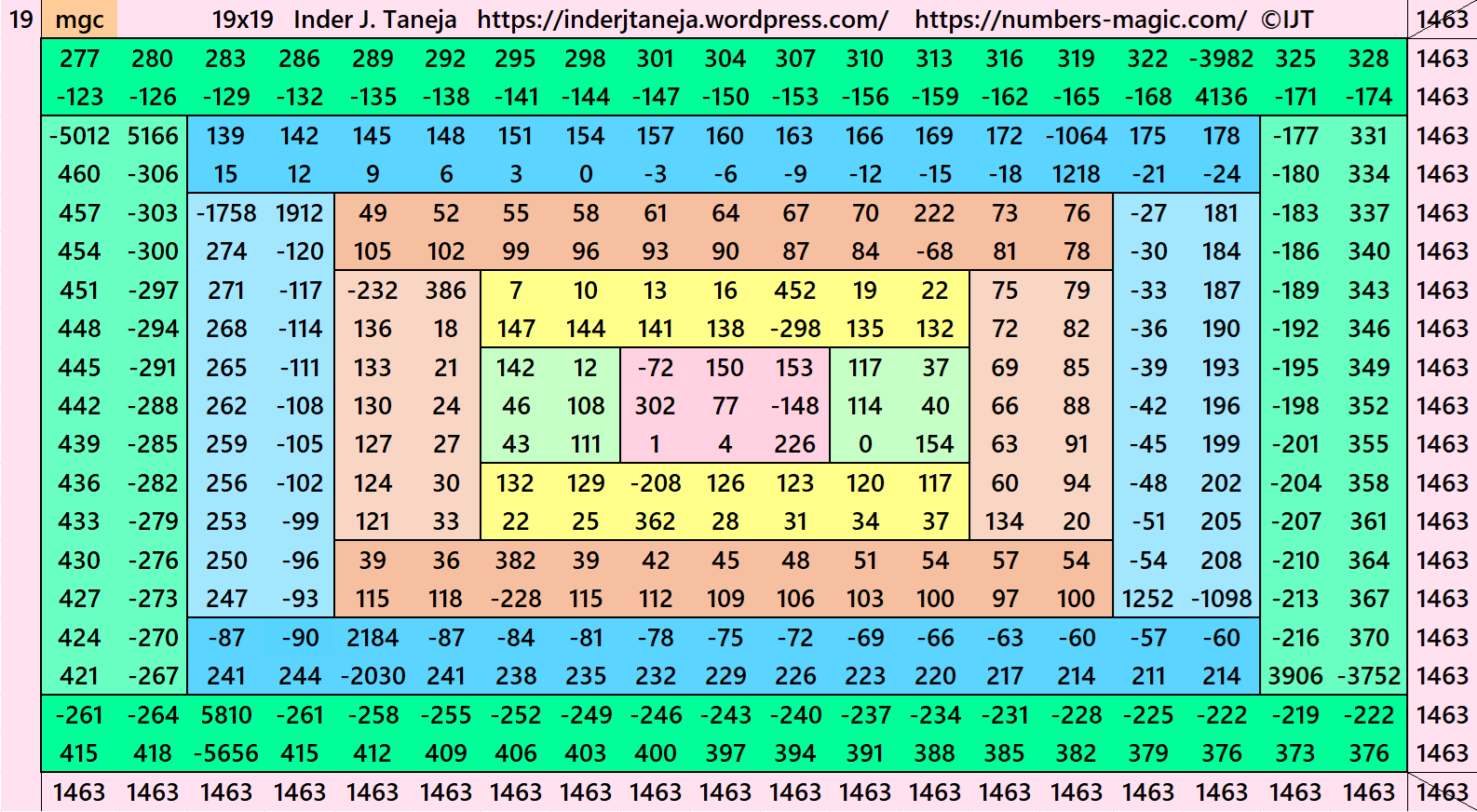
In this example the magic sums are S_3×3:=231, S_7×7:=539, S_11×11:=847, S_15×15:=1155, S_19×19:=1463 and m:=154.

Result 22: Algebraic Cornered Magic Square of Order 19

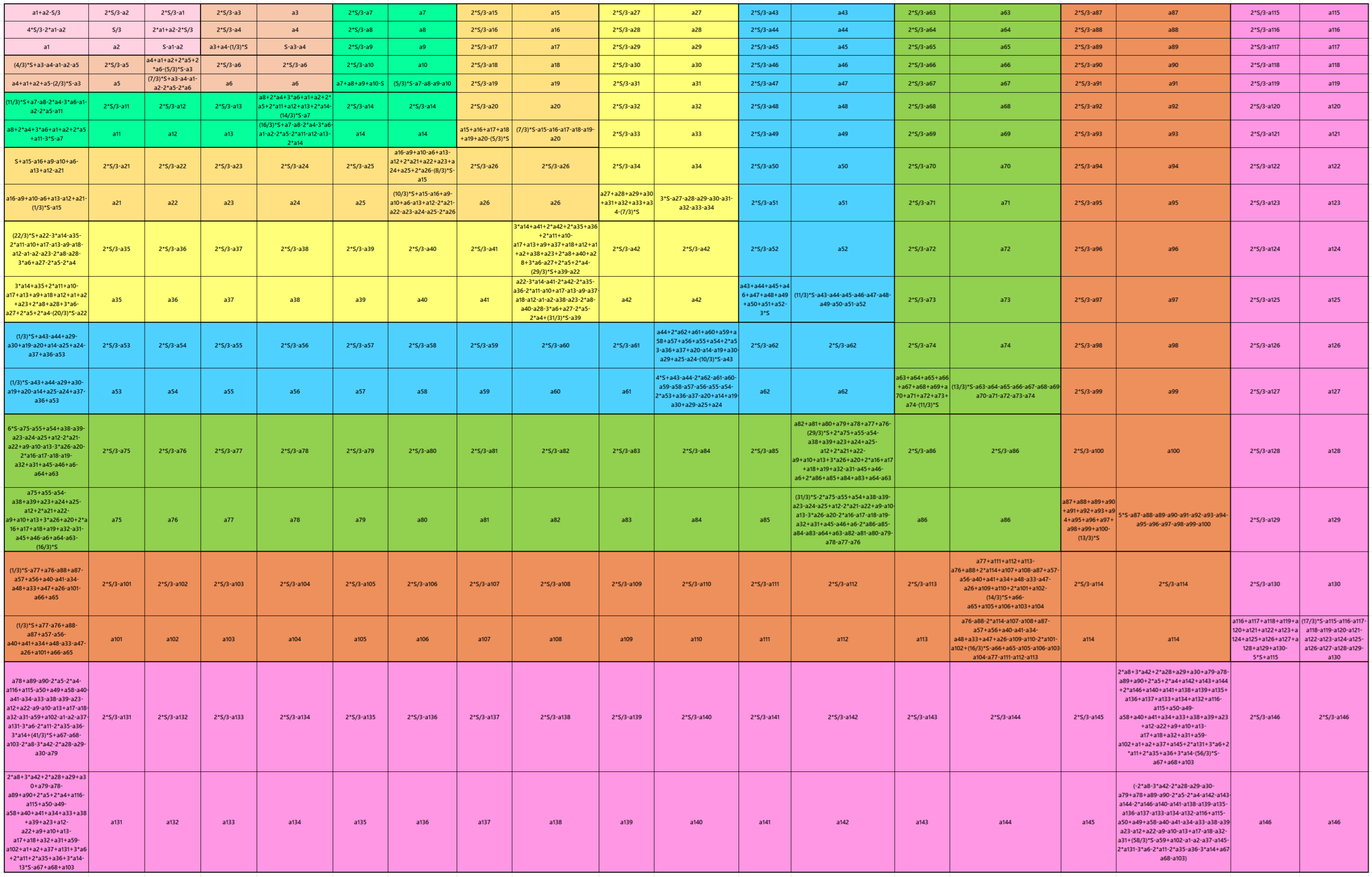
It is an algebraic cornered striped magic square of order 19, where the magic squares of order 3, 5, 7, 9, 11, 13, 15 and 17 are at the upper-left corner. The magic squares of orders 5, 7, 9, 11, 13, 15 and 17 are also algebraic cornered magic squares. In this case the magic sums are S_3×3:=S, S_5×5:=5*S/3, S_7×7:=7*S/3, S_9×9:=3*S, S_11×11:=11*S/3, S_13×13:=13*S/3, S_15×15:=5*S, S_17×17:=17*S/3 and S_19×19:=19*S/3, where S is the magic sum of order 3. In this case, m:=2*S/3 is the width of magic rectangles. To avoid decimal entries the magic sums of order 3 should be multiple of 3. See below two examples:

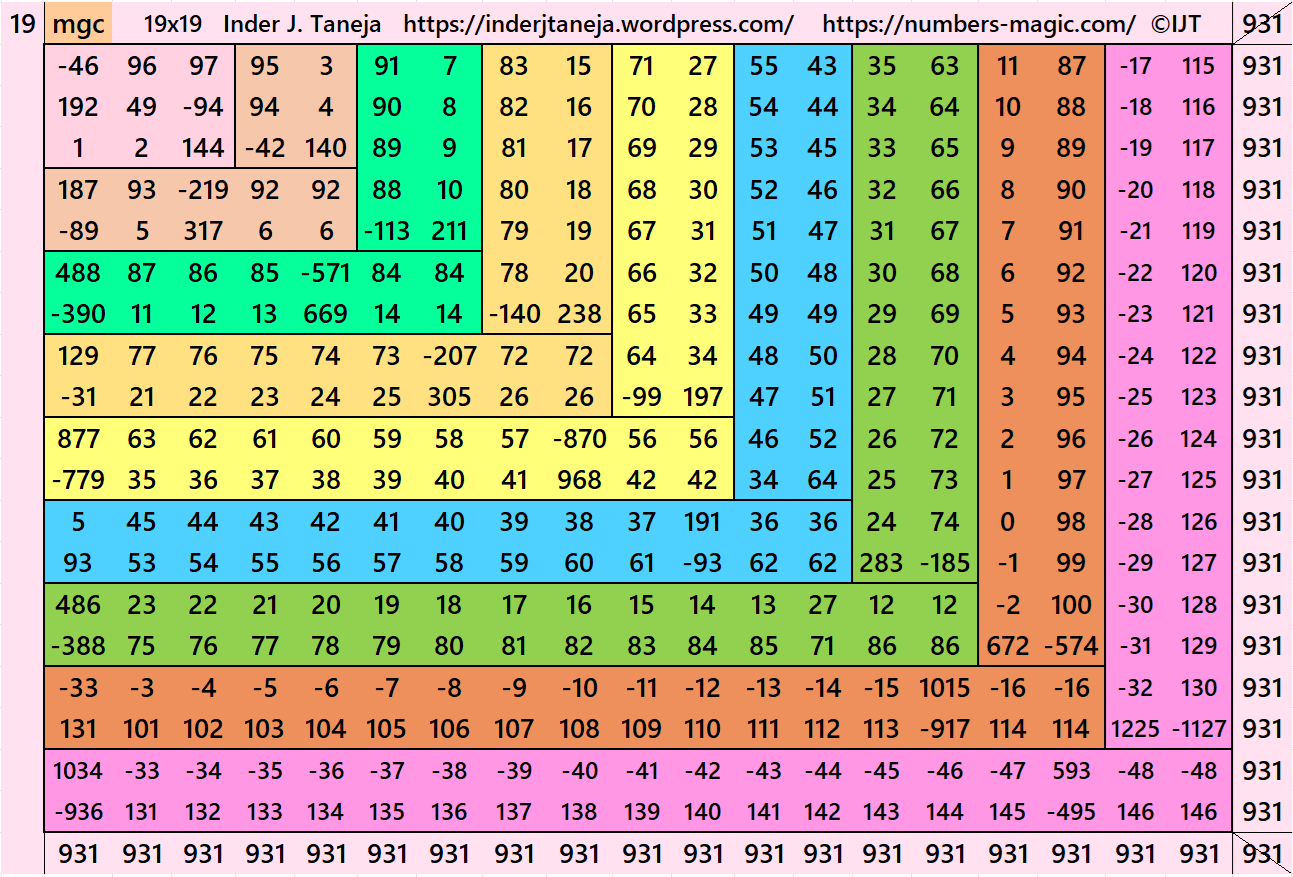
In this example the magic sums are S_3×3:=147 S_5×5:= 245, S_7×7:=343, S_9×9:=441, S_11×11:=539, S_13×13:=637, S_15×15:=735, S_17×17:=833, S_19×19:=931 and m:=98.

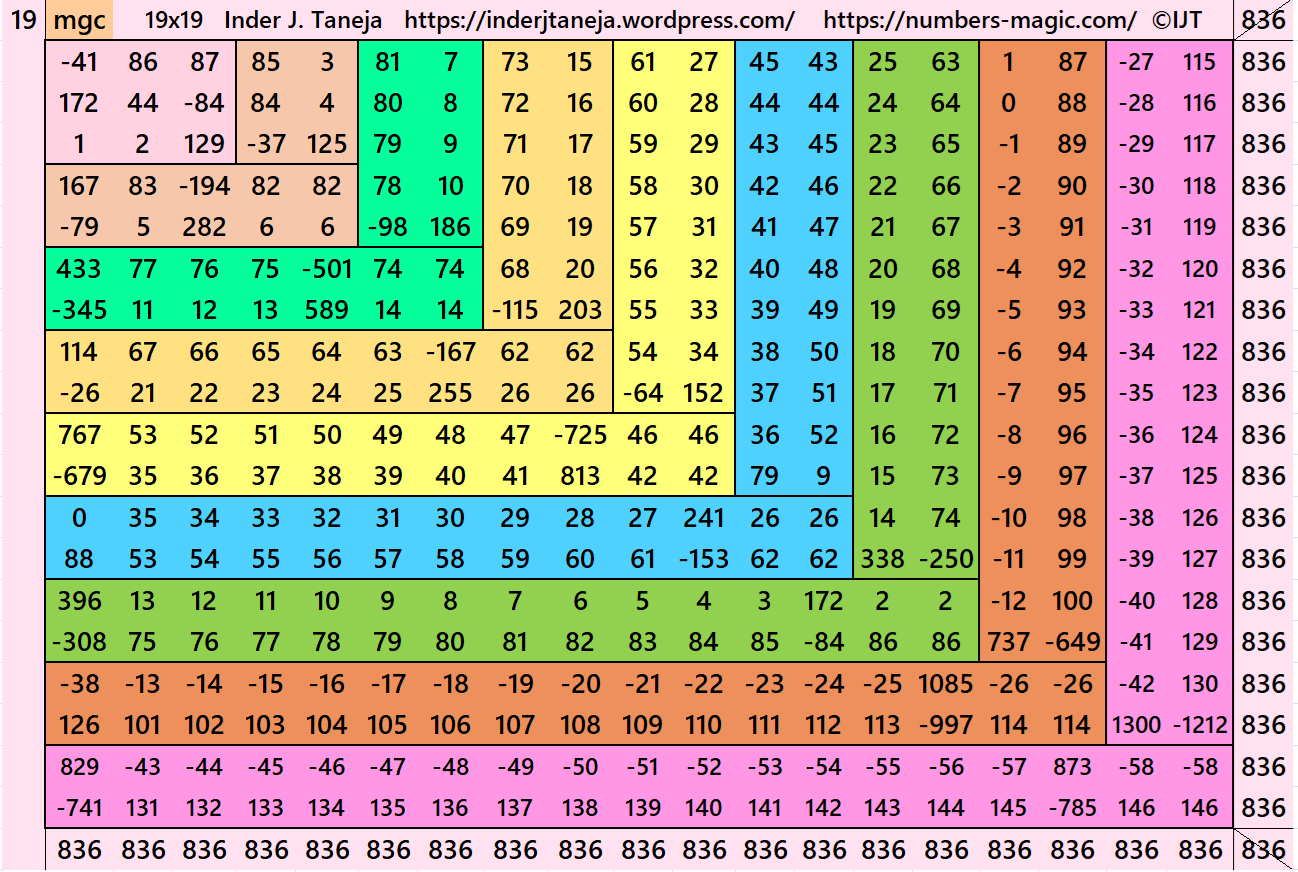
In this example the magic sums are S_3×3:=132, S_5×5:= 220, S_7×7:=308, S_9×9:=396, S_11×11:=484, S_13×13:=572, S_15×15:=660, S_17×17:=748, S_19×19:=836 and m:=88.

References

Part 1: Day and Dates of the Year – 2025 in Terms of Magic Squares

• Inder J. Taneja, Magic Squares of Orders 3 to 7 in Representing Dates and Days of the Year 2025, Zenodo, May 04, 2025, pp. 1-474, https://doi.org/10.5281/zenodo.15338142.
  • Site Link: Magic Squares of Orders 3 to 7 Representing Dates and Days of the Year 2025 (new site)
  • Site Link: Magic Squares of Orders 3 to 7 Representing Dates and Days of the Year 2025 (old site)
• Inder J. Taneja, Magic Squares of Order 8 Representing Days and Dates of the Year 2025, Zenodo, May 04, 2025, pp. 1-134, https://doi.org/10.5281/zenodo.15338246.
  • Site Link: Magic Squares of Order 8 Representing Days and Dates of the Year 2025 (new site)
  • Site Link: Magic Squares of Order 8 Representing Days and Dates of the Year 2025 (old site)
• Inder J. Taneja, Magic Squares of Order 9 Representing Days and Dates of the Year 2025, Zenodo, May 09, 2025, pp. 1-132, https://doi.org/10.5281/zenodo.15375349.
  • Site Link: Magic Squares of Order 9 Representing Days and Dates of the Year 2025 (new site)
  • Site Link: Magic Squares of Order 9 Representing Days and Dates of the Year 2025 (old site)
• Inder J. Taneja, Magic Squares of Order 10 Representing Days and Dates of the Year 2025, Zenodo, May 21, 2025, pp. 1-59, https://doi.org/10.5281/zenodo.15481738.
  • Site Link: Magic Squares of Order 10 Representing Dates and Days of the Year 2025 (new site)
  • Site Link: Magic Squares of Order 10 Representing Dates and Days of the Year 2025 (old site)
• Inder J. Taneja, Magic Squares of Order 12 Representing Days and Dates of the Year 2025 Zenodo, June 10, 2025, pp. 1-43, https://doi.org/10.5281/zenodo.15631884.
  • Site Link: Magic Squares of Order 12 Representing Dates and Days of the Year 2025 (new site)
  • Site Link: Magic Squares of Order 12 Representing Dates and Days of the Year 2025 (old site).

Part 2: Reduced Entries Agebraic Magic Squares

• Inder J. Taneja, Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Orders 3 to 7, Zenodo, September 29, 2025, pp. 1-59, https://doi.org/10.5281/zenodo.17219769.
  • Site Link: Reduced Entries Algebraic Magic Squares of Orders 3, 5, 7 and 9 (new site)
  • Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (new site)
  • Site Link: Reduced Entries Algebraic Magic Squares of Orders 3, 5, 7 and 9 (old site)
  • Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (old site)
• Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 8, Zenodo, September 23, 2025, pp. 1-65, https://doi.org/10.5281/zenodo.17186001.
  • Site Link: Reduced Entries Algebraic Magic Squares of Orders 4, 6, 8 and 10 (new site)
  • Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (new site)
  • Site Link: Reduced Entries Algebraic Pandiagonal Magic Squares of Orders 4 to 8 (old site)
• Inder J. Taneja, Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9, Zenodo, August 27, 2025, pp. 1-92, https://doi.org/10.5281/zenodo.16955571.
  • Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9 (new site)
  • Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 9 (old site)
• Inder J. Taneja. Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 10, Zenodo, September 18, 2025, pp. 1-112,  https://doi.org/10.5281/zenodo.17149185
  • Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 10 (new site)
  • Site Link: Self-Made Algebraic Magic, Semi-Magic and Pandiagonal Magic Squares of Order 10 (old site)
• Inder J. Taneja, Self-Made Algebraic Magic Squares of Order 11, Zenodo, October 12, 2025, pp. 1-58, https://doi.org/10.5281/zenodo.17330815 .
  • Site Link: Self-Made Algebraic Magic Squares of Order 11 (new site)
  • Site Link: Self-Made Algebraic Magic Squares of Order 11 (old site)
• Inder J. Taneja, Self-Made Algebraic Semi-Magic Squares of Order 11, Zenodo, October 12, 2025, pp. 1-77, https://doi.org/10.5281/zenodo.17330822.
  • Site Link: Self-Made Algebraic Semi-Magic Squares of Order 11 (new site)
  • Site Link: Self-Made Algebraic Semi-Magic Squares of Order 11 (old site)
• Inder J. Taneja, Reduced Entries Algebraic Magic and PanMagic Squares of Order 12, Zenodo, July 23, 2025, pp. 1-74, https://doi.org/10.5281/zenodo.16370556.
  • Site Link: Reduced Entries Algebraic Magic and Panmagic Squares of Order 12 (new site)
  • Site Link: Reduced Entries Algebraic Magic and Panmagic Squares of Order 12 (old site)
• Inder J. Taneja, Reduced Entries Algebraic Semi-Magic Squares of Order 12, Zenodo, July 23, 2025, pp. 1-60, https://doi.org/10.5281/zenodo.15692014.
  • Site Link: Reduced Entries Algebraic Semi-Magic Squares of Order 12  (old site)
  • Site Link: Reduced Entries Algebraic Semi-Magic Squares of Order 12 (old site)

Part 3: Double-Digit Cyclic, Flat, Cornered and Striped Agebraic Magic Squares

• Inder J. Taneja, Double-Digit Cyclic-Type Bordered Reduced Entries Algebraic Magic Squares of Orders 7 to 20, Zenodo, November 21, 2025, pp.1-37, https://doi.org/10.5281/zenodo.17675032.
  • Site Link: Double-Digit Cyclic-Type Bordered Algebraic Magic Squares of Orders 7 to 20 for Reduced Entries (New Site)
  • Site Link2: Double-Digit Cyclic-Type Bordered Algebraic Magic Squares of Orders 7 to 20 for Reduced Entries (Old Site)
• Inder J. Taneja, Algebraic Cyclic, Flat and Cornered Striped Magic Squares for Even Orders from 4 to 20, Zenodo, December 02, 2025, pp. 1-58, https://doi.org/10.5281/zenodo.17793845.
  • Site Link1: Algebraic Cyclic, Flat and Cornered Striped Magic Squares of Even Orders from 4 to 20 (New Site).
  • Site Link2: Algebraic Cyclic, Flat and Cornered Striped Magic Squares of Even Orders from 4 to 20 (Old Site)
• Inder J. Taneja, Algebraic Double-Digit and Cornered Magic Squares of Odd Orders from 5 to 19, Zenodo, December 08, 2025, pp. 1-46, https://doi.org/10.5281/zenodo.17859037.
  • Site Link1: Algebraic Double-Digit and Cornered Magic Squares of Odd Orders from 5 to 19 (new site)
  • Site Link2: Algebraic Double-Digit and Cornered Magic Squares of Odd Orders from 5 to 19 (old site)

Double-Digit Magic Squares

• Inder J. Taneja, Two Digits Bordered Magic Squares of Orders 10, 14, 18 and 22, Zenodo, April, 30, 2023, pp. 1-43, https://doi.org/10.5281/zenodo.7880931.
• Inder J. Taneja, Two Digits Bordered Magic Squares of Orders 26 and 30, Zenodo, April, 30, 2023, pp. 1-45, https://doi.org/10.5281/zenodo.7880937.
• Inder J. Taneja, Two Digits Bordered Magic Squares of Orders 36 and 40, Zenodo, May, 04, 2023, pp. 1-41, https://doi.org/10.5281/zenodo.7896709.
• Inder J. Taneja, Two Digits Bordered Magic Squares of Orders 34 and 38, Zenodo, May 10, 2023, pp. 1-45, https://doi.org/10.5281/zenodo.7922571.
• Inder J. Taneja, Two Digits Bordered Magic Squares of Orders 28 and 32, Zenodo, April, 26, 2023, pp. 1-36, https://doi.org/10.5281/zenodo.7866981.
• Inder J. Taneja, Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24, Zenodo, April, 26, 2023, pp. 1-43, https://doi.org/10.5281/zenodo.7866956.
• Inder J. Taneja, New Concepts in Magic Squares: Double Digits Bordered Magic Squares of Orders 7 to 108, Zenodo, August 09, 2023, pp. 1-30, https://doi.org/10.5281/zenodo.8230214.

Cornered Magic Squares

• Inder J. Taneja, Cornered Magic Squares of Order 6, Zenodo, May 23, 2023, pp. 1-23, https://doi.org/10.5281/zenodo.7960679.
• Inder J. Taneja, Cornered Magic Squares of Orders 5 to 13, Zenodo, June 03, 2023, pp. 1-71, https://doi.org/10.5281/zenodo.8000467.
• Inder J. Taneja, Cornered Magic Squares of Orders 14 to 24, Zenodo, June 03, 2023, pp. 1-39, https://doi.org/10.5281/zenodo.8000471.
• Inder J. Taneja, New Concepts in Magic Squares: Cornered Magic Squares of Orders 5 to 81, Zenodo, August 09, 2023, pp. 1-27, https://doi.org/10.5281/zenodo.8231157.
• Inder J. Taneja, Cornered Magic Squares in Construction of Magic Squares of Orders 16, 20, 24 and 28, August 23, 2023, https://numbers-magic.com/?p=10172
• Inder J. Taneja, Striped and Semi-Striped Cornered Magic Squares of Orders 6 to 50 – Recreating Numbers and Magic Squares, March 17, 2025.
• Inder J. Taneja, New Concepts in Magic Squares: Cornered Magic Squares of Orders 5 to 108, Zenodo, January 29, 2025, pp. 1-33, https://doi.org/10.5281/zenodo.14759238.