Beauty of Magic Squares: Multiple Order Bordered Magic Squares of Order 90

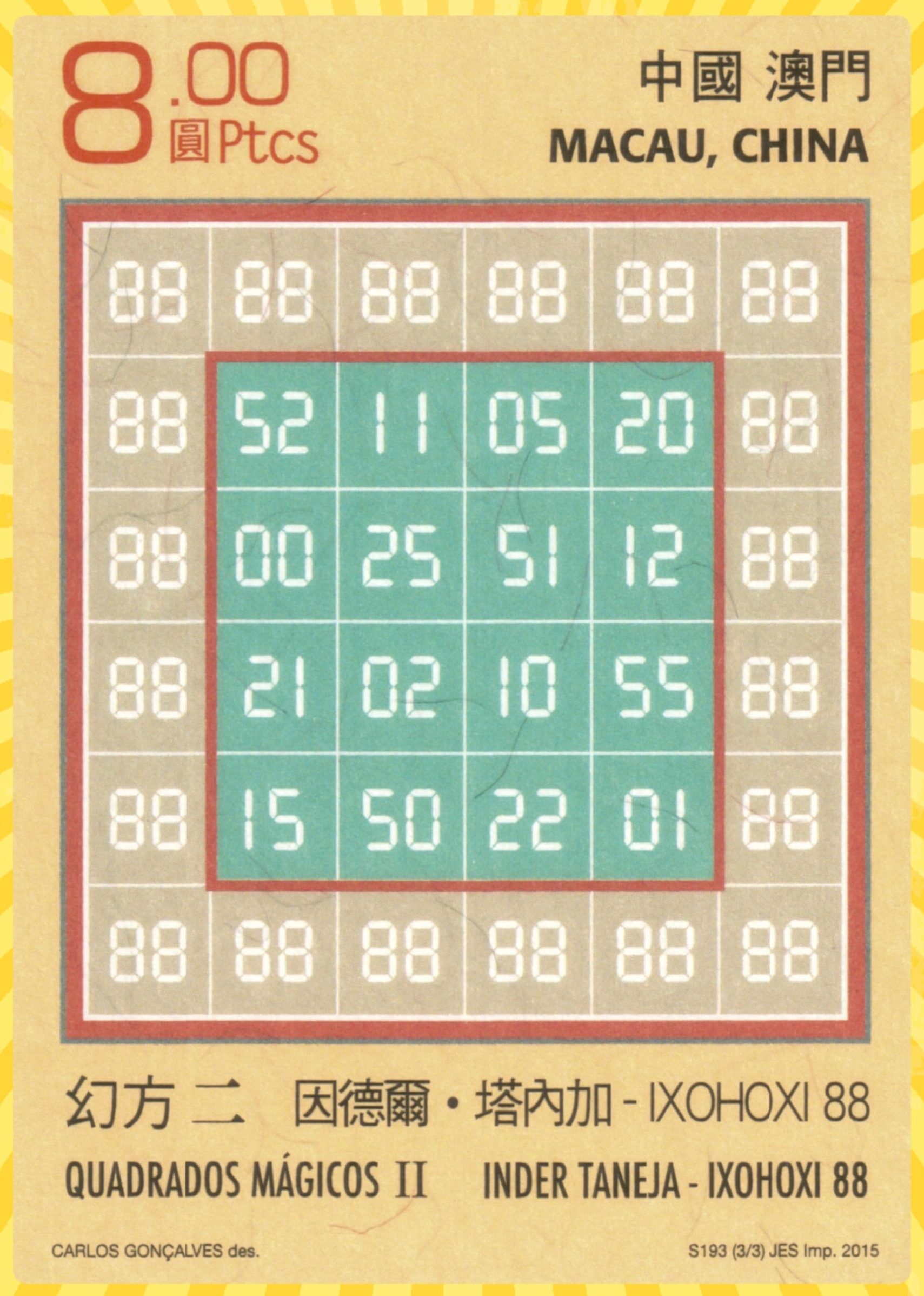
During past years author worked with block-wise bordered magic squares multiples of even and odd number blocks. This means, multiples of 3, 4, 5, 6, etc. These works can be accessed at the following links.
1. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 3
2. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 4.
3. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 5.
4. Block-Wise Bordered Magic Squares Multiples of Magic and Bordered Magic Squares of Order 6.
5. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 7.
6. Block-Wise Bordered Magic Squares Multiples of 8.
7. Block-Wise Bordered Magic Squares Multiples of 9.
8. Block-Wise Bordered Magic Squares Multiples of 10.
9. Block-Wise Bordered Magic Squares Multiples of 11.
10. Block-Wise Bordered Magic Squares Multiples of 12.
11. Block-Wise Bordered Magic Squares Multiples of 14.

The advantage in studying block-wise bordered magic squares is that when we remove external borders, still we are left with magic squares with sequential entries. The bordered magic squares also have the same property. The difference is that instead of numbers here we have blocks of magic squares.

This work bring magic squares, based on multiple order magic squares in the same magic squares. This means same magic square contains borders of order 3, 4, 5, etc. It can be accessed at the following link:

Inder J. Taneja, Multiple Orders Bordered Magic Squares, Zenodo, Jun 9, 2023, pp. 1-43

This work brings brodered magic squares in such a way that in the beginning there is magic square of order 12 with different sums magic squares of order 3. The upper borders are magic squares of orders 4, 5, 6, 7, 8 and 9. The even order borders are with magic squares, such as of orders 4, 6, 8 and 10 are with equal sums magic squares. The odd order borders are with magic squares, such as of orders 5, 7 and 9 are with different sums magic squares. See below the details of each order:

• 0 Border: Different sums magic squares of order 3.
  • Initially, we have a magic square of order 12 formed by different sums magic squares of order 3.
• 1^st Border: Equal sums pandiagnonal magic squares of order 4.
• 2^nd Border: Different sums magic squares of order 5.
  • In this case there are two ways. One is pandiagonal magic squares of order 5. The second is bordered magic square of order 3 with inner part as a magic square of order 3. In both the cases the magic sums of order 5 are different.
• 3^rd Border: Equal sums magic squares of order 6.
  • In this case there are two ways. One is magic squares of order 6. The second is bordered magic square of order 6 with inner part as a pandiagonal magic square of order 4.
• 4^th Border: Different sums magic squares of order 7.
  • In this case also there are two ways. One is pandiagonal magic squares of order 7. The second one is bordered magic square of order 7 with inner parts as a magic square of orders 5 and 3. In both the cases the magic sums of order 7 are different.
• 5^th Border: Equal sums magic squares of order 8.
  • In this case there are three ways. One is pandiagonal magic squares of order 8 with equal sums pandiagonal magic squares of order 4. The second one is flat-type magic square of order 8 with inner part as a magic square of order 4, and the magic rectangles are of orders 2×8 and 2×4. The third one is cyclic-type double-digit magic squares of order 8 with inner part as a magic square of order 4 with four magic rectangles of orders 2×6 are of equal sums.
• 6^th Border: Different sums magic squares of order 9.
  • In this case also there are three ways. One is equal sum semi-magic squares of 3 resulting in magic square of order 9. The second one is bordered magic squares of order 9 having magic squares of orders 7, 5 and 3 in the middle as magic square of order 3, while the orders 7 and 5 again bordered magic squares.

For the previous results on multiple bordered magic squares of orders 20, 30, 42, 56 and 72 refer to the link:

• Inder J. Taneja, Multiple Orders Bordered Magic Squares, Zenodo, Jun 9, 2023, pp. 1-43, https://doi.org/10.5281/zenodo.8019330.
  • Site link: Beauty of Magic Squares: Multiple Order Bordered Magic Squares of Orders 20, 30, 42, 56 and 72

Magic Squares of Order 90

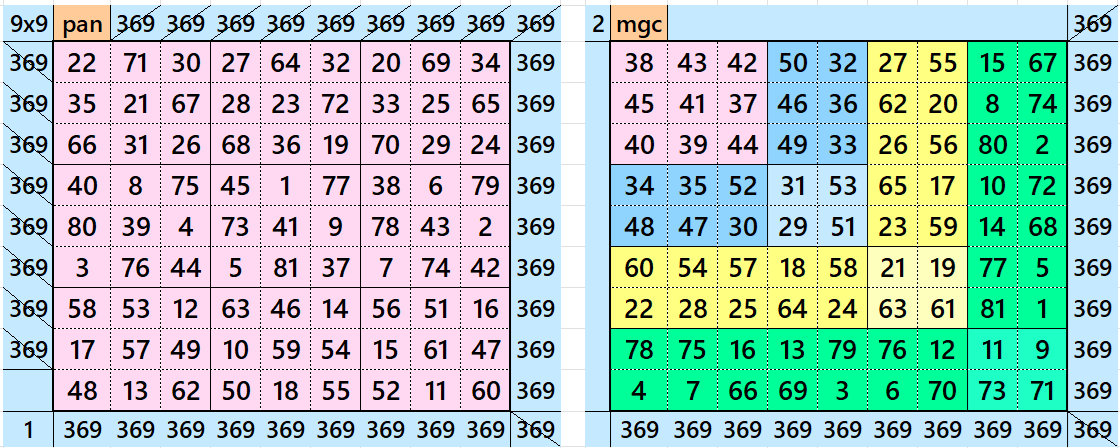
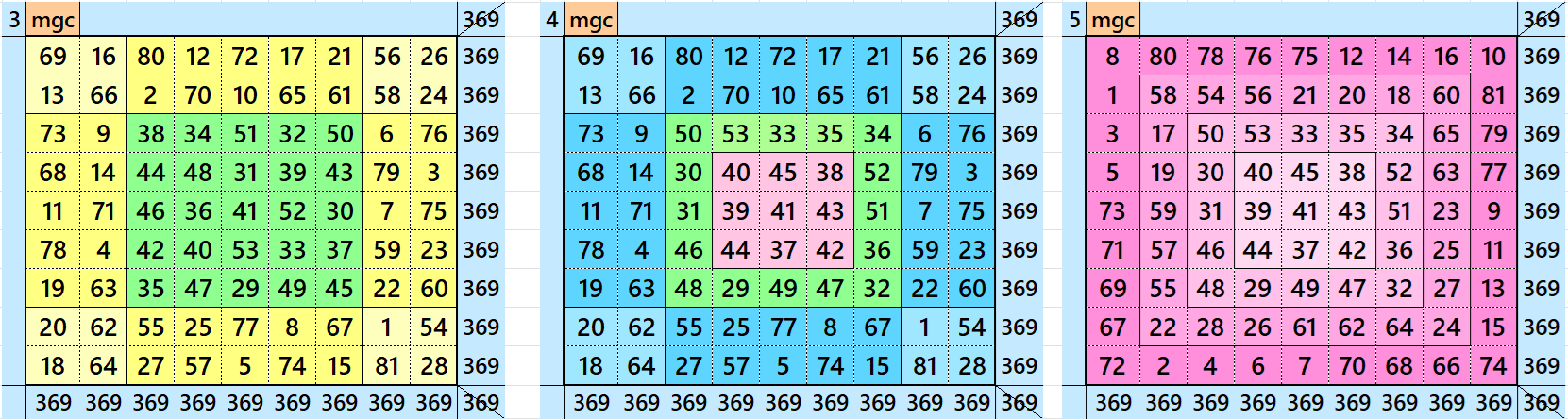
There are 160 different types of magic squares of order 90. These are formed by external border of order 9 in five different ways. These are considered as follows:

• One with 9 blocks of magic squares of order 3.
• The second with a double digit cornered magic square of order 9.
• The third with a double digit magic square of order 9 having four equal sums magic rectangles of order 2×5 and a pandiagonal magic square of order 5 in the middle.
• The forth with a a double digit magic square of order 9 having four equal sums magic rectangles of order 2×5 and a bordered magic square of order 5 in the middle.
• The fifth as a single-digit bordered magic squares of order 9.
  
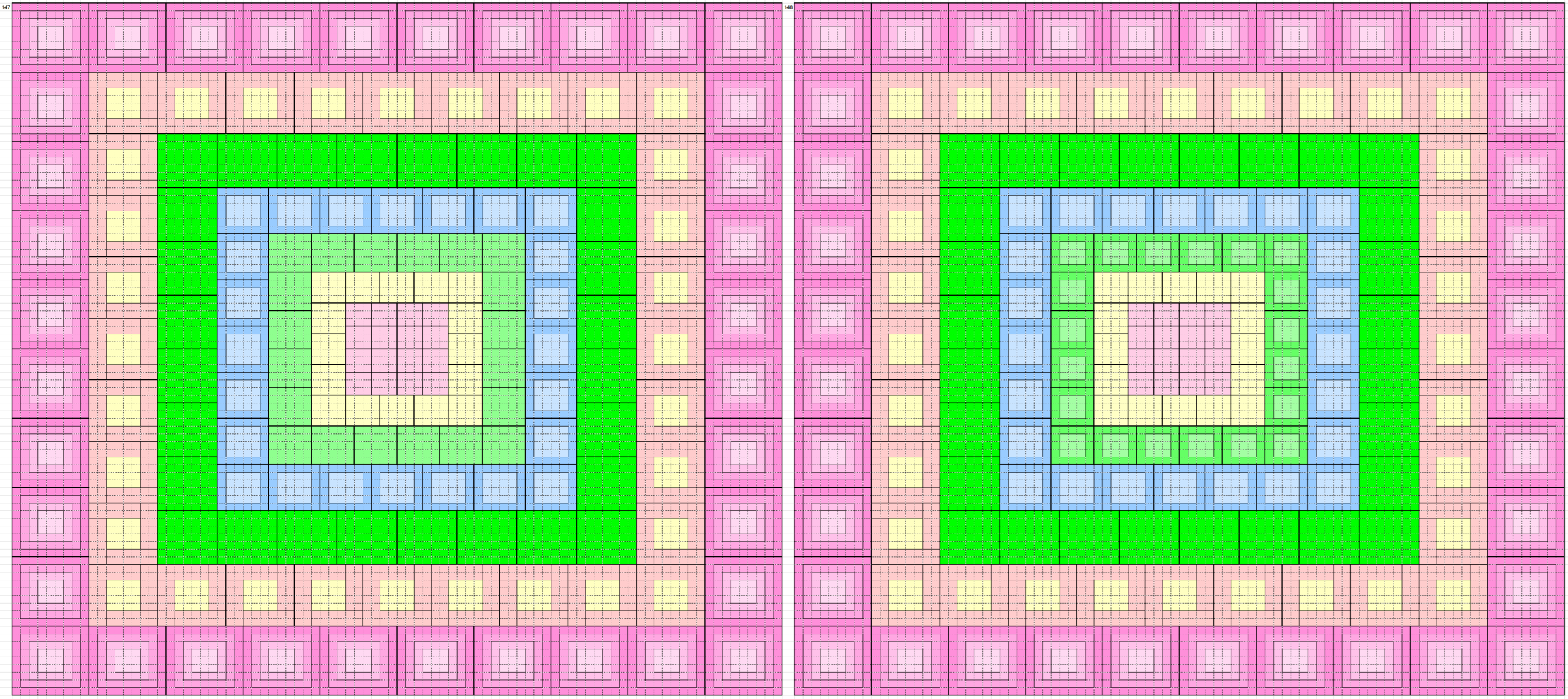
  These forms and external border to magic squares of order 90. Thus, we have 160 magic squares order 90 formed by blocks of order 3, 4, 5, 6, 7, 8 and 9. See below the five magic squares of order 9 used:

Below are 160 magic borderd magic squares of order 90 in figures or designs. These are written in five blocks:

In Figures or Designs

1^st Block of 32: 1-32

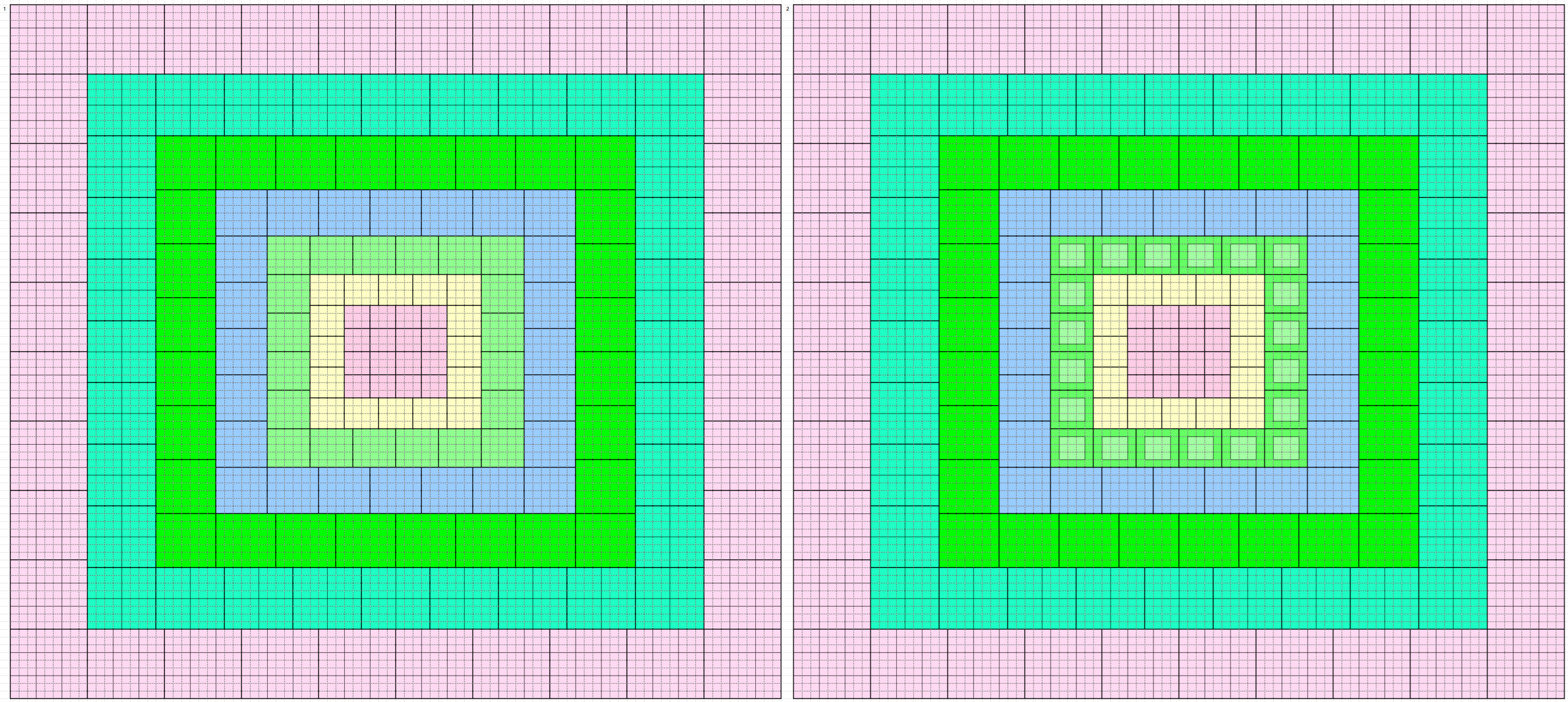
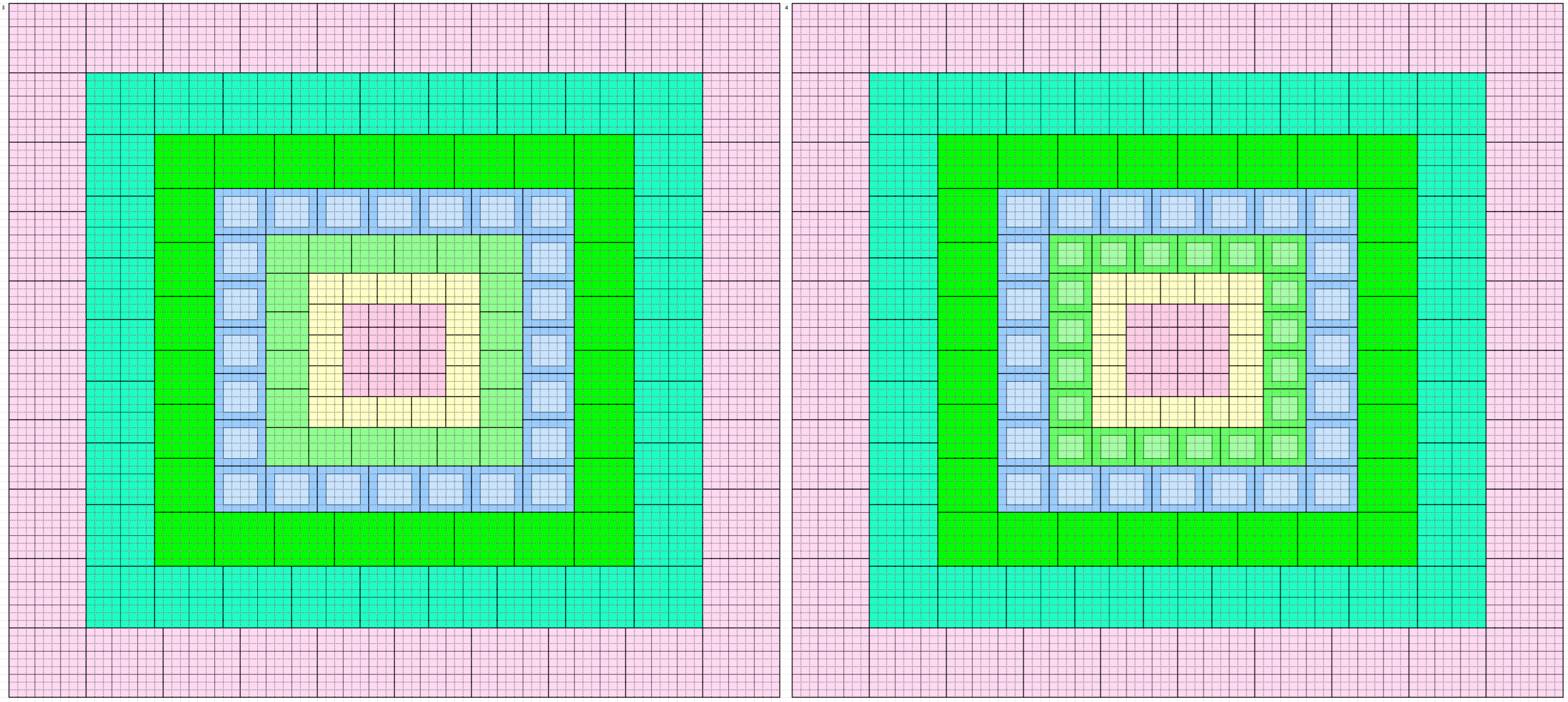
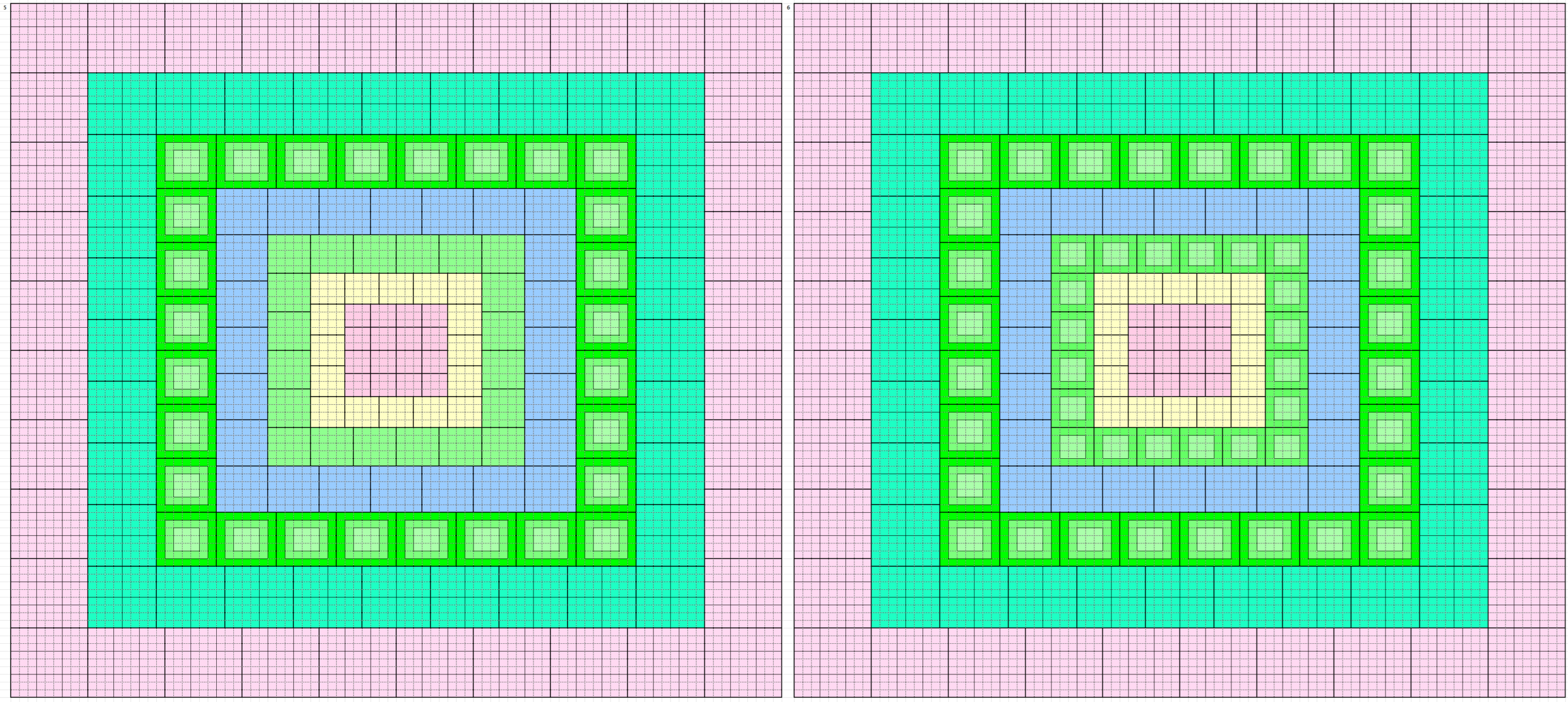
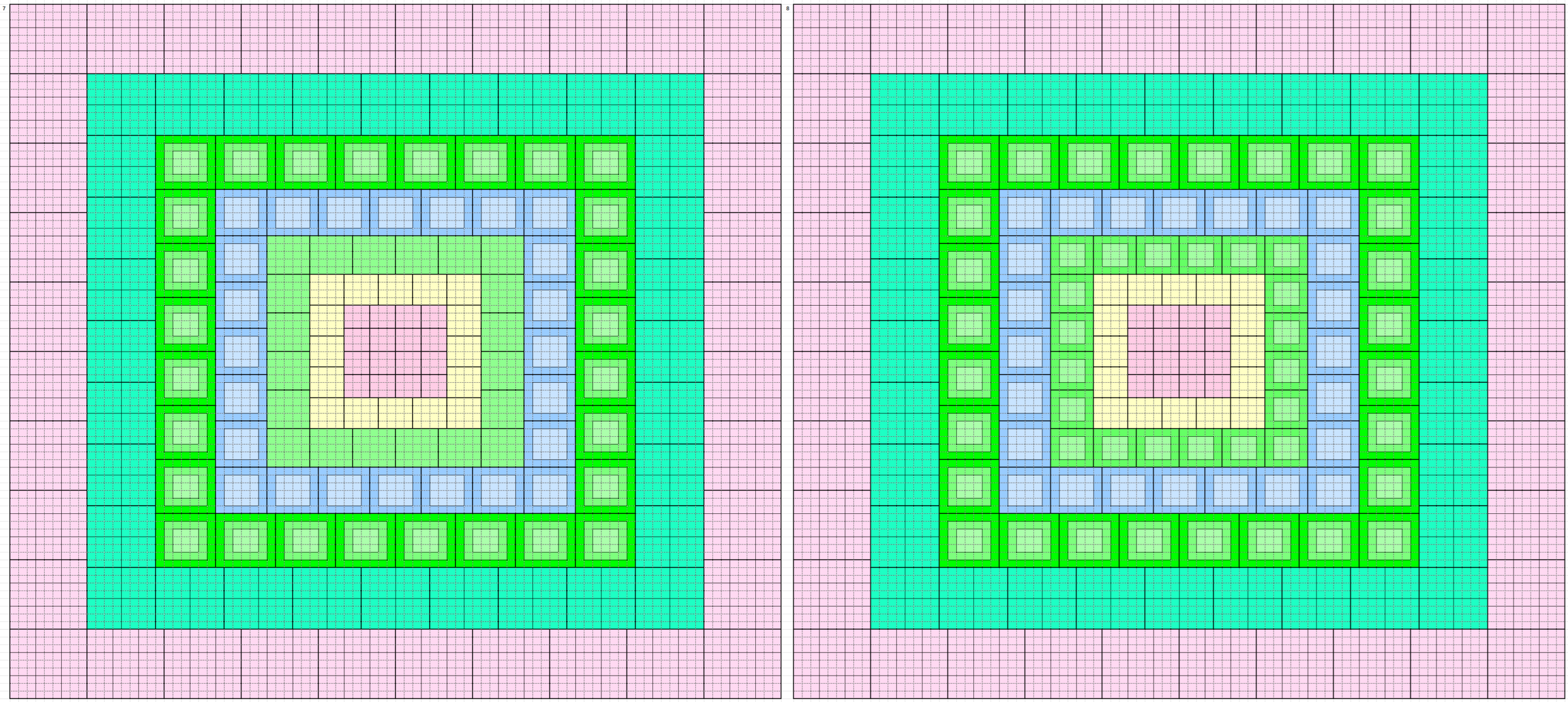
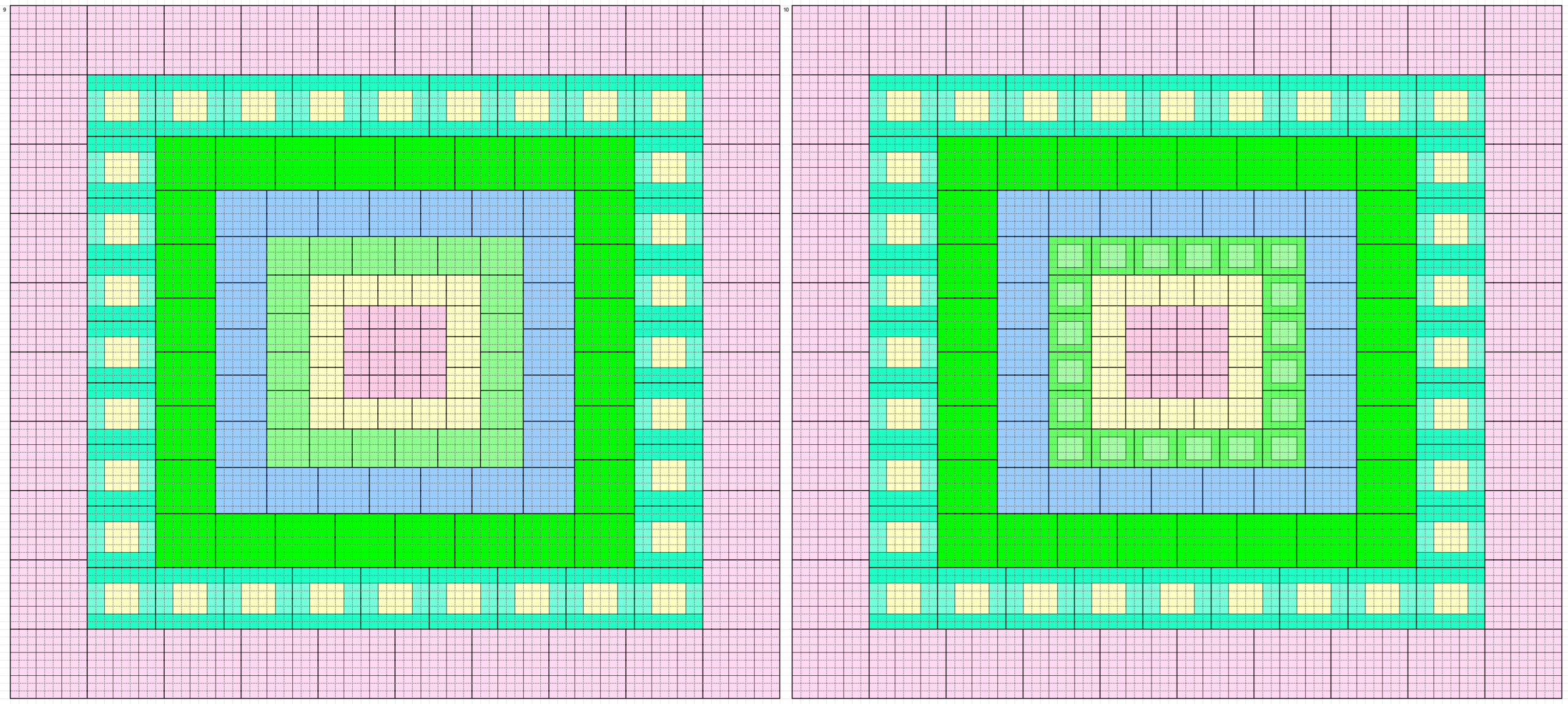
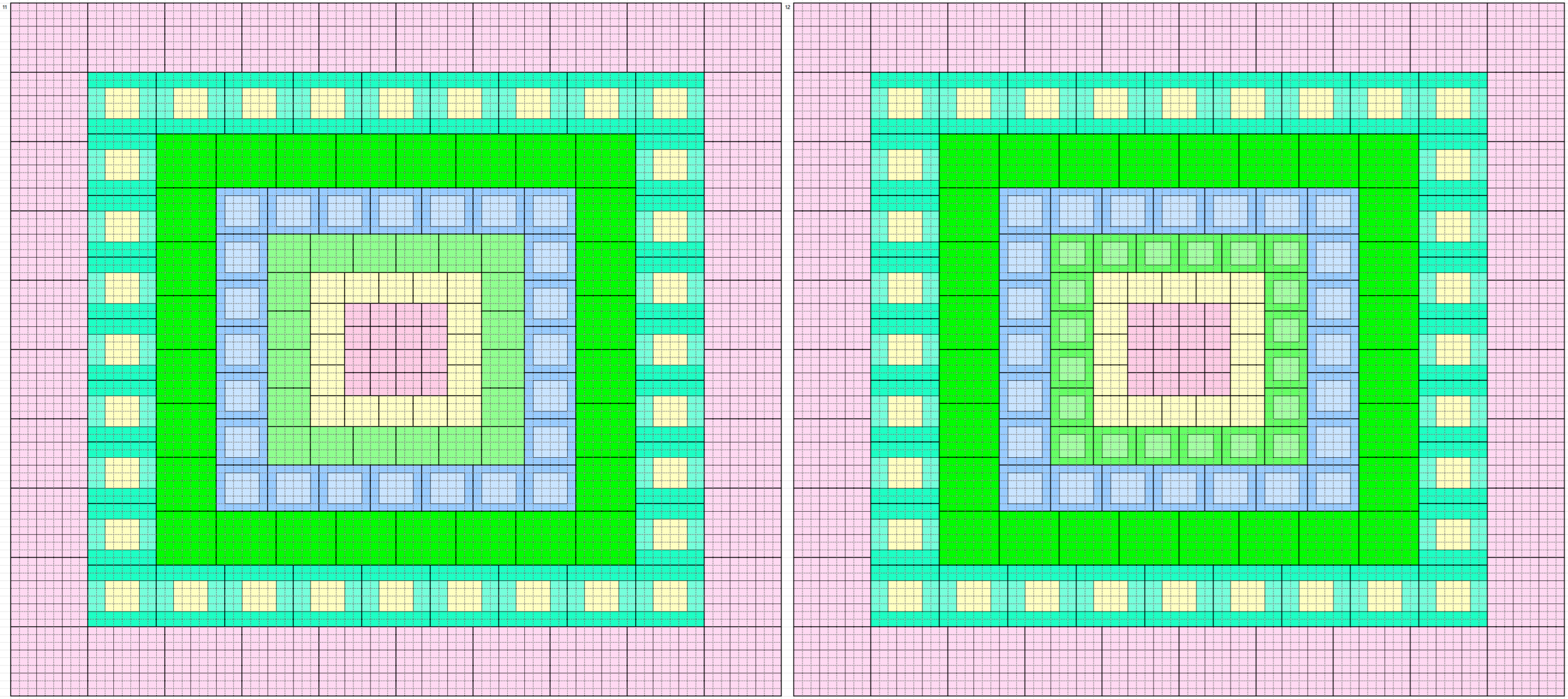
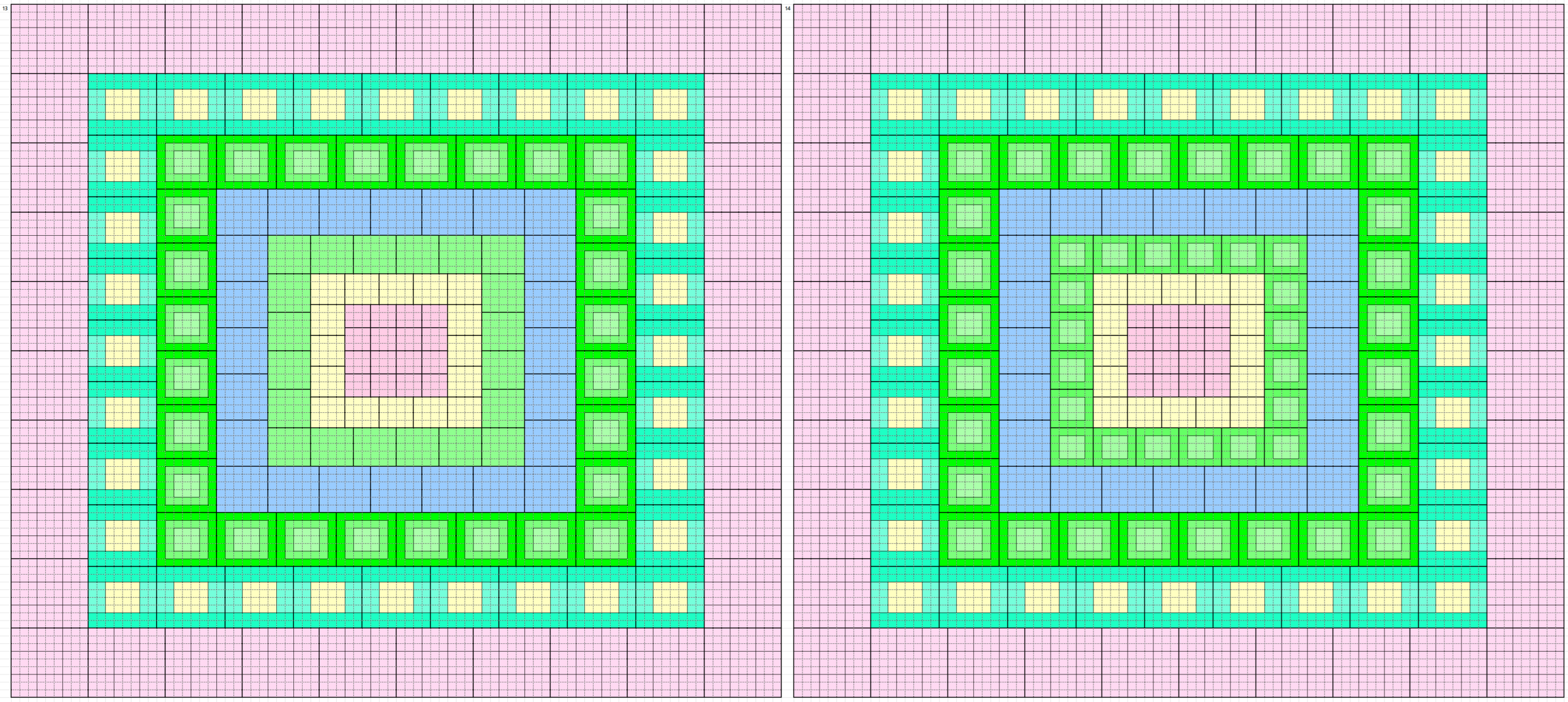
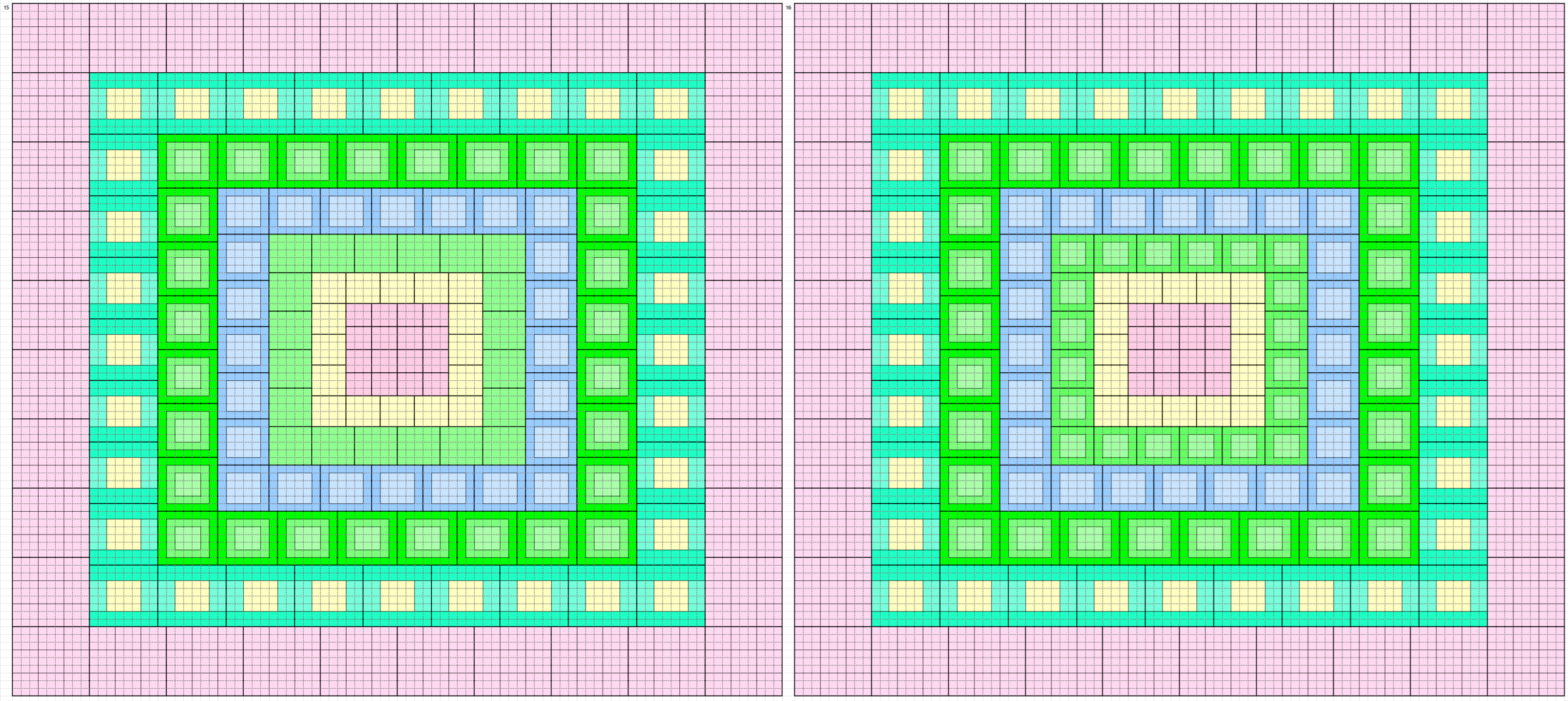
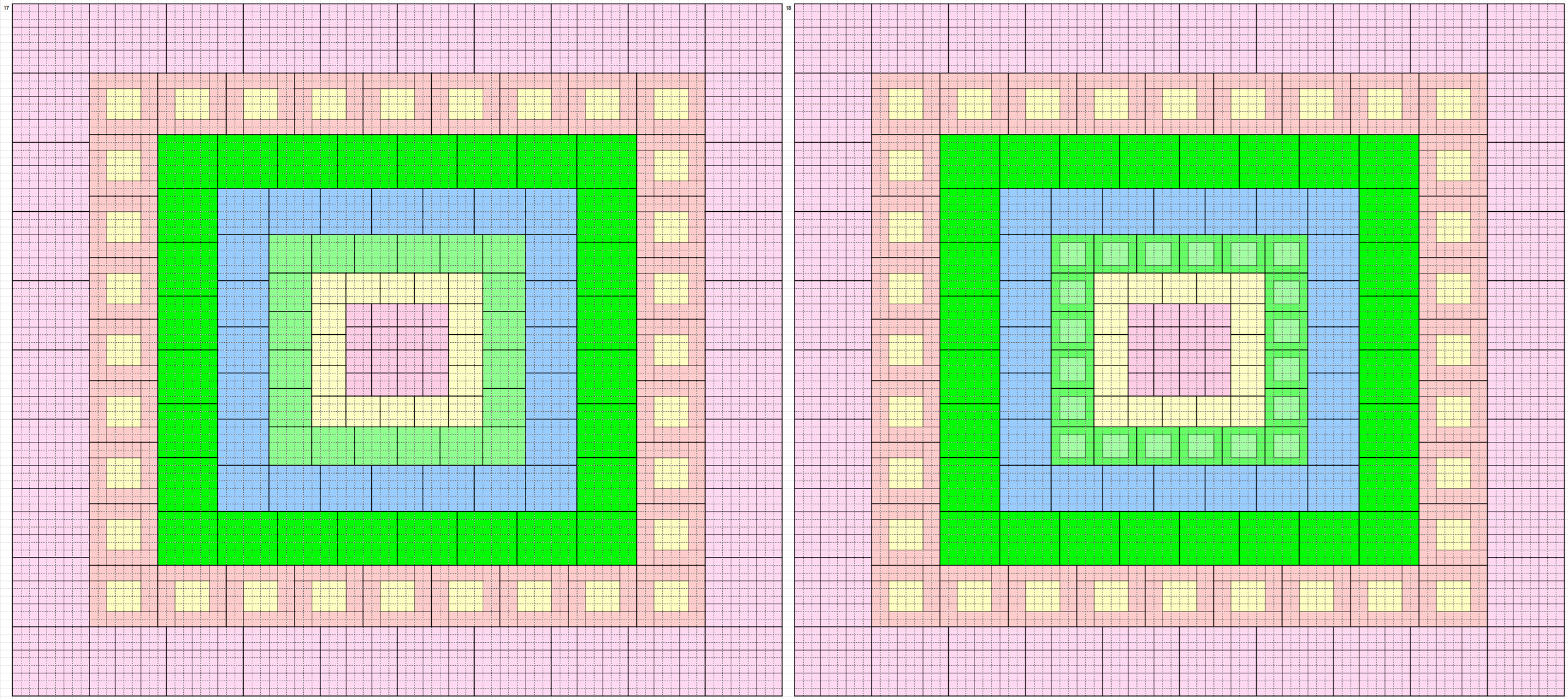
2^nd Block of 32: 33-64

3^rd Block of 32:

4^th Block of 32:

5^th Block of 32:

Excel file for download

References

Even Orders Magic Squares

1. Inder J. Taneja, Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 4, Zenodo, August 31, 2021, pp. 1-148, https://doi.org/10.5281/zenodo.5347897.
2. Inder J. Taneja, Bordered Magic Squares Multiples of 6, Zenodo, July 25, 2023, pp. 1-32, https://doi.org/10.5281/zenodo.8184983.
3. Inder J. Taneja, Bordered and Pandiagonal Magic Squares Multiples of 8, Zenodo, July 26, 2023, pp. 1-58, https://doi.org/10.5281/zenodo.8187791.
4. Inder J. Taneja, Bordered Magic Squares Multiples of 10, Zenodo, July 26, pp. 1-40, https://doi.org/10.5281/zenodo.8187888.
5. Inder J. Taneja, Bordered and Pandiagonal Magic Squares Multiples of 12, Zenodo, July 27, 2023, pp. 1-31, https://doi.org/10.5281/zenodo.8188293.
6. Inder J. Taneja, Bordered Magic Squares Multiples of 14, Zenodo, July 27, pp. 1-33, https://doi.org/10.5281/zenodo.8188395.
7. Inder J. Taneja, Bordered and Pandiagonal Magic Squares Multiples of 16, Zenodo, July 27, pp. 1-30, https://doi.org/10.5281/zenodo.8190884.
8. Inder J. Taneja, Bordered Magic Squares Multiples of 18, Zenodo, July 28, pp. 1-31, https://doi.org/10.5281/zenodo.8191223.
9. Inder J. Taneja, Bordered and Pandiagonal Magic Squares Multiples of 20, Zenodo, July 28, pp. 1-45, https://doi.org/10.5281/zenodo.8191426.

Odd Orders Magic Squares

1. Inder J. Taneja, Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 3, Zenodo, May 05, pp. 1-29, 2023, https://doi.org/10.5281/zenodo.7898383.
2. Inder J. Taneja, Bordered and Pandiagonal Magic Squares Multiples of 5, Zenodo, July 23, 2023, pp. 1-36, https://doi.org/10.5281/zenodo.8175759.
3. Inder J. Taneja, Bordered and Pandiagonal Magic Squares Multiples of 7, Zenodo, July 23, pp. 1-34, 2023, https://doi.org/10.5281/zenodo.8176061.
4. Inder J. Taneja, Bordered Magic Squares Multiples of 9, Zenodo, July 23, 2023, pp. 1-28, https://doi.org/10.5281/zenodo.8176357.
5. Inder J. Taneja, Bordered Magic Squares Multiples of 11, Zenodo, July 24, pp. 1-34, 2023, https://doi.org/10.5281/zenodo.8176475.
6. Inder J. Taneja, Bordered Magic Squares Multiples of 13, Zenodo, July 24, pp. 1-32, 2023, https://doi.org/10.5281/zenodo.8178879.
7. Inder J. Taneja, Bordered Magic Squares Multiples of 15, Zenodo, July 24, pp. 1-35, 2023, https://doi.org/10.5281/zenodo.8178935.
8. Inder J. Taneja, Bordered Magic Squares Multiples of 17, Zenodo, July 25, pp. 1-26, 2023, https://doi.org/10.5281/zenodo.8180706.
9. Inder J. Taneja, Bordered Magic Squares Multiples of 19, Zenodo, July 25, pp. 1-31, 2023, https://doi.org/10.5281/zenodo.8180919.

Mixed Orders Magic Squares

1. Inder J. Taneja, Multiple Orders Bordered Magic Squares, Zenodo, Jun 9, 2023, pp. 1-43,
   https://doi.org/10.5281/zenodo.8019330.