During past years author worked with block-wise bordered magic squares multiples of even and odd number blocks. This means, multiples of 3, 4, 5, 6, etc. These works can be accessed at the following links.
1. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 3
2. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 4.
3. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 5.
4. Block-Wise Bordered Magic Squares Multiples of Magic and Bordered Magic Squares of Order 6.
5. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 7.
6. Block-Wise Bordered Magic Squares Multiples of 8.
7. Block-Wise Bordered Magic Squares Multiples of 9.
8. Block-Wise Bordered Magic Squares Multiples of 10.
9. Block-Wise Bordered Magic Squares Multiples of 11.
10. Block-Wise Bordered Magic Squares Multiples of 12.
11. Block-Wise Bordered Magic Squares Multiples of 14.
The advantage in studying block-wise bordered magic squares is that when we remove external borders, still we are left with magic squares with sequential entries. The bordered magic squares also have the same property. The difference is that instead of numbers here we have blocks of magic squares.
We observe that the above study of even and odd number orders starts from 3. Recently, author studied the two digits borders resulting in interesting magic squares. These studies can be accessed at the following link:
1. Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.
2. Two Digits Bordered Magic Squares of Orders 28 and 32.
3. Two digits Bordered Magic Squares of Order 36.
4. Two digits Bordered Magic Squares of Order 40.
The work is for the order of type 4k+2, where k>1, i.e., for the orders 10, 14, 18, etc. can be access at the following links:
1. Two digits Bordered Magic Squares of Orders 10, 14, 18 and 22.
2. Two digits Bordered Magic Squares of Orders 26 and 30.
3. Two digits Bordered Magic Squares of Order 34.
4. Two digits Bordered Magic Squares of Order 38.
This work bring magic squares, based on multiple order magic squares in the same magic squares. This means same magic square contains borders of order 3, 4, 5, etc. It can be accessed at the following link:
Inder J. Taneja, Multiple Orders Bordered Magic Squares, Zenodo, Jun 9, 2023, pp. 1-43
https://doi.org/10.5281/zenodo.8019330.
See Examples below:
Magic Square of Order 12
Below is a magic square of order 12. It is with blocks of magics squares of order 3.

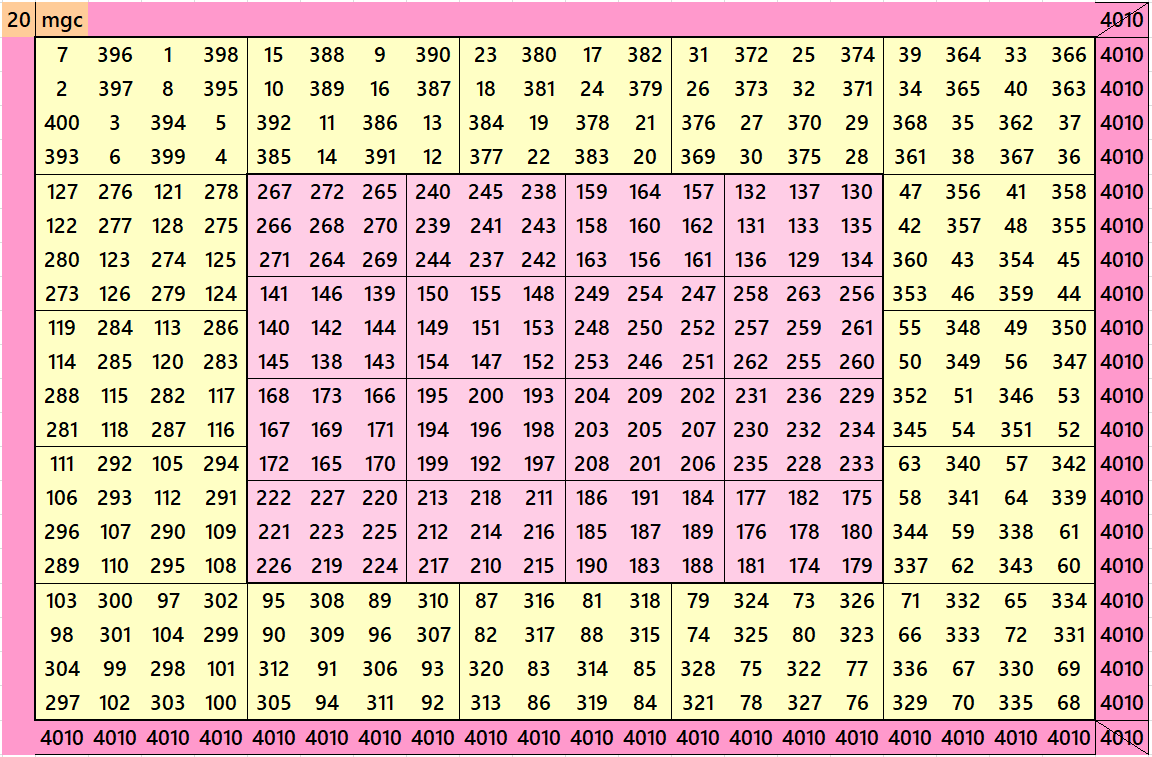
Magic Square of Order 20
Below in a magic square of order 20. It is with blocks of order 3 and 4. Blocks of order 3 are forming a magic square of order 12. The border magic squares of order 4 give us a magic square of order 4. The block of order 4 are pandiagonal magic squares.
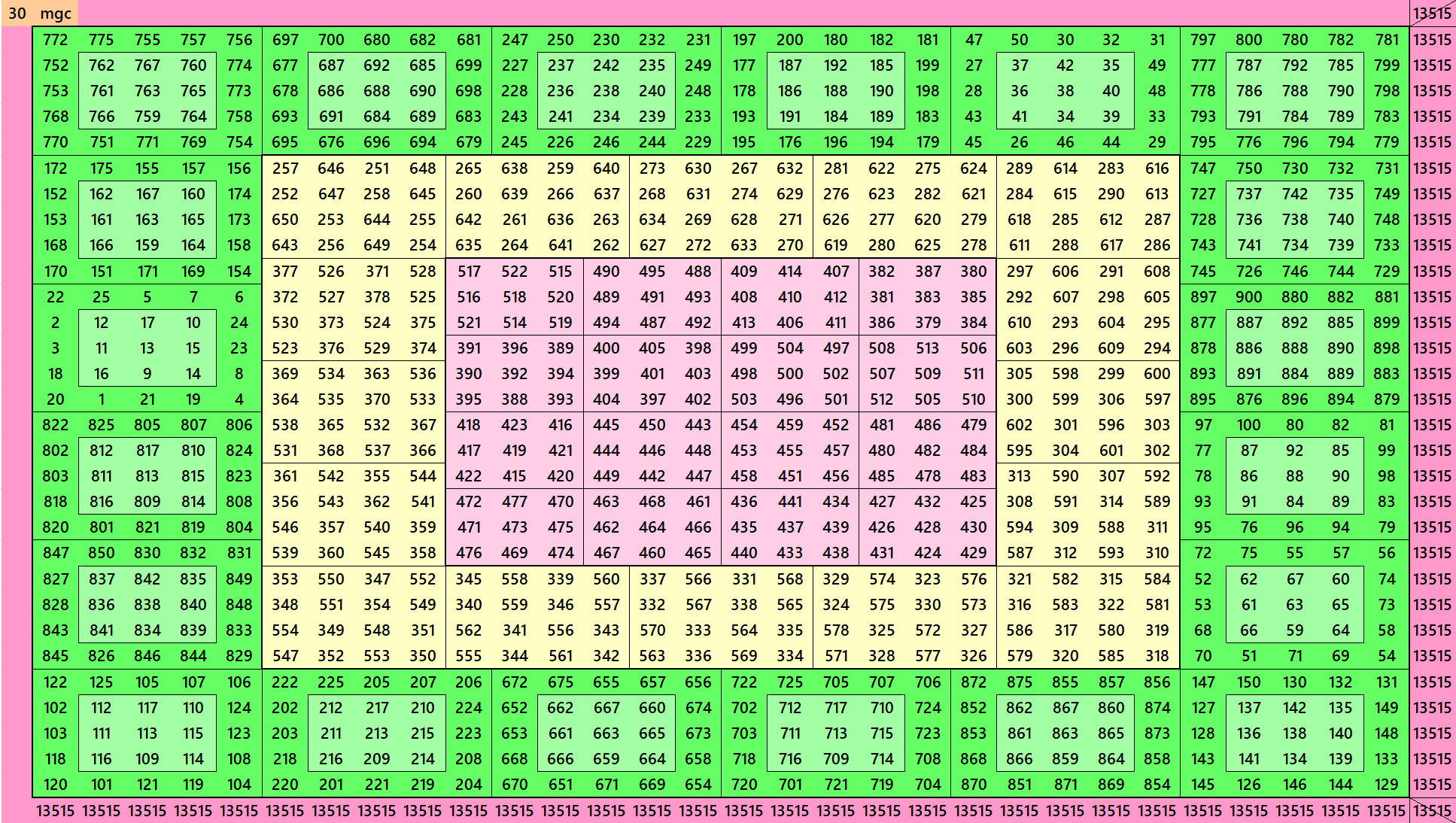
Magic Squares of Order 30
Below are two different types of magic squares of order 30. These are formed by external border of order 5 in two different ways. One with pandiagonal magic squares of order 5. The second with bordered magic squares of order 5. In the blocks are of order 20 age given above formed by blocks of orders 3 and 4.

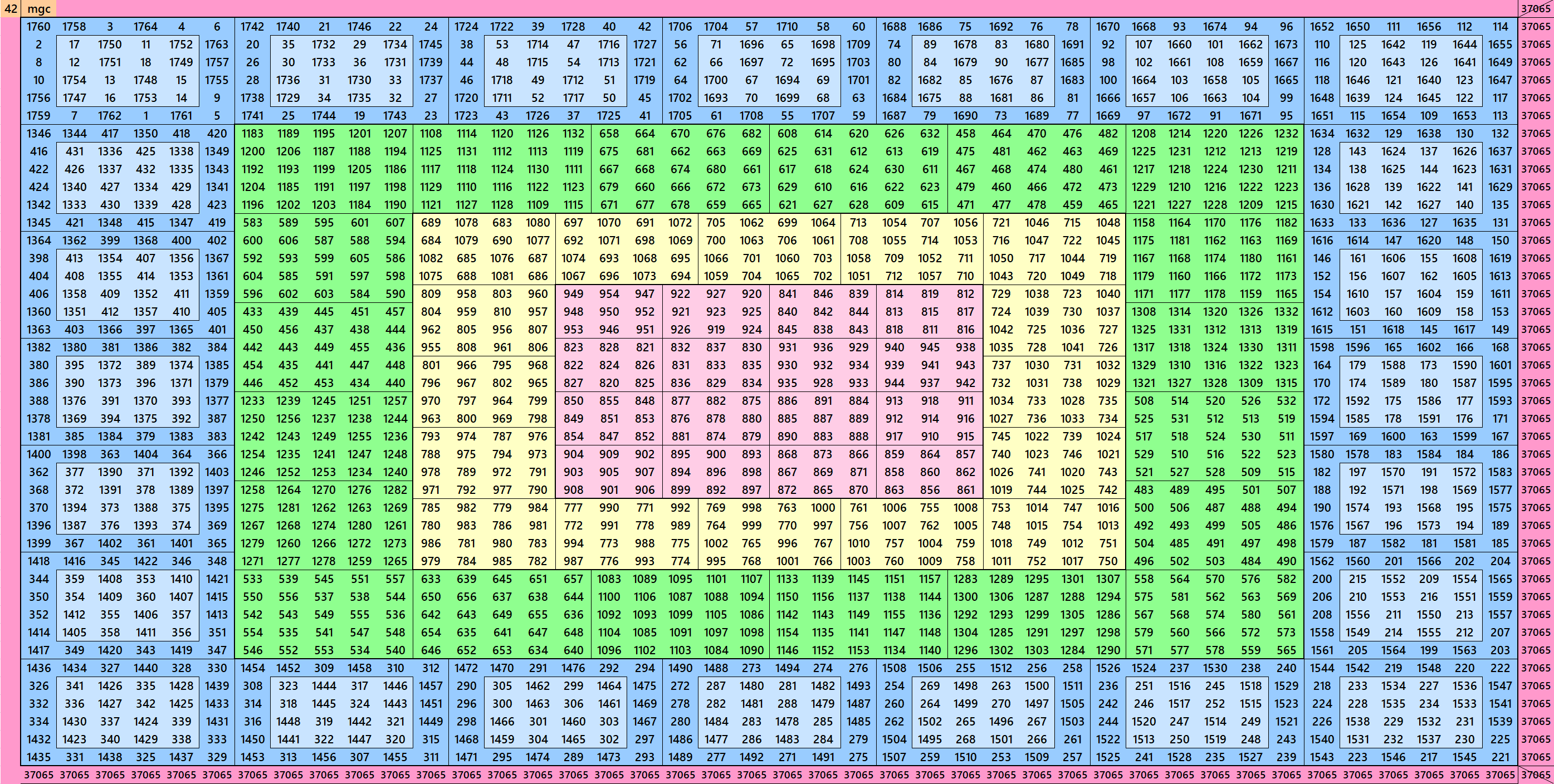
Magic Squares of Order 42
Below are four different types of magic squares of order 42. These are forms external border of order 6 in two different ways. One with magic square of order 6 and another with bordered magic squares of order 6. These forms external borders to magic squares of order 30 given above formed by blocks of orders 3, 4 and 5.



Magic Squares of Order 56
Below are eight different types of magic squares of order 56. These are formed by external border of order 7 in two different ways. One with pandiagonal magic square of order 7 and another with bordered magic squares of order 7. These forms external borders to magic squares of order 42. Since there are four magic squares of order 42. This results in 8 magic squares of order 56. Thus we have 8 magic squares order 56 formed by blocks of order 3, 4, 5, 6 and 7.







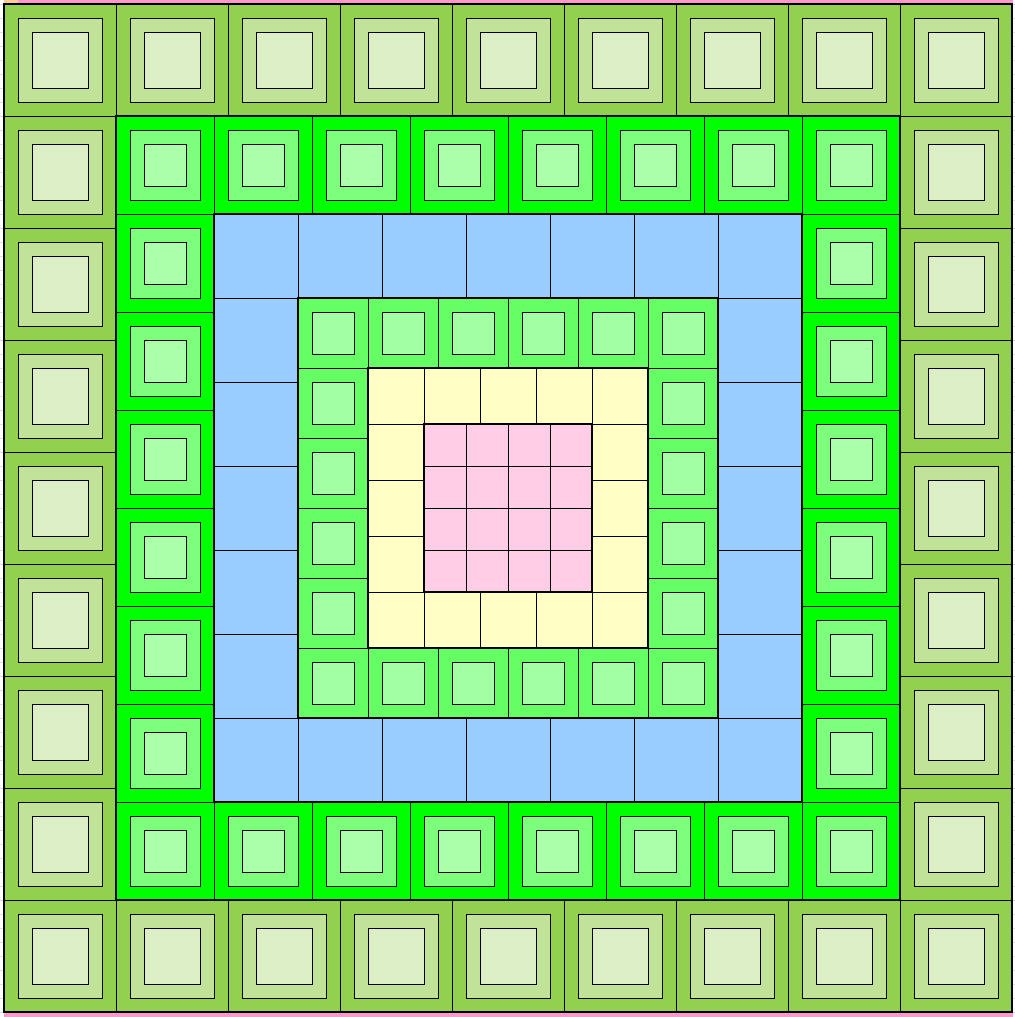
Magic Squares of Order 72
There are 24 different types of magic squares of order 72. These are formed by external border of order 8 in two three ways. One with pandiagonal magic square of order 8 formed by four pandiagonal magic squares of order 4. The second as bordered magic squares of order 8. The third one is two digits bordered magic square with a pandiagonal magic square of order 4 in the middle. These forms external borders to magic squares of order 72. Since there are 8 magic squares of order 56. This results in 24 magic squares of order 72. Thus, we have 24 magic squares order 72 formed by blocks of order 3, 4, 5, 6, 7 and 8. Below are only three examples as figures without numbers. The full work with numbers can be seen in excel file attached with the work.


Magic Squares of Order 90
There are 48 different types of magic squares of order 90. These are formed by external border of order 9 in two ways. One with 9 blocks of magic squares of order 3. The second as bordered magic squares of order 9. These forms and external border to magic squares of order 90. Thus, we have 48 magic squares order 902 formed by blocks of order 3, 4, 5, 6, 7, 8 and 9. Below are only three examples as figures without numbers. The full work with numbers can be seen in excel file attached with the work.



Magic Squares of Order 110
There are 144 different types of magic squares of order 110. These are formed by external border of order 10 in three ways. One with magic square of order 10. The second with block border magic squares of order 10 with four magic squares of order 4. The third as bordered magic squares of order 10. These give external borders to magic squares of order 110. Thus, we have 144 magic squares order 110 formed by blocks of order 3, 4, 5, 6, 7, 8, 9 and 10. Below are only three examples as figures without numbers. Since there are lot of examples, the excel file contains few of them.



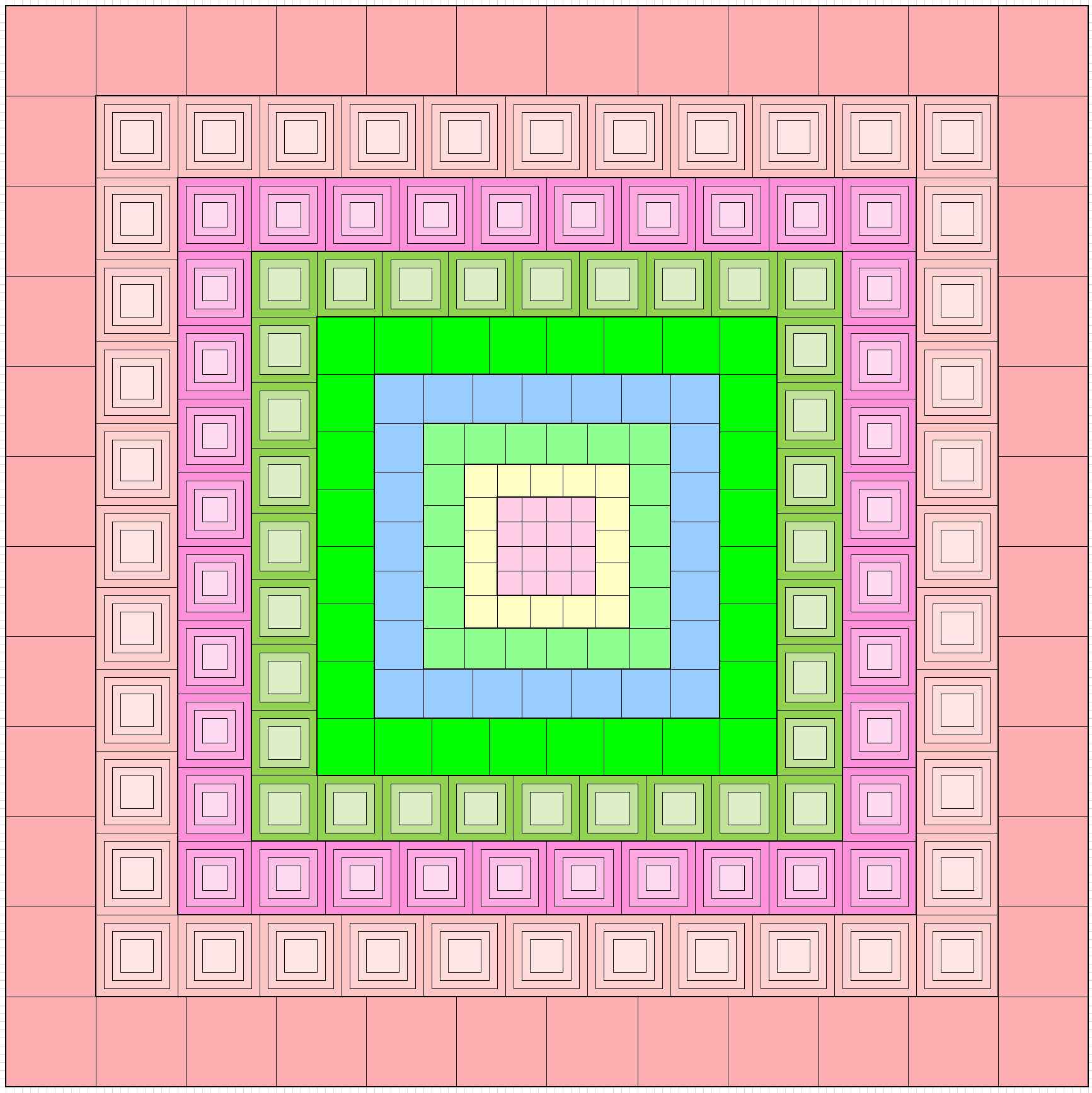
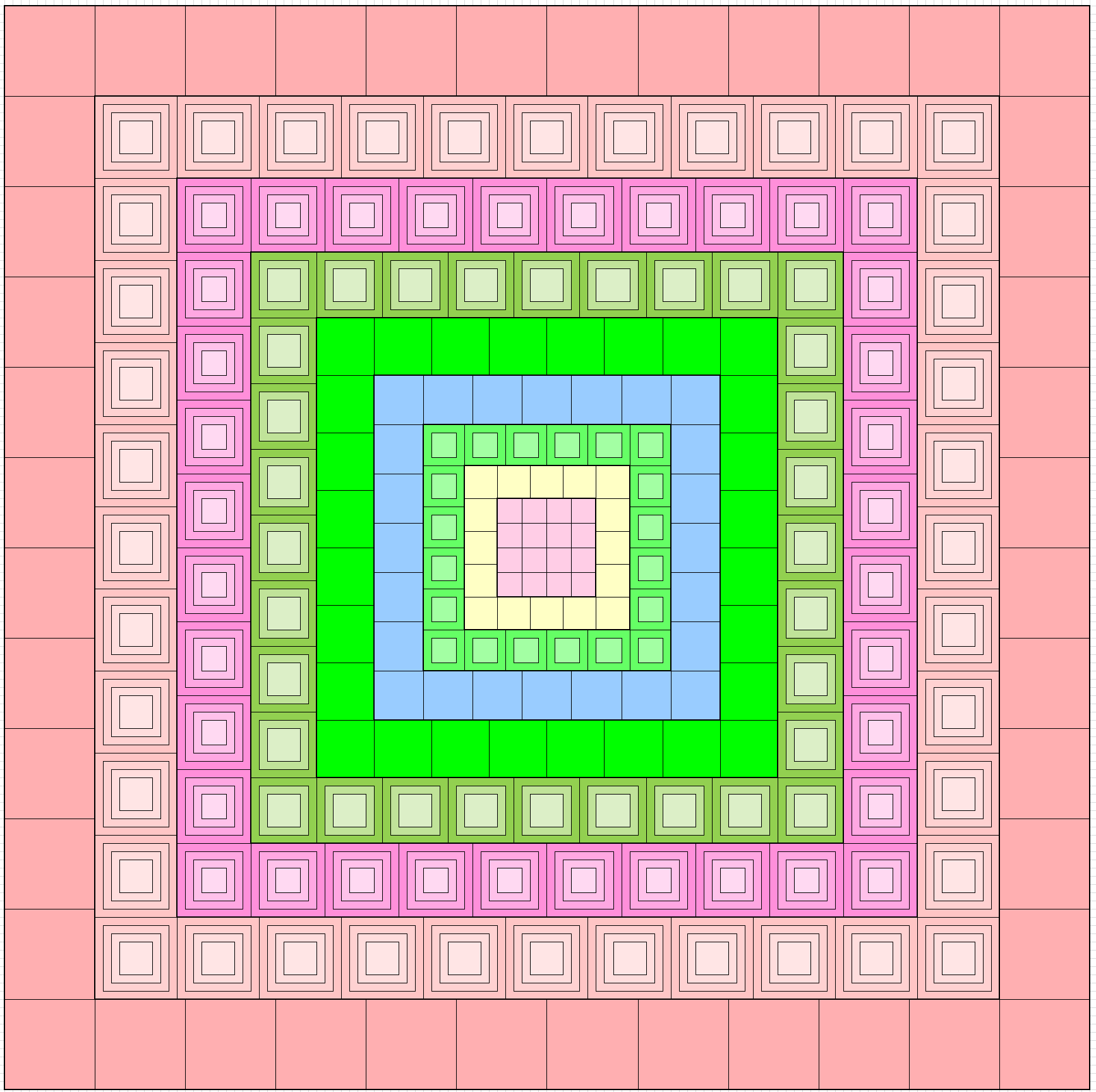
Magic Squares of Order 132
There are 288 different types of magic squares of order 132. These are formed by external border of order 11 in two ways. One with magic square of order 11. The second as bordered magic squares of order 11. These give external borders to magic squares of order 132. Thus, we have 288 magic squares order 132 formed by blocks of order 3, 4, 5, 6, 7, 8, 9, 10 and 11. Below are only three examples as figures without numbers. The full work with numbers can be seen in excel file attached with the work. Since there are lot of examples, the excel file contains few of them.



I can only report being “blown away” by this really amazing work. You are an inspiration to all of us that I know. Lee B. Croft leecroft333@gmail.com.
Thanks