Below are just examples of cornered magic squares of orders 11 to 13. These are in all the four corners of each magic square. This work was possible with the help of Harry White (Magic Squares – budshaw.ca).
This work can be accessed at the following link:
Inder Jeet Taneja, Cornered Magic Squares of Orders 14 to 24, Zenodo, June 03, 2023, pp. 1-39, https://10.5281/zenodo.8000471.
The previous orders can be accessed at the following links:
Inder Jeet Taneja, Cornered Magic Squares of Orders 5 to 10
Inder Jeet Taneja, Cornered Magic Squares of Orders 11 to 13
Cornered Magic Squares of Order 14
Below are 82 examples of cornered magic squares of order 14 only in one direction, i.e., left side up. The other three direction can be obtained easily. In these examples, we have used the aspects of magic squares of orders 6, 8, 10 and 12. In some cases, the idea of bordered magic rectangles is also applied.
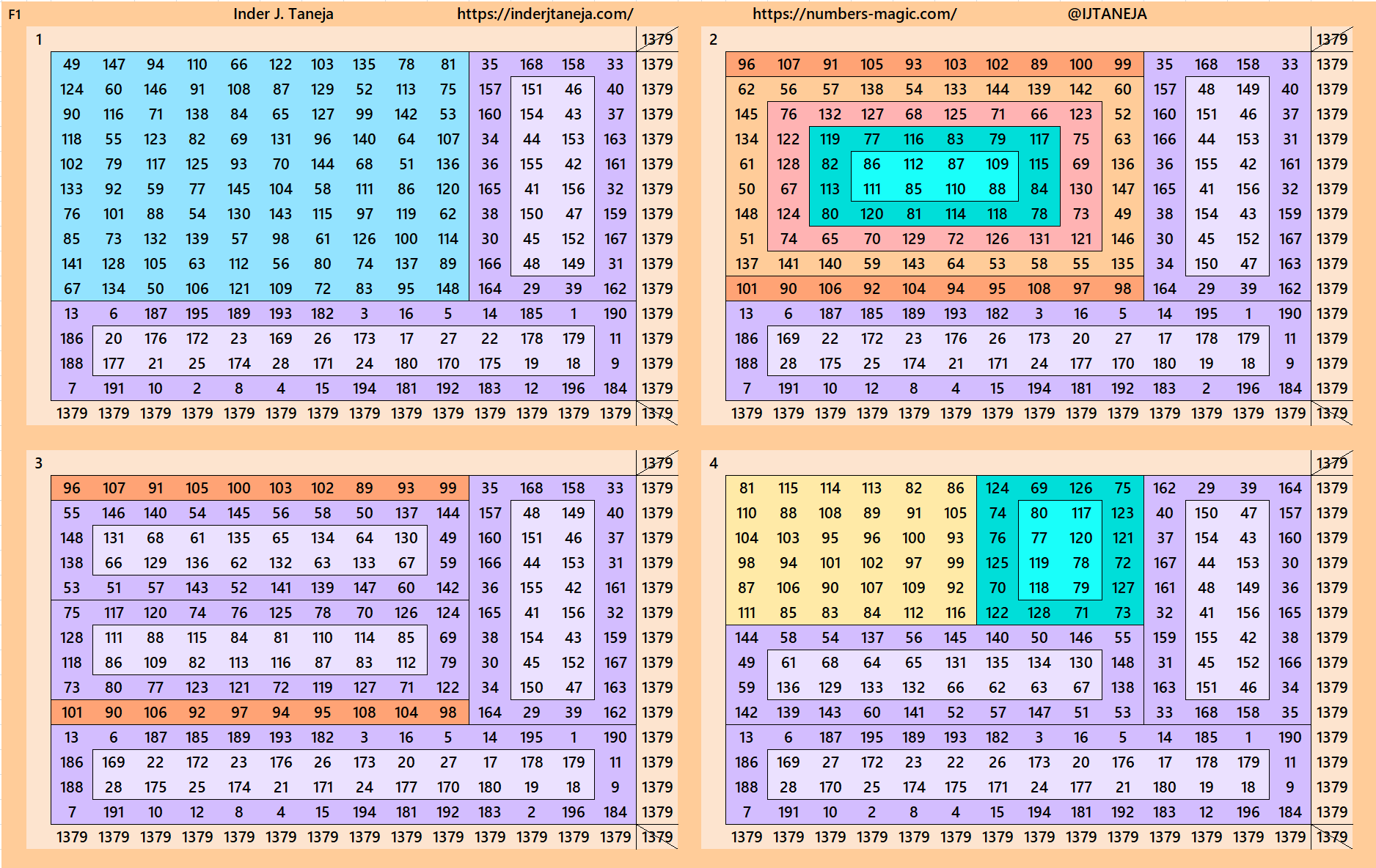
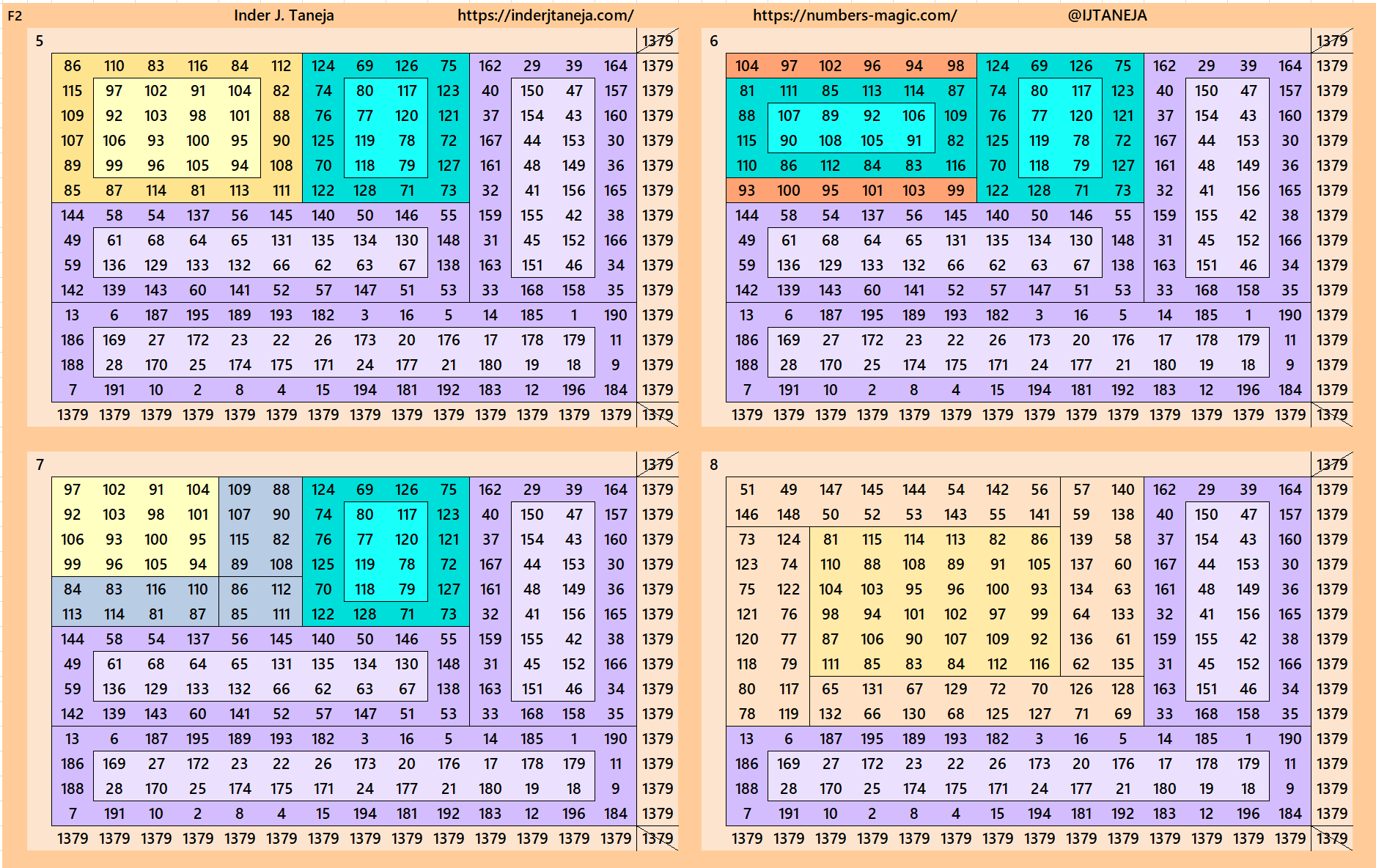
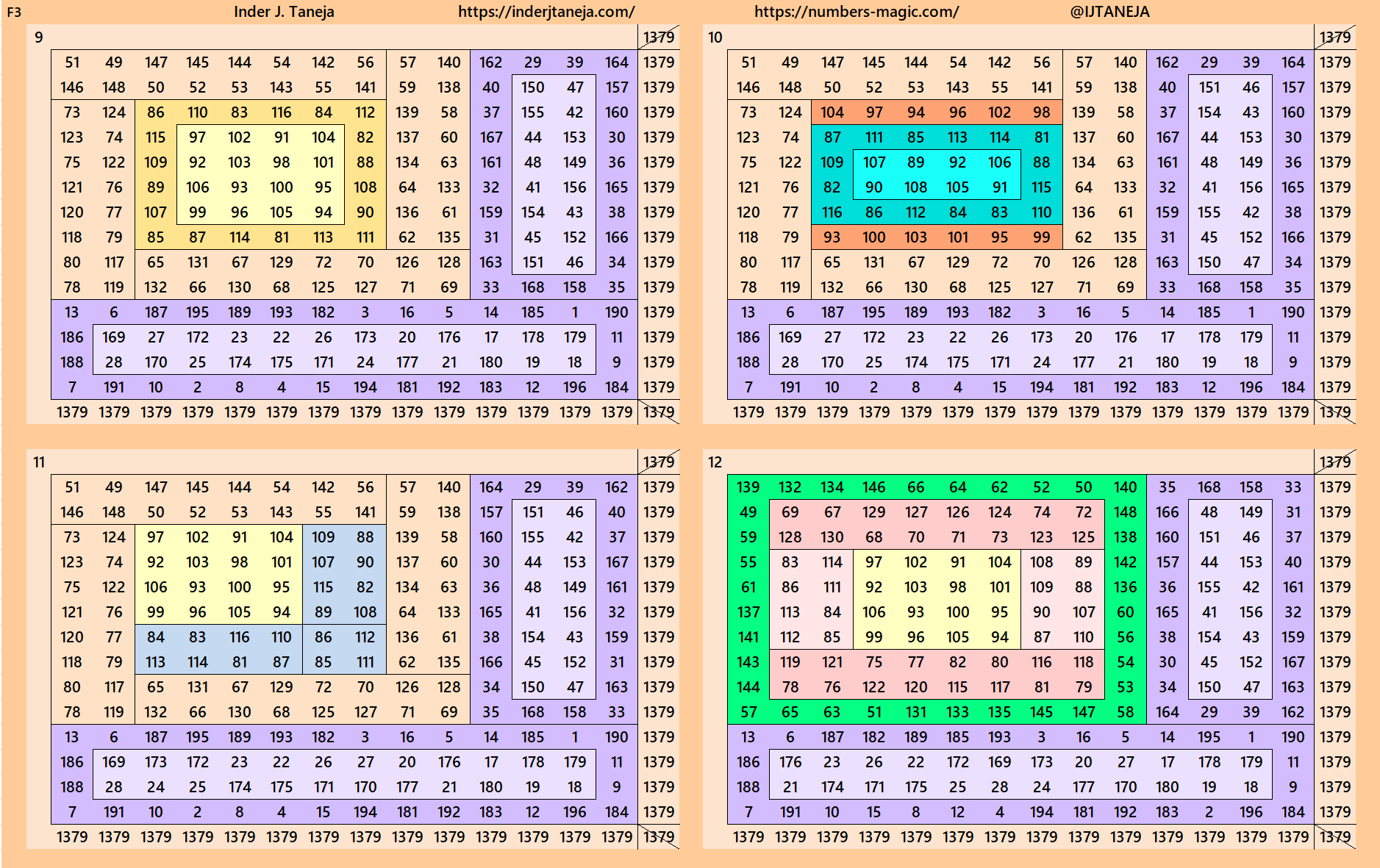
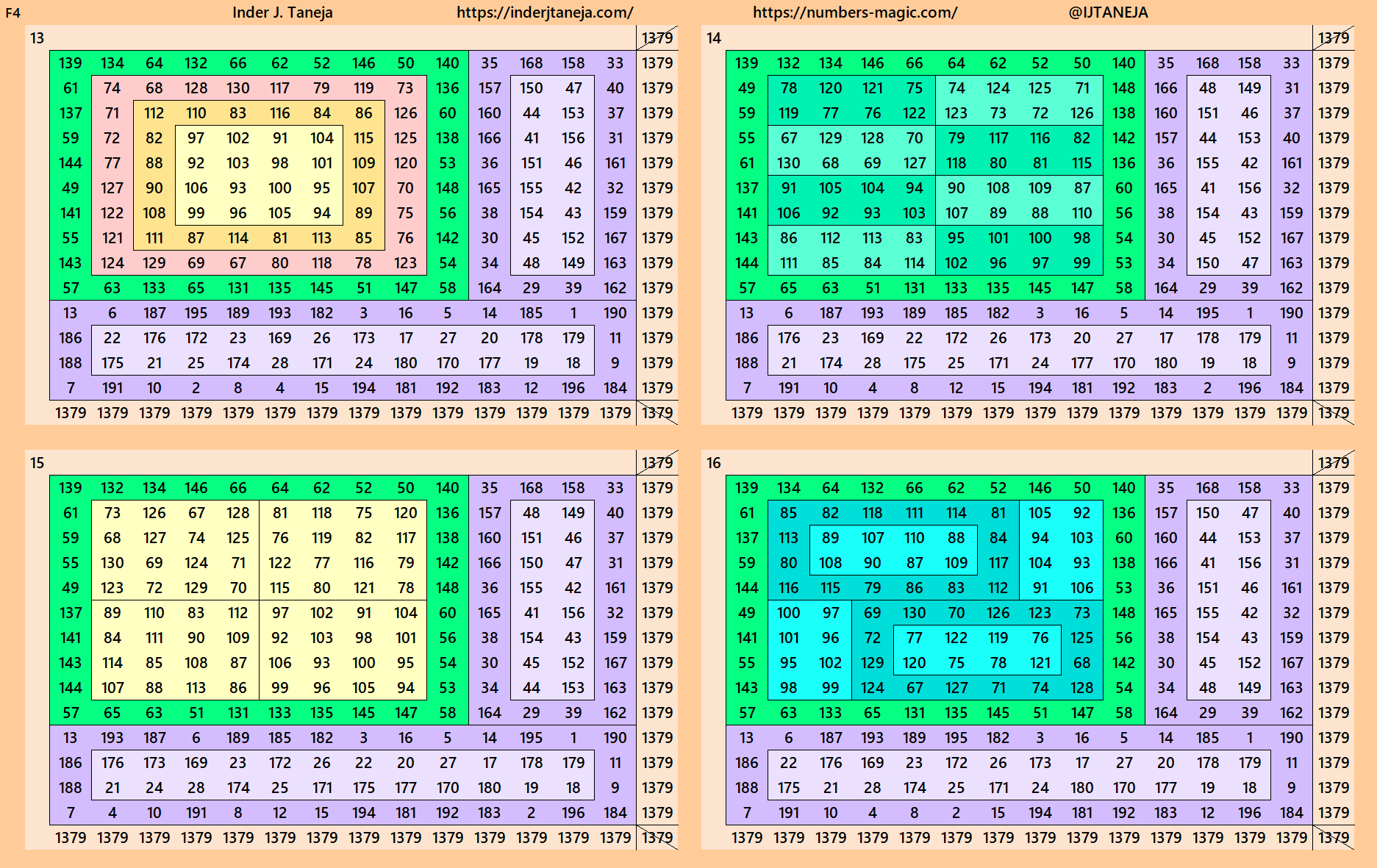
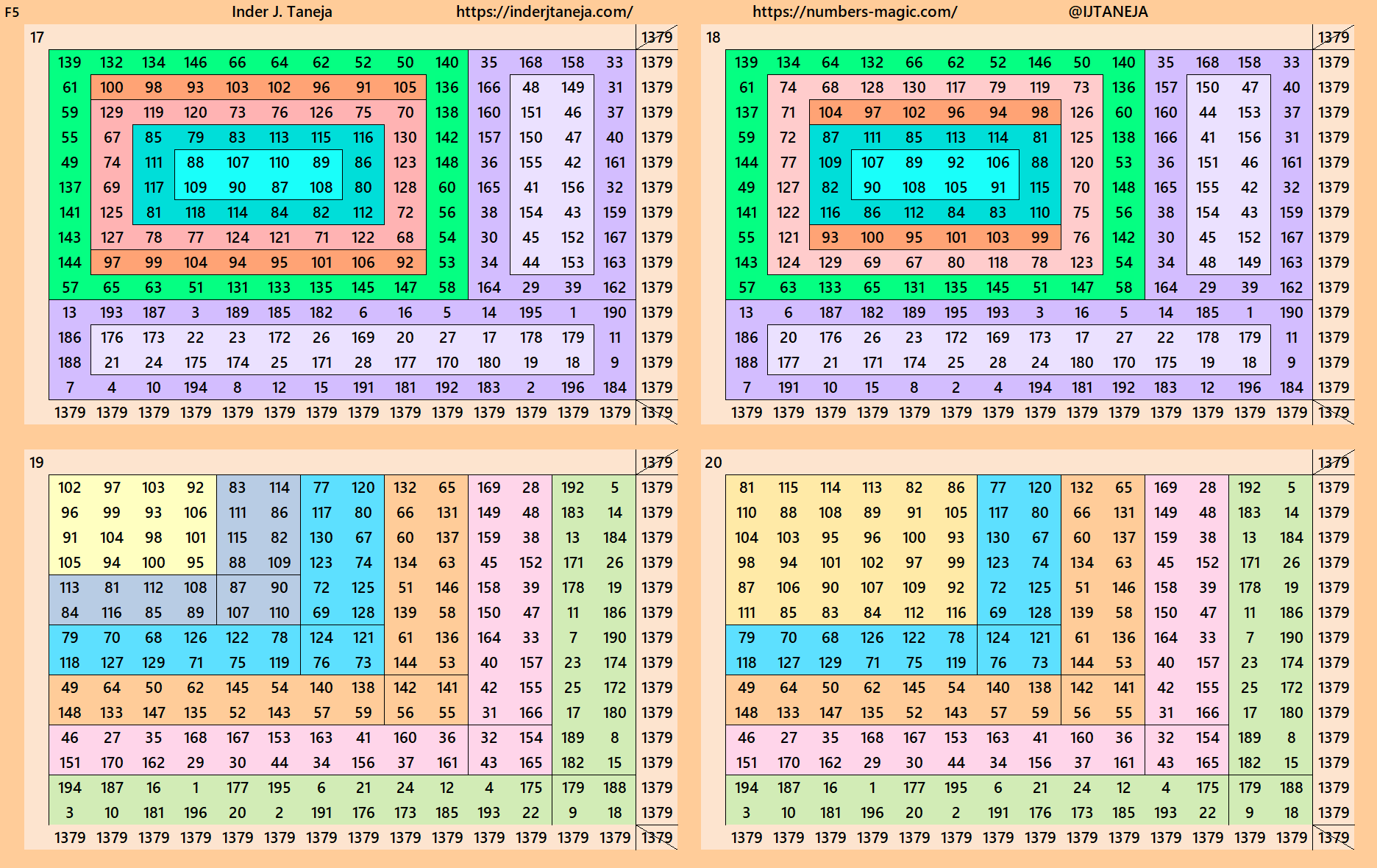
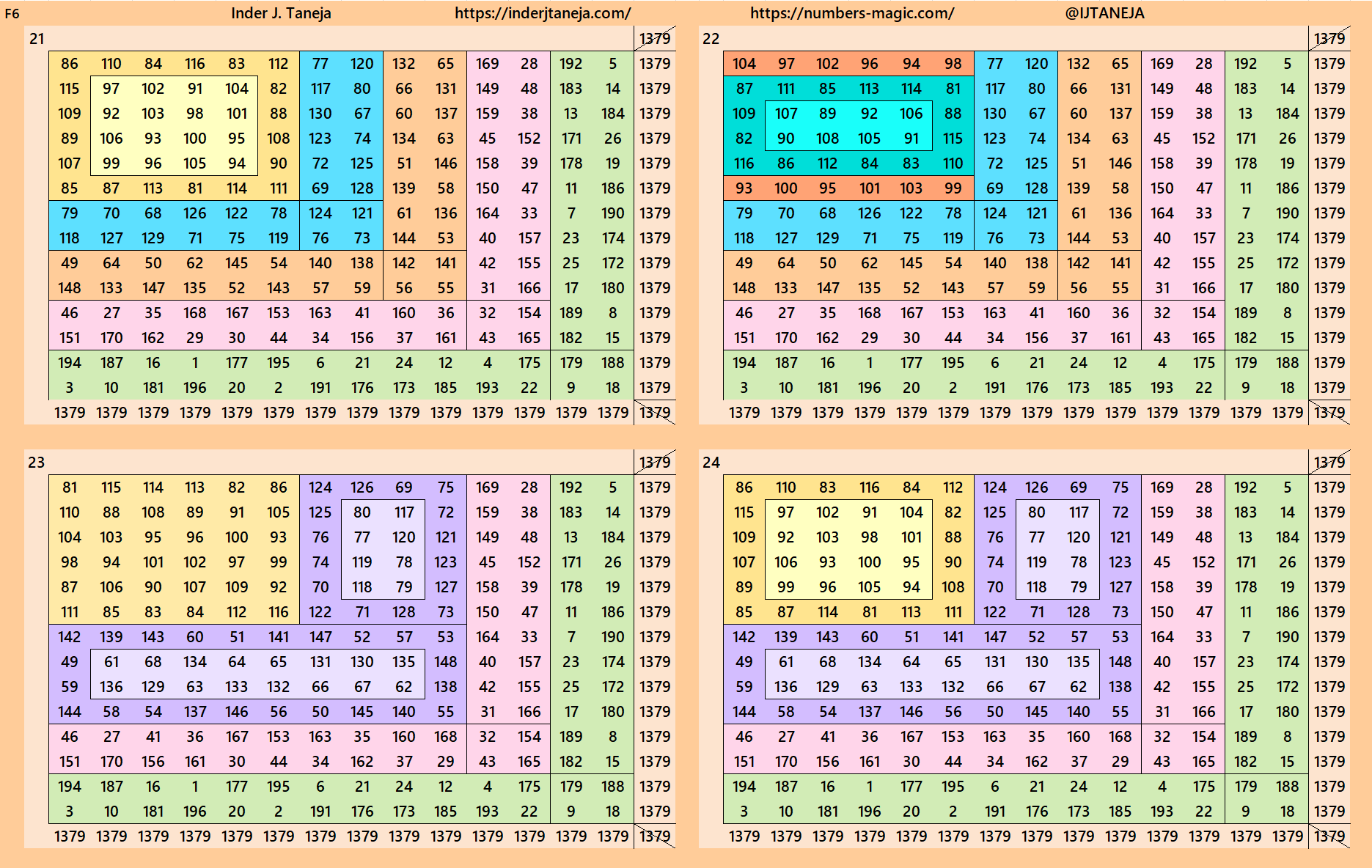
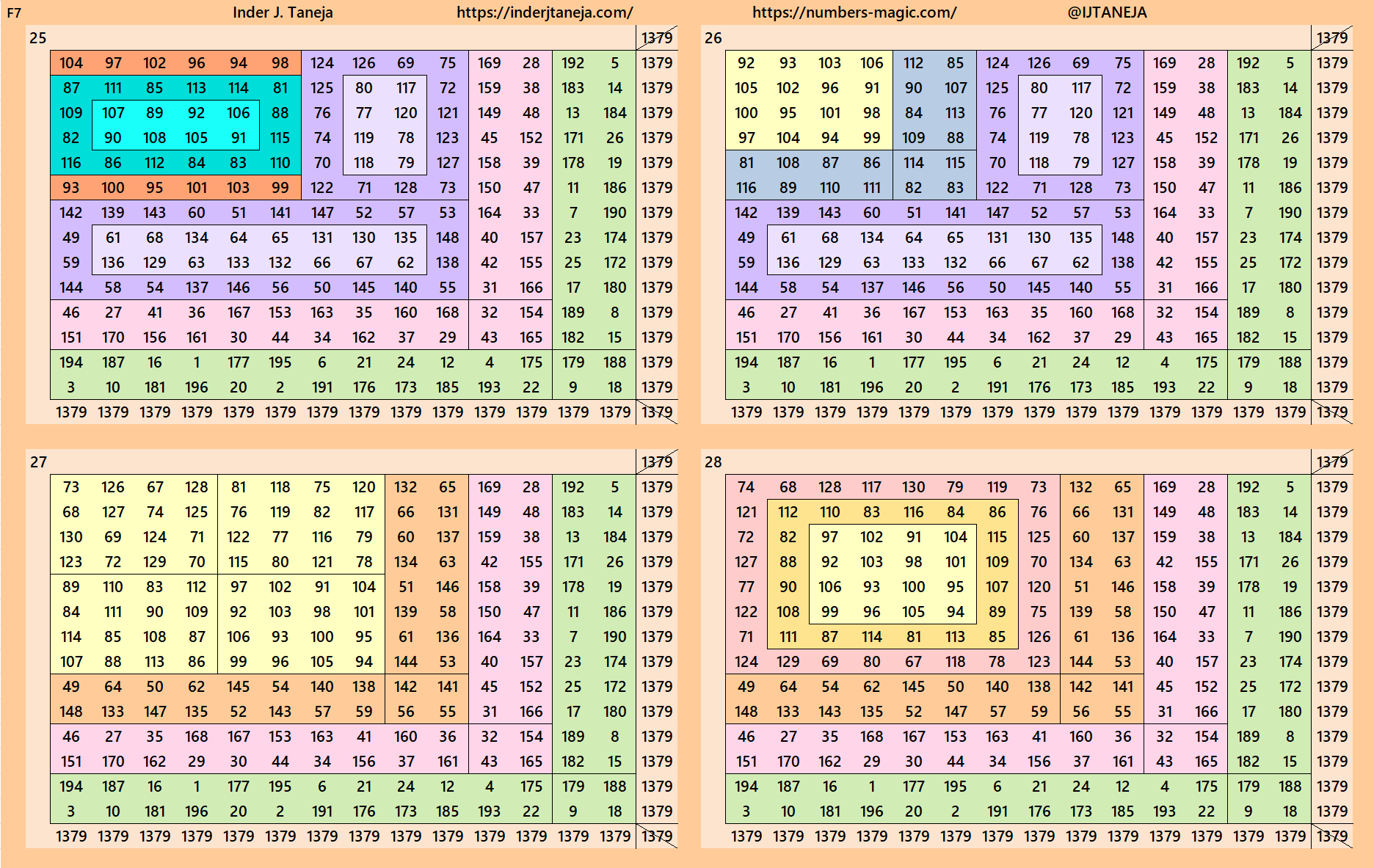
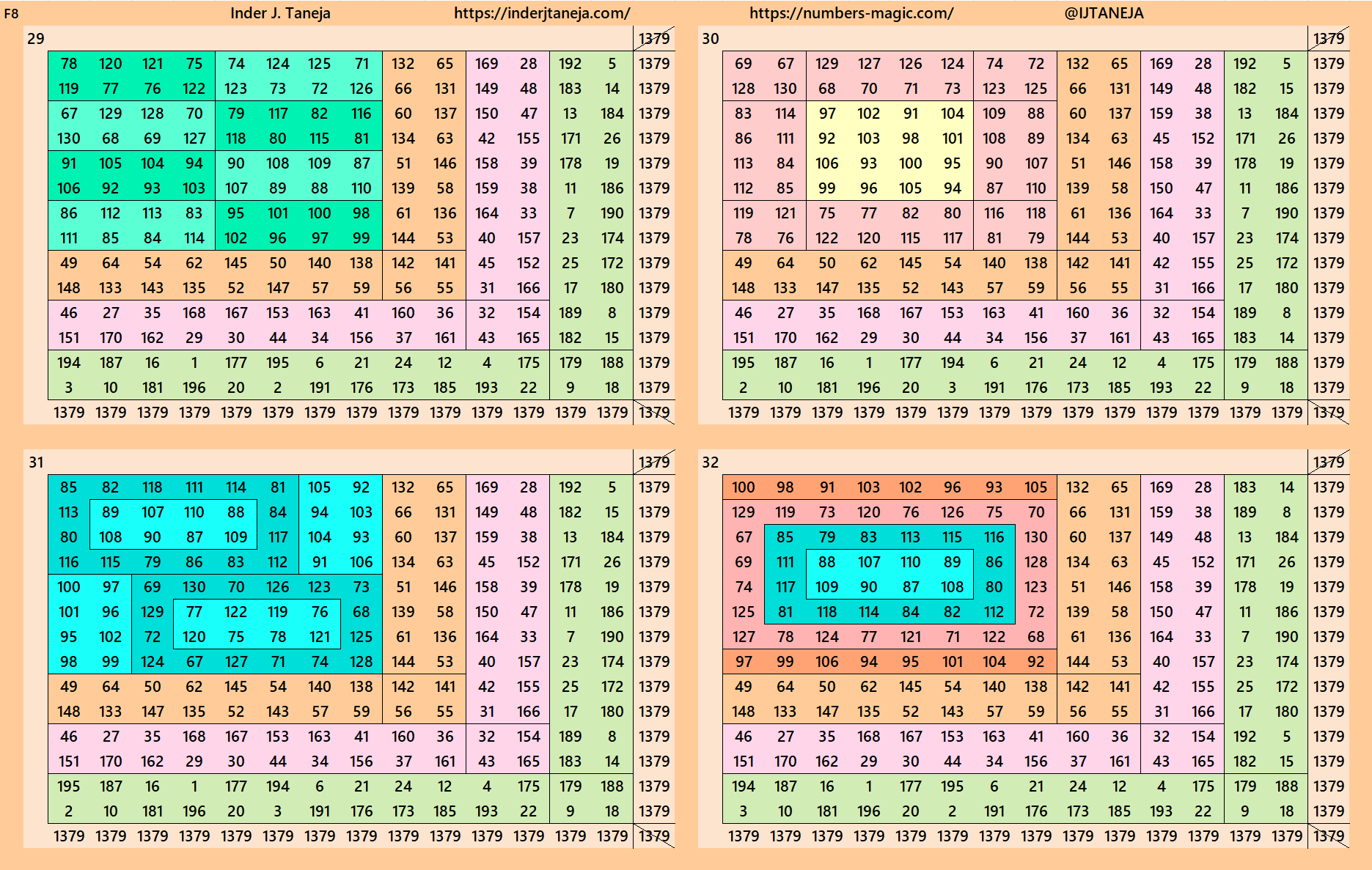
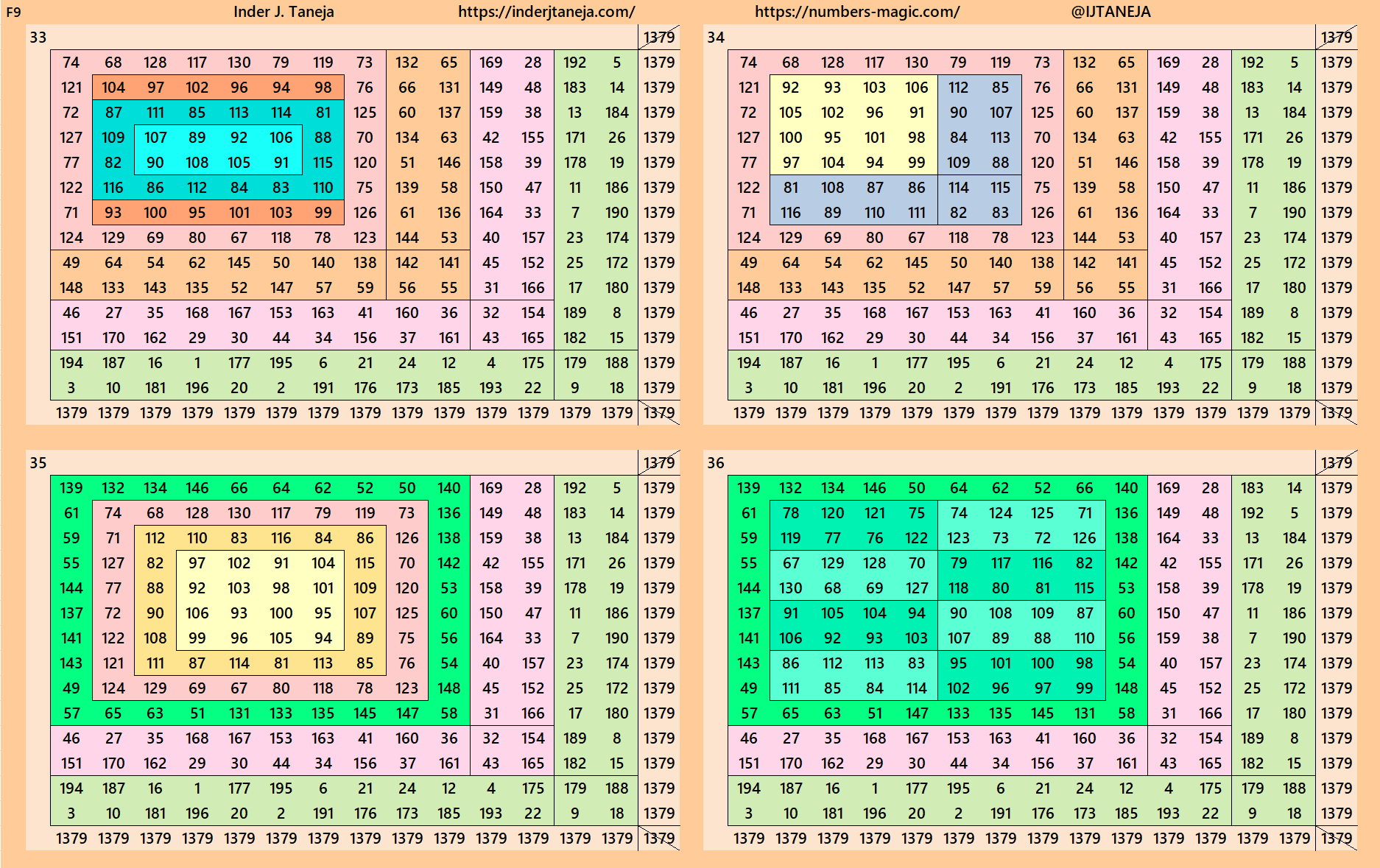
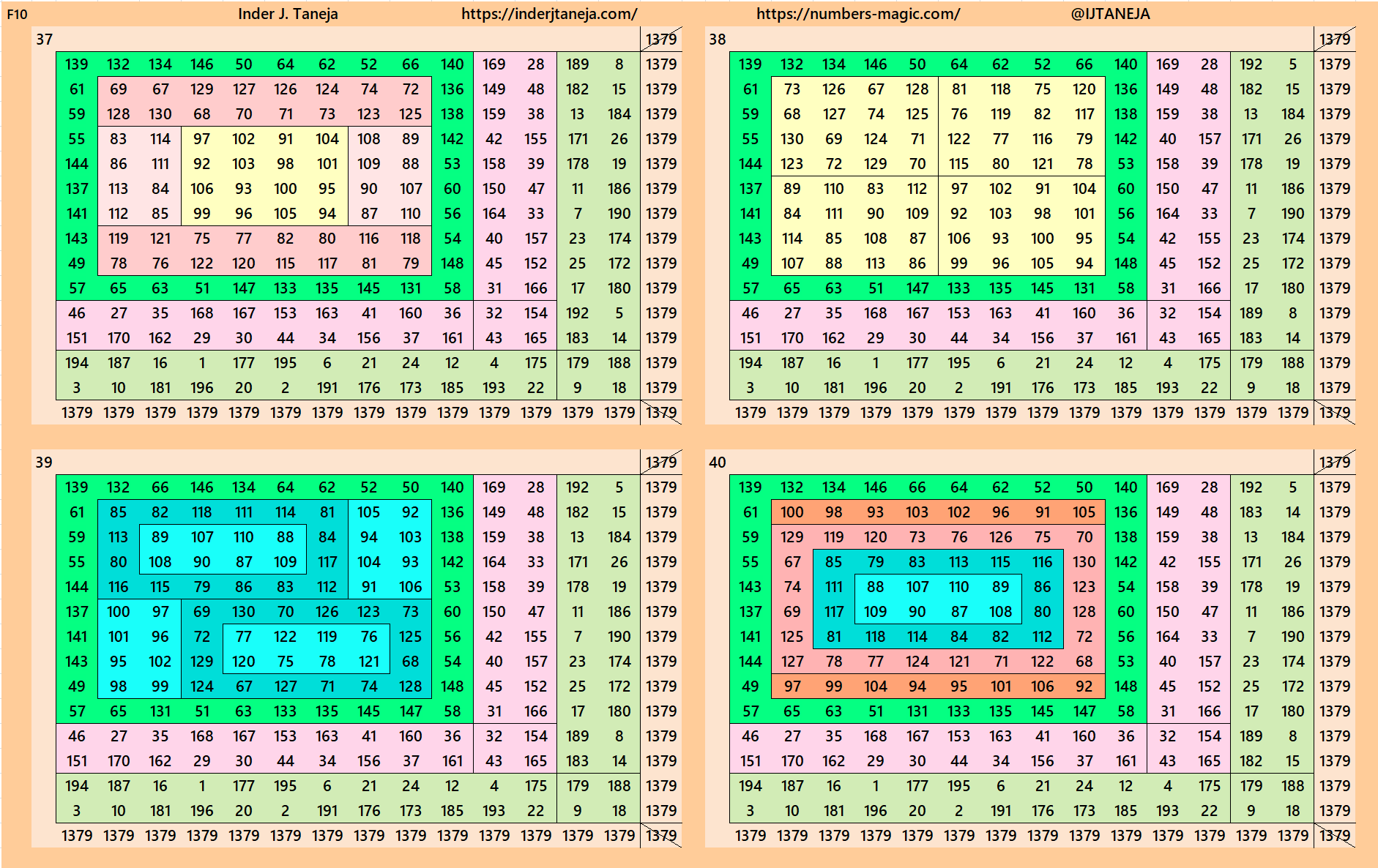
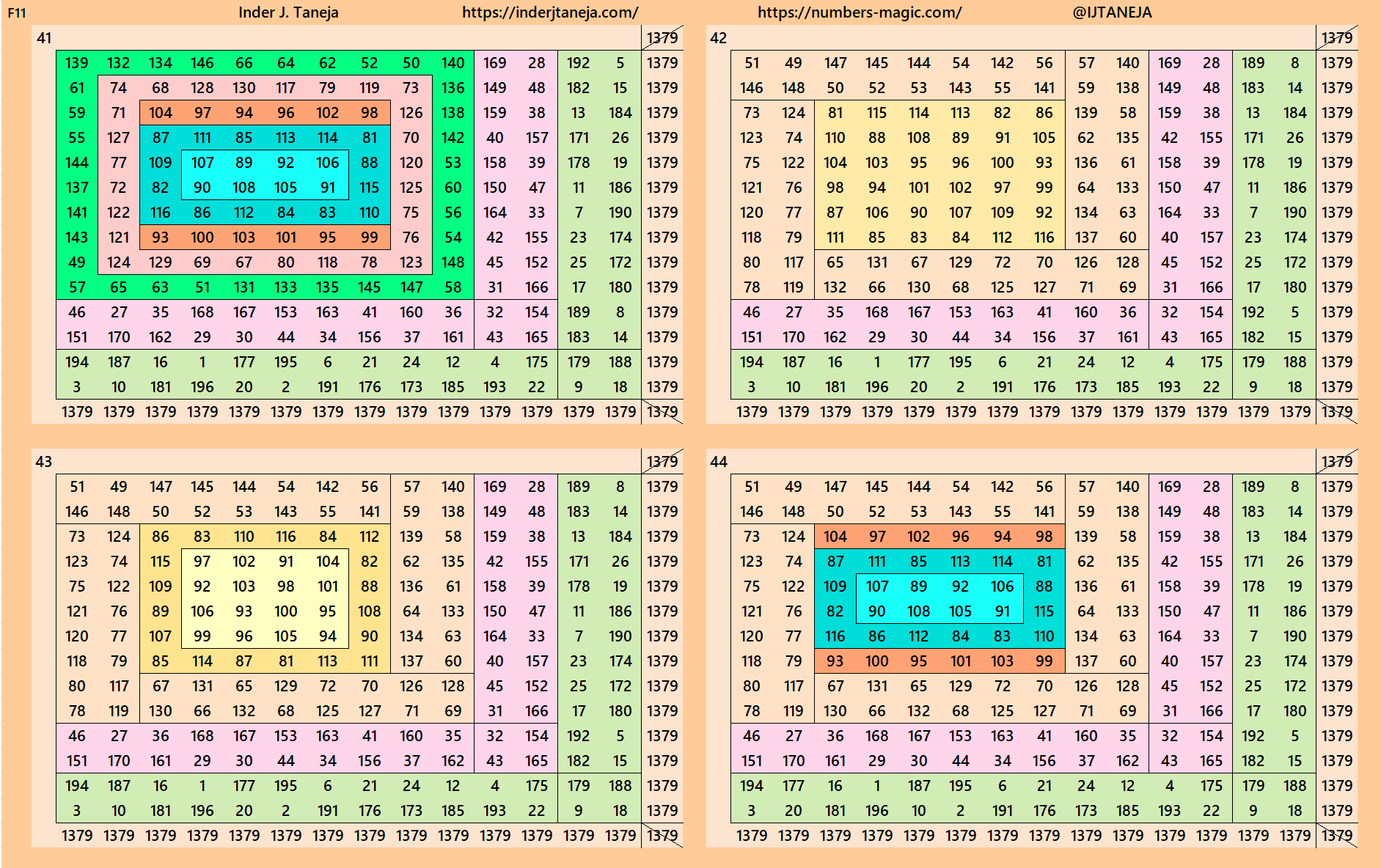
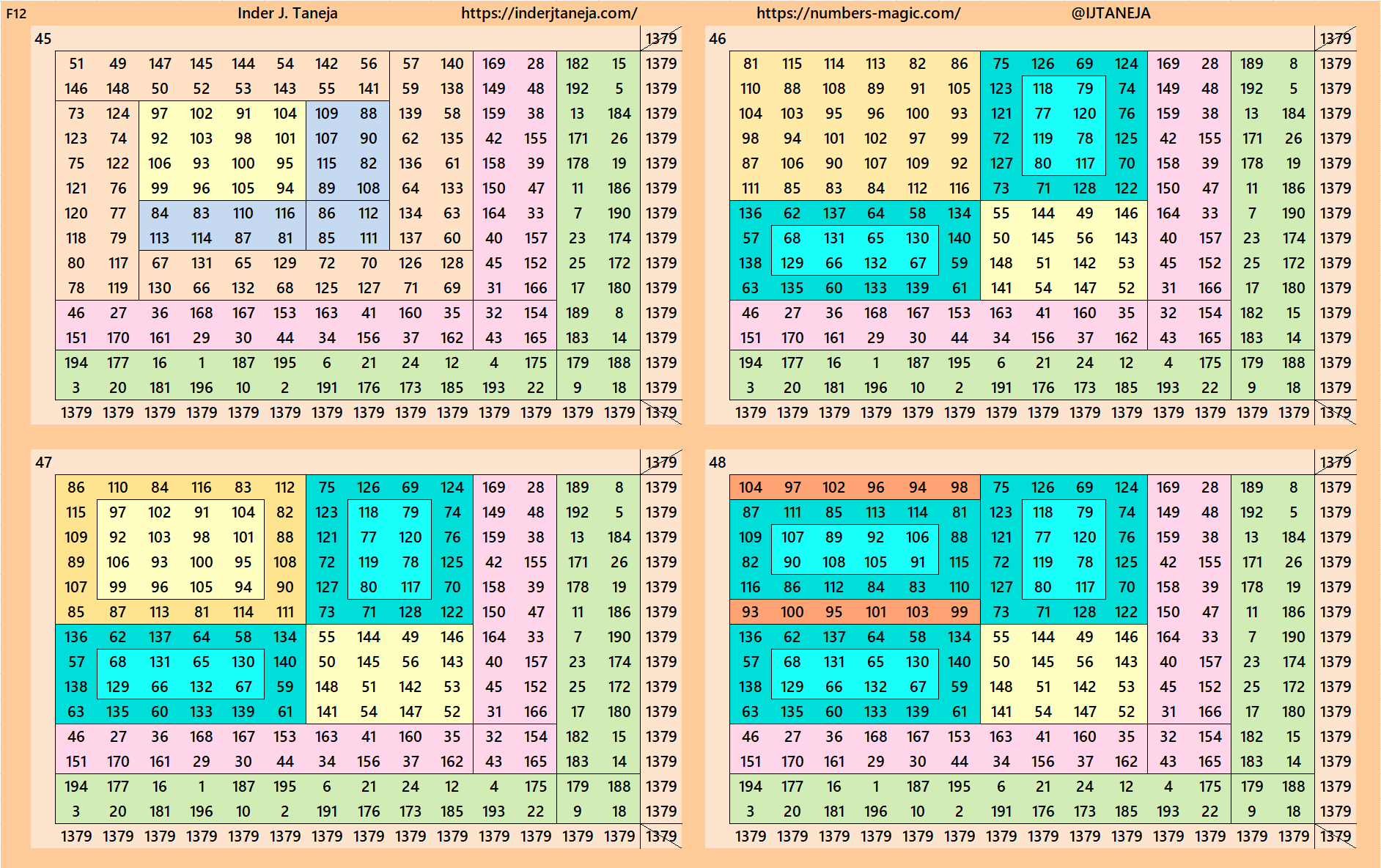
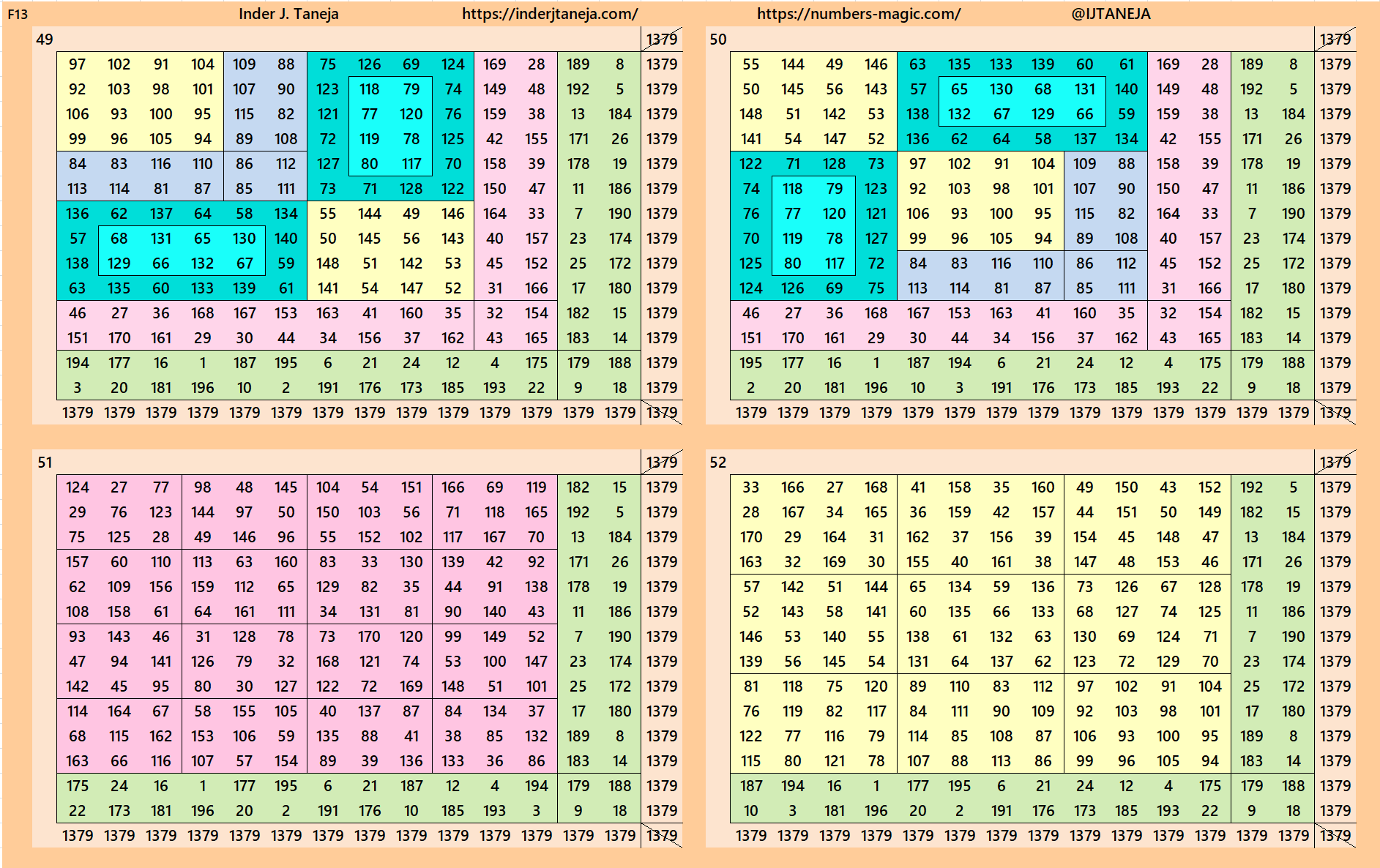
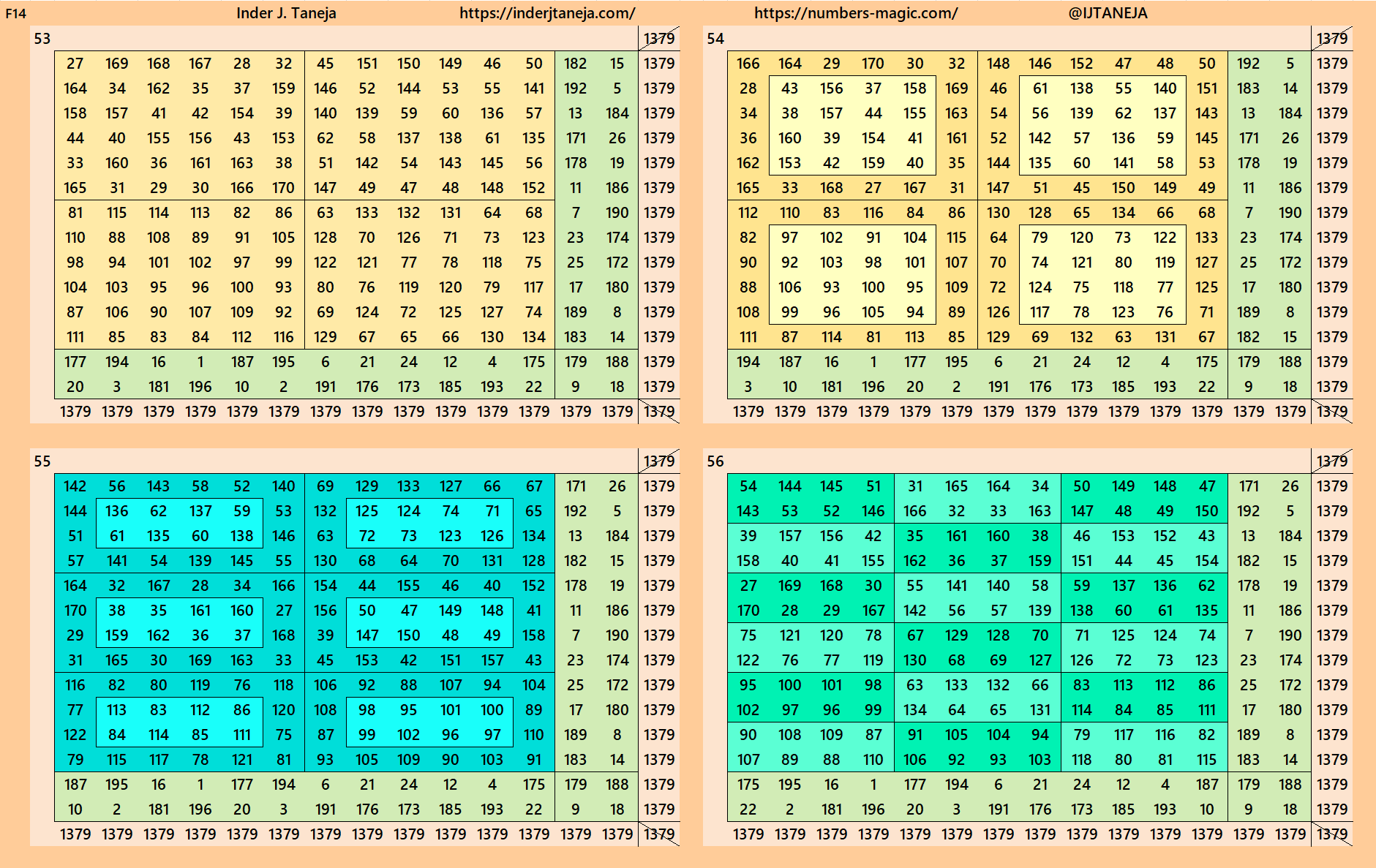
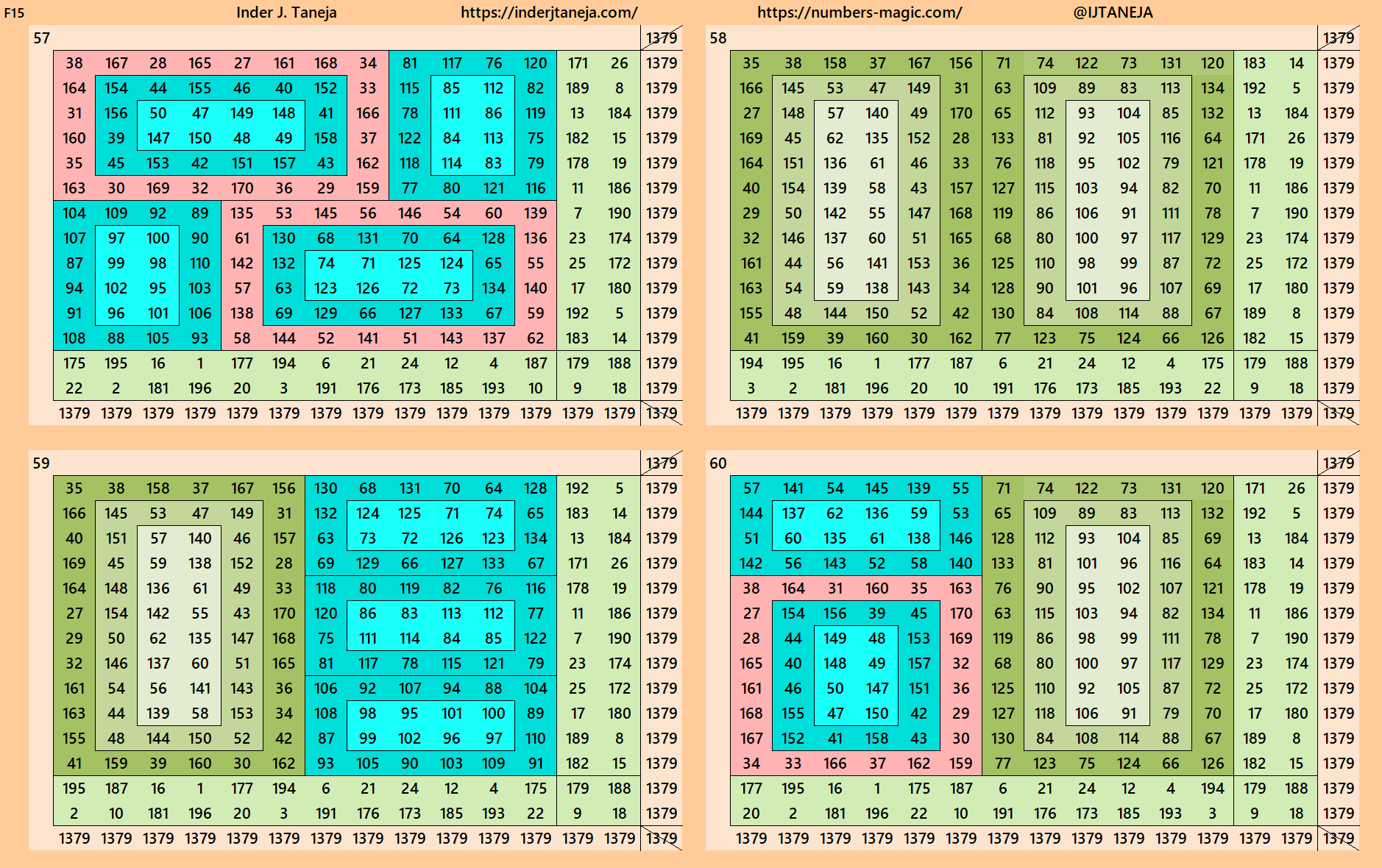
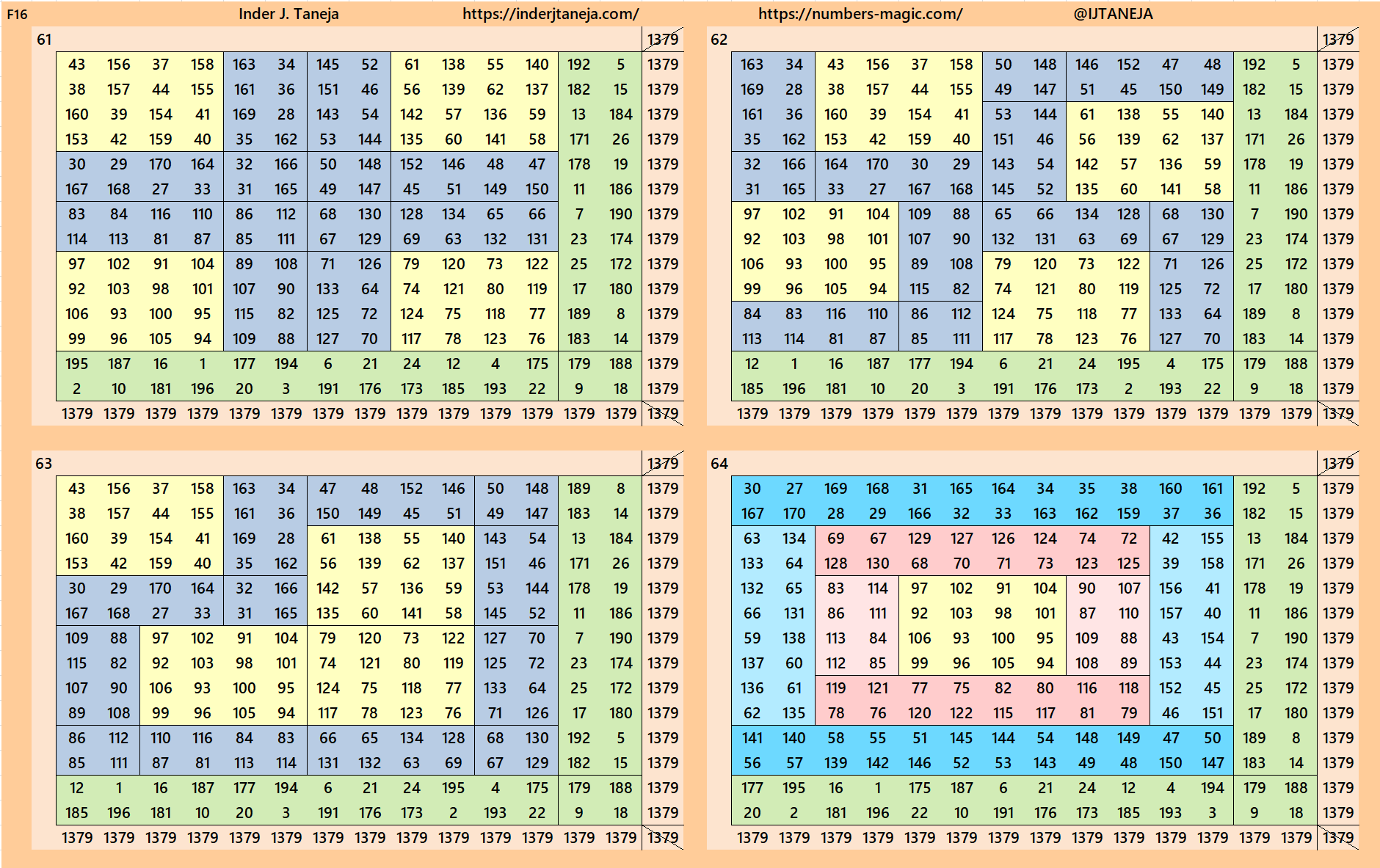
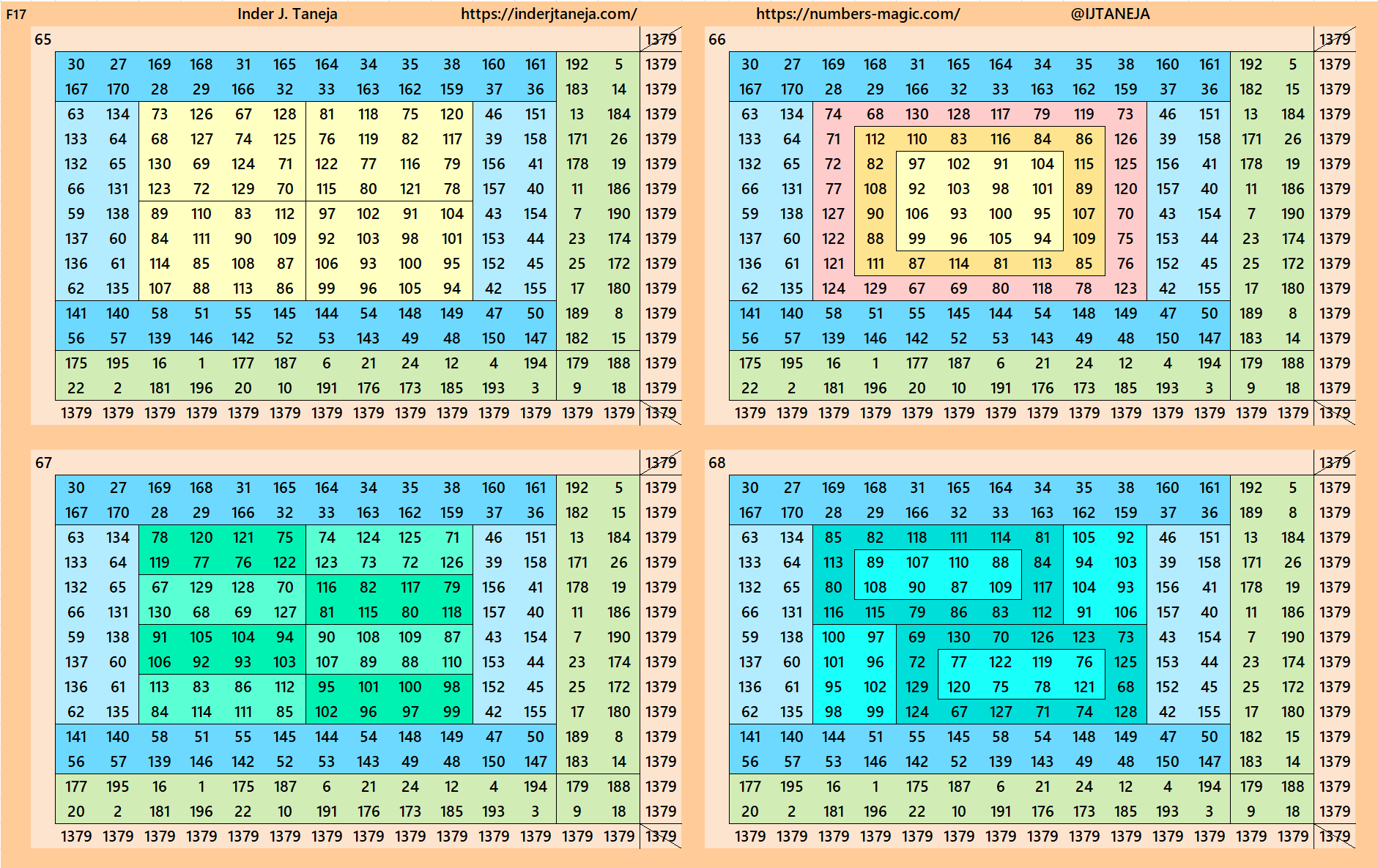
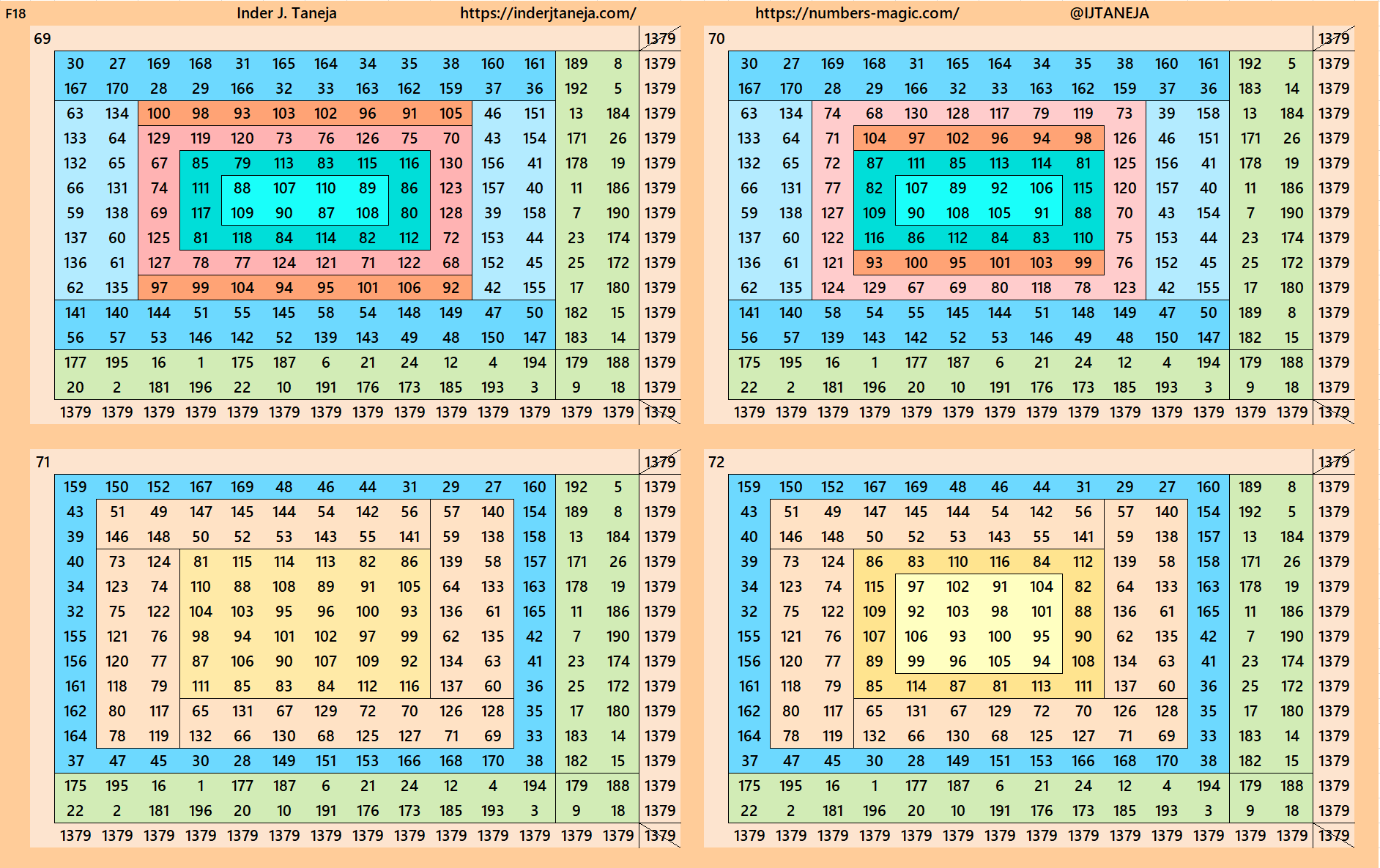
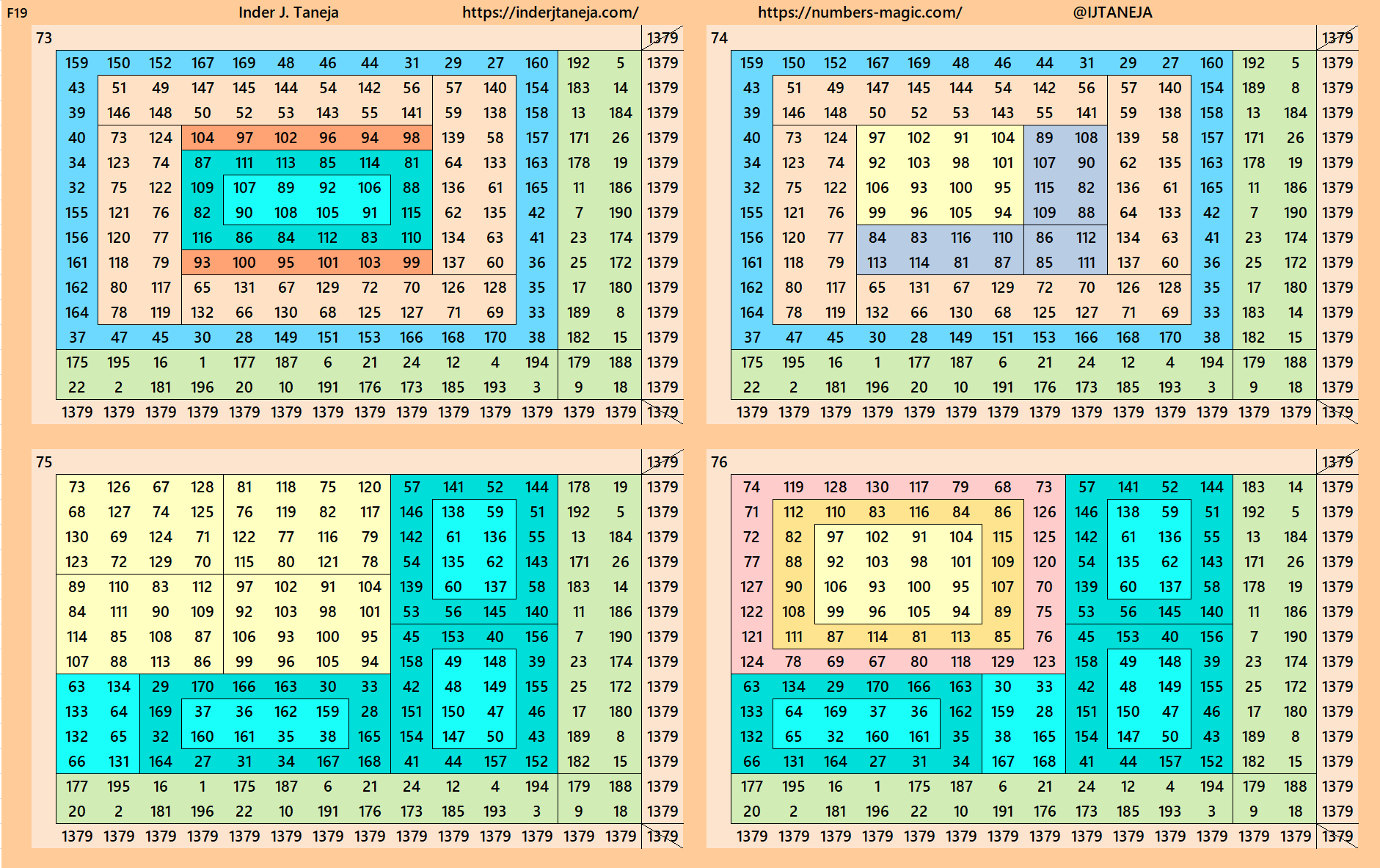
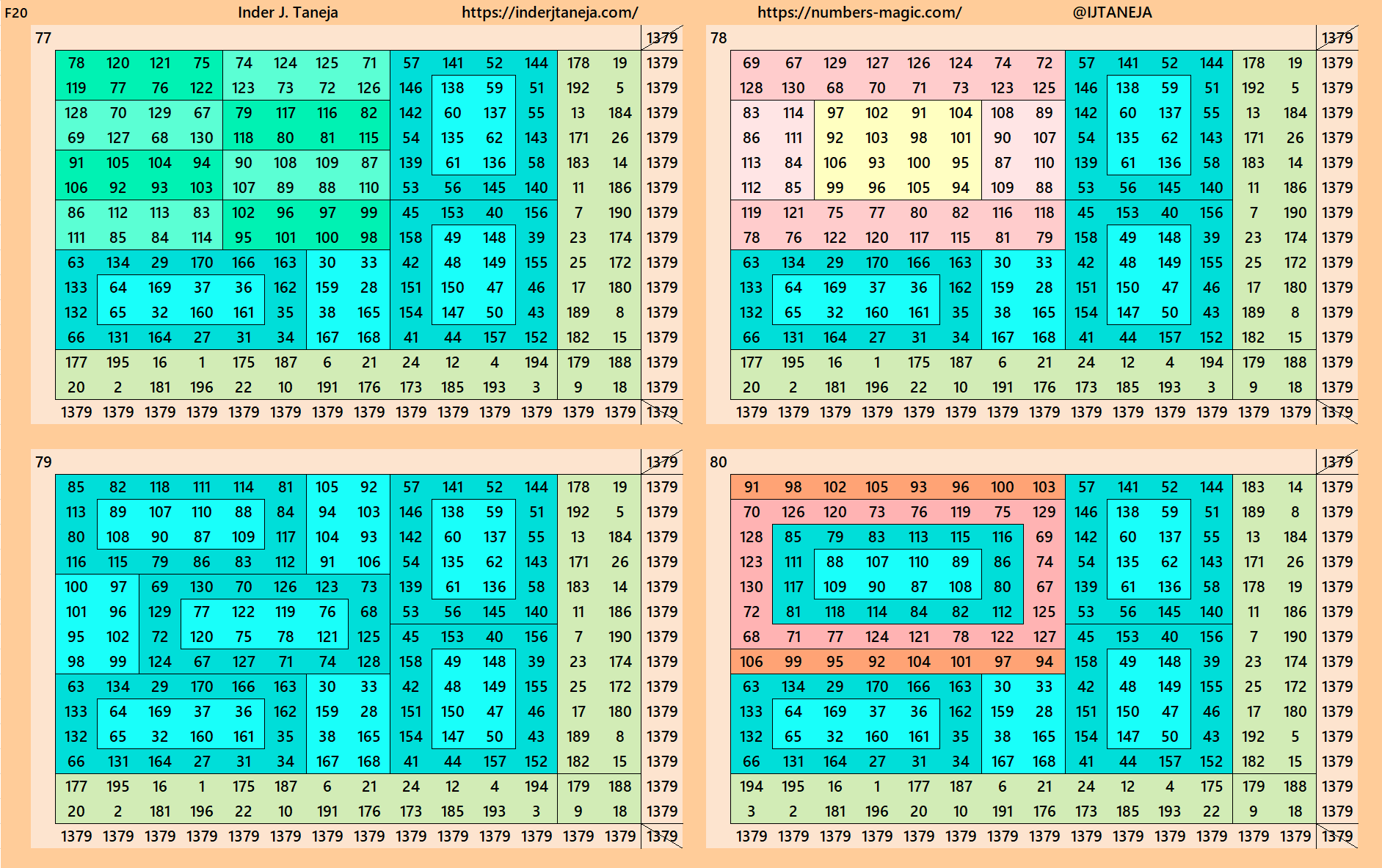
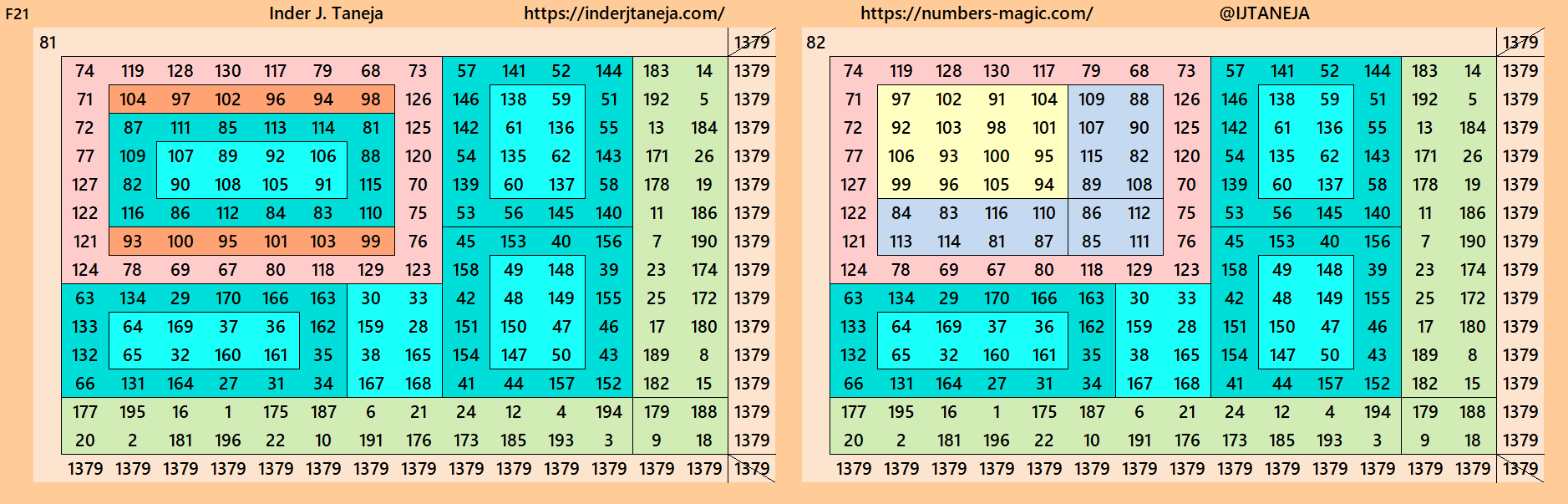
rnered Magic Squares of Orders 15 to 24
Below are cornered magic squares of orders 15 to 24. In each case there is only one example, i.e., of chain-type or nested-type. Extended study of these magic squares shall be done elsewhere.
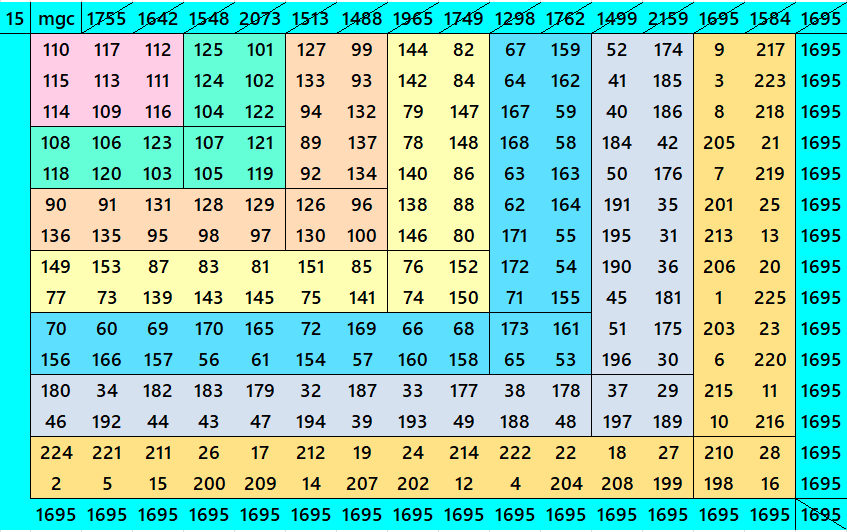
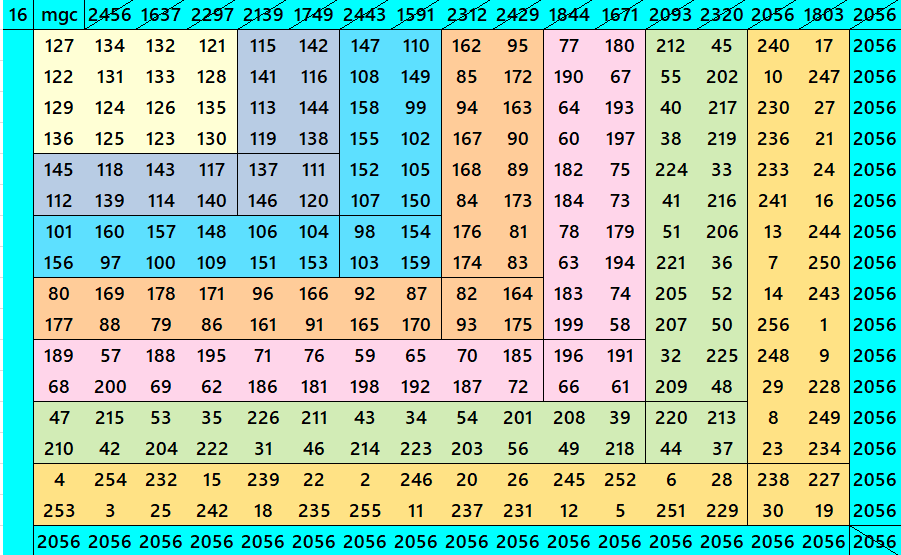
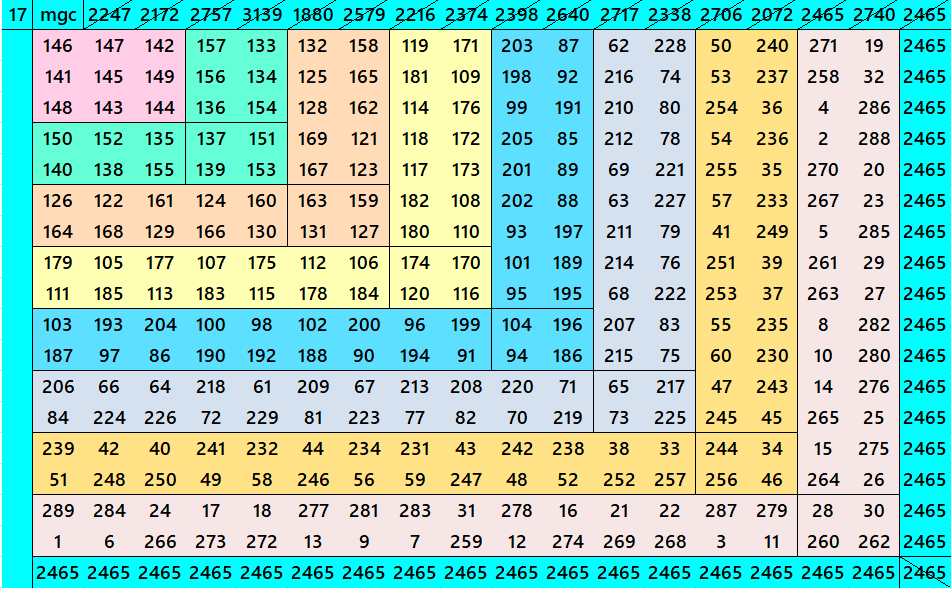
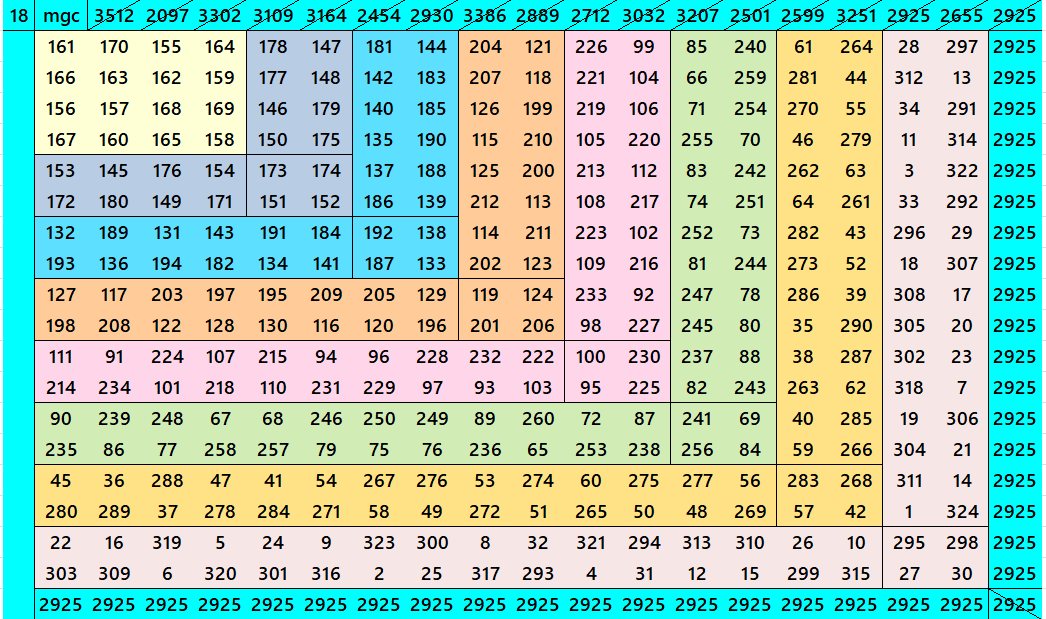
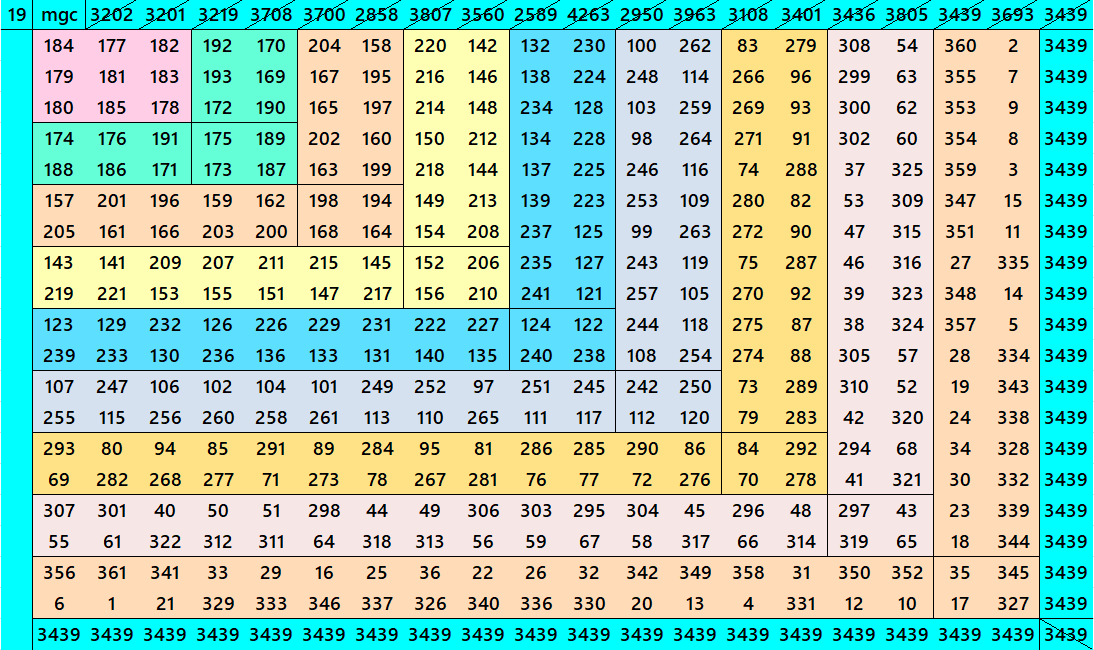
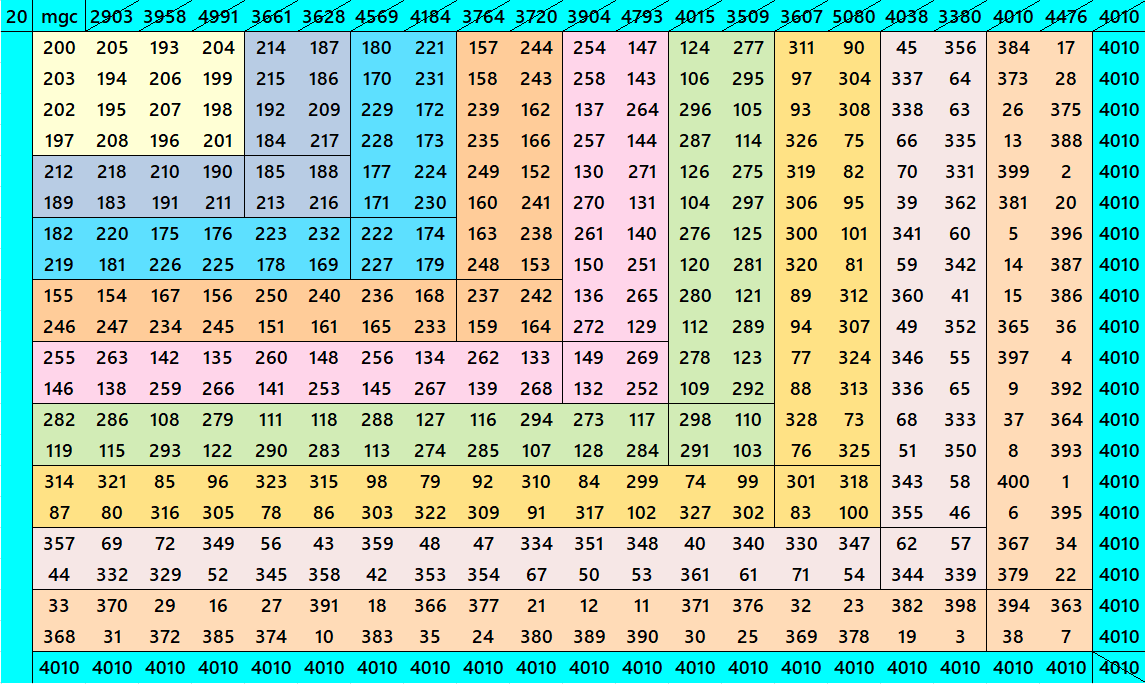
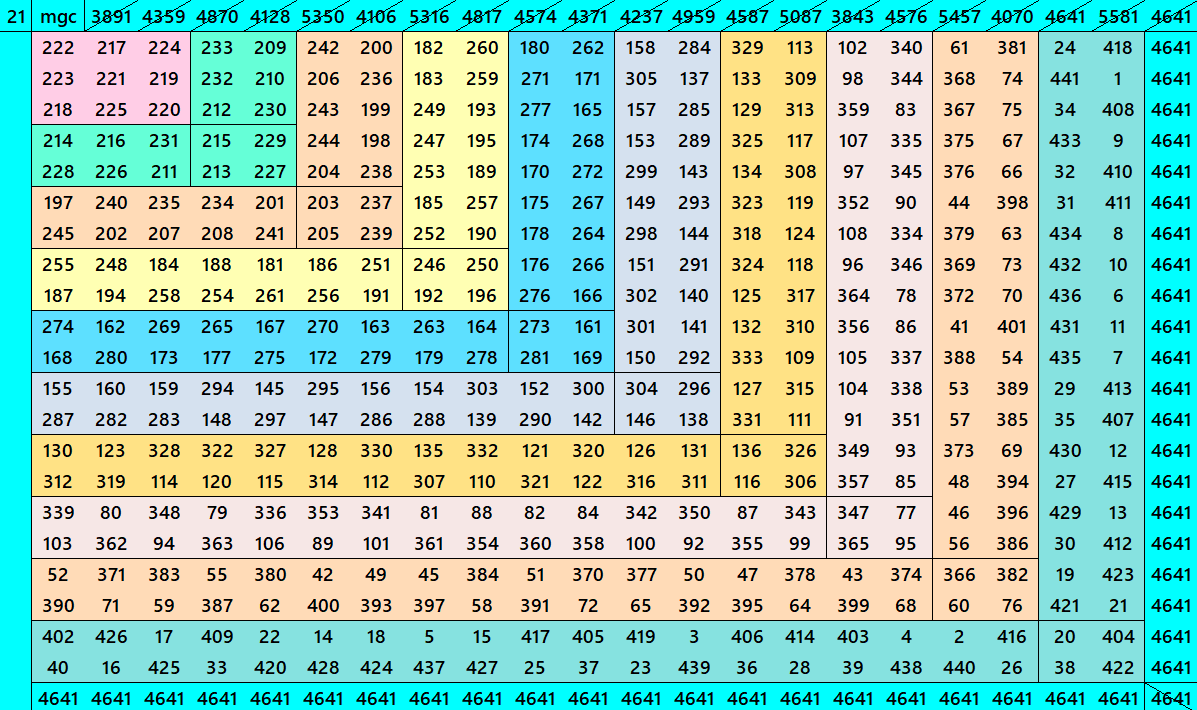
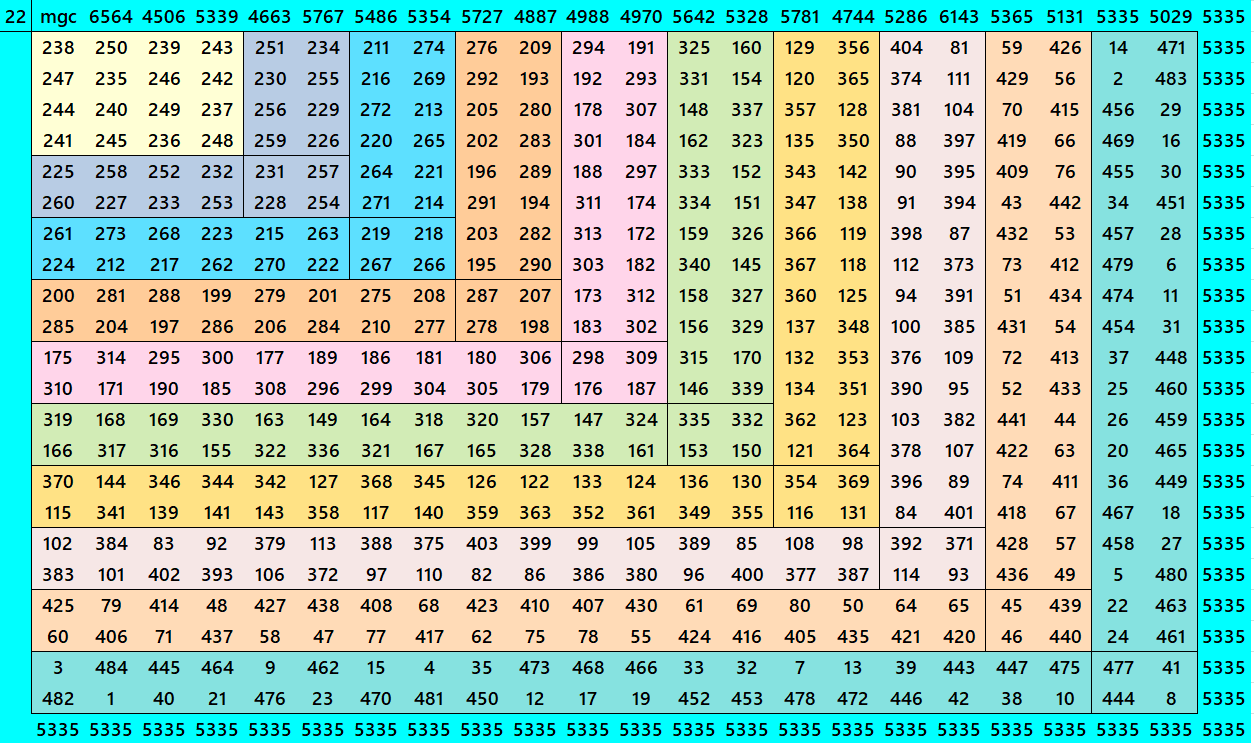
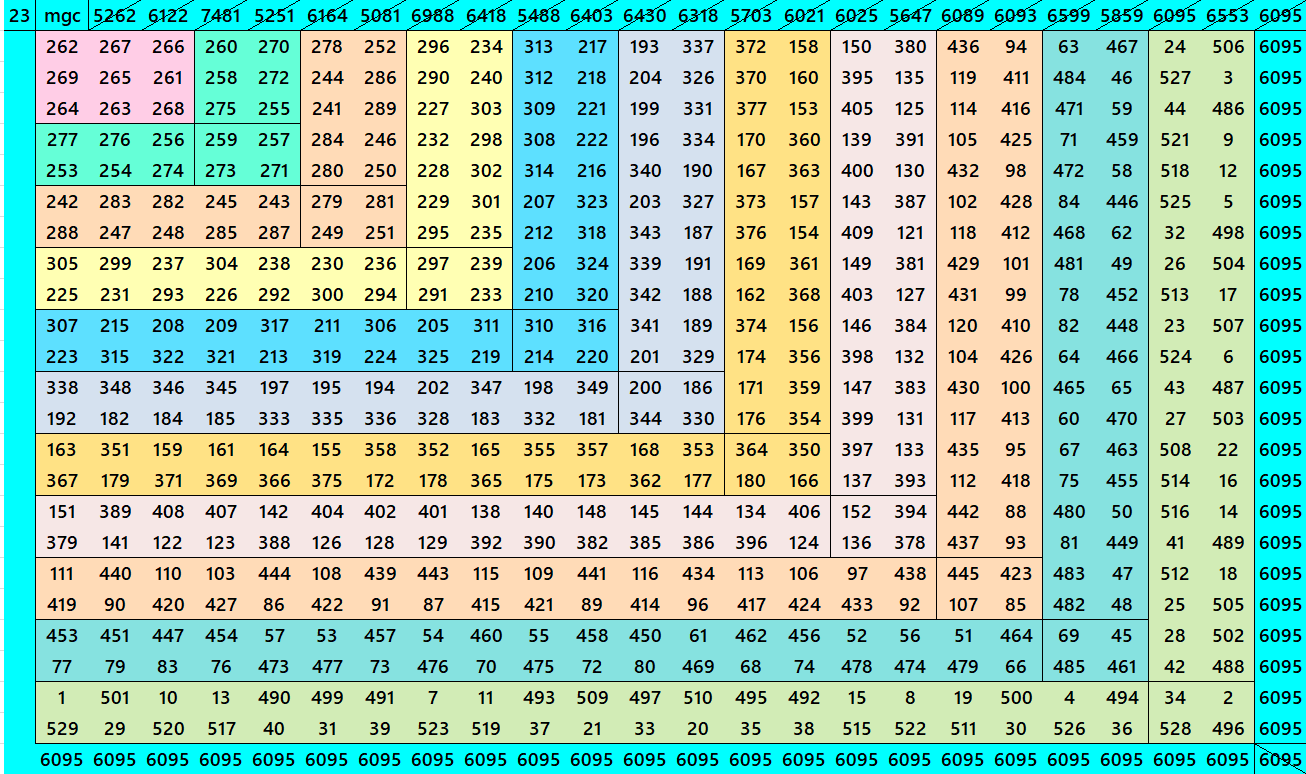
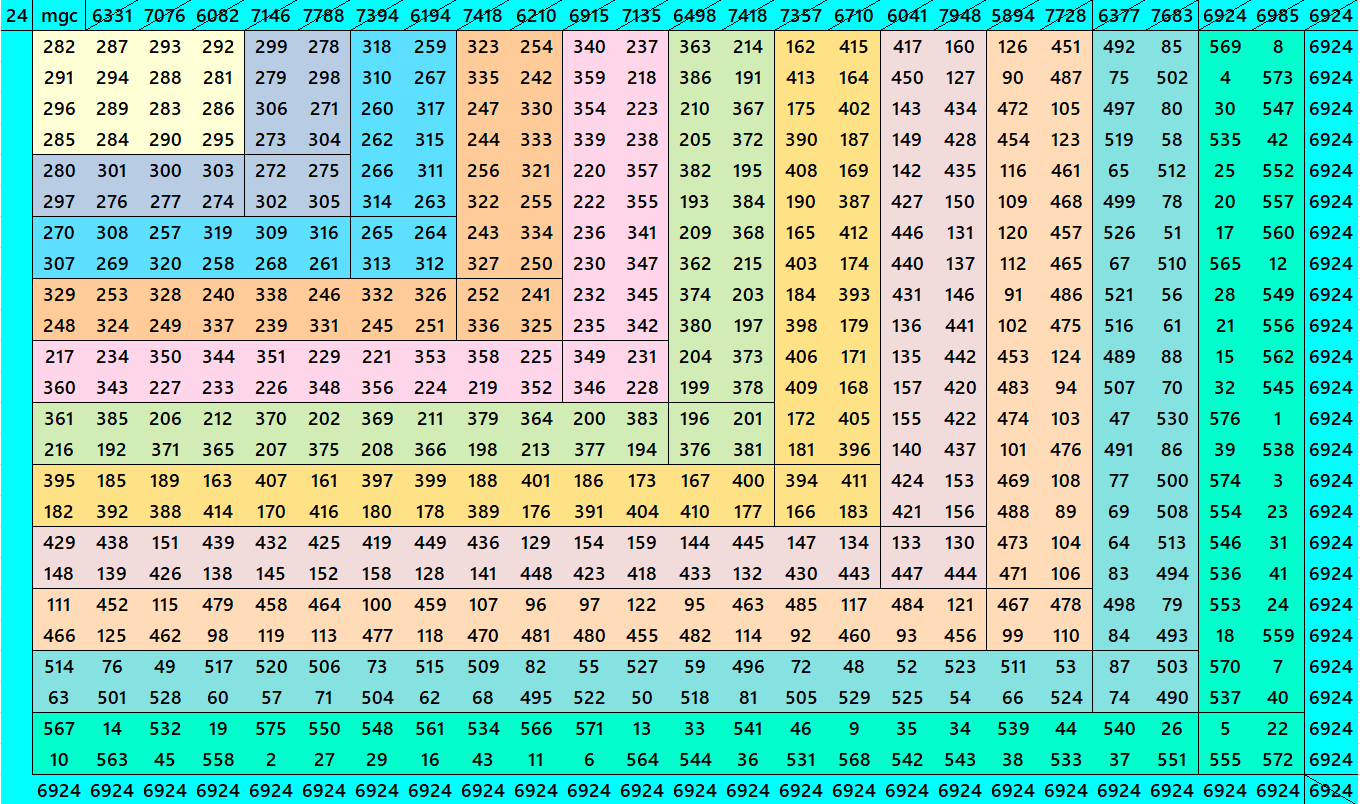
The extended study of these magic squares shall be given later on.


[…] Recently, author worked with cornered Magic Squares based on two-by-two divisions. These works can be accessed at the following links:1. Inder Jeet Taneja, Cornered Magic Squares of Orders 5 to 102. Inder Jeet Taneja, Cornered Magic Squares of Orders 11 to 133. Inder Jeet Taneja, Cornered Magic Squares of Orders 14 to 24 […]
[…] Recently, author worked with cornered Magic Squares based on two-by-two divisions. These works can be accessed at the following links:1. Inder Jeet Taneja, Cornered Magic Squares of Orders 5 to 102. Inder Jeet Taneja, Cornered Magic Squares of Orders 11 to 133. Inder Jeet Taneja, Cornered Magic Squares of Orders 14 to 24 […]
[…] Recently, author worked with cornered Magic Squares based on two-by-two divisions. These works can be accessed at the following links:1. Inder Jeet Taneja, Cornered Magic Squares of Orders 5 to 102. Inder Jeet Taneja, Cornered Magic Squares of Orders 11 to 133. Inder Jeet Taneja, Cornered Magic Squares of Orders 14 to 24 […]
[…] Recently, author worked with cornered Magic Squares based on two-by-two divisions. These works can be accessed at the following links:1. Inder Jeet Taneja, Cornered Magic Squares of Orders 5 to 102. Inder Jeet Taneja, Cornered Magic Squares of Orders 11 to 133. Inder Jeet Taneja, Cornered Magic Squares of Orders 14 to 24 […]
[…] Recently, author worked with cornered Magic Squares based on two-by-two divisions. These works can be accessed at the following links:1. Inder Jeet Taneja, Cornered Magic Squares of Orders 5 to 102. Inder Jeet Taneja, Cornered Magic Squares of Orders 11 to 133. Inder Jeet Taneja, Cornered Magic Squares of Orders 14 to 24 […]
[…] Inder J. Taneja, Cornered Magic Squares of Orders 14 to 24, Zenodo, June 03, 2023, pp. 1-39, https://doi.org/10.5281/zenodo.8000471.Site Link: Cornered Magic Squares of Orders 14 to 24. […]
[…] Recently, author worked with cornered Magic Squares based on two-by-two divisions. These works can be accessed at the following links:1. Inder Jeet Taneja, Cornered Magic Squares of Orders 5 to 102. Inder Jeet Taneja, Cornered Magic Squares of Orders 11 to 133. Inder Jeet Taneja, Cornered Magic Squares of Orders 14 to 24 […]
[…] Recently, author worked with cornered Magic Squares based on two-by-two divisions. These works can be accessed at the following links:1. Inder Jeet Taneja, Cornered Magic Squares of Orders 5 to 102. Inder Jeet Taneja, Cornered Magic Squares of Orders 11 to 133. Inder Jeet Taneja, Cornered Magic Squares of Orders 14 to 24 […]
[…] Recently, author worked with cornered Magic Squares based on two-by-two divisions. These works can be accessed at the following links:1. Inder Jeet Taneja, Cornered Magic Squares of Orders 5 to 10.2. Inder Jeet Taneja, Cornered Magic Squares of Orders 11 to 13.3. Inder Jeet Taneja, Cornered Magic Squares of Orders 14 to 24. […]
[…] We observe that the above study of even order blocks starting from 4. Recently, author studied the double digit or two digits borders resulting in interesting magic squares. These studies can be accessed at the following link:1. Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.2. Two Digits Bordered Magic Squares of Orders 28 and 32.3. Two digits Bordered Magic Squares of Order 36.4. Two digits Bordered Magic Squares of Order 40.The work is for the order of type 4k+2, where k>1, i.e., for the orders 10, 14, 18, 22, 26 and 30 can be access at the following links:1. Two digits Bordered Magic Squares of Orders 10, 14, 18 and 22.2. Two digits Bordered Magic Squares of Orders 26 and 30.3. Two Digits Bordered Magic Squares of Orders 28 and 32.Some studies towards cornered magic squares are also made. See the following links:1. Cornered Magic Squares of Orders 5 to 10.2. Cornered Magic Squares of Orders 11 to 13.3. Cornered Magic Squares of Orders 14 to 24. […]
[…] We observe that the above study of even order blocks starting from 4. Recently, author studied the double digit or two digits borders resulting in interesting magic squares. These studies can be accessed at the following link:1. Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.2. Two Digits Bordered Magic Squares of Orders 28 and 32.3. Two digits Bordered Magic Squares of Order 36.4. Two digits Bordered Magic Squares of Order 40.The work is for the order of type 4k+2, where k>1, i.e., for the orders 10, 14, 18, 22, 26 and 30 can be access at the following links:1. Two digits Bordered Magic Squares of Orders 10, 14, 18 and 22.2. Two digits Bordered Magic Squares of Orders 26 and 30.3. Two Digits Bordered Magic Squares of Orders 28 and 32.Some studies towards cornered magic squares are also made. See the following links:1. Cornered Magic Squares of Orders 5 to 10.2. Cornered Magic Squares of Orders 11 to 13.3. Cornered Magic Squares of Orders 14 to 24. […]
[…] We observe that the above study of even order blocks starting from 4. Recently, author studied the double digit or two digits borders resulting in interesting magic squares. These studies can be accessed at the following link:1. Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.2. Two Digits Bordered Magic Squares of Orders 28 and 32.3. Two digits Bordered Magic Squares of Order 36.4. Two digits Bordered Magic Squares of Order 40.The work is for the order of type 4k+2, where k>1, i.e., for the orders 10, 14, 18, 22, 26, 28, 30 and 32 can be access at the following links:1. Two digits Bordered Magic Squares of Orders 10, 14, 18 and 22.2. Two digits Bordered Magic Squares of Orders 26 and 30.3. Two Digits Bordered Magic Squares of Orders 28 and 32.Some studies towards cornered magic squares are also made. See the following links:1. Cornered Magic Squares of Orders 5 to 10.2. Cornered Magic Squares of Orders 11 to 13.3. Cornered Magic Squares of Orders 14 to 24. […]
[…] We observe that the above study of even order blocks starting from 4. Recently, author studied the double digit or two digits borders resulting in interesting magic squares. These studies can be accessed at the following link:1. Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.2. Two Digits Bordered Magic Squares of Orders 28 and 32.3. Two digits Bordered Magic Squares of Order 36.4. Two digits Bordered Magic Squares of Order 40.The work is for the order of type 4k+2, where k>1, i.e., for the orders 10, 14, 18, 22, 26, 28, 30 and 32 can be access at the following links:1. Two digits Bordered Magic Squares of Orders 10, 14, 18 and 22.2. Two digits Bordered Magic Squares of Orders 26 and 30.3. Two Digits Bordered Magic Squares of Orders 28 and 32.Some studies towards cornered magic squares are also made. See the following links:1. Cornered Magic Squares of Orders 5 to 10.2. Cornered Magic Squares of Orders 11 to 13.3. Cornered Magic Squares of Orders 14 to 24. […]
[…] Recently, author also studied the double digits borders resulting in interesting magic squares. These studies can be accessed at the following link:1. Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.2. Two Digits Bordered Magic Squares of Orders 28 and 32.3. Two digits Bordered Magic Squares of Order 36.4. Two digits Bordered Magic Squares of Order 40.The work is for the order of type 4k+2, where k>1, i.e., for the orders 10, 14, 18, 22, 26, 28, 30 and 32 can be access at the following links:1. Two digits Bordered Magic Squares of Orders 10, 14, 18 and 22.2. Two digits Bordered Magic Squares of Orders 26 and 30.3. Two Digits Bordered Magic Squares of Orders 28 and 32.Some studies towards cornered magic squares are also made. See the following links:1. Cornered Magic Squares of Orders 5 to 10.2. Cornered Magic Squares of Orders 11 to 13.3. Cornered Magic Squares of Orders 14 to 24. […]
[…] links:1. Cornered Magic Squares of Orders 5 to 10.2. Cornered Magic Squares of Orders 11 to 13.3. Cornered Magic Squares of Orders 14 to 24.Below are examples of bordered magic squares multiples of order 15. These examples are only for the […]
[…] links:1. Cornered Magic Squares of Orders 5 to 10.2. Cornered Magic Squares of Orders 11 to 13.3. Cornered Magic Squares of Orders 14 to 24.Below are examples of bordered magic squares multiples of order 13 up to order 52. Total we worked […]
[…] We observe that the above study of even order blocks starting from 4. Recently, author studied the double digit or two digits borders resulting in interesting magic squares. These studies can be accessed at the following link:1. Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.2. Two Digits Bordered Magic Squares of Orders 28 and 32.3. Two digits Bordered Magic Squares of Order 36.4. Two digits Bordered Magic Squares of Order 40.The work is for the order of type 4k+2, where k>1, i.e., for the orders 10, 14, 18, 22, 26 and 30 can be access at the following links:1. Two digits Bordered Magic Squares of Orders 10, 14, 18 and 22.2. Two digits Bordered Magic Squares of Orders 26 and 30.3. Two Digits Bordered Magic Squares of Orders 28 and 32.Some studies towards cornered magic squares are also made. See the following links:1. Cornered Magic Squares of Orders 5 to 10.2. Cornered Magic Squares of Orders 11 to 13.3. Cornered Magic Squares of Orders 14 to 24. […]
[…] We observe that the above study of even order blocks starting from 4. Recently, author studied the double digit or two digits borders resulting in interesting magic squares. These studies can be accessed at the following link:1. Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.2. Two Digits Bordered Magic Squares of Orders 28 and 32.3. Two digits Bordered Magic Squares of Order 36.4. Two digits Bordered Magic Squares of Order 40.The work is for the order of type 4k+2, where k>1, i.e., for the orders 10, 14, 18, 22, 26, 28, 30 and 32 can be access at the following links:1. Two digits Bordered Magic Squares of Orders 10, 14, 18 and 22.2. Two digits Bordered Magic Squares of Orders 26 and 30.3. Two Digits Bordered Magic Squares of Orders 28 and 32.Some studies towards cornered magic squares are also made. See the following links:1. Cornered Magic Squares of Orders 5 to 10.2. Cornered Magic Squares of Orders 11 to 13.3. Cornered Magic Squares of Orders 14 to 24. […]
[…] Inder J. Taneja, Cornered Magic Squares of Orders 14 to 24, Zenodo, June 03, 2023, pp. 1-39, https://doi.org/10.5281/zenodo.8000471.Site Link: Cornered Magic Squares of Orders 14 to 24. […]