Recently, author worked with cornered Magic Squares based on two-by-two divisions. These works can be accessed at the following links:
1. Inder Jeet Taneja, Cornered Magic Squares of Orders 5 to 10
2. Inder Jeet Taneja, Cornered Magic Squares of Orders 11 to 13
3. Inder Jeet Taneja, Cornered Magic Squares of Orders 14 to 24
Also, the author worked on even order double digits bordered magic squares. This works starts from order 8 and goes up to order 40. See below the links:
The work for order of type 4k, k=1, 2, 3, … i.e., for orders 8, 12, 16, 20, 24, 28, 32, 36 and 40:
1. Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.
2. Two Digits Bordered Magic Squares of Orders 28 and 32.
3. Two digits Bordered Magic Squares of Order 36.
4. Two digits Bordered Magic Squares of Order 40.
The work is for the order of type 4k+2, k=1, 2, 3, …, i.e., for the orders 10, 14, 18, 22, 26, 30, 34 and 38:
1. Two digits Bordered Magic Squares of Orders 10, 14, 18 and 22.
2. Two digits Bordered Magic Squares of Orders 26 and 30.
3. Two digits Bordered Magic Squares of Order 34.
4. Two digits Bordered Magic Squares of Order 38.
This work is for magic square of order 25. It includes three types of magic squares:
1. Traditional centered magic squares.
2. Bordered with Magic Squares of Order 5.
3. Double digits bordered magic squares.
For the previous work on odd orders from 3 to 23 see the following links:
1. Inder J. Taneja, Odd Order Magic Squares: Orders 3 to 15.
2. Inder J. Taneja, Magic Squares of Orders 17 and 19.
3. Inder J. Taneja, Magic Squares of Order 21.
4. Inder J. Taneja, Magic Squares of Order 23.
Previous to other orders, here we don’t have cornered magic squares of order 25. Anyway, these are as embedded here up to order 21. Double digits magic squares can also be constructed using software, the reader can follow H. White’s site: Magic Squares. This work can also be accessed online at:
Inder J. Taneja, Magic Squares of Order 25, Zenodo, June 15, 2023, pp. 1-27, https://doi.org/10.5281/zenodo.8043228.
To have better idea, pdf file of total 300 magic squares of order 23 is attached for download.
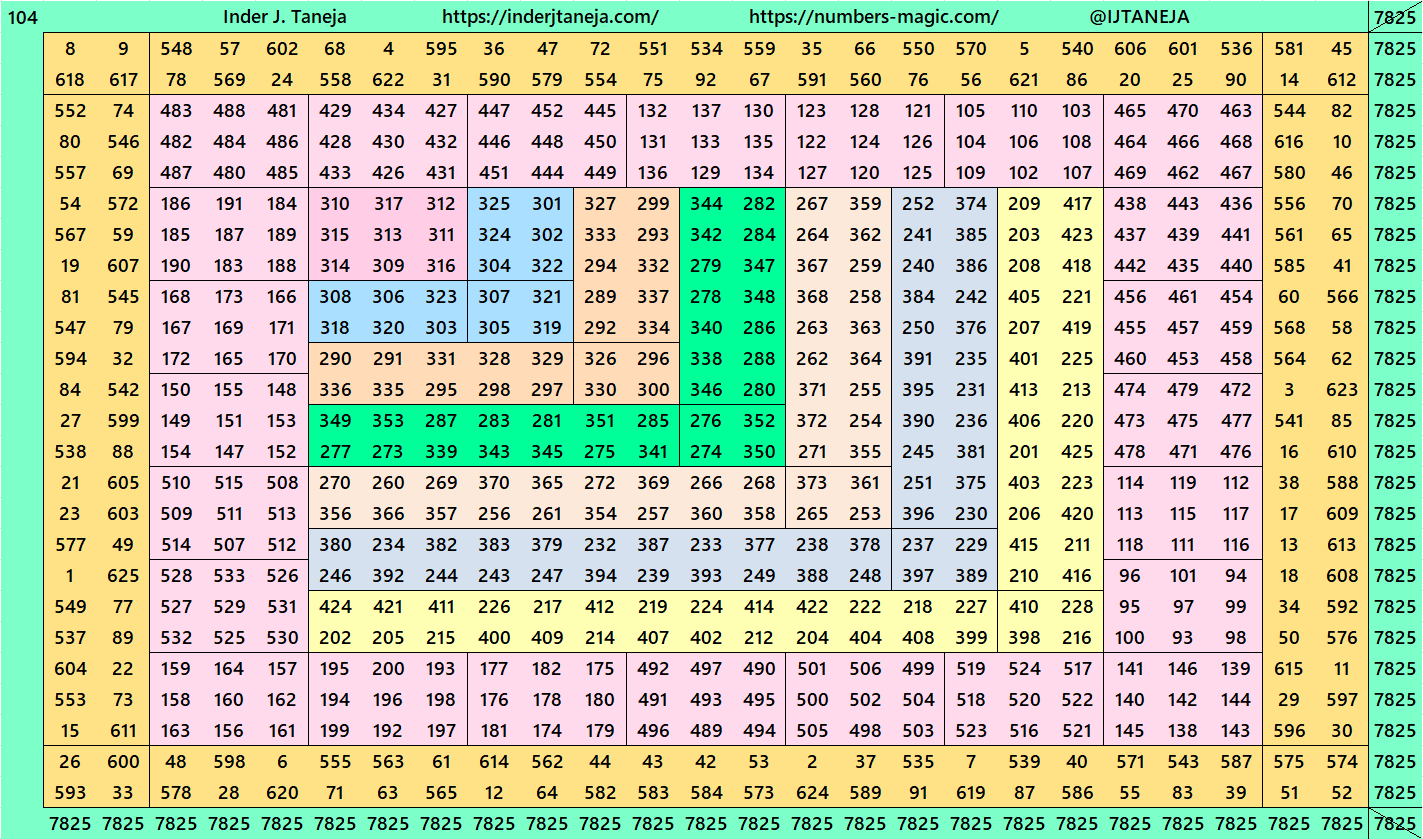
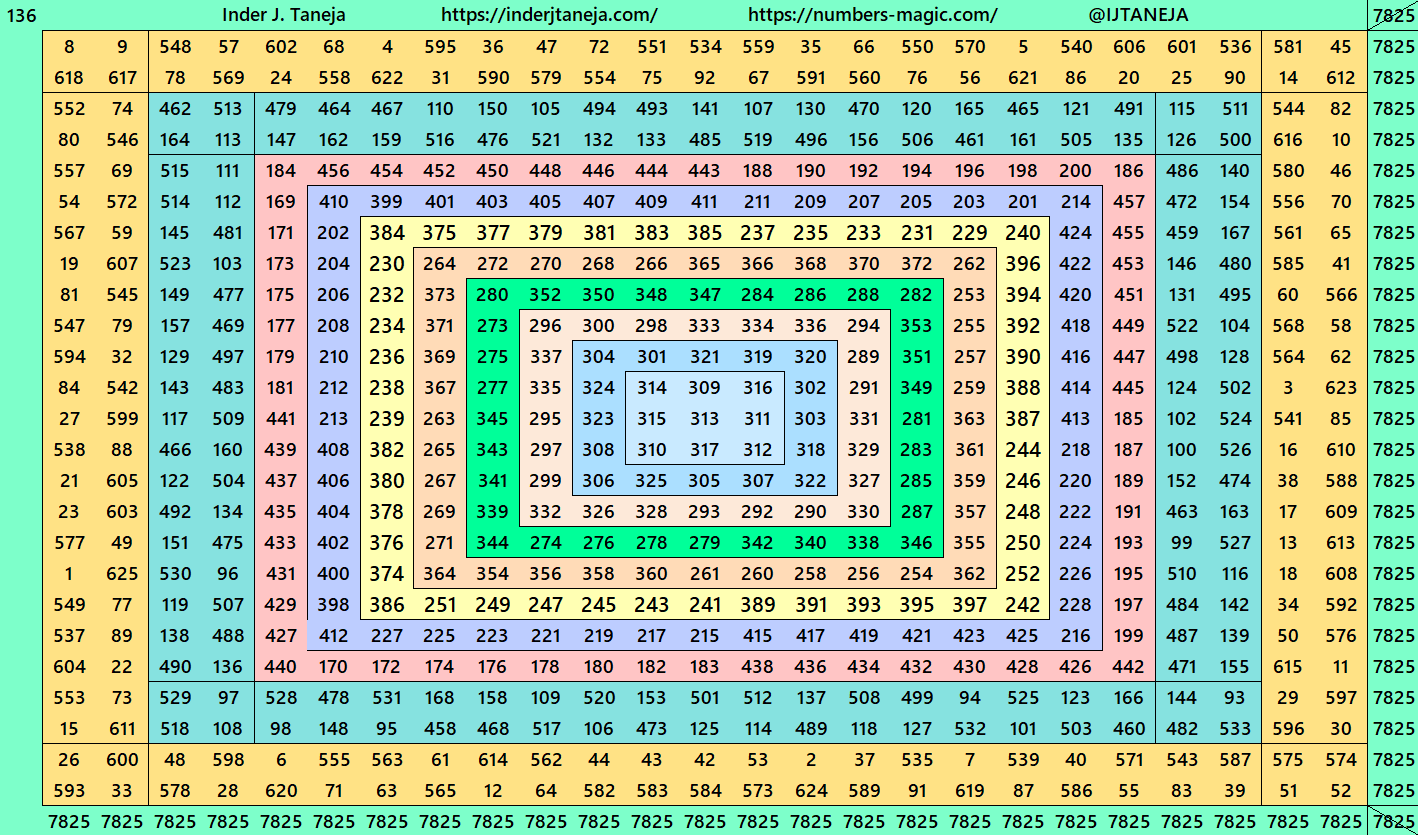
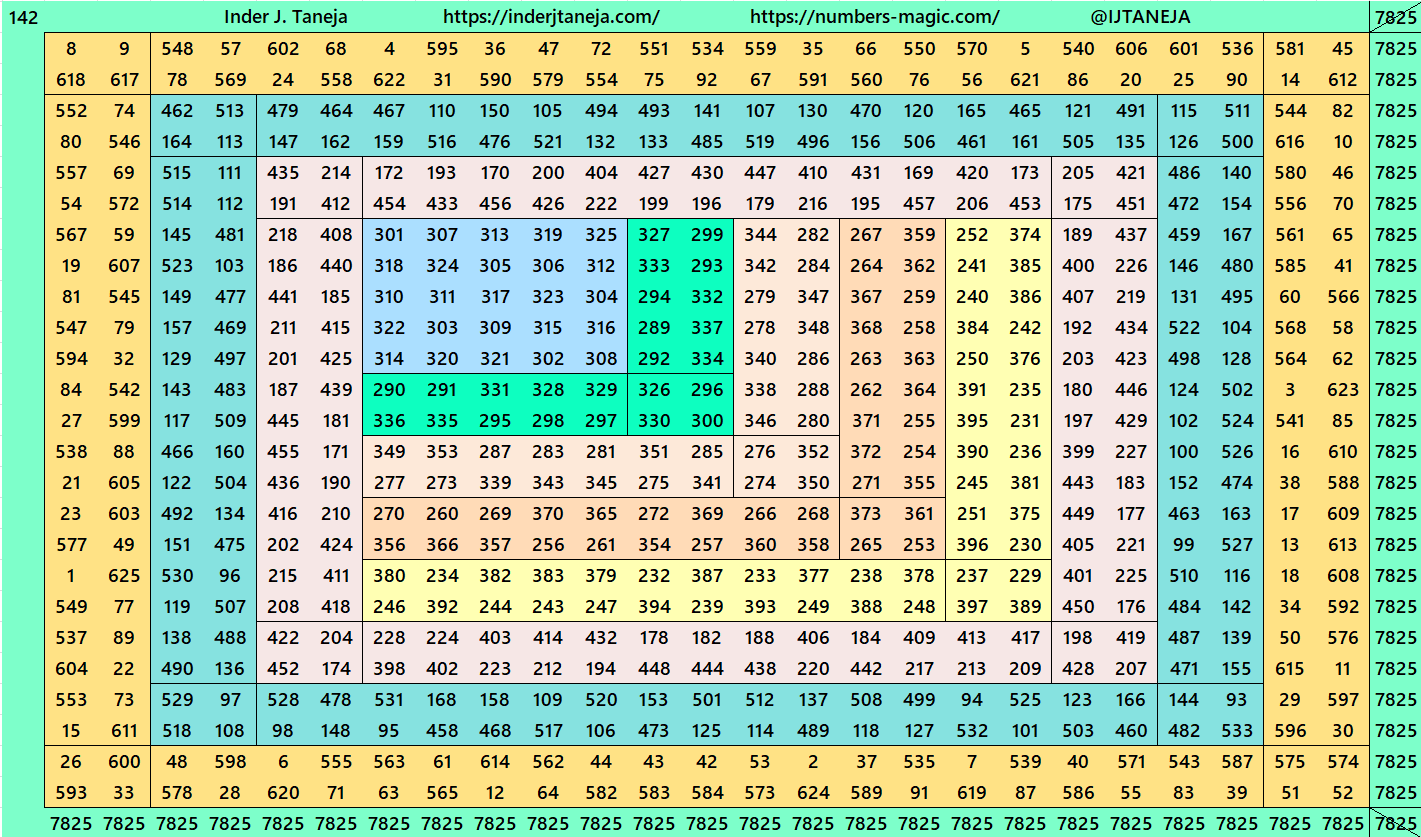
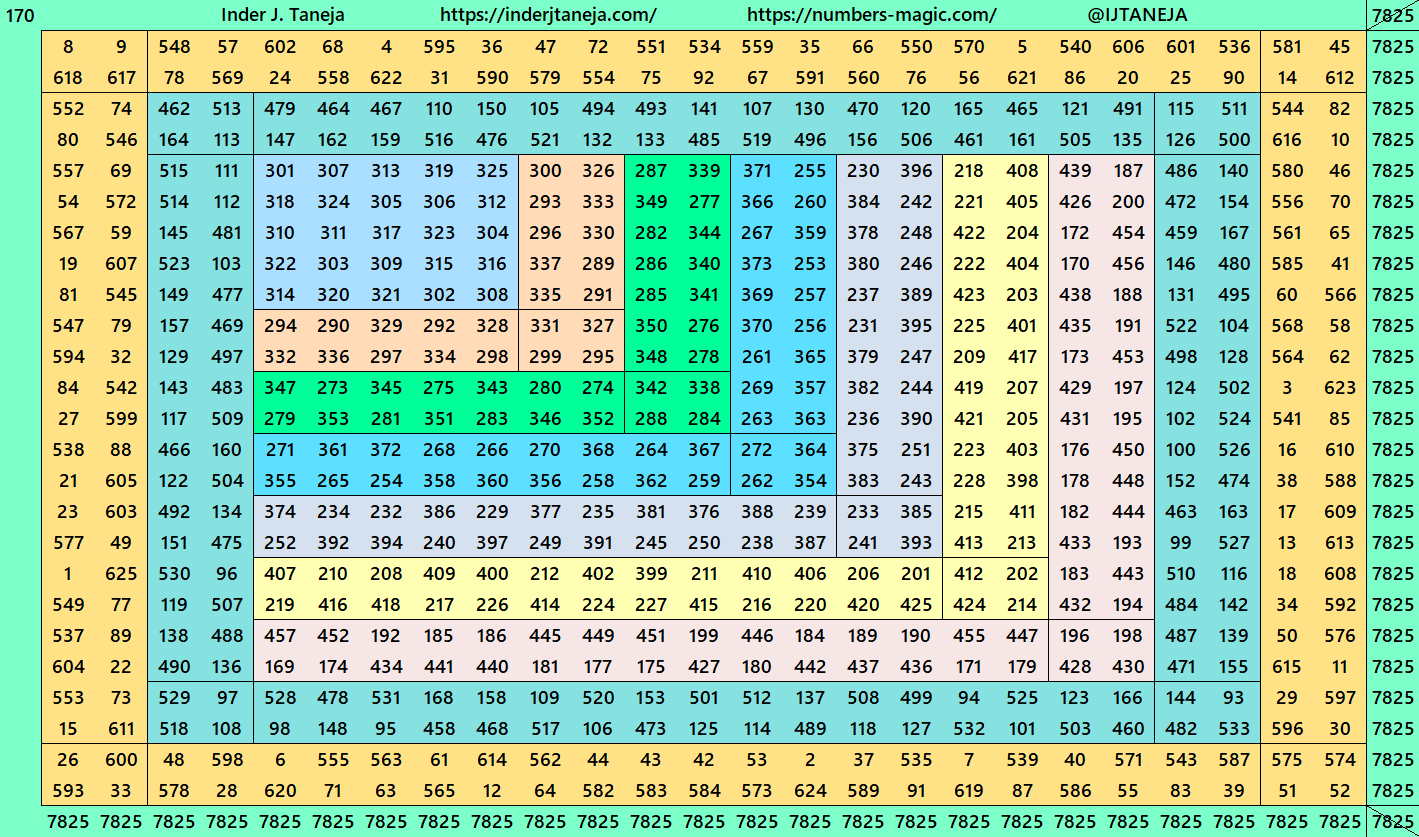
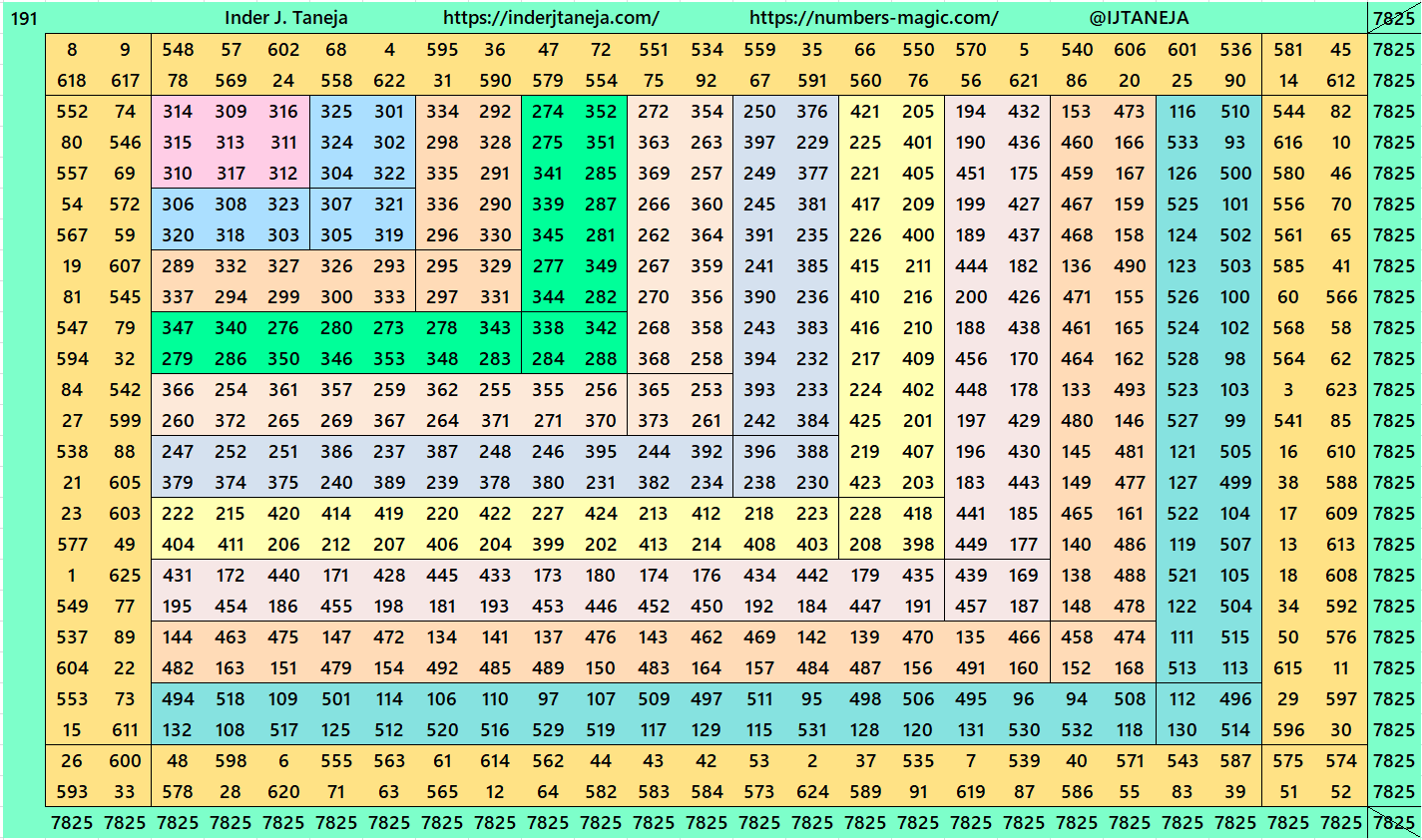
Magic Squares of Order 25
As explained above, the construction of magic squares of order 25 are of three types. Below are examples in each case. The second type is with two possibilities. One with magic squares of order 5 and another with bordered magic squares of order 5. More studies on bordered magic squares multiples of order 5 can be seen at author’s site link:
Inder J. Taneja, Block-Wise Bordered and Pan diagonal Magic Squares Multiples of 5
1. Traditional Centered Magic Squares
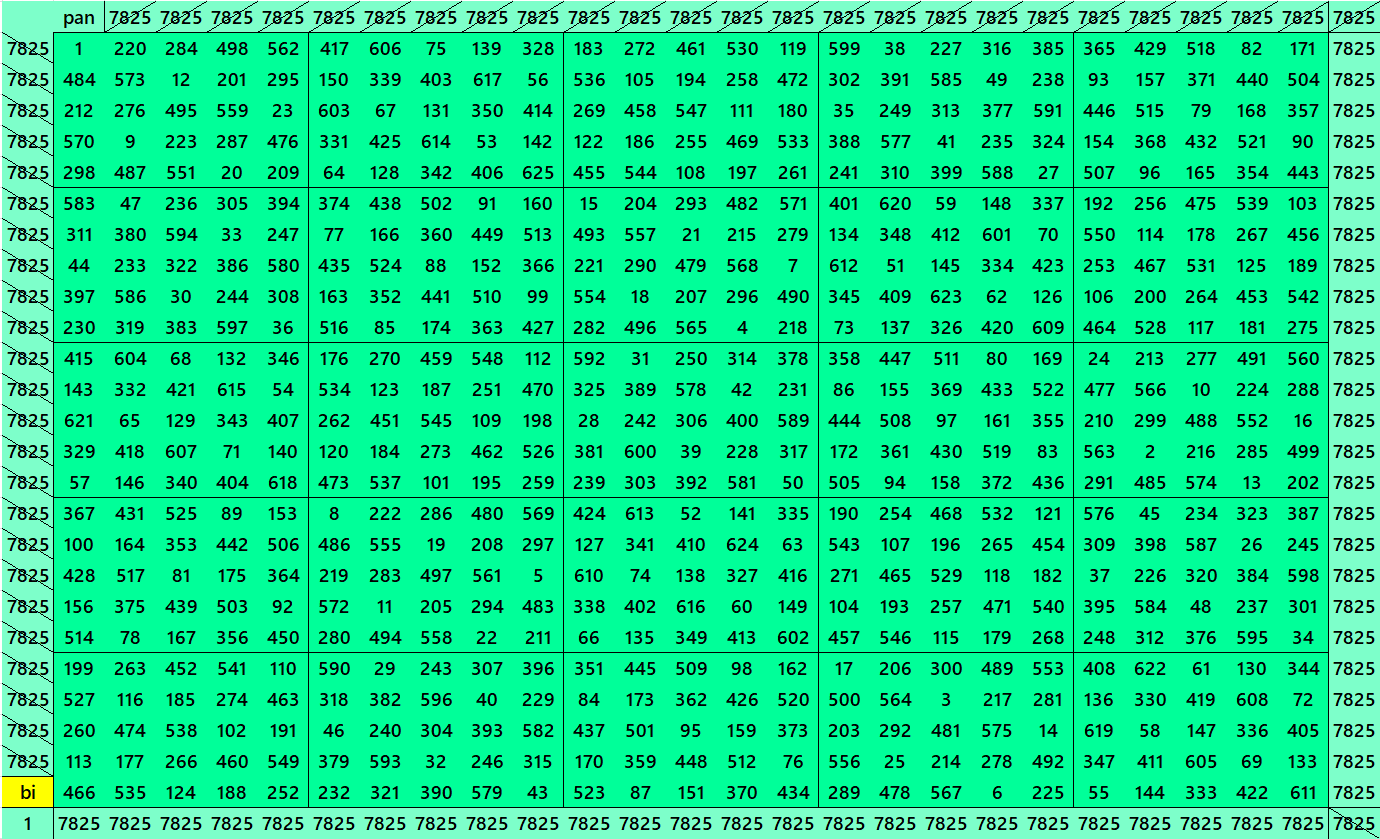
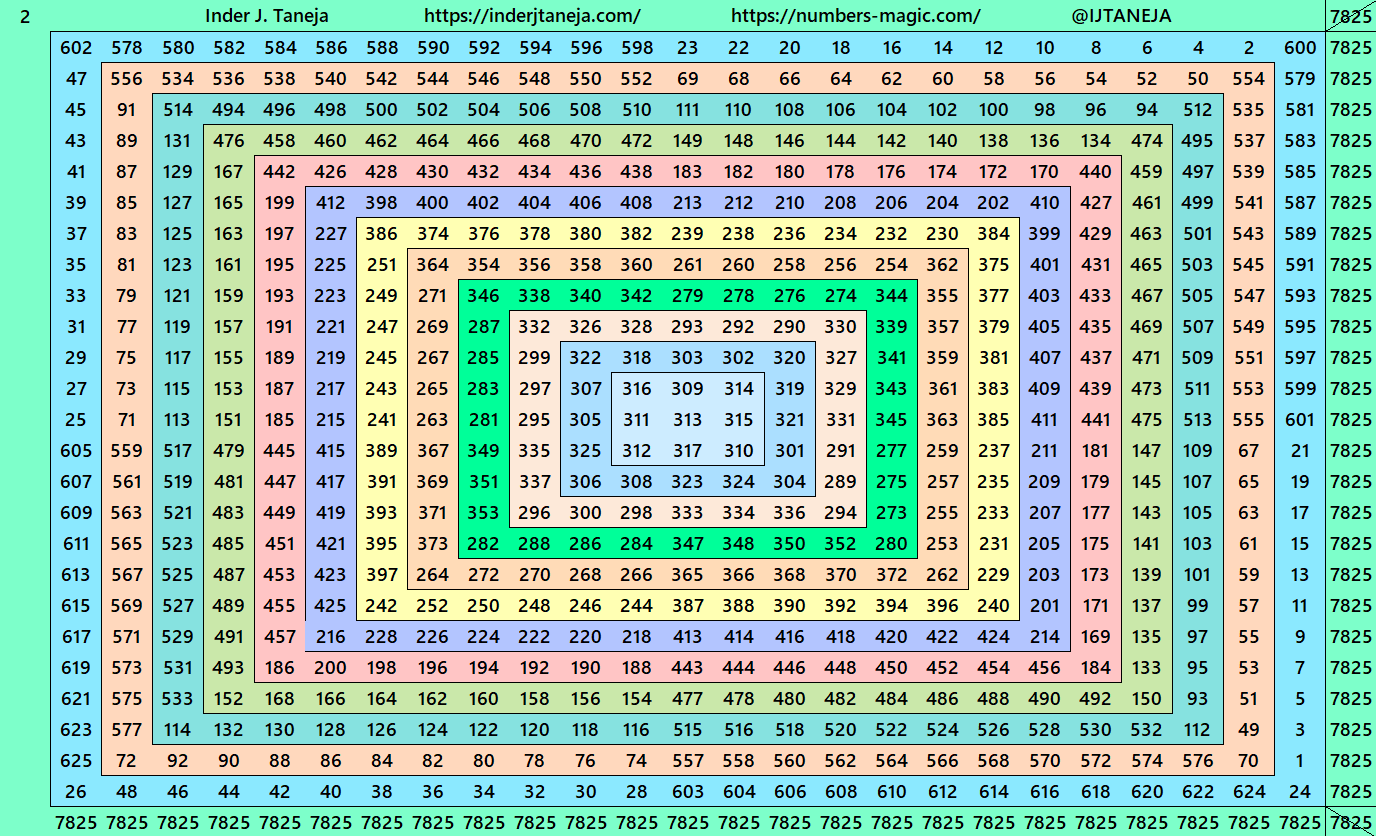
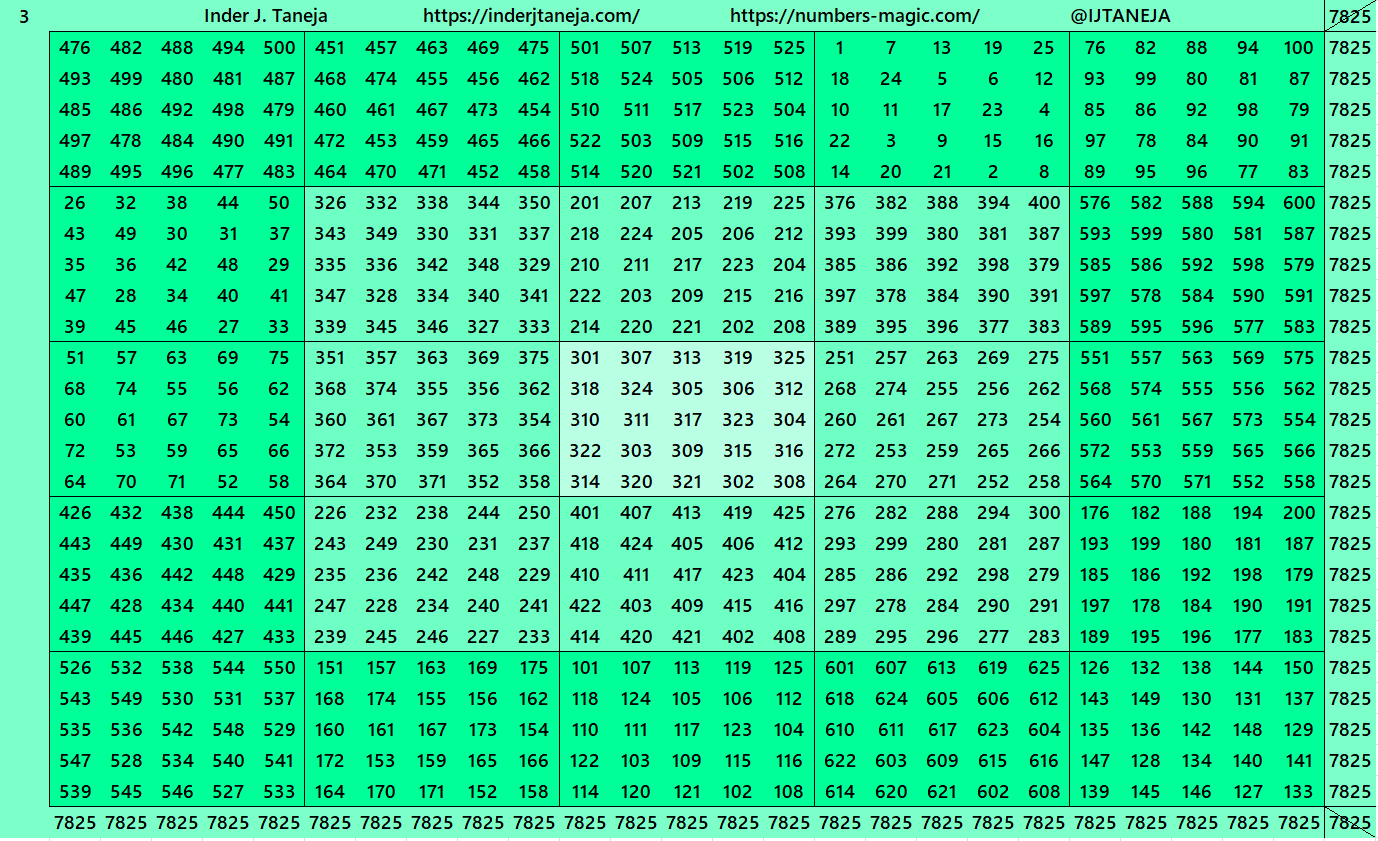
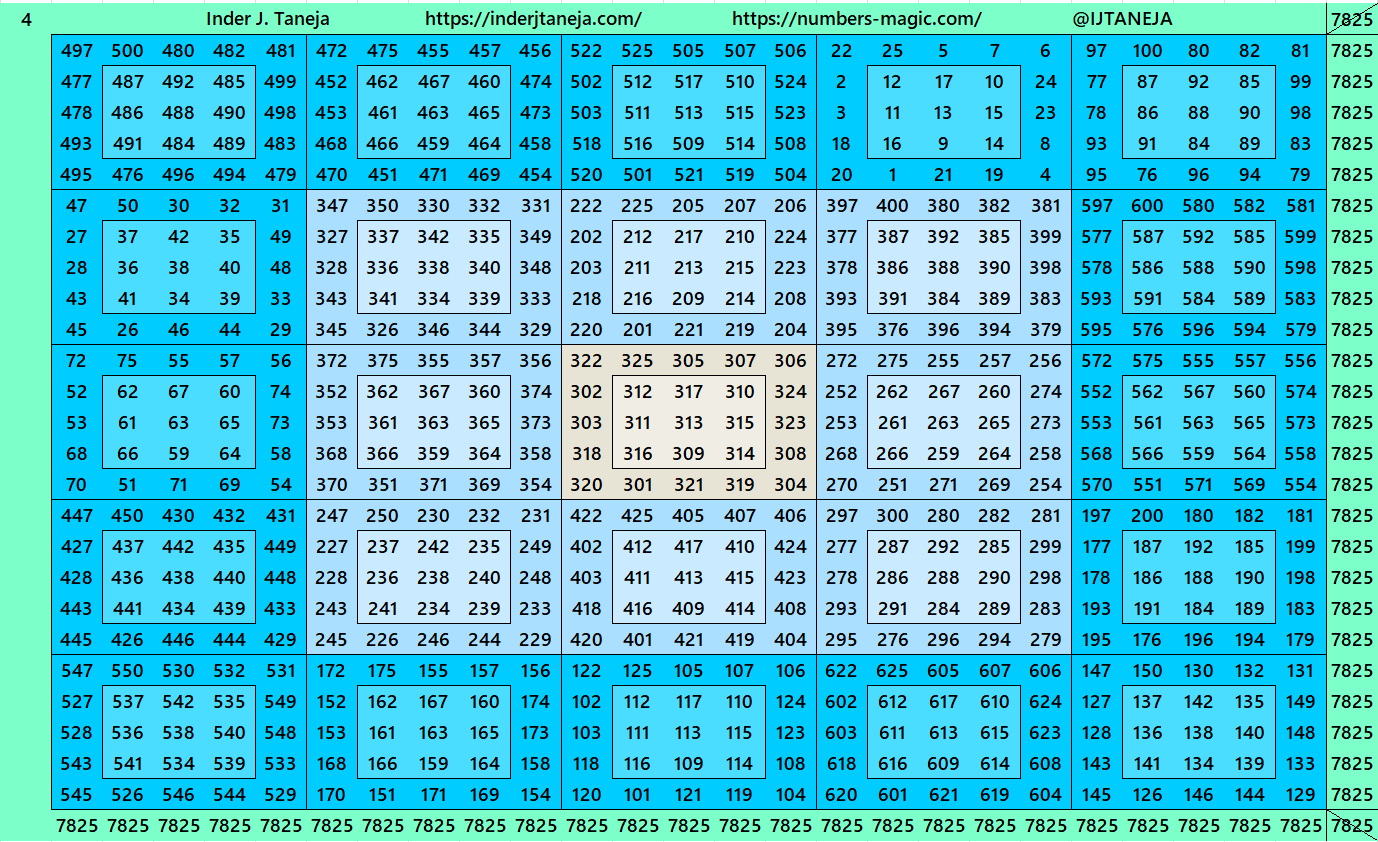
The first example is pandiagonal bimagic squares of order 25.
2. Part 1: Bordered with Magic Squares of Order 5
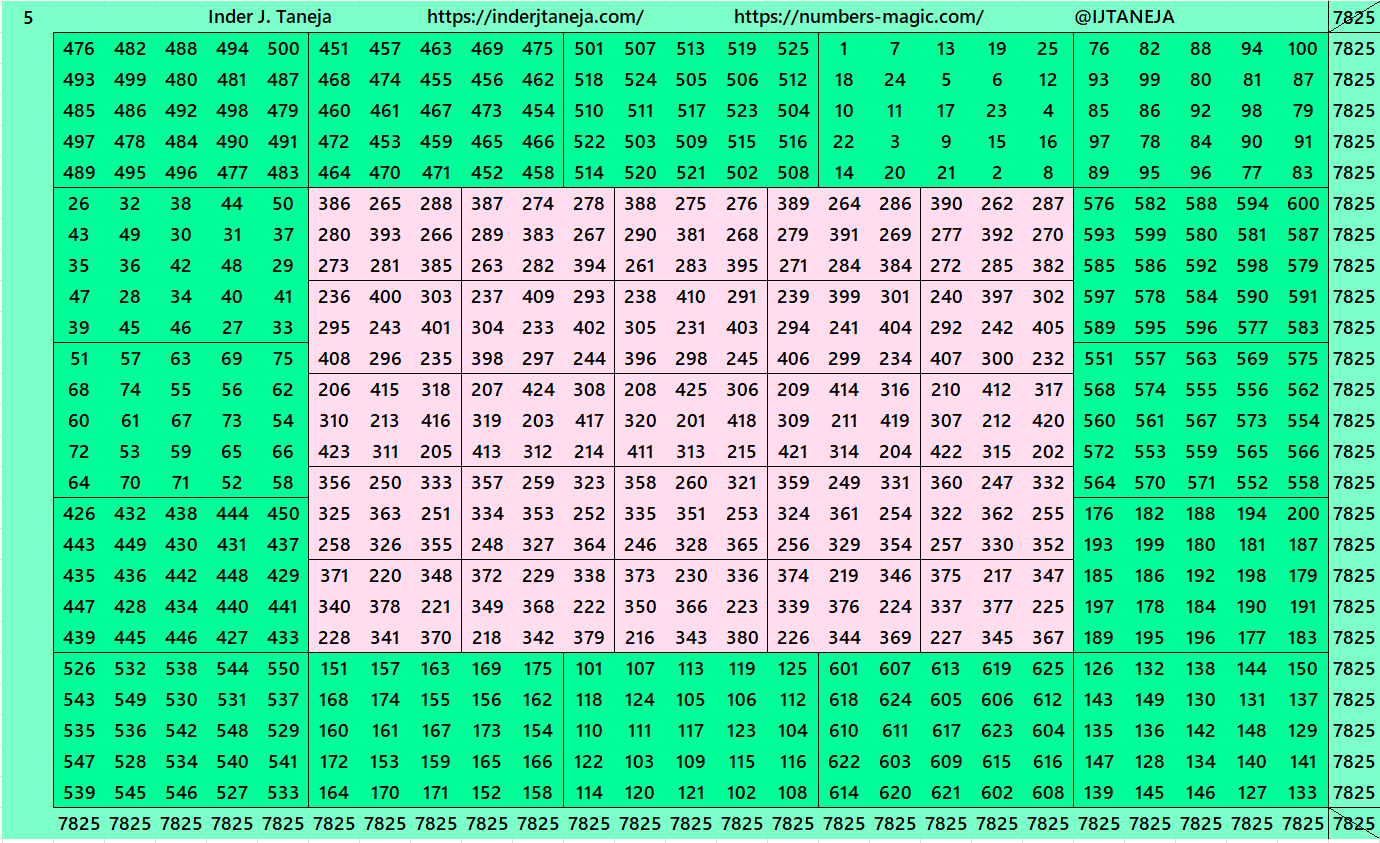
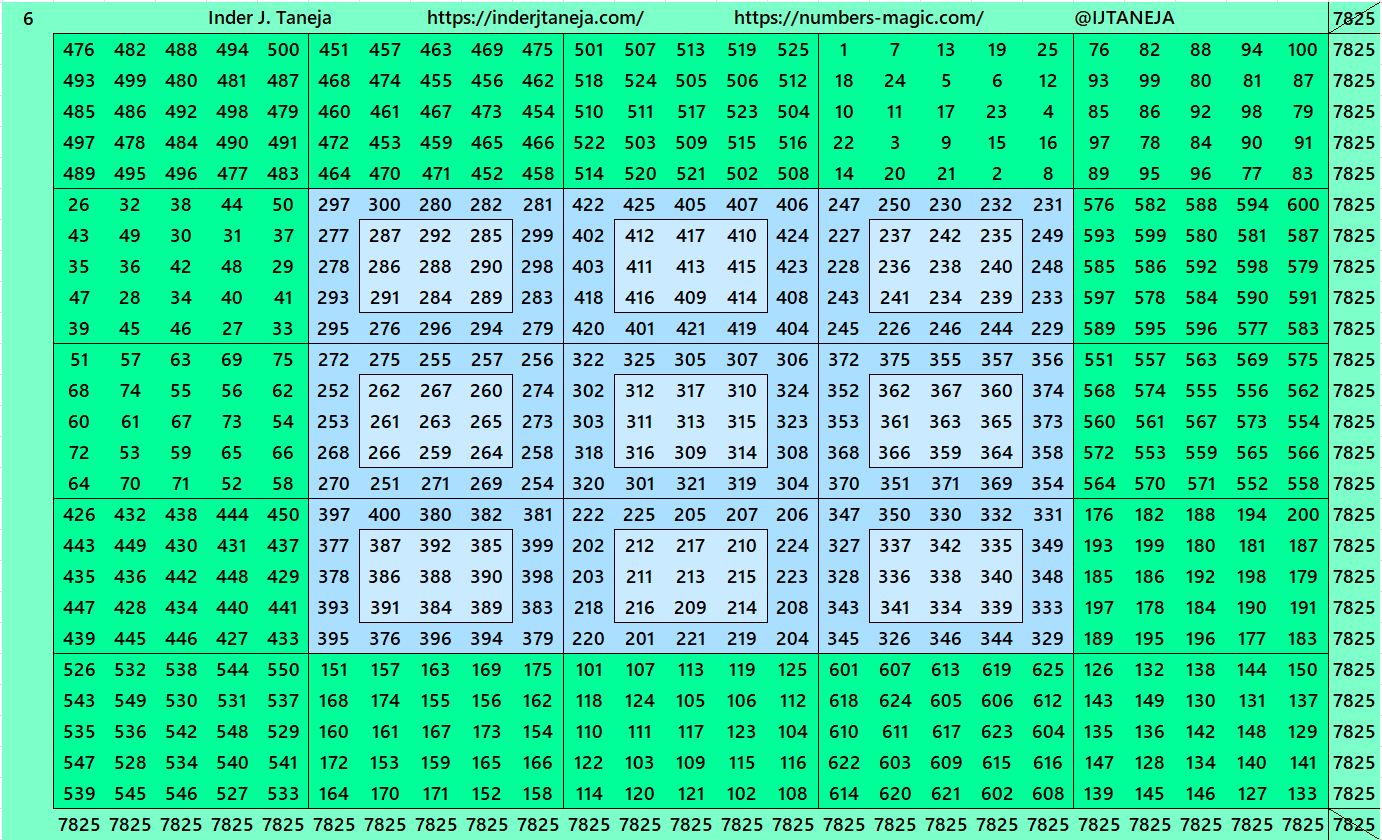
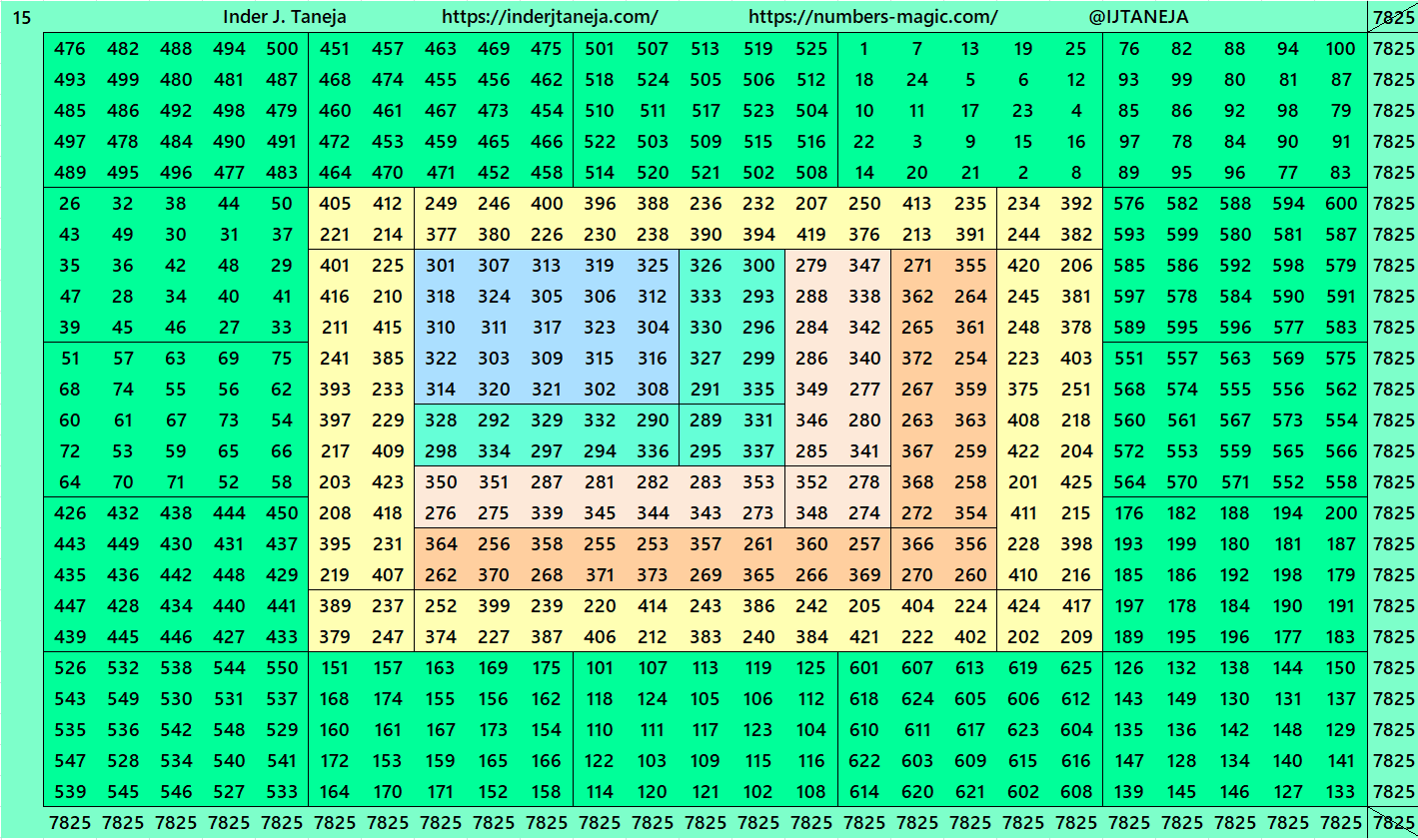
2. Part 2: Bordered with Bordered Magic Squares of Order 5
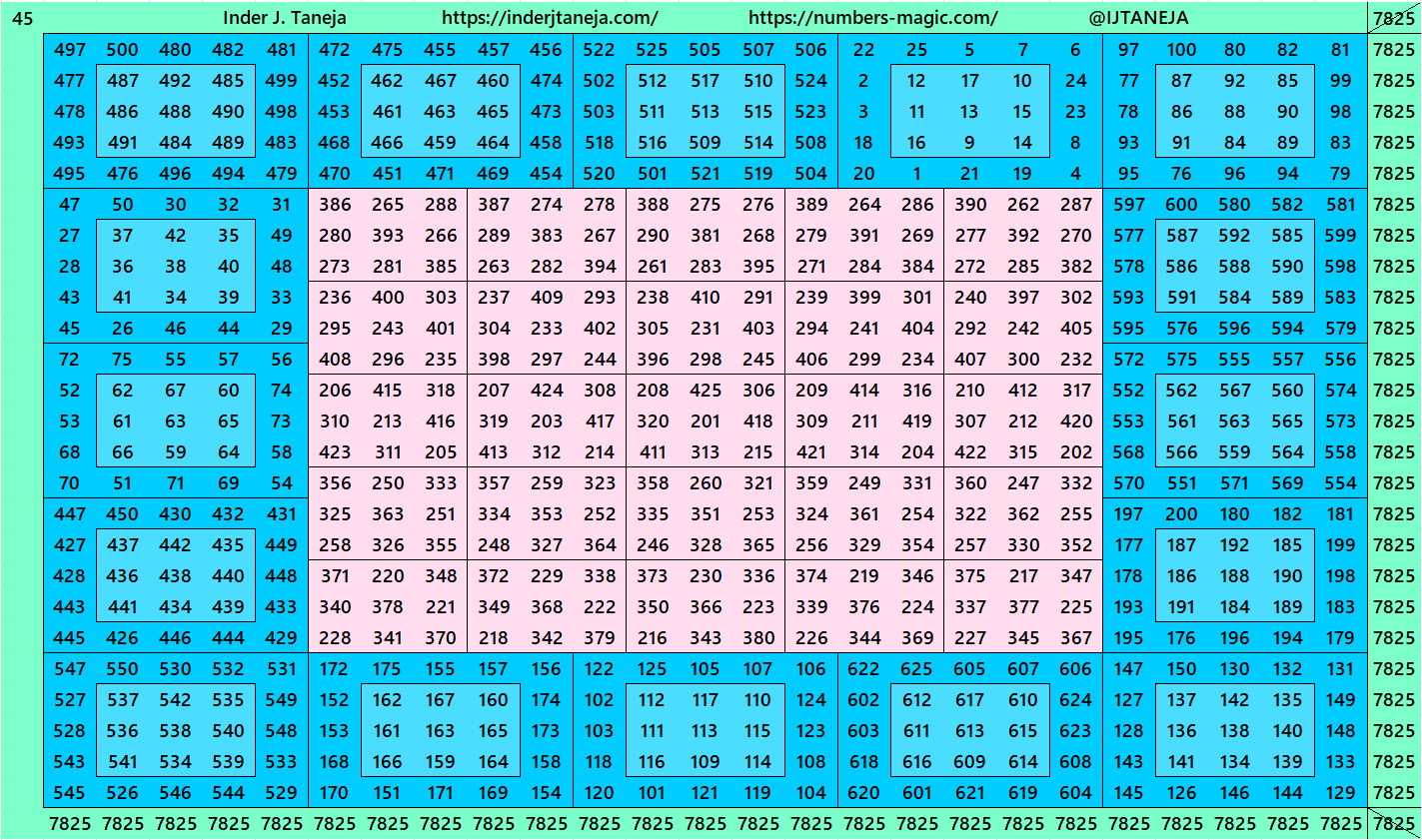
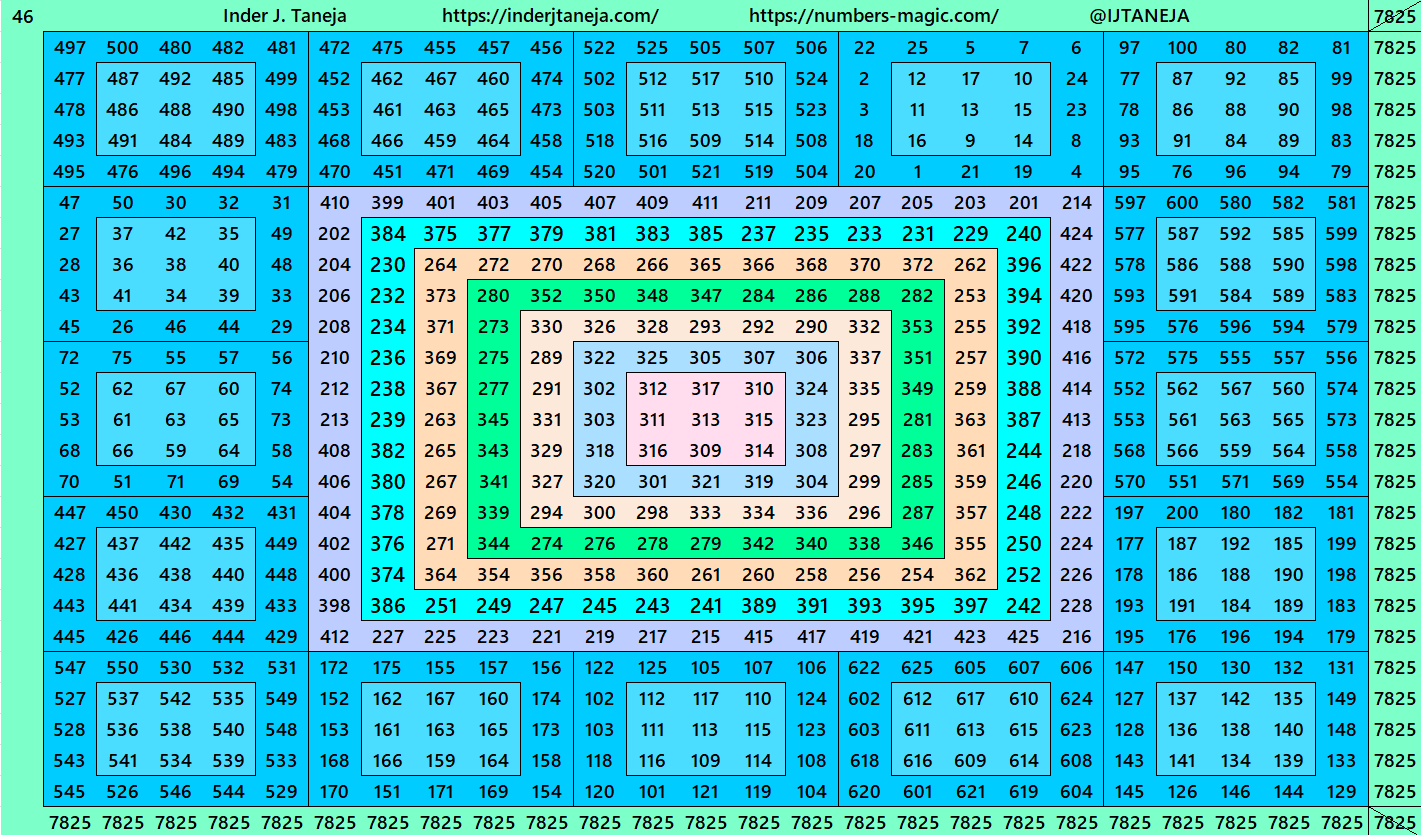
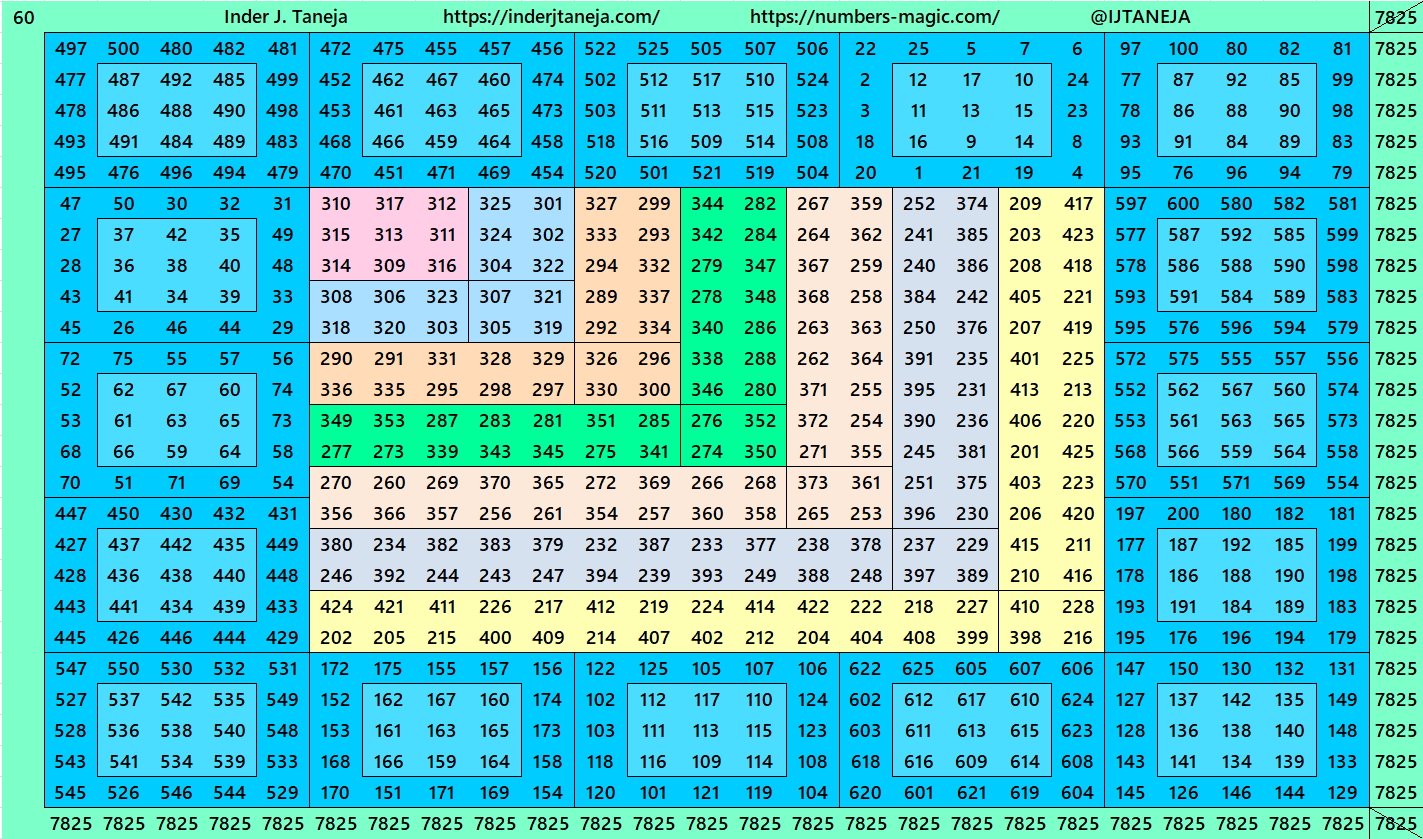
3. Double Digits Bordered Magic Squares
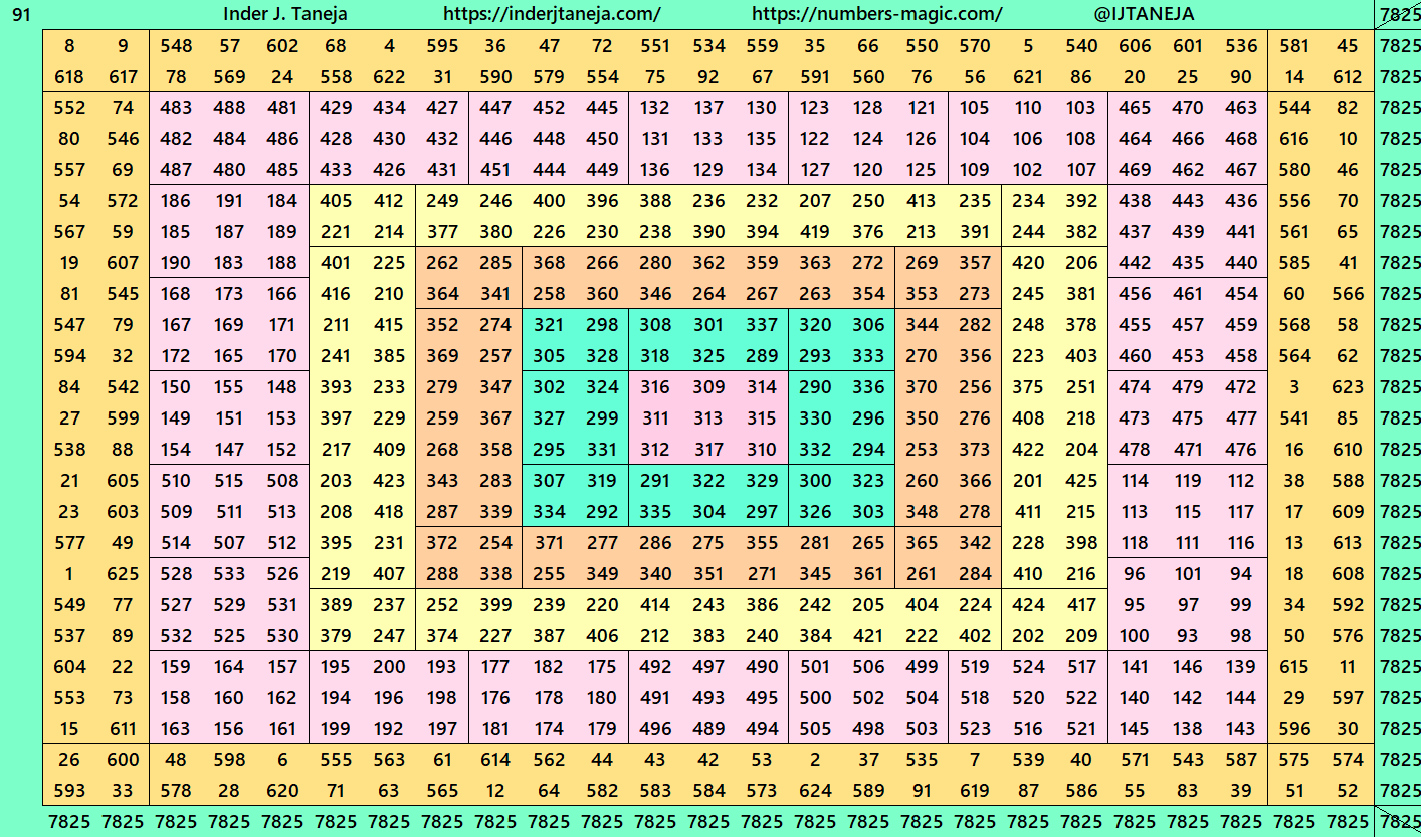
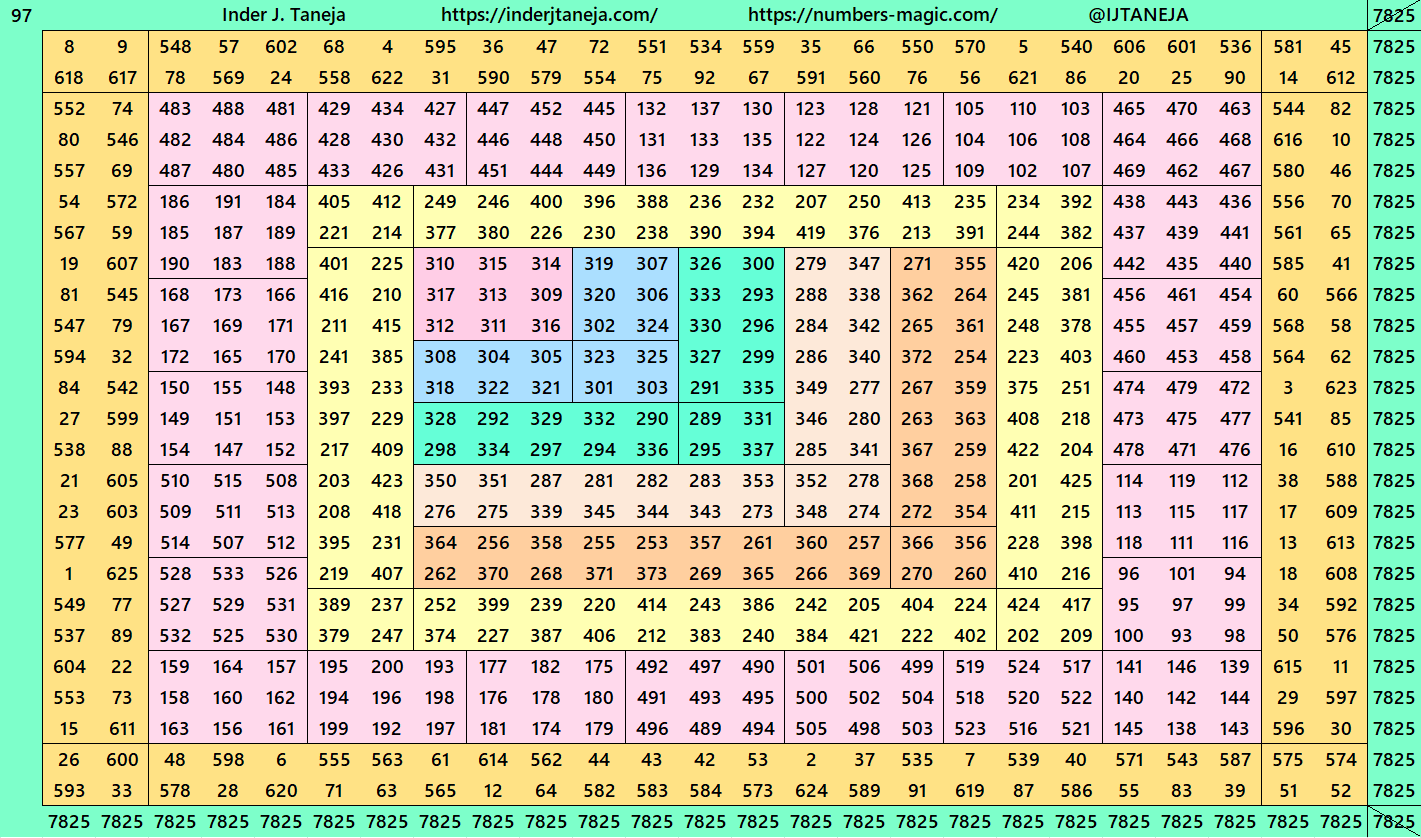


[…] Inder J. Taneja, Site Links: Magic Squares of Order 25. […]