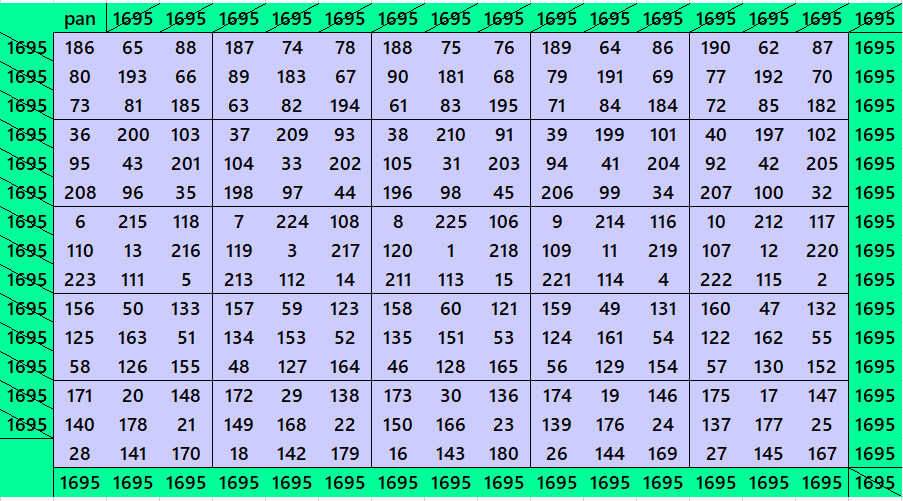
During past years author worked with block-wise bordered magic squares multiples of even number blocks. This means, multiples of 4, 6, 8, etc. These works can be accessed at the following links.
1. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 4
2. Block-Wise Bordered Magic Squares Multiples of Magic and Bordered Magic Squares of Order 6
3. Block-Wise Bordered Magic Squares Multiples of 8
3. Block-Wise Bordered Magic Squares Multiples of 10
4. Block-Wise Bordered Magic Squares Multiples of 12
5. Block-Wise Bordered Magic Squares Multiples of 14
The advantage in studying block-wise bordered magic squares is that when we remove external borders, still we left with magic squares with sequential entries. The bordered magic squares also have the same property. The difference is that instead of numbers here we have blocks of equal sum magic squares multiples of 14.
We observe that the above study of even order blocks starting from 4. Recently, author studied the double digit or two digits borders resulting in interesting magic squares. These studies can be accessed at the following link:
We observe that the above study of even order blocks starting from 4. Recently, author studied the double digit or two digits borders resulting in interesting magic squares. These studies can be accessed at the following link:
1. Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.
2. Two Digits Bordered Magic Squares of Orders 28 and 32.
3. Two digits Bordered Magic Squares of Order 36.
4. Two digits Bordered Magic Squares of Order 40.
The work is for the order of type 4k+2, where k>1, i.e., for the orders 10, 14, 18, 22, 26 and 30 can be access at the following links:
1. Two digits Bordered Magic Squares of Orders 10, 14, 18 and 22.
2. Two digits Bordered Magic Squares of Orders 26 and 30.
Below is a classification of bordered magic squares according to number of digits.
- Single Digit: Bordered magic squares based on single digit
- Two Digits: Bordered magic squares based on magic rectangles of order 2k (k=4, 8, 12, …).
- Three Digits: Bordered magic squares based on magic squares of order 3:
- Four Digits: Bordered magic squares based on magic squares of order 4.
- Five Digits: Bordered magic squares based on magic squares of order 5.
- Six Digits: Bordered magic squares based on magic squares of order 6, etc.
As we see that we are lacking with odd number borders. This work brings bordered magic squares multiples of 3. That means the bordered are made with different sums of magic squares of order 3. Total work is up to order 120. Whole the work with Excel file can be accessed at the following link:
- Inder J. Taneja, Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 3, Zenodo, May 05, pp. 1-29, 2023, https://doi.org/10.5281/zenodo.7898383.
- Excel file of whole the work can be accessed from the above work. Also, it given at the end of this work for download.
Below are examples of bordered magic squares multiples of order 3 up to order 36.
Block-Wise Bordered Magic Squares Multiples of 3









Pandigonal Magic Squares Multiples of 3