Revised on July 12, 2023
During past years author worked with block-wise, bordered and block-bordered magic squares. This work make connection between block-wise and bordered magic squares. We started with block-wise bordered magic squares of orders 140 and 126. Based on these two big magic squares, the inner order magic squares multiples of 14 are studied. By inner orders we understand that magic squares of orders 112, 98, 84, etc. The construction of the block-wise bordered magic squares multiples of 14 is based on equal sum blocks of magic squares of order 14. We have taken 46 different types of magic squares of order 14. The advantage in studying block-wise bordered magic squares is that when we remove external border, still we are left with magic squares with sequential entries. It is the same property of bordered magic squares with single digits. The difference is that instead of numbers here we have blocks of equal sum magic squares of order 14. For multiples of orders 4, 6, 8, 10 and 12 see the links below:
1. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 4.
2. Block-Wise Bordered Magic Squares Multiples of Magic Squares of Order 6.
3. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 8 – Revised
4. Block-Wise Bordered Magic Squares Multiples of 10 – Revised.
5. Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 12 – Revised.
This work is up to order 140. Examples below are only up to order 42. The higher order examples can be seen in Excel file attached at the end. This work also can be seen as online:
Below are few examples up to order 42 studied in this work. The work is up to order 140.
The complete excel files with 46 examples in each case are given at the end for download.
Magic Squares of Order 16
Below are few examples of magic squares of order 14. It includes bordered, double digits, cornered magic squares, etc. The complete list of 46 magic squares of order 14 is given as pdf file for download.
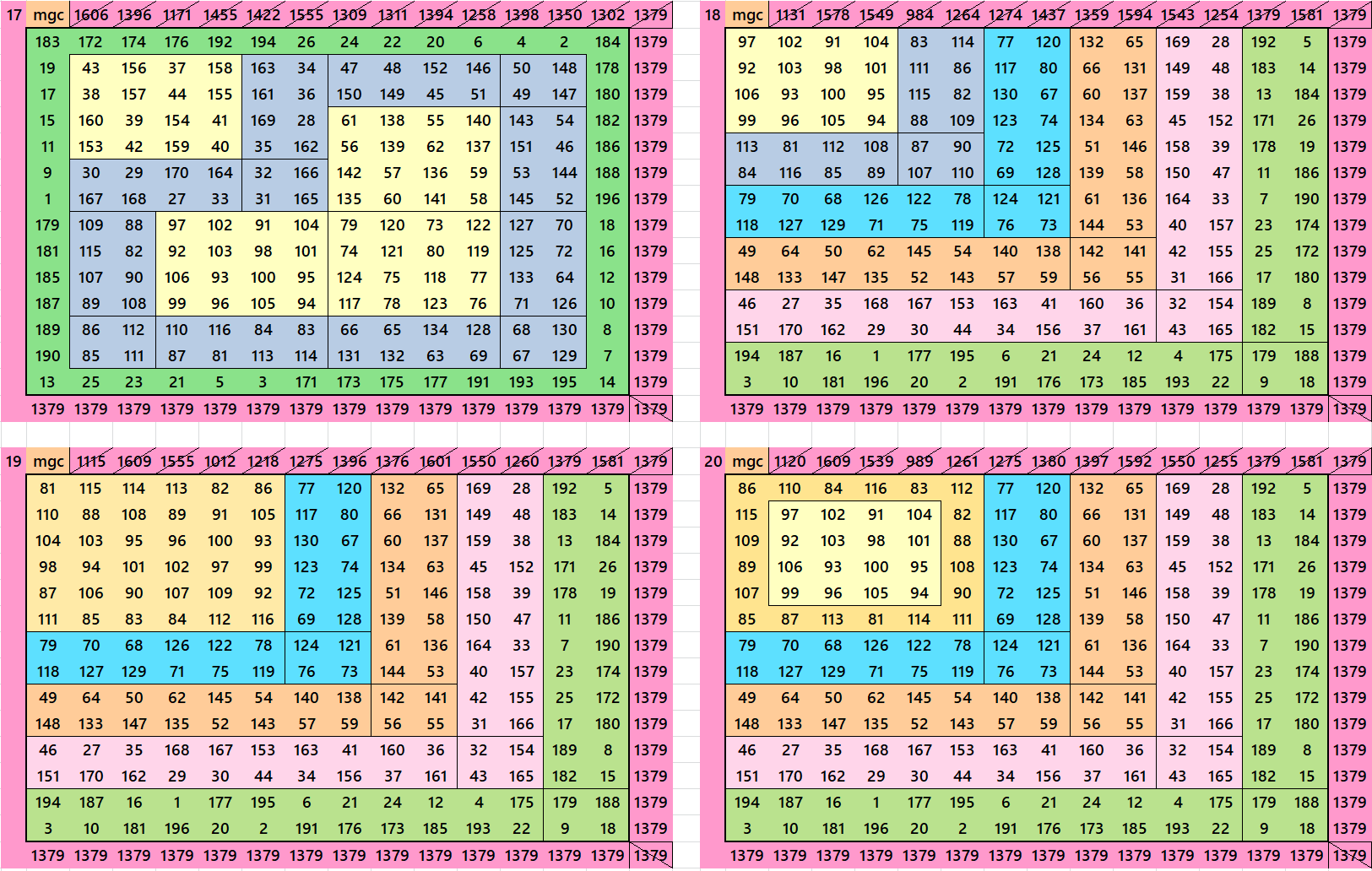
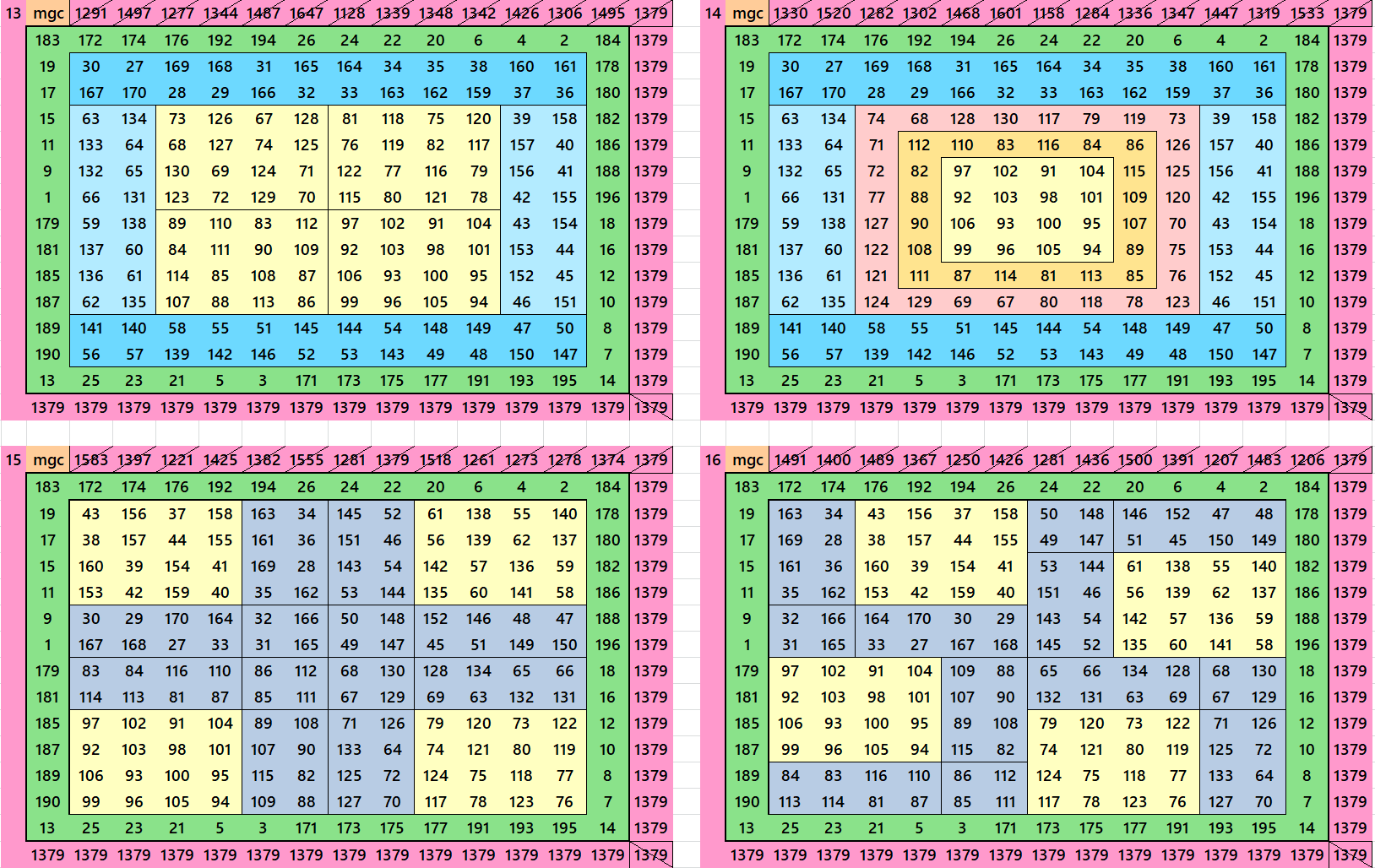
Pdf file of 46 Magic Squares of Order 14
Magic Squares of Order 28
Below are only 3 examples of magic squares of order 28. The others are given as pdf file.
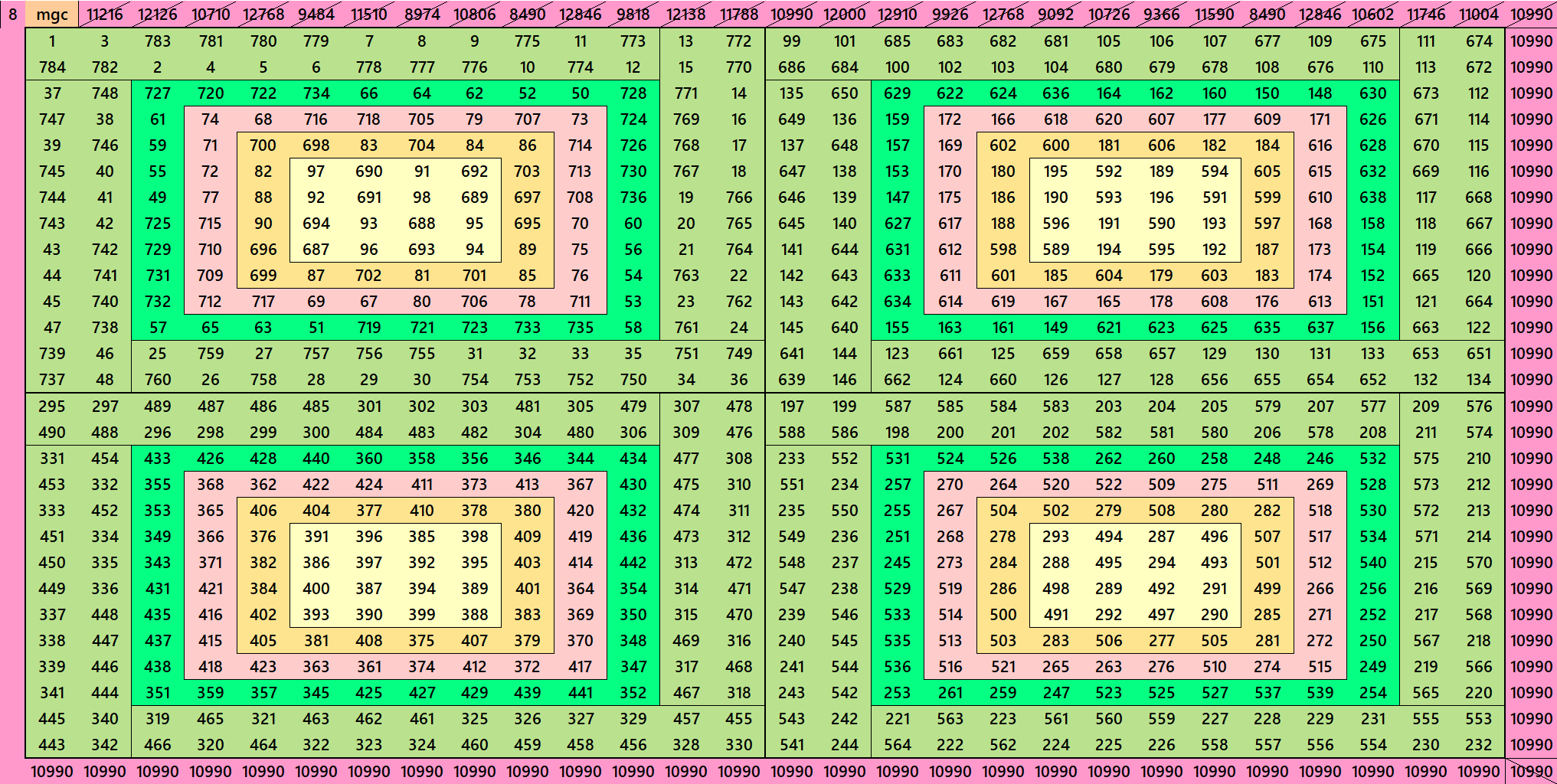
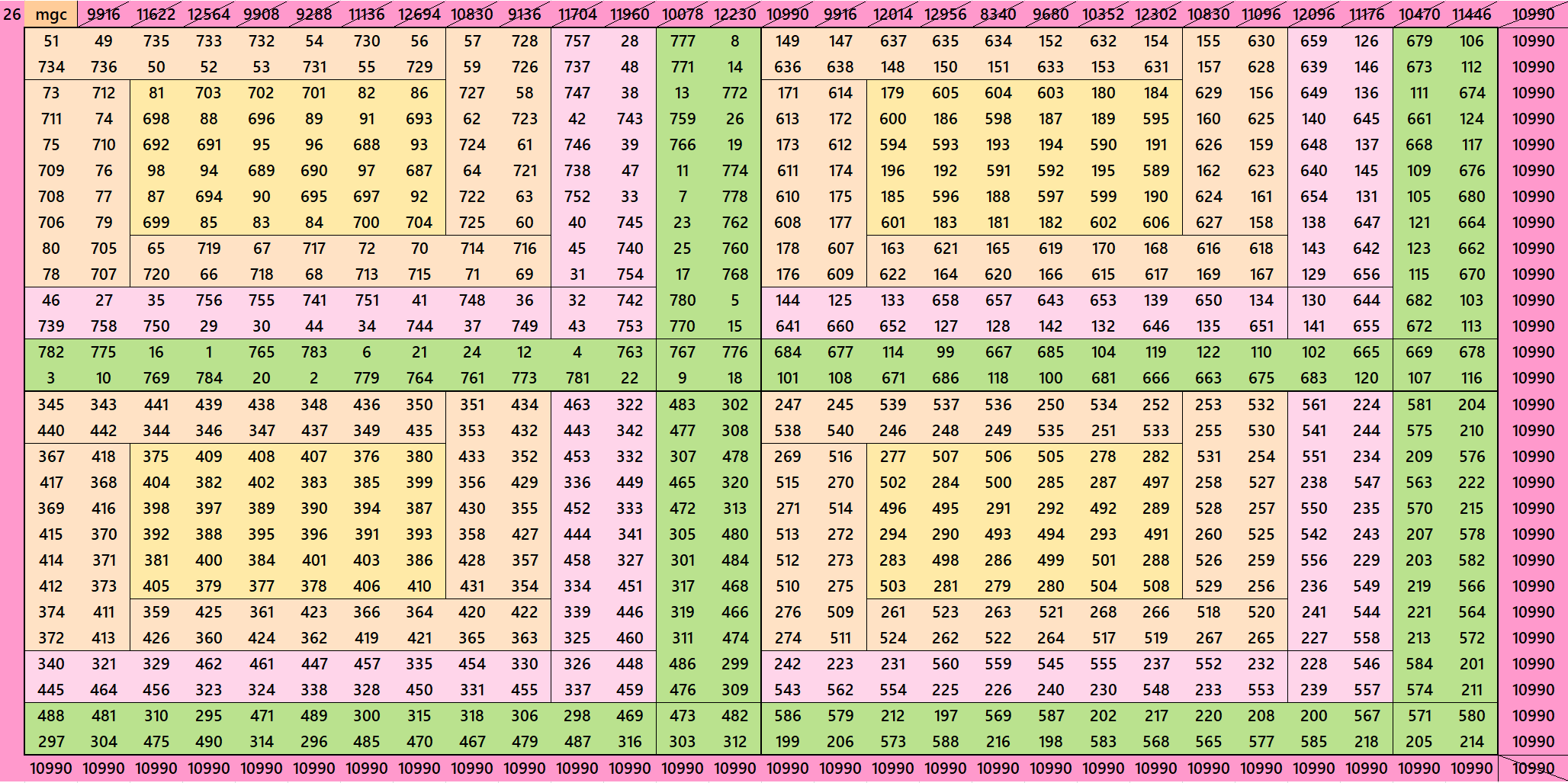
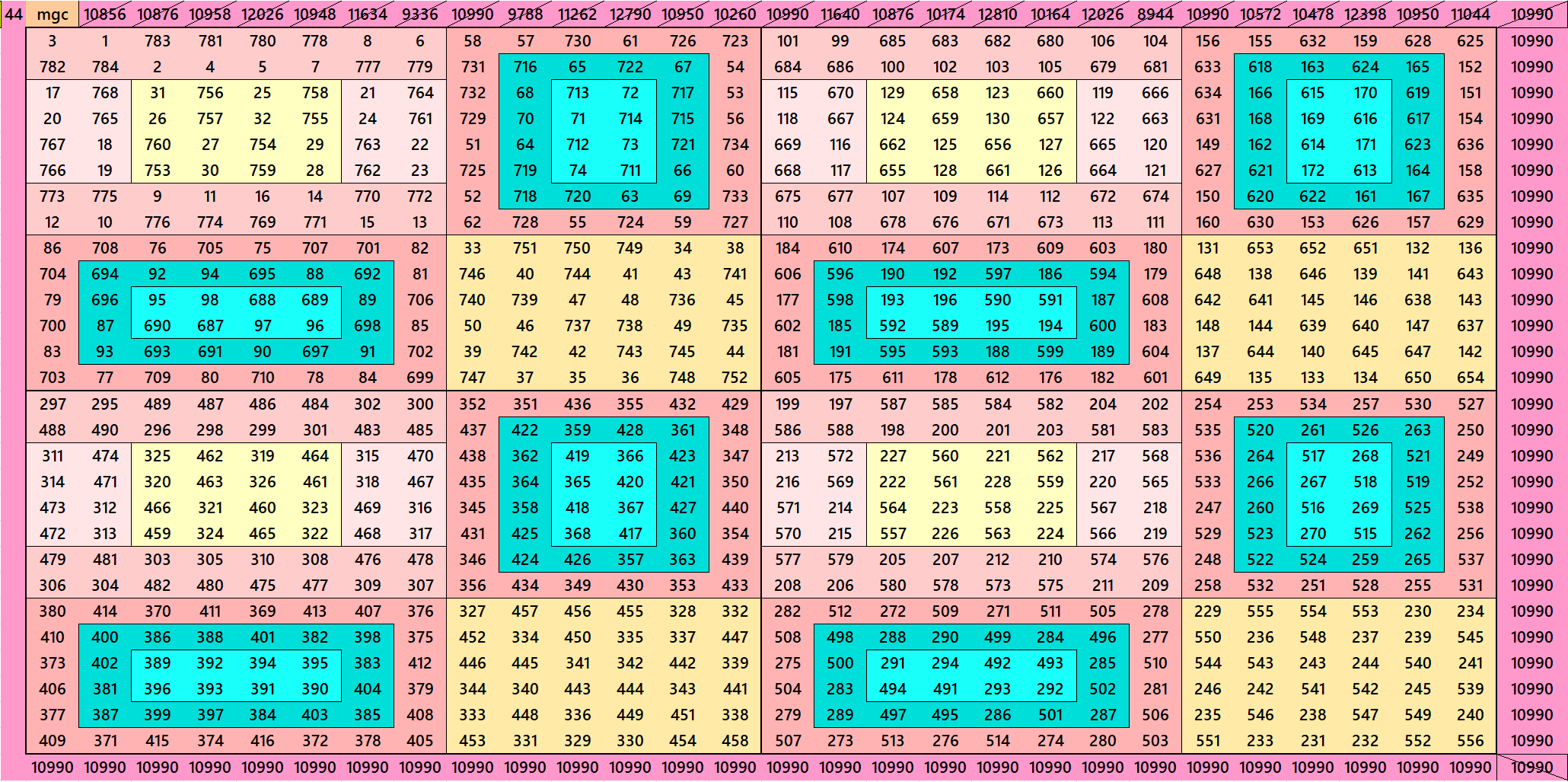
Pdf file of 46 Magic Squares of Order 28
Magic Squares of Order 42
Below are only 3 examples of magic squares of order 42. The others are given as pdf file.
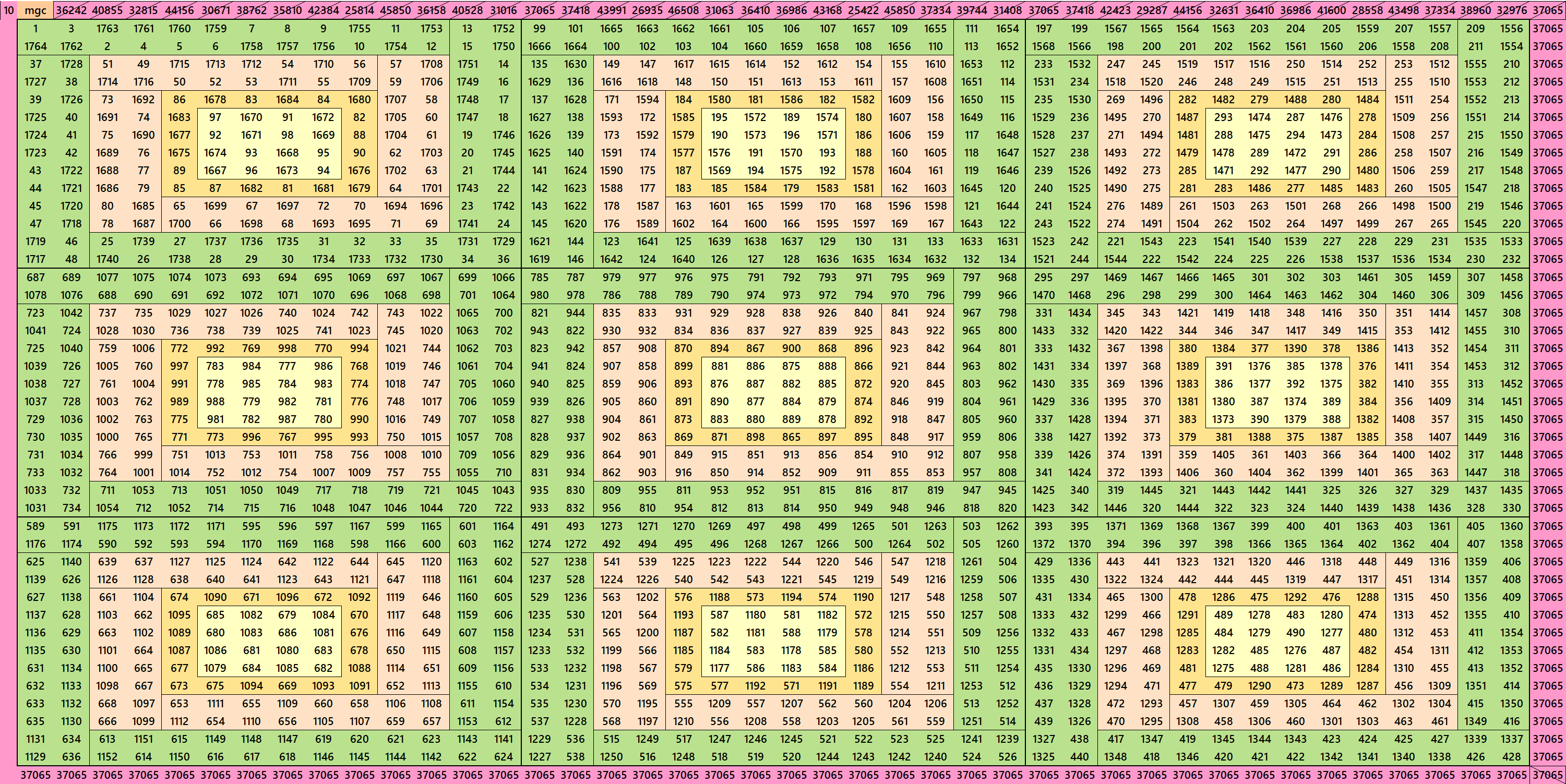
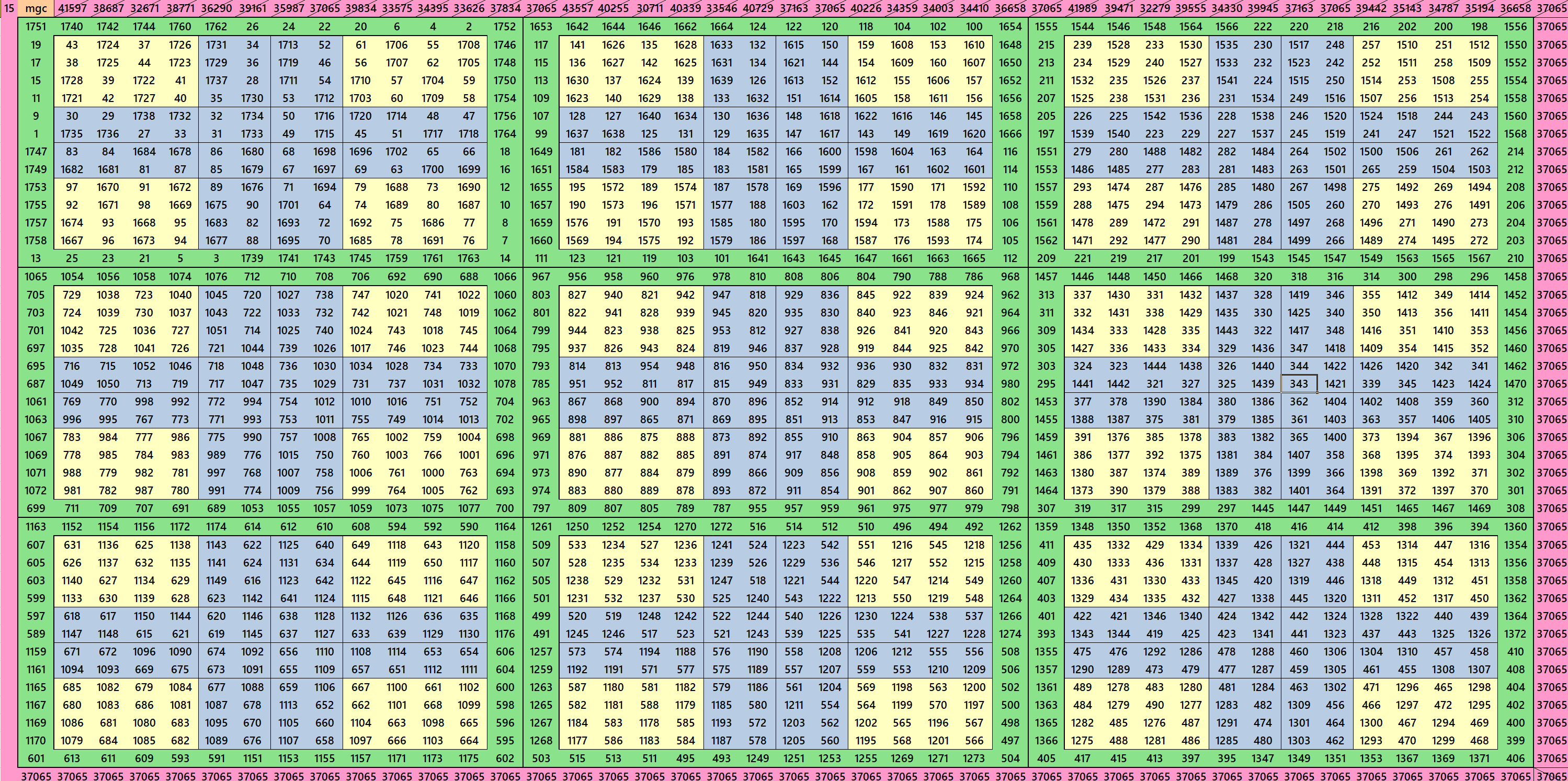
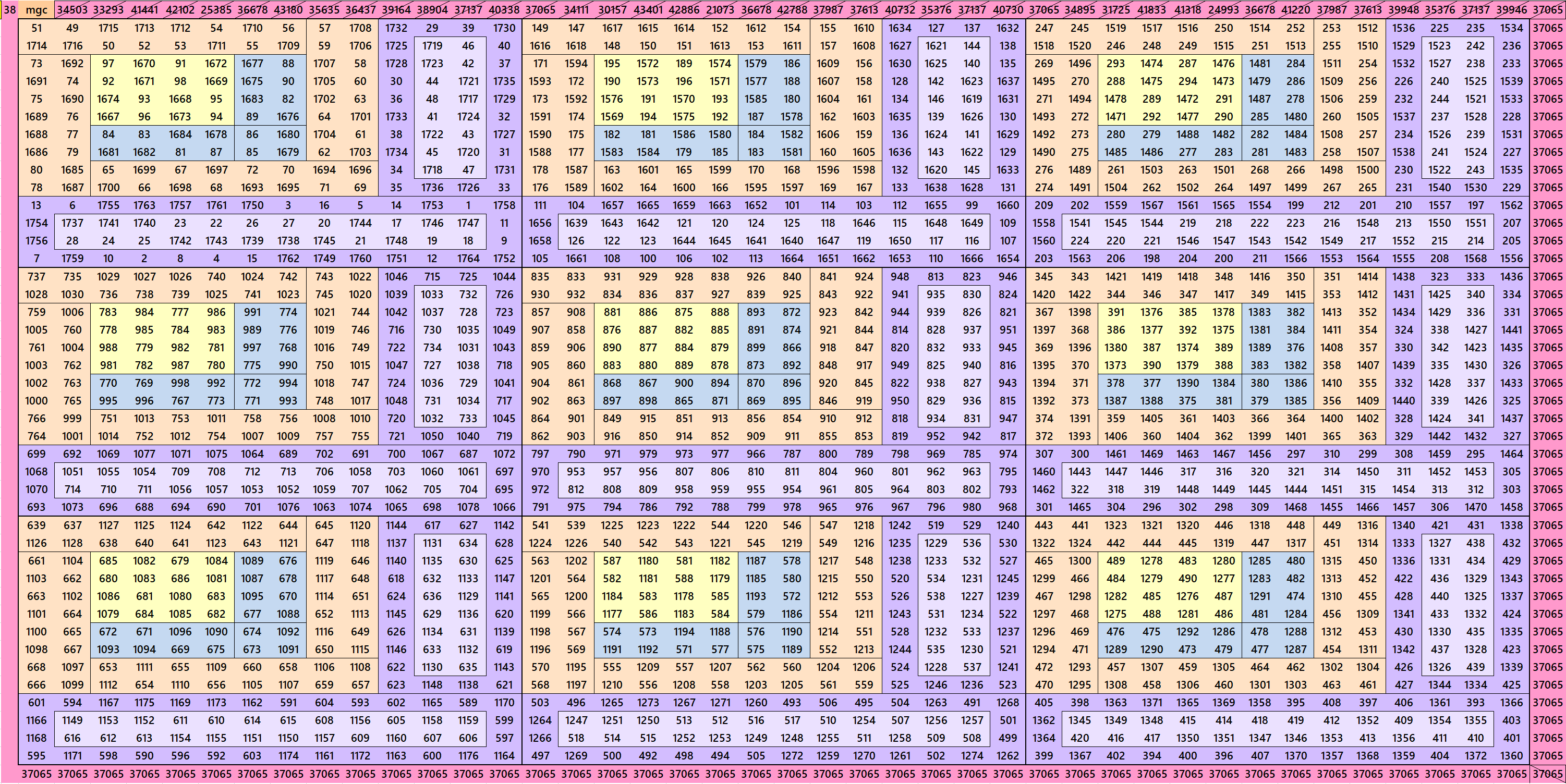
Pdf file of 46 Magic Squares of Order 42
Excel file of Magic Squares Multiples of 14
The excel files below for download contains magic squares multiples of order 14 from order 14 to 140. There are 46 examples in each case. These are given in two files. One with orders 140 and 126. The second file with remaining orders from 112 to 14.