Recreating Numbers and Magic Squares

Magic Squares

207 Magic Squares in Honor of the 138th Anniversary of S. Ramanujan with Hardy-Ramanujan Number 1729

ByInder J. Taneja

Dec 21, 2025

138th Birth Anniversary of S. Ramanujan,
December 22, 1887-April 26, 1920

National Mathematics Day, India – December 22

This work brings magic squares connected with S. Ramanujan’s life and with Hardy-Ramanujan number 1729. On december 22, 2025 there is 138th aniversiory of S. Ramanujan. This work brings magic squares of orders 3 to 20 having magic sum either 1729 or multiple of 1729. Some special entries are considered such as 2212, 1887, 2025 and 138. See below the table of total 207 magic squares according to each order.

The whole work can be accessed at the following link:

For previous work see the following links:

See below magic squares. Most of the work is based on three types of magic squares.
1. General Magic Squares
2. Single-Digit Bordered Magic Squares.
3. Double-Digit Bordered Magic Squares.
4. Cornered Magic Squares.

The construction of these magic squares is based on reduced entries algebraic magic sqaures recently studied by the author. For details see the reference list. If any of the magic square is not found according to above table. It can be accessed at the link of the work given above.

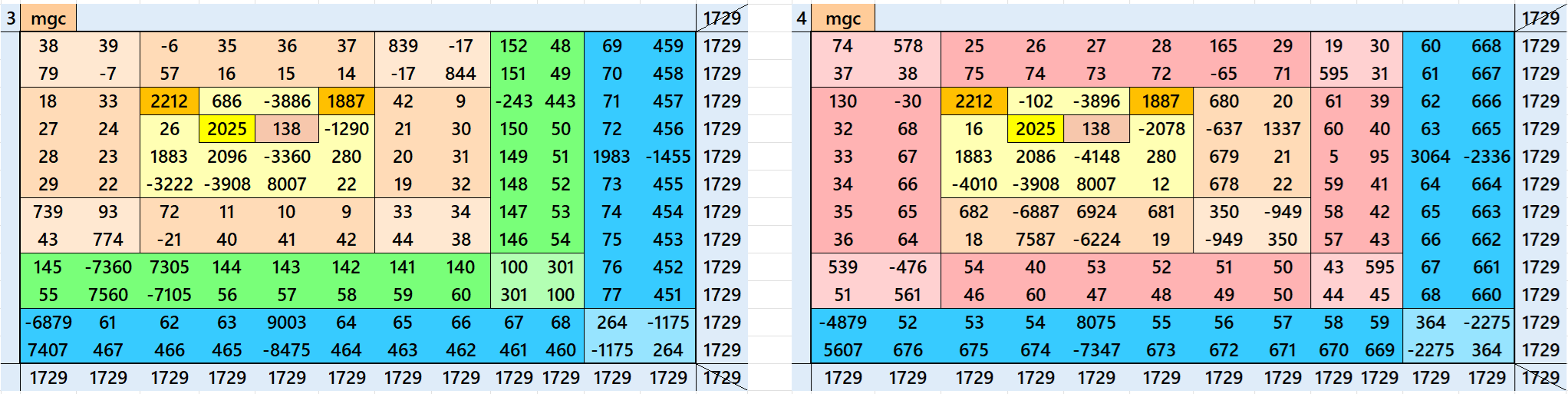
Magic Squares of Order 3

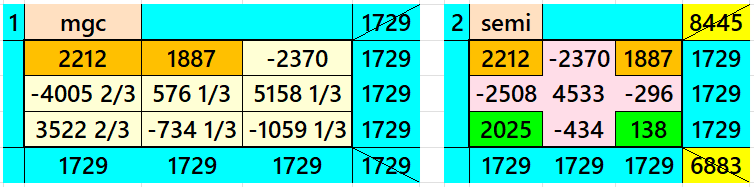
Above there are two examples magic squares of order 3 with magic sum 1729. The first example is magic squares but there are fractional entries. The second one is semi-magic having four special entreis, such as. date of birth of S. Ramanujan 2212-1887 and 138th aniversary on 2212-2025.

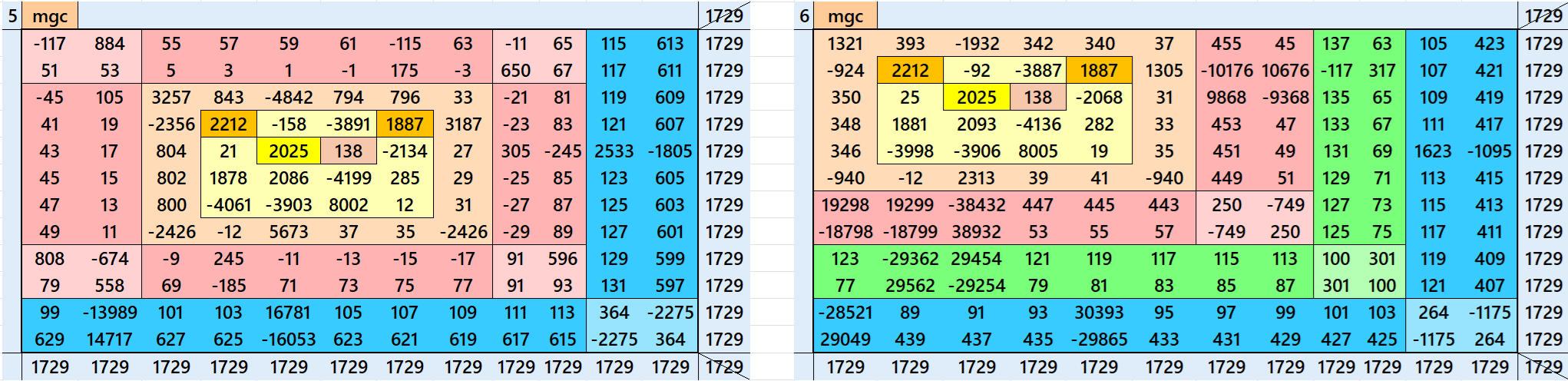
Magic Squares of Order 4

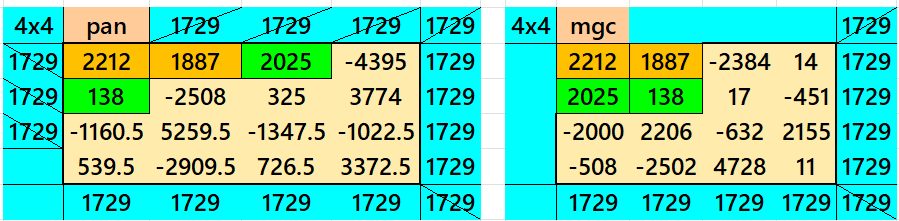
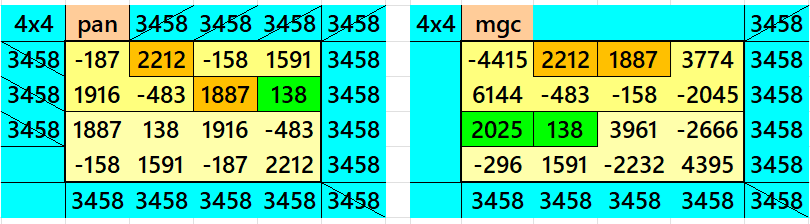
Above there are two examples magic squares of order 4 with magic sum 1729. The first example is in two diffeernt ways. First one is pandiagonal but having decimal entries. The second way is not pandiagonal but don’t require decimal entries. The example is also written in two parts. Both are with two equal sums magic rectangles of orders 2×4. Here the magic sum is 2×1729. This is to avoid decimal entries.

Both the examples uses special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

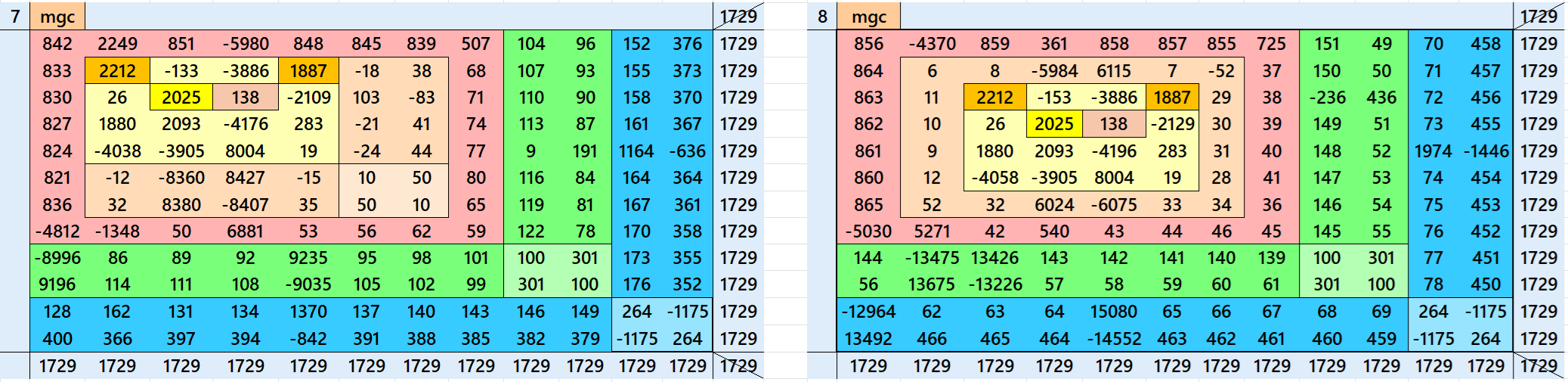
Magic Squares of Order 5

Above there are three examples magic squares of order 5 with magic sum 1729. The first example is a pandiagonal . The second example is a cornered magic square having magic square of order 3 at the upper left corner. The third example is a single-digit bordered semi-magic square

All 3 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

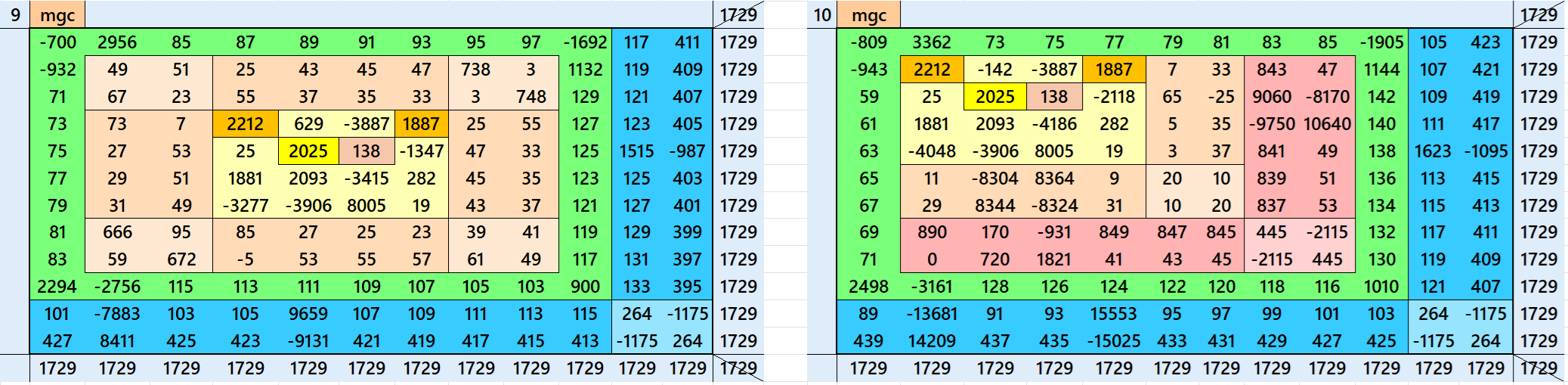
Magic Squares of Order 6

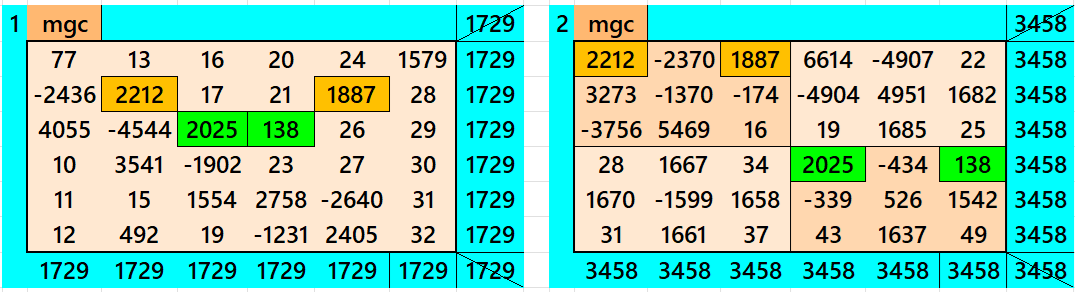
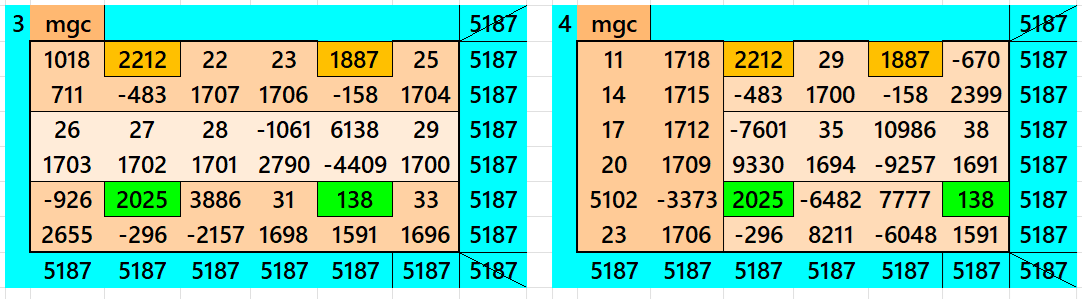
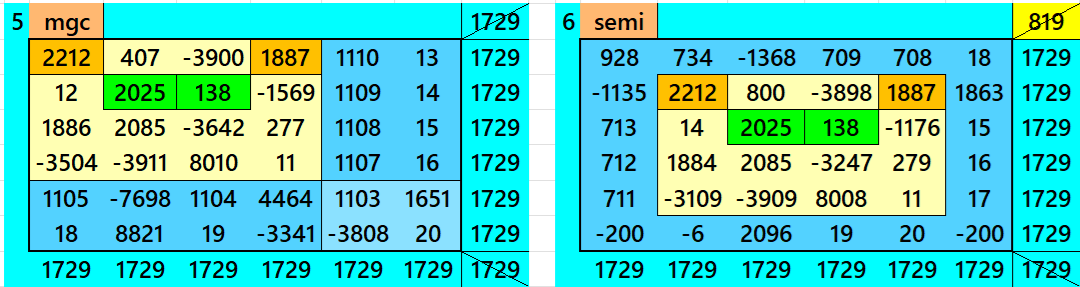
Above there are six examples magic squares of order 6 with magic sum 1729. The first example is a normal magic square of order 6. The second example is with four equal sums semi-magic squares of order 3. The third and forth examples are with magic rectangles. The fifth one is cornrered magic square of order 6. The the last example is a single-digit bordered semi-magic square of order 6.

All 6 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

Magic Squares of Order 7

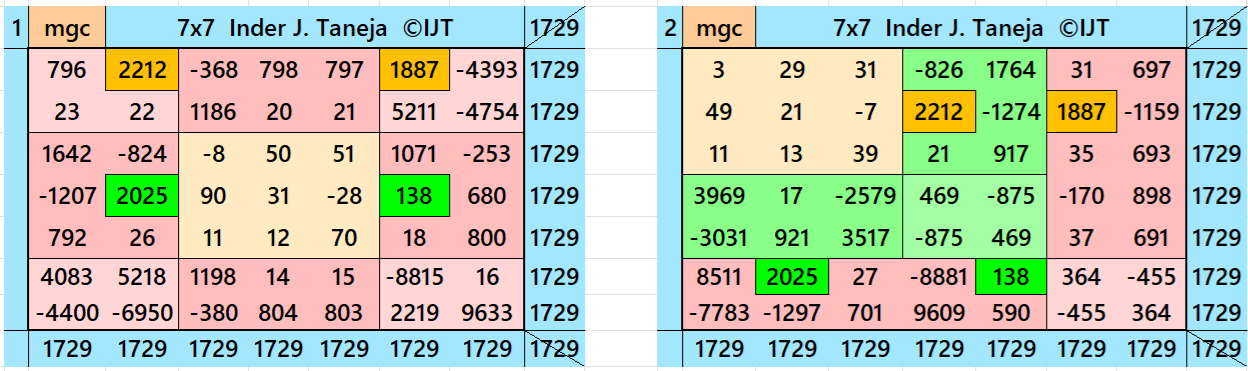
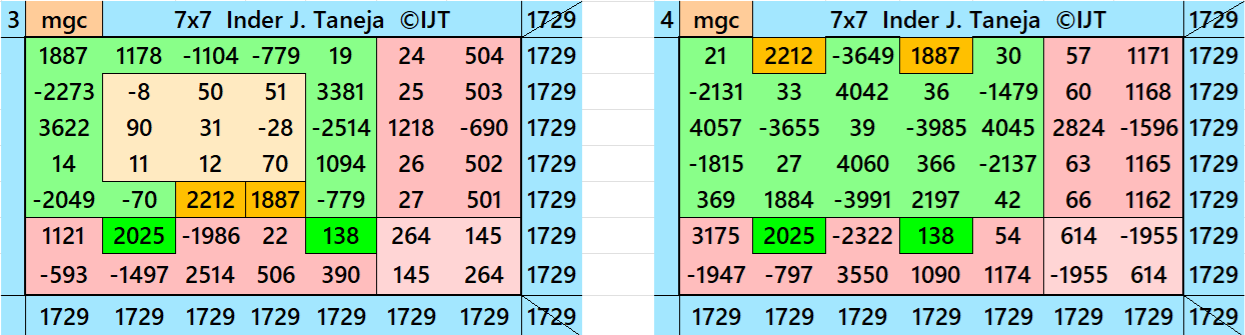
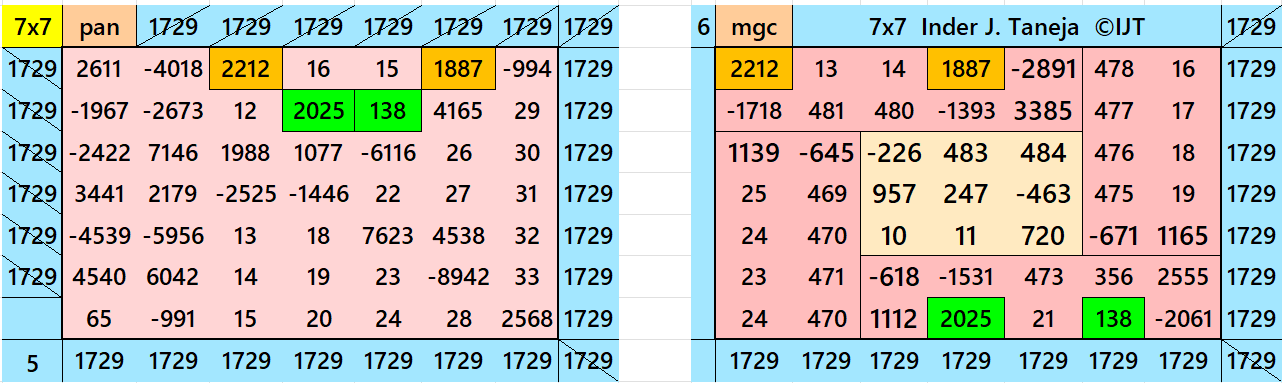
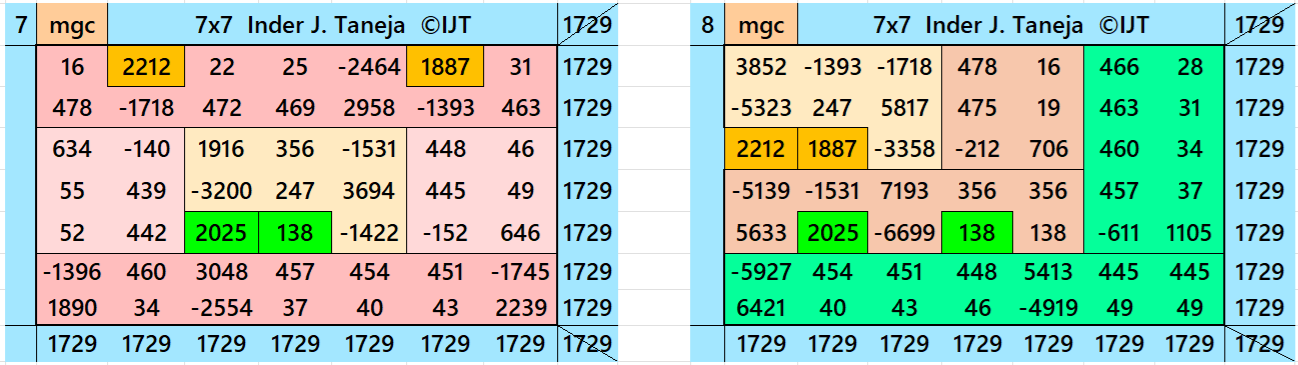
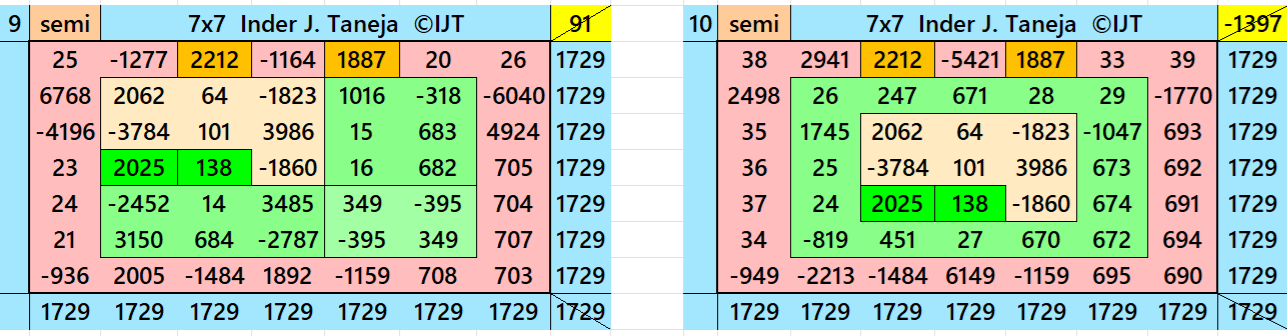
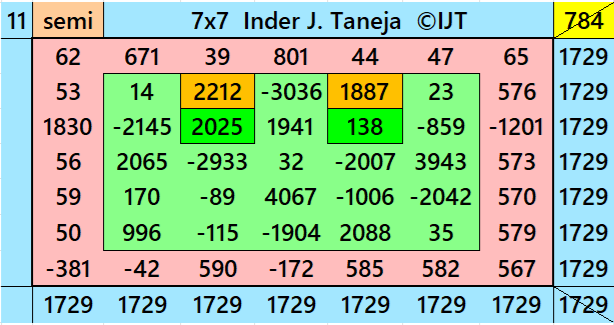
Above there are eleven examples magic squares of order 7 with magic sum 1729. The first eight examples are based on the different types of magic squares as written in the bignninig of this wotk. The last three examples are of semi-magic squares of order 7 .

All 11 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

Magic Squares of Order 8

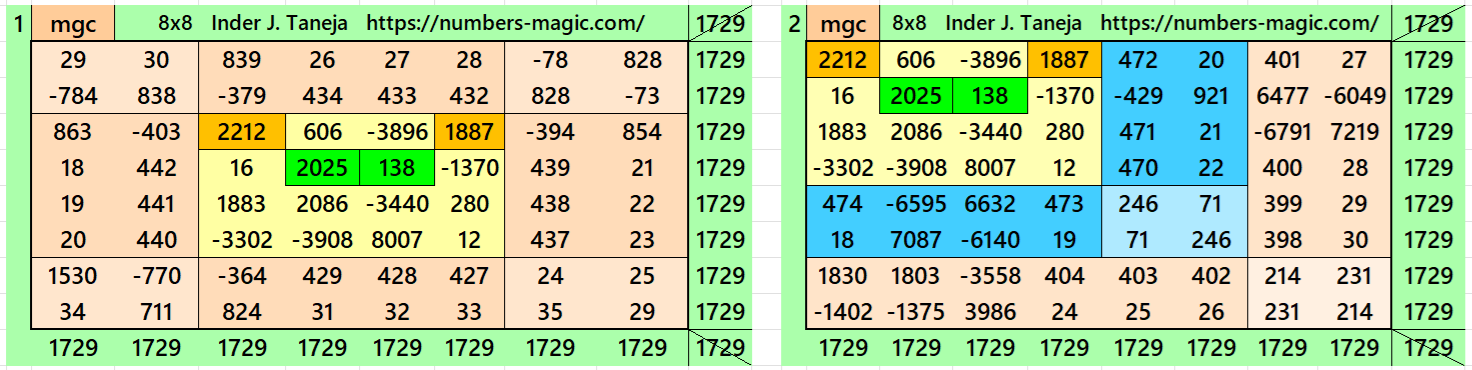
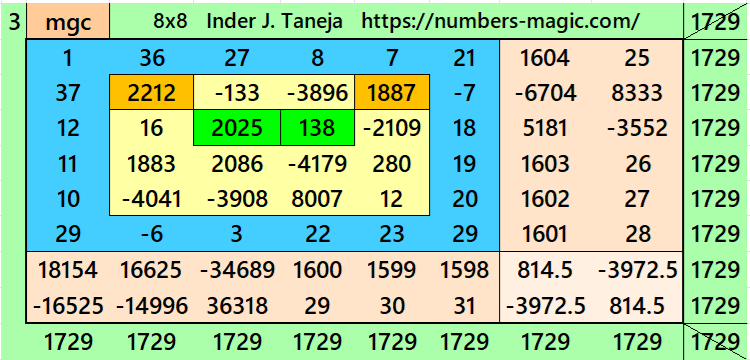
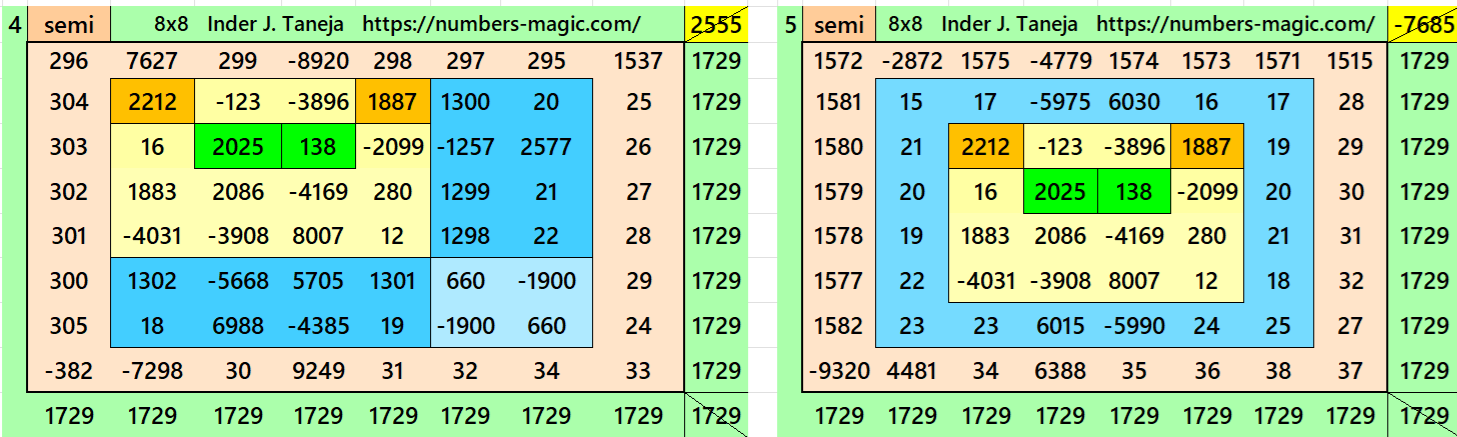
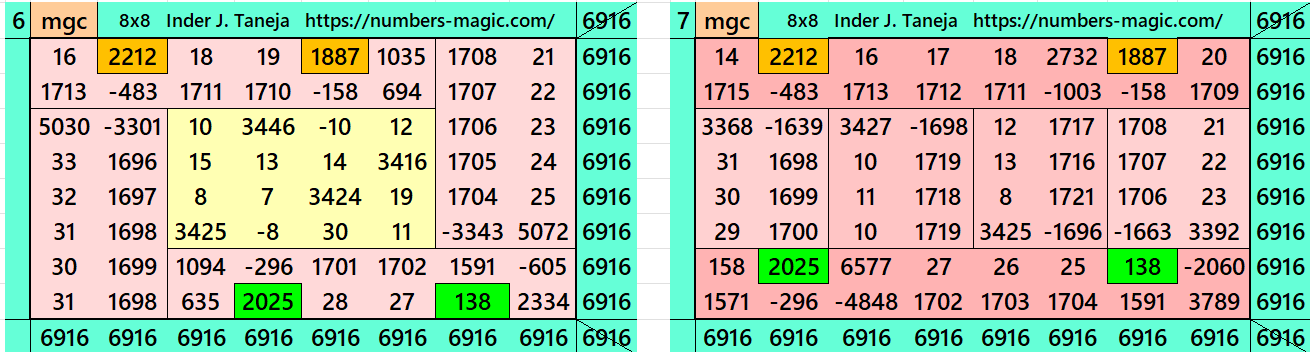
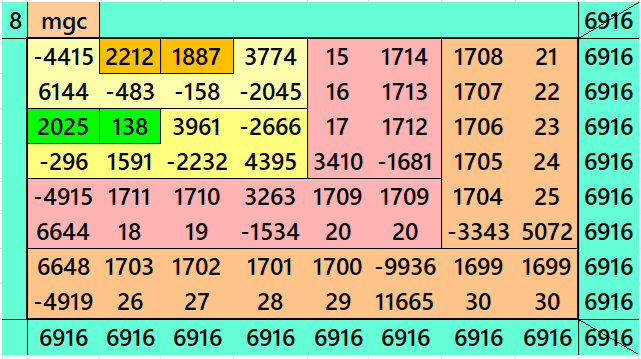
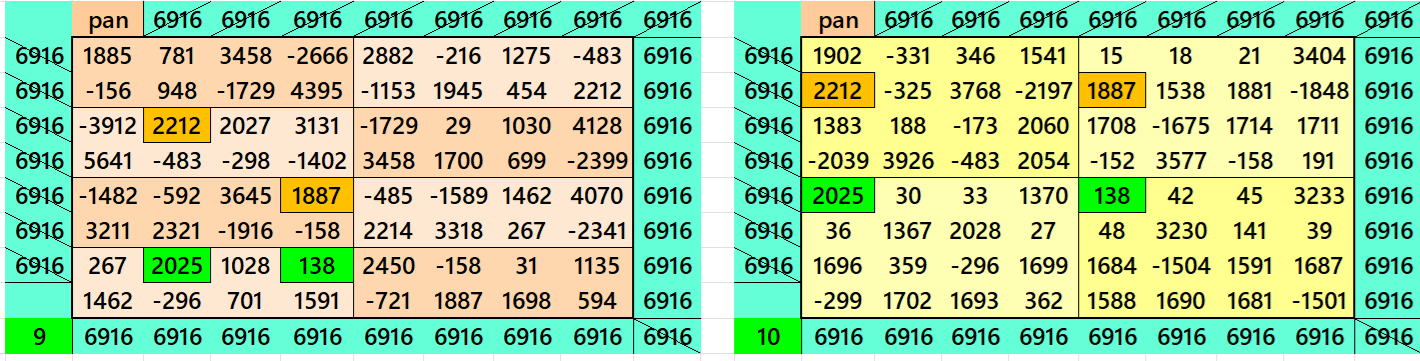
Above there are ten examples magic squares of order 8 with magic sum 1729. The first three examples are based on the different types of magic squares as written in the bignninig of this wotk. The examples 4 and 5 are of semi-magic square of order 8. The examples 8, 9 and 10 are little different. The examples 8 and 9 are stripled magic square of order 8. The example 10 is based on four equazl sums pandiagonal magic squares of order 4. The examples 9 and 10 both are pandiagonal. In both these examples the magic sums ie 6916=4*1729. This we have considered to avoid decimal entries.

All 10 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

Magic Squares of Order 9

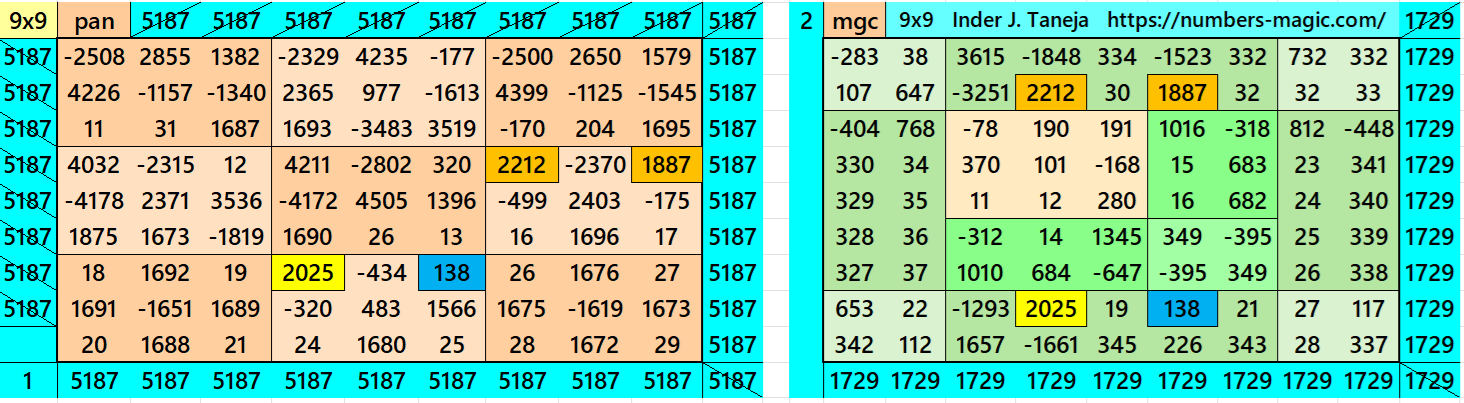
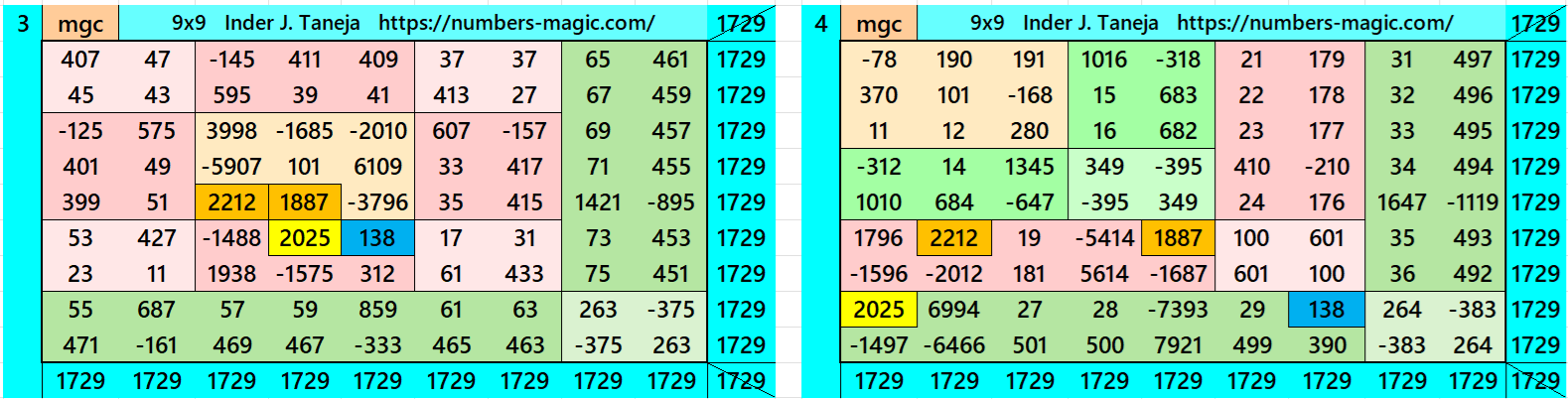
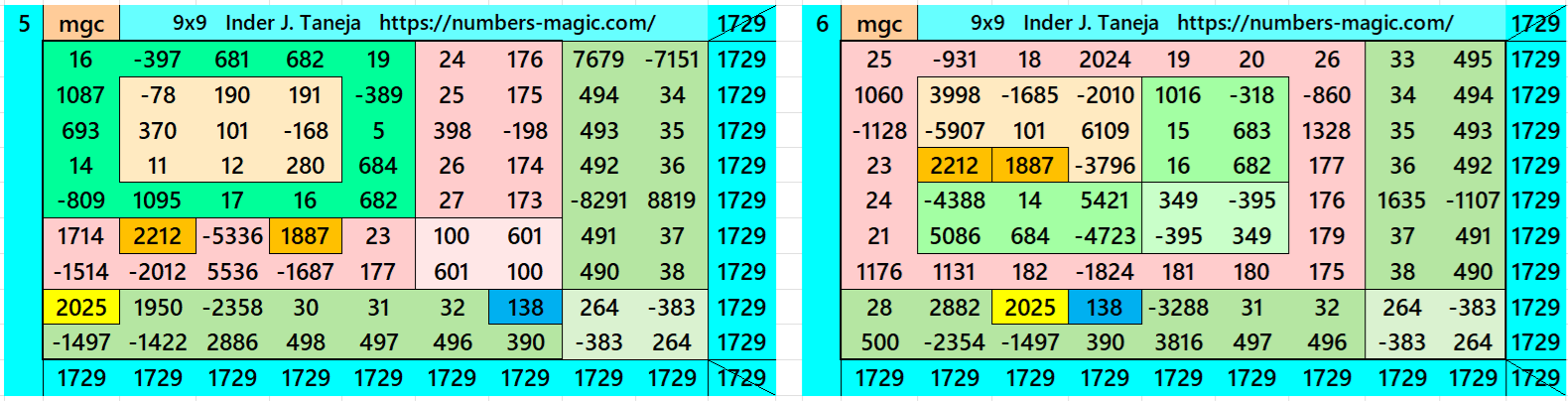
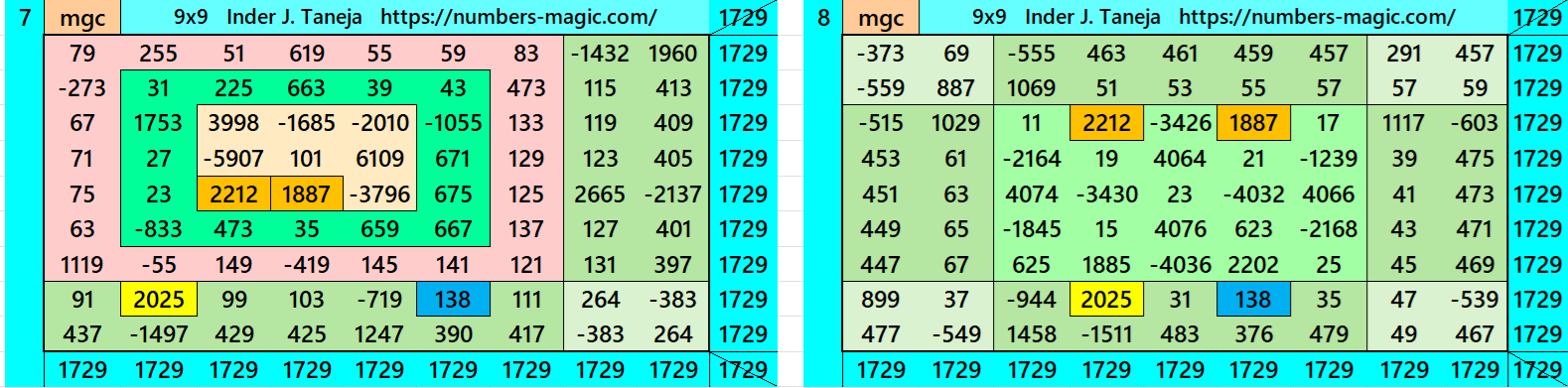
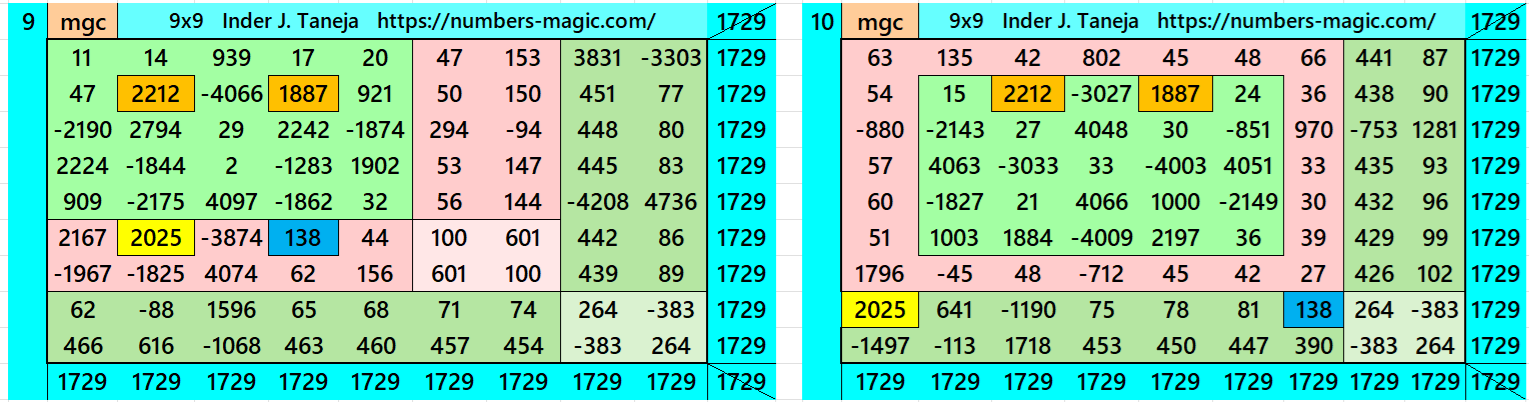
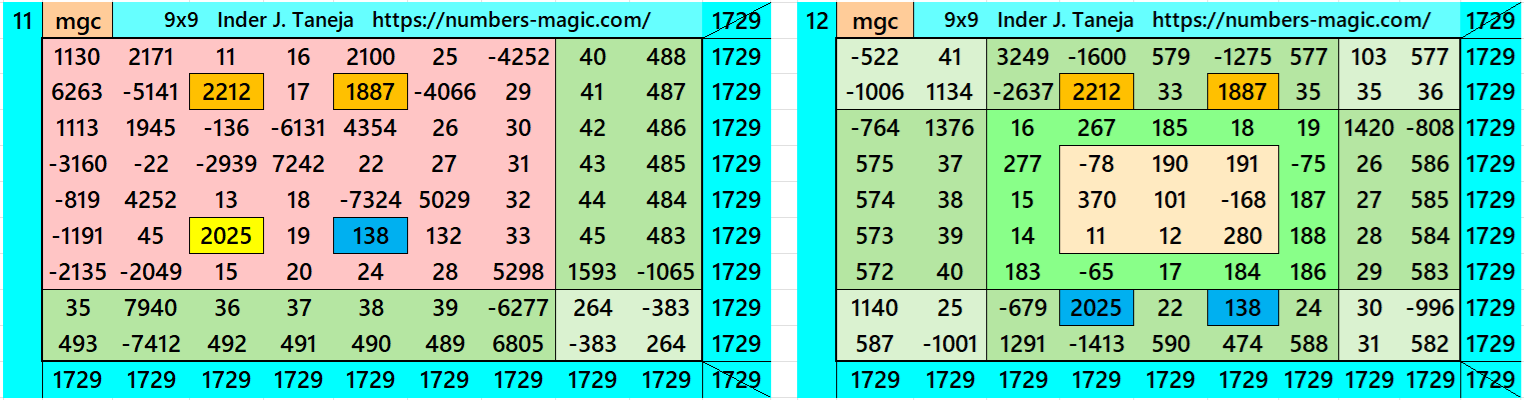
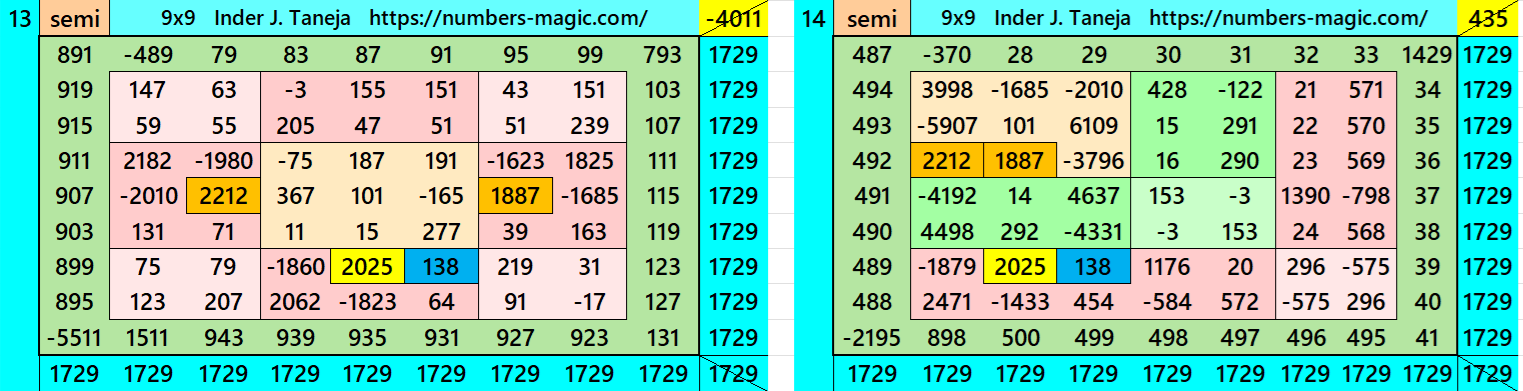
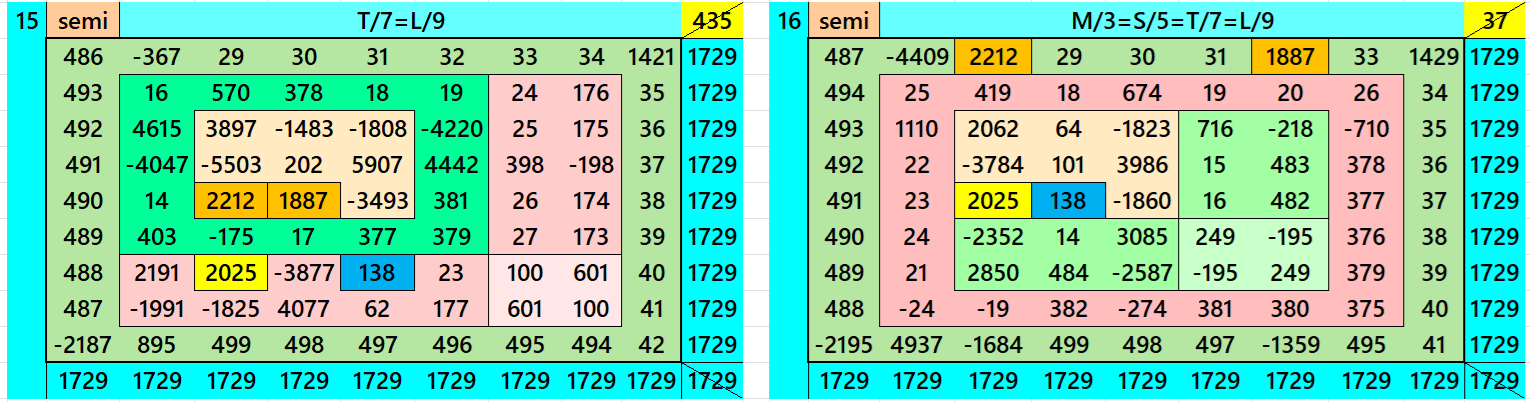
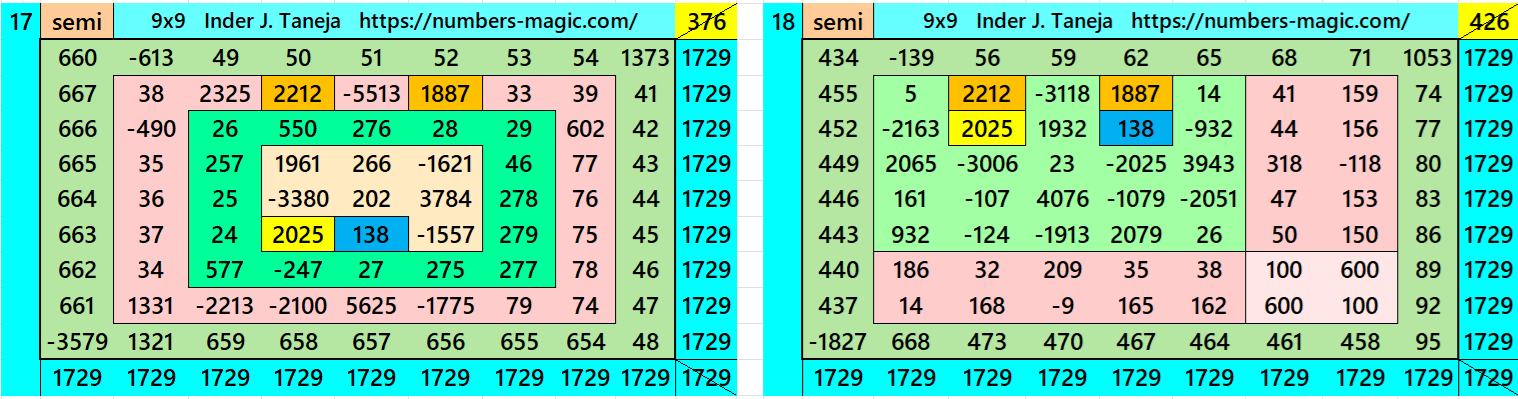
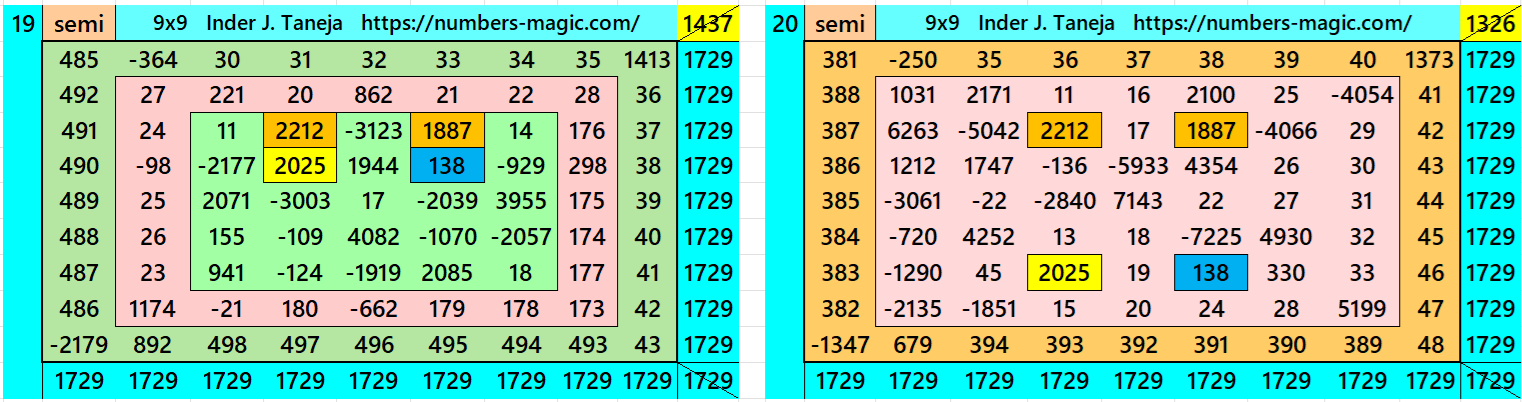
Above there are twenty examples magic squares of order 9 with magic sum 1729. The first example is pandiagonal with 9 equal sums semi-magic squres of order 3. The next 11 examples, i.e., from 2 to 12 are different types of magic squares as written in the bignninig of this work. The last 8 examples, i.e., from 13 to 20 are of semi-magic squares of order 9.

All 20 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

Magic Squares of Order 10

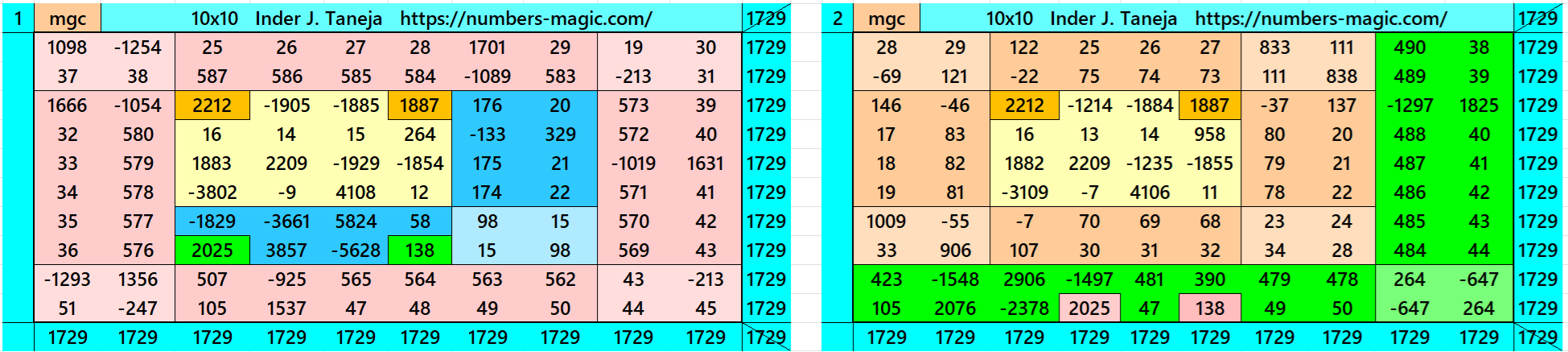
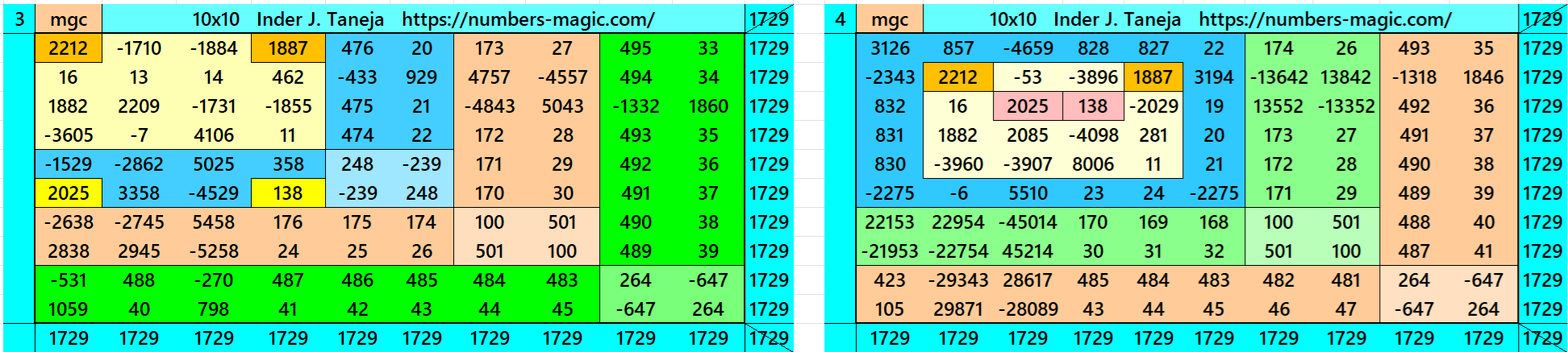
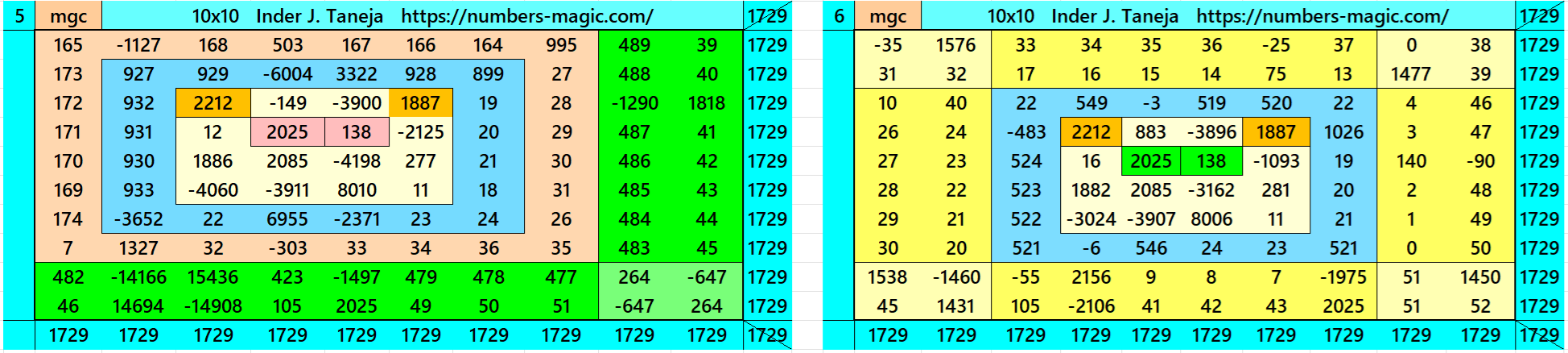
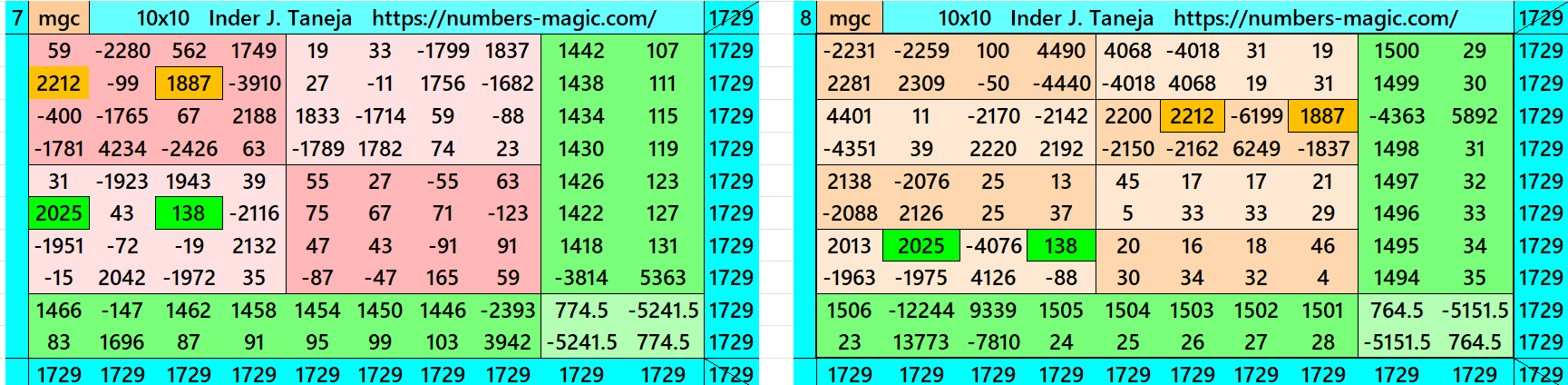
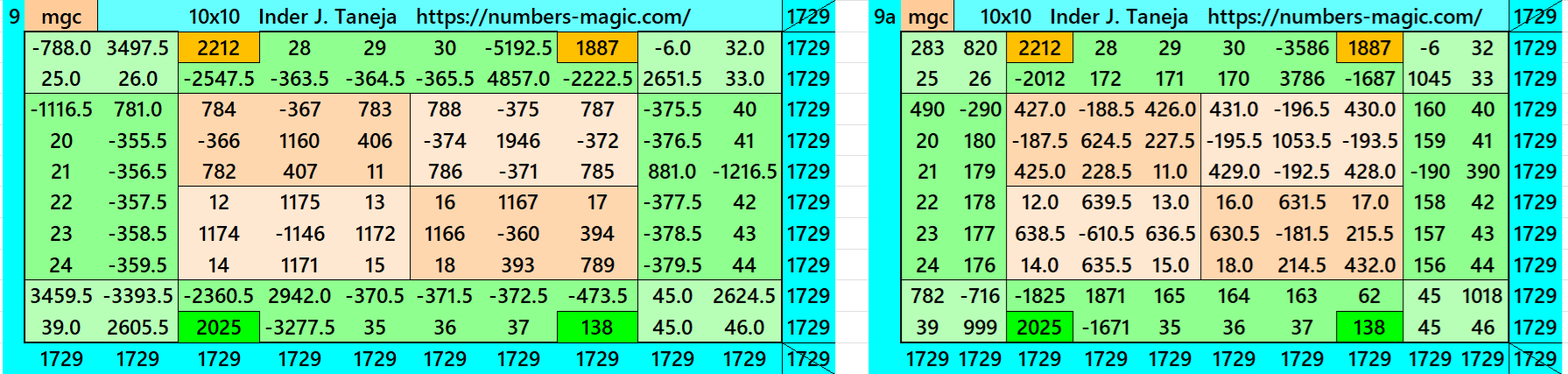
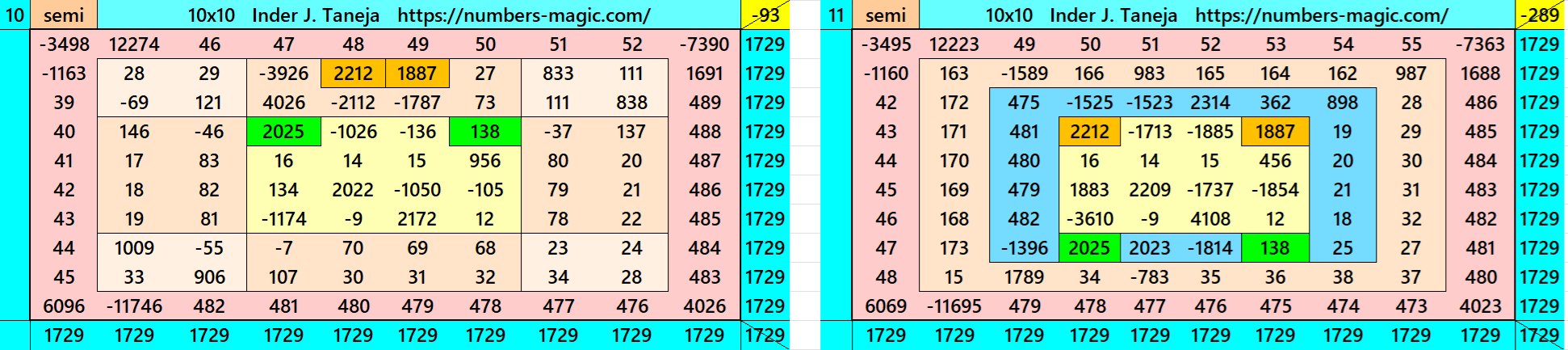
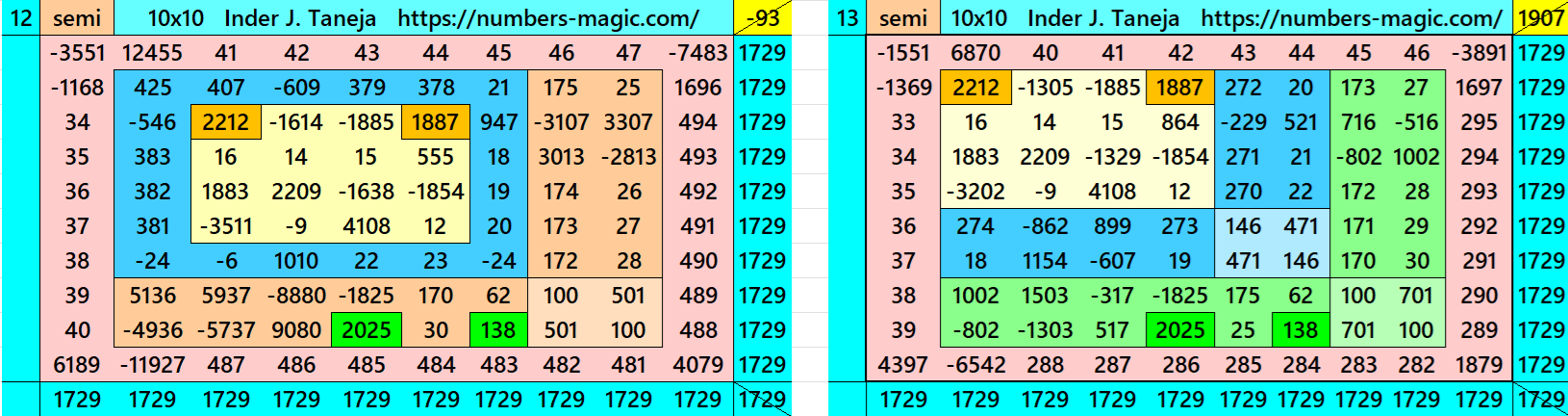
Above there are therteen examples magic squares of order 10 with magic sum 1729. The first 9 examples are different types of magic squares.. The last 4 examples are of semi-magic squares of order 10. The example 9 is written in two different ways. One the decimal entries are only in the inner part, i.e., in magic square of order 6. The one is with decimal entries in the outer part.

All 13 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

Magic Squares of Order 11

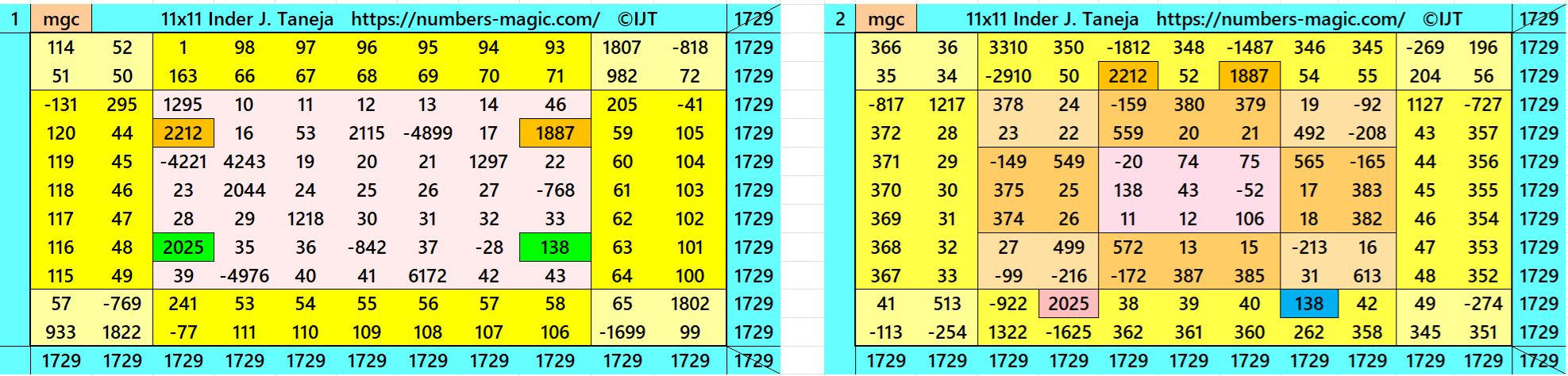
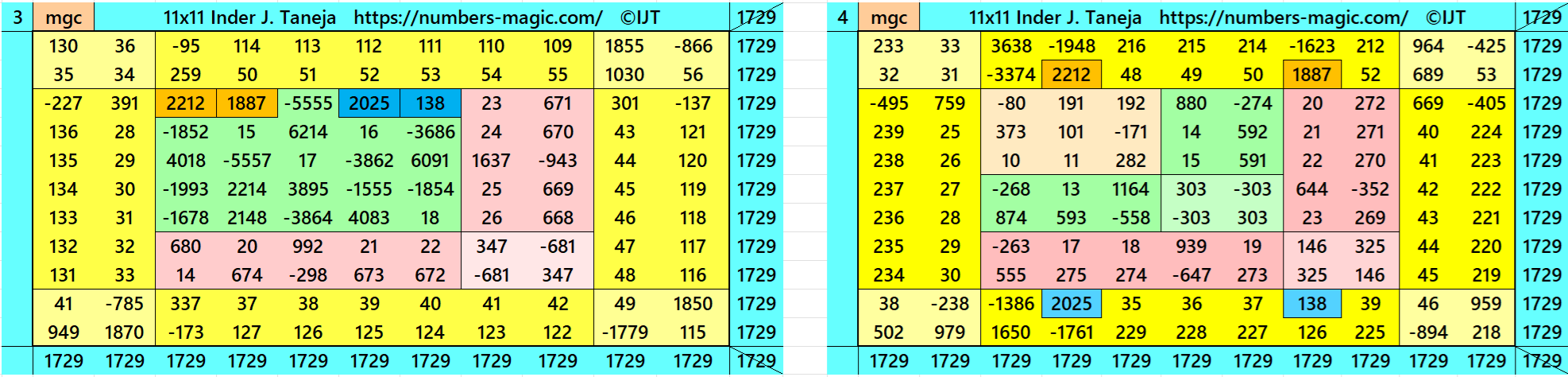
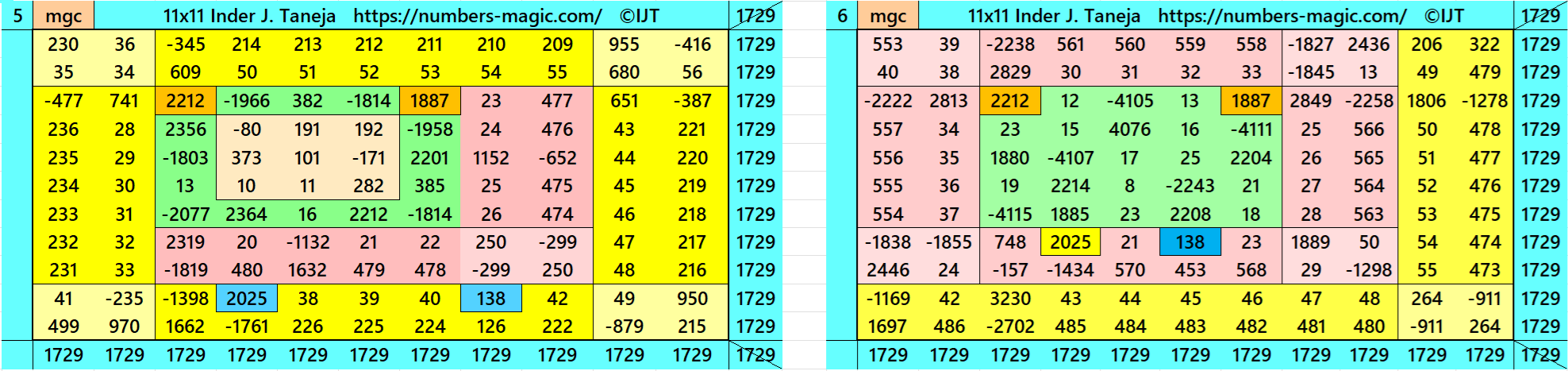
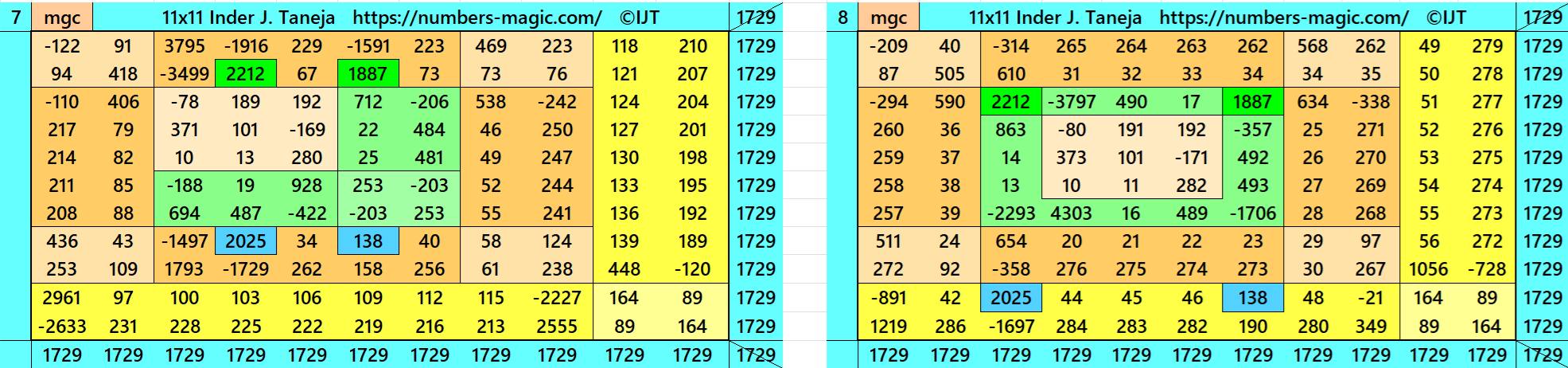
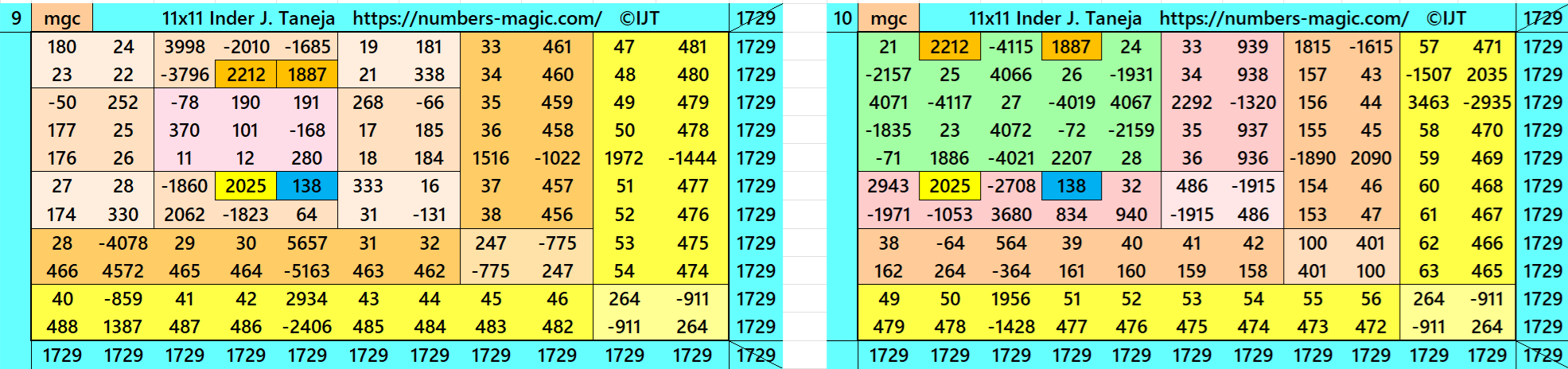
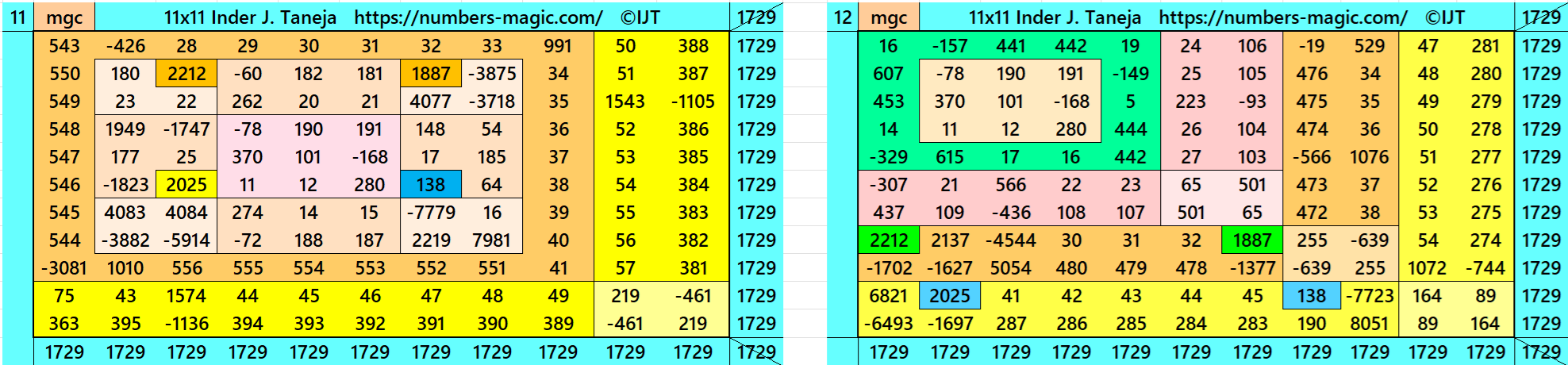
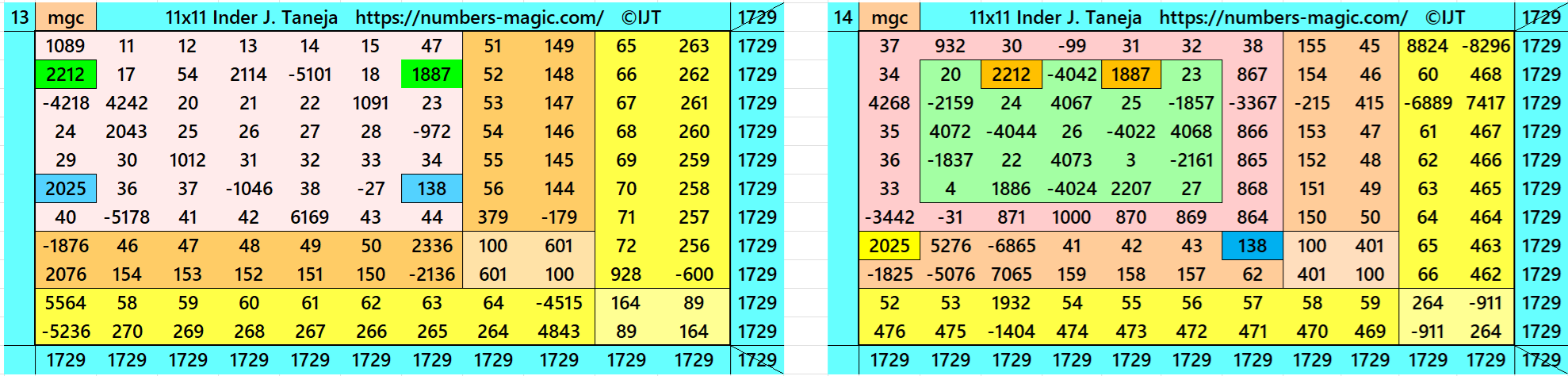
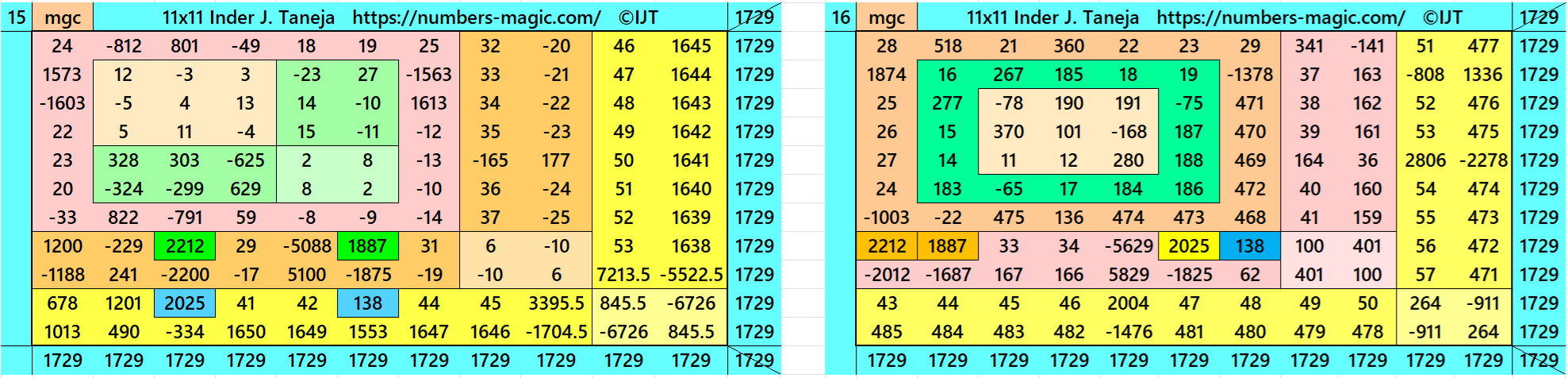
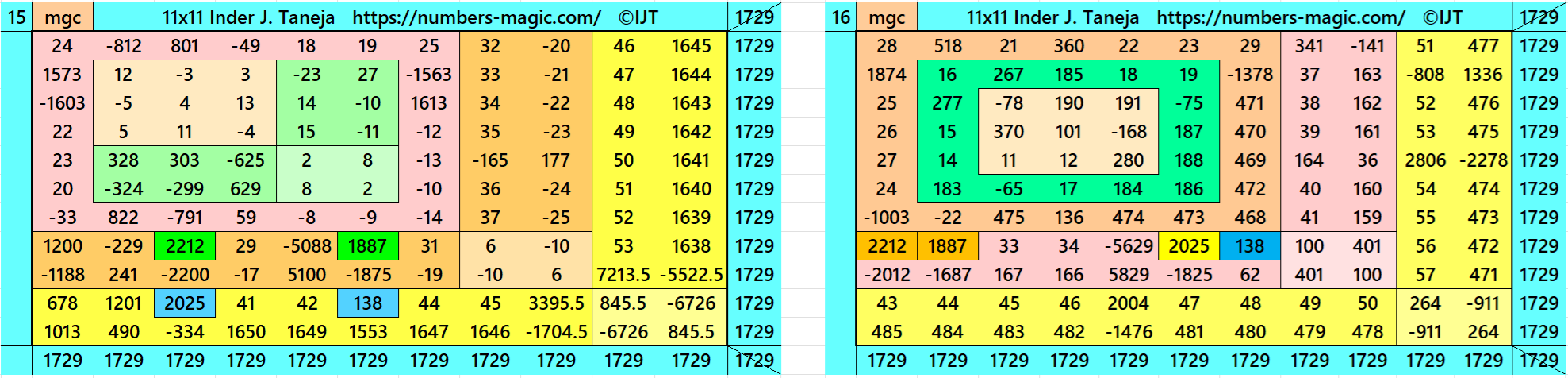
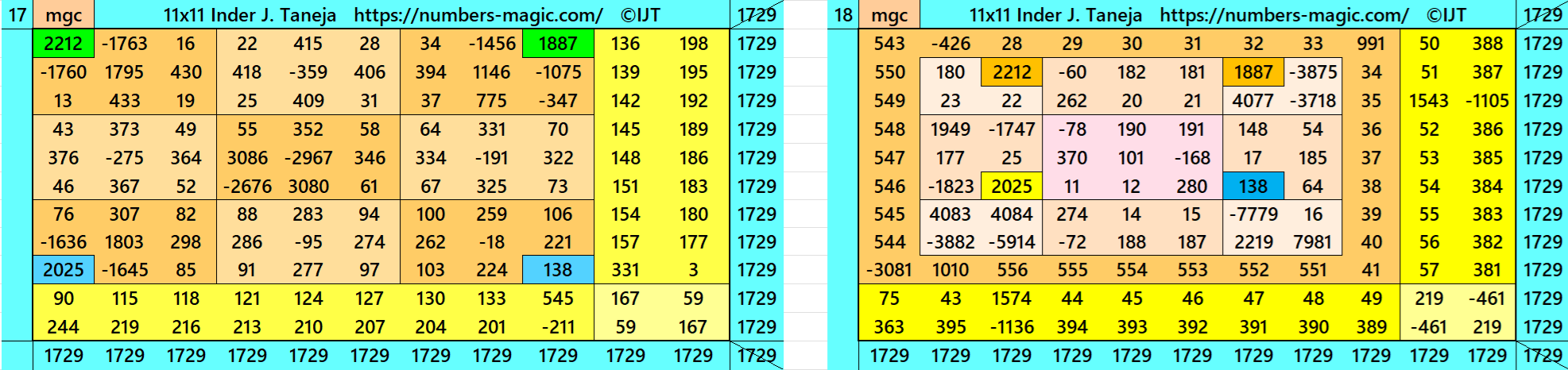
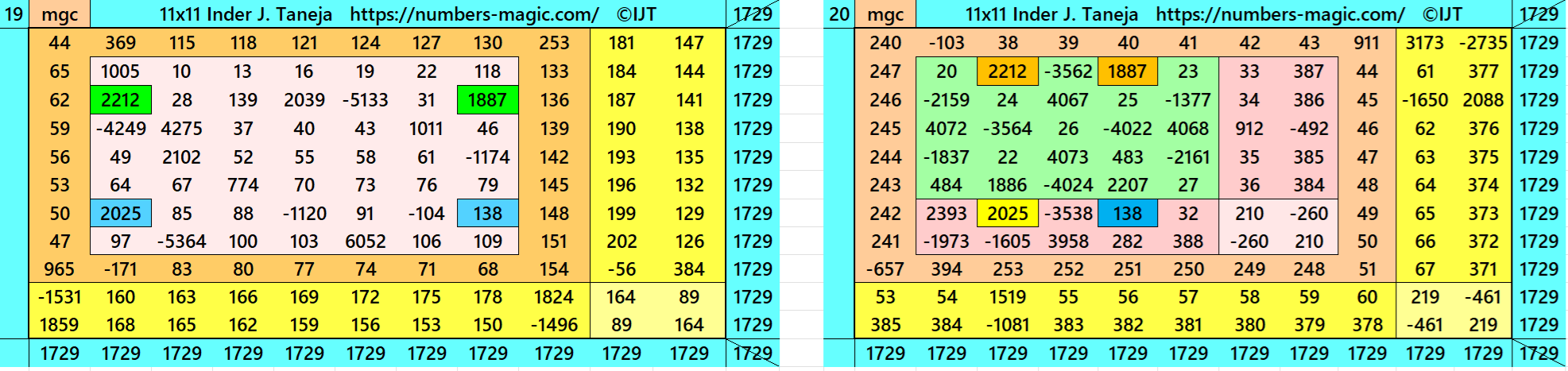
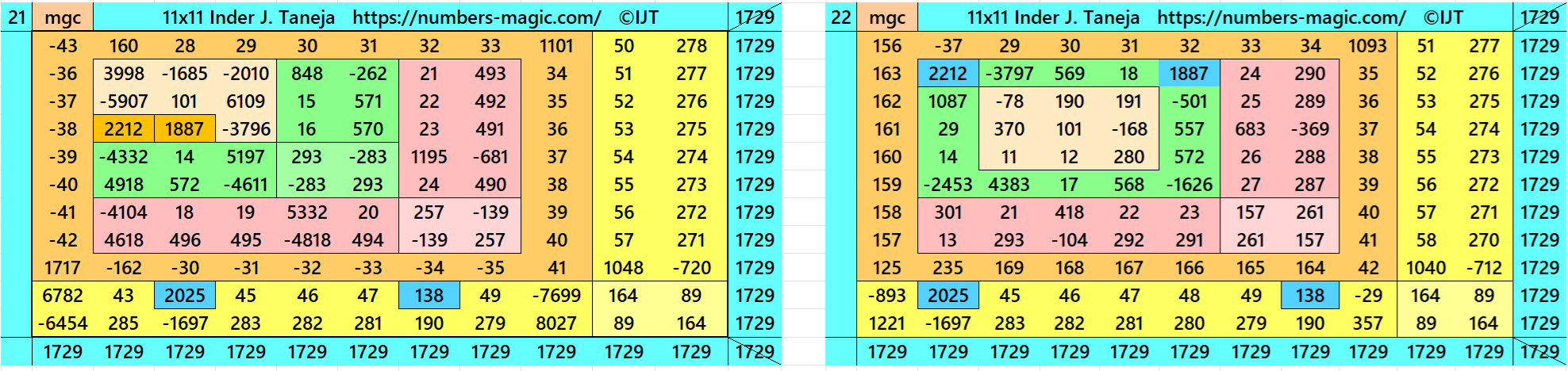
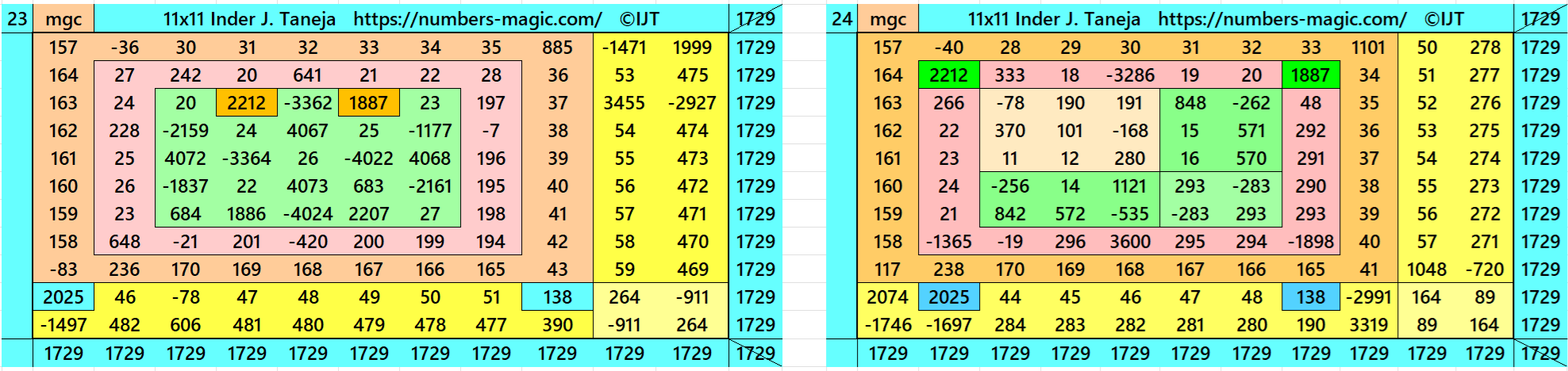
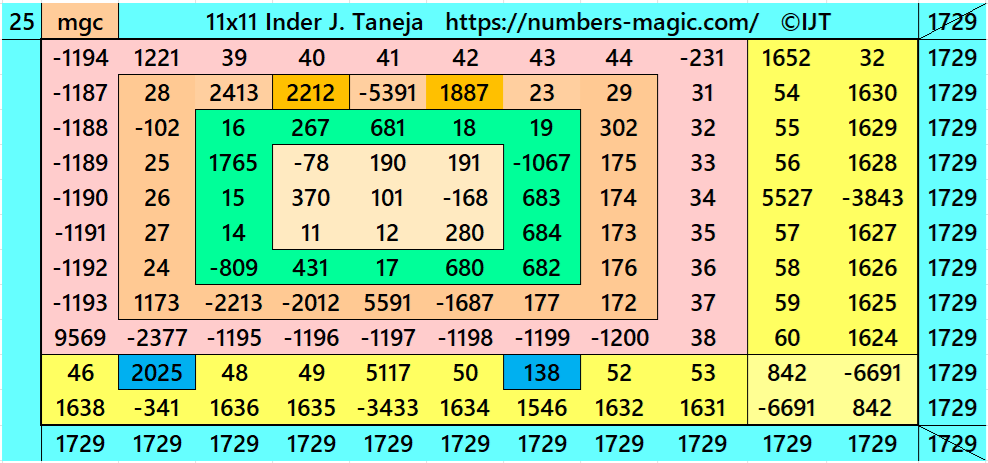
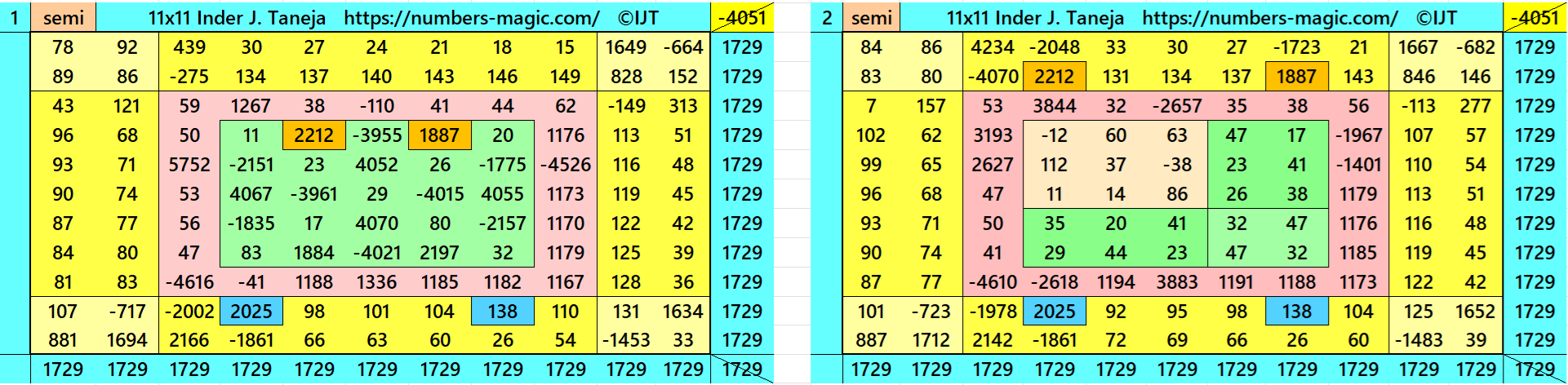
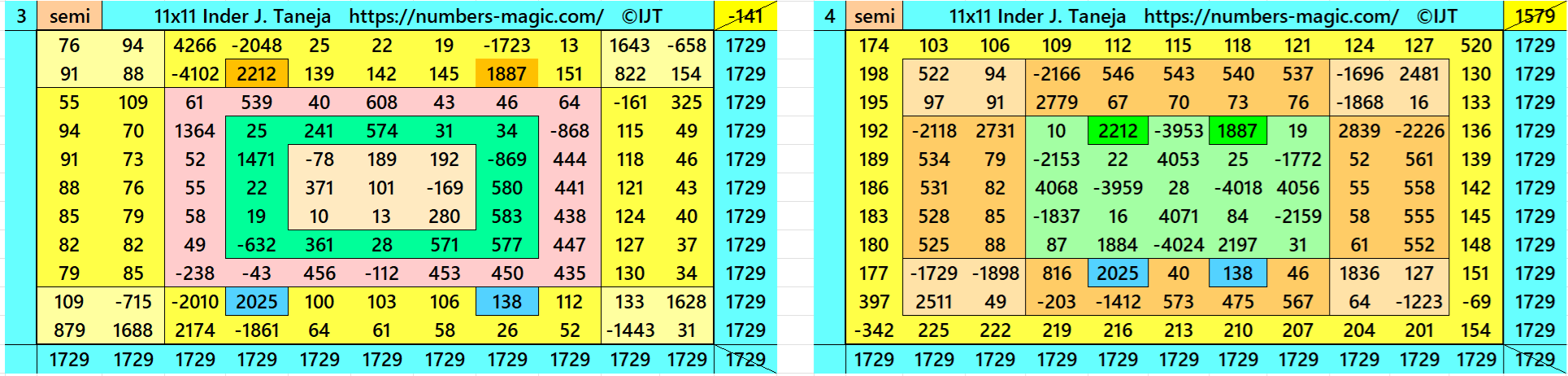
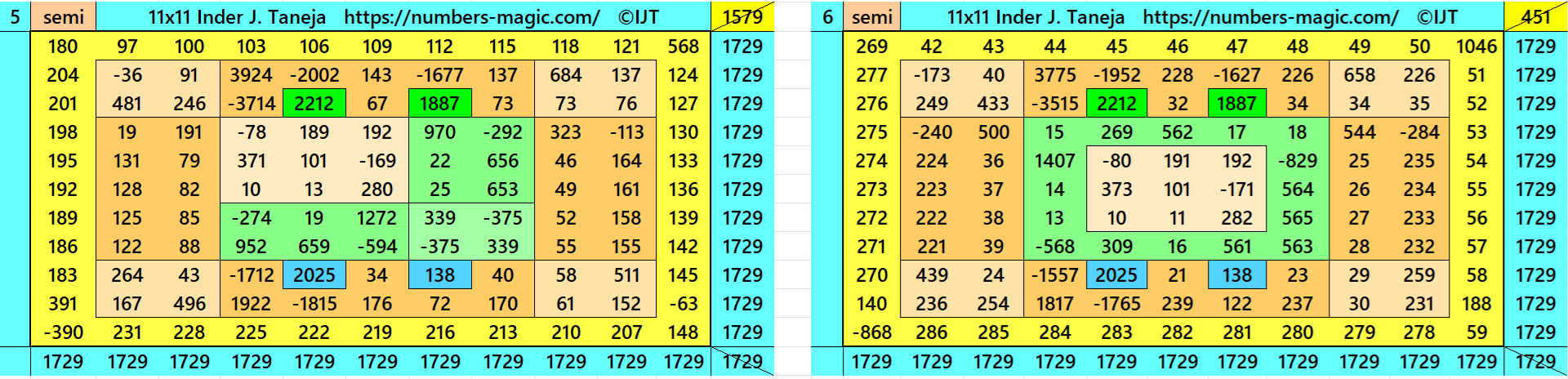
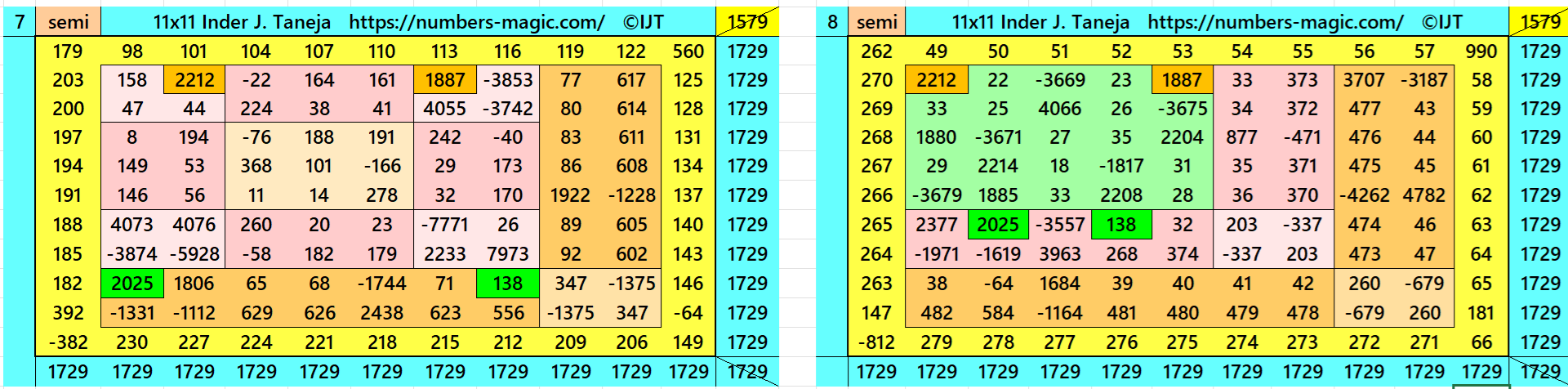
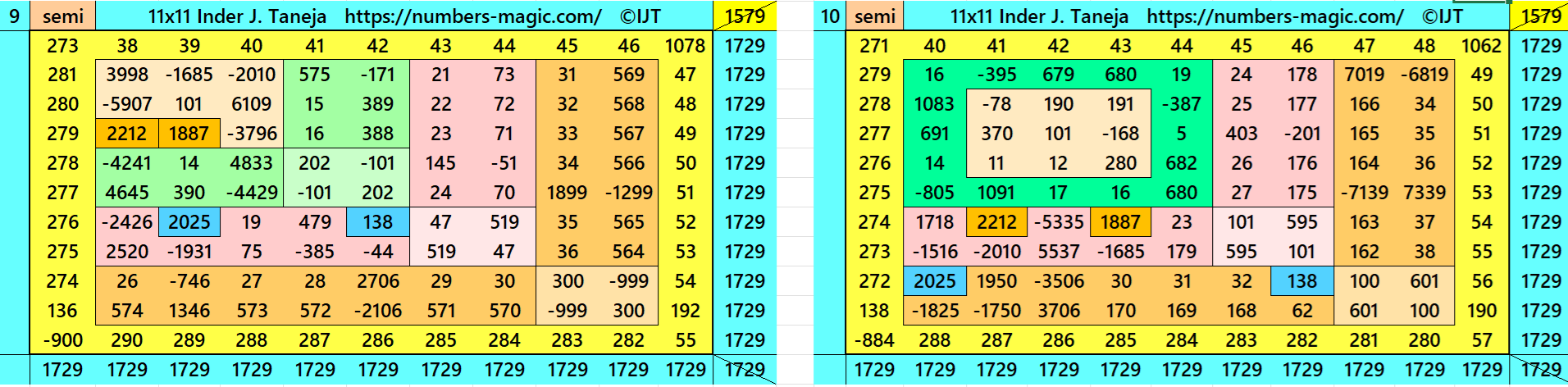
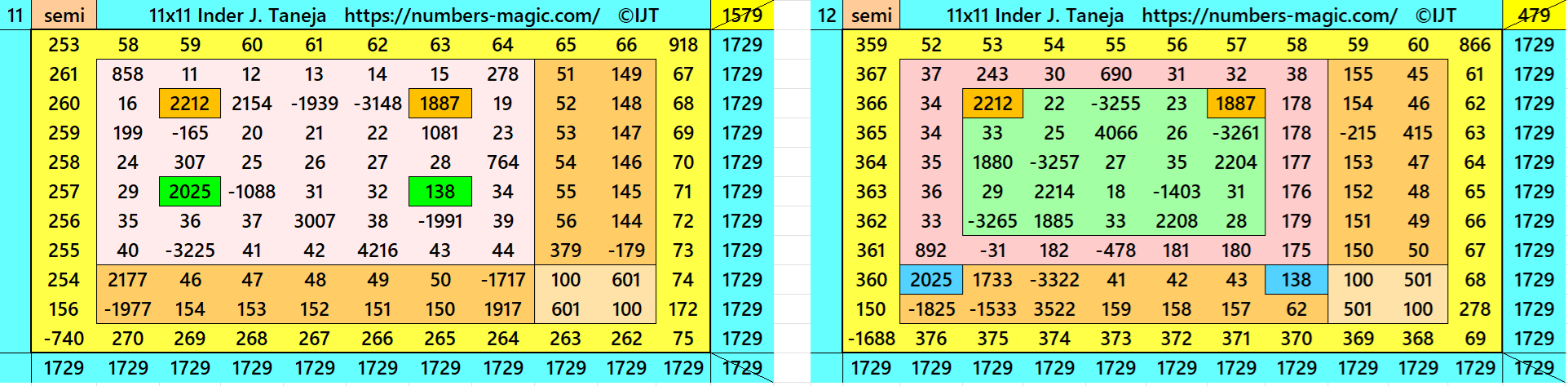
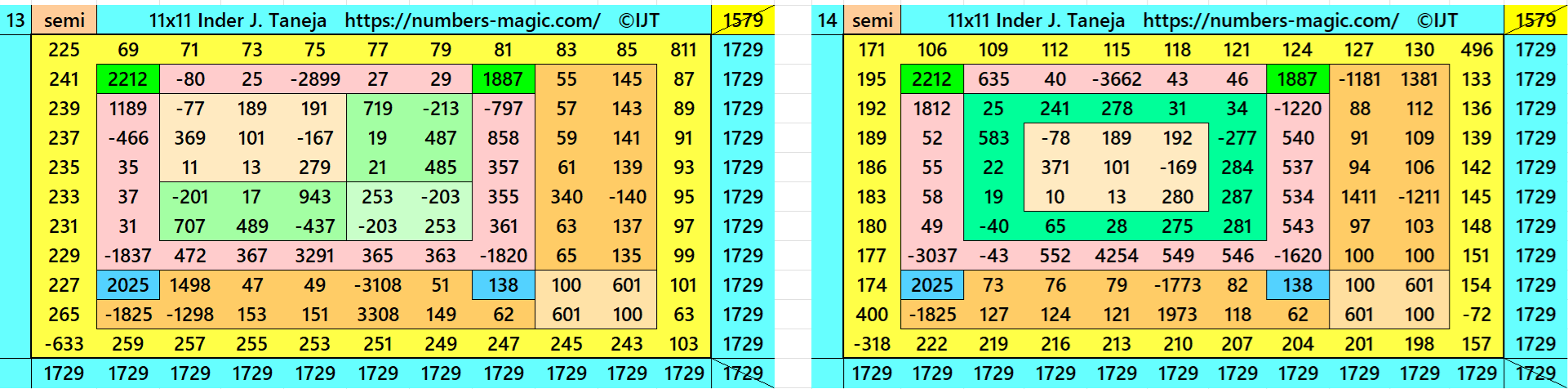
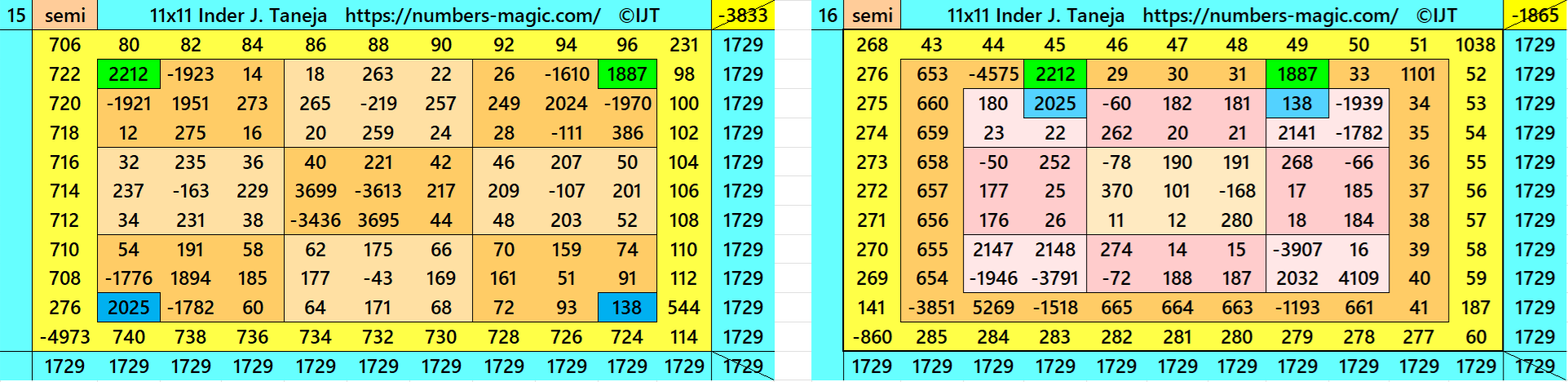
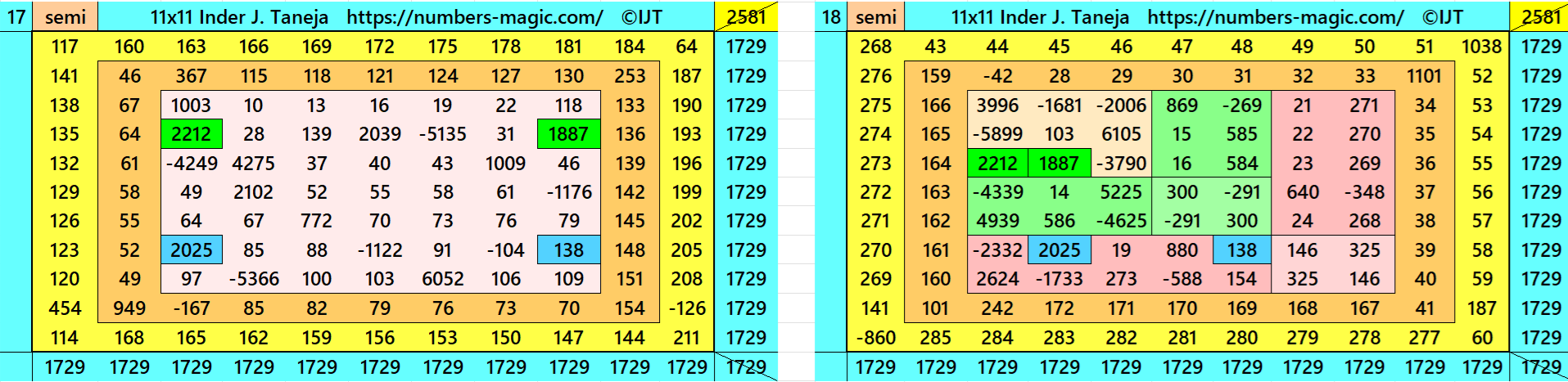
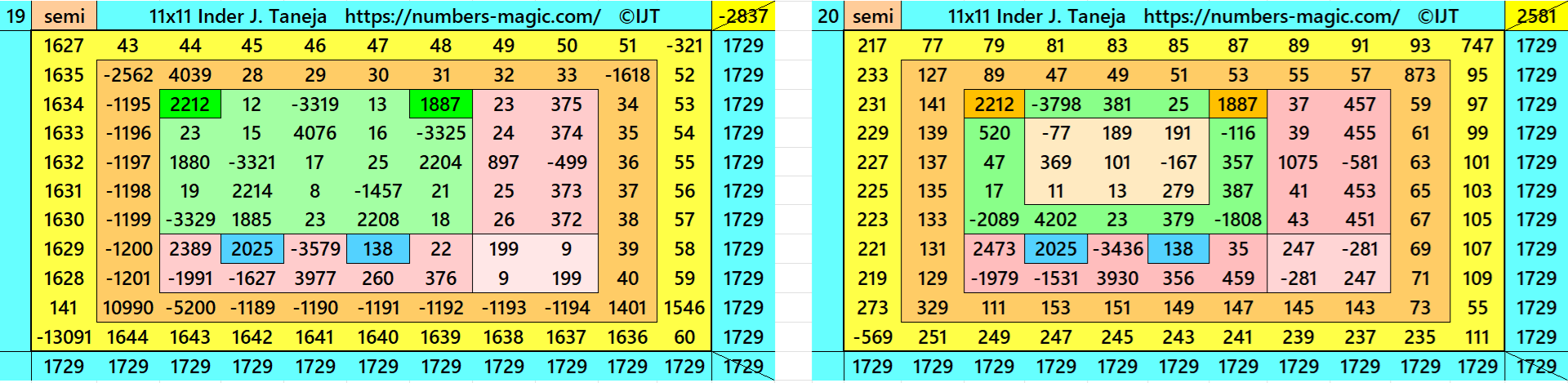
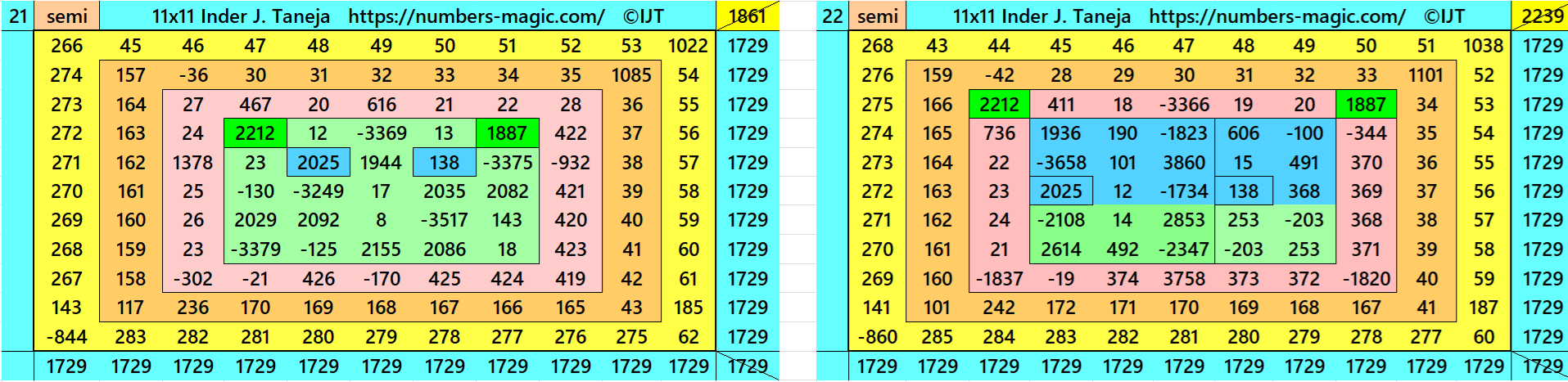
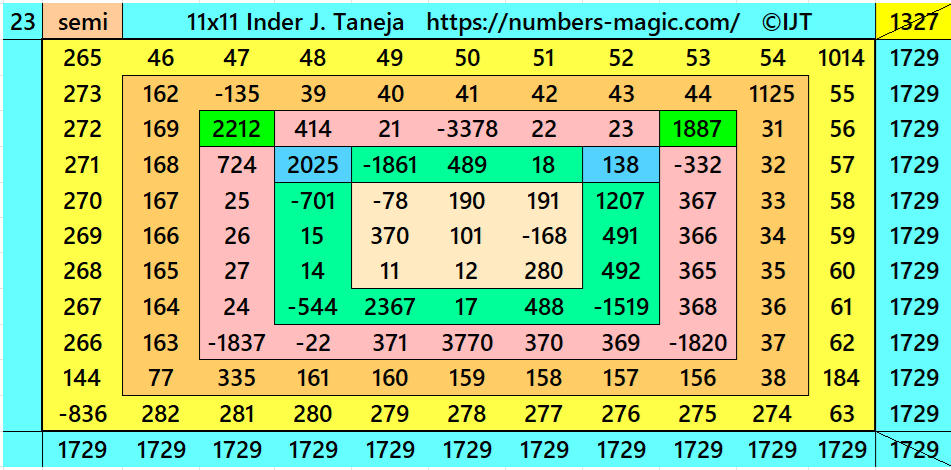
Above there are 48 examples magic squares of order 11 with magic sum 1729. The first 25 examples are different types of magic squares.. The last 23 examples are of semi-magic squares of order 11.

All 48 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

Magic Squares of Order 12

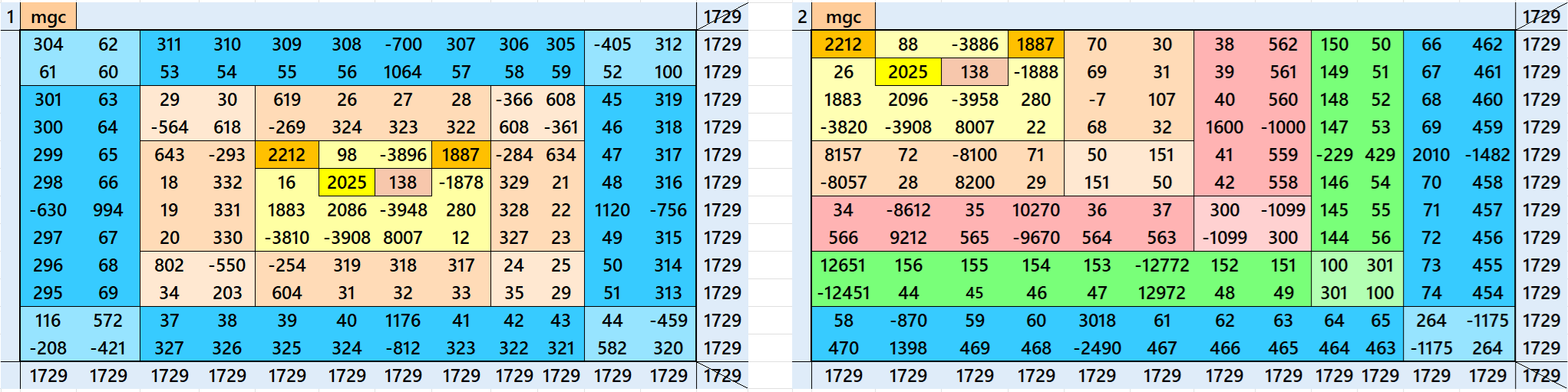
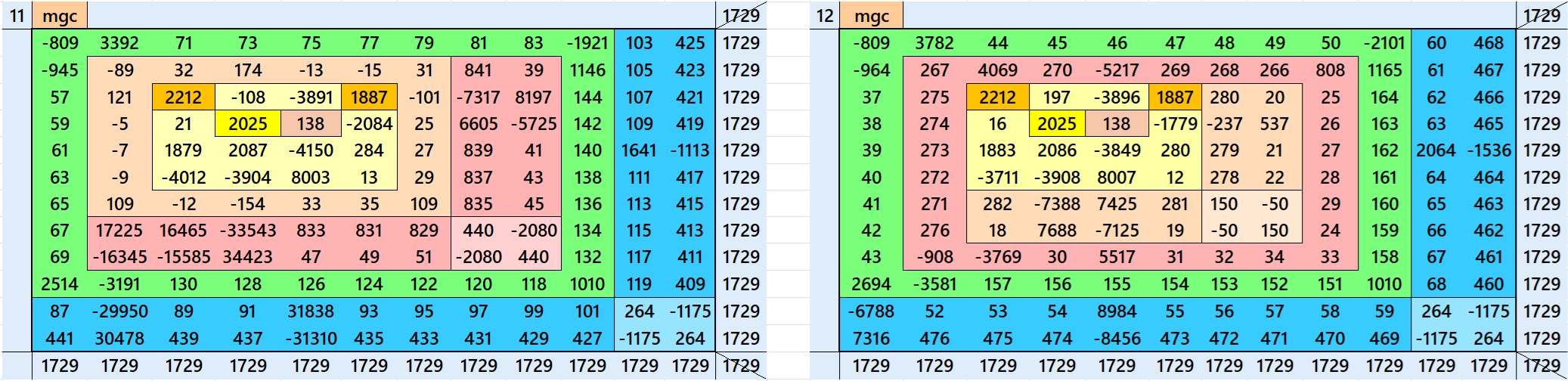
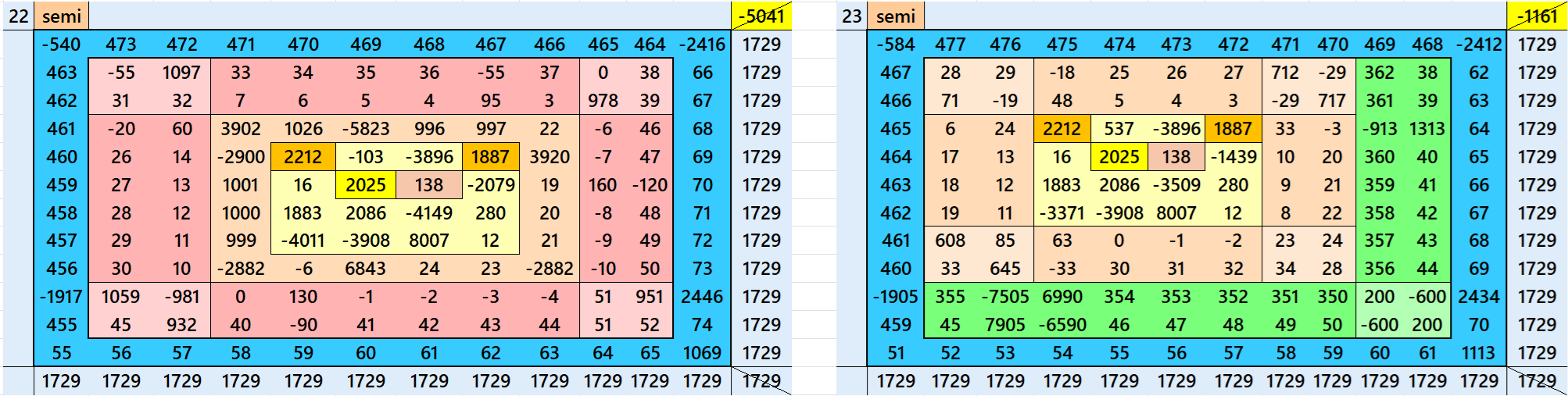
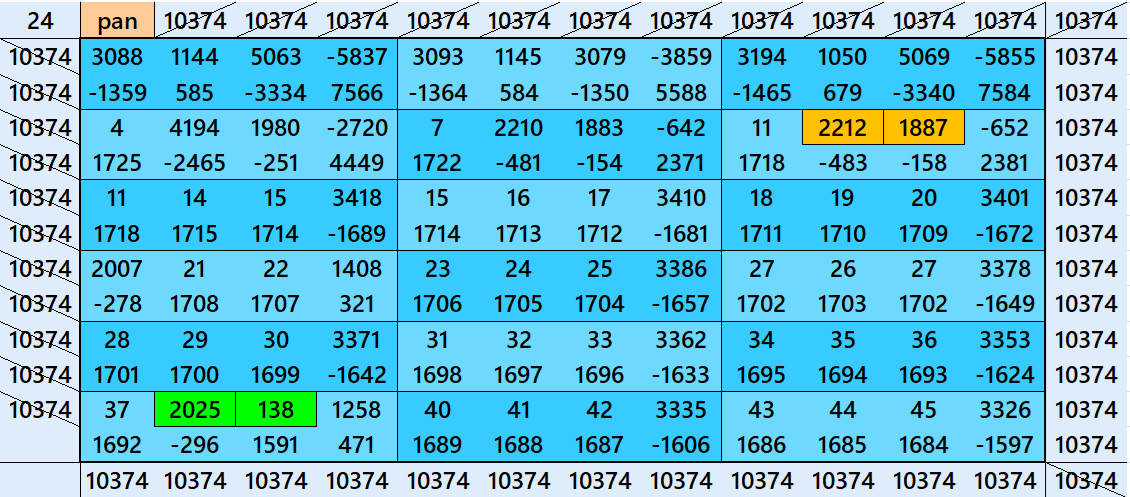
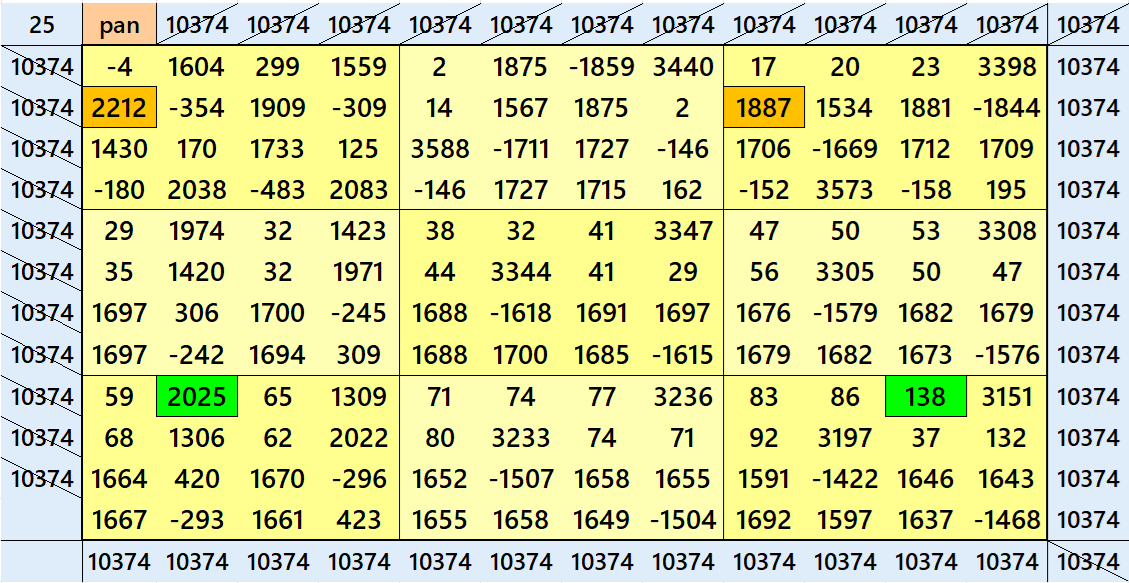
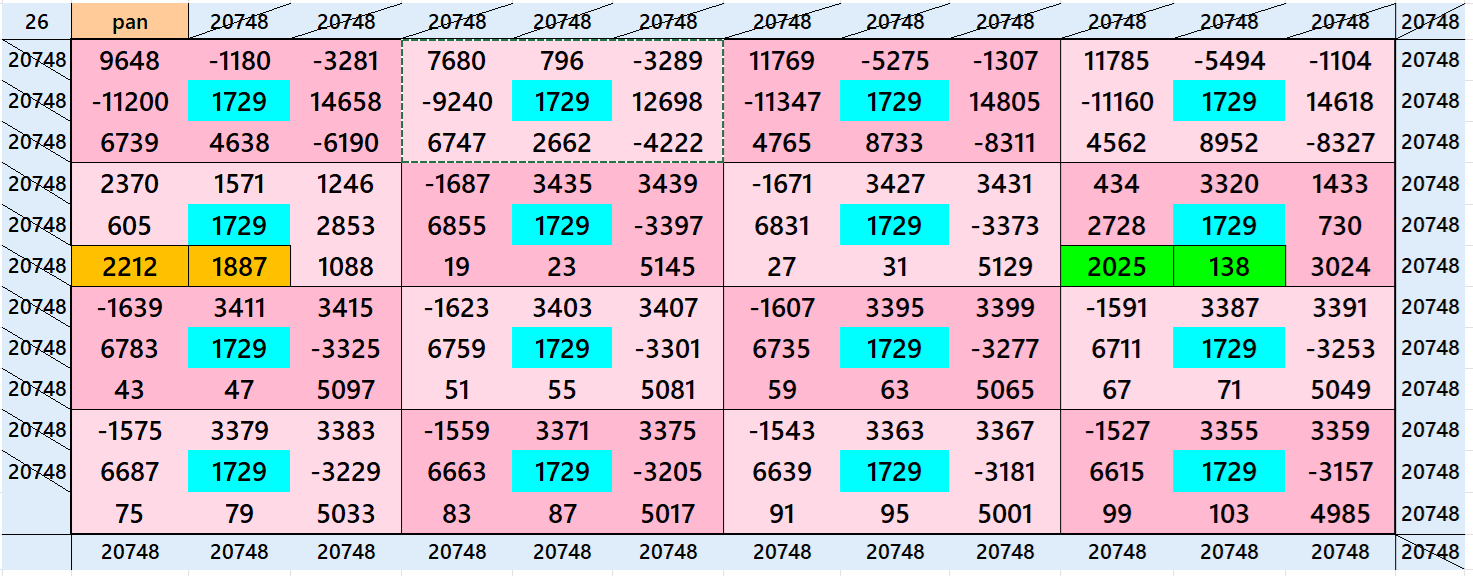
Above there are 26 examples magic squares of order 12 with magic sum 1729. The first 13 examples are different types of magic squares. The next 10, i.e., 14 to 23 examples are of semi-magic squares of order 12. The last three examples are of different type. All the three examples are pandiagonal. The example 24 is based on 18 equal sums magic rectangles of order 2×4. The example 25 is with 9 equal sums pandiagonal magic squares of order 4. The example 26 is based on 12 equal sums magic squares of order 3. The magic sums of examples 24, 25 and 26 are S12×12:=10374=6*1729, S12×12:=10374=6*1729 and S12×12:=20748=12*1729 respectively. See below the sums of magic rectangles and magic squares of lower orders of examples 24, 25 and 26:

  • Magic Rectangles Sums for Example 24:

  • Pandiagonal Magic Square Sums of Order 4 for Example 25:

  • Magic Square Sums of Order 3 for Example 26:

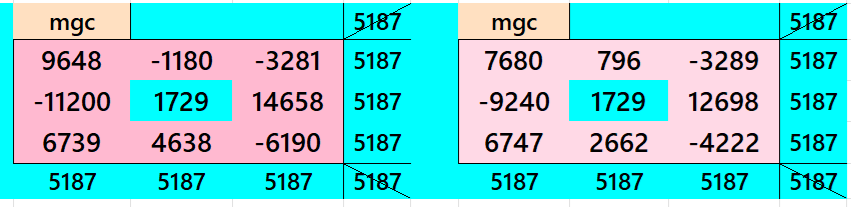
In this case there are only two magic squares are there. In the similar way we can write sum of other magic squares of order 3 for the example 26.

All 26 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

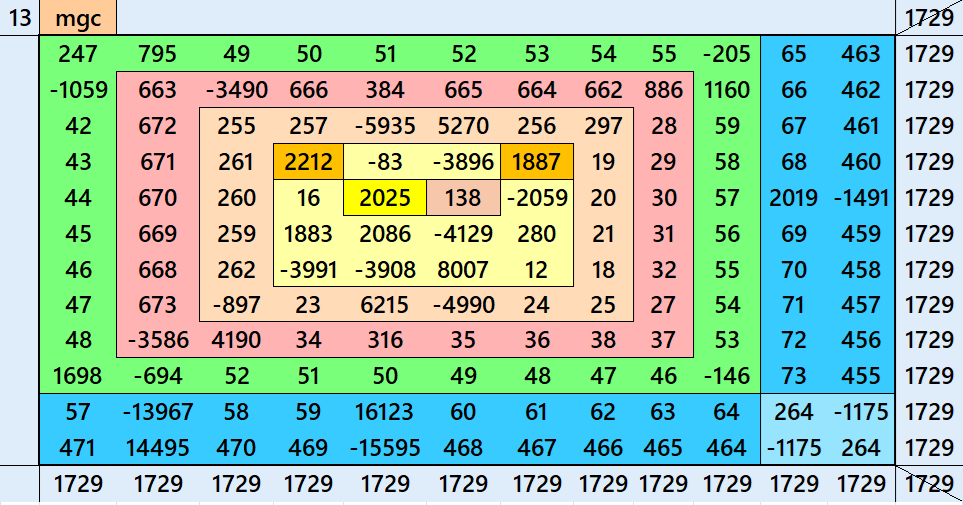
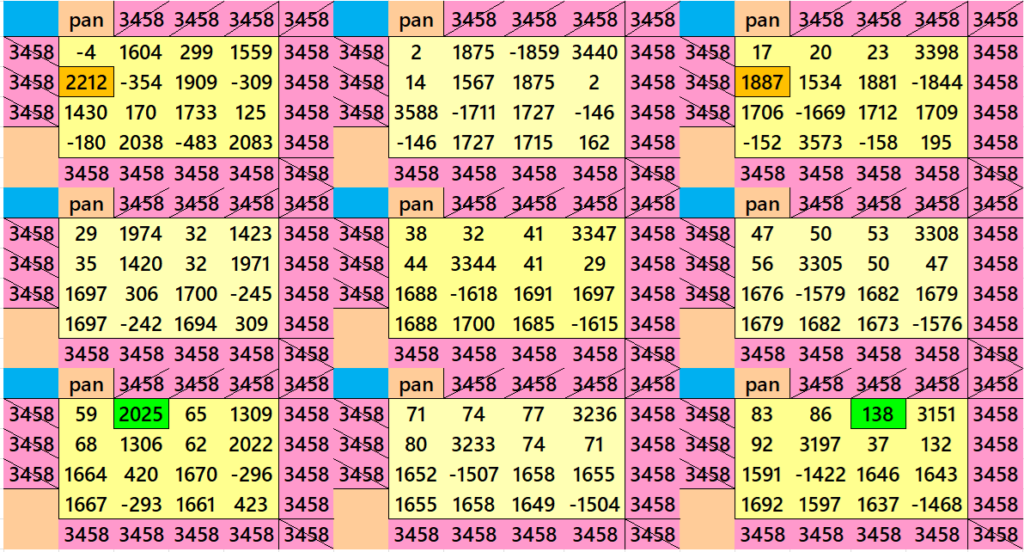
Magic Squares of Order 13

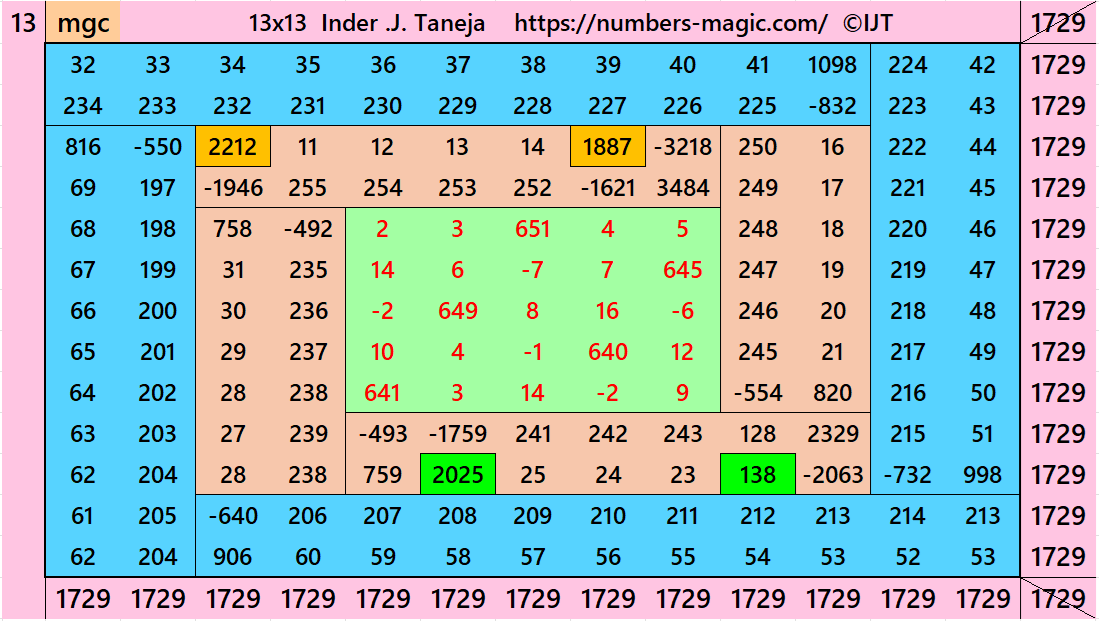
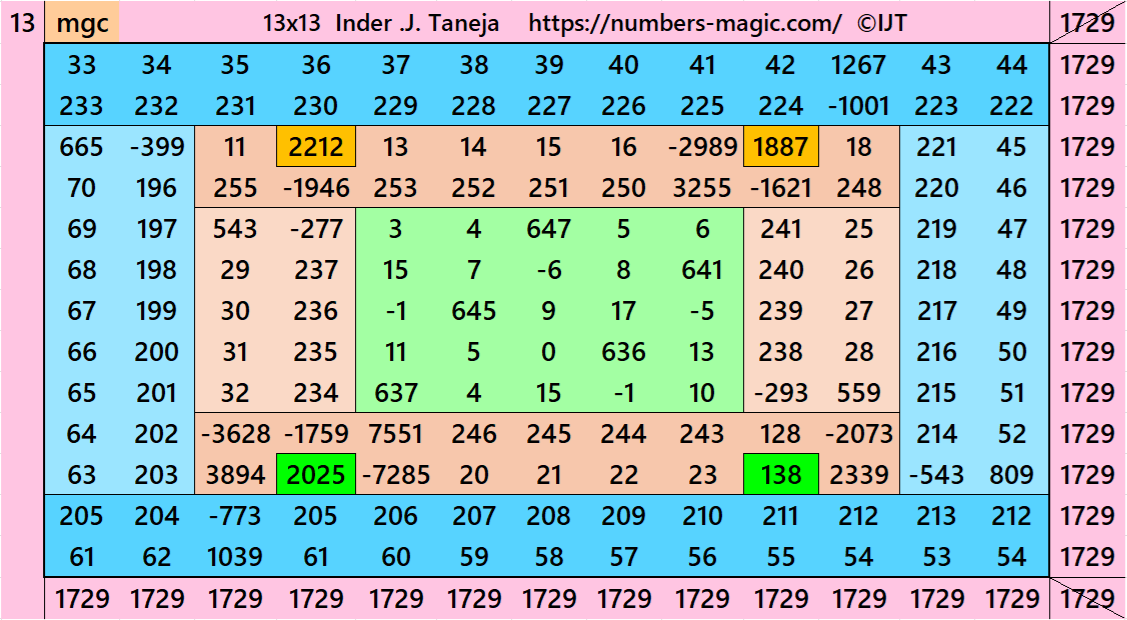
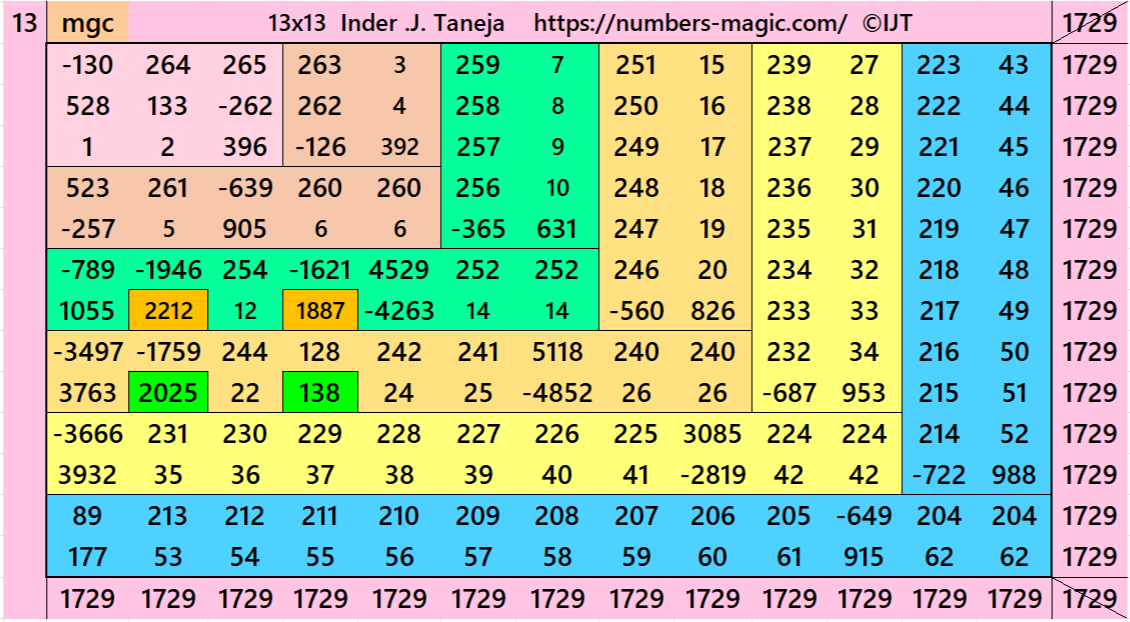
Above there are 3 examples magic squares of order 13 with magic sum 1729. All 3 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

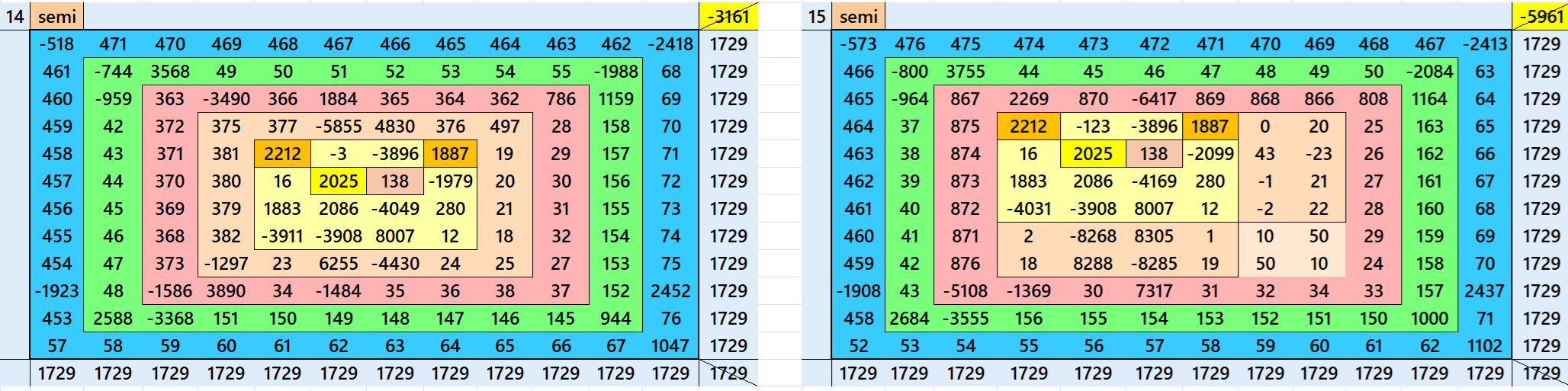
Magic Squares of Order 14

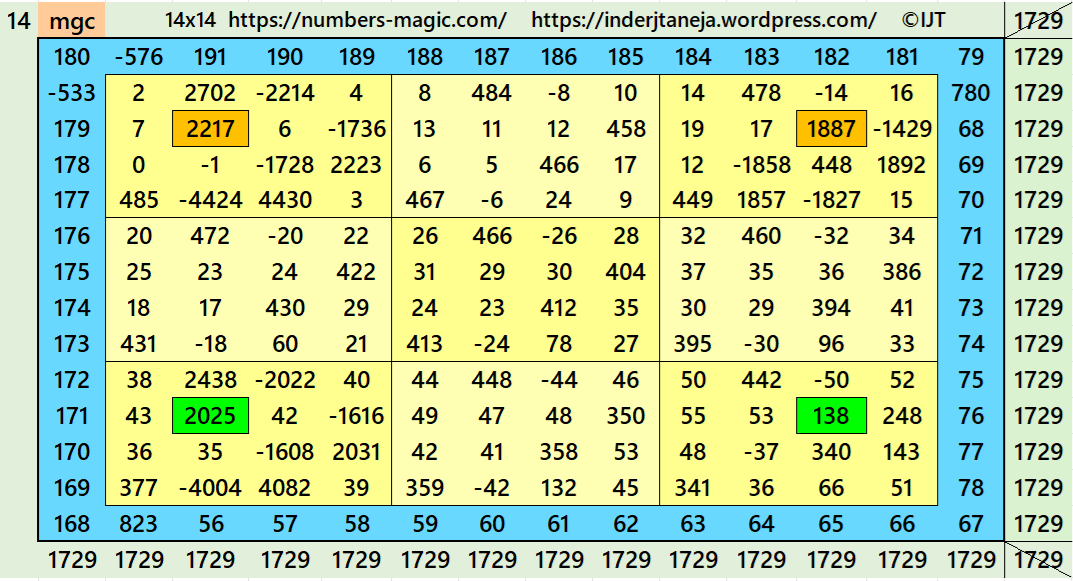
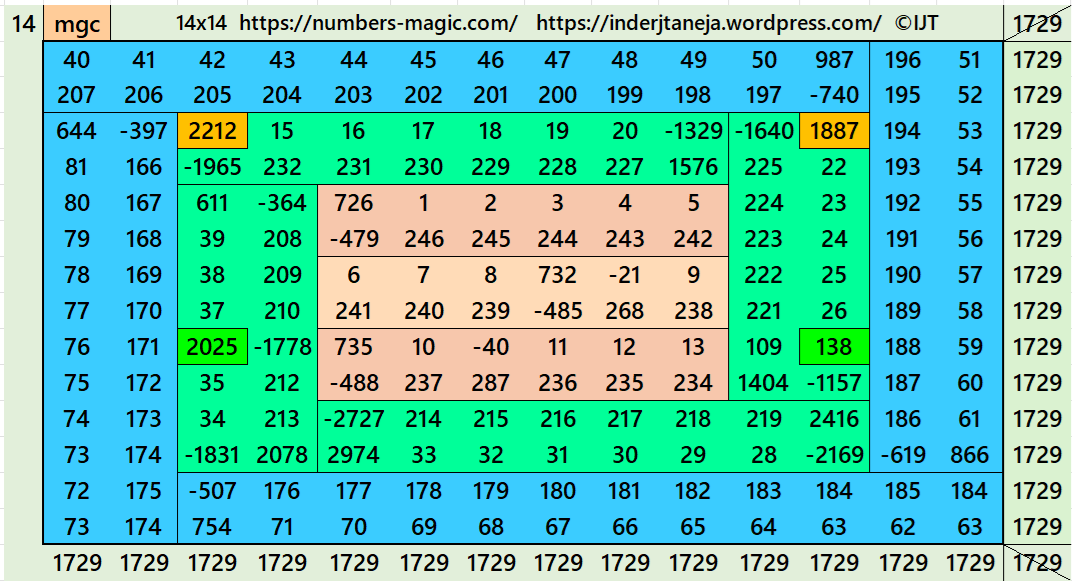
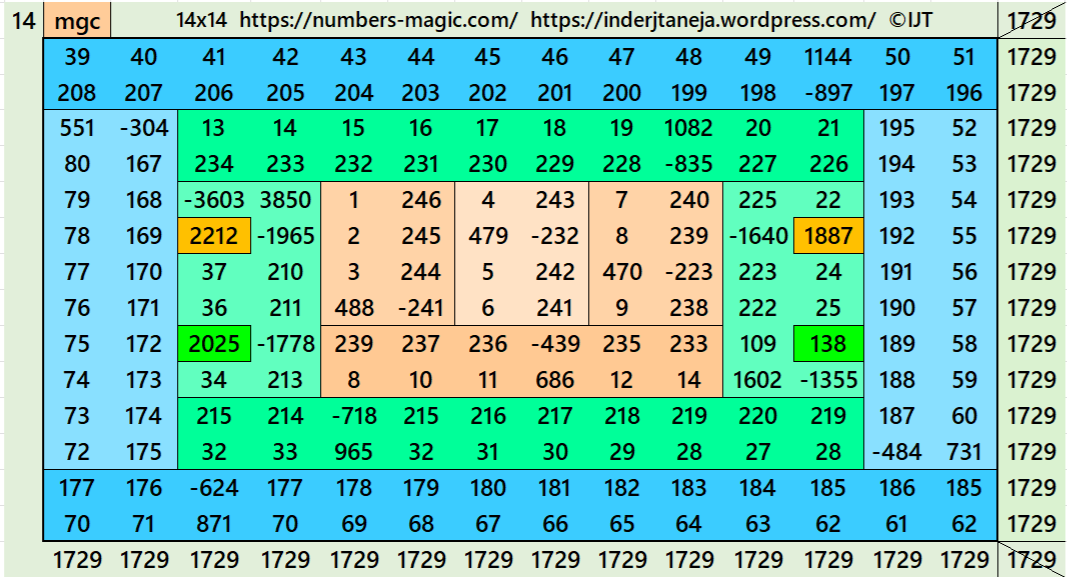
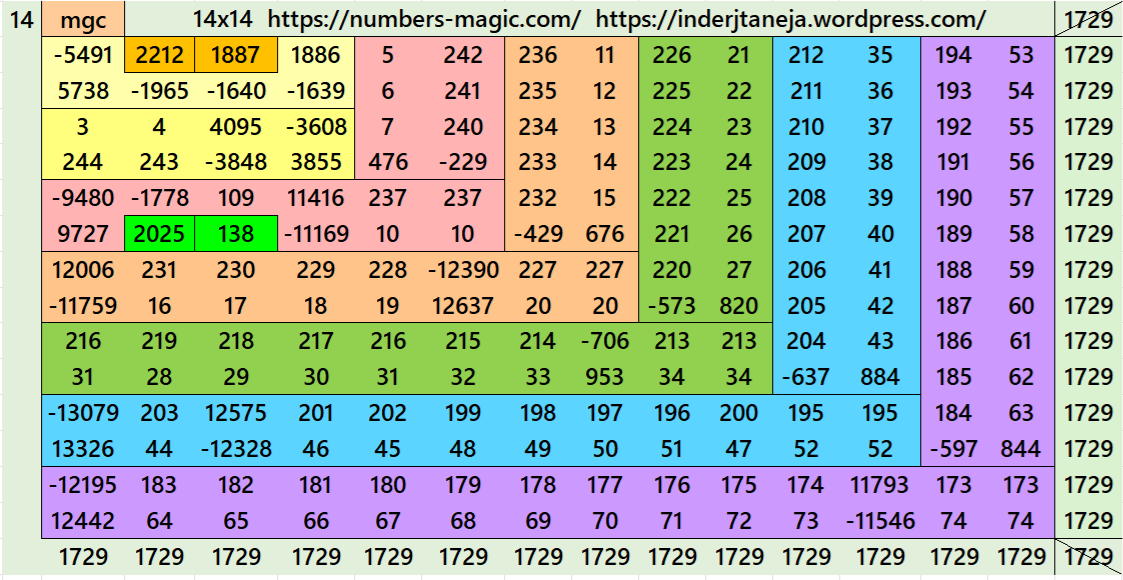
Above there are 4 examples magic squares of order 14 with magic sum 1729. All 4 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

Magic Squares of Order 15

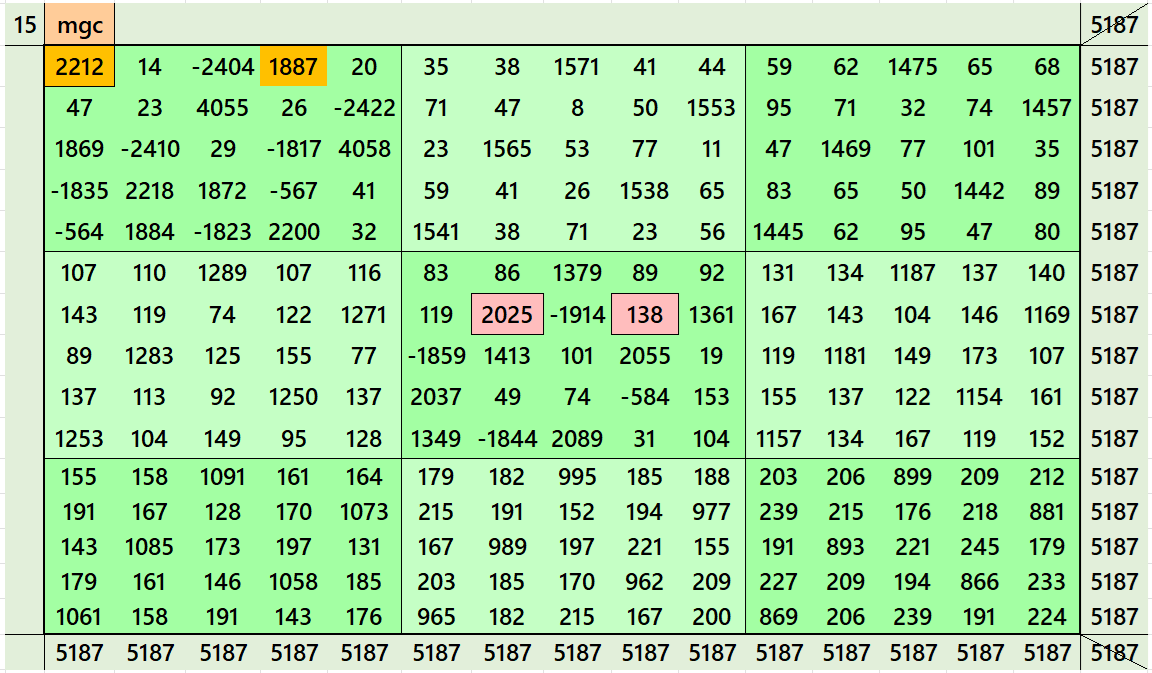
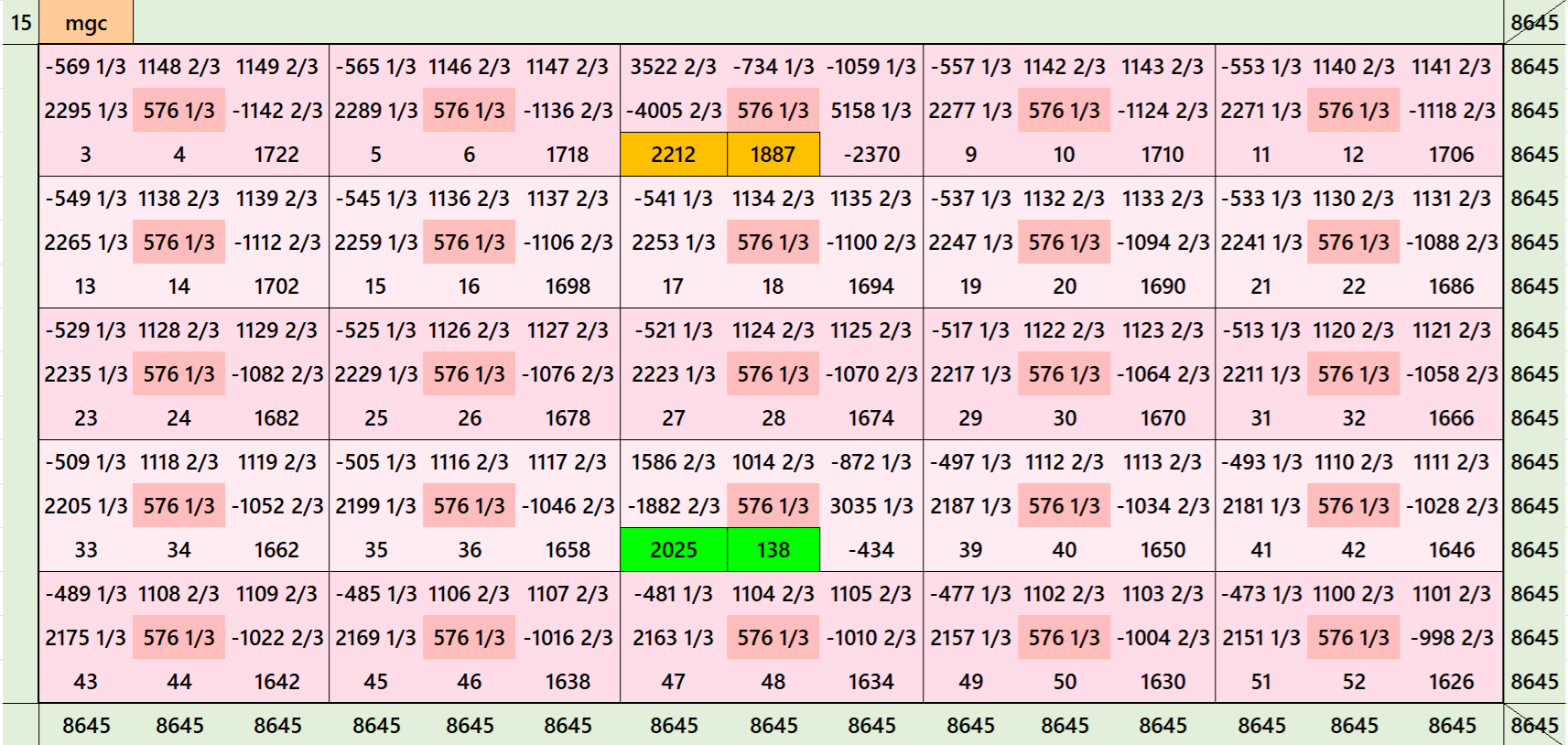
Above there are 2 examples magic squares of order 15 with magic sum 1729. First examples is based on 9 equal sums pandiagonal magic squares of order 5. The second example is based on 25 equal sums magic squares of order 3. It contains fractional entries.

Both the examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

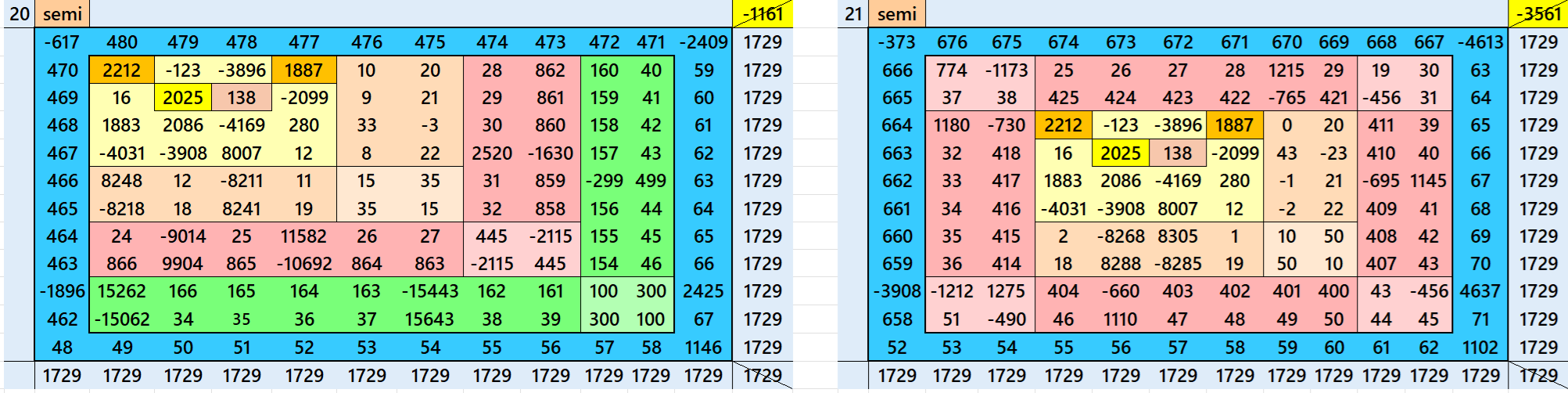
Magic Squares of Order 19

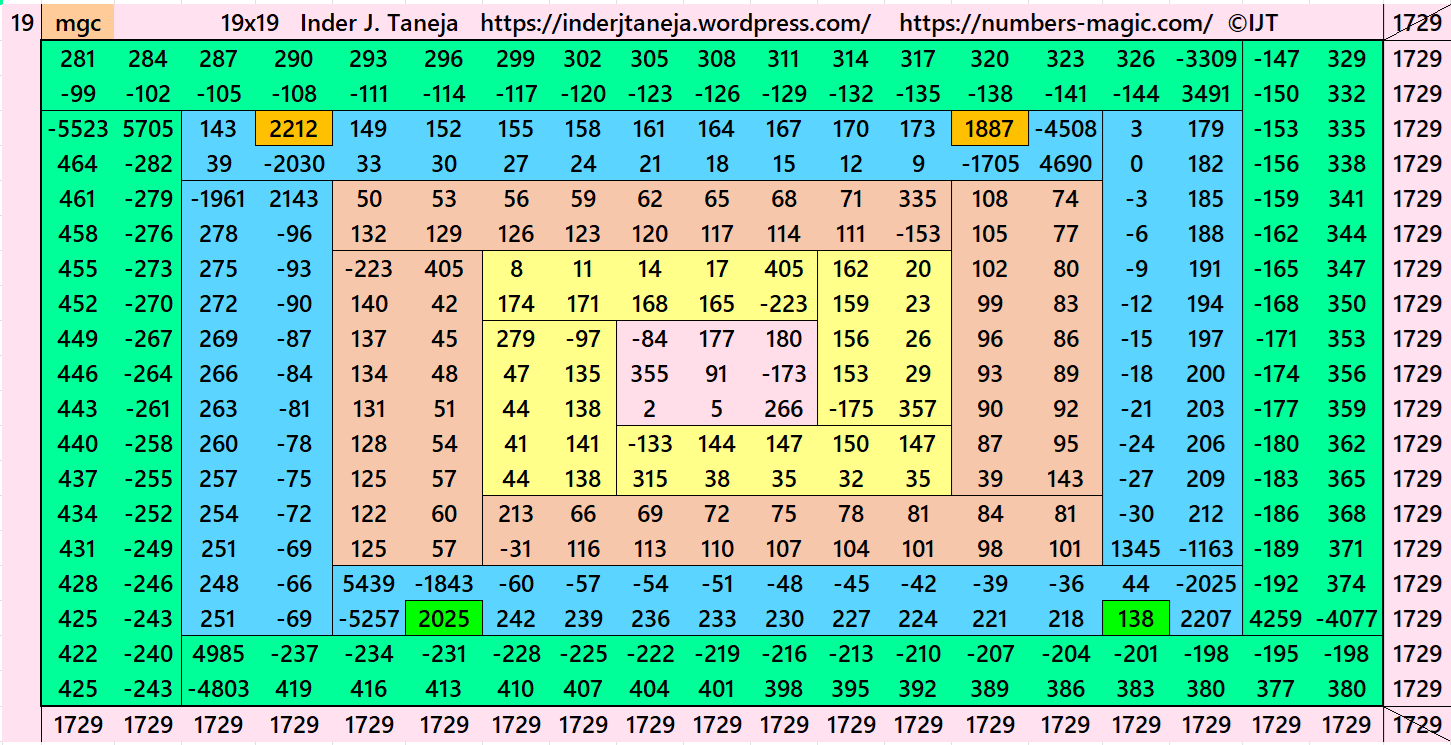
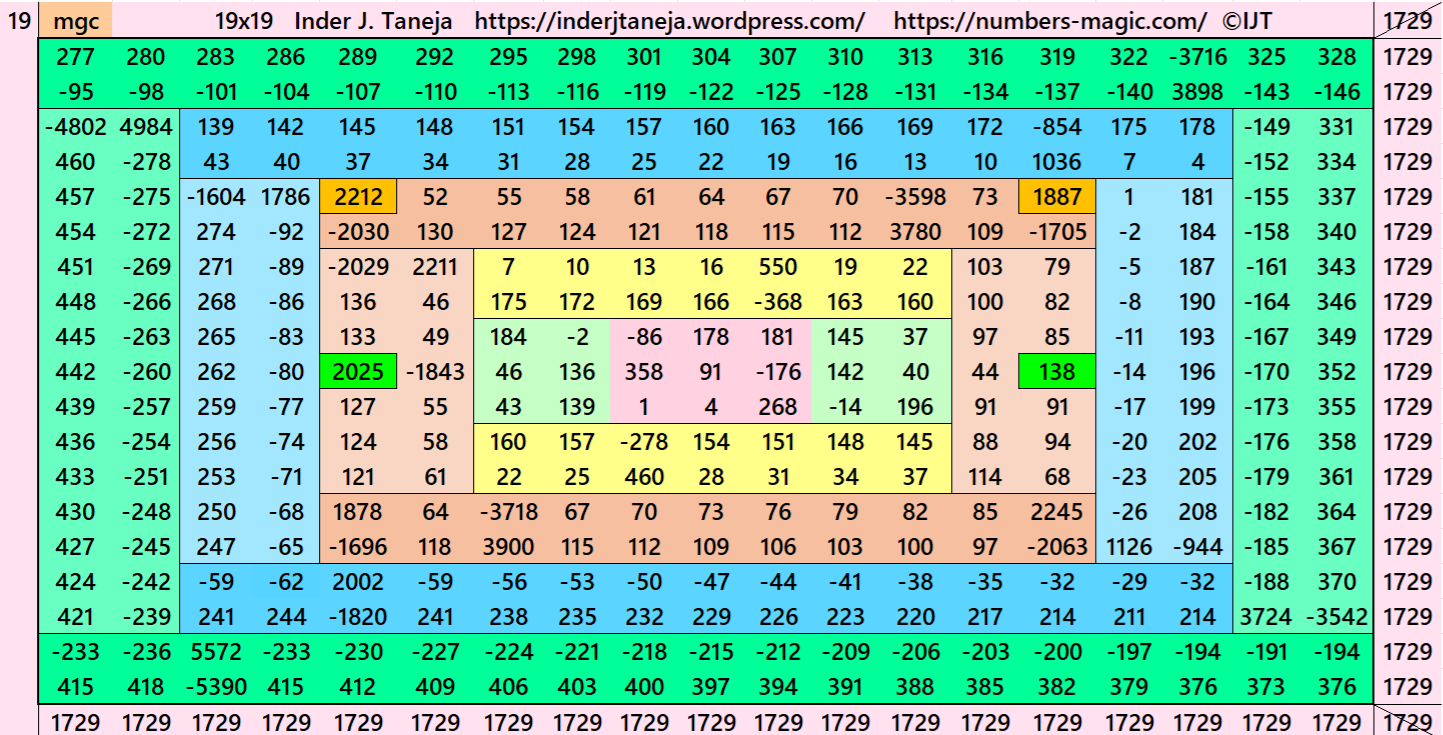
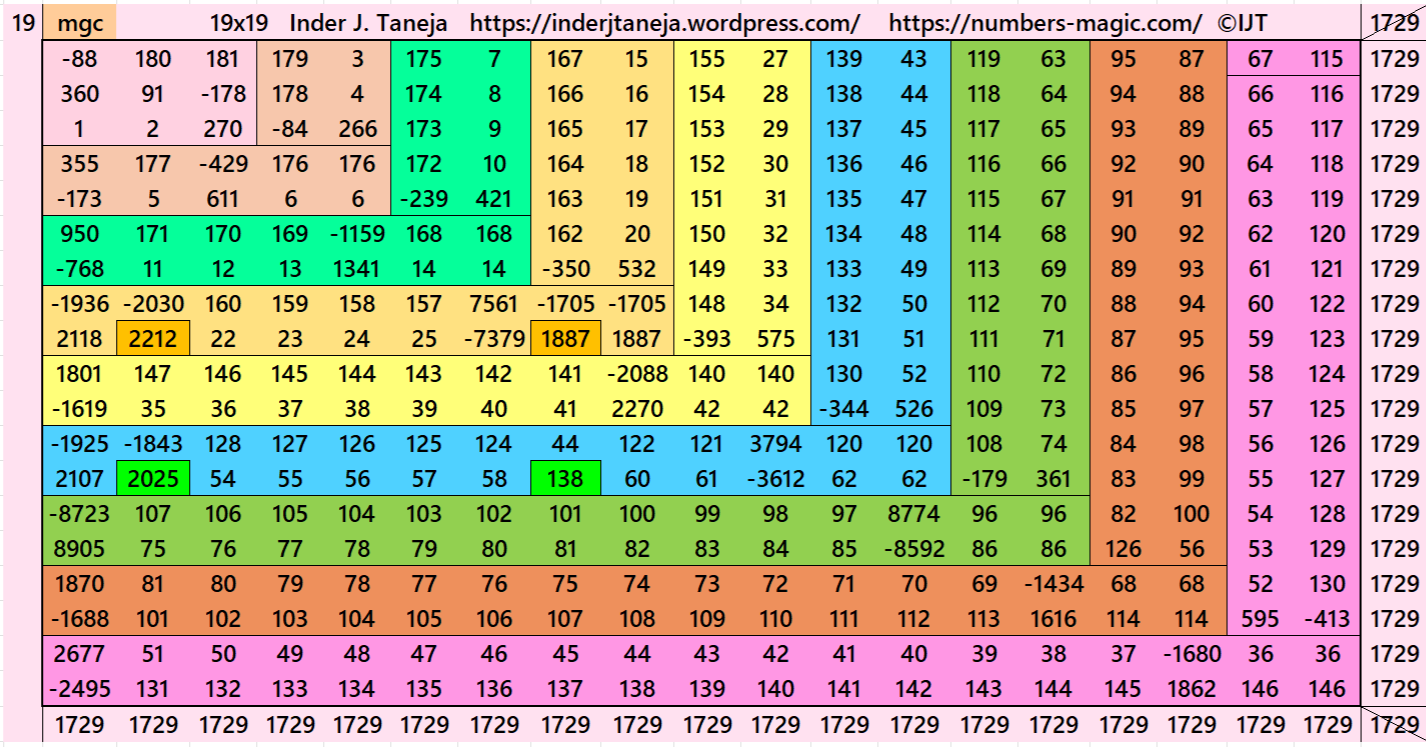
Above there are 3 examples magic squares of order 19 with magic sum 1729. All 3 examples use special entries, namely the date of birth of S. Ramanujan (22.12.1887) and his 138th anniversary on 22.12.2025. These contain the four numbers 2212, 1887, 2025, and 138. The construction of these magic squares is based on reduced-entry algebraic magic squares recently studied by the author. See the reference list for details.

References

Part 1: Work on S. Ramanujan

Part 2: Day and Dates of the Year – 2025 in Terms of Magic Squares

Part 3: Reduced Entries Agebraic Magic Squares

Part 4: Agebraic Magic Squares: Double-Digits, Cornered and Striped

Post Views: 68

By Inder J. Taneja

Related Post

Magic Squares

Algebraic Double-Digit and Cornered Magic Squares of Odd Orders from 5 to 19

Dec 7, 2025 Inder J. Taneja
Magic Squares

Algebraic Double-Digit and Cornered Magic Squares of Even Orders from 4 to 20

Nov 30, 2025 Inder J. Taneja
Magic Squares

Double-Digit Cyclic-Type Bordered Algebraic Magic Squares of Orders 7 to 20 for Reduced Entries

Nov 18, 2025 Inder J. Taneja

Leave a Reply

Your email address will not be published. Required fields are marked *

More to See

Curiosities

26 and 2026 in Numbers and Magic Squares

December 22, 2025 Inder J. Taneja
Magic Squares

207 Magic Squares in Honor of the 138th Anniversary of S. Ramanujan with Hardy-Ramanujan Number 1729

December 21, 2025 Inder J. Taneja
Days of Year

353rd to 358th Days of the Year – 19.12.2025 and 24.12.2025: Magic Squares of Order 12

December 19, 2025 Inder J. Taneja
Days of Year

347th to 352nd Days of the Year – 13.12.2025 and 18.12.2025: Magic Squares of Order 12

December 15, 2025 Inder J. Taneja
WP Twitter Auto Publish Powered By : XYZScripts.com