Bimagic Squares of Orders 200 and 1000: Blocks of Order 8

Whole the work is done manually on excel sheets.

Below are bimagic squares written in blocks multiples of orders 8. These are bimagic squares of order 200 and 1000. Most of the work is done manually by author in 2011.

Inder J. Taneja, Bimagic Squares of Bimagic Squares and an Open Problem, Febuarary 11, 2011, 2011, pp. 1-14, (22.02.2011), https://doi.org/10.48550/arXiv.1102.3052.

Before proceeding further below are the basic formulas to check the sums of magic and bimagic squares

• Magic Sum

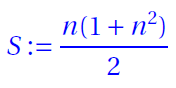
• Bimagic Sum

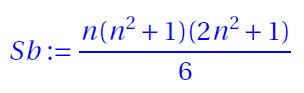
where n is the order the magic square.

Bimagic Square of Order 8

In this case, we have

S_8×8:=260; Sb_8×8:= 11180

2×4 blocks are of equal sums as of magic square, i.e., 260. See below the bimagic square of order 8.

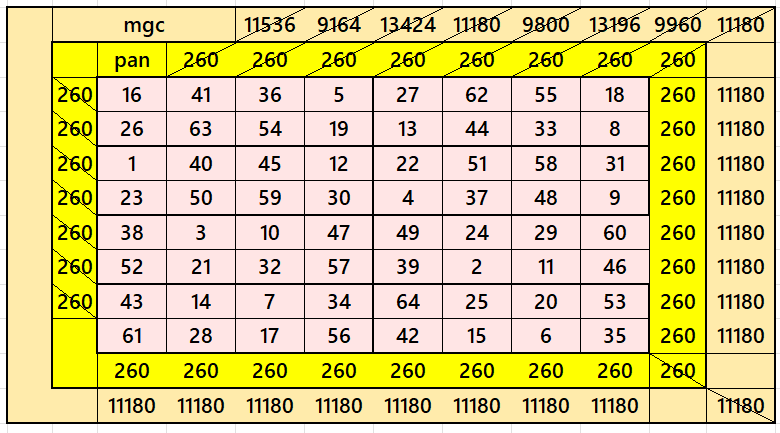
The construction of bimagic square of order 8 is well known in the history, and is done by G. Pfeffermann in 1891. In this case, we have a pandiagonal bimagic square of order 8, where the blocks of order 2×4 are of same sum as of magic square of order 8.

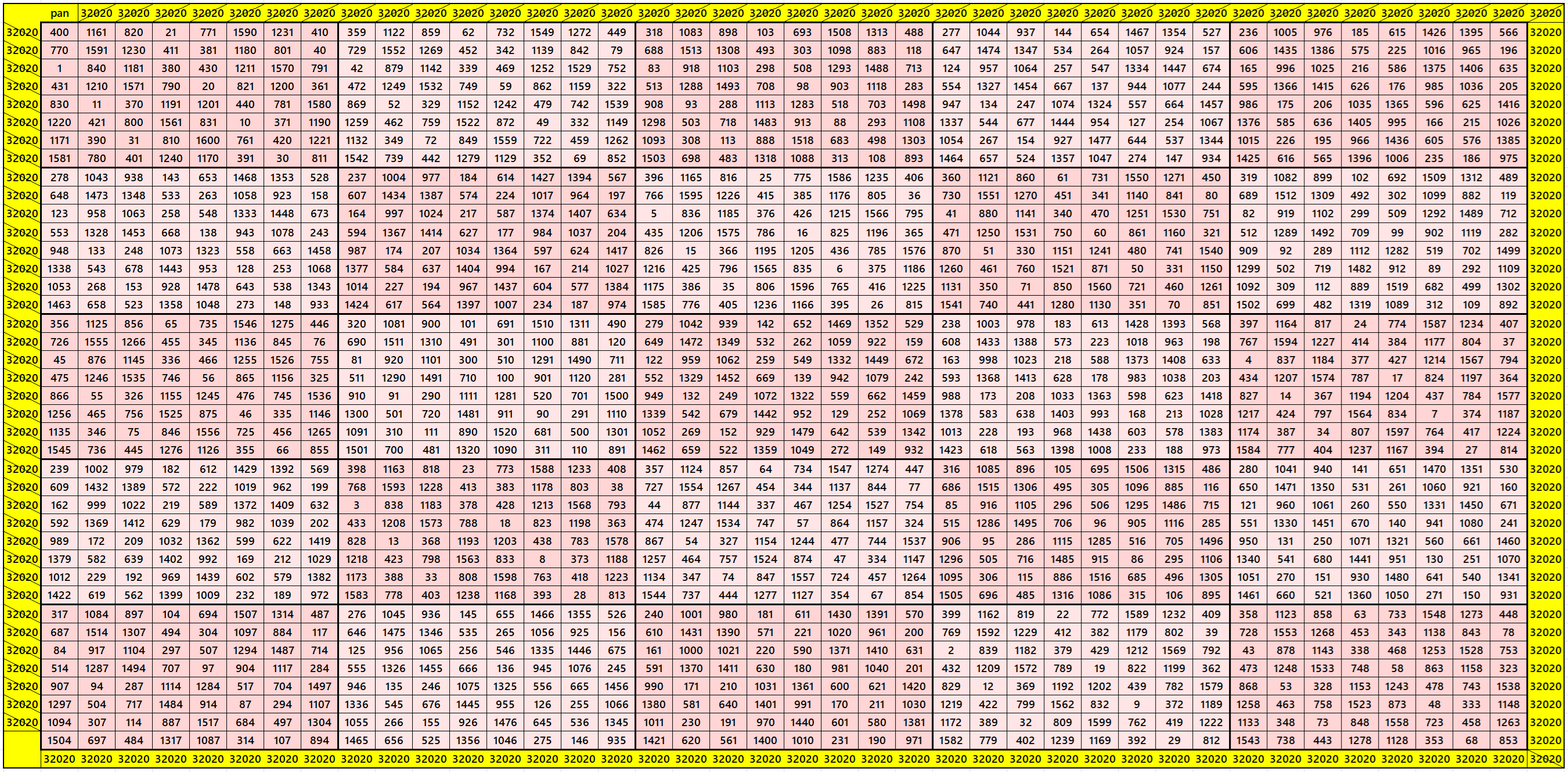
Bimagic Square of Order 40: Blocks of Order 8

In this case, we have

S_40×40:=32020; Sb_40×40:= 34165340, S_8×8:=6404.

Magic squares of order 8 are of equal sums. These are either bimagic or semi-bimagic. See bimagic square of order 40. It is also pandiagonal.

Bimagic Square of Order 200: Blocks of Orders 8 and 40

Bimagic square of order 200×200 has the the following properties:

1. 8×8 are pandiagonal magic squares with equal magic sums, i.e., S_8×8:=160004. These are with different bimagic or semi-bimagic sums.
2. 40×40 are pandiagonal equal sums magic squares with different bimagic sums, i.e., S_40×40:=800020. These are with different bimagic or semi-bimagic sums.
3. 200×200 is a pandiagonal bimagic squares with magic and bimagic sums S_200×200:=4000100 and Sb_200×200:=106670666700.

Summarizing, we have a pandiagonal bimagic square of order 200×200, where blocks of orders 8×8 and 40×40 are also pandiagonal with equal magic sums, but different bimagic or semi-bimagic sums. These values are given in tables in an excel sheet attached with the work.

• Excel file for download

Bimagic Square of Order 1000: Blocks of Orders 8, 40 and 200

Bimagic square of order 1000×1000 has the the following properties:

1. 8×8 are pandiagonal equal sums magic squares, i.e., S_8×8:=4000004. These are with different bimagic or semi-bimagic sums.
2. 40×40 are pandiagonal equal sums magic squares, i.e., S_40×40:=20000020. These are with different bimagic or semi-bimagic sums.
3. 200×200 are pandiagonal equal sum magic squares, i.e, S_200×200:=100000100. These are with different bimagic or semi-bimagic sums.
4. 1000×1000 is a pandiagonal bimagic square with magic and bimagic sums, S_1000×1000:=500000500 and Sb_1000×1000:=333333833333500.

Summarizing, we have a pandiagonal bimagic square of order 1000×1000, where blocks of orders 8×8, 40×40 and 200×200 are also pandiagonal with equal magic sums, but different bimagic or semi-bimagic sums. These values are given in tables in an excel sheet attached with the work.

• Excel file for download

References:

1. Inder J. Taneja, Block-Wise Construction of Bimagic Squares: Multiples of Orders 8 and 16.
2. Inder J. Taneja, Block-Wise Construction of Bimagic Squares Multiples of 25: Orders 25, 125 and 625.
3. Inder J. Taneja, Block-Wise Construction of Bimagic Squares Multiples of 9: Orders 9, 81 and 729.
4. Inder J. Taneja, Block-Wise Construction of Bimagic Squares of Orders 121 and 1331.
5. Inder J. Taneja, Bimagic Squares of Orders 256, 512 and 1024: Blocks of Order 16.