Below are bimagic squares written in blocks multiples of order 9. These are of orders 9, 81 and 729 The work is done manually by author in 2011. The work is summarized in the link below:
Inder J. Taneja, Bimagic Squares of Bimagic Squares and an Open Problem, Febuarary 11, 2011, 2011, pp. 1-14, (22.02.2011), https://doi.org/10.48550/arXiv.1102.3052.
Before proceeding further below are the basic formulas to check the sums of magic and bimagic squares
- Magic Sum
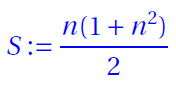
- Bimagic Sum
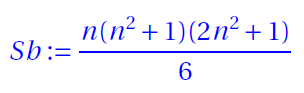
where n is the order the magic square.
Bimagic Square of Order 9
In this case, we have
S9×9:=369; Sb9×9:= 20049,
Sum of entries of blocks of order 3×3 are the same as of magic square. i.e., S9×9:=369. Below is an example of bimagic square of order 9. It is constructed by G. Pfeffermann in 1891.
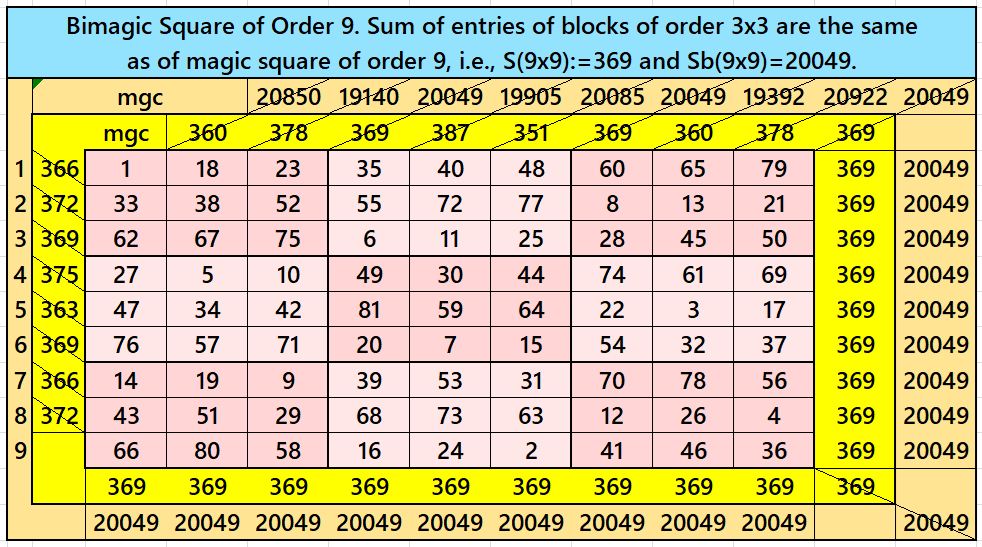
We shall use the idea of this bimagic square to bring bimagic squares of orders 81 and 729.
Bimagic Square of Order 81: Blocks of Order 9
Bimagic Square of order 81×81 with magic and bimagic sums
S81×81:=265761 and Sb81×81:=1162527201
Each block of order 9 is a magic square with equal magic sums, S9×9:=29529. It also has the same property as of order 9, i.e., sum of entries of blocks of order 3×3 are the same as of magic square of order 9, i.e., S9×9:=29529.
Excel sheet of Bimagic Square of Order 81
Bimagic Square of Order 729: Blocks of Order 9 and 81
Bimagic Square of order 729 with magic and bimagic sums
S729×729 :=193710609 and Sb729×729 := 68630571075249
Blocks of orders 9 and 81 are only magic squares with equal magic sums:
S81×81 := 21523401 and S9×9 := 2391489.
Similar to magic squares of orders 9 and 81 as given above, in this case also the sum of entries of blocks of order 3×3 are the same as of magic square of orderr 9, i.e., S9×9 := 2391489.
Unfortunately, in this case, we don’t have sub-groups of orders 9 or 81 as bimagic squares. These are only magic squares of equal sums.

