Block-Wise Construction of Bimagic Squares Multiples of 25: Orders 25, 125 and 625

Whole the work is done manually on excel sheets.

Below are bimagic squares written in blocks multiples of order 25. These are orders 25, 125 and 625 The work is done manually by author in 2011. See the reference below:

Inder J. Taneja, Bimagic Squares of Bimagic Squares and an Open Problem, Febuarary 11, 2011, 2011, pp. 1-14, (22.02.2011), https://doi.org/10.48550/arXiv.1102.3052.

Before proceeding further below are the basic formulas to check the sums of magic and bimagic squares

• Magic Sum

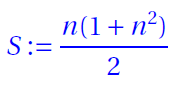
• Bimagic Sum

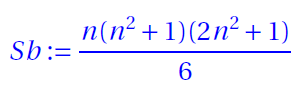
where n is the order the magic square.

Bimagic Square of Order 25

In this case, we have

S_25×25:=7825; Sb_25×25:= 3263025,

Blocks of order 5 are pandiagonal and of equal sums, S_5×5 := 1565. The magic squares of order 25 is also pandiagonal. See below the bimagic square of order 25.

Bimagic Square of Order 125: Blocks of Order 25

Bimagic Square of order 125×125 with magic and bimagic sums

S_125×125:=976625 and Sb_125×125:= 1073502625

Each block of order 25 is a pandiagonal bimagic square with different bimagic sums, S_25×25:=195325.

Using H. White’s software we can easily check that the bimagic square of order 125 is pandiagonal.

Excel sheet of Bimagic Square of Order 125

Bimagic Square of Order 625: Blocks of Order 25 and 125

Bimagic Square of order 625×625 with magic and bimagic sums

S_625×625:=122070625 and Sb_625×625:= 31789265950625

Each block of order 125 is a pandiagonal bimagic square with equal magic and bimagic sums

S_125×125:=24414125 and Sb_125×125:= 6357853190125

Each block of order 25×25 is bimagic square of same magic sums, S_25×25:=4882825, but different bimagic sums given in a table in excel sheet attached with this work.

Blocks of order 5 are also pandiagonal magic squares with equal magic sums S_5×5:=(1/5)S_25×25:=976565.

Using H. White’s software, we can easily check that the bimagic square of order 625 is pandiagonal.

Excel sheet of Bimagic Square of Order 625