Block-Wise Construction of Bimagic Squares: Multiples of Orders 8 and 16

Whole the work is done manually on excel sheets.

Below are bimagic squares written in blocks multiples of orders 8 and 16. Most of the work is done manually by author in 2011. Few of them are with the help of Aale de Winkel <aaledewinkel@magichypercubes.com>, Magic Encyclopedia magic square, magic cube, magic tesseract, magic hypercube. See the reference below:

• Inder J. Taneja, Bimagic Squares of Bimagic Squares and an Open Problem, Febuarary 11, 2011, 2011, pp. 1-14, (22.02.2011), https://doi.org/10.48550/arXiv.1102.3052.

Before proceeding further below are the basic formulas to check the sums of magic and bimagic squares

• Magic Sum

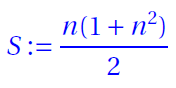
• Bimagic Sum

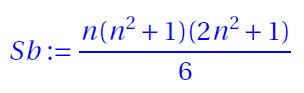
where n is the order the magic square.

Bimagic Square of Order 8

In this case, we have

S_8×8:=260; Sb_8×8:= 11180

2×4 blocks are of equal sums as of magic square, i.e., 260. See below the bimagic square of order 8.

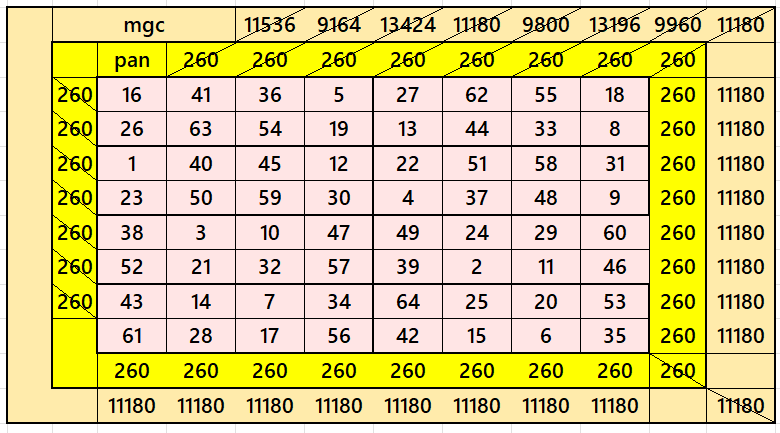
The construction of bimagic square of order 8 is well known in the history, and is done by G. Pfeffermann in 1891. In this case, we have a pandiagonal bimagic square of order 8, where the blocks of order 2×4 are of same sum as of magic square of order 8.

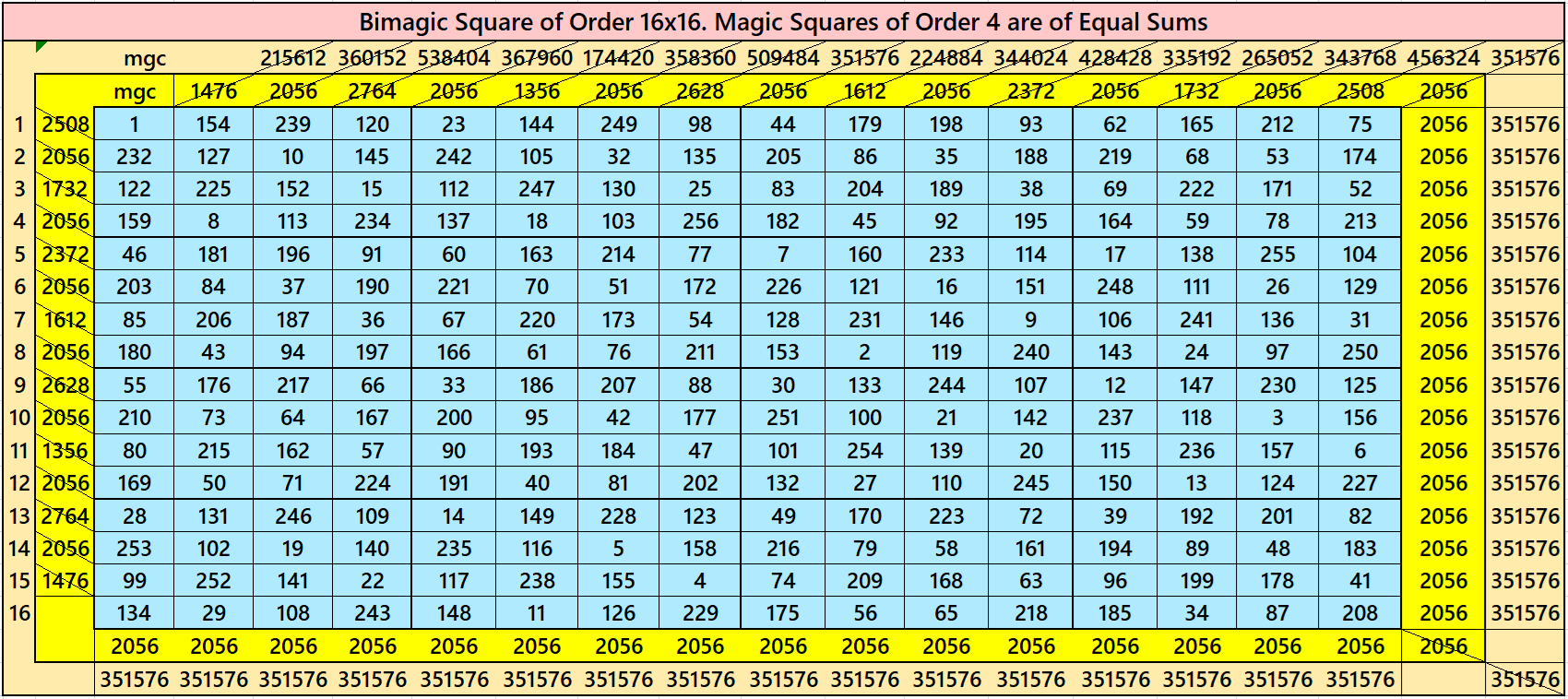
Bimagic Square of Order 16

In this case, we have

S_16×16:=2056; Sb_16×16:= 351576, S_4×4:=(1/4) S_16×16=514.

See below the bimagic square of order 16.

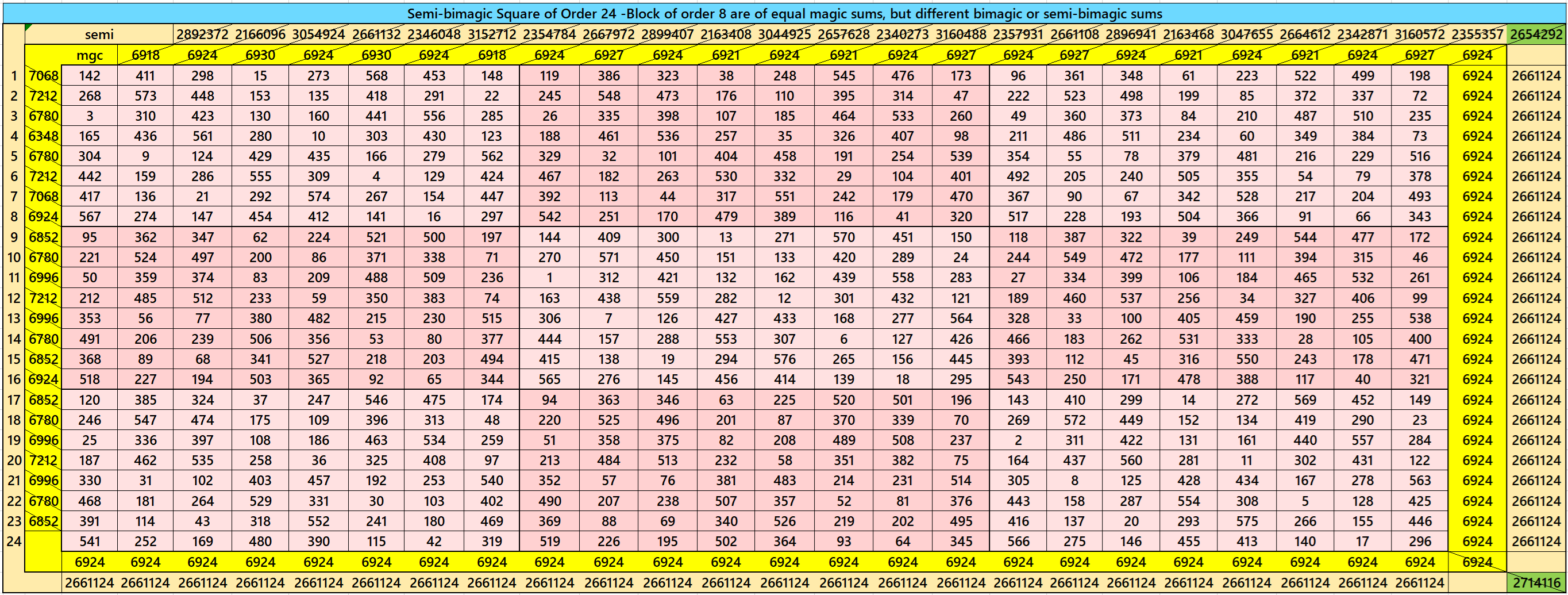
Semi-Bimagic Square of Order 24: Blocks of Order 8

In this case, we have

S_24×24:=6924; Sb_24×24:= 2661124 (semi), S_8×8:=2308.

Magic squares of order 8 are of equal sums. These are either bimagic or semi-bimagic. See semi-bimagic square of order 24

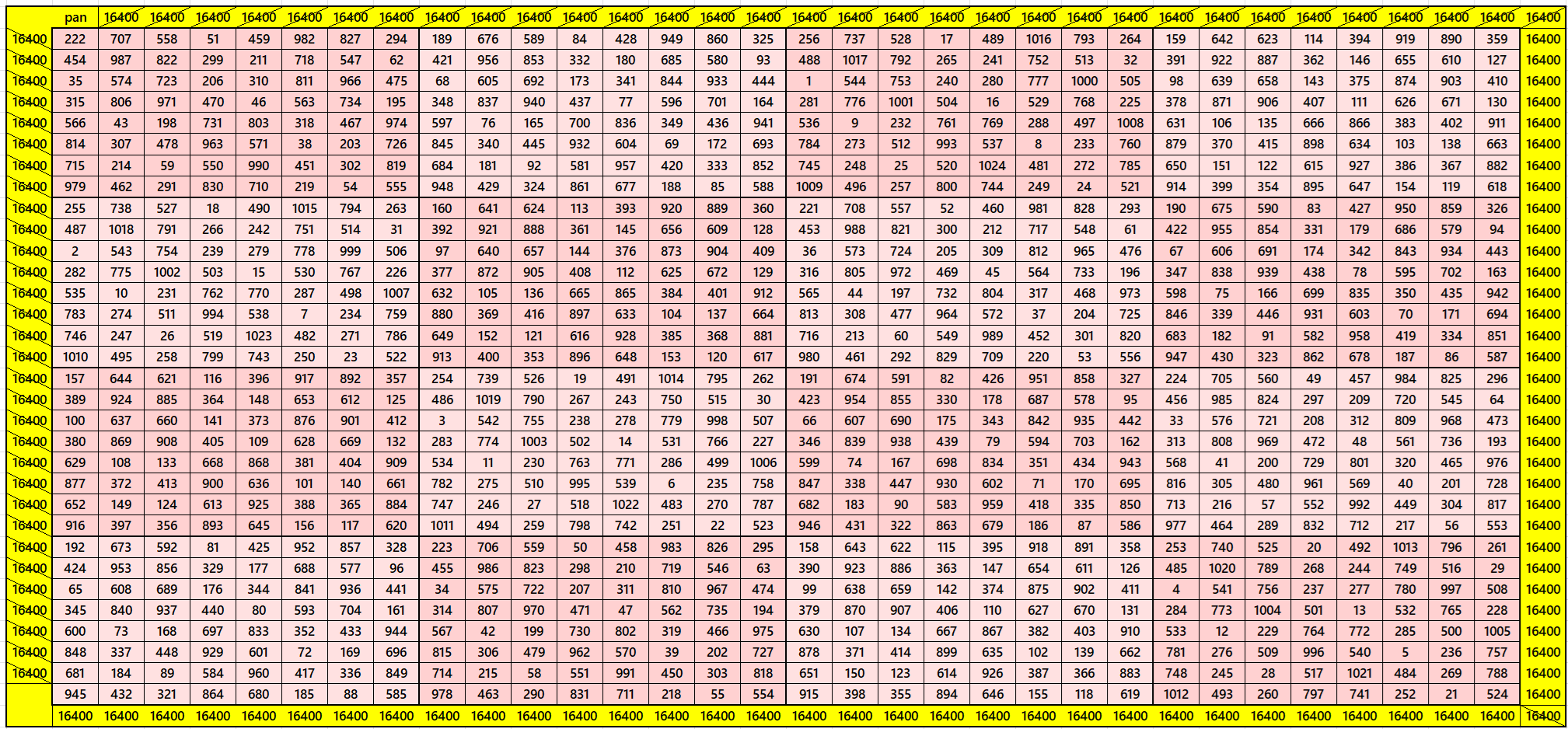
Bimagic Square of Order 32: Blocks of Order 8

In this case, we have

S_32×32:=16400; Sb_32×32:= 11201200, S_8×8:=4100.

Magic squares of order 8 are of equal sums. These are either bimagic or semi-bimagic. See bimagic square of order 32. It is also pandiagonal.

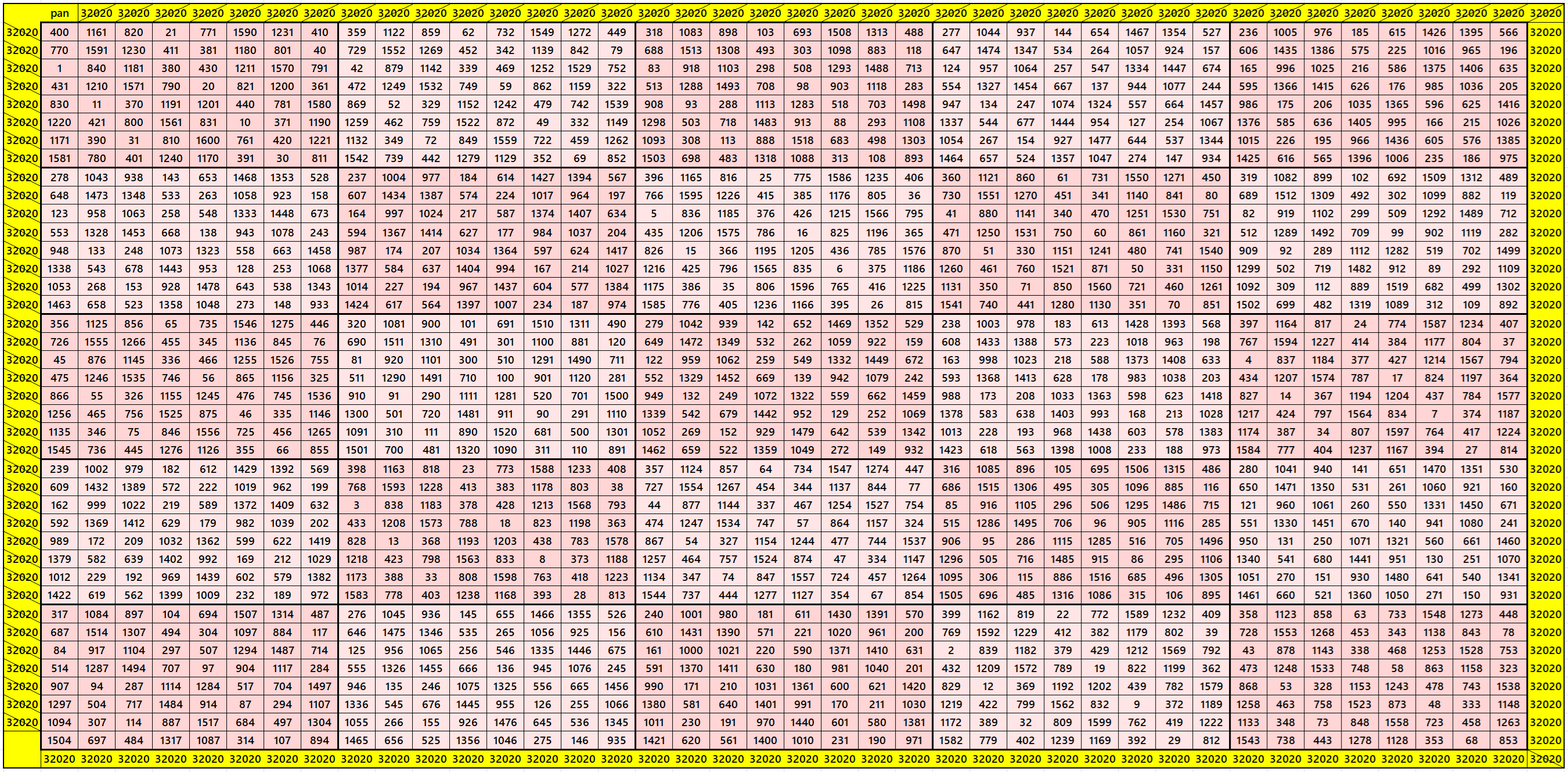
Bimagic Square of Order 40: Blocks of Order 8

In this case, we have

S_40×40:=32020; Sb_40×40:= 34165340, S_8×8:=6404.

Magic squares of order 8 are of equal sums. These are either bimagic or semi-bimagic. See bimagic square of order 40. It is also pandiagonal.

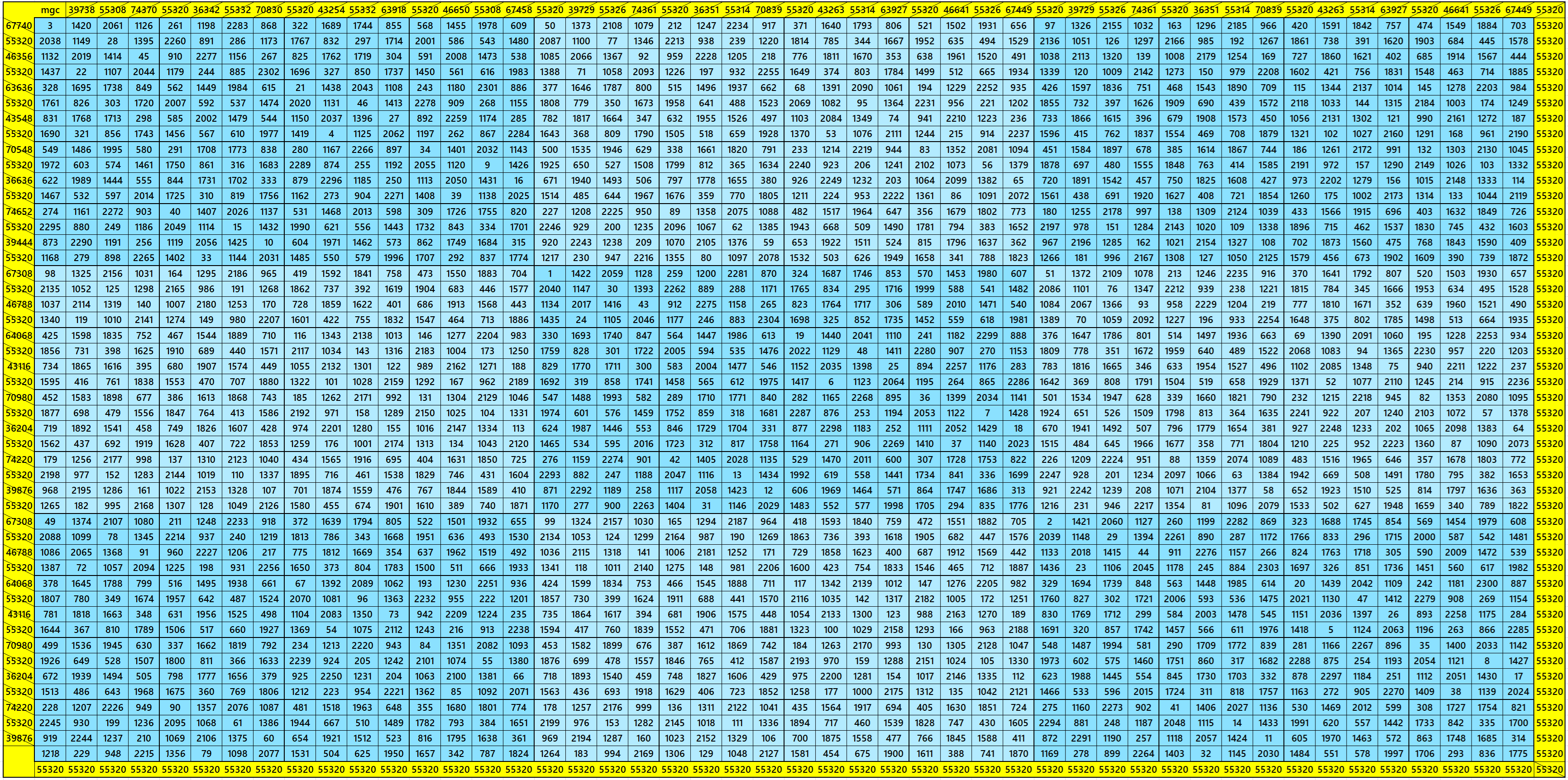
Semi-Bimagic Square of Order 48: Blocks of Order 16

In this case, we have

S_48×48:=55320; Sb_48×48:= 84989960 (semi-bimagic); S_16×16:=18440.

Magic squares of order 16 are of equal sums. These are all bimagic. See below semi-bimagic square of order 48.

Bimagic Square of Order 56: Blocks of Order 8

In this case, we have

S_56×56:=87836; Sb_56×56:= 183665076; S_8×8:=12548.

Magic squares of order 8 are of equal sums. These are either bimagic or semi-bimagic squares of order 8. See below bimagic square of order 56.

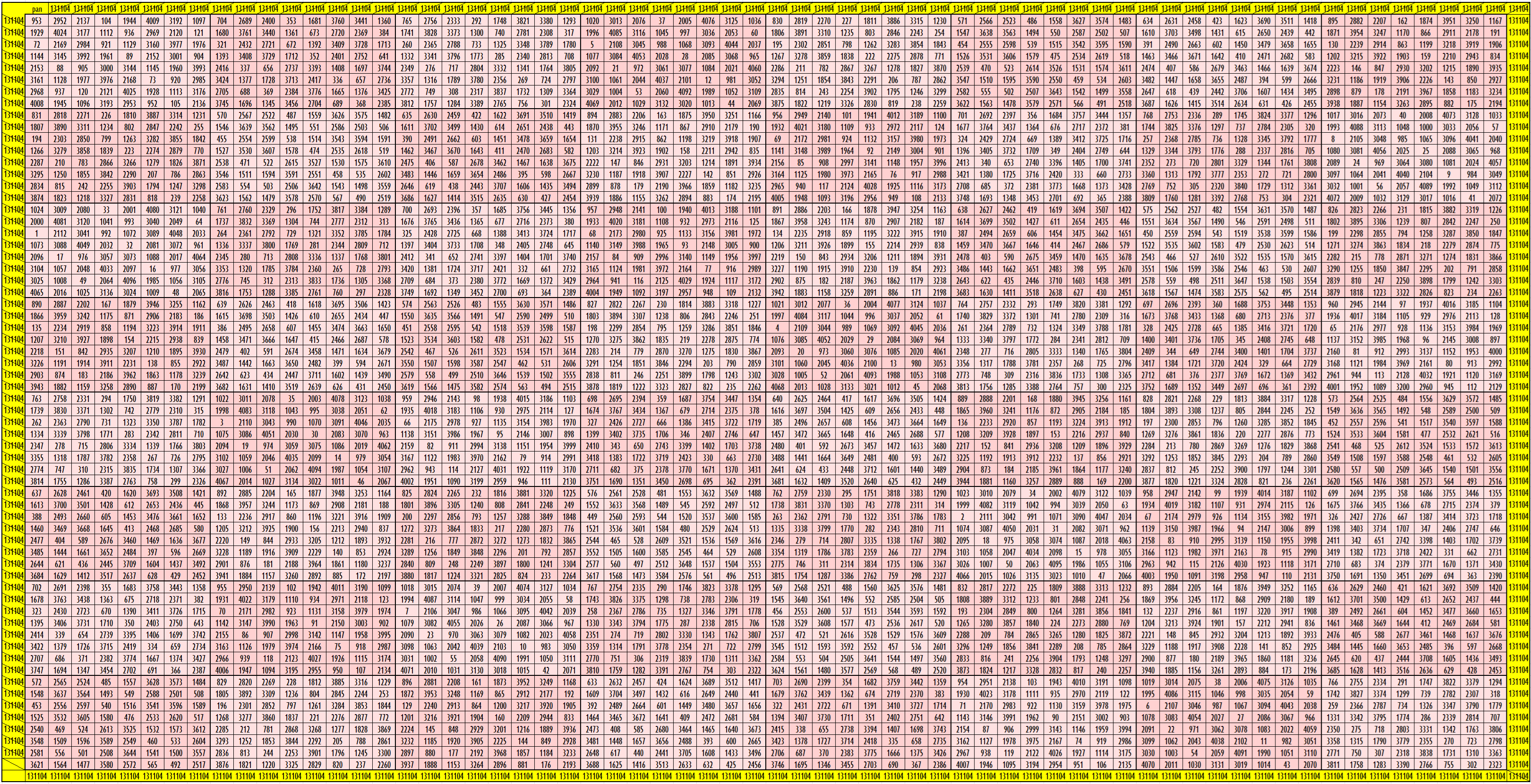
Bimagic Squares of Order 64: Blocks of Orders 8 and 16

Below are two types of bimagic squares of order 64:

First Type: Blocks of Order 8

In this case, we have

S_64×64:=131104; Sb_64×64:= 358045024; S_8×8:=16338.

See below bimagic square of order 64 with blocks of order 8. These blocks of order 8 are either bimagic or semi-bimagic with different sums, but the magic sum of all order magic squares is same.

Second Type: Blocks of Order 16

In this case, we have

S_64×64:=131104; Sb_64×64:= 358045024; S_16×16:=32776 and S_4×4:==8194.

Magic squares of order 16 are of equal sums. These are all bimagic. See below bimagic square of order 64 with blocks of order 16. These blocks of order 16 are bimagic squares with different sums, but the magic sum of all order 16 magic squares is same.

Bimagic Square of Order 72: Blocks of Order 8

In this case, we have

S_72×72:=186660; Sb_72×72:= 645159180; S_8×8:=20740.

Magic squares of order 8 are of equal sums. These are either bimagic ou semi-bimagic squares of different sums. See the excel sheet given at the end.

Bimagic Squares of Order 80: Blocks of Orders 8 and 16

Similar to order 64, here also we have two ways to write bimagic square of order 80.

First Type: Blocks of Order 8

In this case, we have

S_80×80:=256040; Sb_80×80:= 1092522680; S_8×8:=25604.

These blocks of order 8 are either bimagic or semi-bimagic with different sums, but the magic sum of all order magic squares is same. See the magic square of order 80 in excel sheet given at the end.

Second Type: Blocks of Order 16

In this case, we have

S_80×80:=256040; Sb_80×80:= 1092522680; S_16×16:=51208 and S_4×4:=12802.

Magic squares of order 16 are of equal sums. See below bimagic square of order 80 with blocks of order 16. These blocks of order 16 are bimagic squares with different bimagic sums, but the magic sum of all order 16 magic squares is same. See the magic square of order 80 in excel sheet given at the end.

Bimagic Square of Order 88: Blocks of Order 8

In this case, we have

S_88×88:=340780; Sb_88×88:= 1759447140; S_8×8:=30980.

Magic squares of order 8 are of equal sums. These are either bimagic ou semi-bimagic squares of different sums. See the excel sheet given at the end.

Bimagic Square of Order 96: Blocks of Order 8

In this case, we have

S_96×96:=442416; Sb_96×96:= 2718351376; S_8×8:=36868.

Magic squares of order 8 are of equal sums. These are either bimagic ou semi-bimagic squares of different sums. See the excel sheet given at the end.

Even though 96 is divisible by 16, still, we don’t have bimagic square of order 96 with blocks of order 16.

Bimagic Square of Order 104: Blocks of Order 8

In this case, we have

S_104×104:=562484; Sb_104×104:=4056072124; S_8×8:=43268.

Magic squares of order 8 are of equal sums. These are either bimagic ou semi-bimagic squares of different sums. See the excel sheet given at the end.

Bimagic Squares of Order 112: Blocks of Orders 8 and 16

Similar to orders 64 and 80, here also we have two ways to writing bimagic square of order 112.

First Type: Blocks of Order 8

In this case, we have

S_112×112:=702520; Sb_112×112:= 5875174760; S_8×8:=50180.

These blocks of order 8 are either bimagic or semi-bimagic with different sums, but the magic sum of all order magic squares is same. See the magic square of order 112 in excel sheet given at the end.

Second Type: Blocks of Order 16

In this case, we have

S_112×112:=702520; Sb_112×112:= 5875174760; S_16×16:=100360 and S_4×4:=25090.

See below bimagic square of order 80 with blocks of order 16. These blocks of order 16 are bimagic squares with different bimagic sums, but the magic sums of all order 16, and order 4 are of equal sums.

Bimagic Square of Order 120: Blocks of Order 8

In this case, we have

S_120×120:=864060; Sb_120×120:=8295264020; S_8×8:=57604.

Magic squares of order 8 are of equal sums. These are either bimagic ou semi-bimagic squares of different sums. See the excel sheet given at the end.

Bimagic Square of Order 128: Blocks of Orders 8 and 16

Similar to orders 64, 80 and 112, here also we have two ways to writing bimagic square of order 128.

First Type: Blocks of Order 8

In this case, we have

S_128×128:=1048640; Sb_128×128:=11454294720; S_8×8:=65540.

These blocks of order 8 are either bimagic or semi-bimagic with different sums, but the magic sum of all order magic squares is same. See the magic square of order 128 in excel sheet given at the end.

Second Type: Blocks of Order 16

In this case, we have

S_128×128:=1048640; Sb_128×128:=11454294720; S_16×16:=131080 and S_4×4:=32770.

See below bimagic square of order 128 with blocks of order 16. These blocks of order 16 are bimagic squares with different bimagic sums, but the magic sums of all order 16, and order 4 are of equal sums.

Bimagic Square of Order 136: Blocks of Order 8

In this case, we have

S_136×136:=1257796; Sb_136×136:=15509882476; S_8×8:=73988.

Magic squares of order 8 are of equal sums. These are either bimagic ou semi-bimagic squares of different sums. See the excel sheet given at the end.

Bimagic Square of Order 144: Blocks of Order 16

In this case, we have

S_144×144:=1493064; Sb_144×144:=20640614424; S_16×16:=165896 and S_4×4:=41474.

See below bimagic square of order 128 with blocks of order 16. These blocks of order 16 are bimagic squares with different bimagic sums, but the magic sums of all order 16, and order 4 are of equal sums.

Bimagic Square of Order 152: Blocks of Order 8

In this case, we have

S_152×152:=1755980; Sb_152×152:=27047359940; S_8×8:=92420.

Magic squares of order 8 are of equal sums. These are either bimagic ou semi-bimagic squares of different sums. See the excel sheet given at the end.

Bimagic Square of Order 160: Blocks of Order 16

In this case, we have

S_144×144:=2048080; Sb_144×144:=34954581360; S_16×16:=204808 and S_4×4:=51202.

See below bimagic square of order 128 with blocks of order 16. These blocks of order 16 are bimagic squares with different bimagic sums, but the magic sums of all order 16, and order 4 are of equal sums.

Excel file of Bimagic Squares Multiples of Orders 8 and 16.