This work brings pandiagonal magic squares in different situations. These are multiples of order 3, 4, 5, etc. We can always write pandiagonal magic squares multiples of any order, except of type 4k+2, where k=1, 2, 3, … etc. These orders are 6, 10, 14, 18, etc. Below are magic squares of orders 3, 4, 5 and 7:
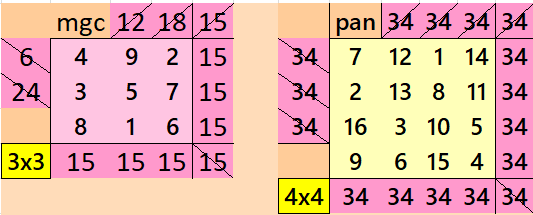
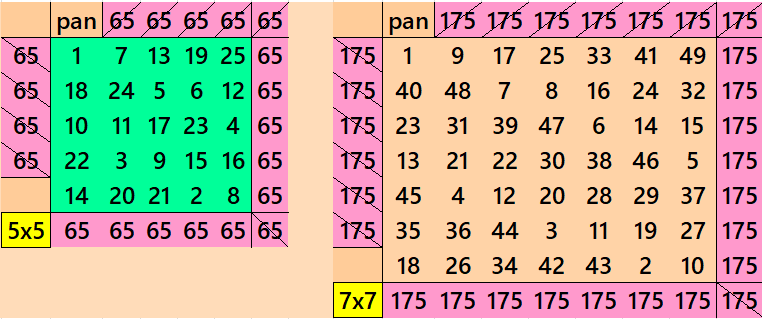
We observe that except order 3 other magic squares are pandiagonal. Except order 4, the orders 5 and 7 are prime numbers. Starting from order 5, we can always write pandiagonal magic squares of prime orders. See below examples prime orders up to order 23:
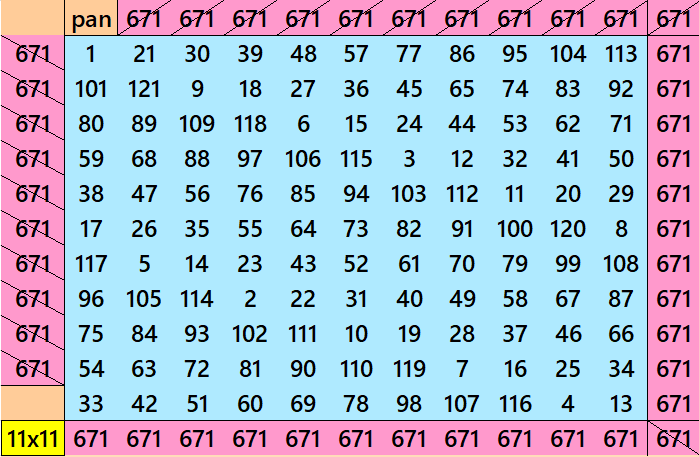
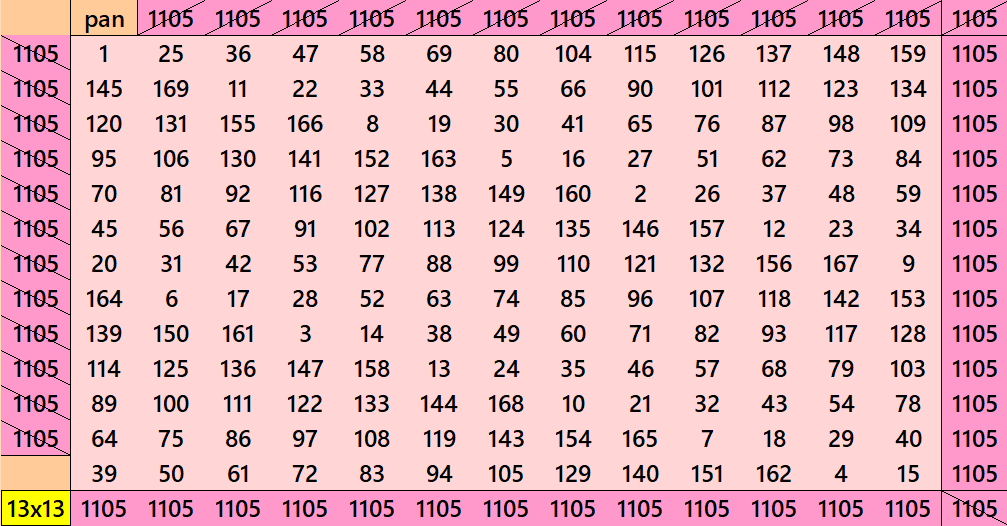
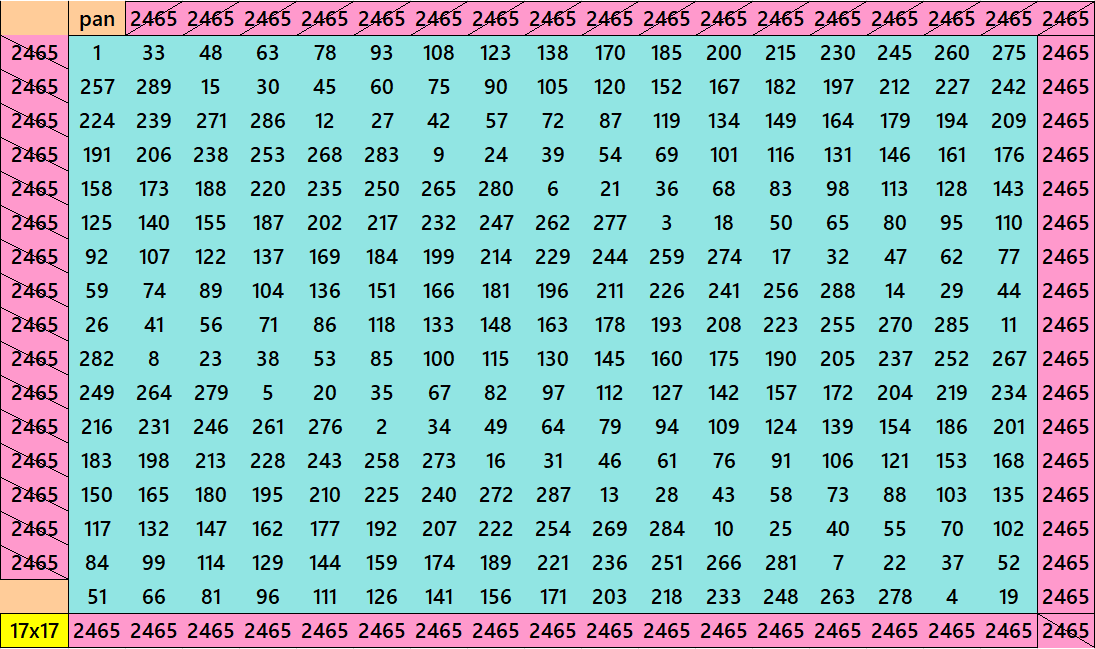
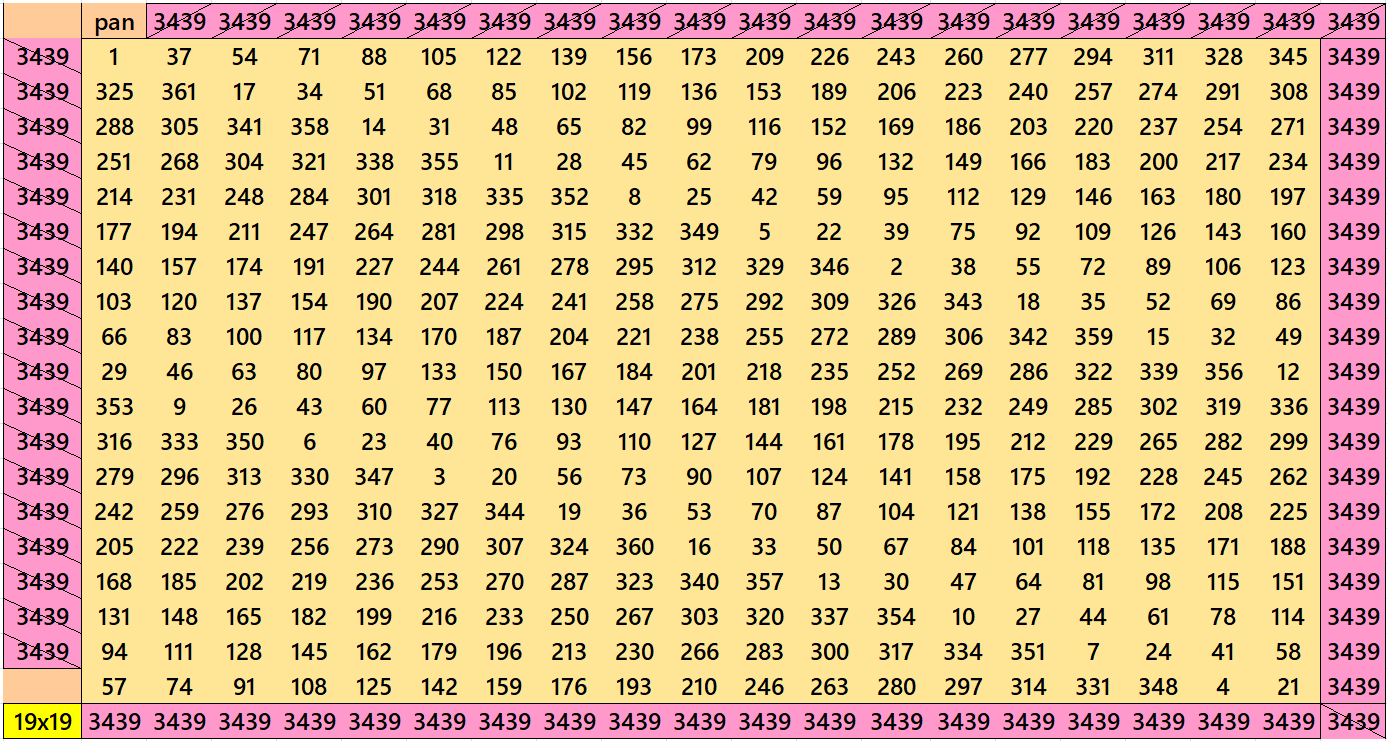
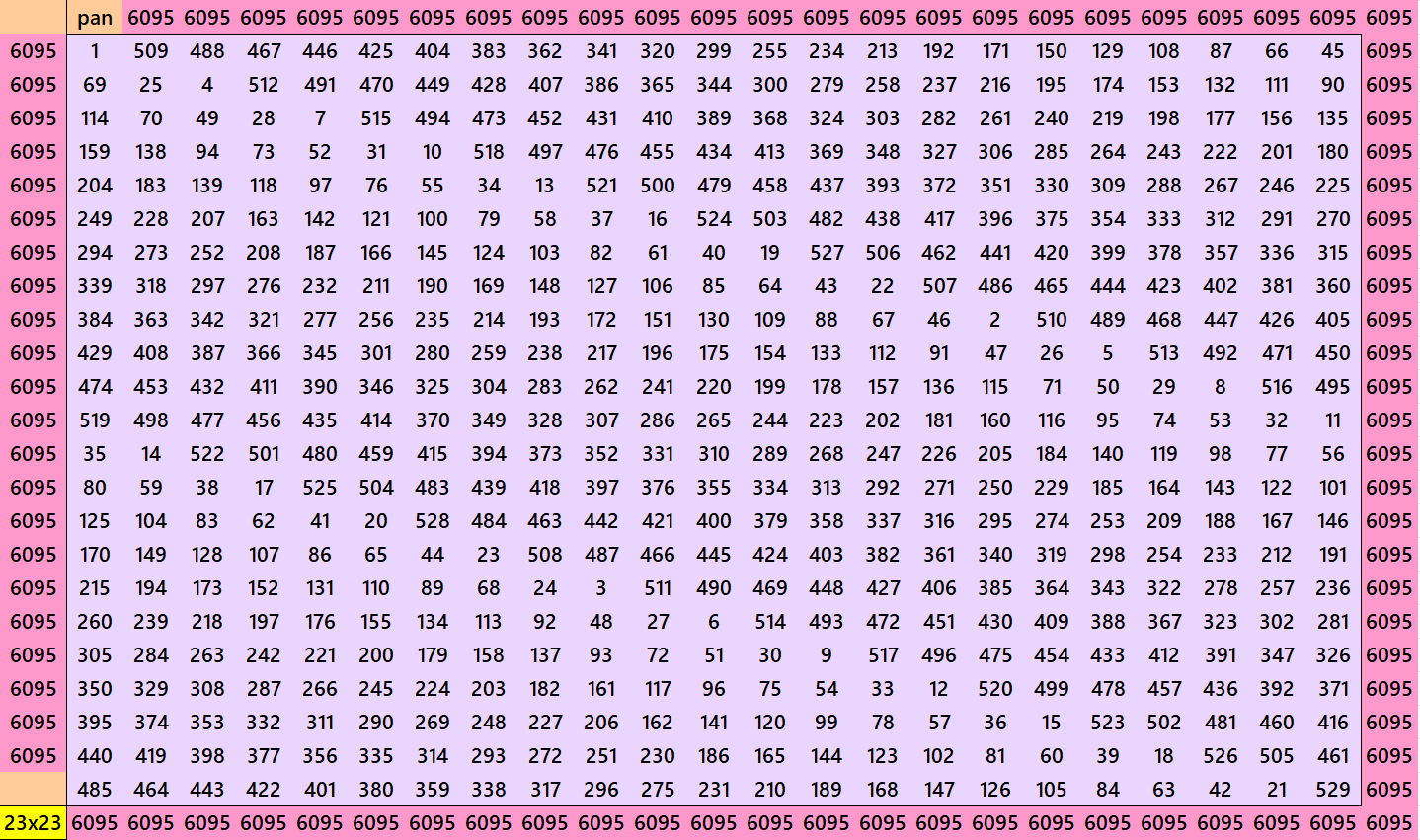
Further orders such as 29, 31, 37, 41, etc. can also be written as pandiagonal magic squares with the same procedure as above.
Below are pandiagonal magic squares of non prime orders, such as 8, 12, 15, 16, 20, 21, etc. In these cases, we have pandiagonal magic squares with blocks of orders 3, 4, 5, 7, 11, 13, etc. These blocks are of two types. Either equal sums or non-equal sums.
For construction details the readers see the following author’s work. In some cases, magic rectangles are used to bring these pandiagonal magic squares:
- Inder J. Taneja, Block-Wise Equal Sums Pandiagonal Magic Squares of Order 4k, Zenodo, January 31, 2019, pp. 1-17, https://doi.org/10.5281/zenodo.2554288.
- Inder J. Taneja, Magic Rectangles in Construction of Block-Wise Pandiagonal Magic Squares, Zenodo, January 31, 2019, pp. 1-49, http://doi.org/10.5281/zenodo.2554520.
- Inder Jeet Taneja, Block-Wise and Block-Bordered Magic and Bimagic Squares of Orders 10 to 47. Zenodo, January 14, 2021, pp. 1-185, http://doi.org/10.5281/zenodo.4437783.
- Inder Jeet Taneja, Block-Wise Bordered and Pandiagonal Magic Squares Multiples of 4, Zenodo, August 31, 2021, pp. 1-148, https://doi.org/10.5281/zenodo.5347897.
- Inder J. Taneja, A Simplified Procedure to Construct Pandiagonal Magic Squares Multiples of 4 (Revised), Zenodo, August 10, 2023, pp. 1-27, https://doi.org/10.5281/zenodo.8236754.
Pandiagonal Magic Square of Order 8
Below is a pandiagonal magic square of order 8, constructed with equal sums of pandiagonal magic squares of order 4.
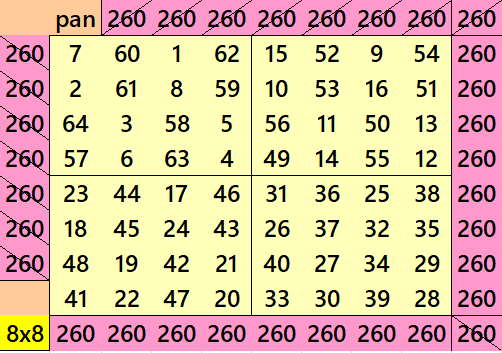
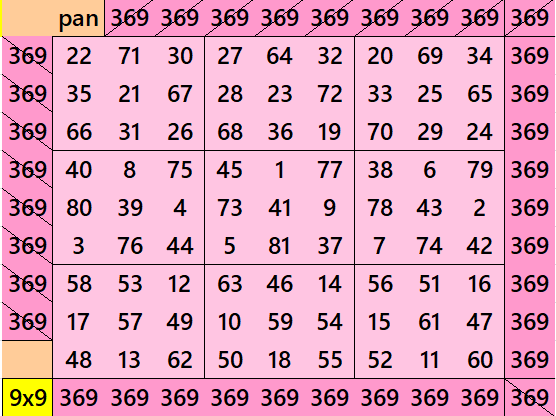
Pandiagonal Magic Square of Order 9
Below is a pandiagonal magic square of order 9, constructed with blocks of equal sums of semi-magic squares of order 3.
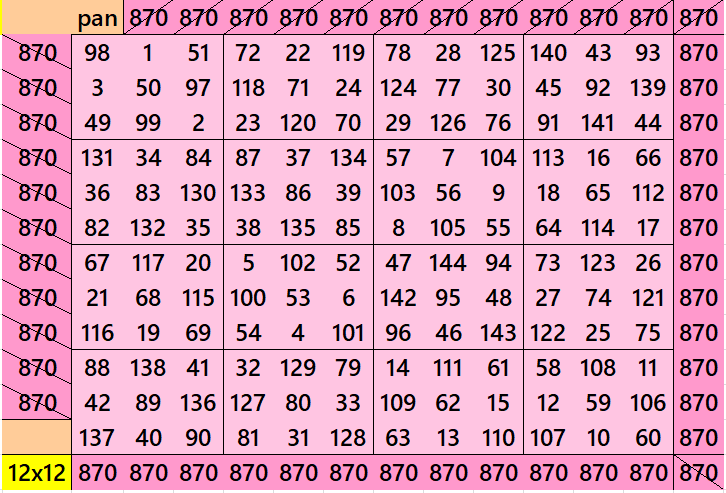
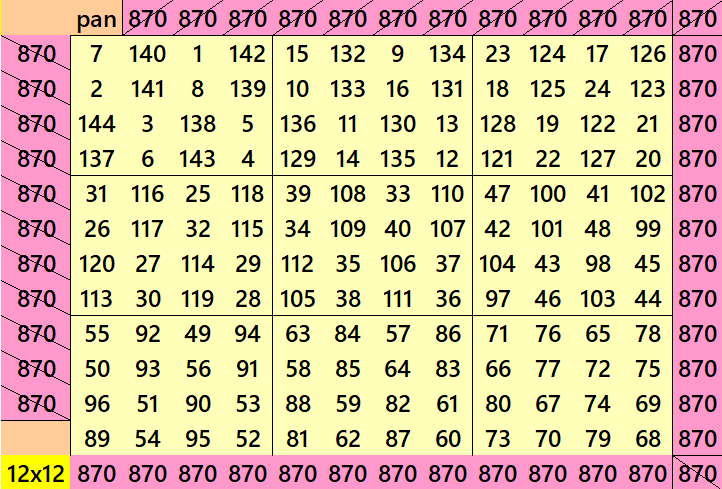
Pandiagonal Magic Square of Order 12
We can write 12=3×4. In this we have pandiagonal magic squares of order 12 with blocks of order 3 and 4. The first magic squares of order 12 is with different sums magic squares of order 3. The second magic square of order 12 is with equal sums pandiagonal magic squares of order 4. See below:
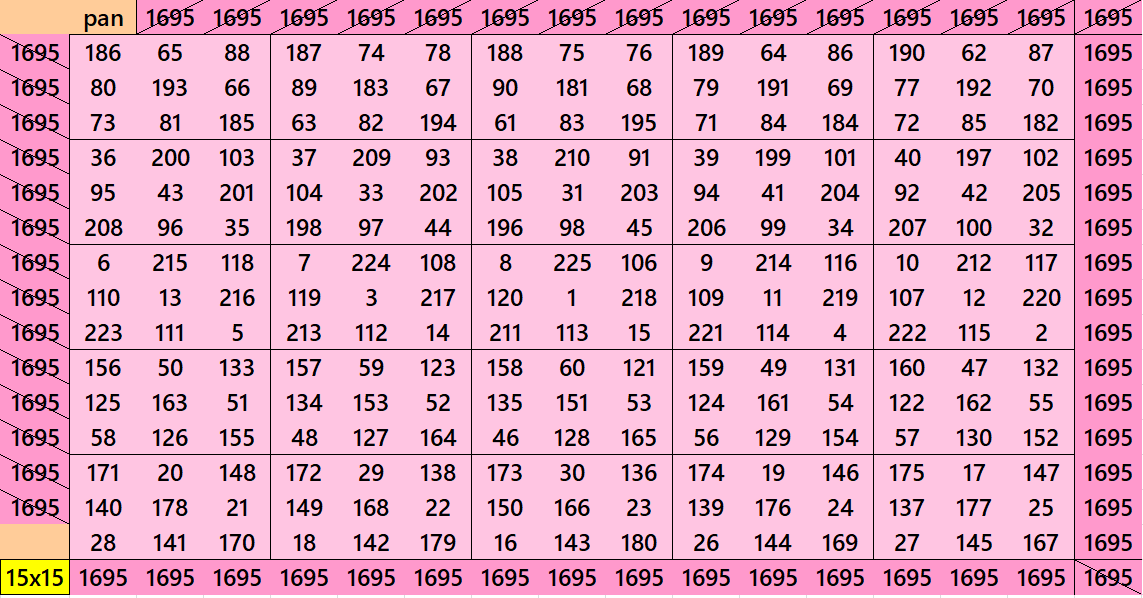
Pandiagonal Magic Squares of Order 15
We can write 15=3×5. In this we have pandiagonal magic squares of order 15 with blocks of order 3 and 5. The first magic squares of order 15 is with equal sums semi-magic squares of squares of order 3. The second magic square of order 15 is with equal sums pandiagonal magic squares of order 5. See below:
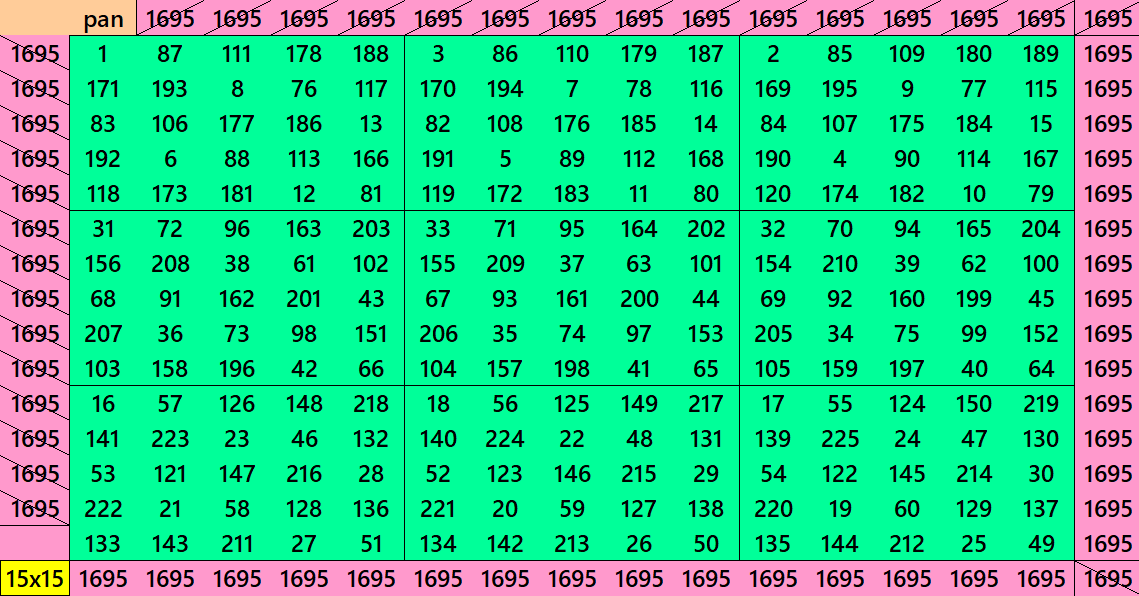
We observe that the further orders in each alternative case have equal sums blocks. For blocks of order 3, the equal sums are for the magic squares of order 21, 27, 33, etc. In this case, we always have semi-magic squares of order 3. For blocks of order 5, the equal sums are for orders, 25, 35, 45, etc.
Pandiagonal Magic Square of Order 16
Below is a pandiagonal magic square of order 16, constructed with equal sums pandiagonal magic squares of order 4.
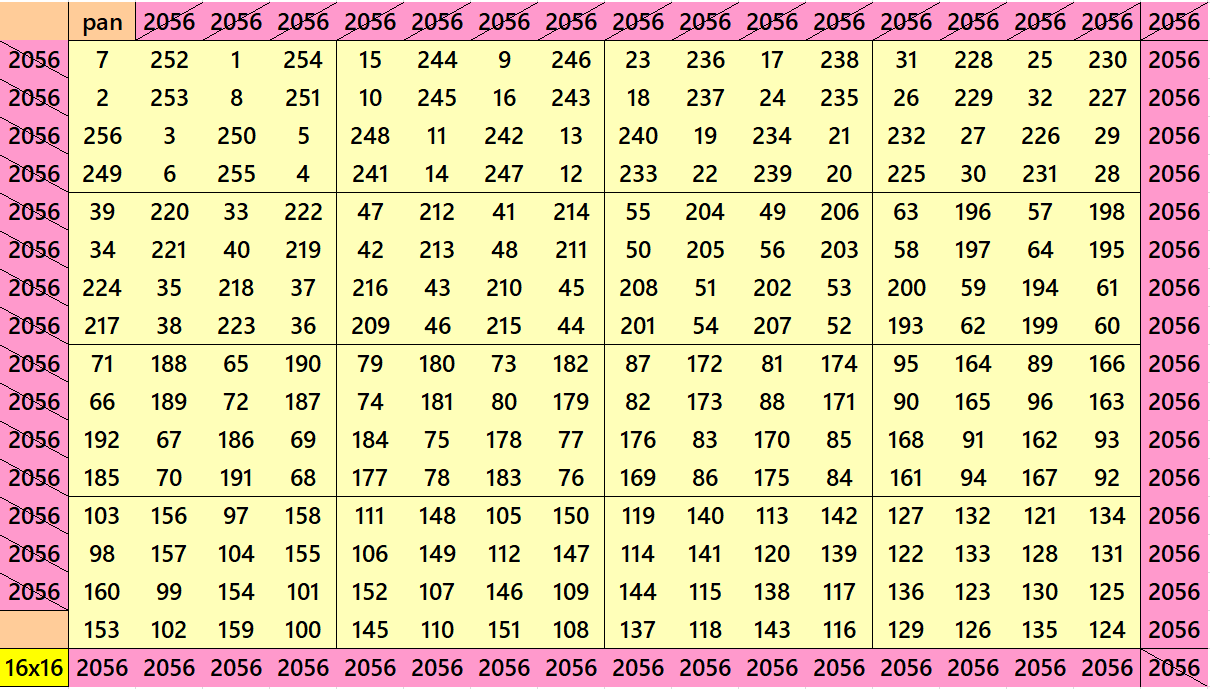
Pandiagonal Magic Squares of Order 20
We can write 20=4×5. In this we have pandiagonal magic squares with blocks of orders 4 and 5. The first pandiagonal magic square of order 20 is with equal sums pandiagonal magic squares of order 4. The second pandiagonal magic squares is with different sums pandiagonal magic squares of order 5.
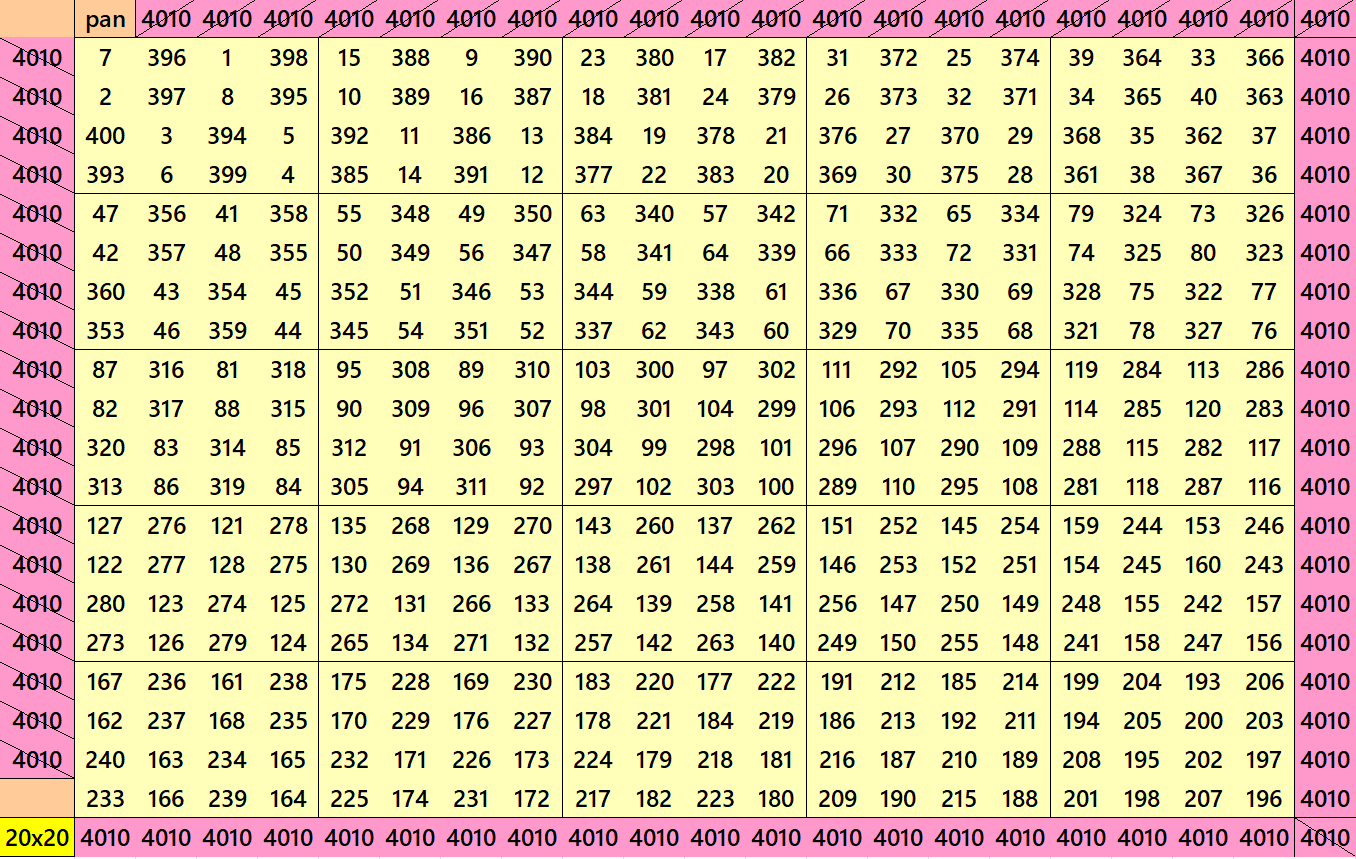
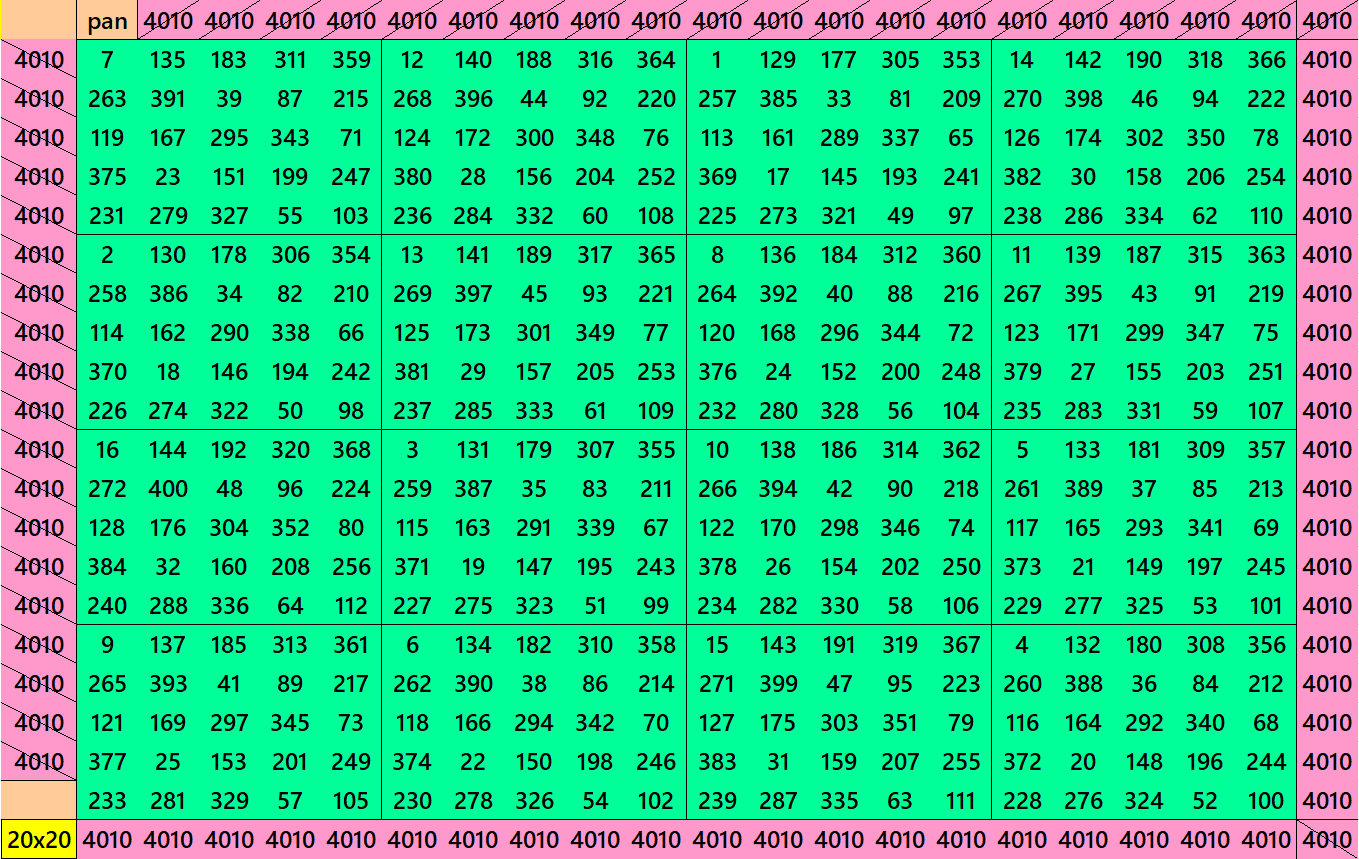
Pandiagonal Magic Squares of Order 21
We can write 21=3×7. In this we have pandiagonal magic squares with blocks of orders 3 and 7. The first magic square of order 21 is with equal sums semi-magic squares of order 3. The second magic square of order 21 is with equal sums pandiagonal magic squares of order 7. See below
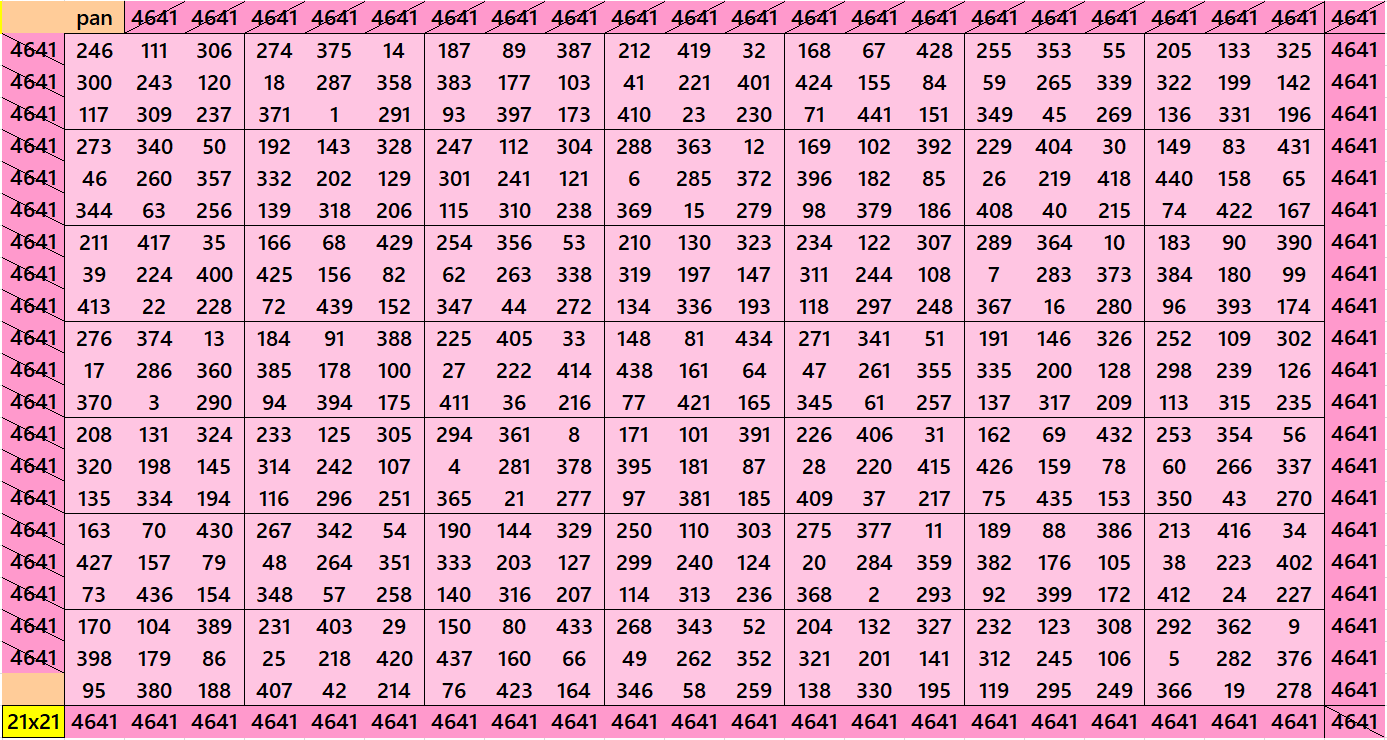
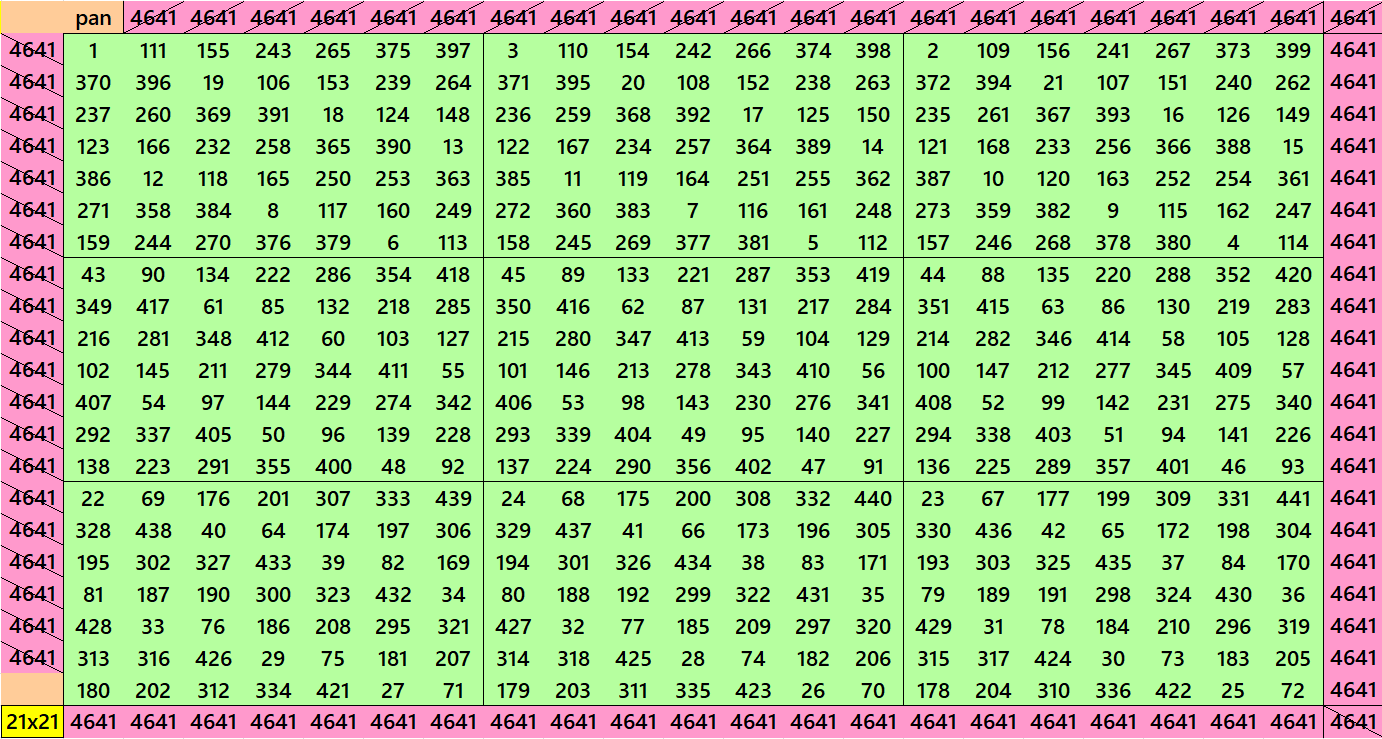
We observe that the further orders in each alternative case, for order 7, we have equal sums blocks. For examples, magic squares of orders 35, 49, 63, etc. are with equal sums pandiagonal blocks of order 7
Pandiagonal Magic Squares of Order 24
We can write 24=2x3x4. In this we have pandiagonal magic squares with blocks of orders 3 and 4. The first magic square is made with 4 equal sums pandiagonal magic square of order 12. Each block of order 12 is formed by unequal sums of magic squares of order 3. The second magic square is made with equal sums pandiagonal magic squares of order 4.
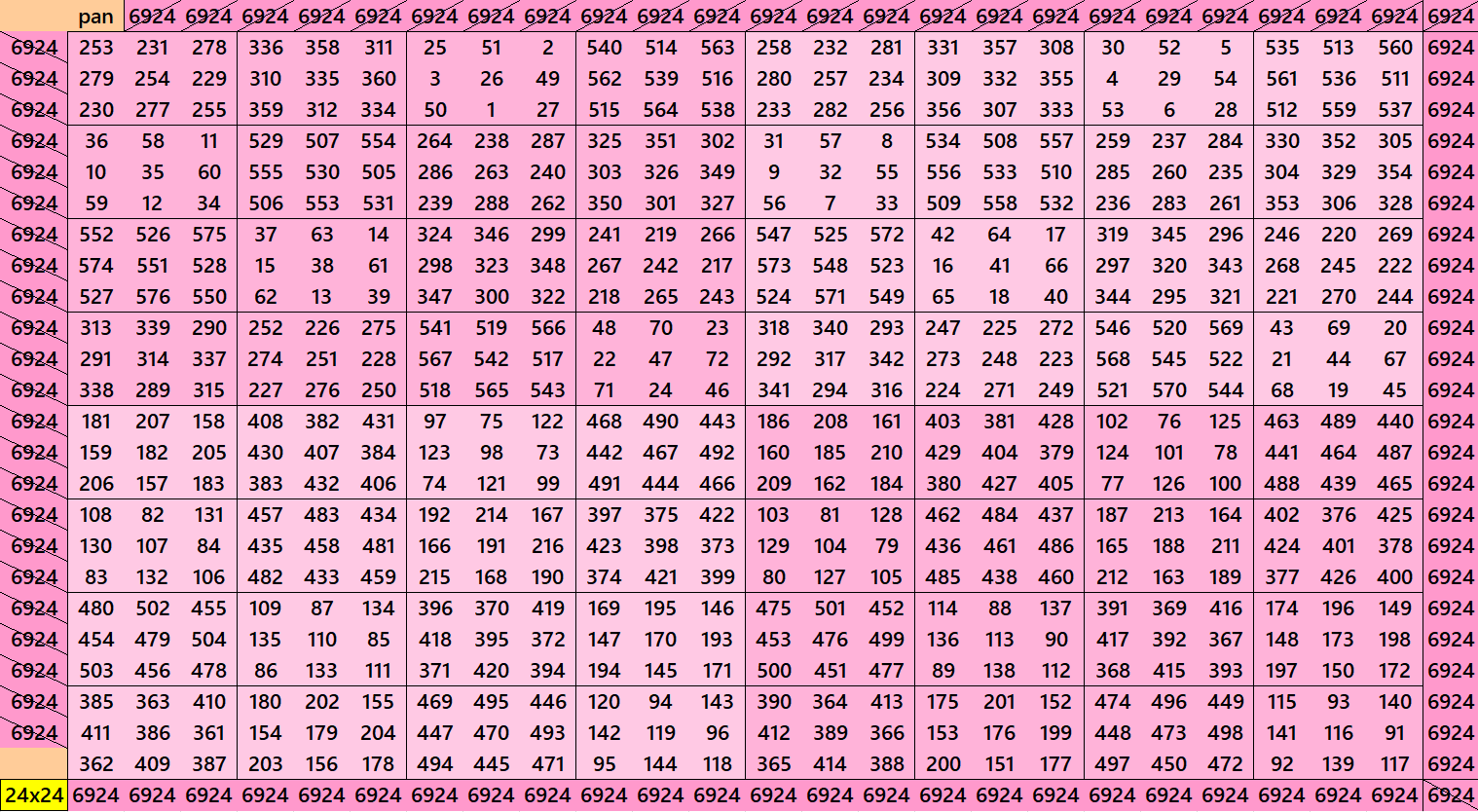
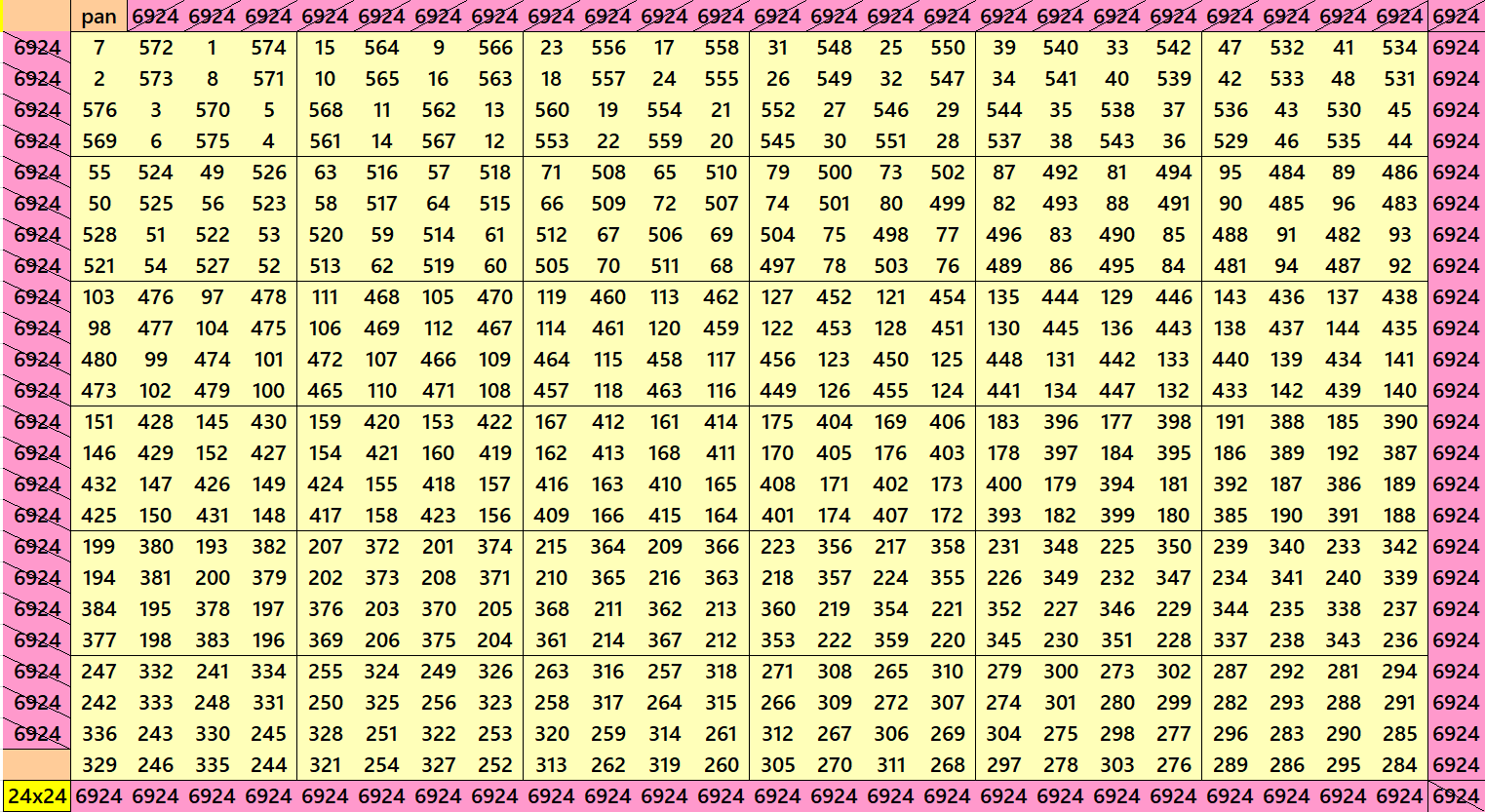
Pandiagonal Magic Square of Order 25 – Bimagic Square
Below is a pandiagonal bimagic square of order 25. It is made with equal sums pandiagonal magic squares of order 5.
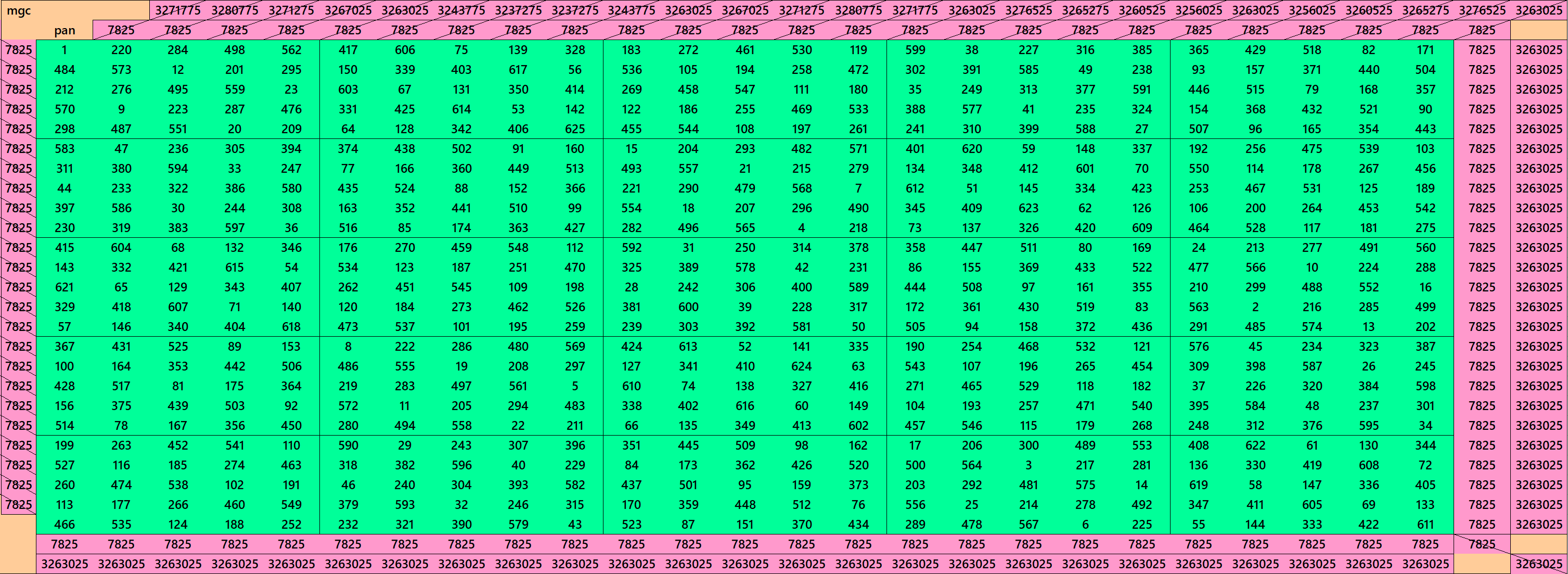
Pandiagonal Magic Square of Order 27
We can write 27=3^3. In this case we have pandiagonal magic square of order 27 with equal sums blocks of order 3.
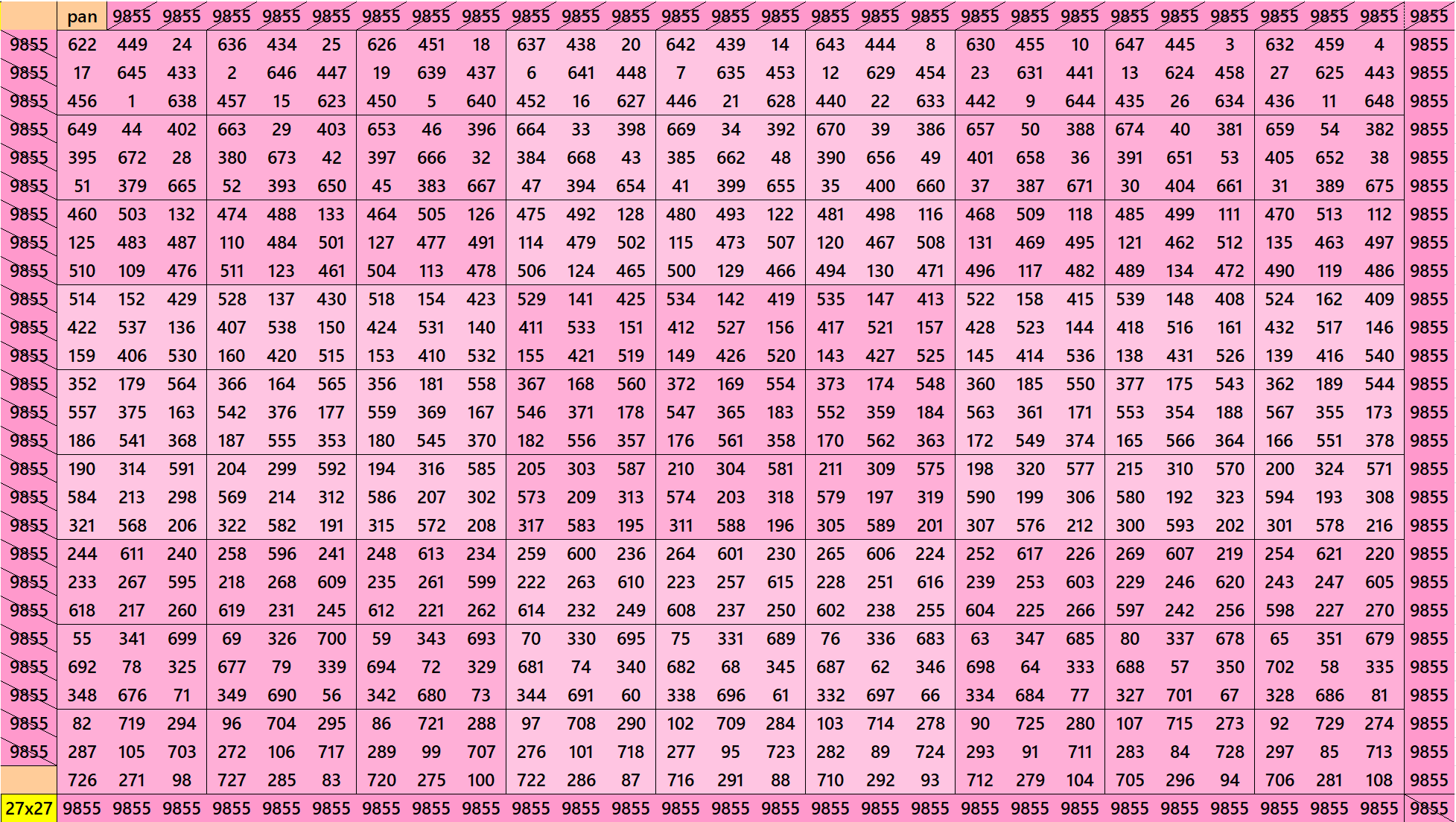
Above we have considered blocks of order 9 formed by equal sums semi-magic squares of order 3. The blocks of order 9 are also equal sums and semi-magic squares.
Pandiagonal Magic Squares of Order 28
We can write 28=4×7. This allow us to write pandiagonal magic squares of 28 with blocks of order 4 and 7. The first magic square is with equal sums pandiagonal magic squares of order 4. The second magic squares is with different sums pandiagonal magic squares of order 7.
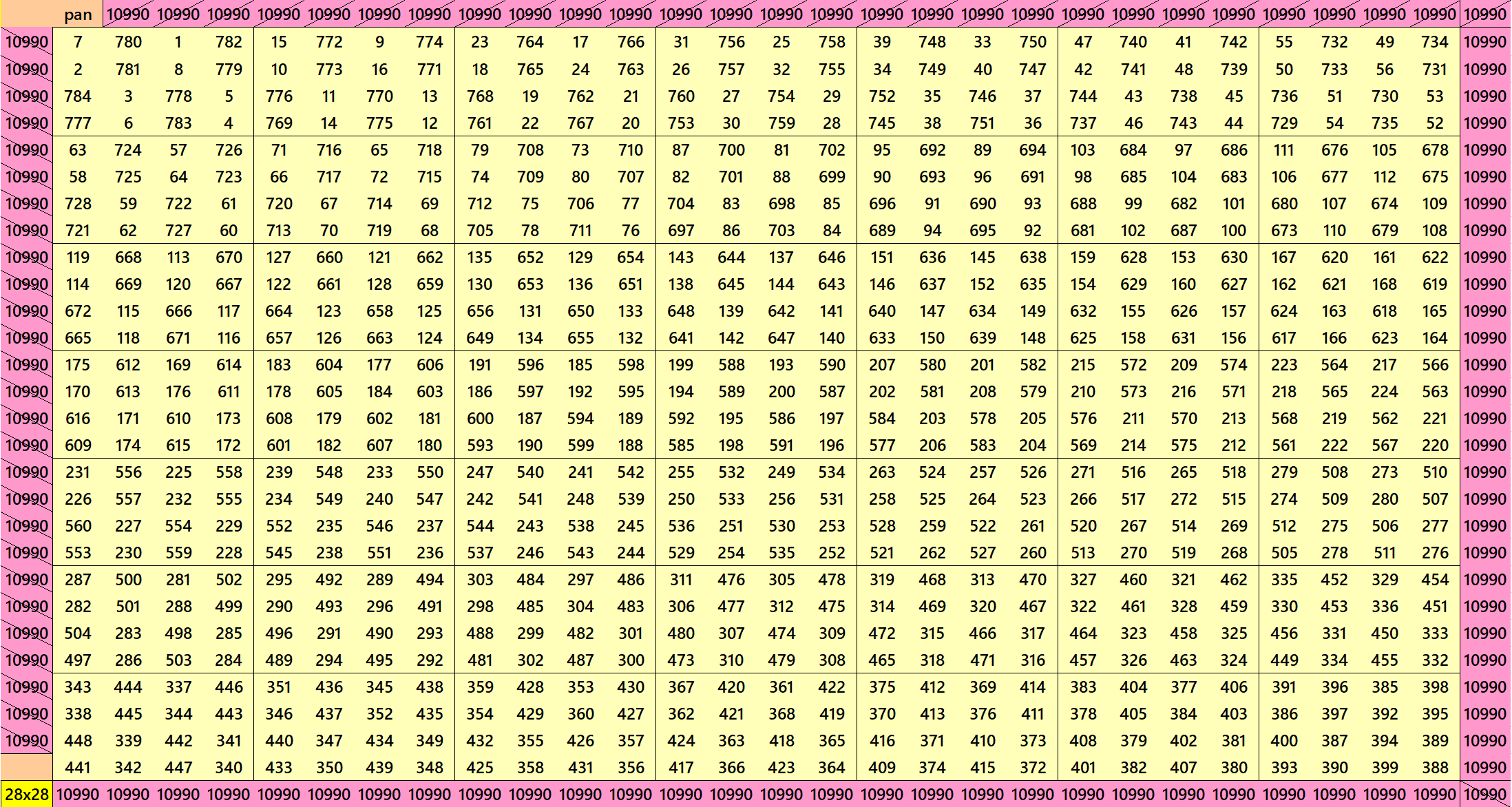
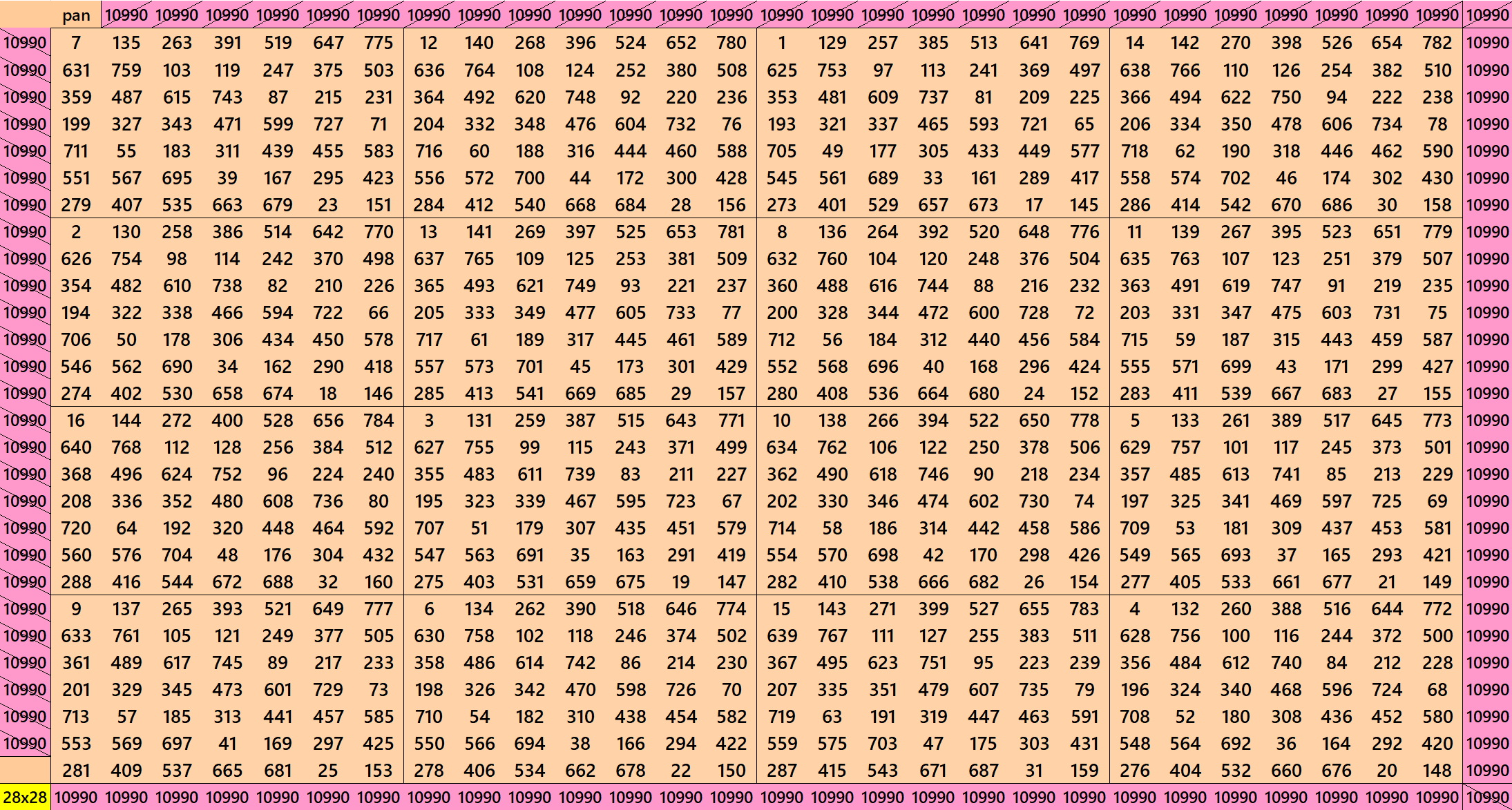
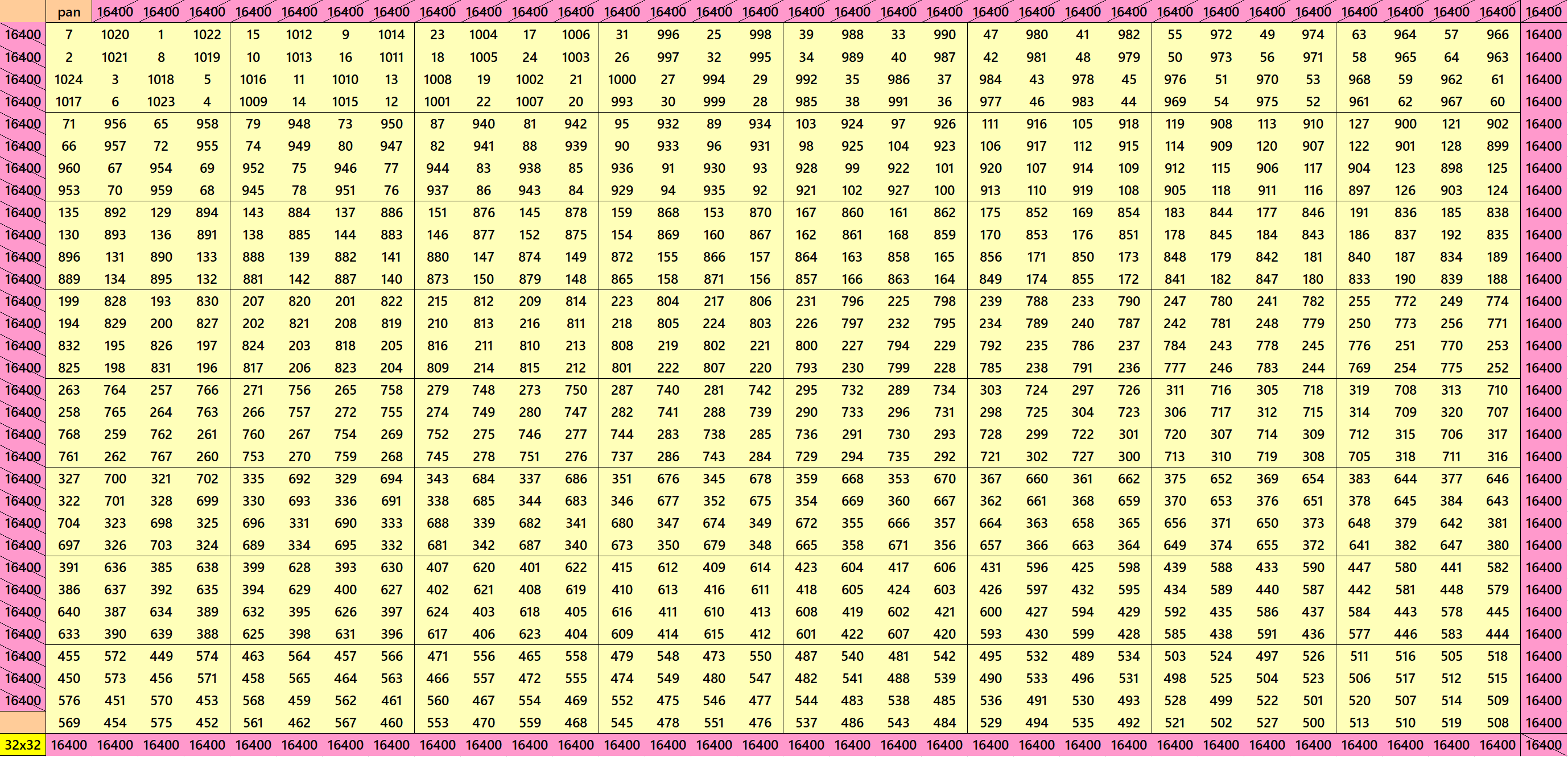
Pandiagonal Magic Square of Order 32
Below is a pandiagonal magic square of order 32, constructed with equal sums of pandiagonal magic squares of order 4.
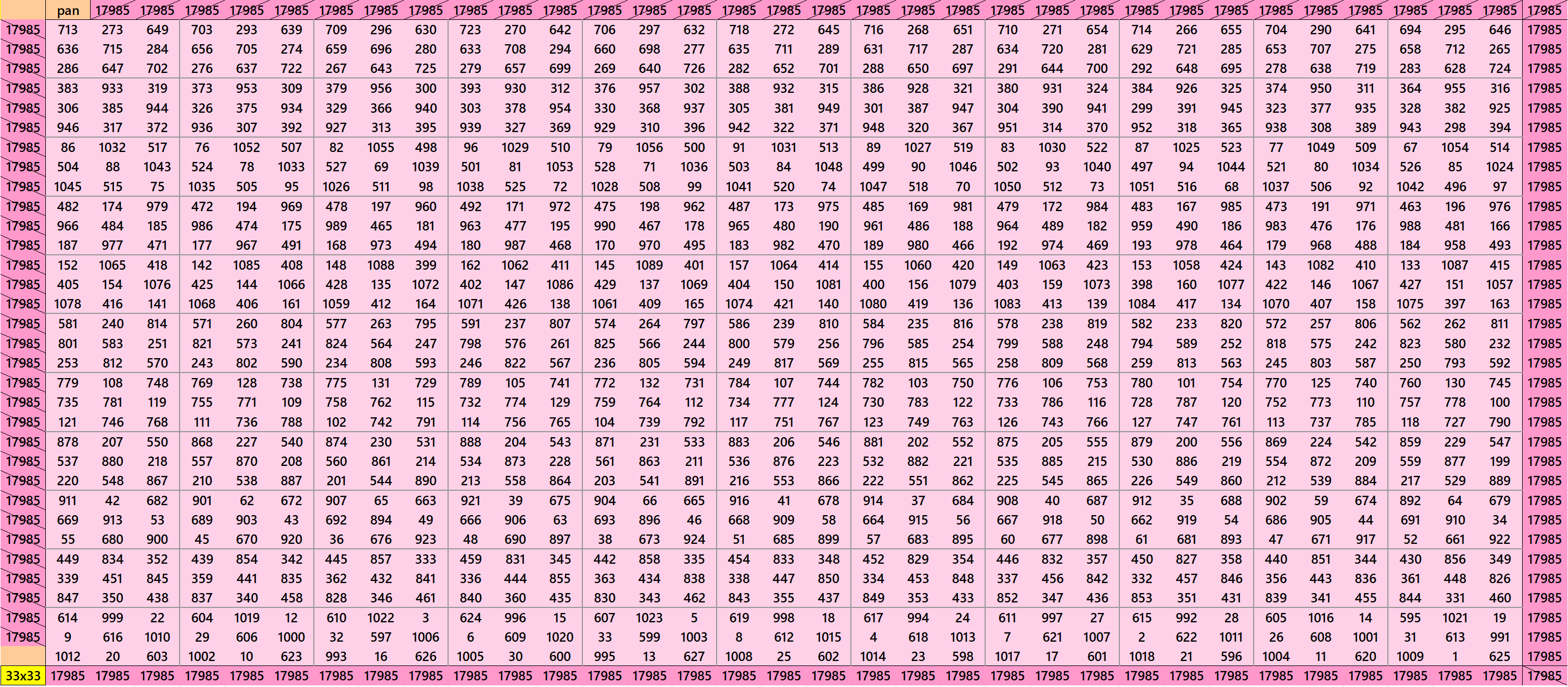
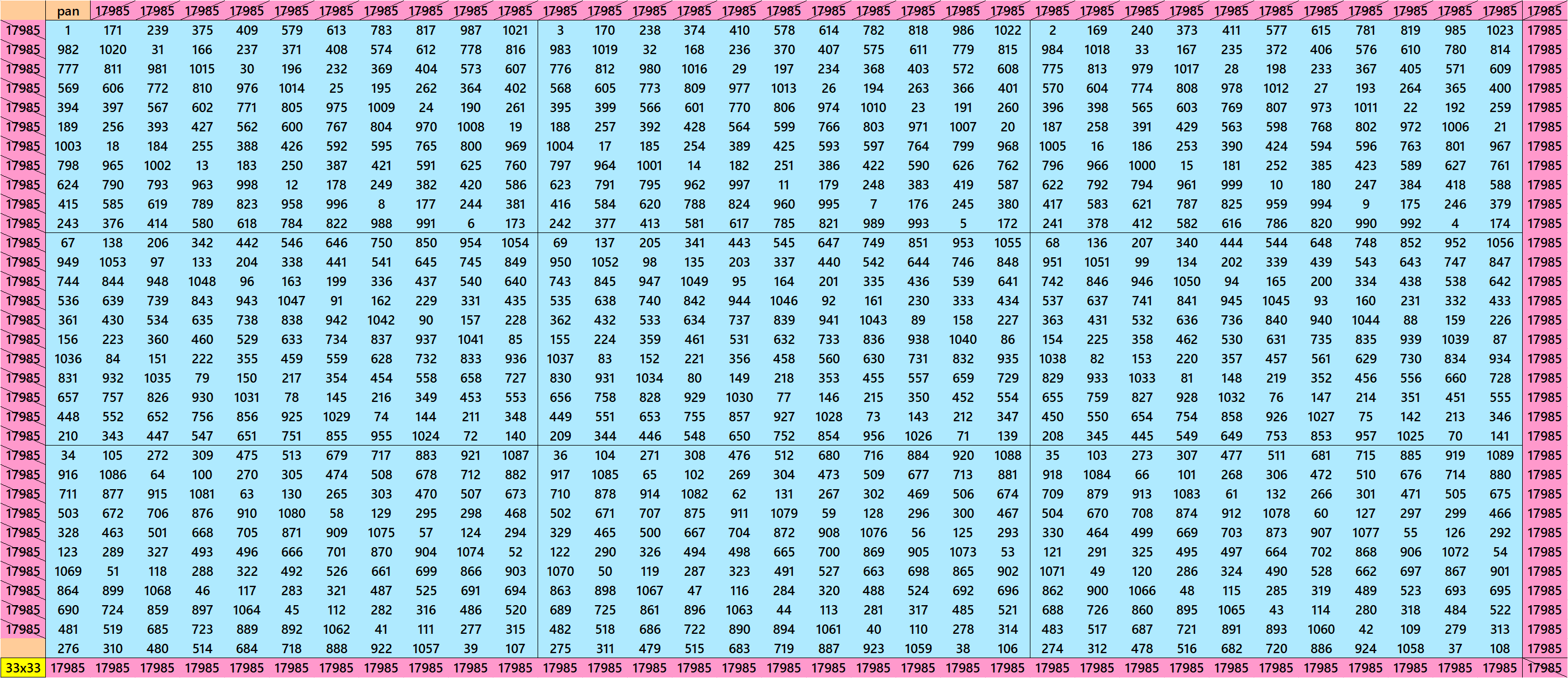
Pandiagonal Magic Squares of Order 33
We can write 33=3×11. This allows us to write pandigonal magic squares with blocks of order 3 and 11. The first magic square is made with equal sums semi-magic squares of order 3. The second magic square is made with equal sums pandiagonal magic squares of order 11. See below:
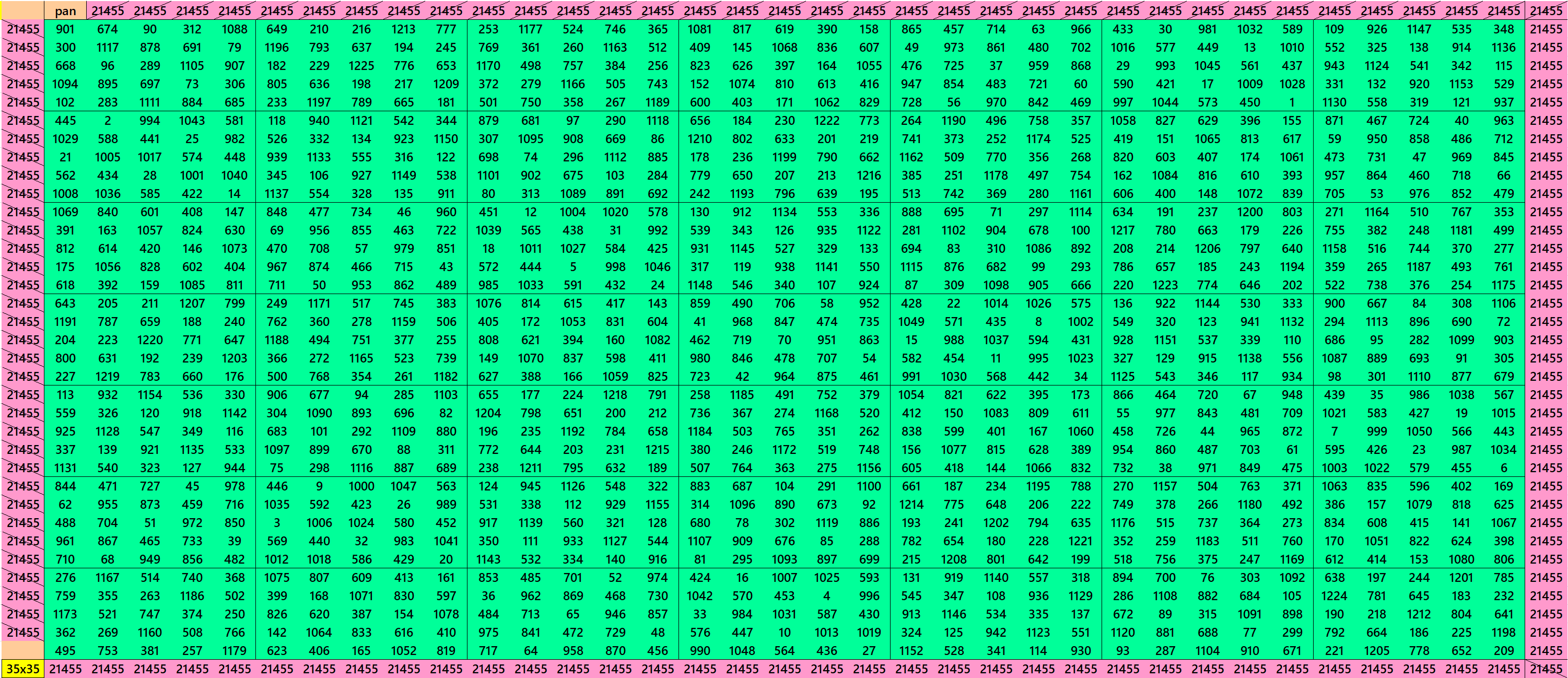
Pandiagonal Magic Squares of Order 35
We can write 35=5×7. This allows us to write pandigonal magic squares with blocks of orders 5 and 7. The first magic square of order 35 given below is made with equal sums pandiagonal magic squares of order 5. The second magic square of order 35 given below is made with equal sums pandiagonal magic squares of order 7. See below:
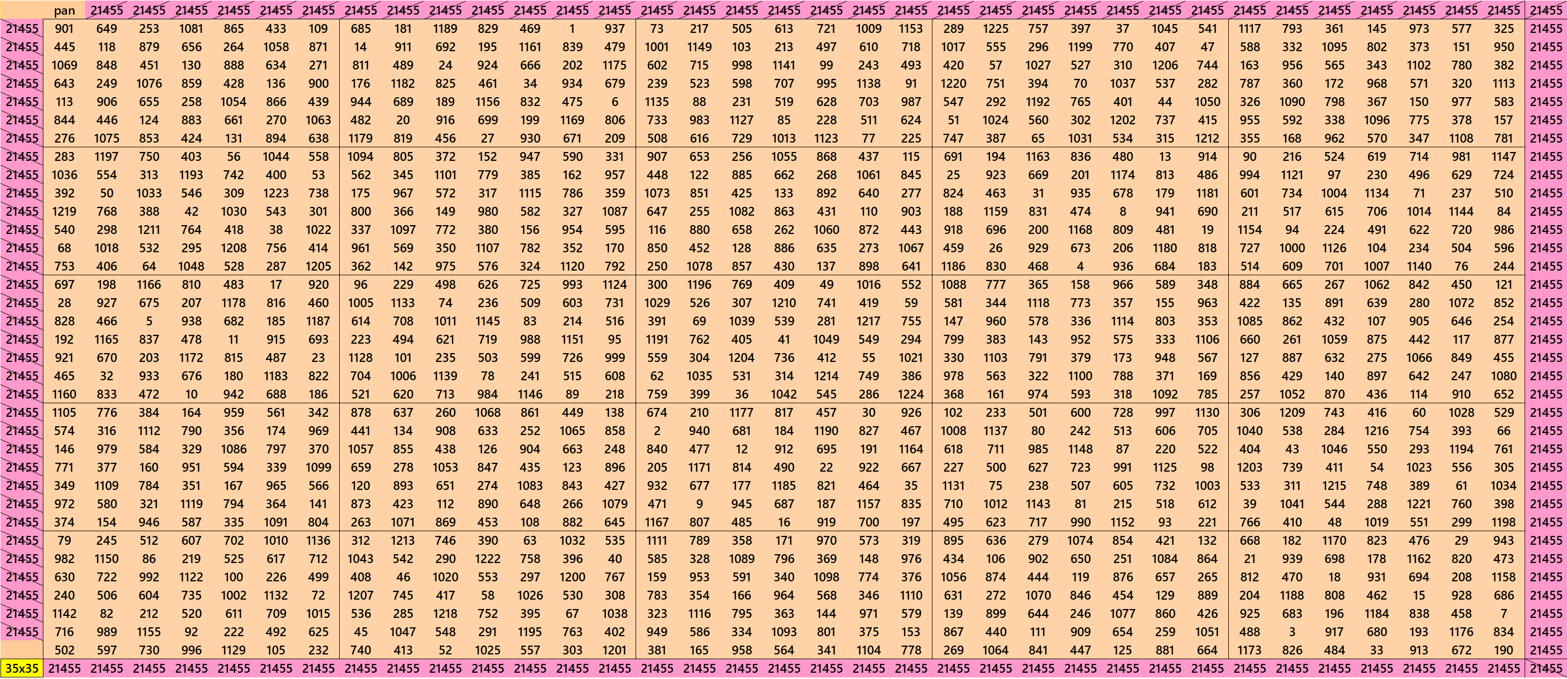
Pandiagonal Magic Squares of Order 36
We can write 36=3x3x4. This allows us to write pandigonal magic squares with blocks of orders 3 and 4. The first two magic square of order 36 given below are made with equal sums pandiagonal magic squares of order 12 and different sums magic squares of order 3. Each pandiagonal magic square of order 12 is formed by different sums magic squares of order 3. The third magic square of order 36 given below is made with equal sums pandiagonal magic squares of order 4. See below:
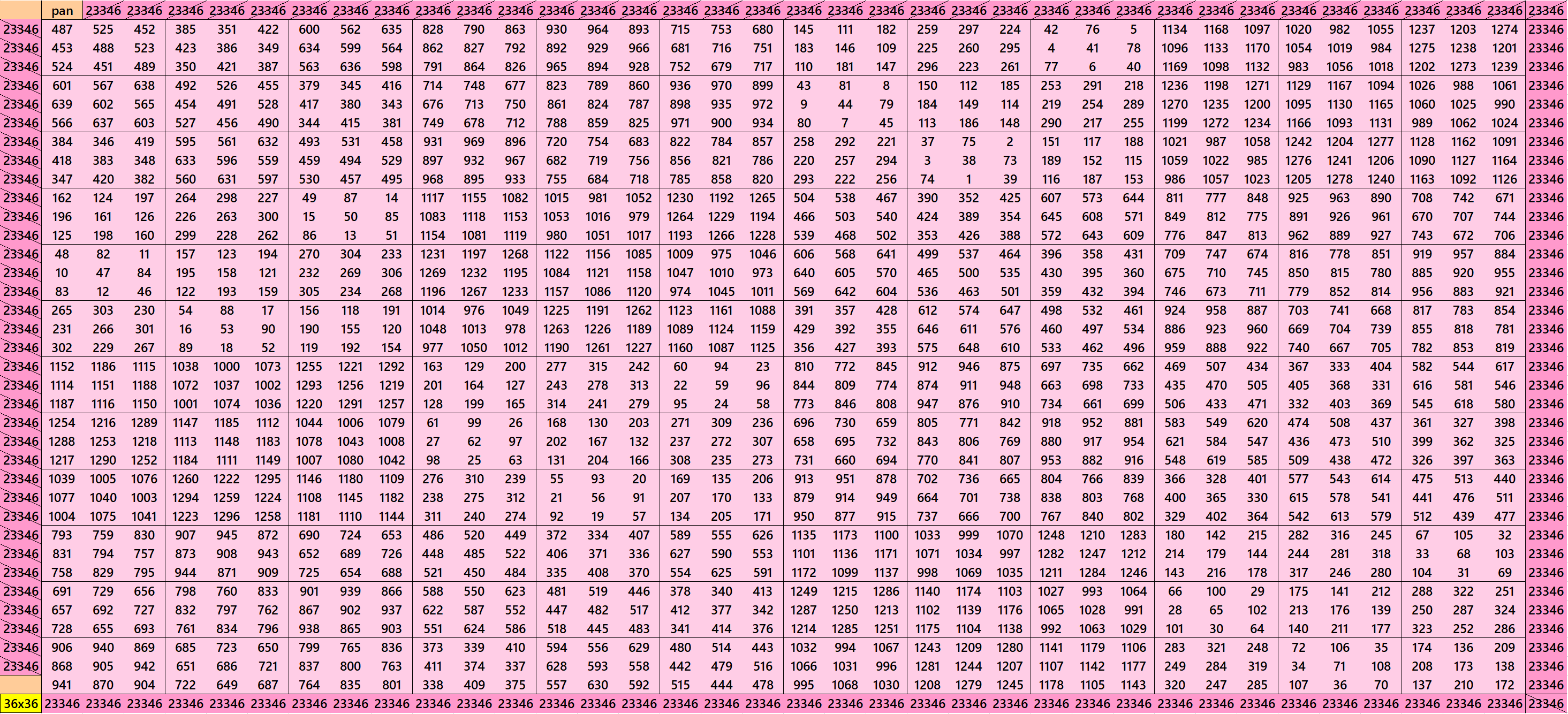
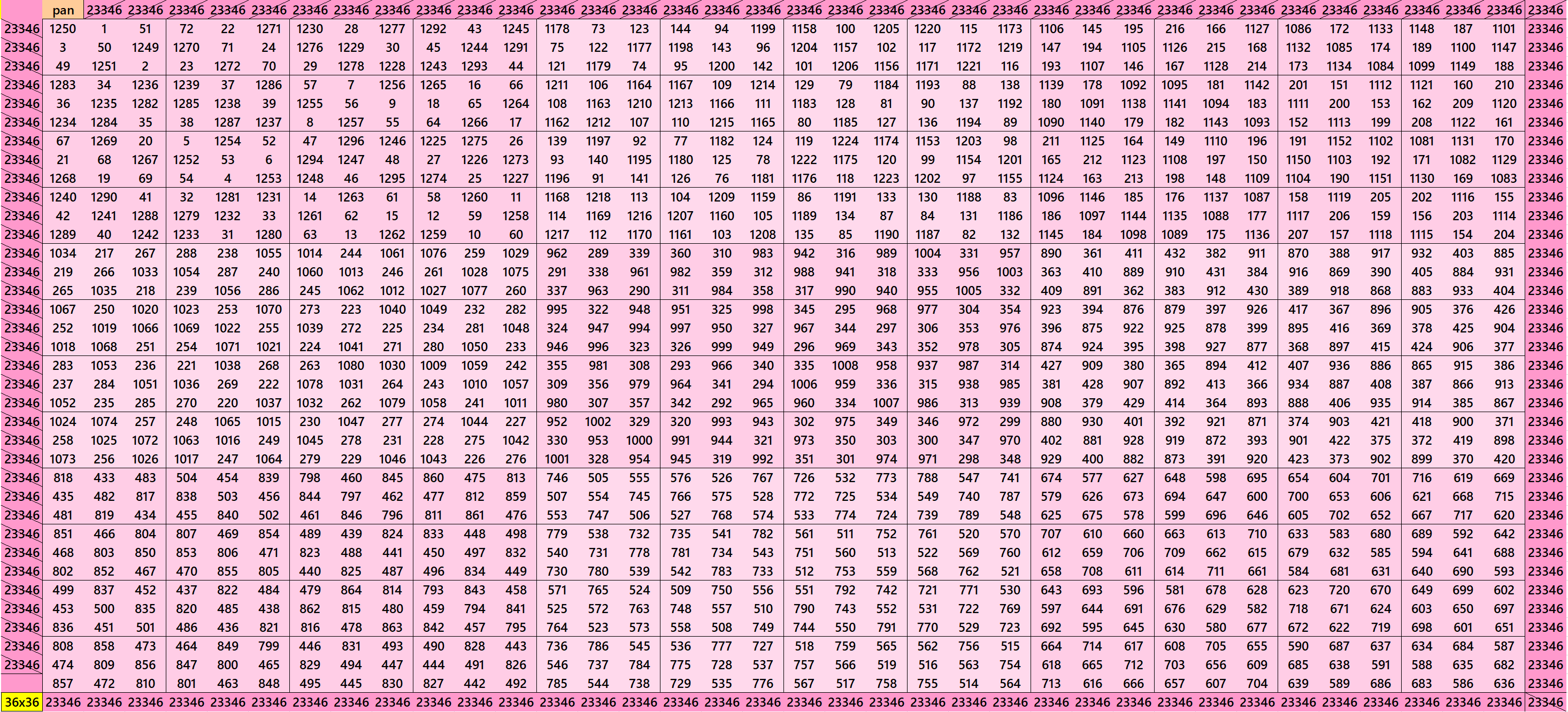
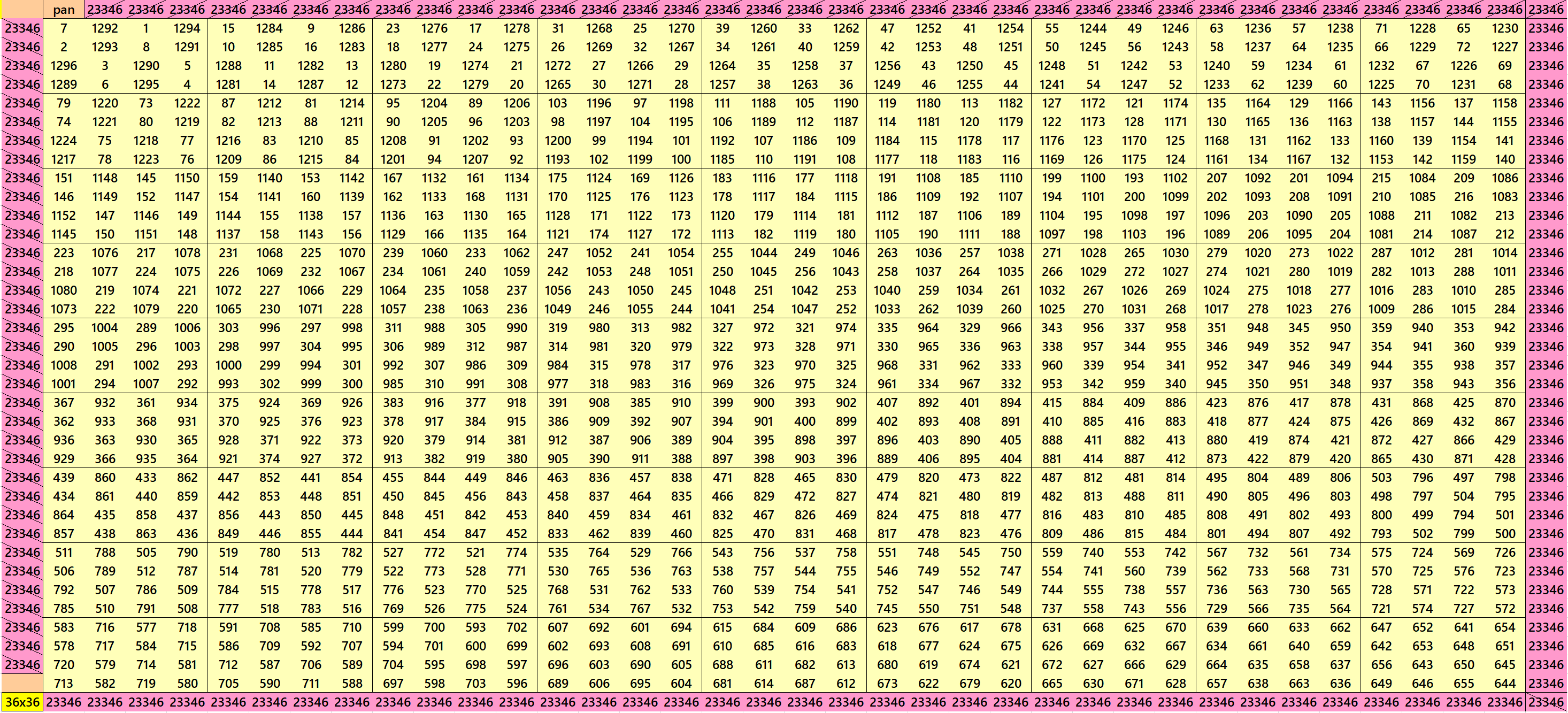
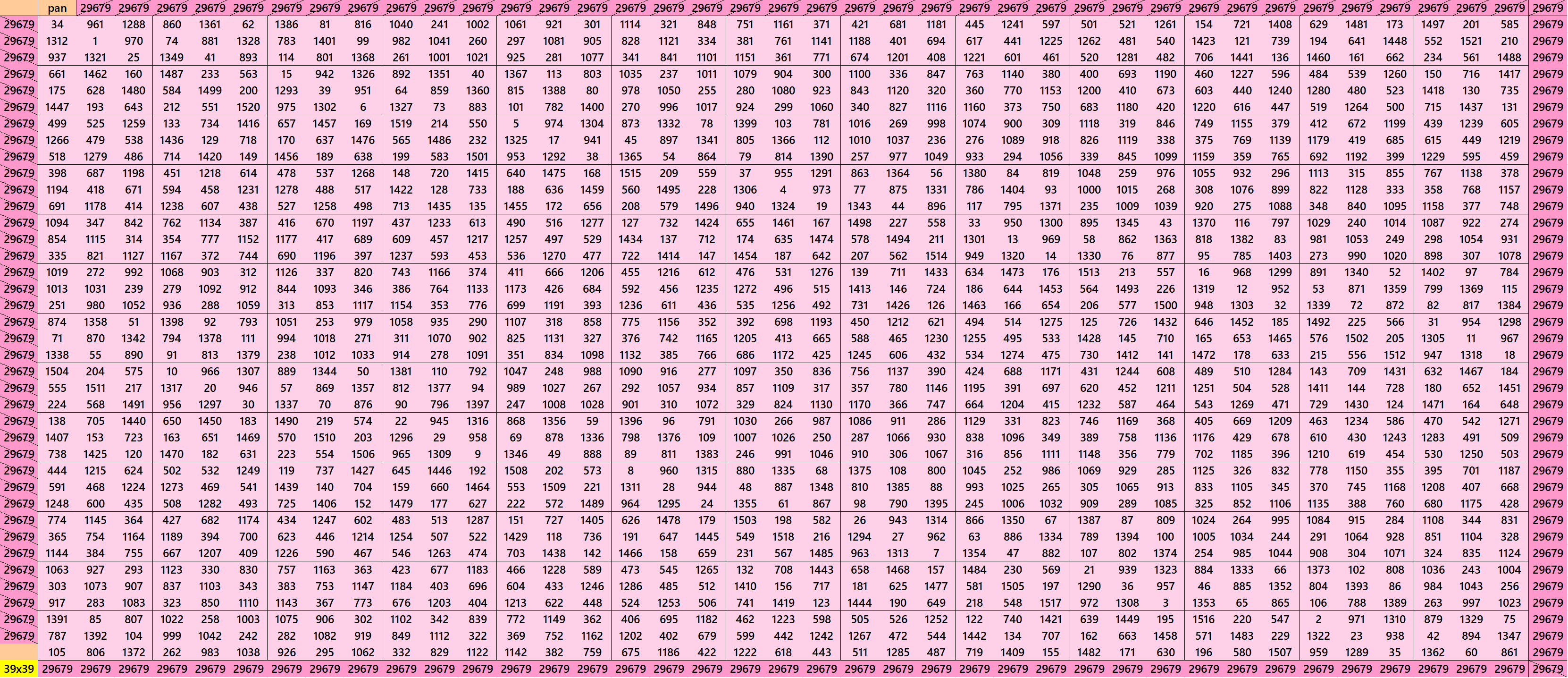
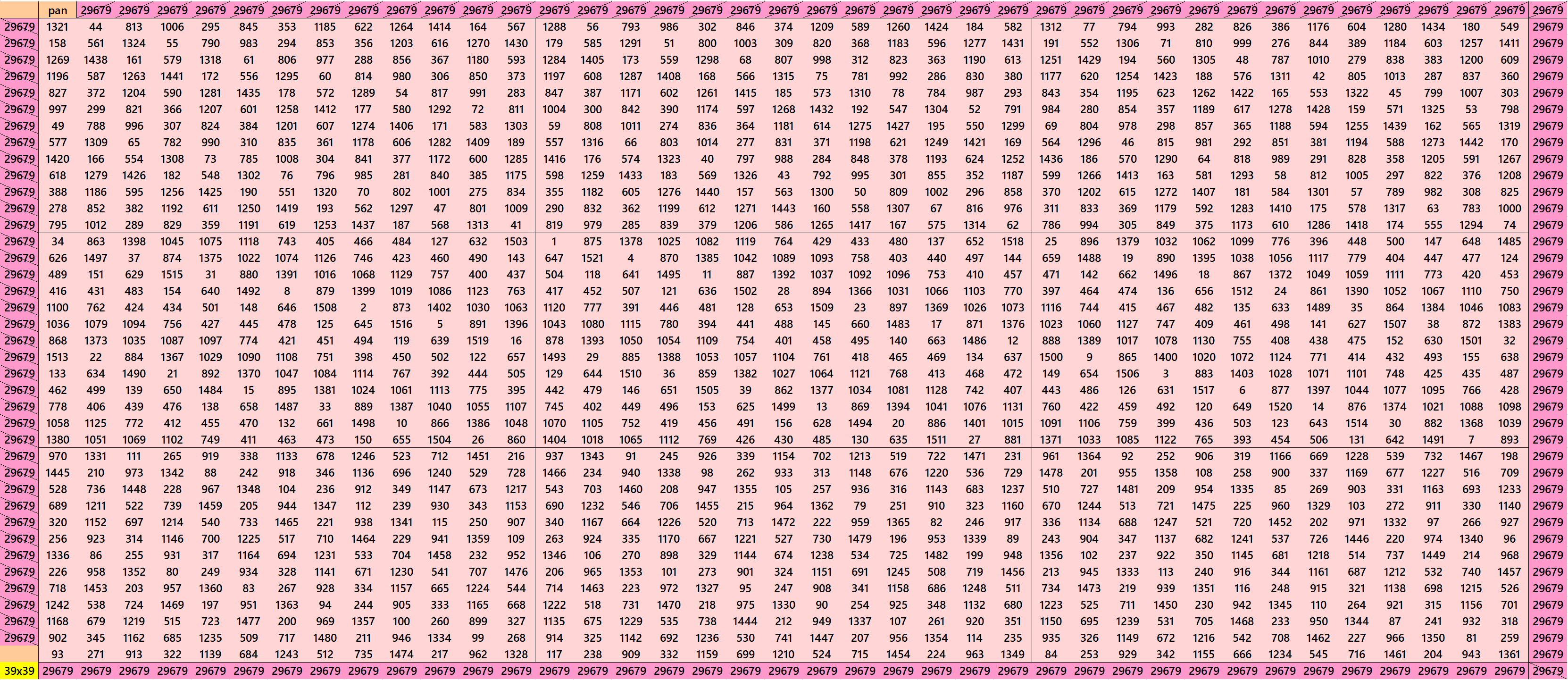
Pandiagonal Magic Squares of Order 39
We can write 39=3×11. This allows us to write pandigonal magic squares with blocks of orders 3 and 13. The first magic square of order 39 given below is made with equal sums semi-magic squares of order 3. The second magic square of order 39 is made with equal sums pandiagonal magic squares of order 13. See below:
Pandiagonal Magic Squares of Order 40
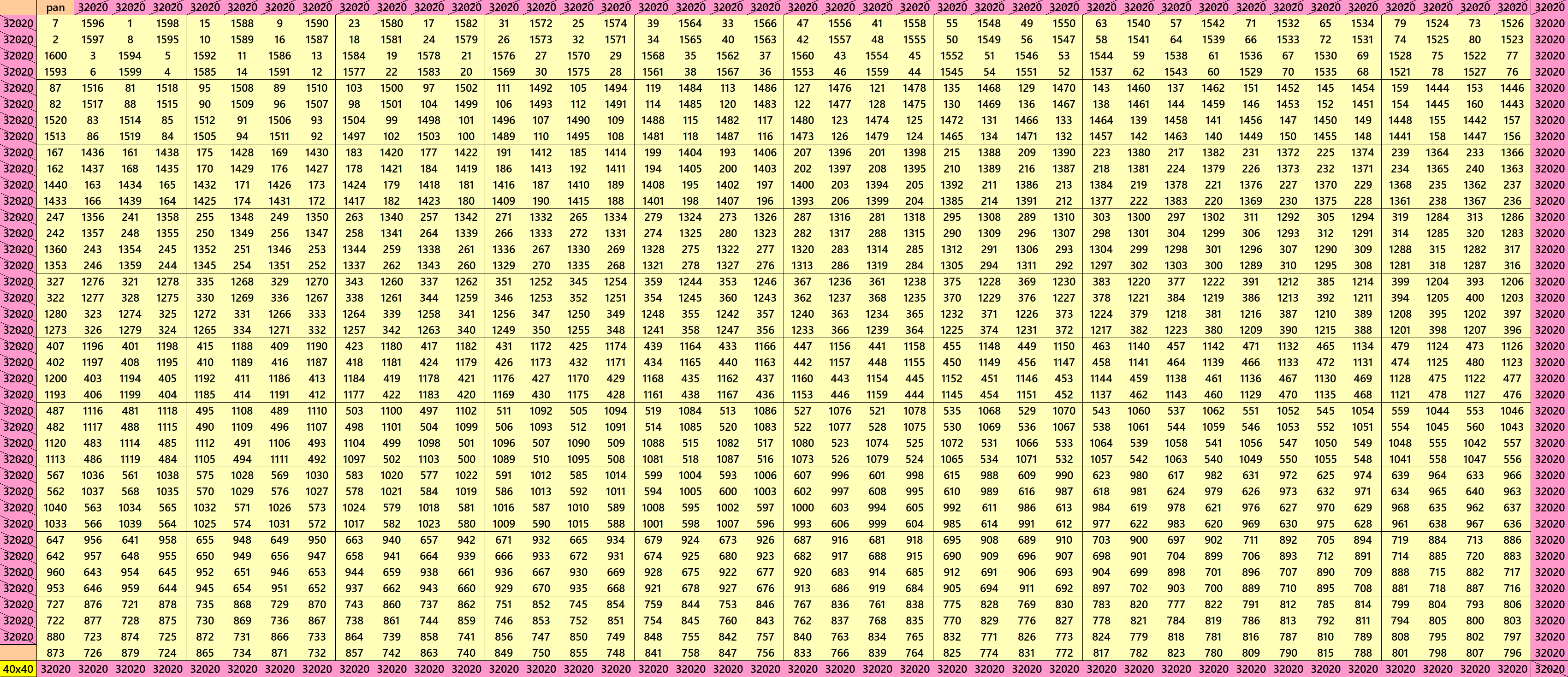
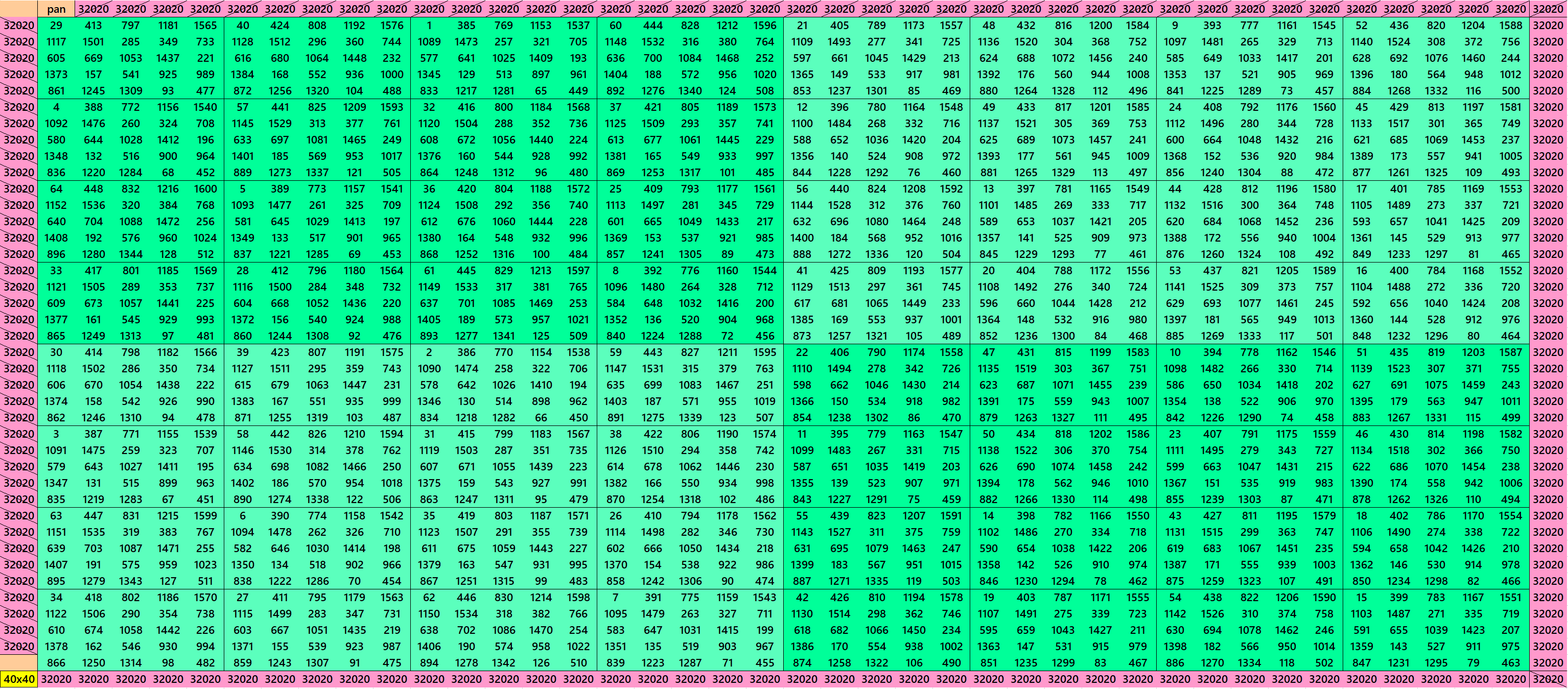
We can write 40=2x4x5. This allows us to write pandigonal magic squares with blocks of orders 4 and 5. The first magic square of order 40 is made with equal sums pandiagonal magic squares of order 4. The second magic square of order 40 is made with 4 equal sums pandiagonal magic squares of order 20, where each pandiagonal magic square of order 20 is made with different sums magic squares of order 5. See below:
Pandiagonal Magic Squares of Order 44
We can write 44=4×11. This allows us to write pandigonal magic squares with blocks of orders 4 and 11. The first magic square of order 44 is made with equal sums pandiagonal magic squares of order 4. The second magic square of order 44 is made with equal sums pandiagonal magic squares of order 11. See below:
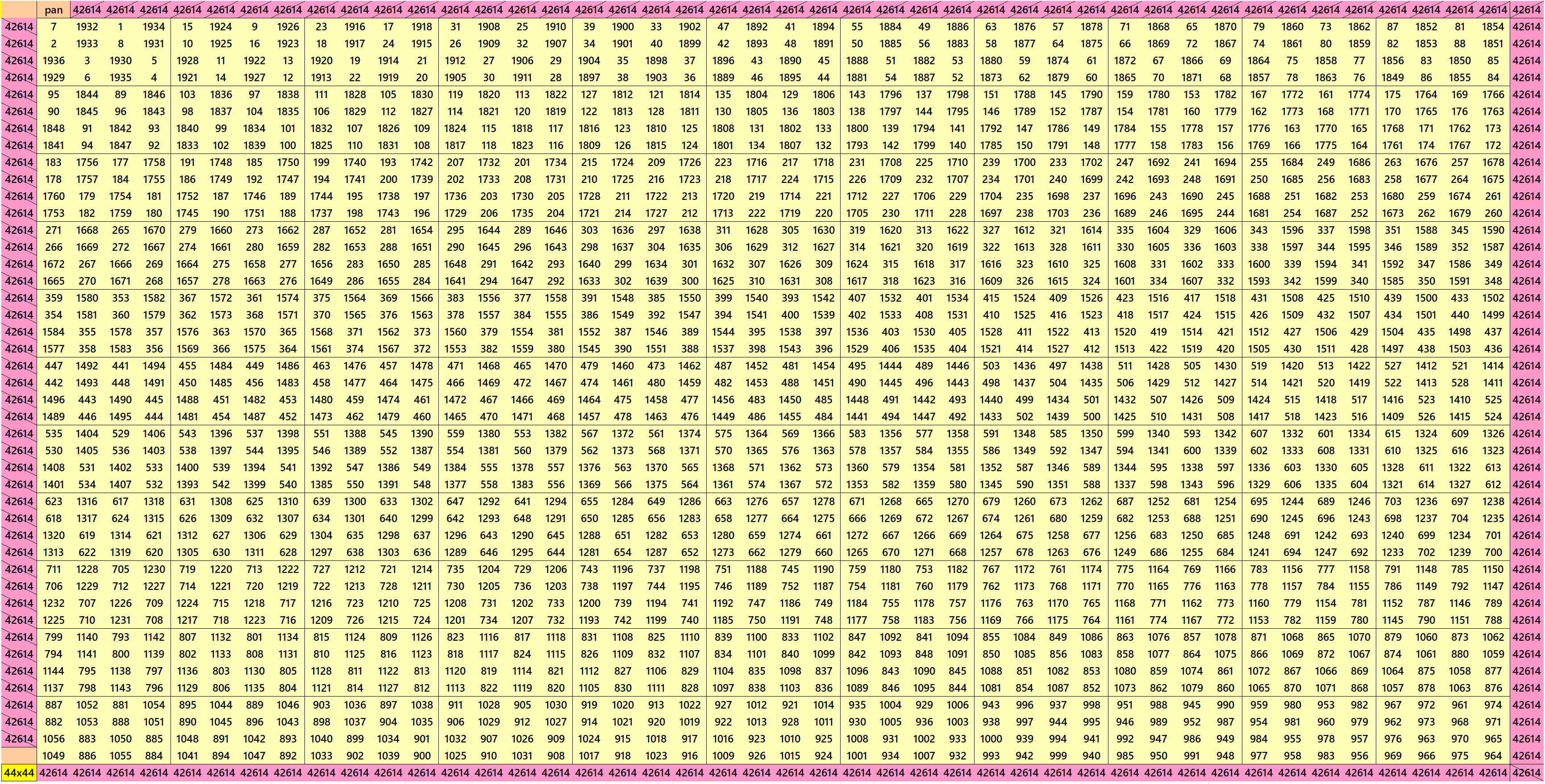
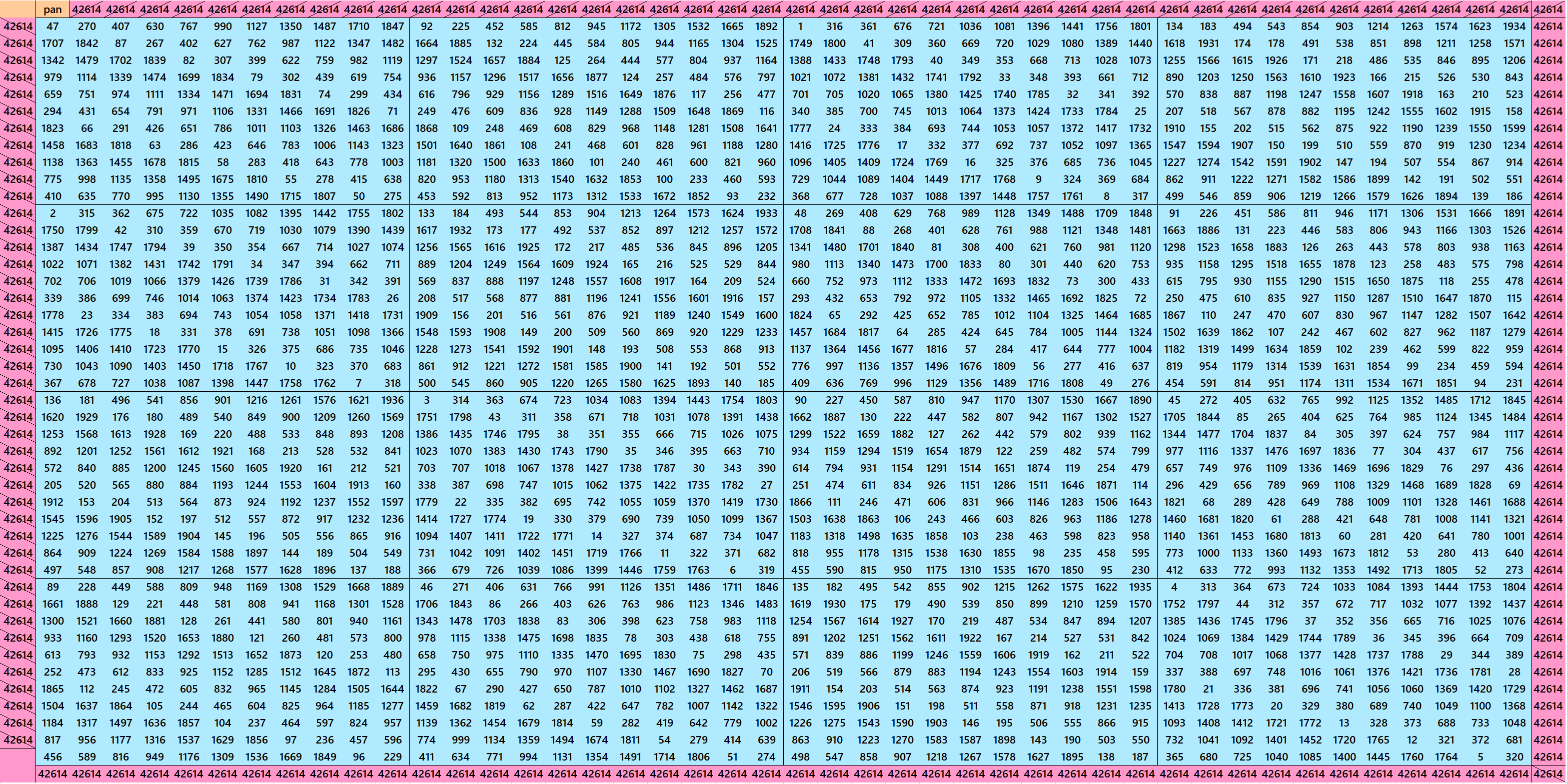
Pandiagonal Magic Squares of Order 45
We can write 45=3x3x5. This allows us to write pandigonal magic squares with blocks of orders 3 and 5. The first magic square of order 45 is made with equal sums semi-magic squares of order 3. The second magic square is made with equal sums pandiagonal magic squares of order 15, where the each magic squares order 15 is made with equal sums pandiagonal magic squares of order 5. After 15, it is second magic square where both the blocks of order 3 and 5 are of equal sums. See below:

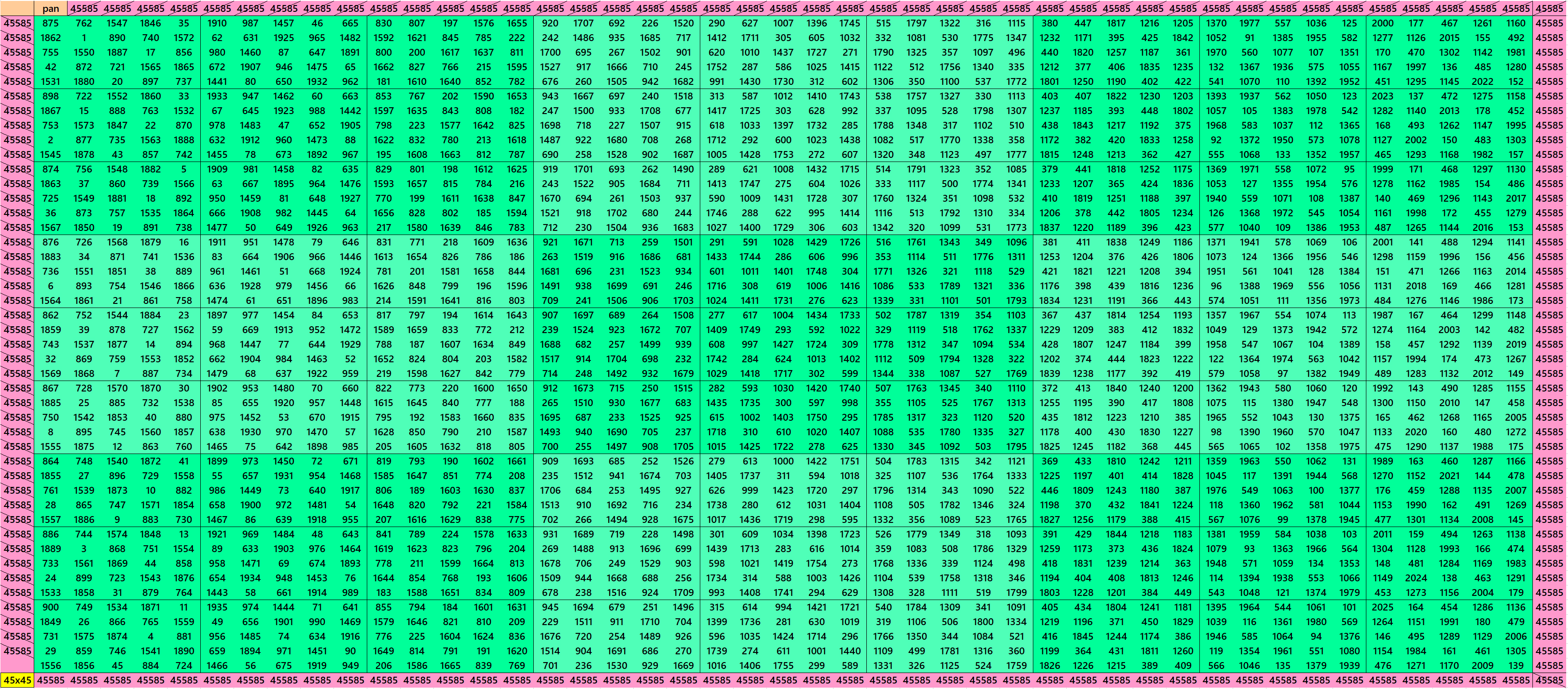
Pandiagonal Magic Squares of Order 48
We can write 48=3x4x4. This allows us to write pandigonal magic squares with blocks of orders 3 and 4. The first magic square of order 48 is made with equal sums pandiagonal magic squares of order 12, where each pandiagonal magic square is made with different sums magic squares of order 3. The second magic square of order 48 is made with equal sums pandiagonal magic squares of order 4. See below:
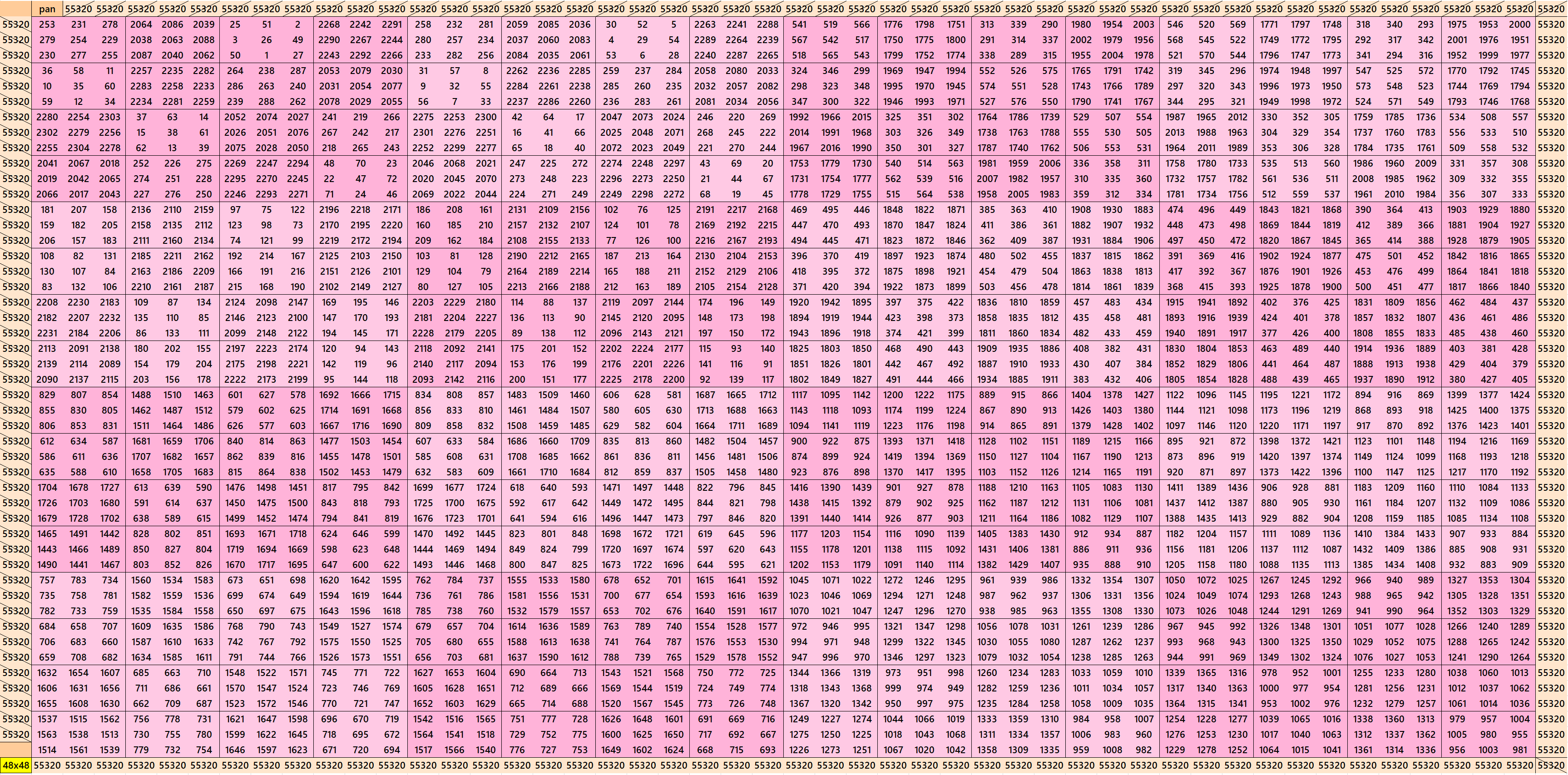
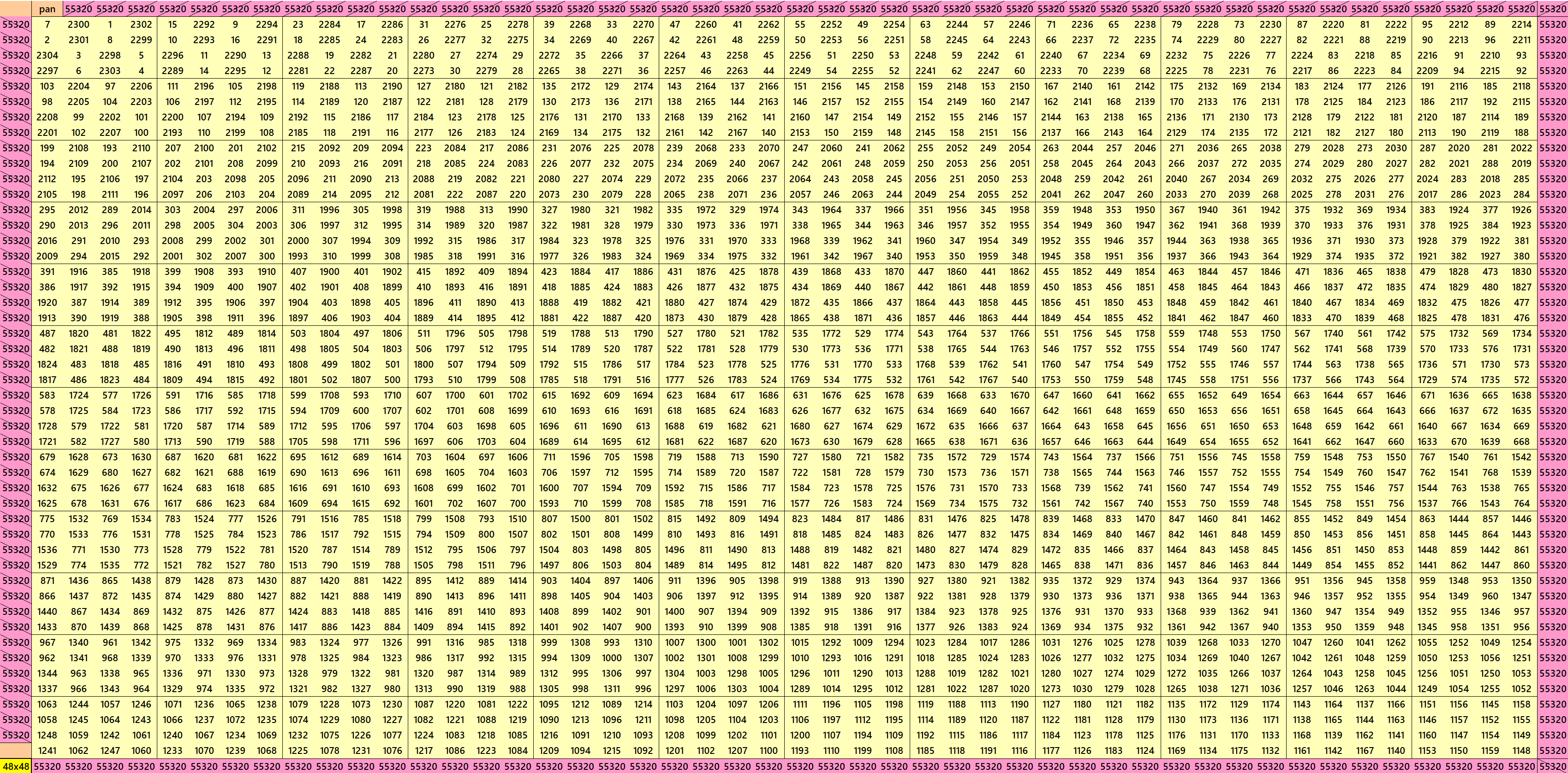
Pandiagonal Bimagic Square of Order 49
We can write 49=7^2. This allows us to write pandigonal magic squares with blocks of order 7. The magic square below is bimagic with equal sums pandiagonal magic squares of order 7. See below:

Pandiagonal Magic Squares of Order 51
We can write 51=3×17. This allows us to write pandigonal magic squares with blocks of orders 3 and 17. The first magic square of order 51 is made with equal sums semi-magic squares of order 3. The second magic square of order 39 is made with equal sums pandiagonal magic squares of order 17. See below:


Pandiagonal Magic Squares of Order 52
We can write 52=4×13. This allows us to write pandigonal magic squares with blocks of orders 4 and 13. The first magic square of order 52 is made with equal sums pandiagonal magic squares of order 4. The second magic square of order 42 is made with unequal sums pandiagonal magic squares of order 13. See below:


Proceeding in the similar way we can write pandiagonal magic squares of higher orders, except the multiple of 4k+2, k=1, 2, 3, …., i.e. of orders 6, 10, 14, etc. Below is are excel files for down the whole work on pandiagonal magic squares of among the orders 4 to 108. The procedure used to write these pandiagonal magic squares is given in the reference list given in the beginning.
Excel file for Download of Pandiagonal Magic Squares among the Orders 4 to 108.
Below are some extra files of equal equal sums blocks of magic squares resulting in pandiagonal magic squares. These blocks of orders 3, 5 and 7.
- Order 3×3
- Order 5×5
- Order 7×7
————————————————————–

