Universal and Upside-Down Magic and Bimagic Squares of Order 16

There are many ways of representing magic squares with palindromic type entries. Also, we can write magic squares in the composite forms based on pair of Latin squares. This paper works with magic and bimagic squares of order 16. By upside-down, we understand than by making 180^o it remains same. When the magic square is of both type, i.e., upside-down and mirror looking, we call it as universal magic square. By mirror looking, we understand that putting in front of mirror, still we see the image as a magic square. In case of mirror looking, writing as digitais fonts, 2 becoms 5 and 5 as 2. In case of upside-down, 6 becomes 9 and 9 as 6.

This work bring 11 examples in different categories of entries. These are divided in three parts.

1. 4-Digits Cell Entries
   • In this case, the work is in 4-digits, such as, (1,6,8,9), (1,2,5,8) and (0,2,5,8). Four digits combinations lead us to 4-digits cell entries.
2. 6-Digits Cell Entries
   • In this case, the work is in 3-digits, such as, (1,6,9) and (2,5,8). Three digits combinations lead us to 6-digits cell entries.
3. 8-Digits Cell Entries
   • In this case, the work is in 2-digits, such as, (6,9), (2,5) and (2,5). Two digits combinations lead us to 4-digits cell entries.

For complete work on universal and upside-down magic, bimagic and pandiagonal squares of orders 3 to 16, the readers can access the following links:

• Inder J. Taneja, Universal and Upside-Down Magic Squares of Orders 3 to 6, Zenodo, September 30, 2024, pp. 1-59, https://doi.org/10.5281/zenodo.13858891.
  • Site link: Universal and Upside-Down Magic Squares of Order 3 to 6 (new site)
  • Site link: Universal and Upside-Down Magic Squares of Order 3 to 6 (old site)
• Inder J. Taneja, Universal and Upside-Down Magic Squares of Orders 7 to 10, Zenodo, September 30, 2024, pp. 1-87, https://doi.org/10.5281/zenodo.13858893.
  • Site link: Universal and Upside-Down Magic Squares of Orders 7 to 10 (new site)
  • Site link: Universal and Upside-Down Magic Squares of Orders 7 to 10 (old site)
• Inder J. Taneja, Universal and Upside-Down Magic Squares of Orders 11 to 15, Zenodo, October 06, 2024, pp. 1-91, https://doi.org/10.5281/zenodo.13896515
  • Site link: Universal and Upside-Down Magic Squares of Orders 11 to 15 (new site)
  • Site link: Universal and Upside-Down Magic Squares of Orders 11 to 15 (old site)
• Inder J. Taneja, Universal and Upside-Down Magic Squares of Order 16, Zenodo, October 16, 2024, pp. 1-28, https://doi.org/10.5281/zenodo.13942620
  • Site link: Universal and Upside-Down Magic and Bimagic Squares of Order 16 (new site)
  • Site link:

Universal and Upside-Down
Magic and Bimagic Squares of Order 16

a) 4-Digits Cell Entries:

Example 1: Upside-Down Bimagic Square in 4-digits (1,6,8,9)

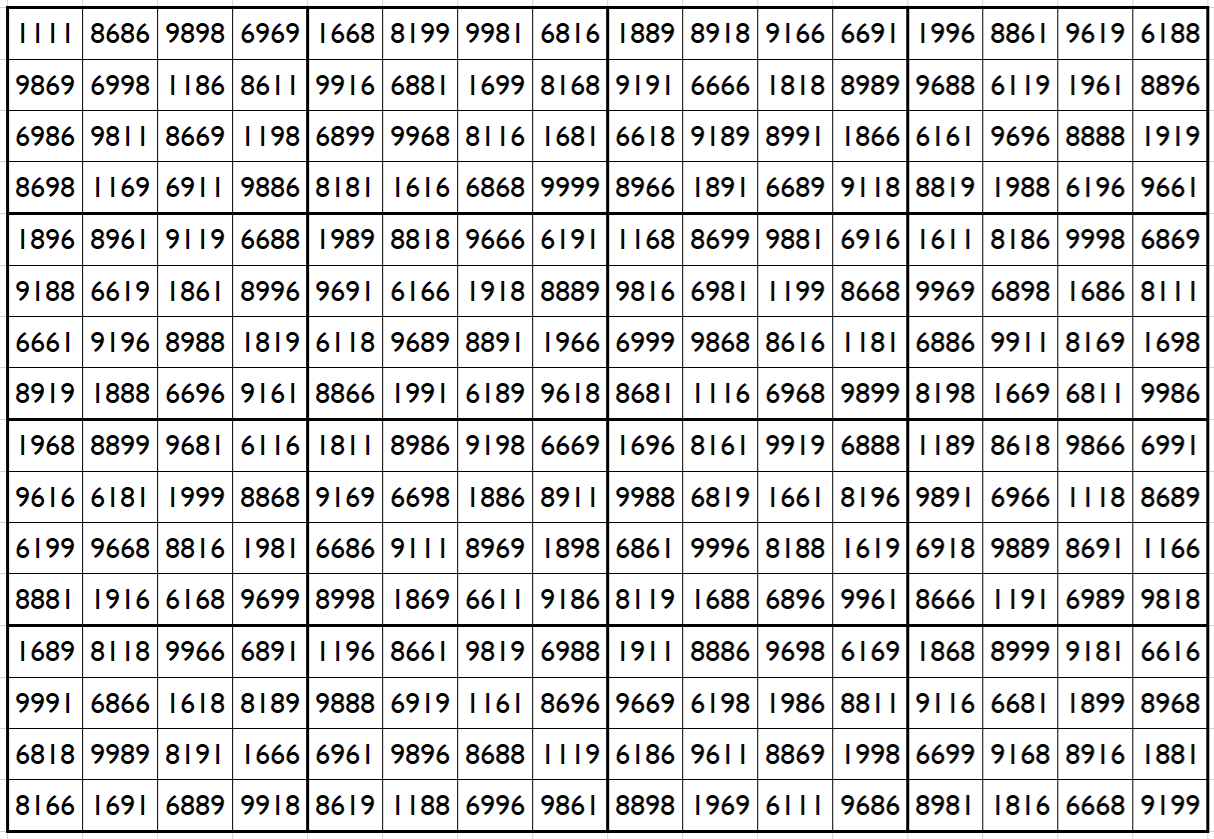
The above magic square is bimagic and upside-down with magic and bimagic sums

S_16×16(1,6,8,9):=106656 and Sb_16×16(1,6,8,9):=864504248.

Blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(1,6,8,9):=26664.

Example 2: Universal Bimagic Square in 4-digits (1,2,5,8)

The above magic square is bimagic and universal with magic and bimagic sums

S_16×16(1,2,5,8):=71104 and Sb_16×16(1,2,5,8):=437198296.

Blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(1,2,5,8):=17776.

Example 3: Universal Bimagic Square in 4-digits (0,2,5,8)

The above magic square is bimagic and universal with magic and bimagic sums

S_16×16(0,2,5,8):=66660 and Sb_16×16(0,2,5,8):= 426207072.

Blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(0,2,5,8):=16665.

b) 6-Digits Cell Entries:

Example 4: Upside-Down Magic Square in 3-digits (1,6,9)

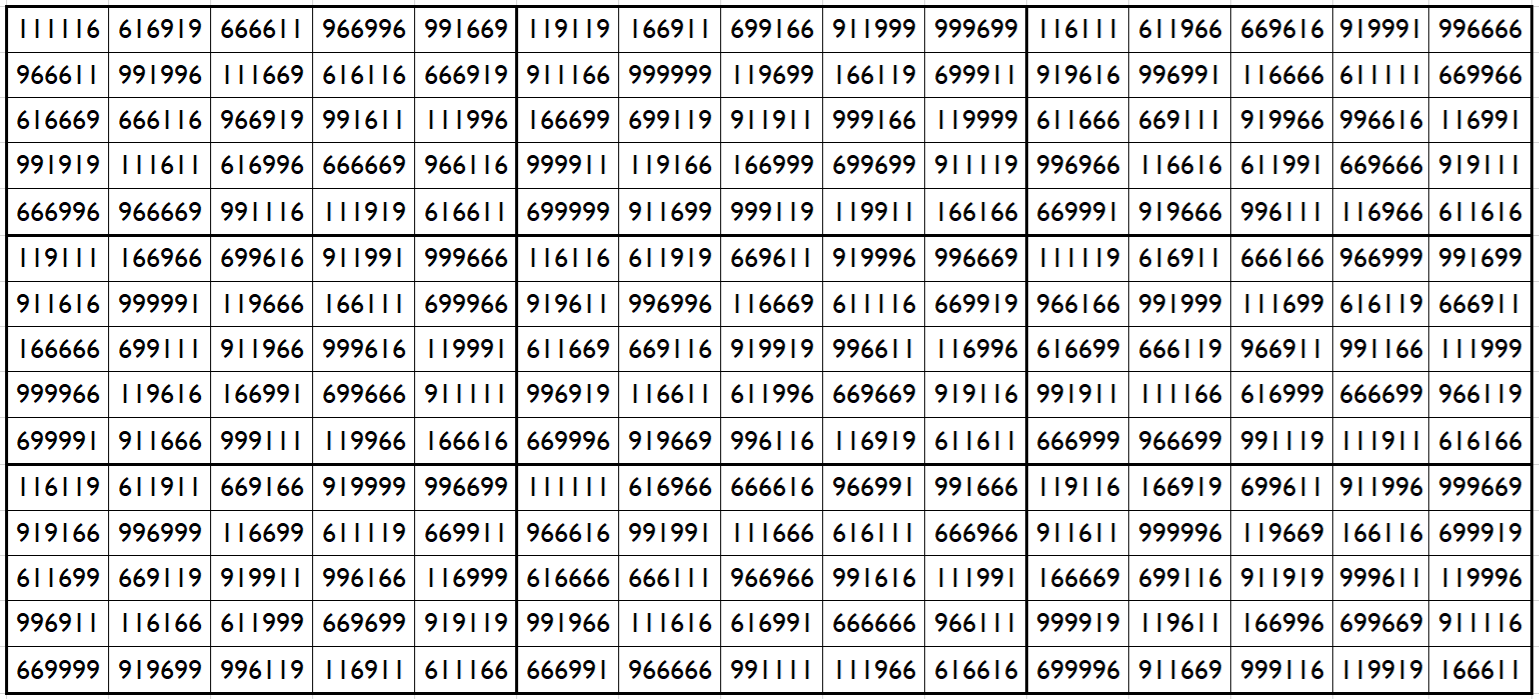
The above magic square in 3-digits (1,6,9) is upside-down with magic sum

S_16×16(2,5,8):=11120109.

Blocks of order 4 are magic squares with different magic sums.

Example 5: Universal Magic Square in 3-digits (2,5,8)

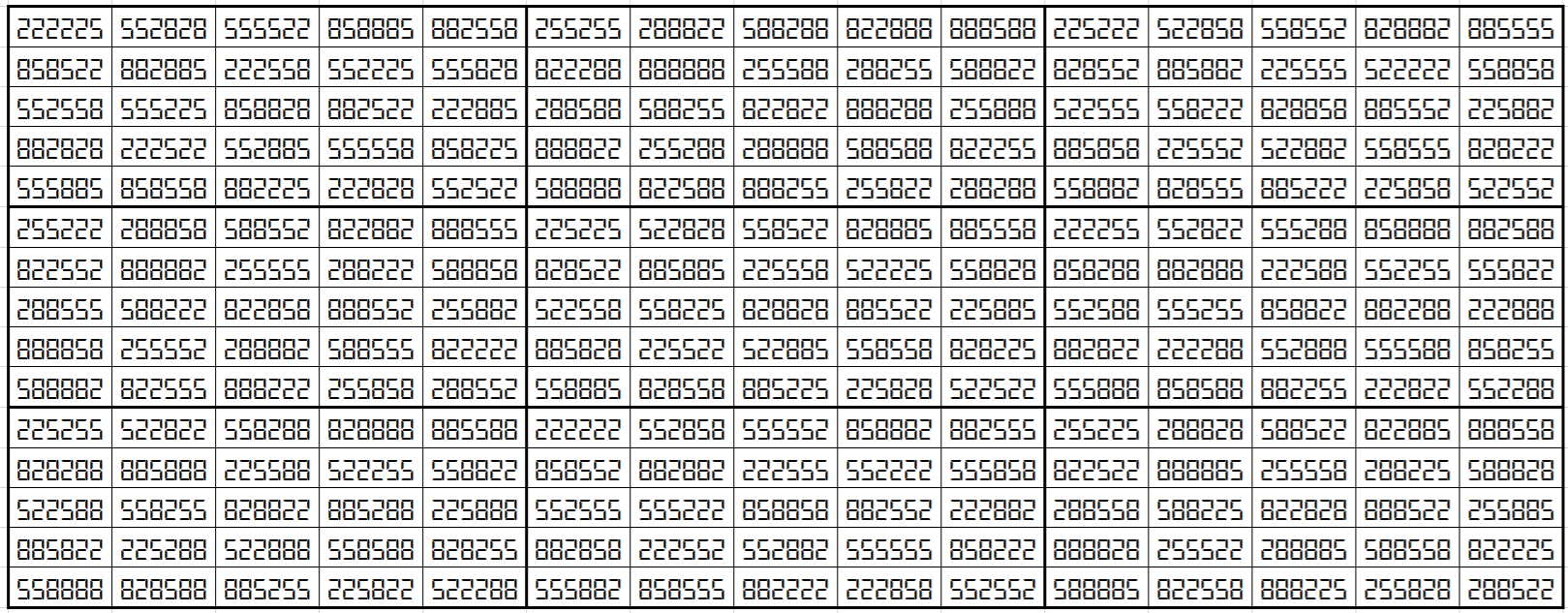
The above magic square in 3-digits (2,5,8) is universal. In case of original and mirror looking versions, the magic sums are same, i.e,

SO_16×16(2,5,8):=SM_16×16(2,5,8):=8005998.

In case of upside-down, the magic sum is different, i.e.,

SU_16×16(2,5,8):=7708701.

The blocks of order 4 are magic squares with different magic sums.

b) 8-Digits Cell Entries:

Example 6. Upside-Down Bimagic Square in 2-digits (6,9)

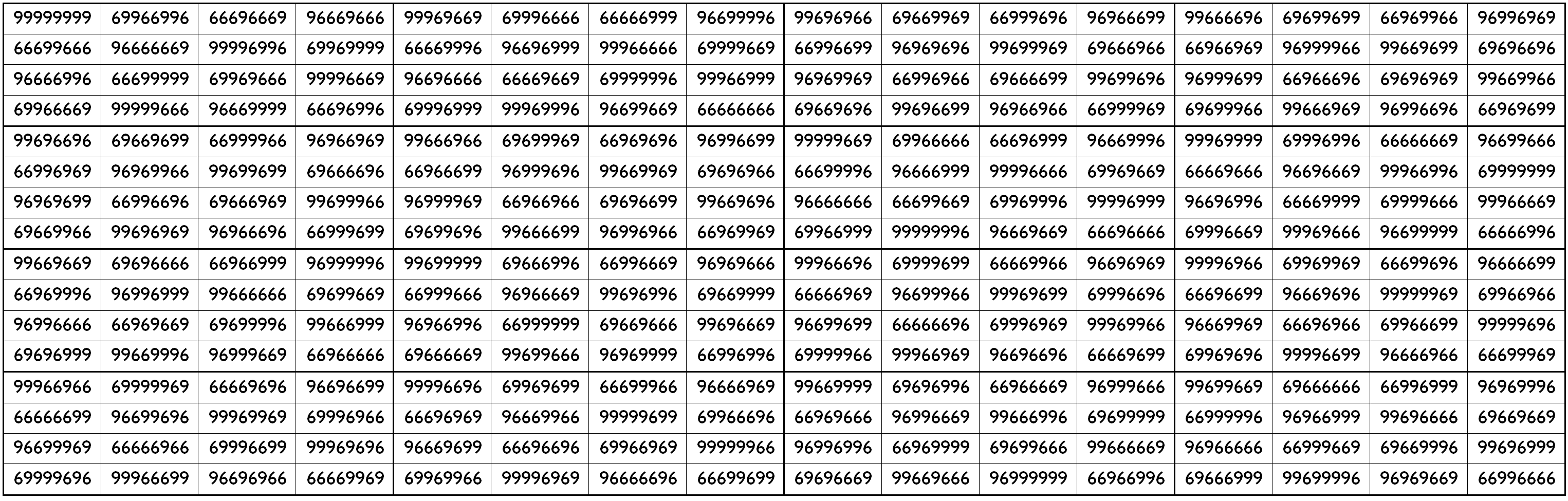
The above magic square is bimagic and upside-down with magic and bimagic sums

S_16×16(6,9):=1333333320 and Sb_16×16(6,9):=114747472525252536.

Blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(6,9):=333333330.

Example 7. Upside-Down Pandiagonal Magic Square in 2-digits (6,9)

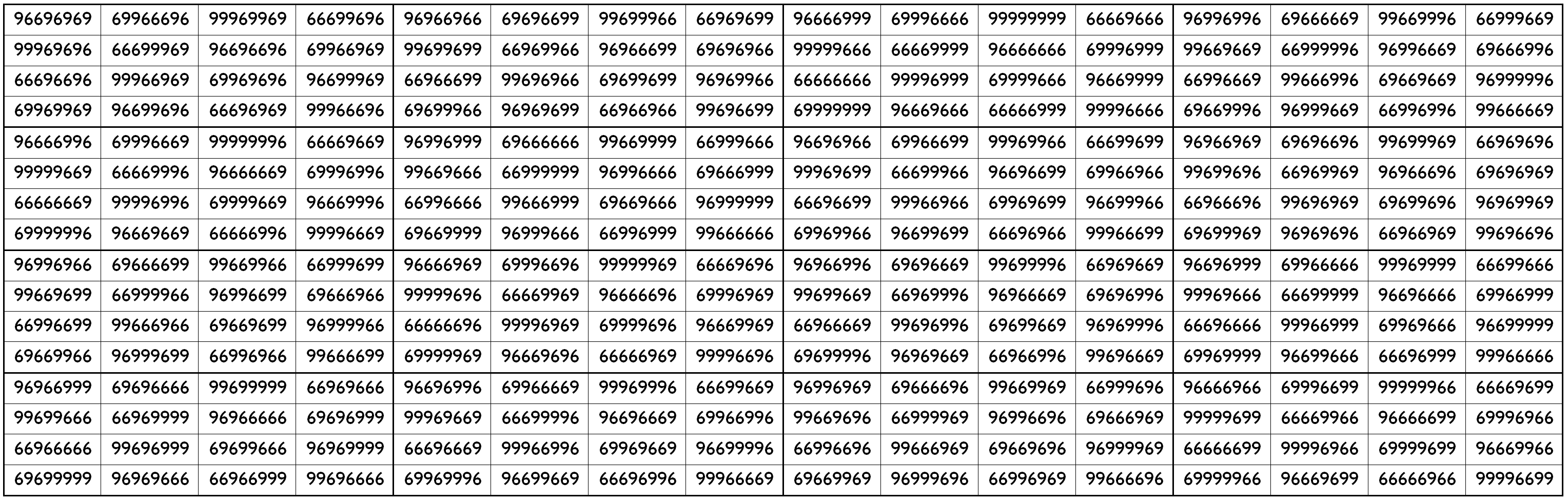
The above magic square is upside-down and pandiagonal with magic sum

S_16×16(6,9):=1333333320

Blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(6,9):=333333330.

Example 8. Universal Bimagic Square in 2-digits (1,8)

The above magic square is bimagic and universal with magic and bimagic sums

S_16×16(1,8):=799999992 and Sb_16×16(1,8):=59797978997979800.

Blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(1,8):=199999998.

Example 9. Universal Pandiagonal Magic Square in 2-digits (1,8)

The above magic square is universal and pandiagonal with magic sum

S_16×16(1,8):=799999992

Blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(1,8):=199999998.

Example 10. Universal Bimagic Square in 2-digits (2,5)

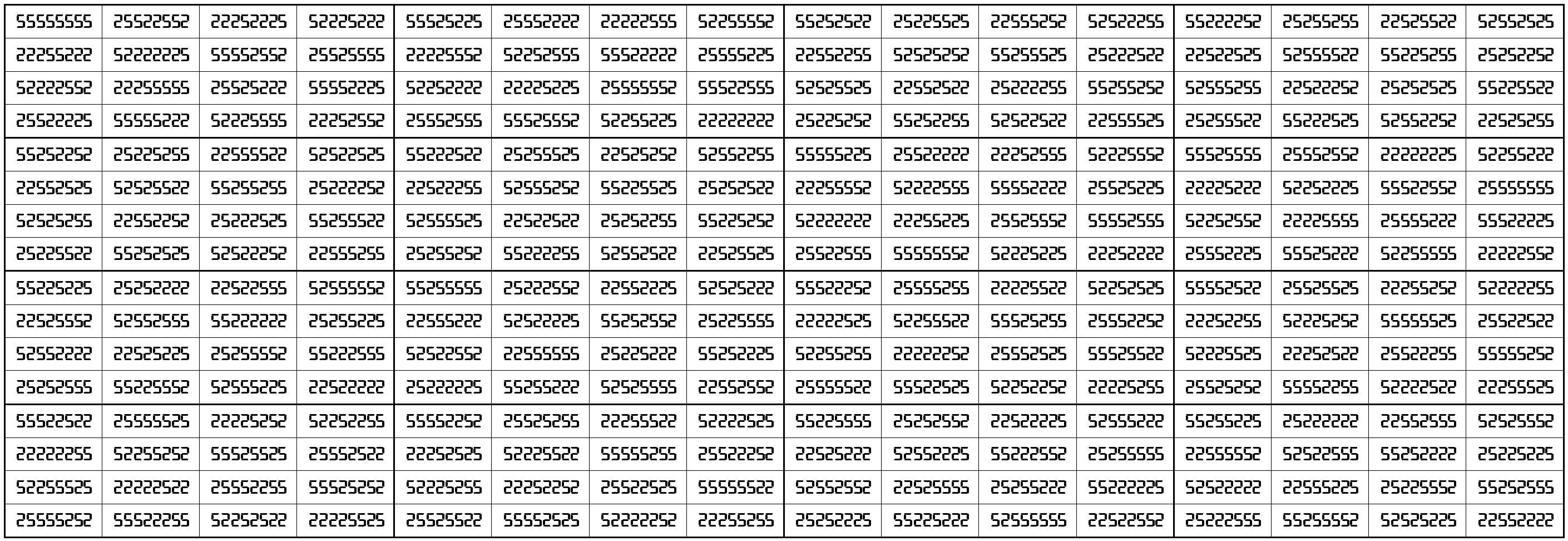
The above magic square is bimagic and universal with magic and bimagic sums

S_16×16(2,5):=622222216 and Sb_16×16(2,5):=27833894016610552.

Blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(2,5):=155555554.

Example 11. Universal Pandiagonal Magic Square in 2-digits (2,5)

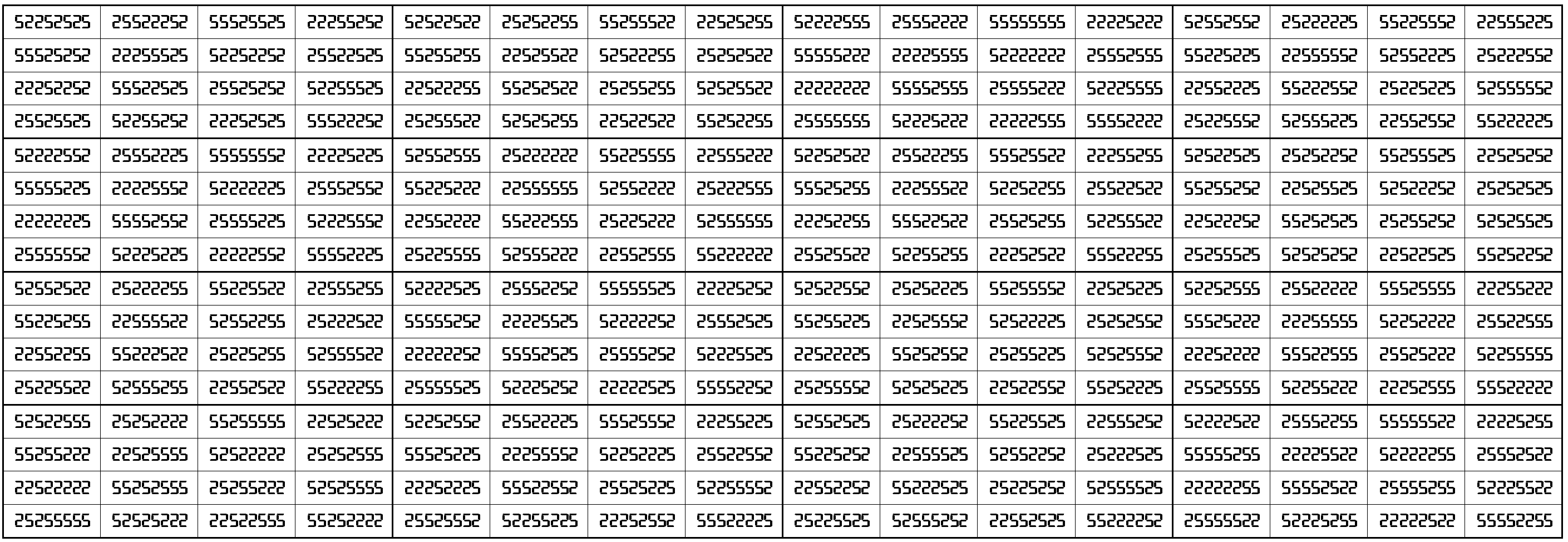
The above magic square is universal and pandiagonal with magic sum

S_16×16(2,5):=622222216.

Blocks of order 4 are magic squares with equal magic sums, i.e., S_4×4(2,5):=155555554.