This work bring magic cubes with six sides as magic squares of orders 3, 4, 5, 7 to 8. Most of the magic squres are with different magic sums. These examples brings only universal and or upside-down magic cubes. By universal we understand that when the magic square is 180o rotatable and are mirror looking, while in case of upside-down the magic squares are only 180o rotatable.
The readers can also access the following links to download the whole work
- Inder J. Taneja, Magic Cubes Based on Magic Squares, Zenodo, October 17, 2024, pp. 1-63, https://doi.org/10.5281/zenodo.13924915.
- Site link: Magic Cubes Based on Magic Squares
- Inder J. Taneja, Universal and Upside-Down Magic Cubes, Zenodo, October 17, 2024, pp. 1-38, https://doi.org/10.5281/zenodo.13947425.
- Site Link: Universal and Upside-down Magic Cubes
Universal and Upside-down Magic Cubes Order 3
Example 1. Univesal Magic Cube
Let’s consider the following six semi-magic squares of order 3
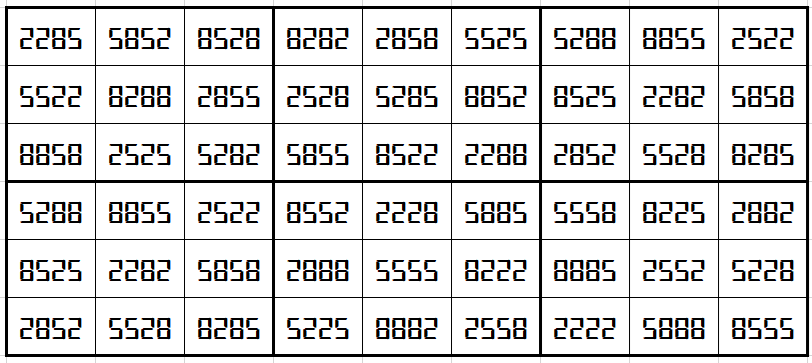
The above six magic squares are constucted using only 3-digits, 2, 5 and 8. All the blocks of order 3×3 are semi-magic with equal semi-magic sum, i.e.,
S3×3(1)=S3×3(2)=S3×3(3)=S3×3(4)=S3×3(5)=S3×3(6):=16665.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
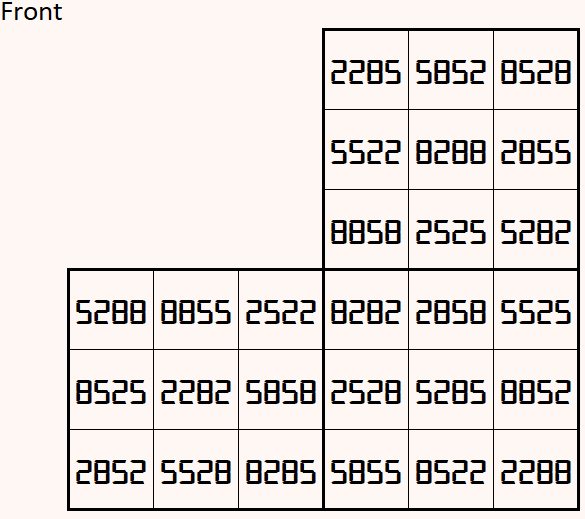

Above magic cube is readable in any position, i.e., upside-down and/or mirror looking.
Example 2. Univesal Magic Cube
Let’s consider the following six semi-magic squares of order 3

The above six magic squares are constucted using only 3-digits, 0, 2 and 5. All the blocks of order 3×3 are semi-magic with equal semi-magic sum, i.e.,
S3×3(1)=S3×3(2)=S3×3(3)=S3×3(4)=S3×3(5)=S3×3(6):=7777.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
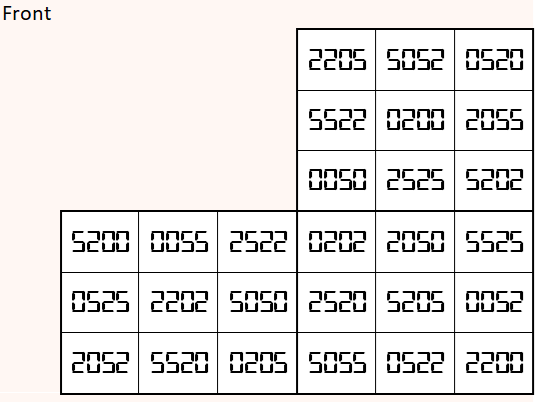
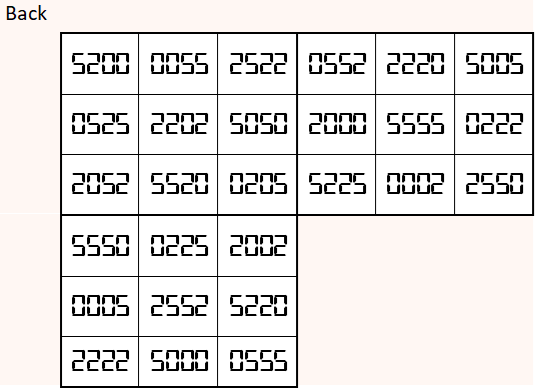
Above magic cube is readable in any position, i.e., upside-down and/or mirror looking.
Example 3. Upside-down
Let’s consider the following six semi-magic squares of order 3
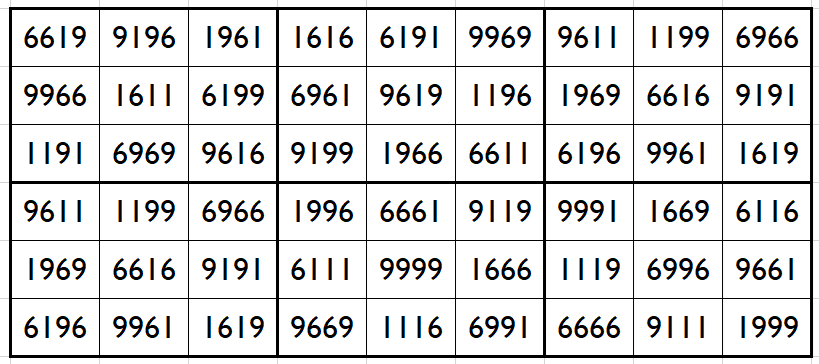
The above six magic squares are constucted using only 3-digits, 1, 6 and 9. All the blocks of order 3×3 are semi-magic with equal semi-magic sum, i.e.,
S3×3(1)=S3×3(2)=S3×3(3)=S3×3(4)=S3×3(5)=S3×3(6):=17776.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
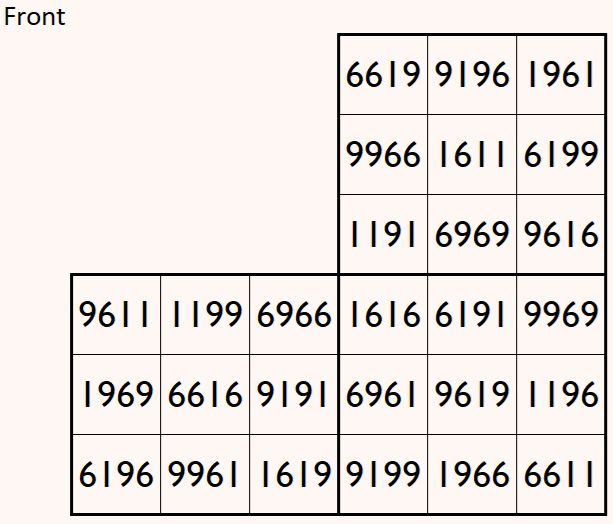
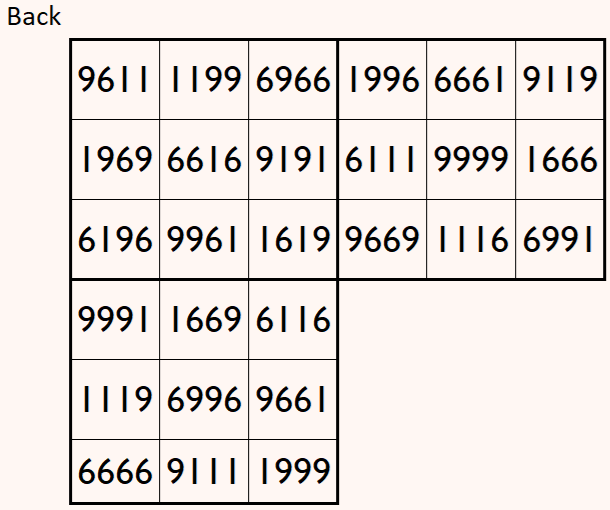
Above magic cube is upside-down, i.e, 180 degrees rotation, still we can read each magic square.
Example 4. Upside-down
Let’s consider the following six semi-magic squares of order 3
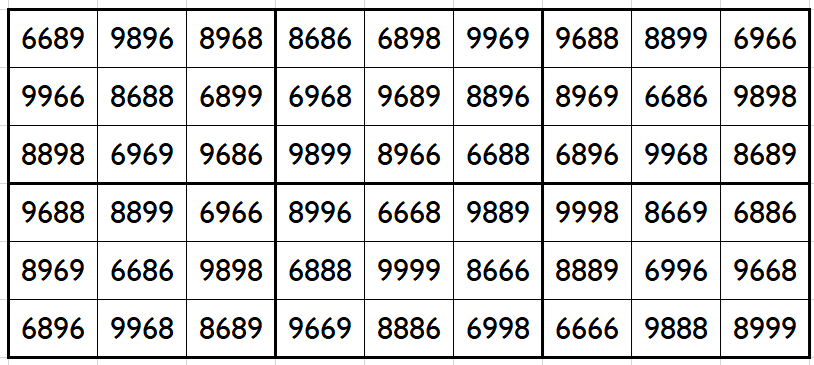
The above six magic squares are constucted using only 3-digits, 6, 8 and 9. All the blocks of order 3×3 are semi-magic with equal semi-magic sum, i.e.,
S3×3(1)=S3×3(2)=S3×3(3)=S3×3(4)=S3×3(5)=S3×3(6):=25553.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
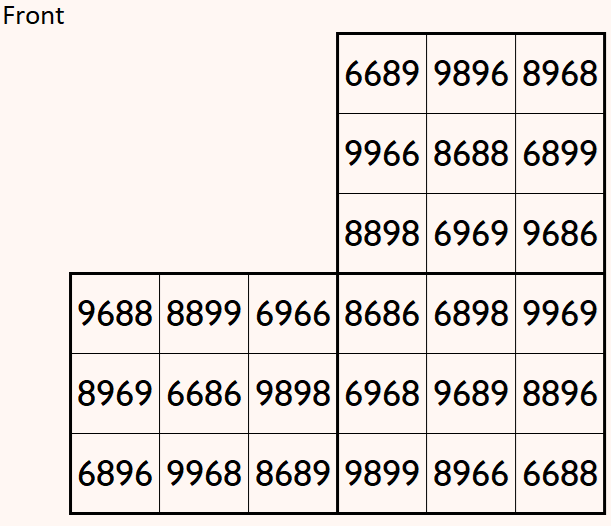
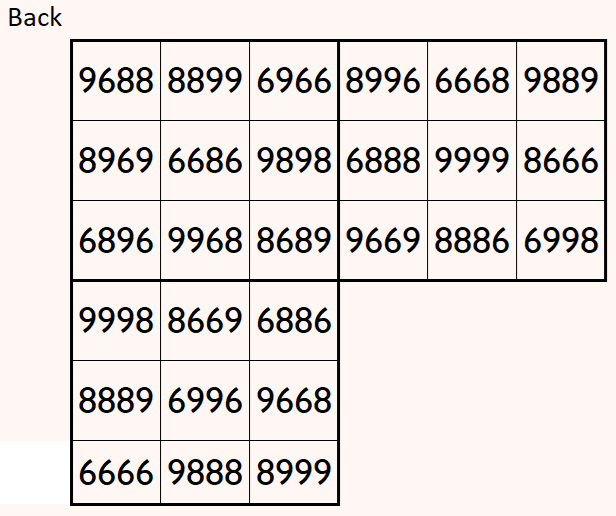
Above magic cube is upside-down, i.e, 180 degrees rotation, still we can read each magic square.
Magic Cubes with Magic Squares of Order 4
Example 1. Upside-down Magic Cube
Let’s consider the following six magic squares of order 4:
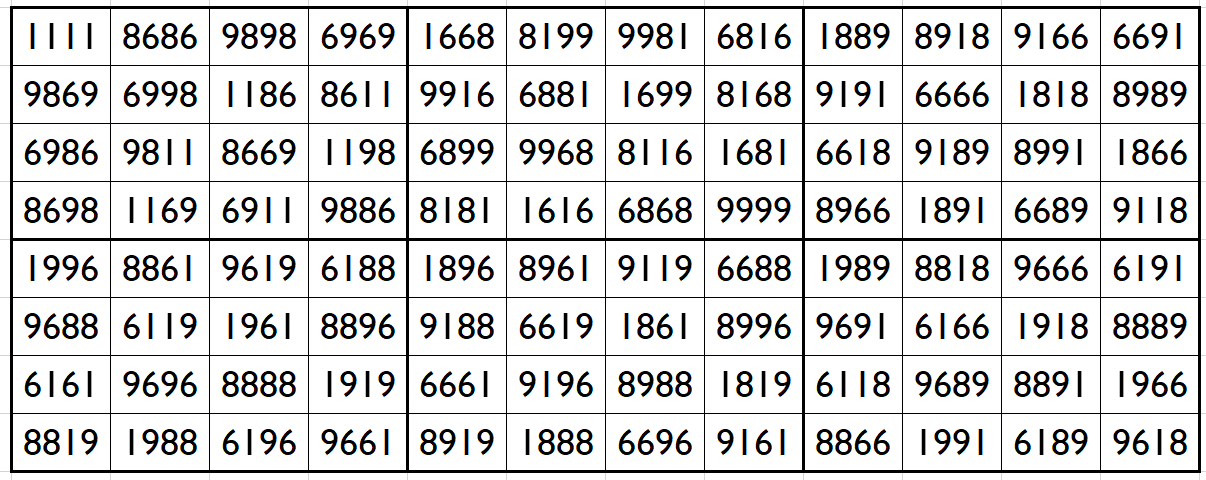
The above six magic squares are constucted using only 4-digits, 1, 6, 8 and 9. All the blocks of order 4×4 are magic squares with equal magic sum, i.e.,
S4×4(1)=S4×4(2)=S4×4(3)=S4×4(4)=S4×4(5)=S4×4(6):=26664.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
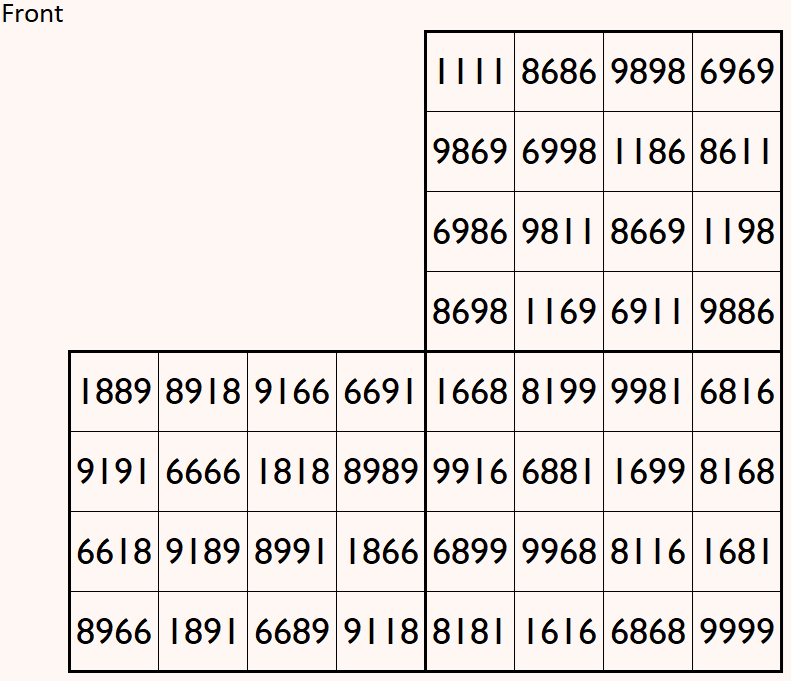
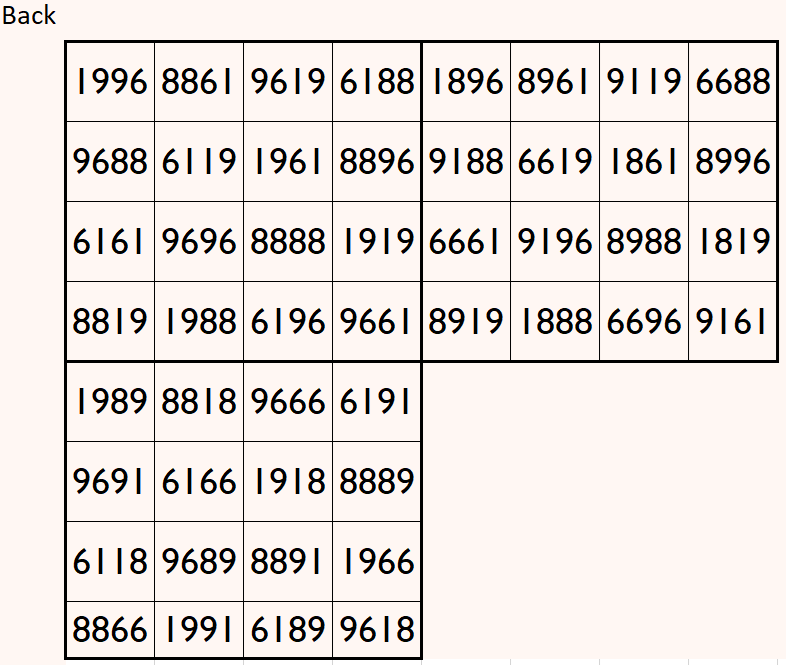
Above magic cube is readable upside-down position.
Example 2. Universal Magic Cube
Let’s consider the following six magic squares of order 4:
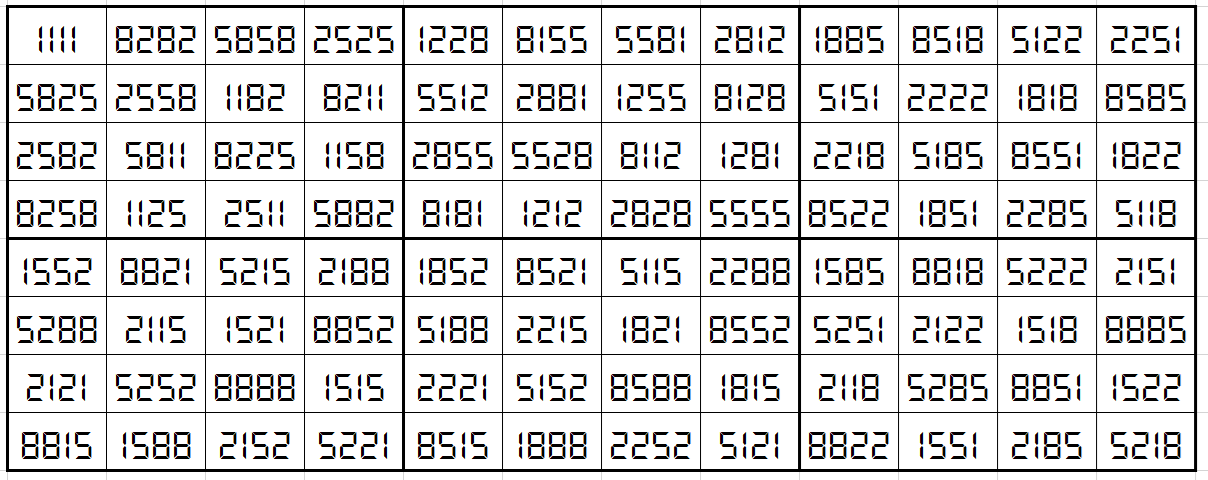
The above six magic squares are constucted using only 4-digits, 1, 2, 5 and 8. All the blocks of order 4×4 are magic squares with equal magic sum, i.e.,
S4×4(1)=S4×4(2)=S4×4(3)=S4×4(4)=S4×4(5)=S4×4(6):=17776.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:

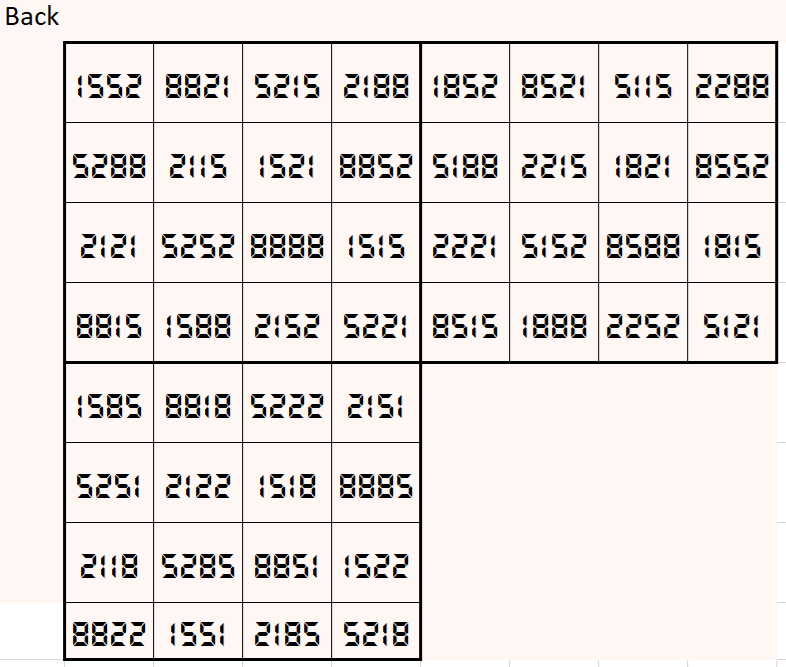
Above magic cube is universal, i.e., it is readable as upside-down and/or mirror looking position.
Example 3. Universal Magic Cube
Let’s consider the following six magic squares of order 4:

The above six magic squares are constucted using only 4-digits, 0, 2, 5 and 8. All the blocks of order 4×4 are magic squares with equal magic sum, i.e.,
S4×4(1)=S4×4(2)=S4×4(3)=S4×4(4)=S4×4(5)=S4×4(6):=16665.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
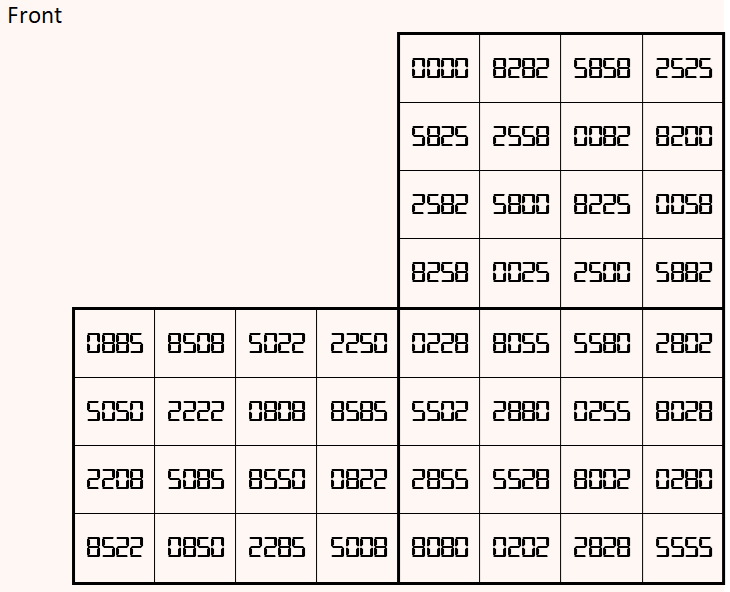

Above magic cube is universal, i.e., it is readable as upside-down and/or mirror looking position.
Magic Cubes with Magic Squares of Order 5
Example 1. Upside-side Magic Cube
Let’s consider the following six pandiagonal magic squares of order 5
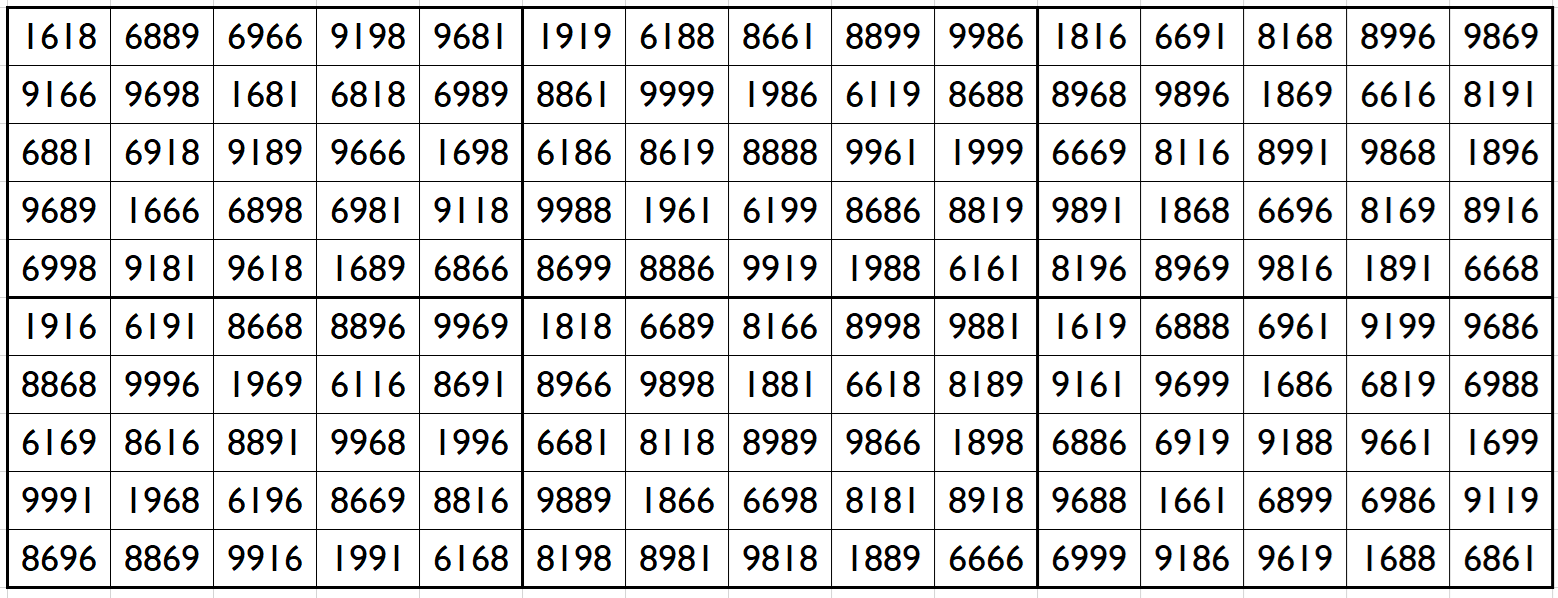
The above six magic squares are constucted using only 4-digits, 1, 6, 8 and 9. All the blocks of order 5×5 are pandiagonal magic squares with different magic sum, i.e.,
S5×5(1):=34352, S5×5(2):=35653, S5×5(3):=35540, S5×5(4):=35640, S5×5(5):=35552 and S5×5(6):=34353.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
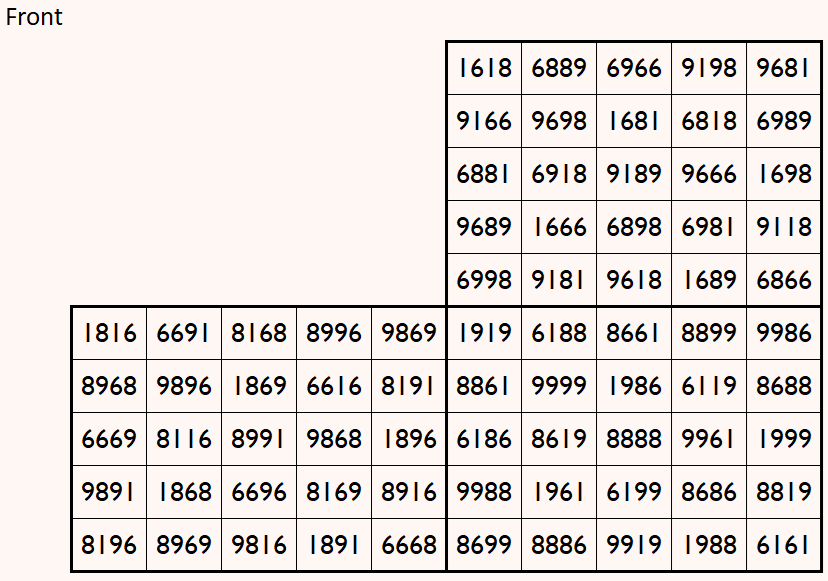
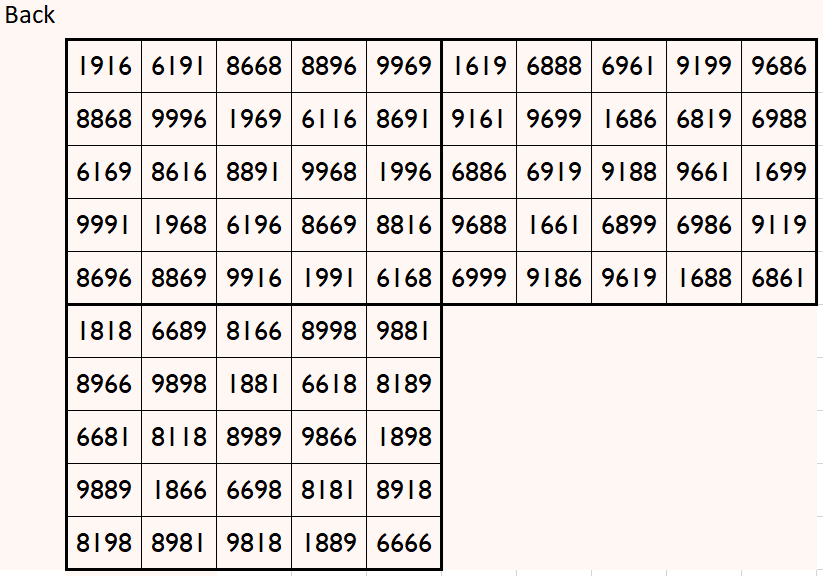
Above magic cube is readable upside-down position.
Example 2. Universal Magic Cube
Let’s consider the following six pandiagonal magic squares of order 5

The above six magic squares are constucted using only 4-digits, 0, 2, 5 and 8. All the blocks of order 5×5 are pandiagonal magic squares with different magic sum, i.e.,
S5×5(1):=15953, S5×5(2):=25250, S5×5(3):=25457, S5×5(4):=25157, S5×5(5):=25553 and S5×5(6):=25553.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
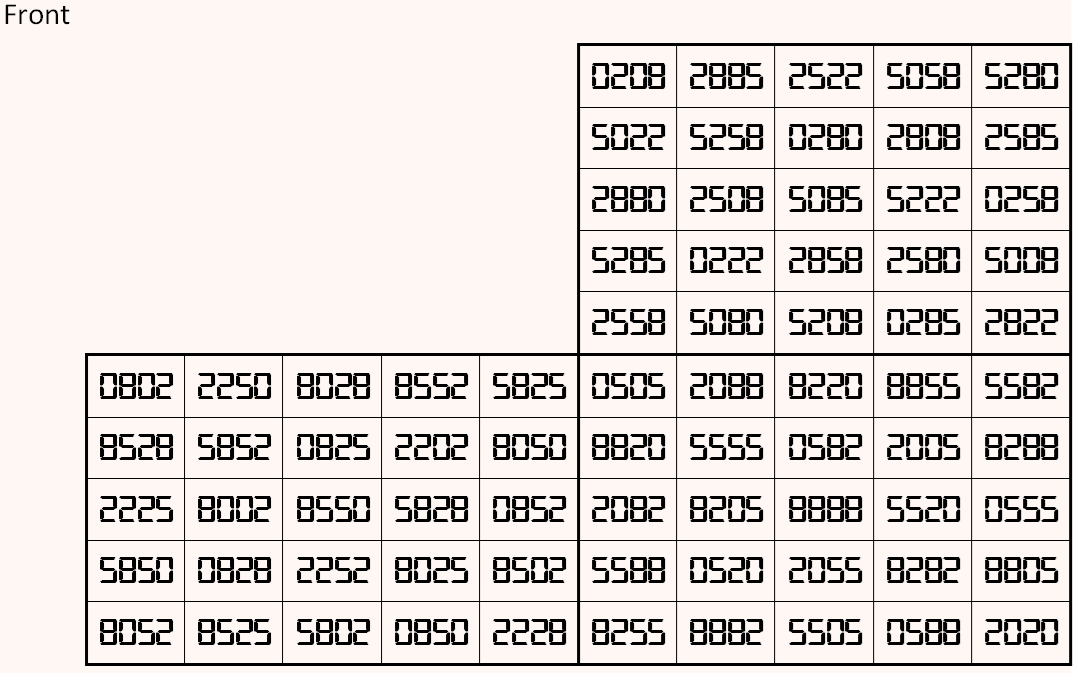
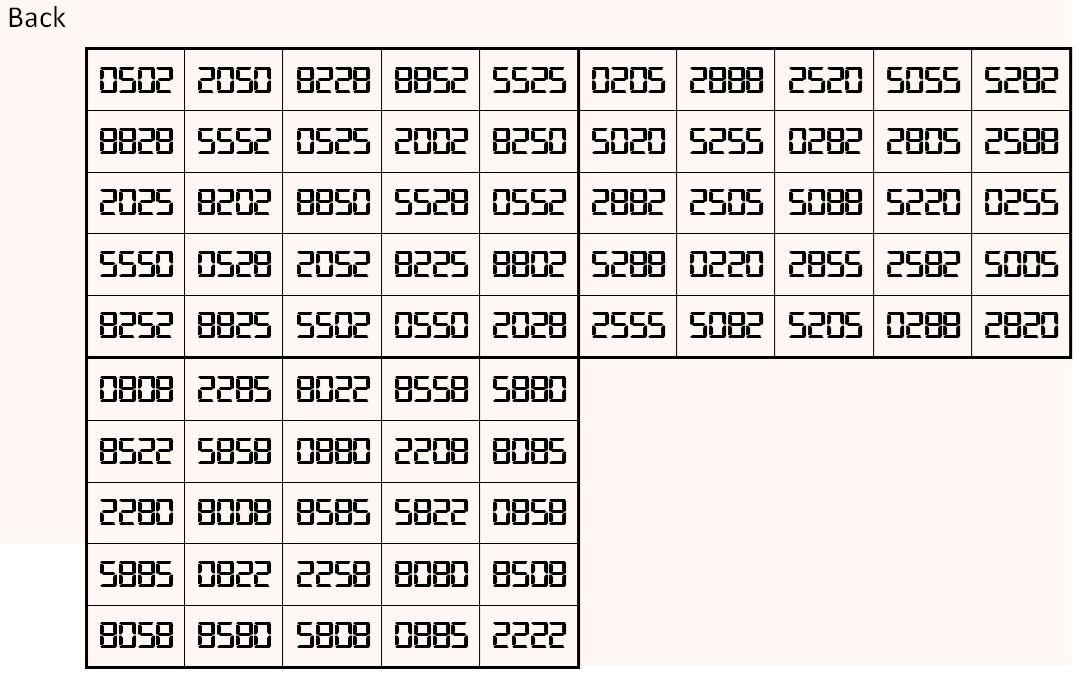
Above magic cube is universal, i.e., it is readable as upside-down and/or mirror looking position.
Example 3. Universal Magic Cube
Let’s consider the following six pandiagonal magic squares of order 5
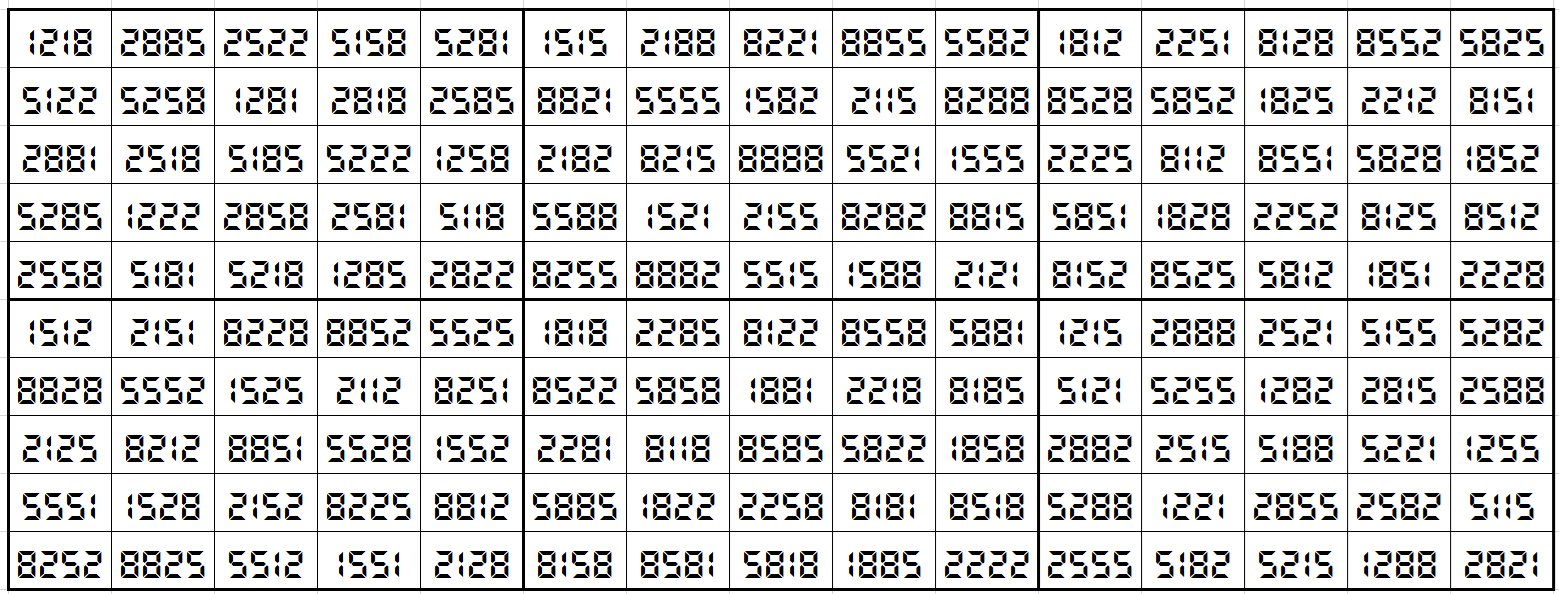
The above six magic squares are constucted using only 4-digits, 1, 2, 5 and 8. All the blocks of order 5×5 are pandiagonal magic squares with different magic sum, i.e.,
S5×5(1):=17064, S5×5(2):=26361, S5×5(3):=26568, S5×5(4):=26268, S5×5(5):=26664 and S5×5(6):=17061.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
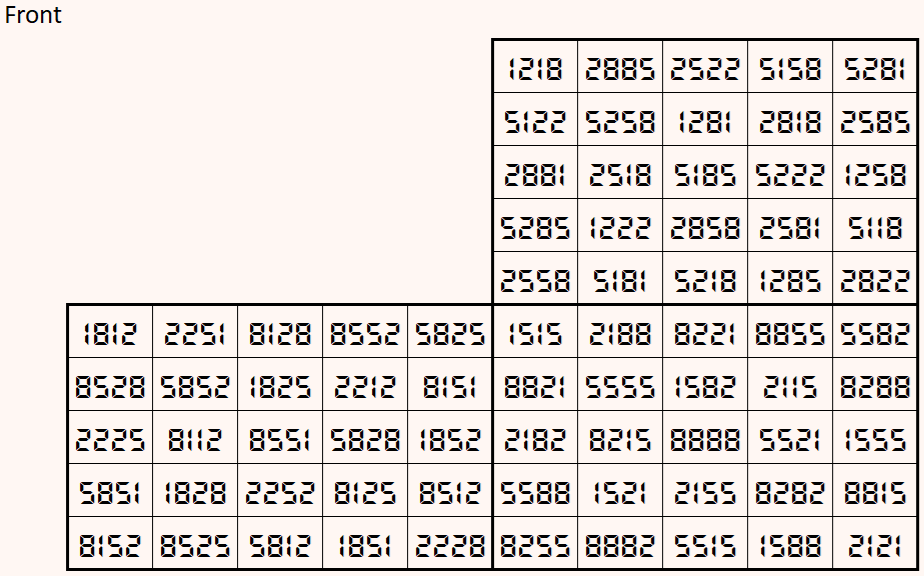

Above magic cube is universal, i.e., it is readable as upside-down and/or mirror looking position.
Magic Cubes with Magic Squares of Order 7
Example 1. Universal Magic Cube
Let’s consider the following six pandiagonal magic squares of order 7
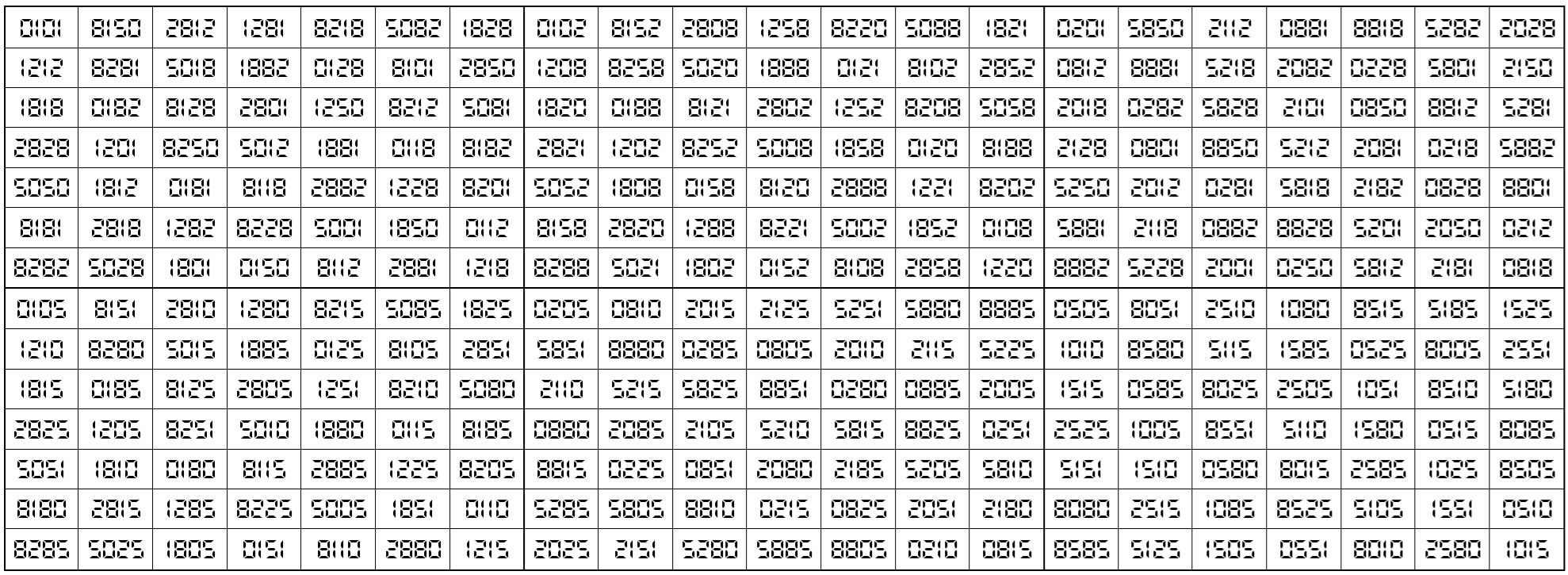
The above six magic squares are constucted using only 5-digits, 0, 1, 2, 5 and 8. All the blocks of order 7×7 are pandiagonal magic squares with different magic sum, i.e.,
S7×7(1):=27472, S7×7(2):=27449, S7×7(3):=27449, S7×7(4):=27471, S7×7(5):=25171 and S7×7(6):=27371.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
Above magic cube is universal, i.e., it is readable as upside-down and/or mirror looking position.
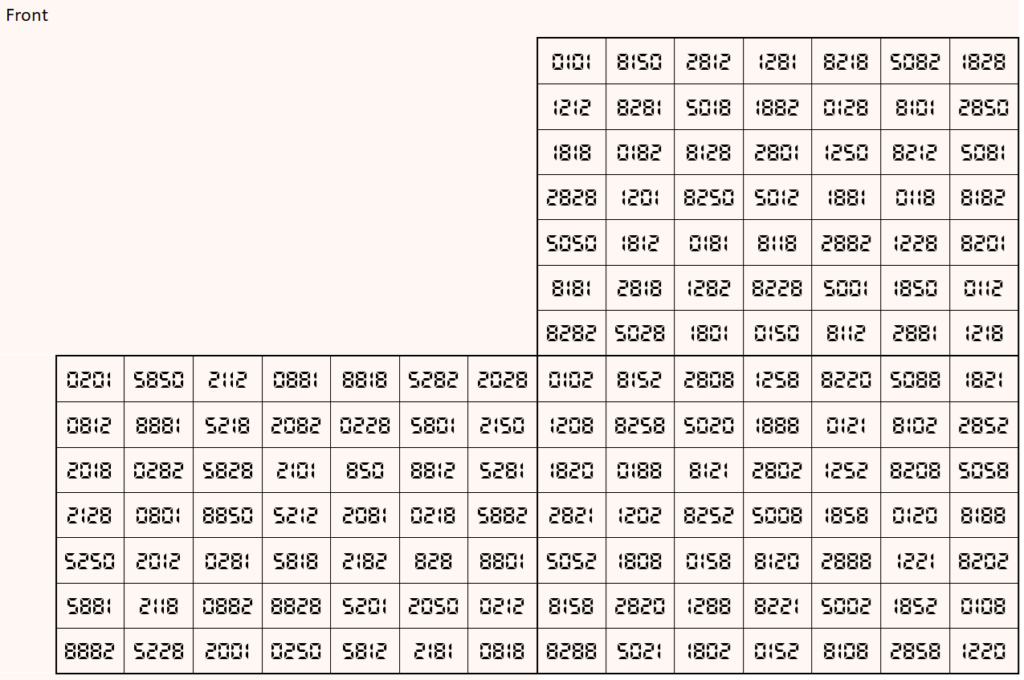

Example 2. Upside-down Magic Cube
Let’s consider the following six pandiagonal magic squares of order 7
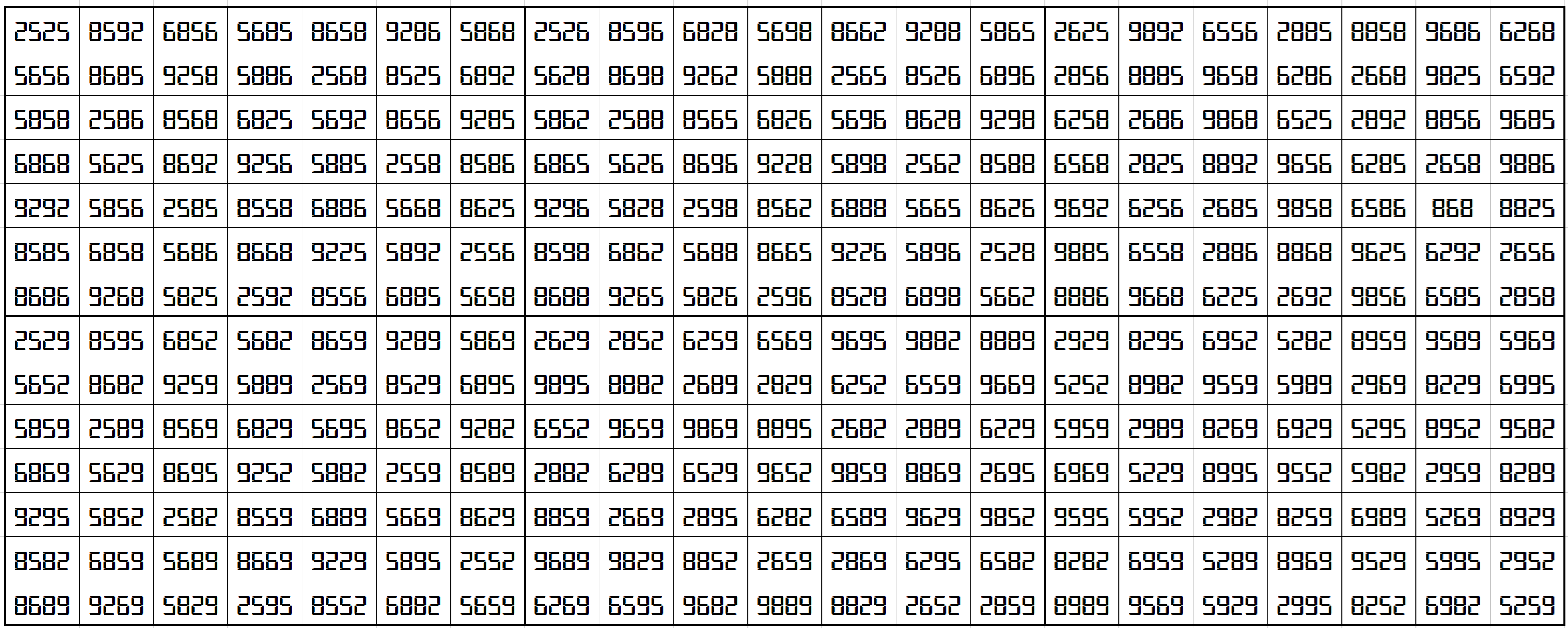
The above six magic squares are constucted using only 5-digits, 2, 5, 6, 8 and 9. All the blocks of order 7×7 are pandiagonal magic squares with different magic sum, i.e.,
S7×7(1):=47470, S7×7(2):=47463, S7×7(3):=47463, S7×7(4):=47475, S7×7(5):=46775 and S7×7(6):=47975.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:


Above magic cube is readable as upside-down.
Example 3. Upside-down Magic Cube
Let’s consider the following six pandiagonal magic squares of order 7
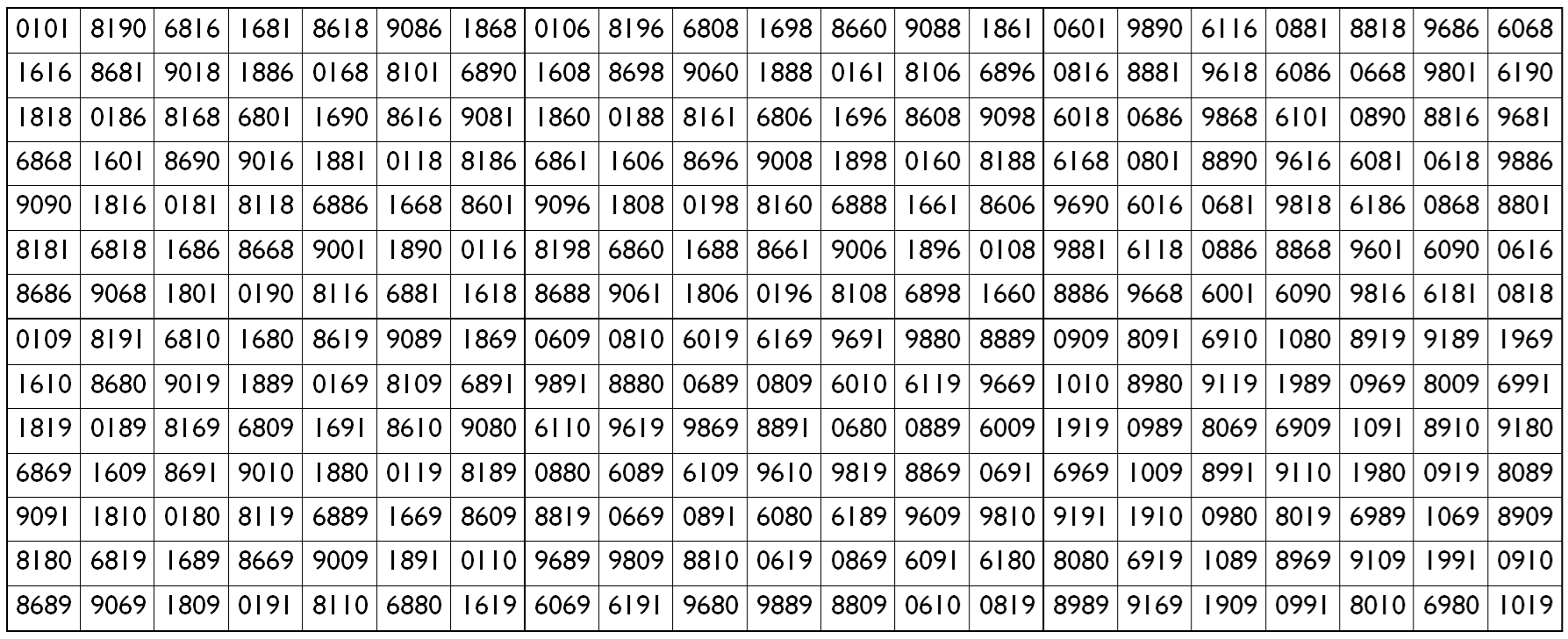
The above six magic squares are constucted using only 5-digits, 0, 1, 6, 8 and 9. All the blocks of order 7×7 are pandiagonal magic squares with different magic sum, i.e.,
S7×7(1):=36360, S7×7(2):=36417, S7×7(3):=42060, S7×7(4):=36367, S7×7(5):=42067 and S7×7(6):=37067.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
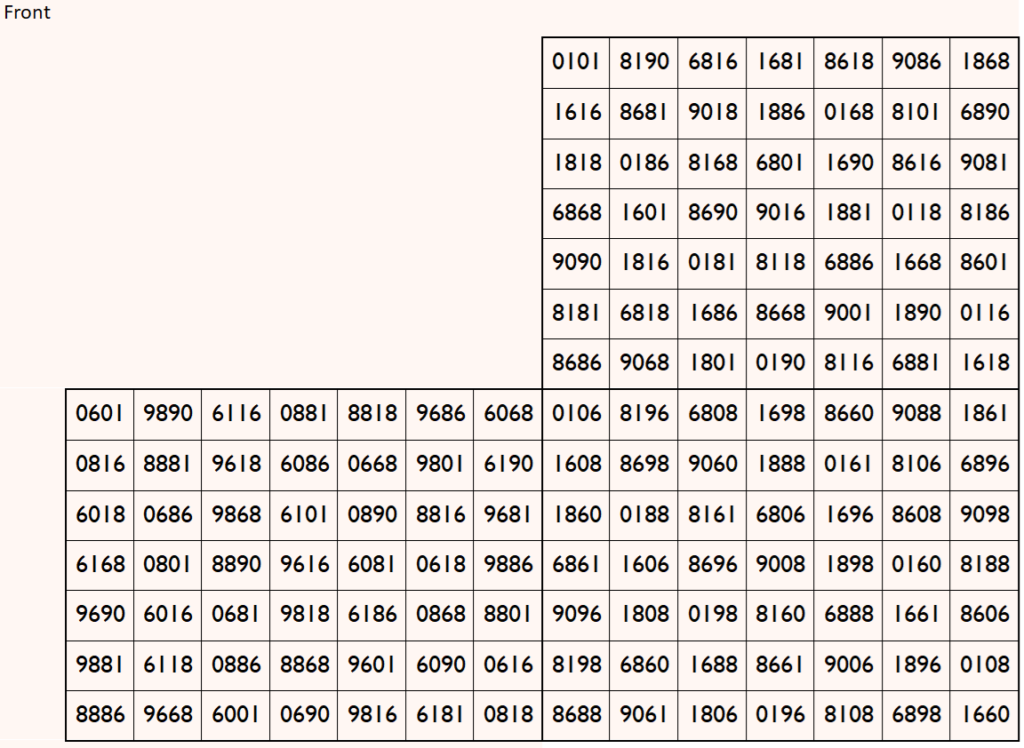
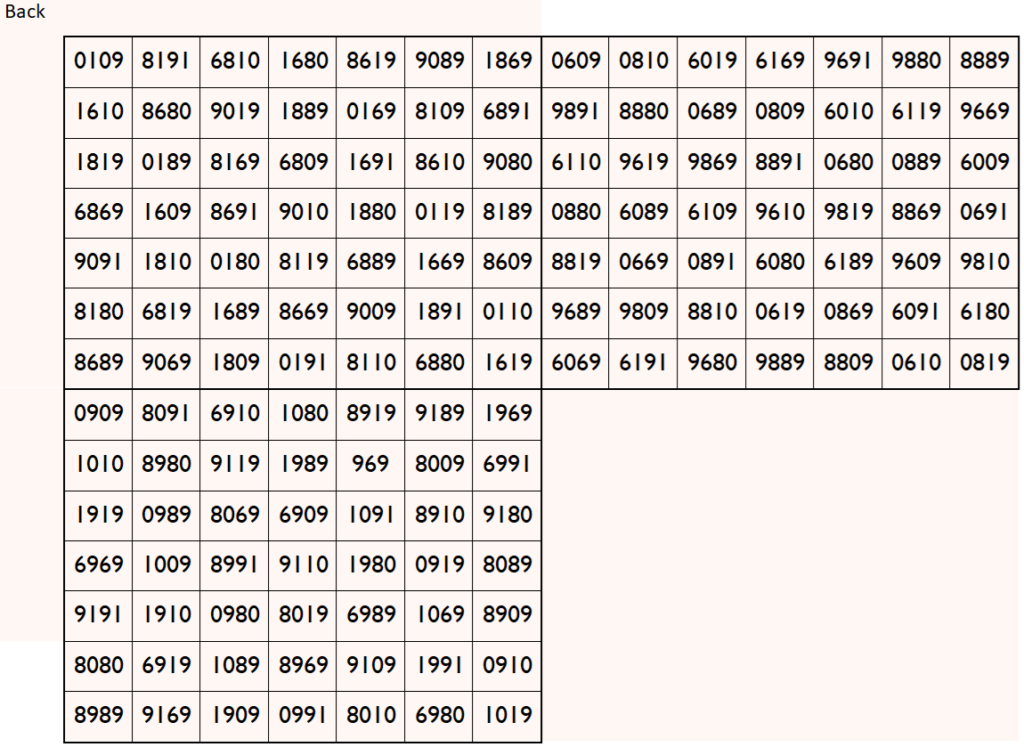
Above magic cube is readable as upside-down.
Magic Cubes with Magic Squares of Order 8
Example 1. Upside-down Magic Cube
Let’s consider the following six magic squares of order 8
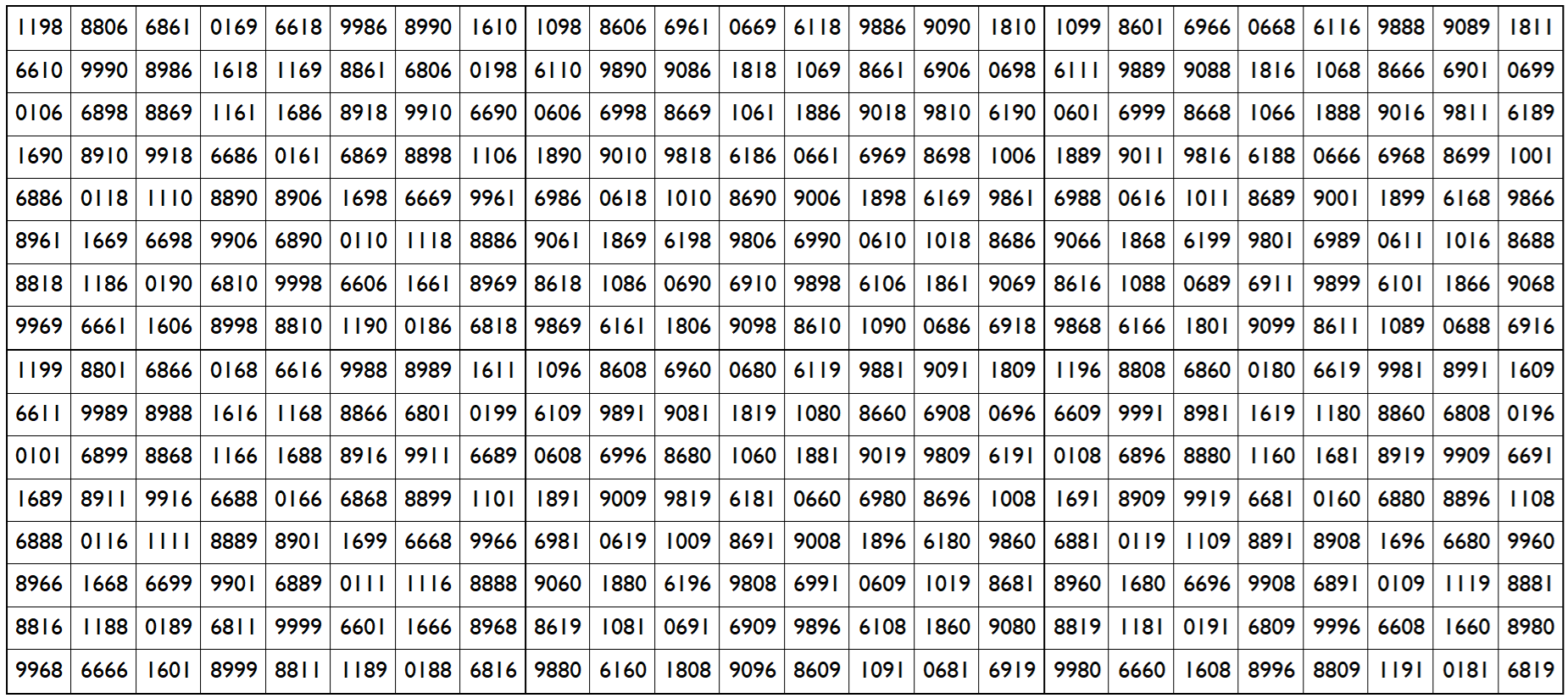
The above six magic squares are constucted using only 5-digits, 0, 1, 6, 8 and 9. The First four magic squares are of equal magic sums, and the last two are also of equal magic sums. See below;
S8×8(1):=44238, S8×8(2):=44238, S8×8(3):=44238, S8×8(4):=44238, S8×8(5):=44244 and S8×8(6):=44244.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
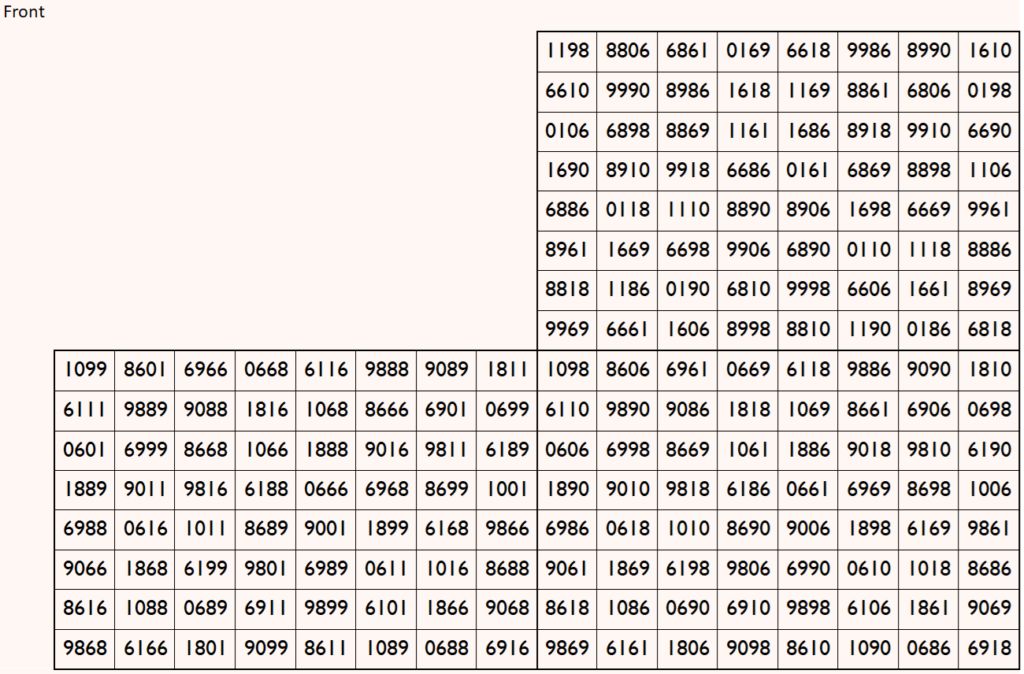

Above magic cube is readable as upside-down.
Example 2. Upside-down Magic Cube
Let’s consider the following six magic squares of order 8

The above six magic squares are constucted using only 5-digits, 2, 5, 6, 8 and 9. The First four magic squares are of equal magic sums, and the last two are also of equal magic sums. See below;
S8×8(1):=55146, S8×8(2):=55146, S8×8(3):=55146, S8×8(4):=55146, S8×8(5):=55136 and S8×8(6):=55136.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:


Above magic cube is readable as upside-down.
Example 3. Universal Magic Cube
Let’s consider the following six magic squares of order 8
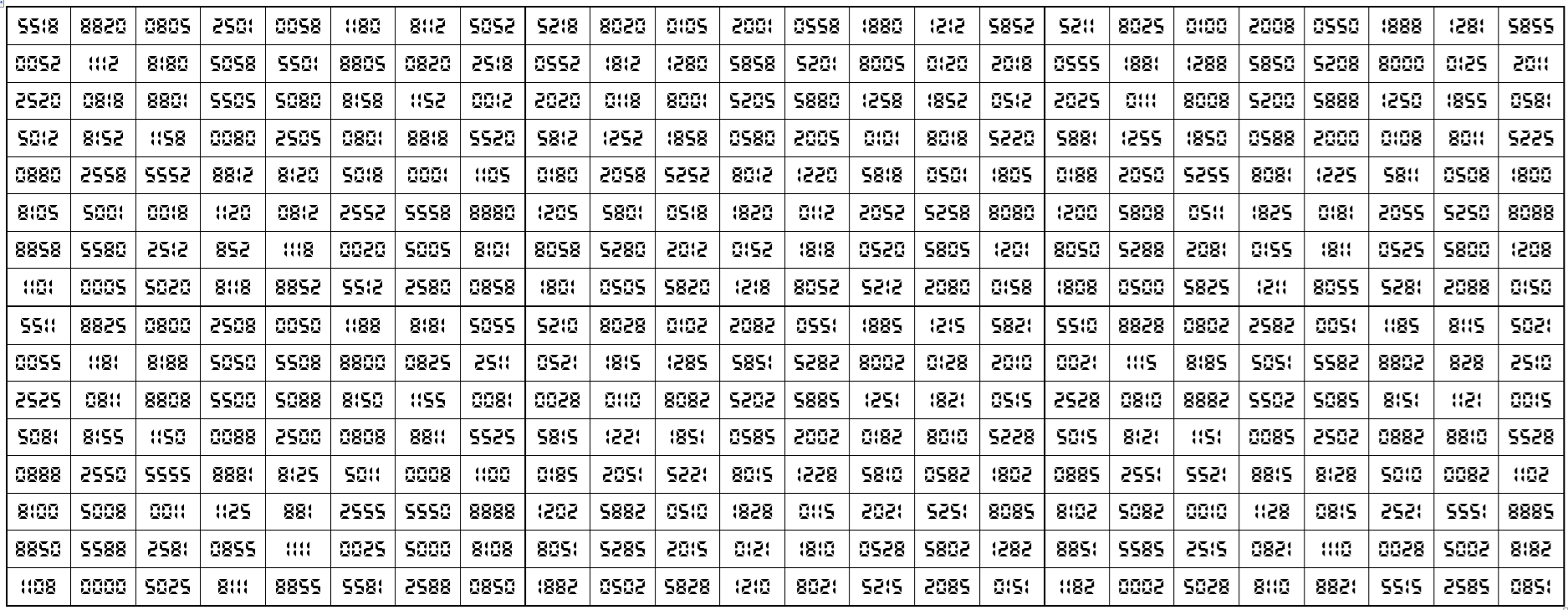
The above six magic squares are constucted using only 5-digits, 0, 1, 6, 8 and 9. The First four magic squares are of equal magic sums, and the last two are also of equal magic sums. See below;
S8×8(1):=32046, S8×8(2):=24846, S8×8(3):=24918, S8×8(4):=32118, S8×8(5):=32118 and S8×8(6):=32094.
Magic cube is composed with six magic squares representing front and back. First three magic squares represent the front part and the last three represent the back part. See below:
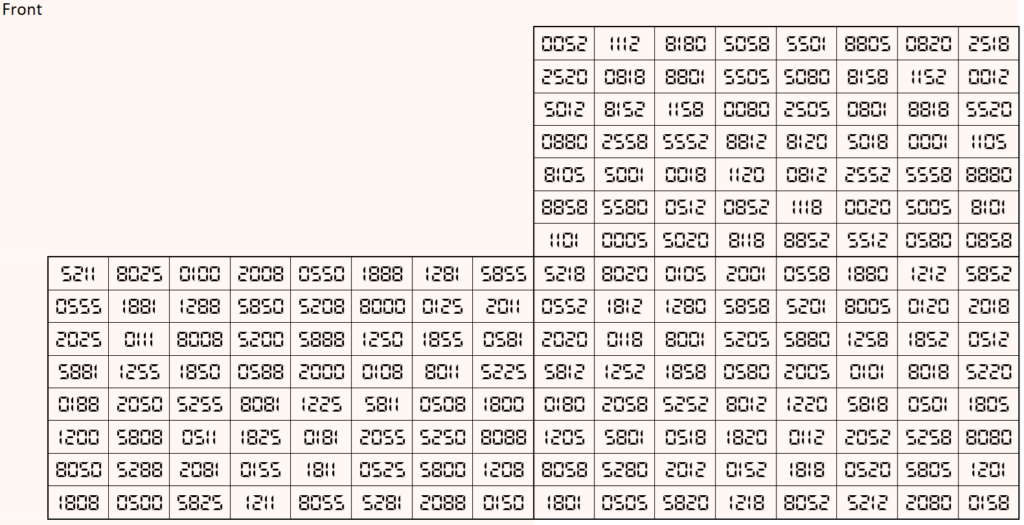
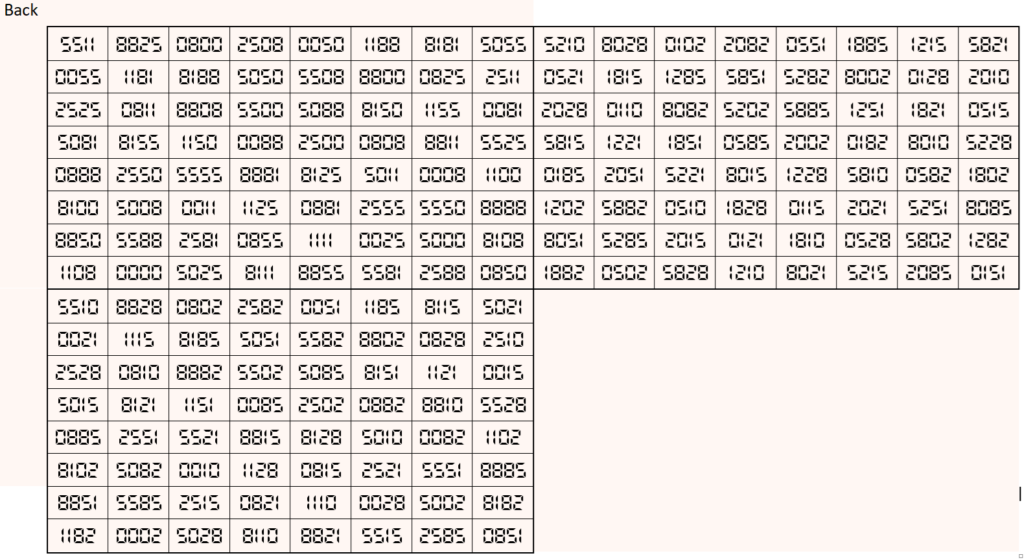
Above magic cube is universal, i.e., it is readable as upside-down and/or mirror looking position.

