This work bring magic cubes with six sides as magic squares of orders 3 to 10. The odd order magic squares are constructed in such a way that they are of equal difference magic sums. In each case, the difference is the order of the magic square. The even order magic squares are of equal sums. Some examples of universal and upside-down magic cubes are also given, but this work is given in another site.
These examples are based on different types of magic squares, such as, single-digit bordered, double-digits bordered, striped, cornered, etc. The readers can also access the following links to download the whole work.
The readers can also access the following links to download the whole work.
- Inder J. Taneja, Magic Cubes Based on Magic Squares, Zenodo, October 17, 2024, pp. 1-63, https://doi.org/10.5281/zenodo.13924915.
- Site Link: Magic Cubes Based on Magic Squares
- Inder J. Taneja, Universal and Upside-Down Magic Cubes, Zenodo, October 17, 2024, pp. 1-38, https://doi.org/10.5281/zenodo.13947425.
- Site Link: Universal and Upside-down Magic Cubes
Magic Cube with Magic Squares of Order 3
Example 1.
Let’s consider the following six magic squares of order 3
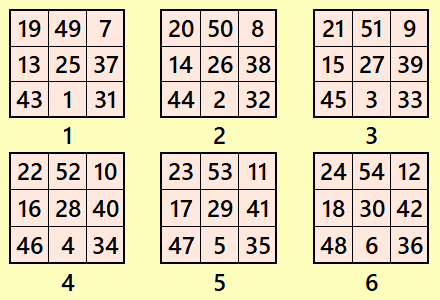
These magic squares are constructed using sequential numbres from 1 to 54. The magic sums are
S3×3(1):=75, S3×3(2):=78, S3×3(3):=81, S3×3(4):=84, S3×3(5):=87 and S3×3(6):=90.
These magic squares are of equal difference magic sums.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
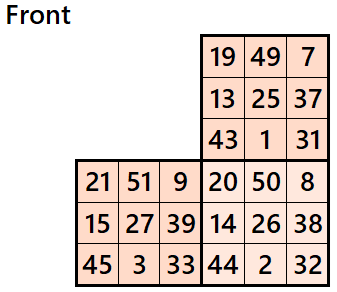
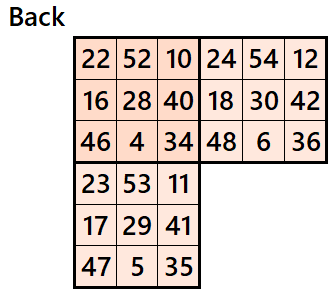
Magic Cubes with Magic Squares of Order 4
Example 1.
Let’s consider the following six magic squares of order 4
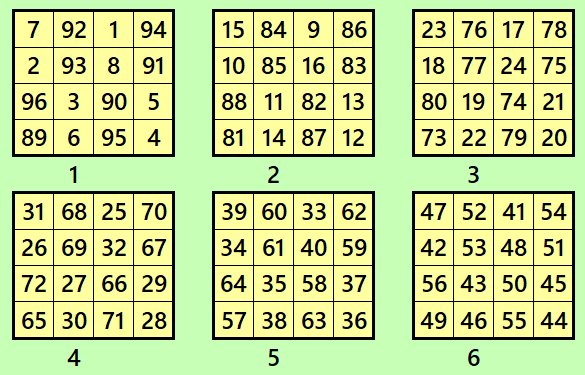
These magic squares are constructed using sequential numbres from 1 to 96. In this case, all the magic squares are pandiagonal and of equal sums, i.e.,
S4×4(1)=S4×4(2)=S4×4(3)=S4×4(4)=S4×4(5)=S4×4(6):=194.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
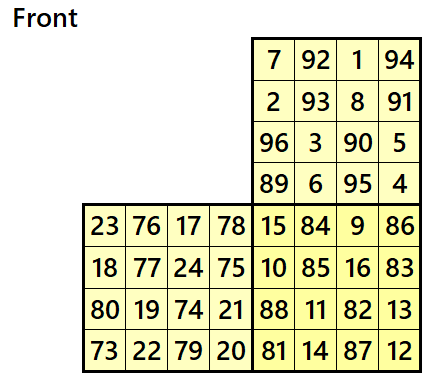
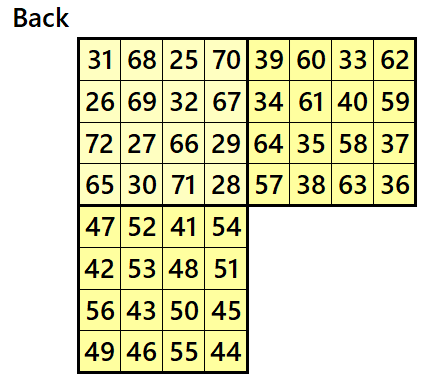
Example 2.
Let’s consider the following six magic squares of order 4
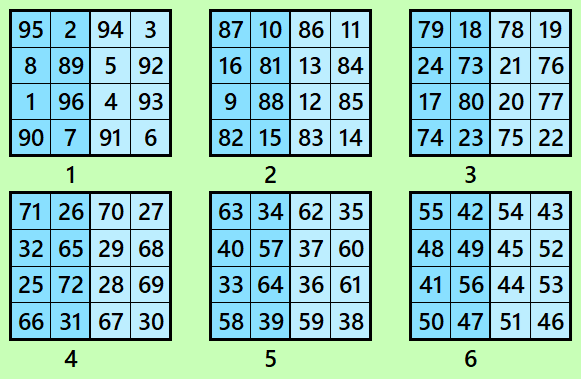
These magic squares are constructed using sequential numbres from 1 to 96. In this case, all the magic squares are of equal sums, i.e.,
S4×4(1)=S4×4(2)=S4×4(3)=S4×4(4)=S4×4(5)=S4×4(6):=194.
These magic squares are constructed with equal sums stripes or magic rectangles of order 2×4.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
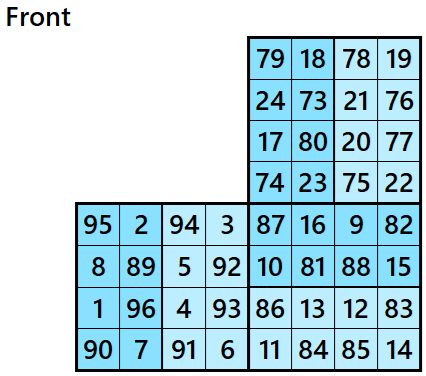
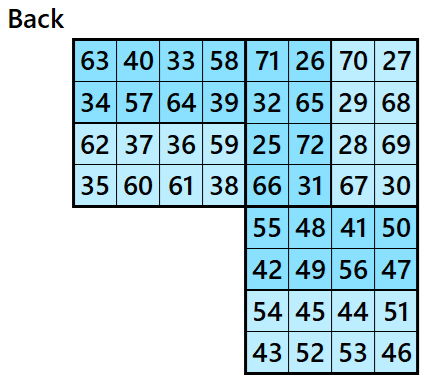
Magic Cubes with Magic Squares of Order 5
Example 1.
Let’s consider the following six magic squares of order 5
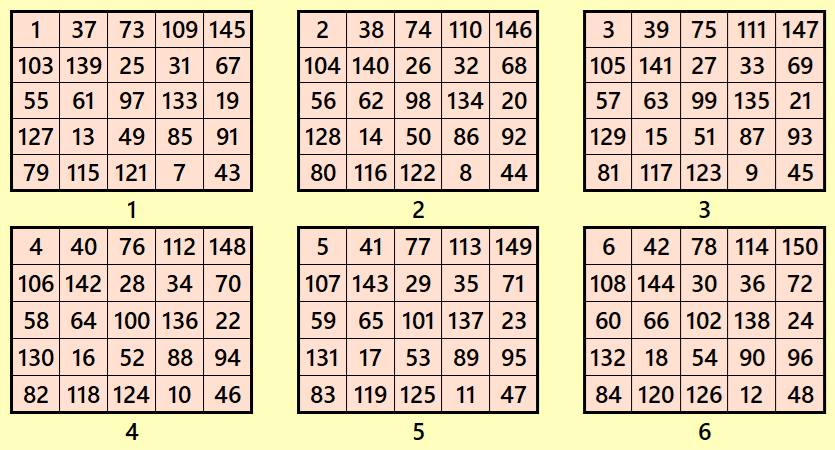
These magic squares are constructed using sequential numbres from 1 to 150. The magic sums are
S5×5(1):=365, S5×5(2):=370, S5×5(3):=375 S5×5(4):=380, S5×5(5):=385 and S5×5(6):=390.
Interestingly, these sums are of equal differences. Each magic square of order 5 is pandiagonal.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
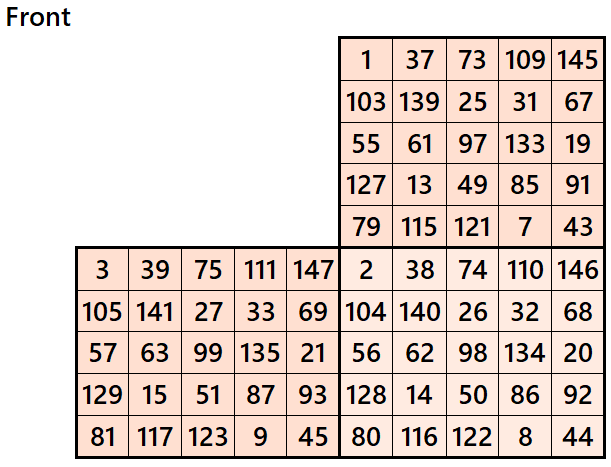
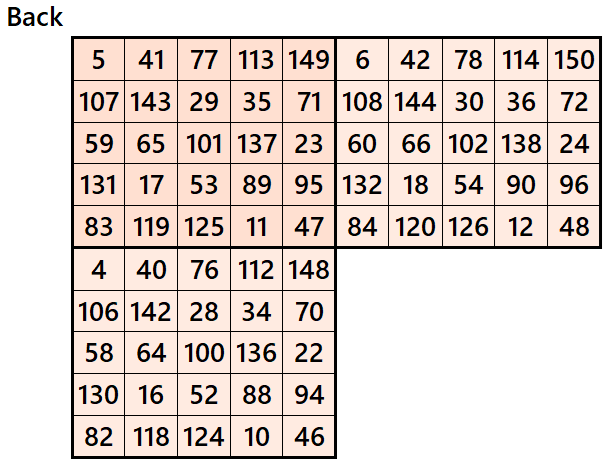
Example 2.
Let’s consider the following six magic squares of order 5
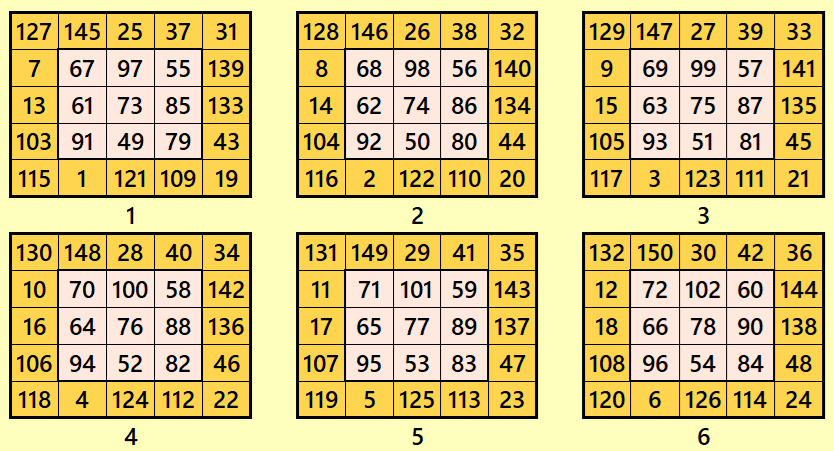
These magic squares are constructed using sequential numbres from 1 to 150. The magic sums are
S5×5(1):=365, S5×5(2):=370, S5×5(3):=375 S5×5(4):=380, S5×5(5):=385 and S5×5(6):=390.
Interestingly, these sums are of equal differences. Magic squares of order 5 are single digit bordred magic squares.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
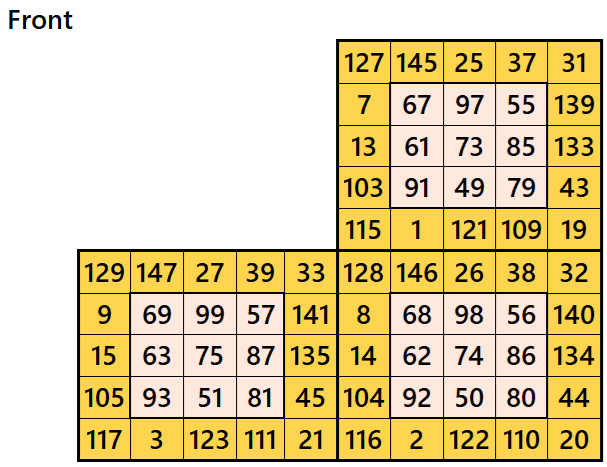
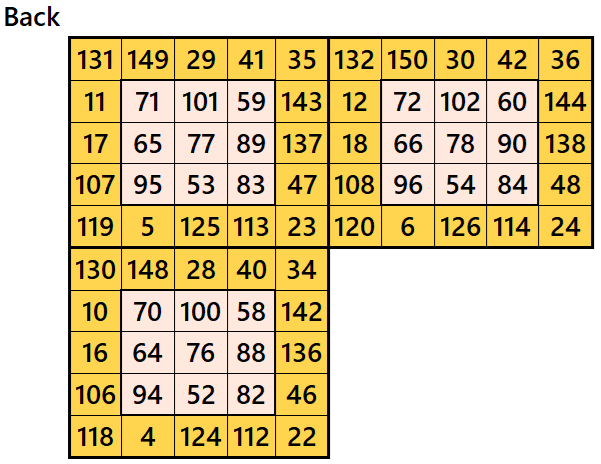
Example 3.
Let’s consider the following six magic squares of order 5
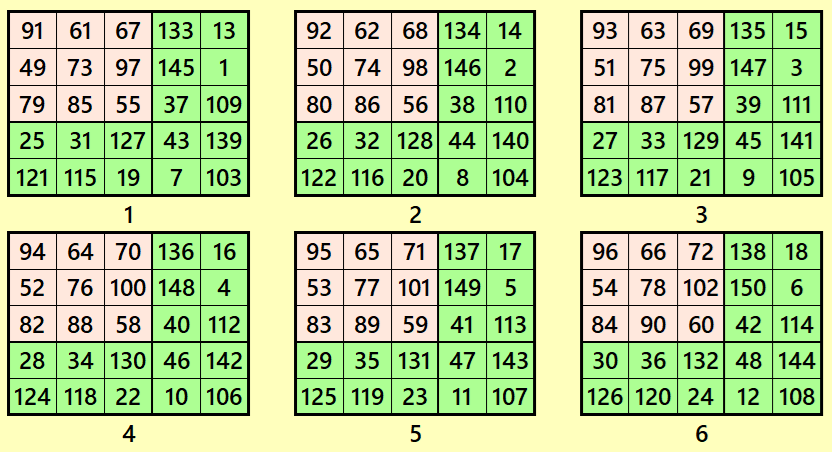
These magic squares are constructed using sequential numbres from 1 to 150. The magic sums are
S5×5(1):=365, S5×5(2):=370, S5×5(3):=375 S5×5(4):=380, S5×5(5):=385 and S5×5(6):=390.
Interestingly, these sums are of equal differences.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
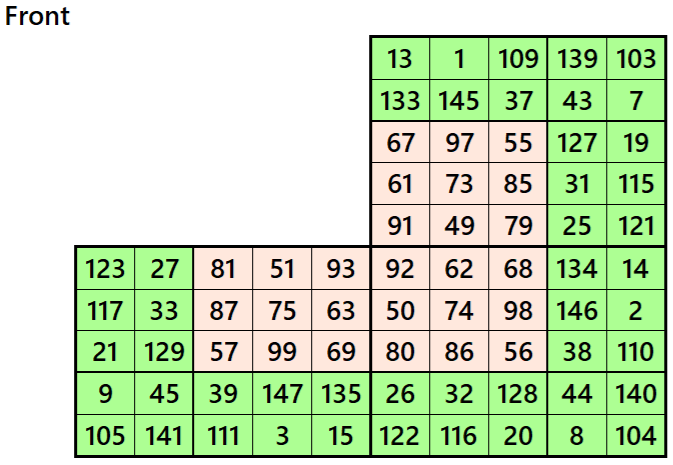
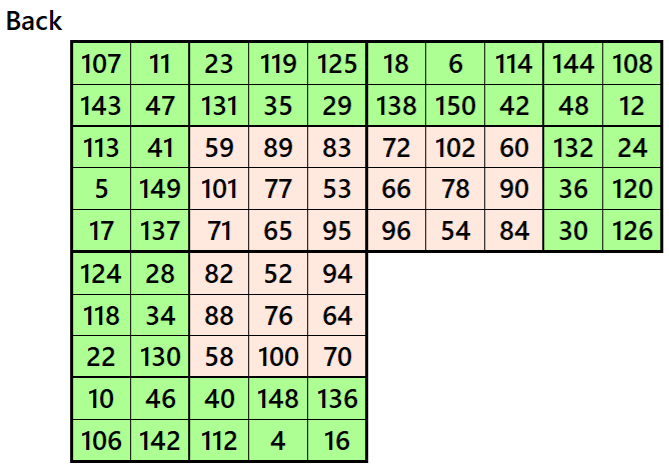
Magic Cubes with Magic Squares of Order 6
Example 1.
Let’s consider the following six magic squares of order 6
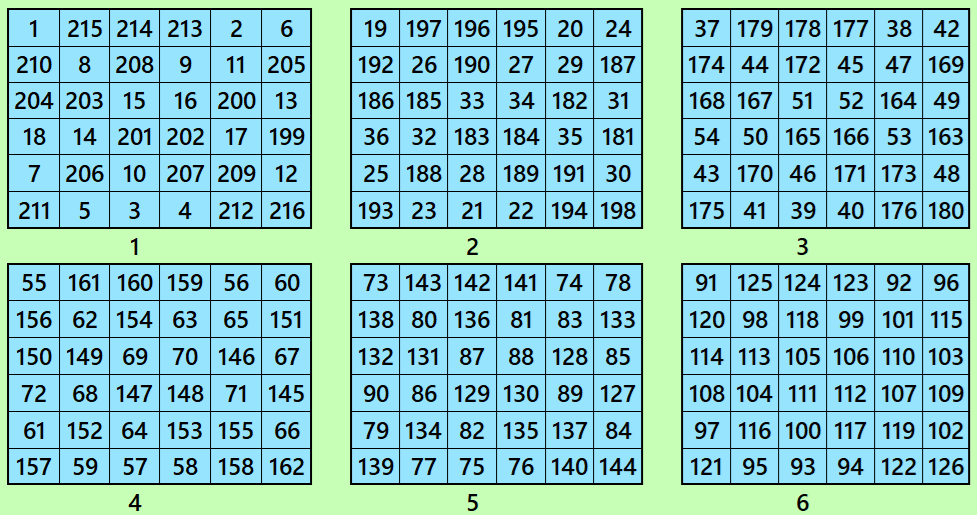
These magic squares are constructed using sequential numbres from 1 to 216. These are of equal sums, i.e,
S6×6(1)=S6×6(2)=S6×6(3)=S6×6(4)=S6×6(5)=S6×6(6):=651.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
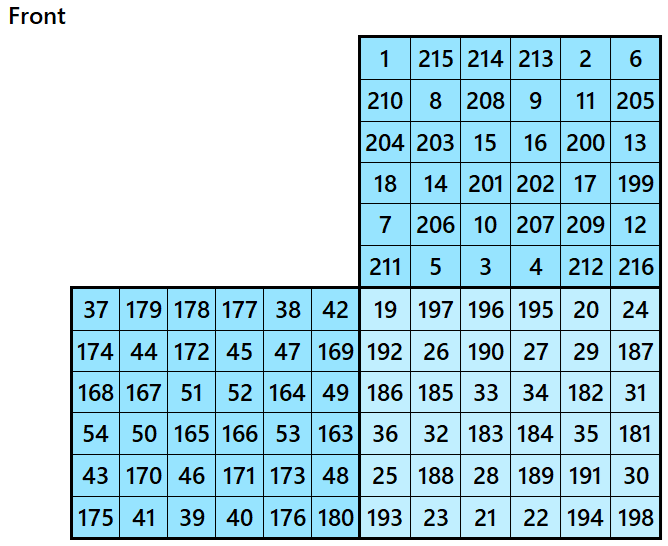
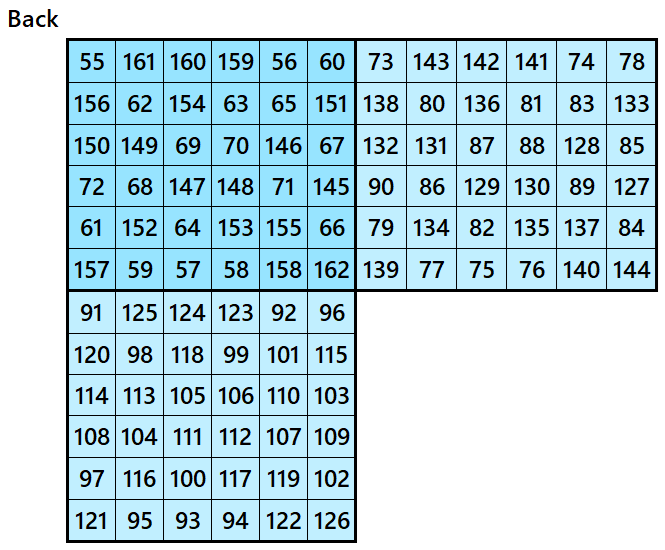
Example 2.
Let’s consider the following six magic squares of order 6
These magic squares are constructed using sequential numbres from 1 to 216. These magic squares are bordered magic squares, where the inner blocks are magic square of order 4. These are of equal sums, i.e,
S6×6(1)=S6×6(2)=S6×6(3)=S6×6(4)=S6×6(5)=S6×6(6):=651.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
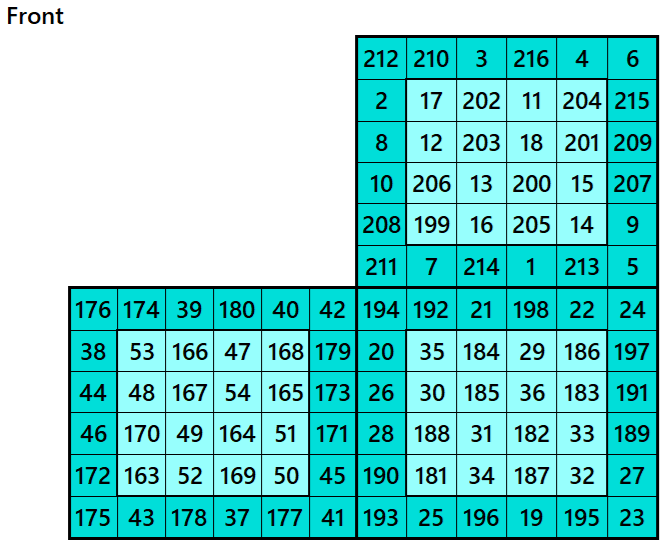
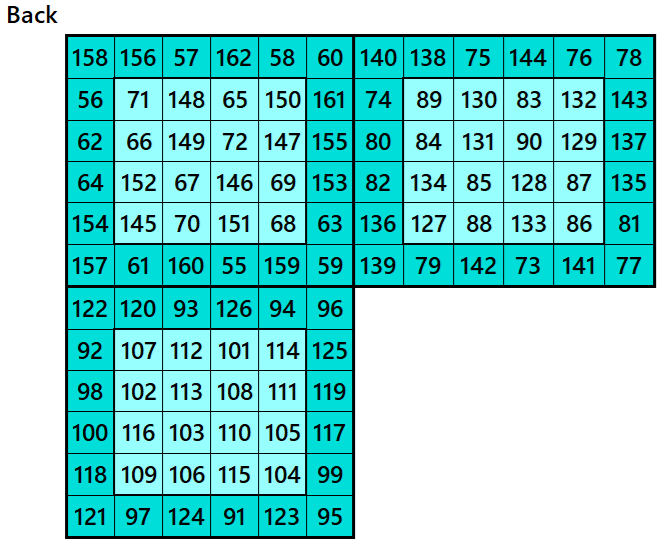
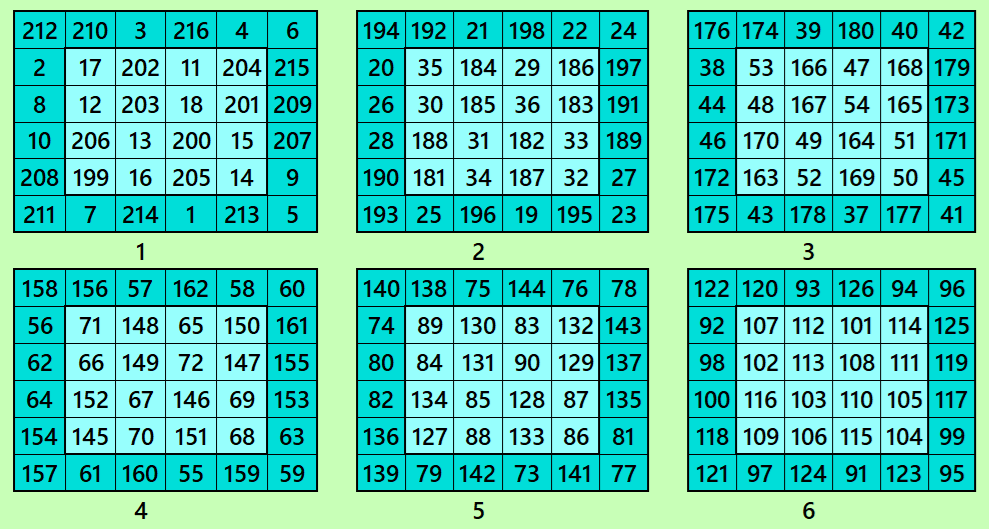
Example 3.
Let’s consider the following six magic squares of order 6
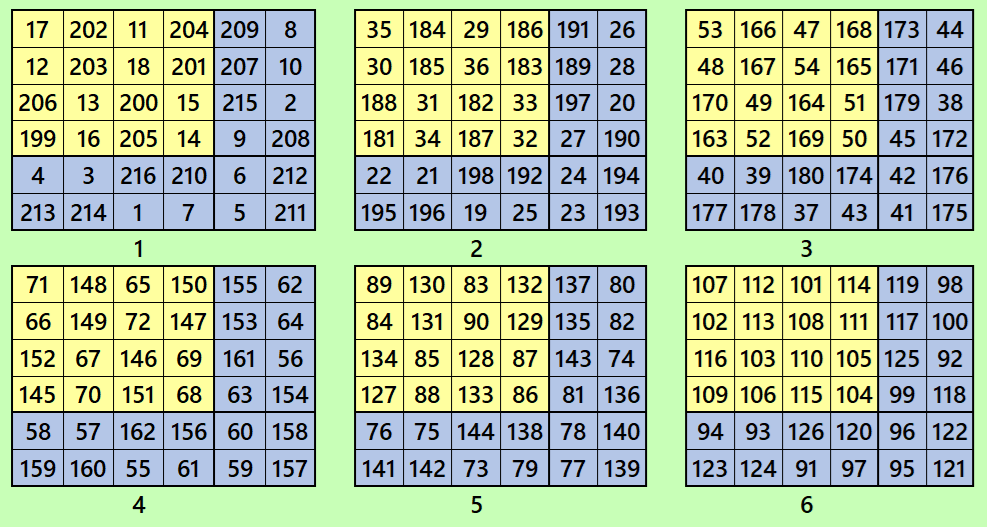
These magic squares are constructed using sequential numbres from 1 to 216. These are of equal sums, i.e,
S6×6(1)=S6×6(2)=S6×6(3)=S6×6(4)=S6×6(5)=S6×6(6):=651.
These magic squares are cornered magic squares, where the superior left corners are magic square of order 4.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:

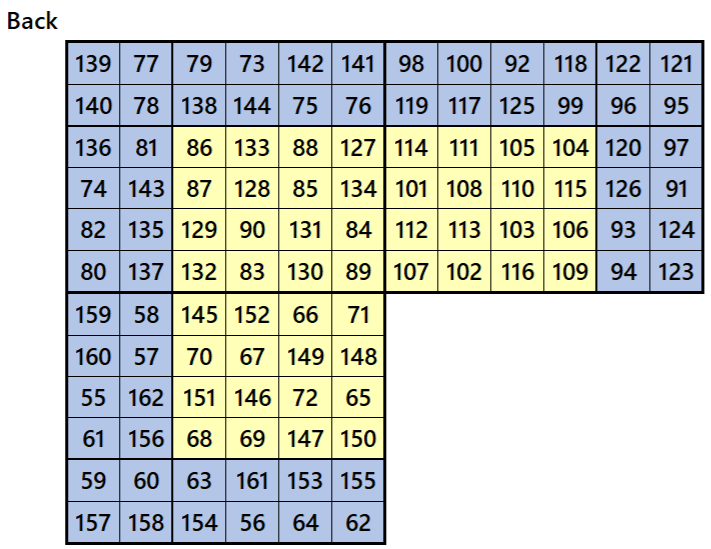
Magic Cubes with Magic Squares of Order 7
Example 1.
Let’s consider the following six magic squares of order 7
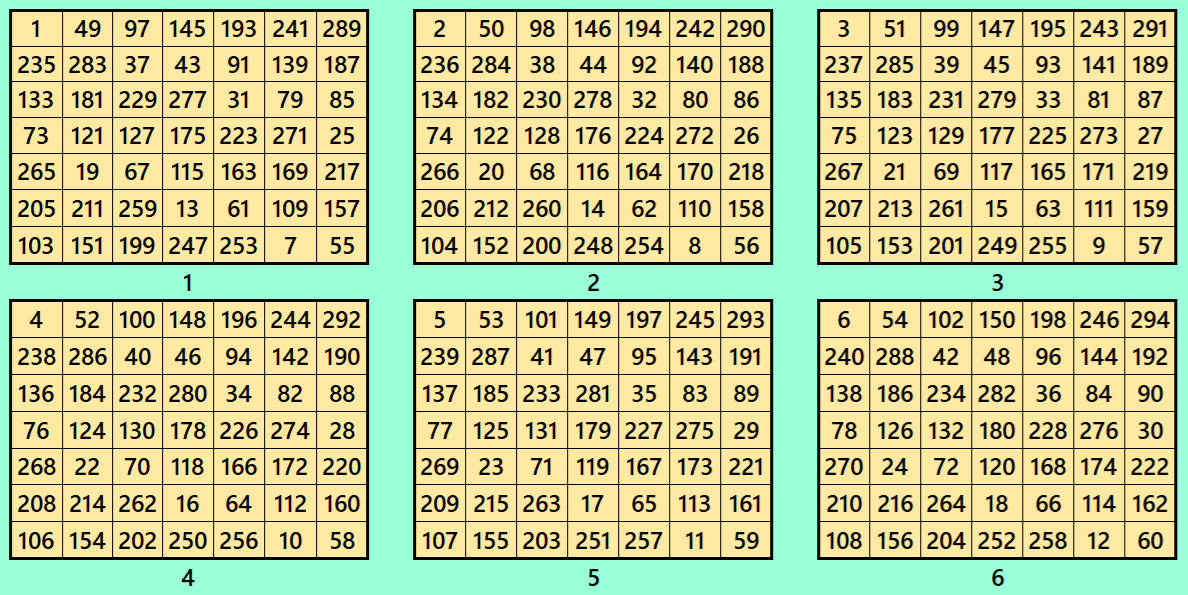
These magic squares are constructed using sequential numbres from 1 to 150. The magic sums are
S7×7(1):=1015, S7×7(2):=1022, S7×7(3):=1029, S7×7(4):=1036, S7×7(5):=1043 and S7×7(6):=1050.
Interestingly, these sums are of equal differences. Each magic square of order 7 is pandiagonal.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
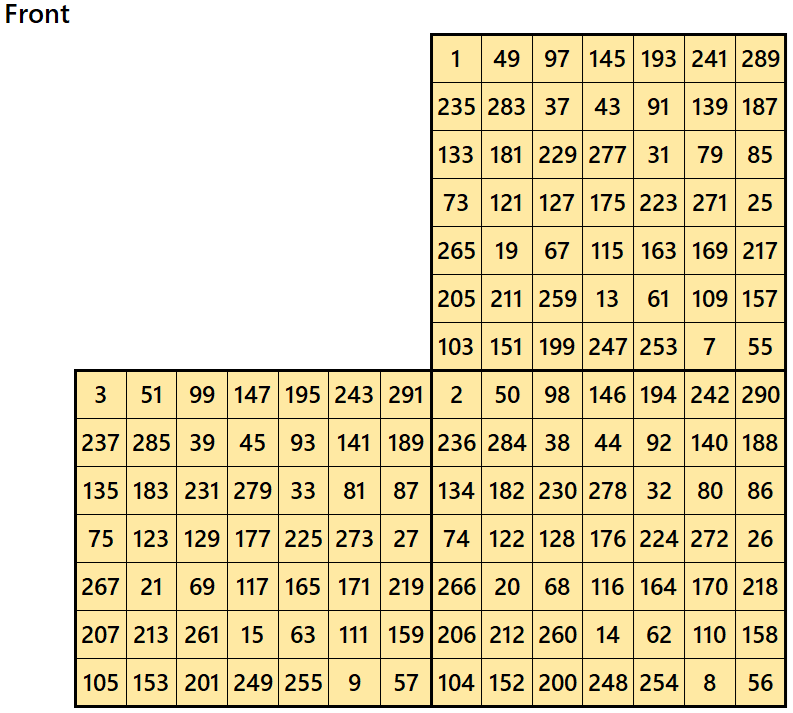
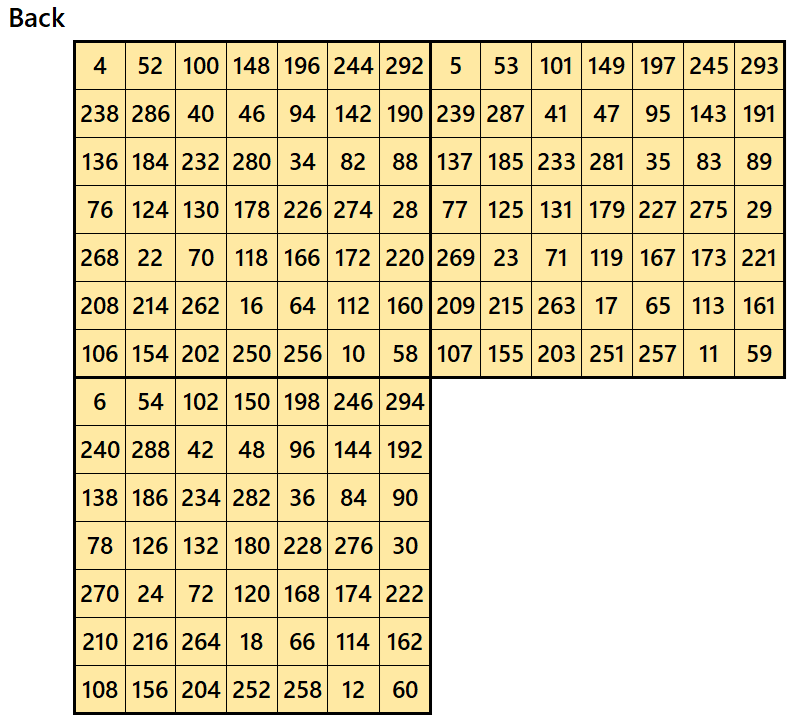
Example 2.
Let’s consider the following six magic squares of order 7
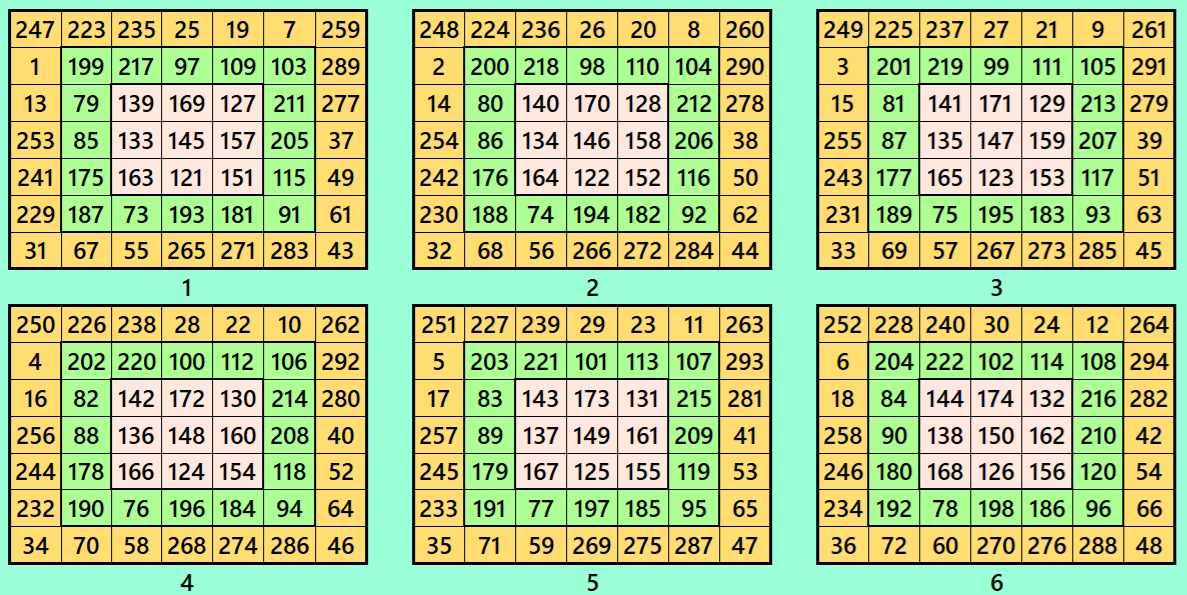
These magic squares are constructed using sequential numbres from 1 to 150. The magic sums are
S7×7(1):=1015, S7×7(2):=1022, S7×7(3):=1029, S7×7(4):=1036, S7×7(5):=1043 and S7×7(6):=1050.
Interestingly, these sums are of equal differences. The magic squares of order 7 are single digit bordered magic squares.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
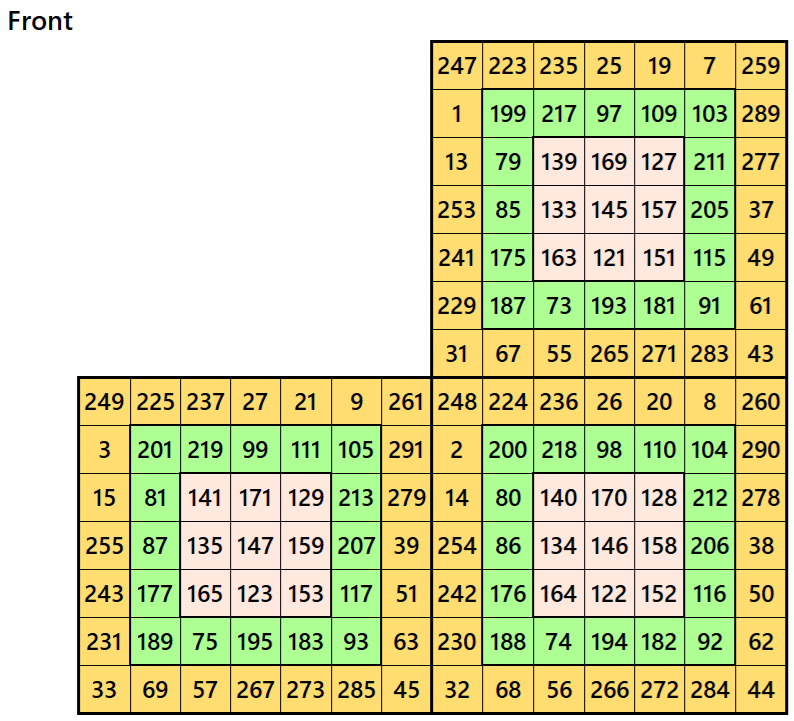
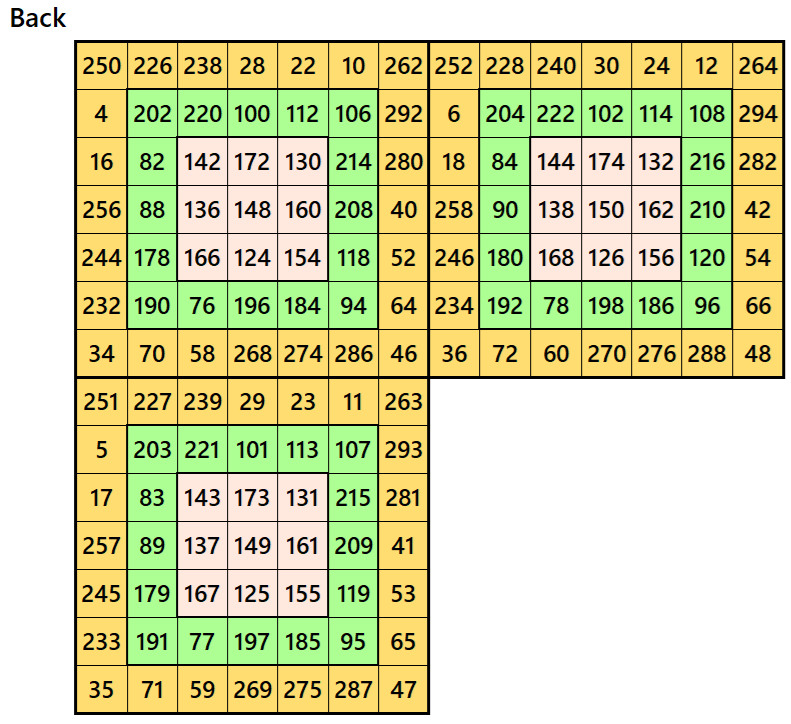
Example 3.
Let’s consider the following six magic squares of order 7
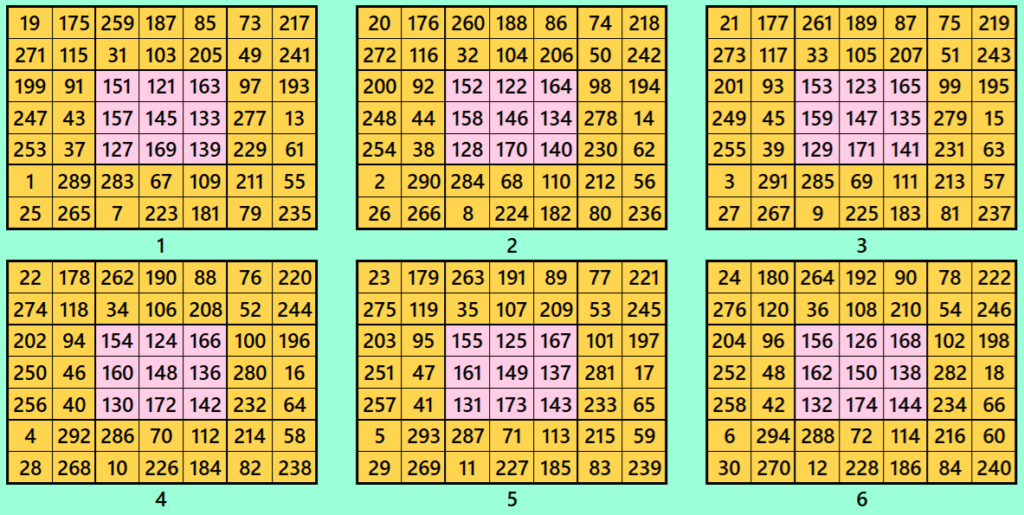
These magic squares are constructed using sequential numbres from 1 to 150. The magic sums are
S7×7(1):=1015, S7×7(2):=1022, S7×7(3):=1029, S7×7(4):=1036, S7×7(5):=1043 and S7×7(6):=1050.
Interestingly, these sums are of equal differences. The magic squares of order 7 are double digit bordered magic squares.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
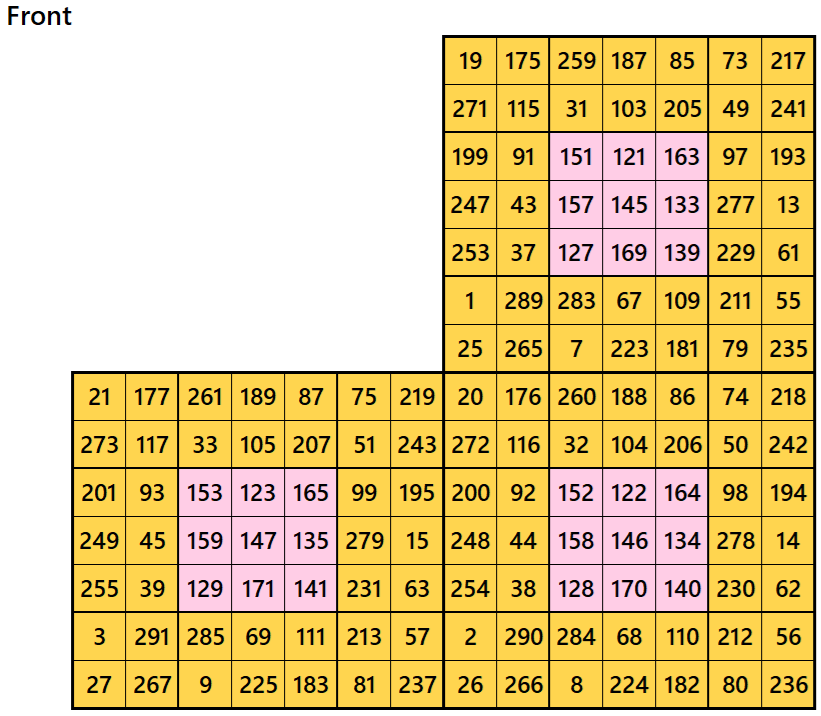

Example 4.
Let’s consider the following six magic squares of order 7
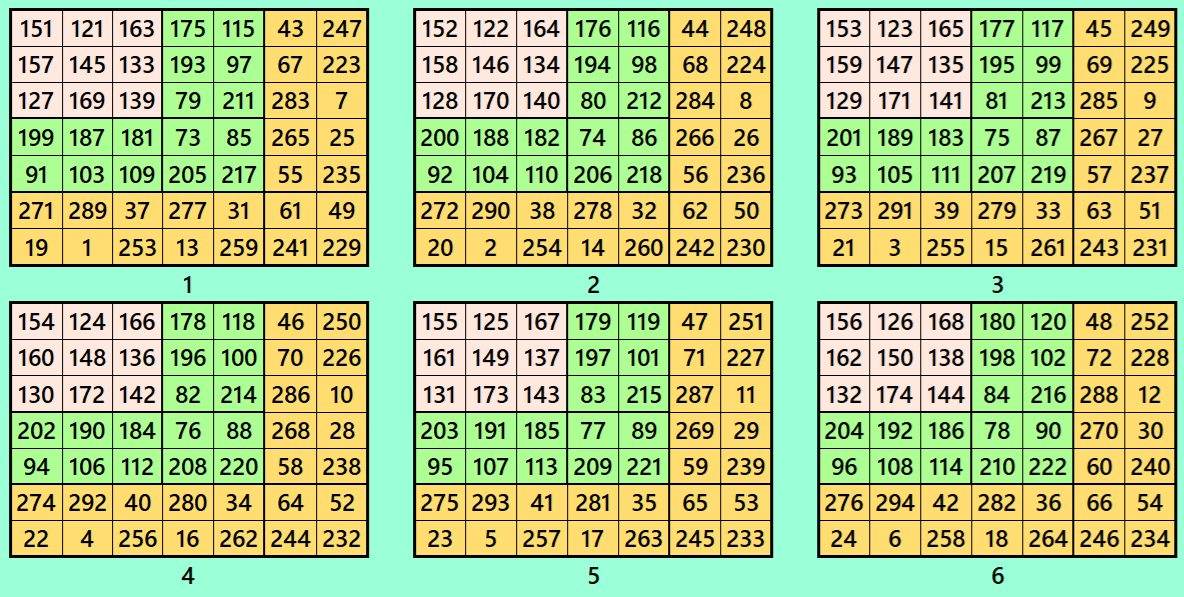
These magic squares are constructed using sequential numbres from 1 to 150. The magic sums are
S7×7(1):=1015, S7×7(2):=1022, S7×7(3):=1029, S7×7(4):=1036, S7×7(5):=1043 and S7×7(6):=1050.
Interestingly, these sums are of equal differences. The magic squares of order 7 are cornered magic squares.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
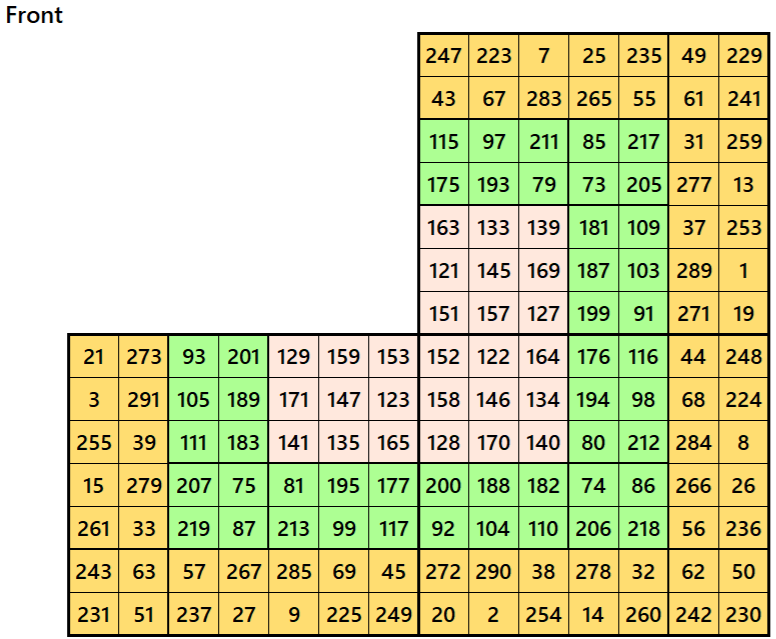
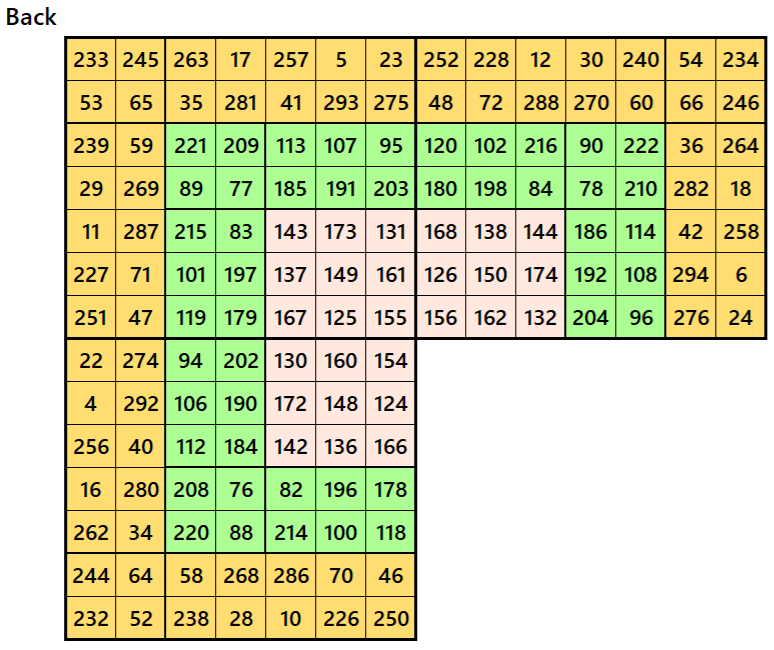
Magic Cubes with Magic Squares of Order 8
Example 1.
Let’s consider the following six magic squares of order 8
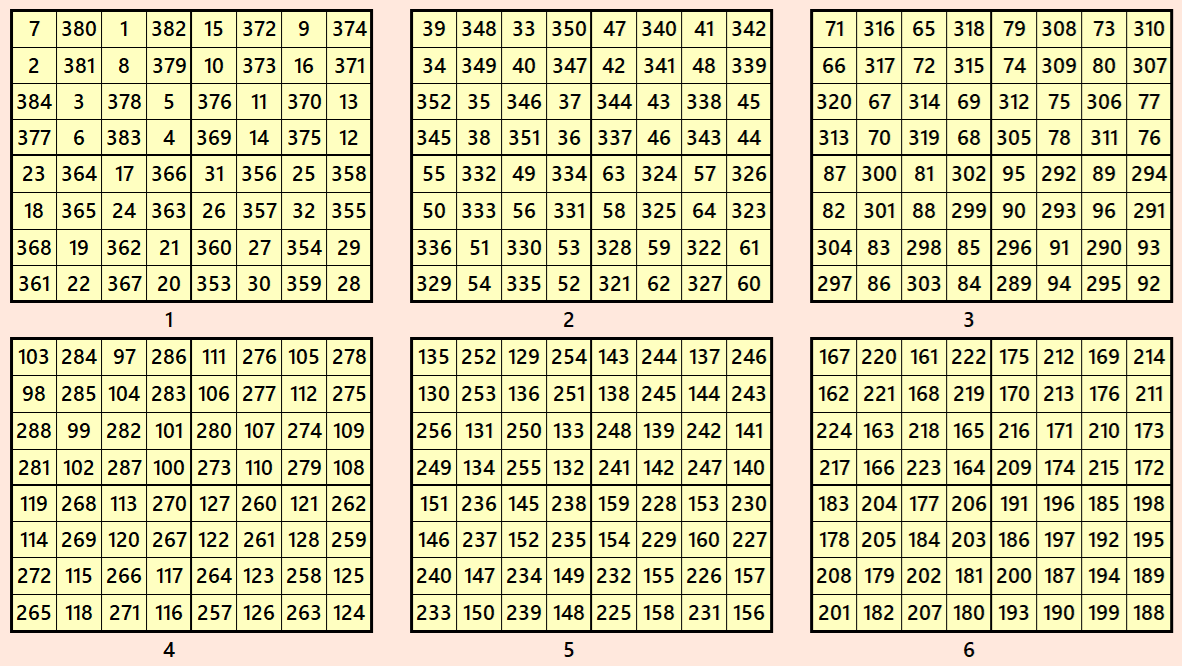
These magic squares are constructed using sequential numbres from 1 to 384. These are of equal sums, i.e,
S8×8(1)=S6×6(2)=S8×8(3)=S8×8(4)=S8×8(5)=S8×8(6):=1540.
All the magic squares of order 4 are pandiagonal of equal magic sums.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
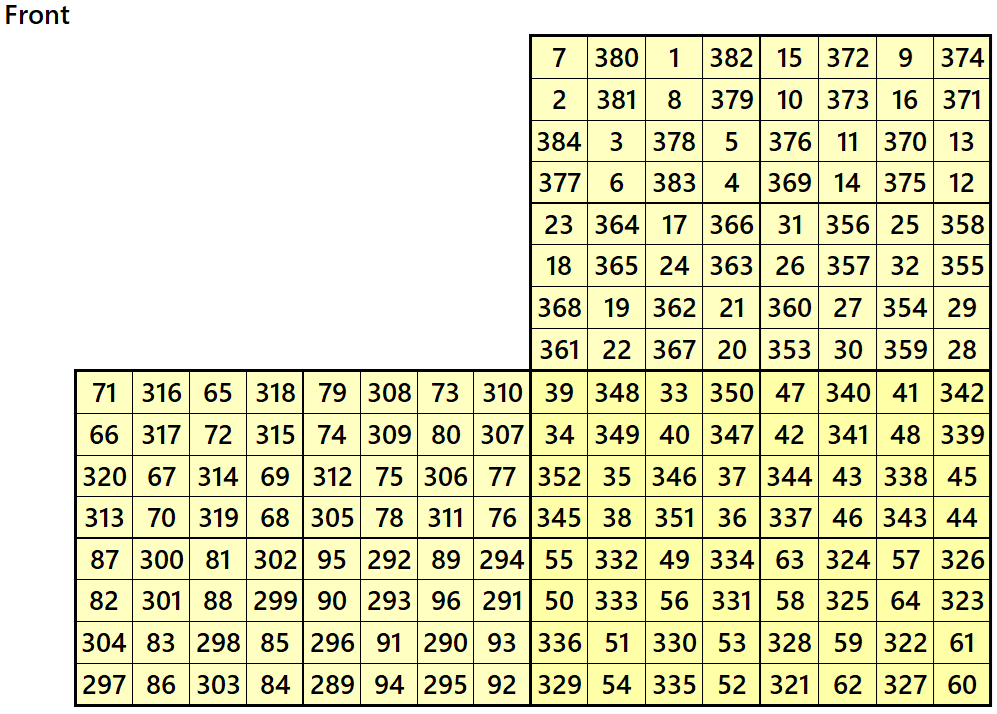

Example 2.
Let’s consider the following six magic squares of order 8
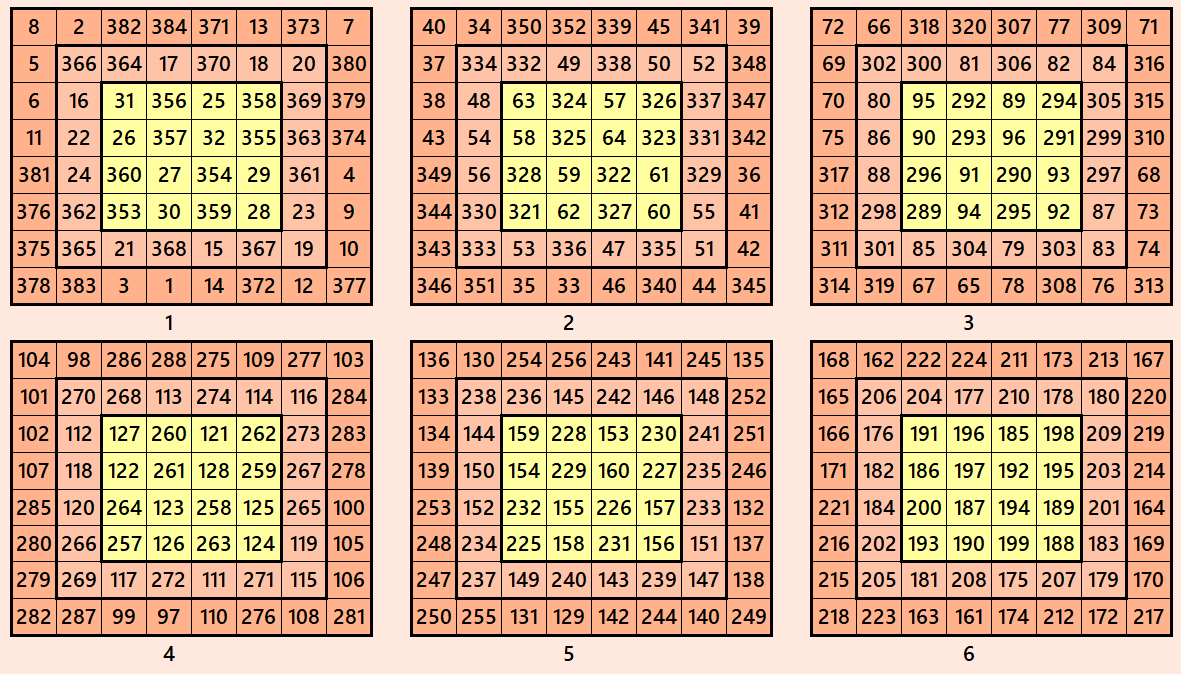
These magic squares are constructed using sequential numbres from 1 to 384. These are of equal sums, i.e,
S8×8(1)=S6×6(2)=S8×8(3)=S8×8(4)=S8×8(5)=S8×8(6):=1540.
These magic squares are known as single digit bordred magic squares. The inner block of order 4 in each case is a magic square of order 4.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
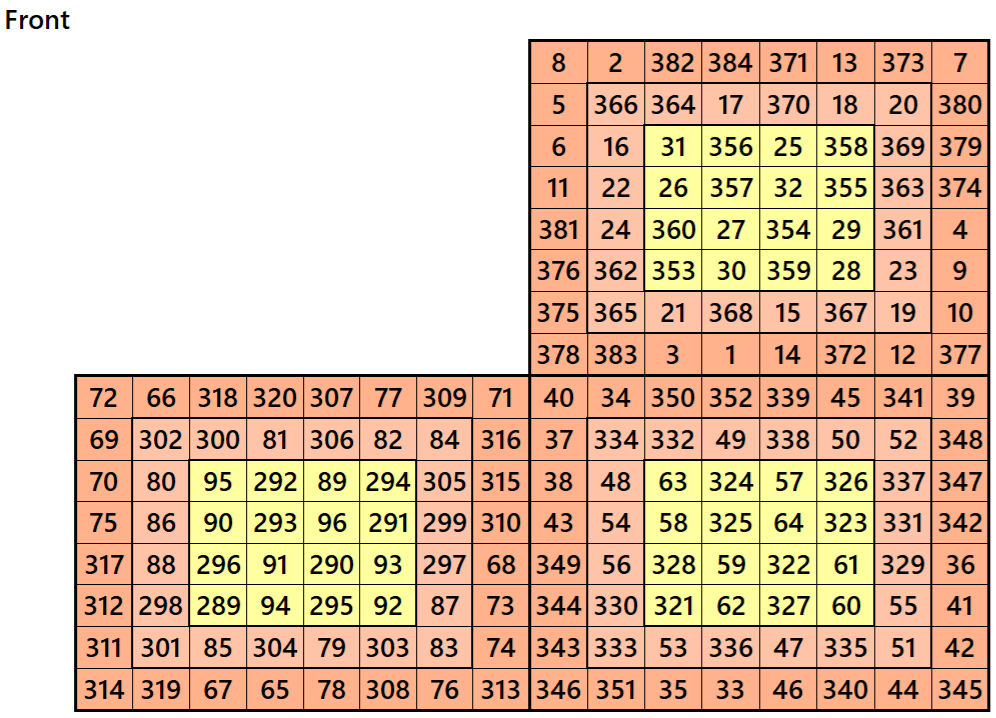
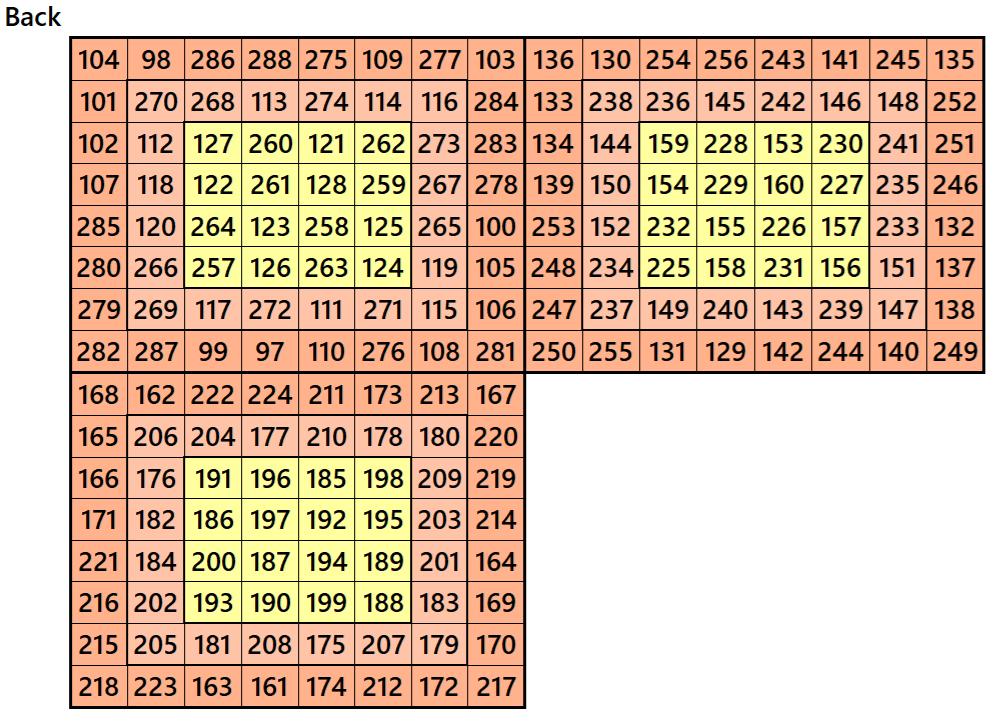
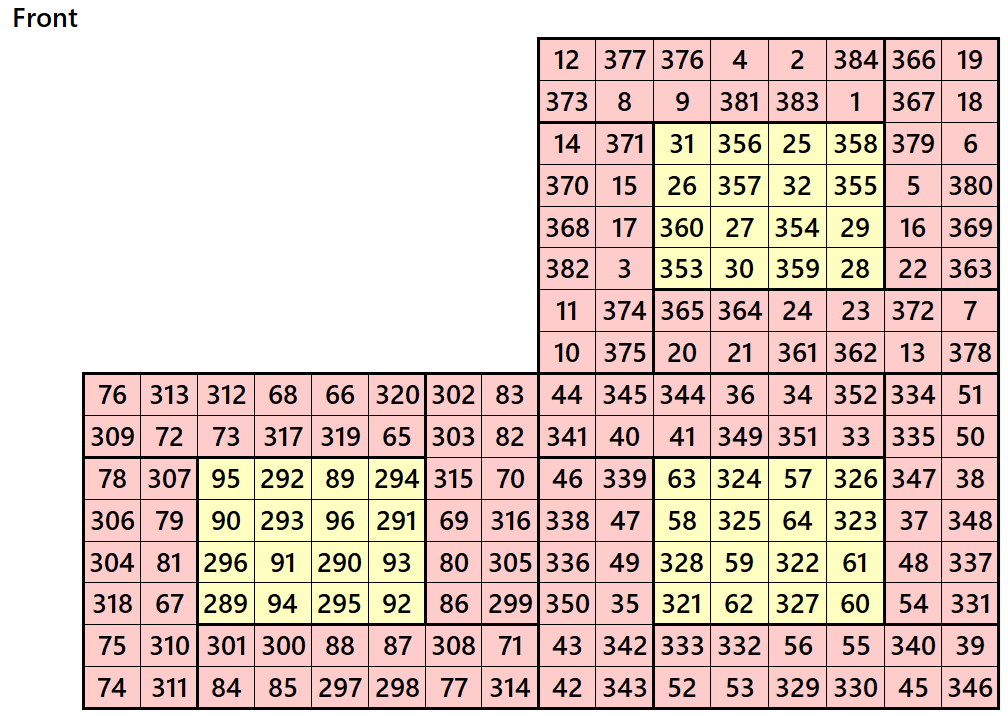
Example 3.
Let’s consider the following six magic squares of order 8
These magic squares are constructed using sequential numbres from 1 to 384. These are of equal sums, i.e,
S8×8(1)=S6×6(2)=S8×8(3)=S8×8(4)=S8×8(5)=S8×8(6):=1540.
These magic squares are known as double digits bordred magic squares. The inner block of order 4 in each case is a magic square of order 4 with equal magic sums.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
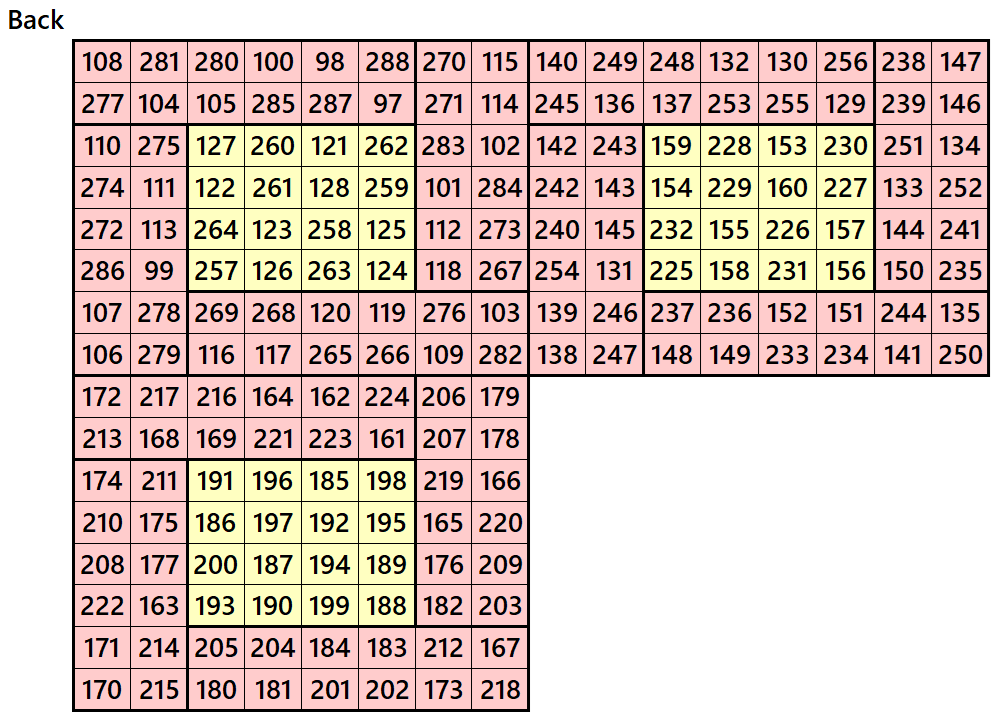
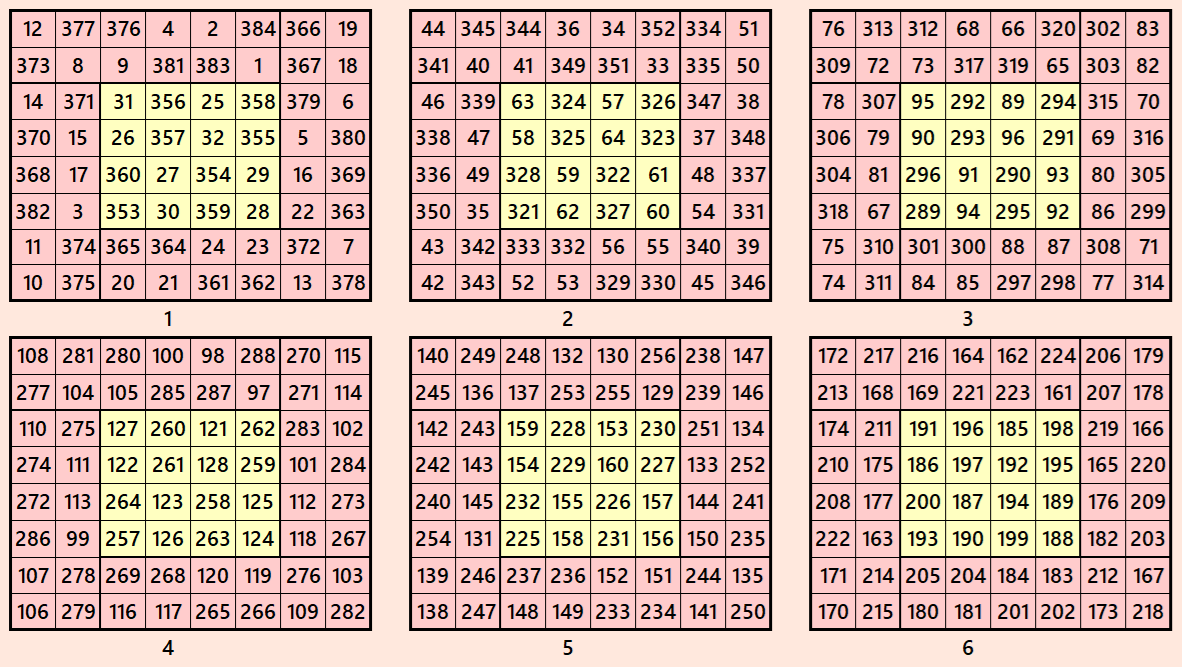
Example 4.
Let’s consider the following six magic squares of order 8
These magic squares are constructed using sequential numbres from 1 to 384. These are of equal sums, i.e,
S8×8(1)=S6×6(2)=S8×8(3)=S8×8(4)=S8×8(5)=S8×8(6):=1540.
These magic squares are constructed using equal sums magic rectangles of order 2×4. These are known by striped magic squares.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
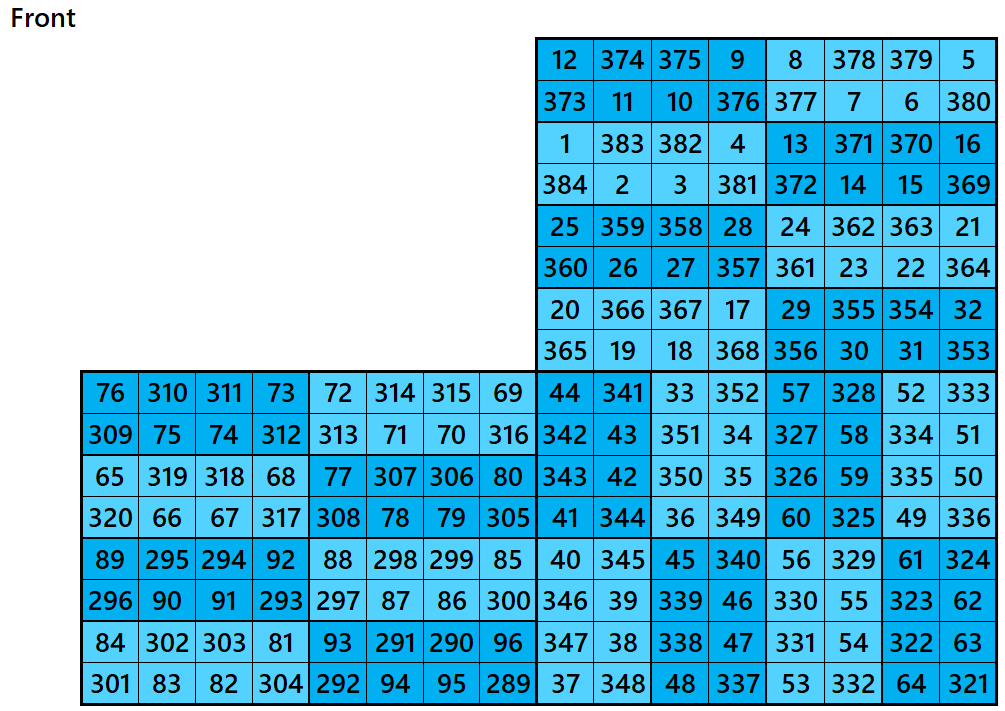
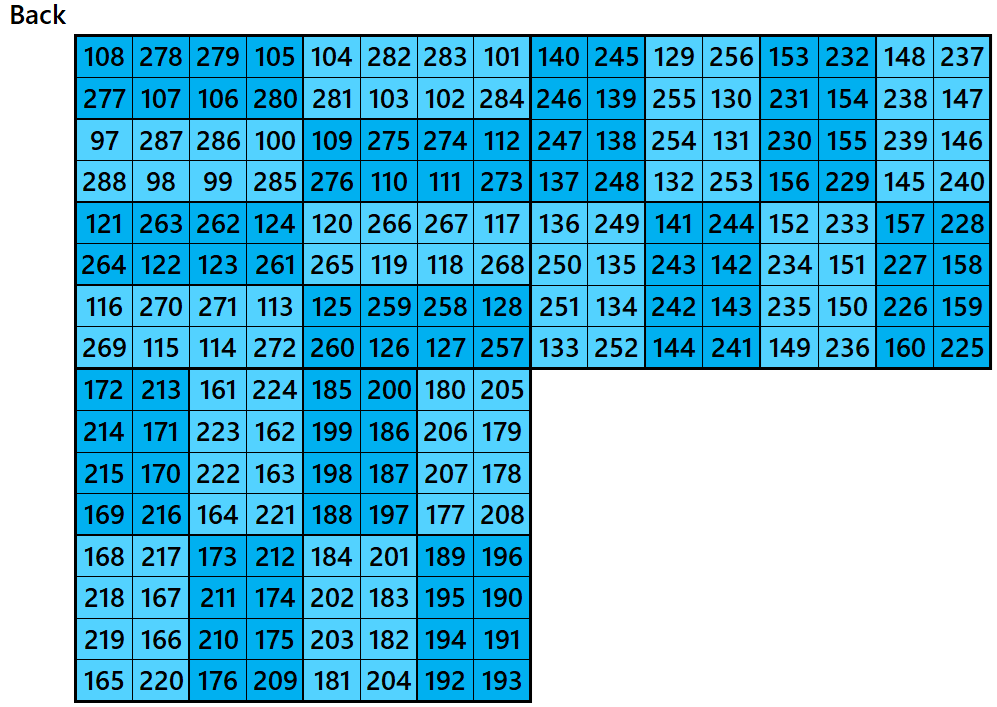
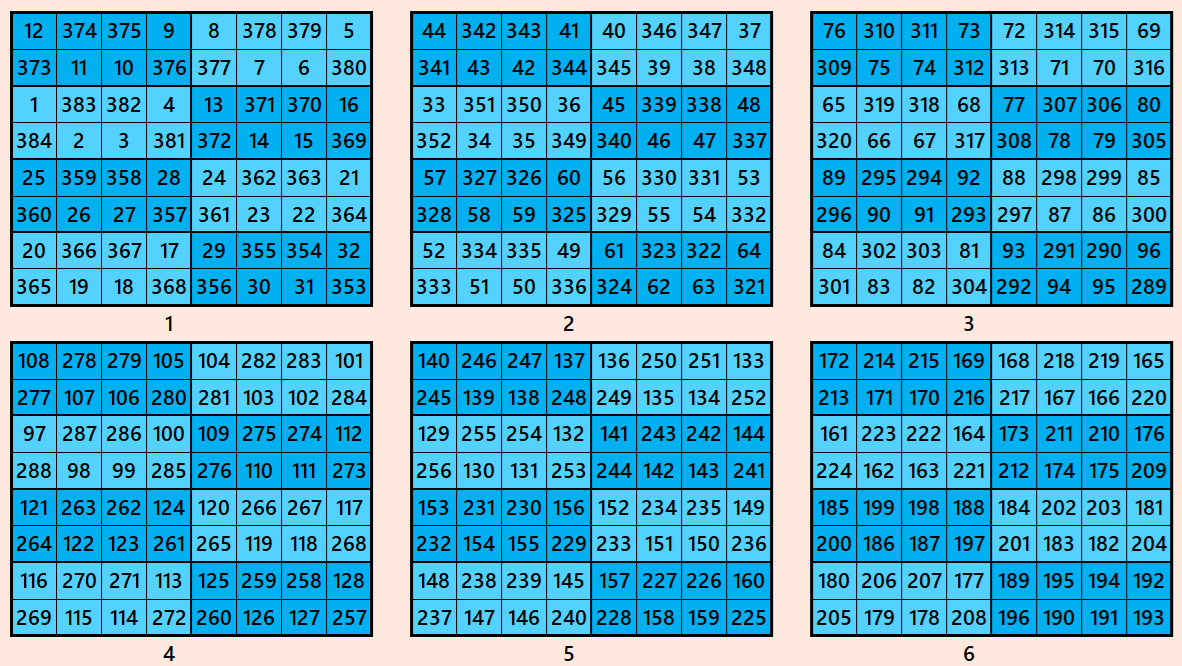
Example 5.
Let’s consider the following six magic squares of order 8
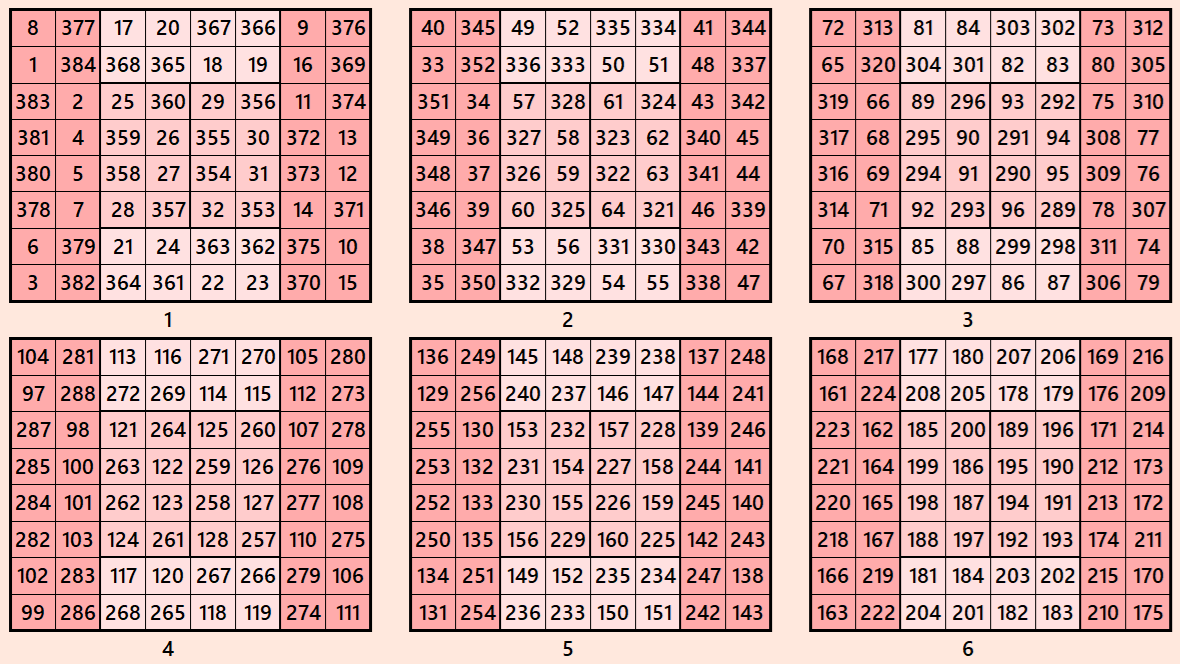
These magic squares are constructed using sequential numbres from 1 to 384. These are of equal sums, i.e,
S8×8(1)=S6×6(2)=S8×8(3)=S8×8(4)=S8×8(5)=S8×8(6):=1540.
These magic squares are known by striped magic squares. These are contructed using magic rectangles of orders 2×4 and 2×8.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
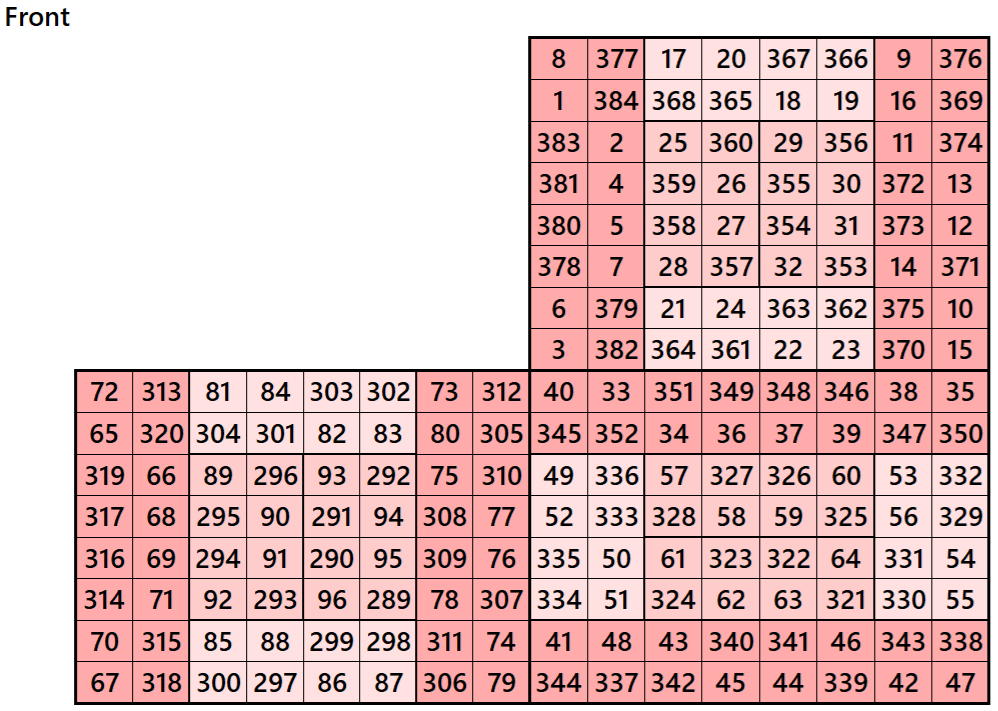
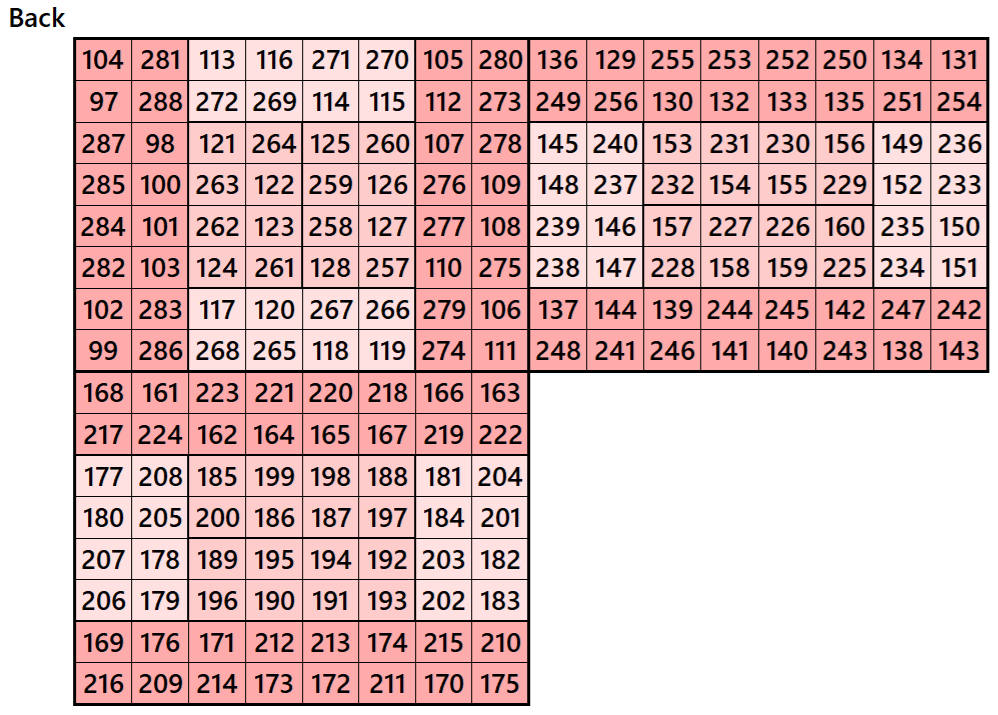
Example 6.
Let’s consider the following six magic squares of order 8
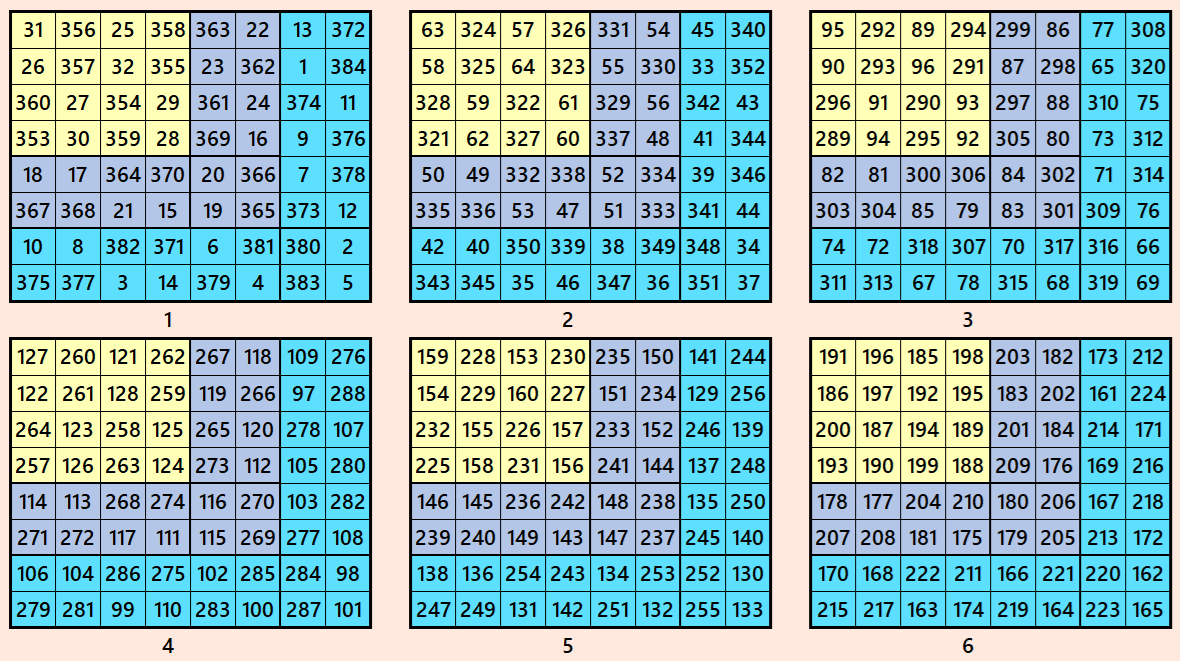
These magic squares are constructed using sequential numbres from 1 to 384. These are of equal sums, i.e,
S8×8(1)=S6×6(2)=S8×8(3)=S8×8(4)=S8×8(5)=S8×8(6):=1540.
These magic squares are known as conered magic squares. Magic squares of order 4 are at corner of each magic square of order 8. These as cornered with magic squares of order 4 and 6. All the magic squares of order 4 are pandiagonal of equal magic sums.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
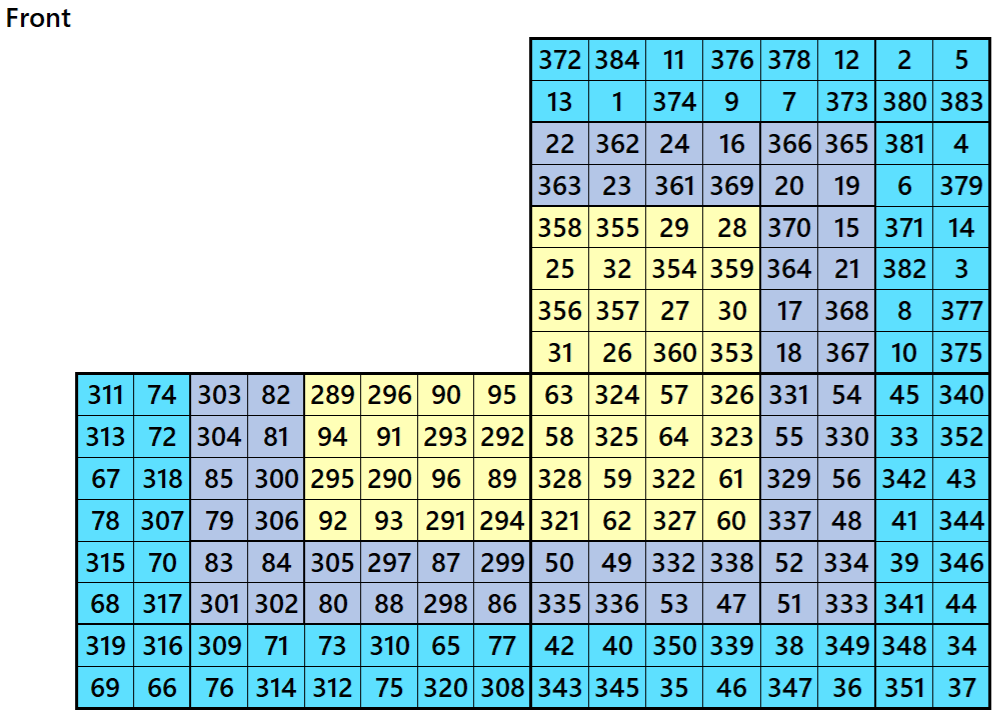
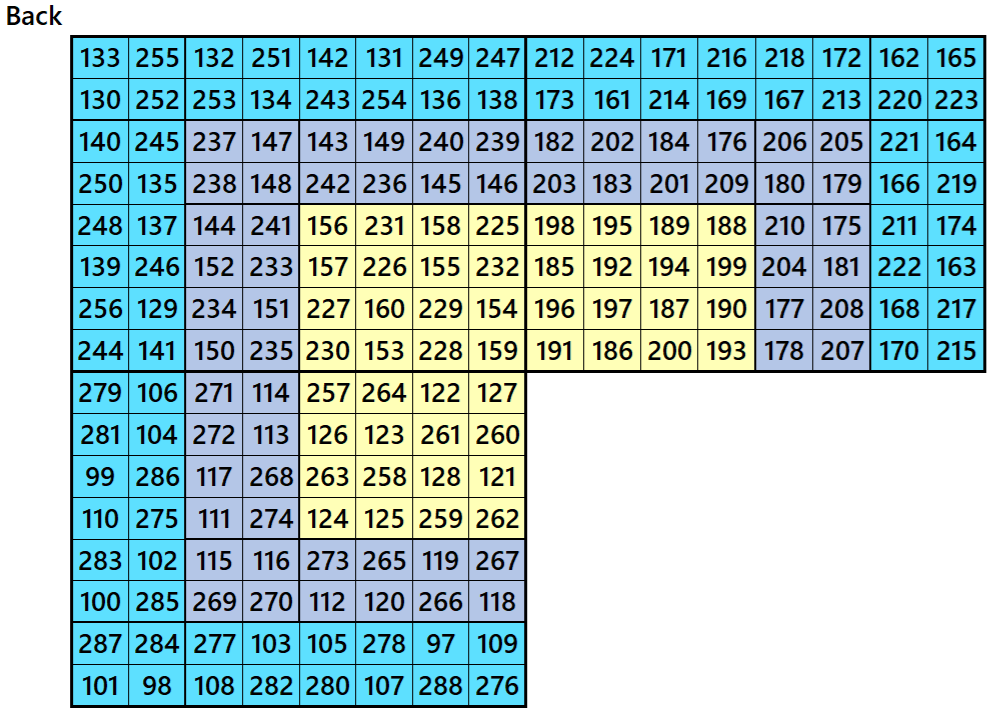
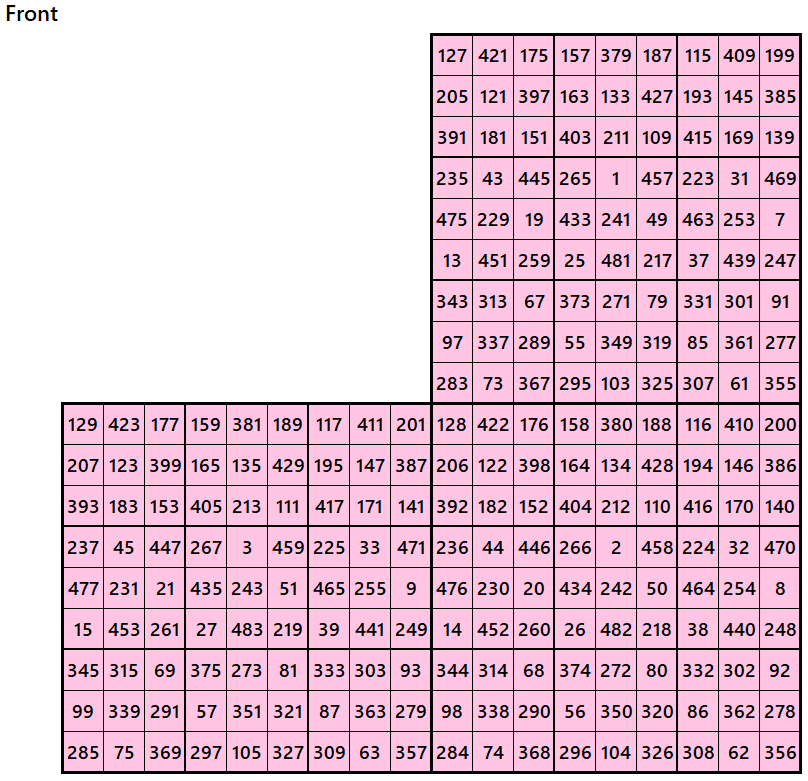
Magic Cubes with Magic Squares of Order 9
Example 1.
Let’s consider the following six magic squares of order 9.
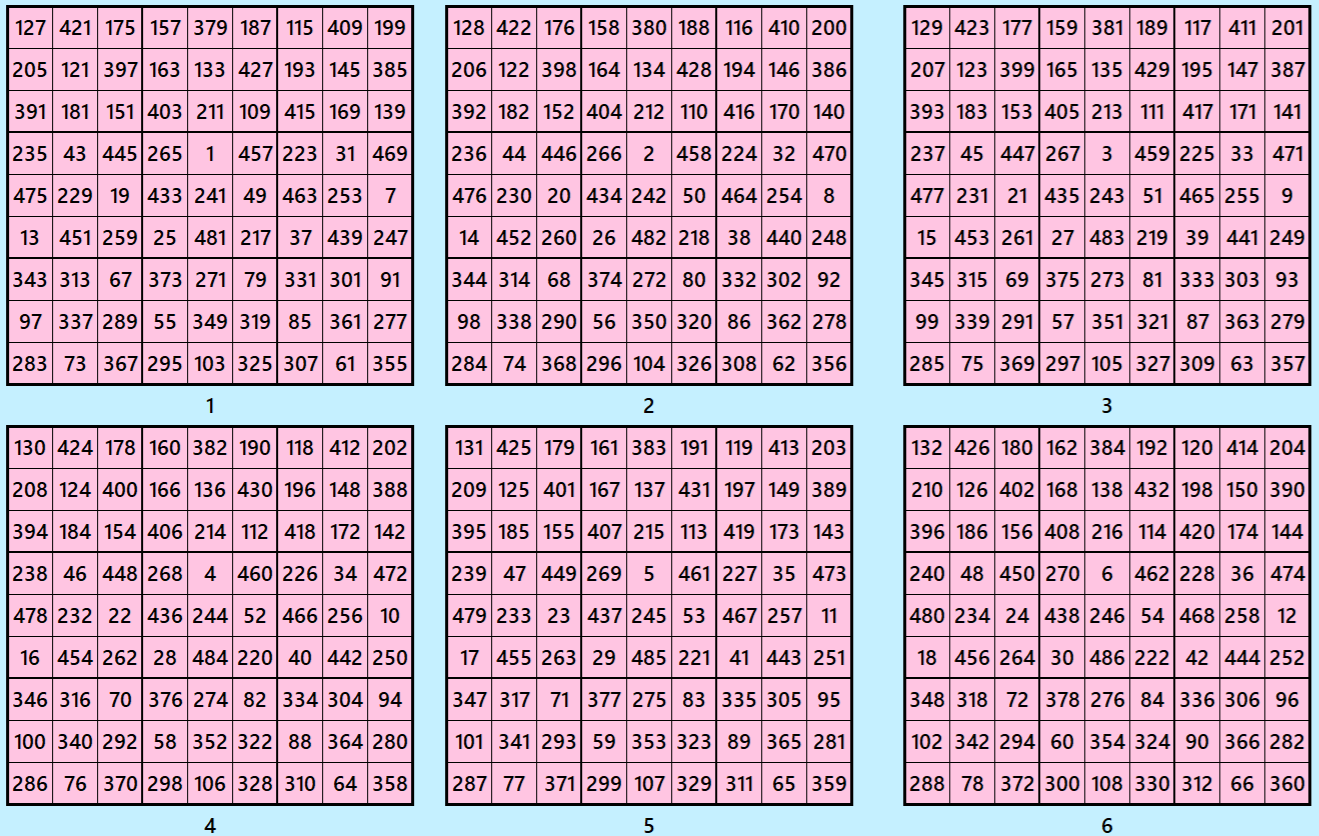
These magic squares are constructed using sequential numbres from 1 to 486. The magic sums are
S9×9(1):=2169, S9×9(2):=2178, S9×9(3):=2187, S9×9(4):=2196, S9×9(5):=2205 and S9×9(6):=2214.
Interestingly, these sums are of equal differences. Magic squares of order 3 are semi-magic squares of equal sums in each case.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:

Example 2.
Let’s consider the following six magic squares of order 9.
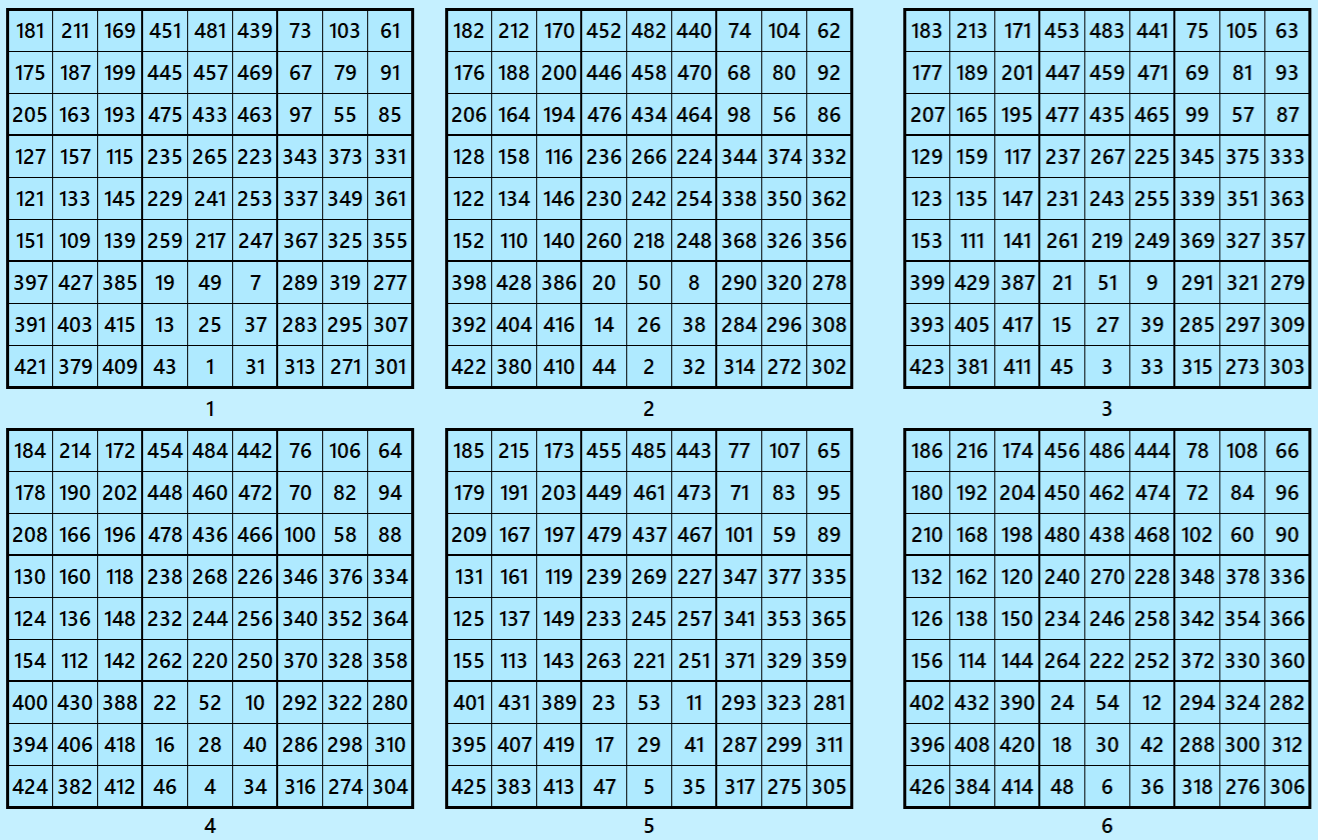
These magic squares are constructed using sequential numbres from 1 to 486. The magic sums are
S9×9(1):=2169, S9×9(2):=2178, S9×9(3):=2187, S9×9(4):=2196, S9×9(5):=2205 and S9×9(6):=2214.
Interestingly, these sums are of equal differences. Magic squares of order 3 are magic squares with different magic sums.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
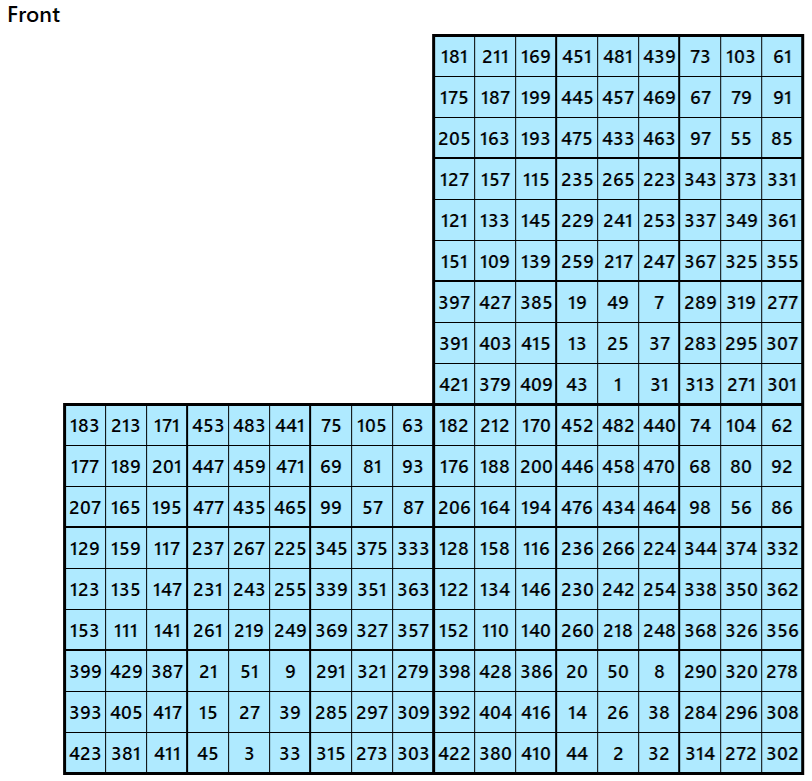
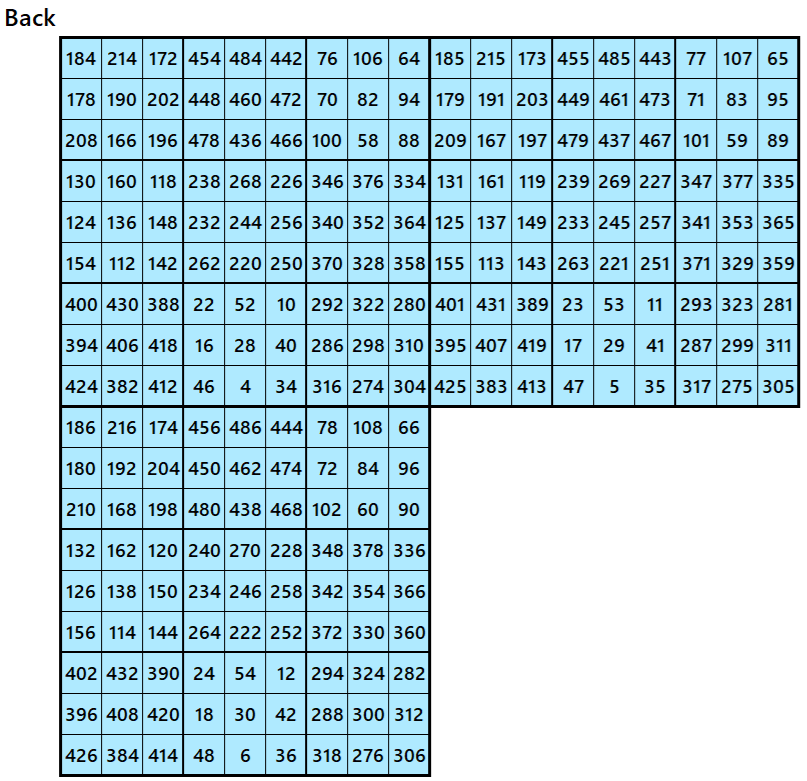
Example 3.
Let’s consider the following six magic squares of order 9.
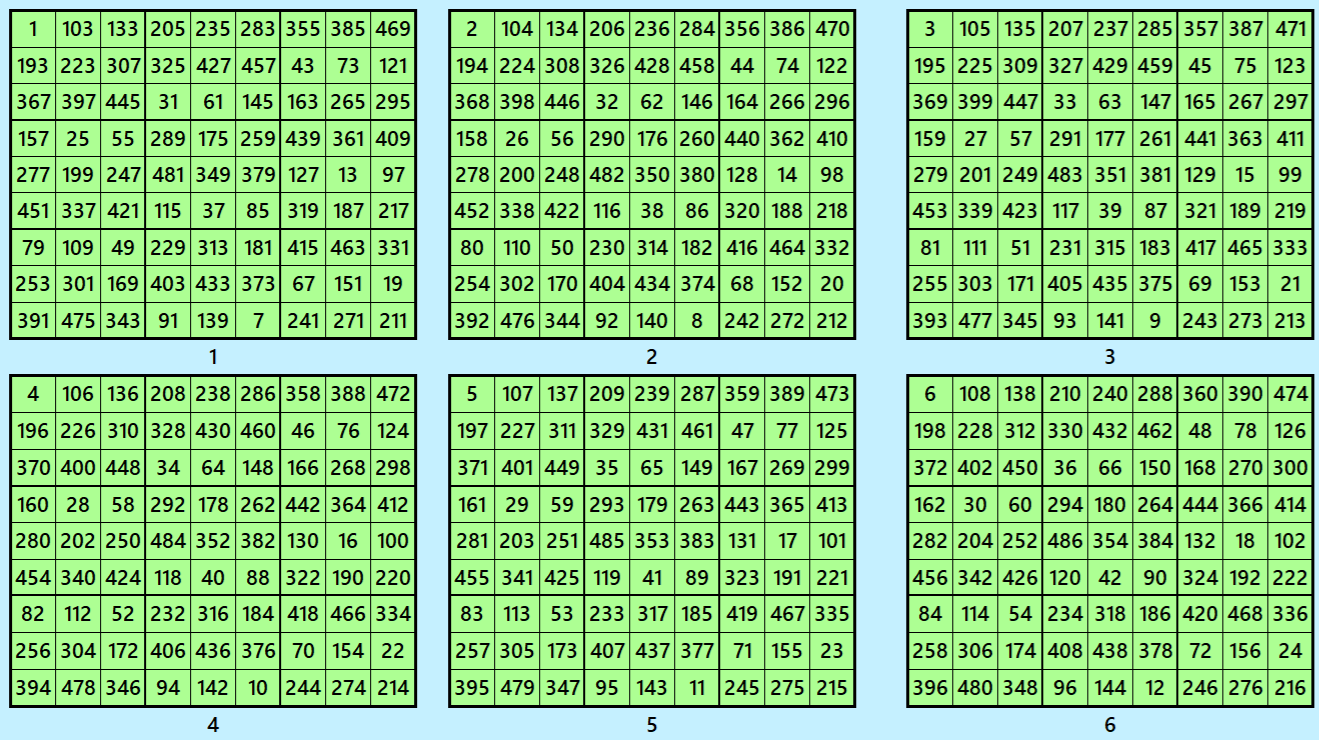
These magic squares are constructed using sequential numbres from 1 to 486. The magic sums are
S9×9(1):=2169, S9×9(2):=2178, S9×9(3):=2187, S9×9(4):=2196, S9×9(5):=2205 and S9×9(6):=2214.
Interestingly, these sums are of equal differences. 9 entries in each block of order 3×3 are of equal sums. The magic squares order 9 are also bimagic.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
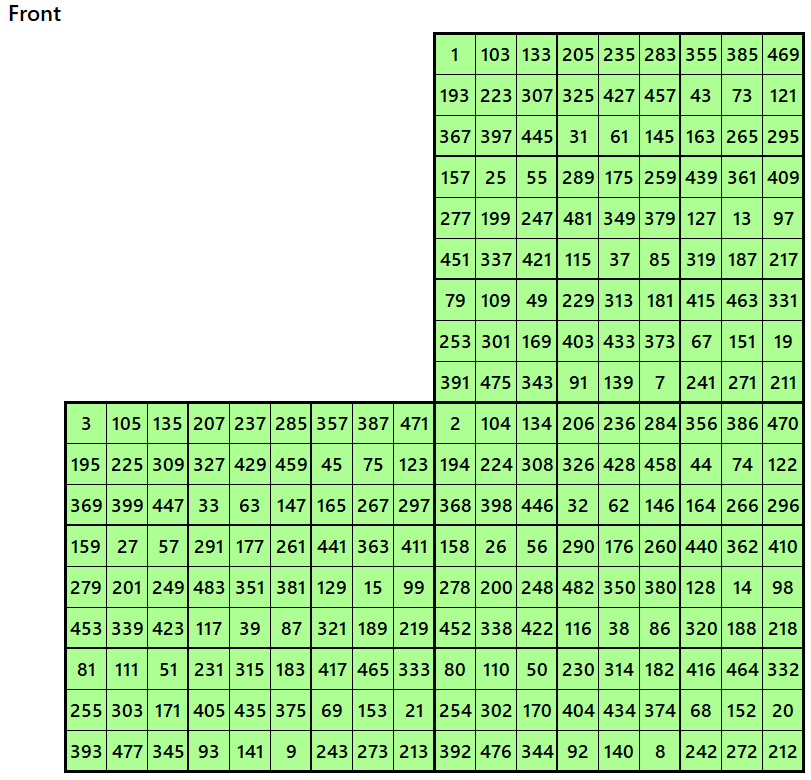
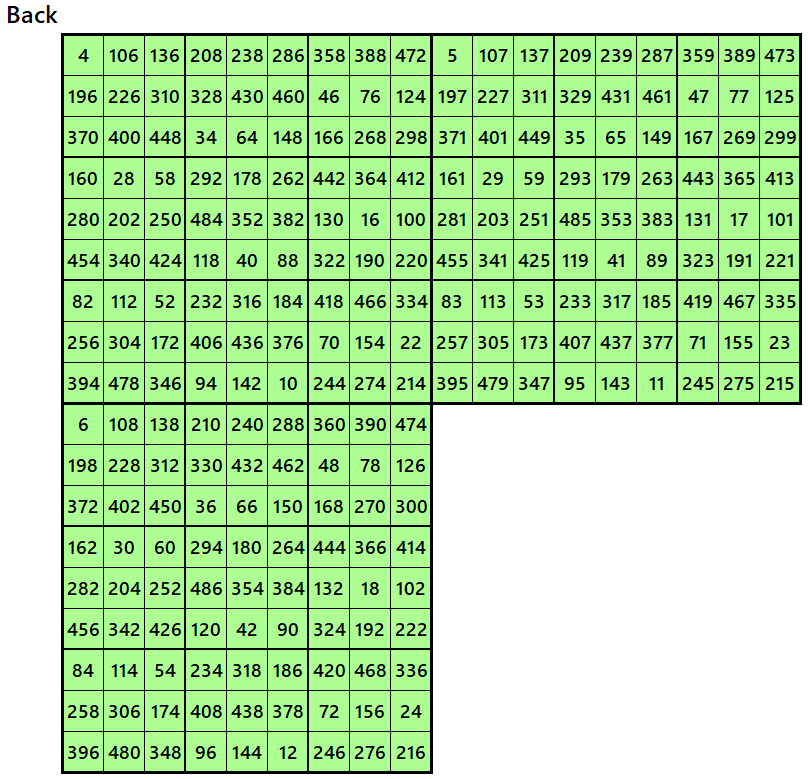
Example 4.
Let’s consider the following six magic squares of order 9.
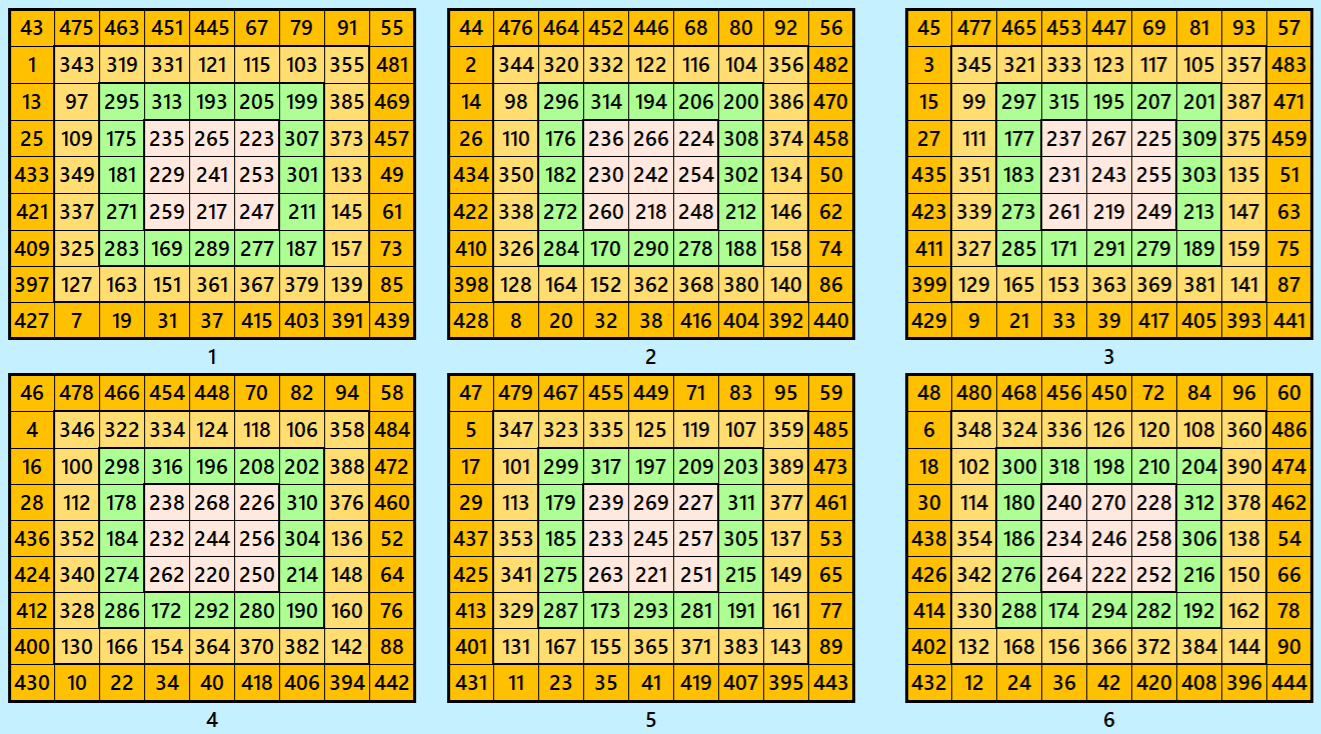
These magic squares are constructed using sequential numbres from 1 to 486. The magic sums are
S9×9(1):=2169, S9×9(2):=2178, S9×9(3):=2187, S9×9(4):=2196, S9×9(5):=2205 and S9×9(6):=2214.
Interestingly, these sums are of equal differences. In this case, the magic squares of order 9 are single digit bordered magic squares.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
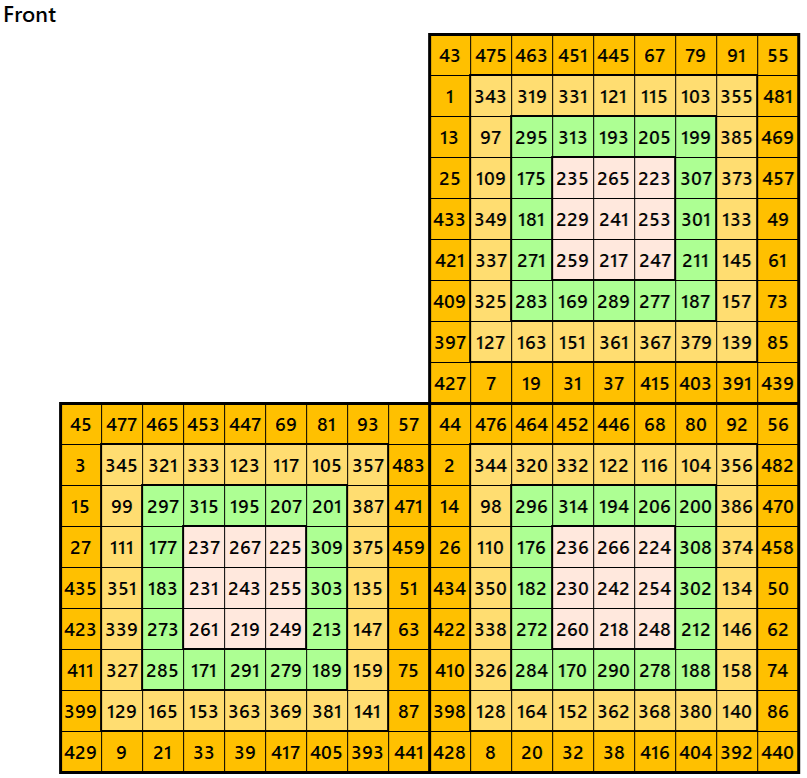
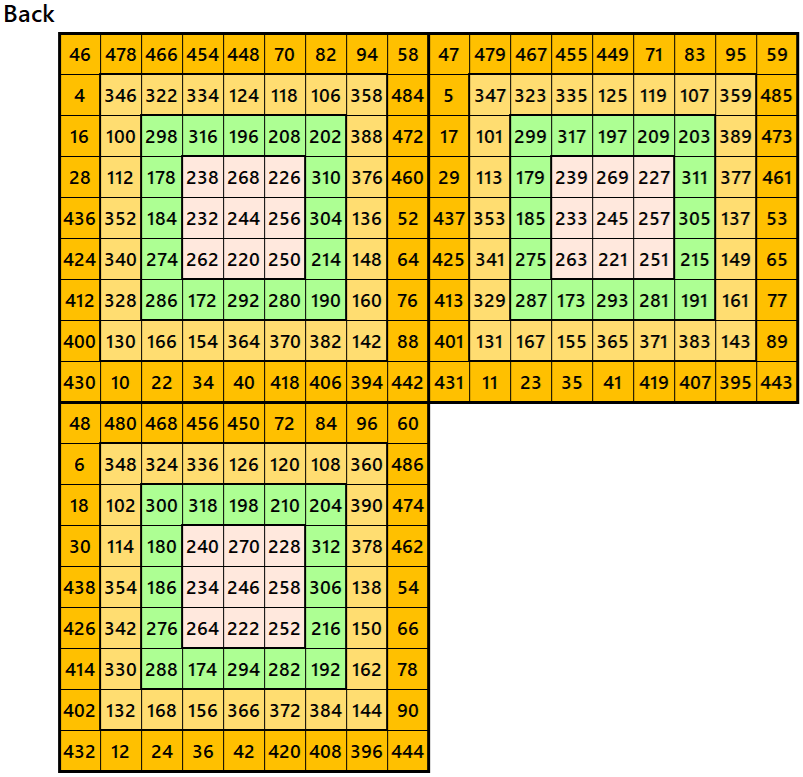
Example 5.
Let’s consider the following six magic squares of order 9.
These magic squares are constructed using sequential numbres from 1 to 486. The magic sums are
S9×9(1):=2169, S9×9(2):=2178, S9×9(3):=2187, S9×9(4):=2196, S9×9(5):=2205 and S9×9(6):=2214.
Interestingly, these sums are of equal differences. In this case, the magic squares of order 9 are doble digits bordered magic squares.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
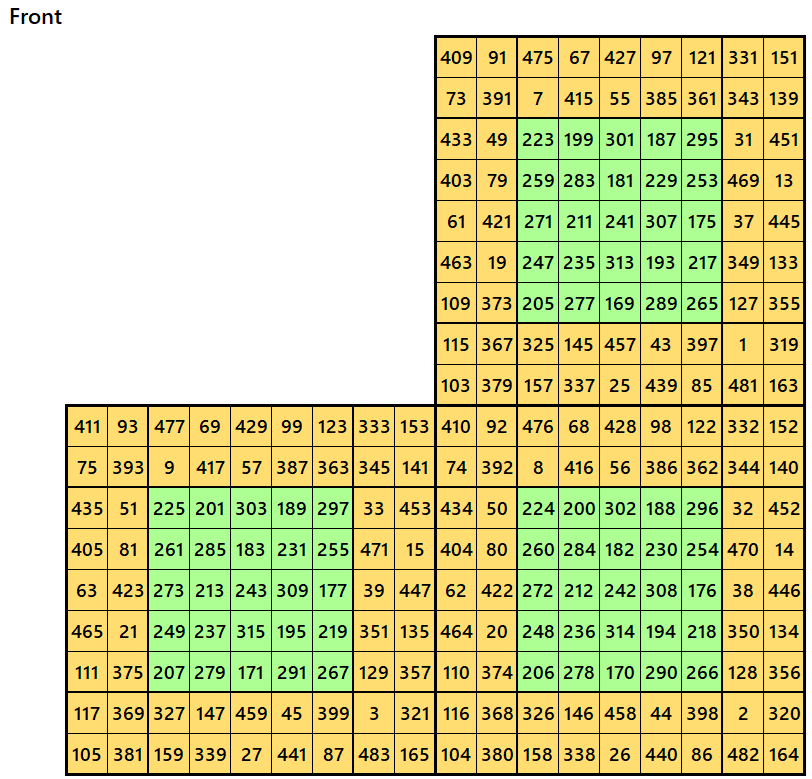
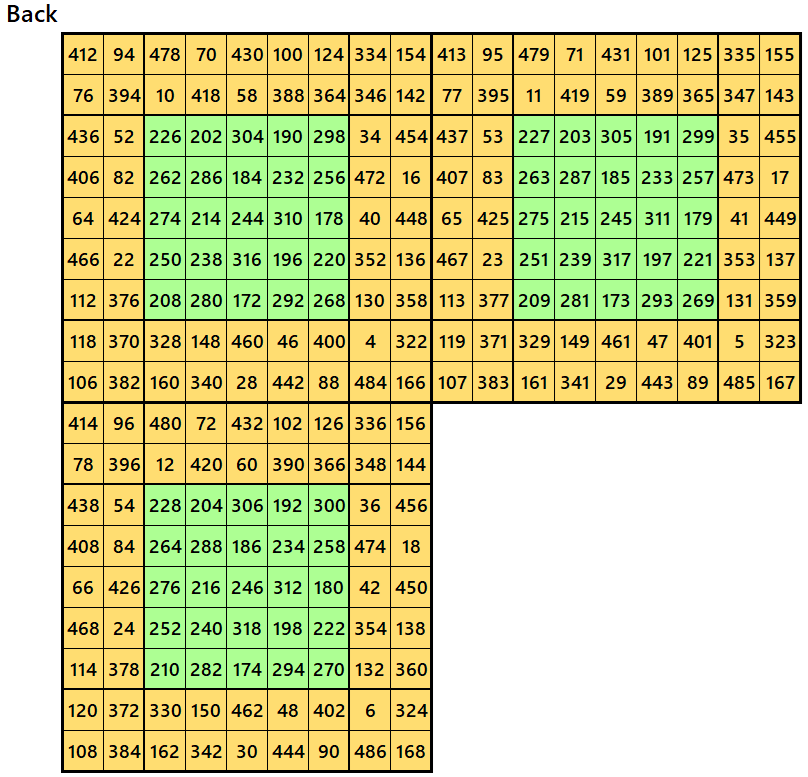
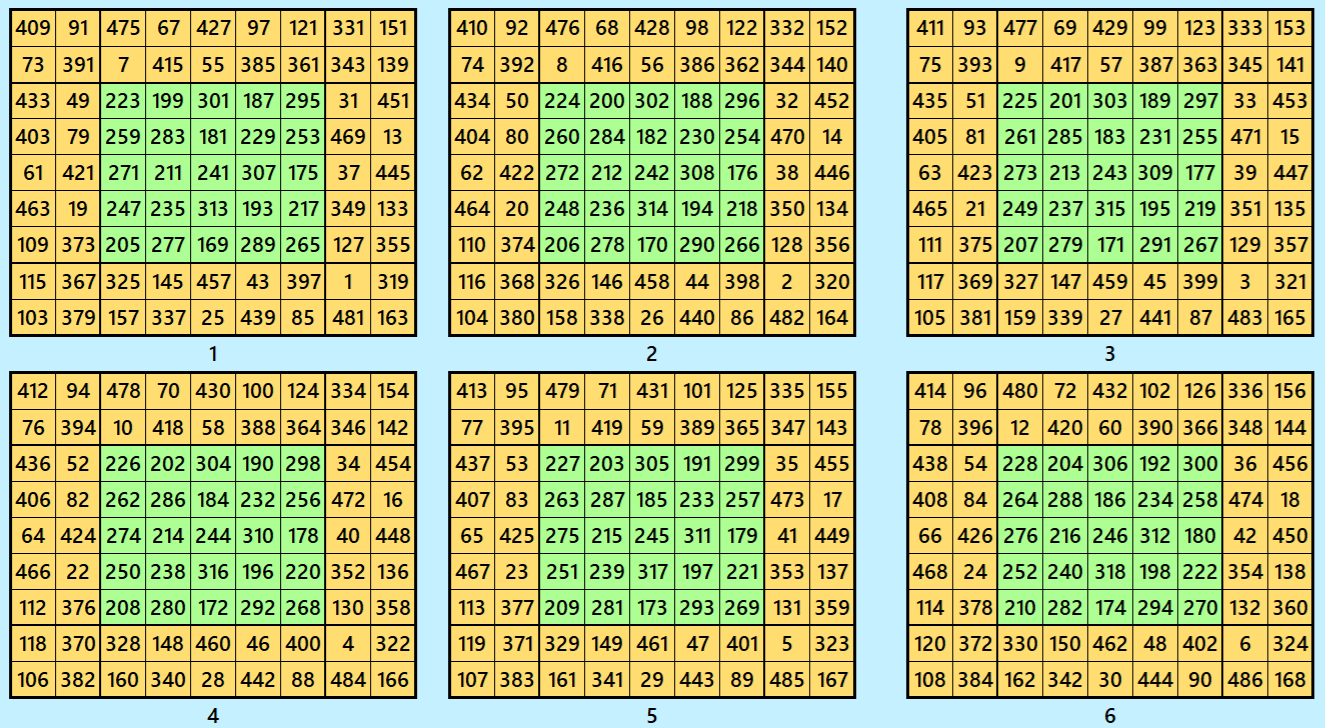
Example 6.
Let’s consider the following six magic squares of order 9.
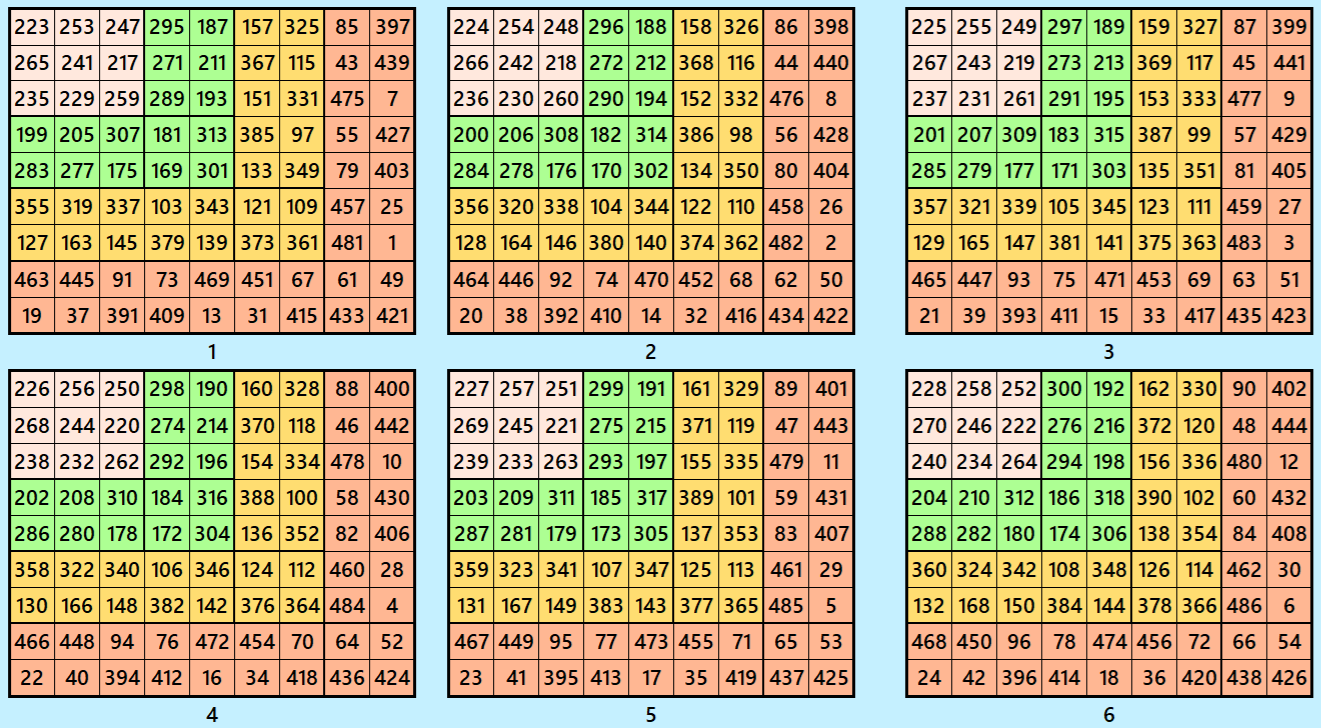
These magic squares are constructed using sequential numbres from 1 to 486. The magic sums are
S9×9(1):=2169, S9×9(2):=2178, S9×9(3):=2187, S9×9(4):=2196, S9×9(5):=2205 and S9×9(6):=2214.
Interestingly, these sums are of equal differences. Magic squares of order 9 are cornered magic squares.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
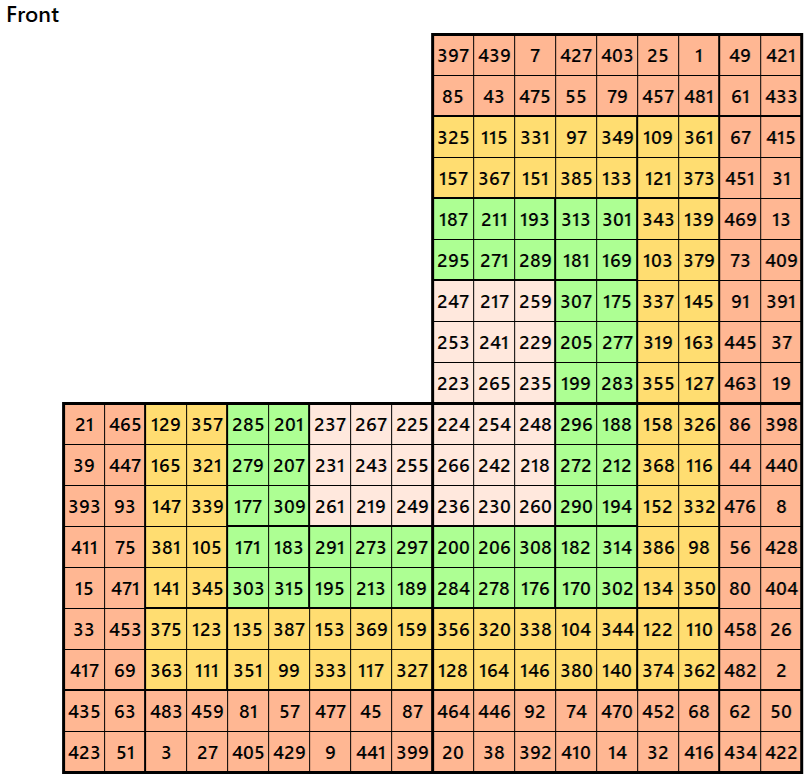
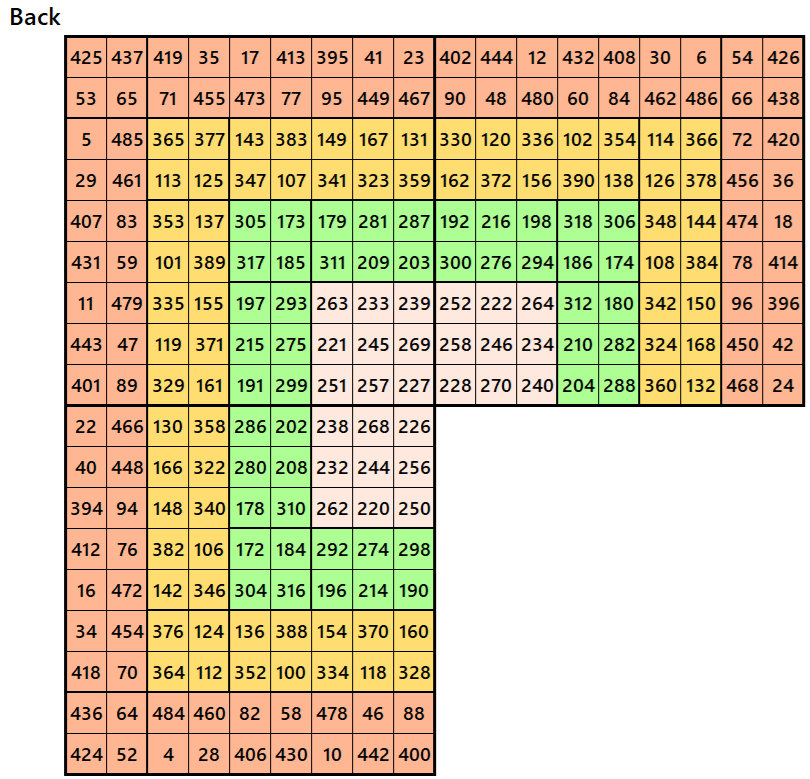
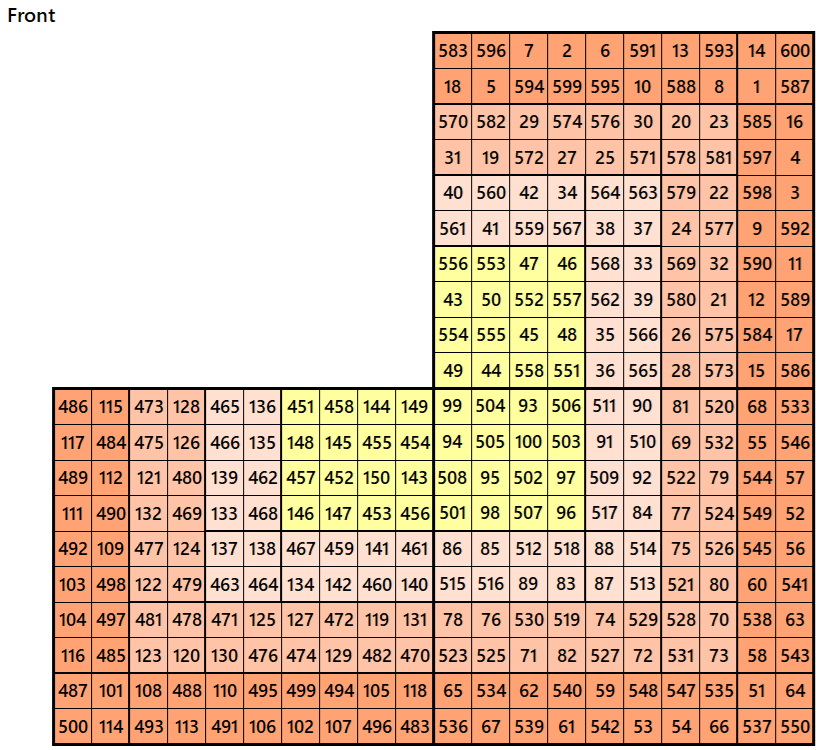
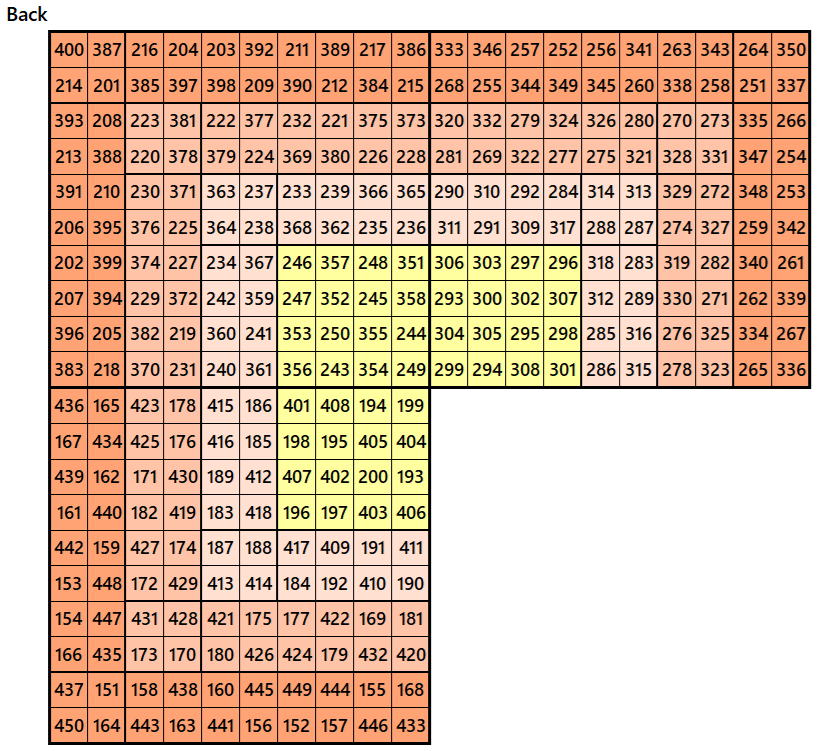
Magic Cubes with Magic Squares of Order 10
Example 1.
Let’s consider the following six magic squares of order 10

These magic squares are constructed using sequential numbres from 1 to 600. These are of equal magic sums, i.e,
S10×10(1)=S10×10(2)=S10×10(3)=S10×10(4)=S10×10(5)=S10×10(6):=3005.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:


Example 2.
Let’s consider the following six magic squares of order 10
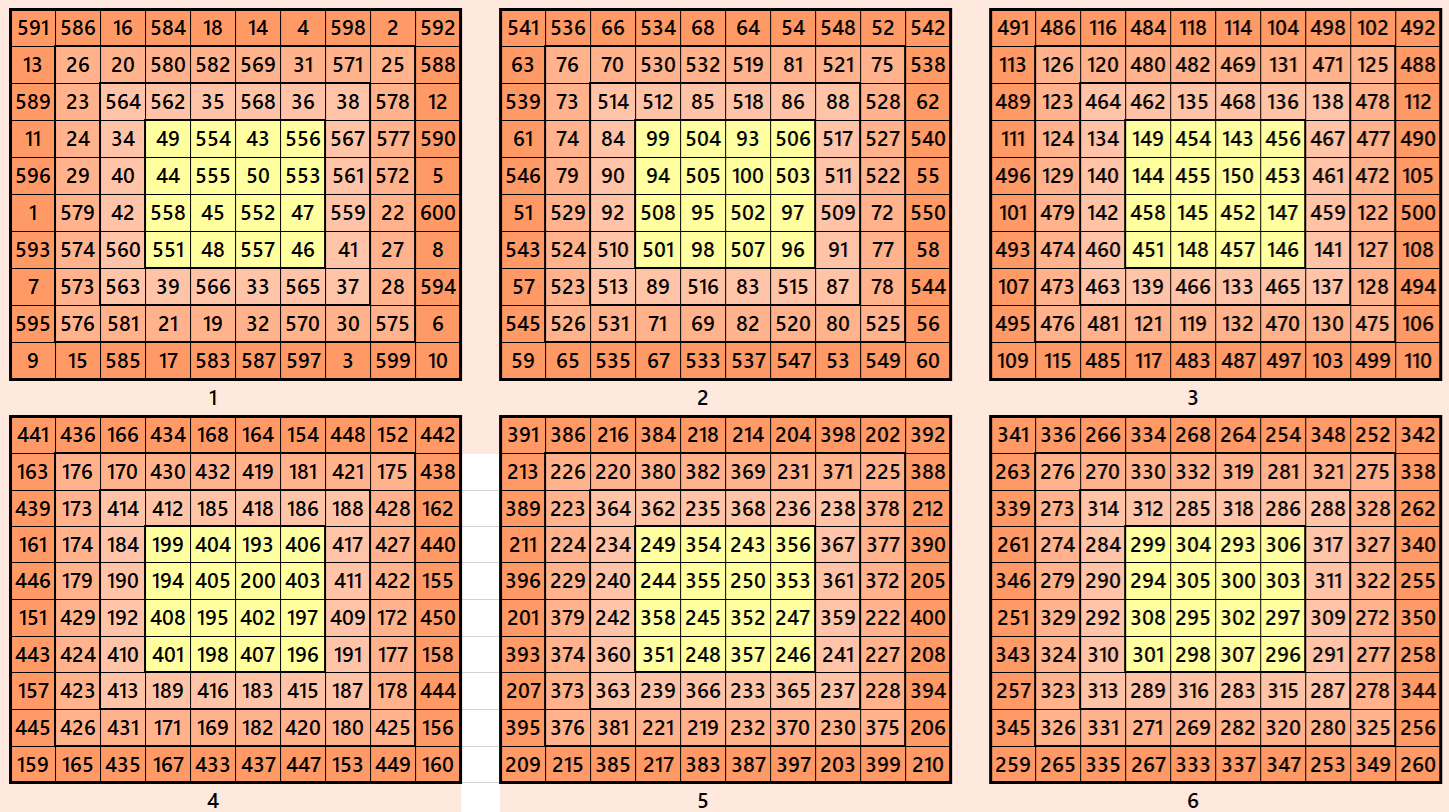
These magic squares are constructed using sequential numbres from 1 to 600. These are of equal magic sums, i.e,
S10×10(1)=S10×10(2)=S10×10(3)=S10×10(4)=S10×10(5)=S10×10(6):=3005.
These magic squares are known as single digit bordered magic squares. The inner block in each case is a pandiagonal magic square of order 4.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
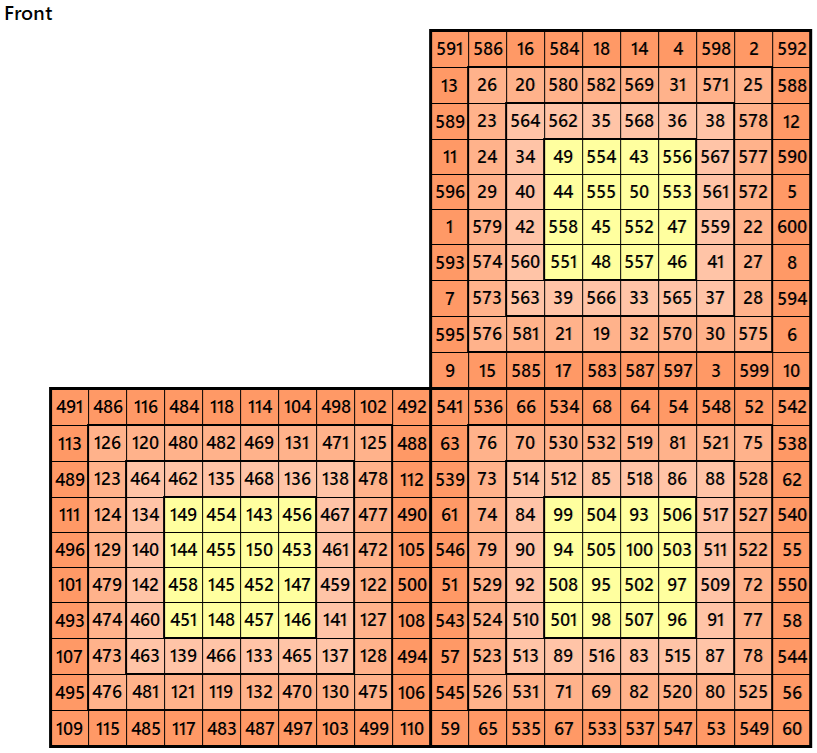
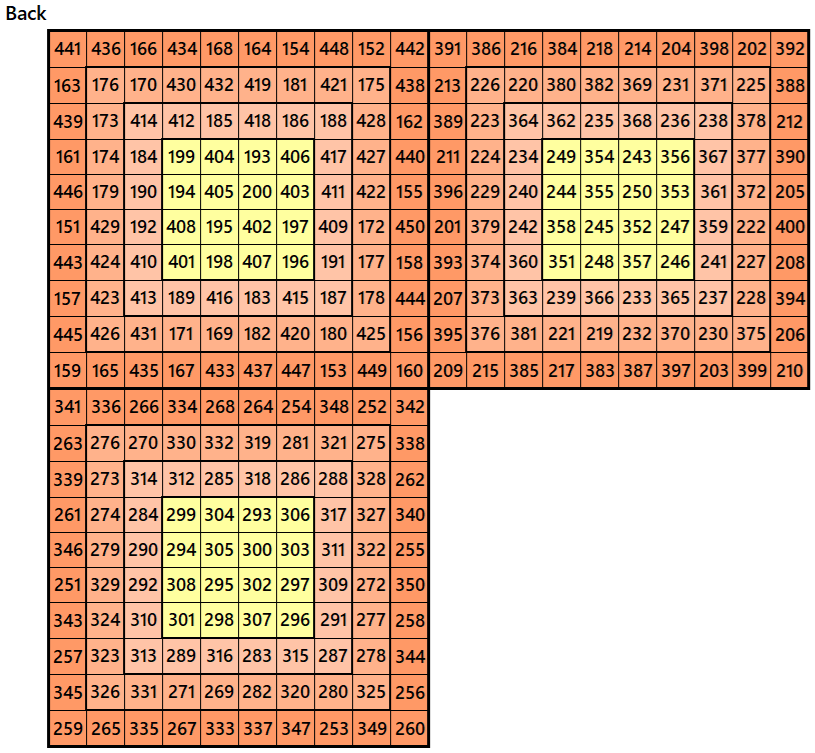
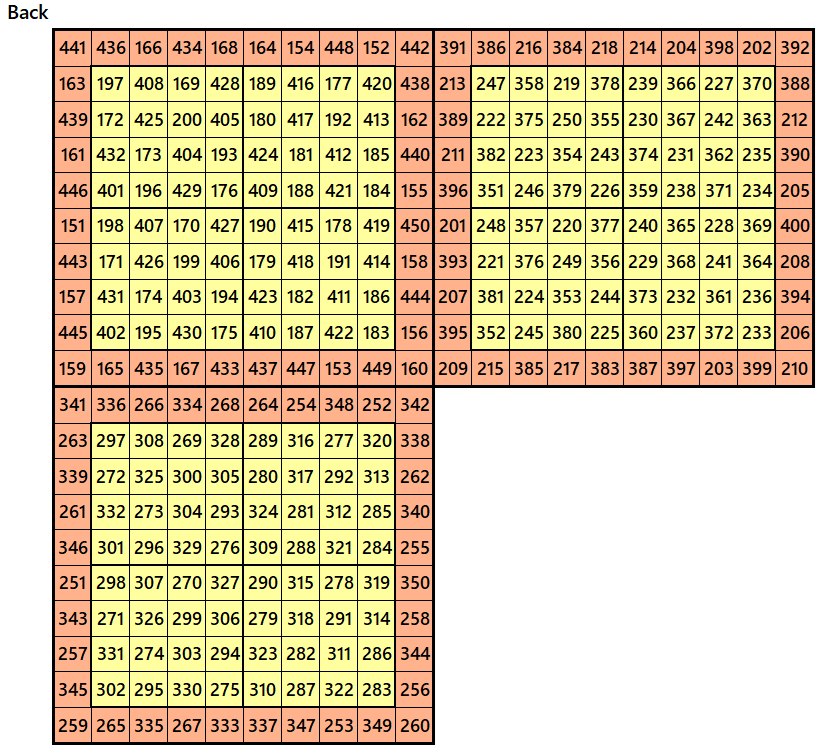
Example 3.
Let’s consider the following six magic squares of order 10
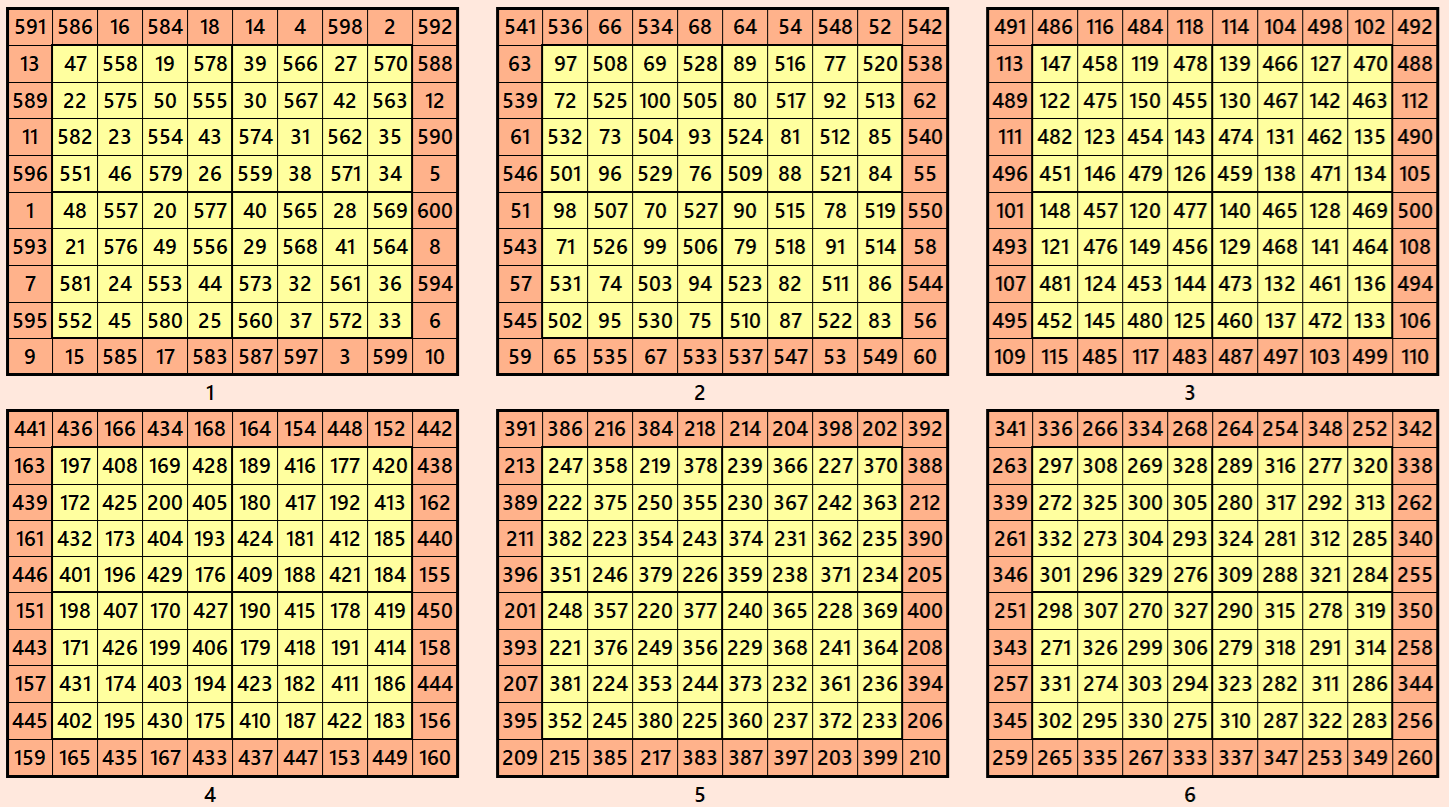
These magic squares are constructed using sequential numbres from 1 to 600. These are of equal magic sums, i.e,
S10×10(1)=S10×10(2)=S10×10(3)=S10×10(4)=S10×10(5)=S10×10(6):=3005.
These magic squares are also block-bordered magic squares. In this case, inner blocks of order 8 are pandigonal magic squares of order 8.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
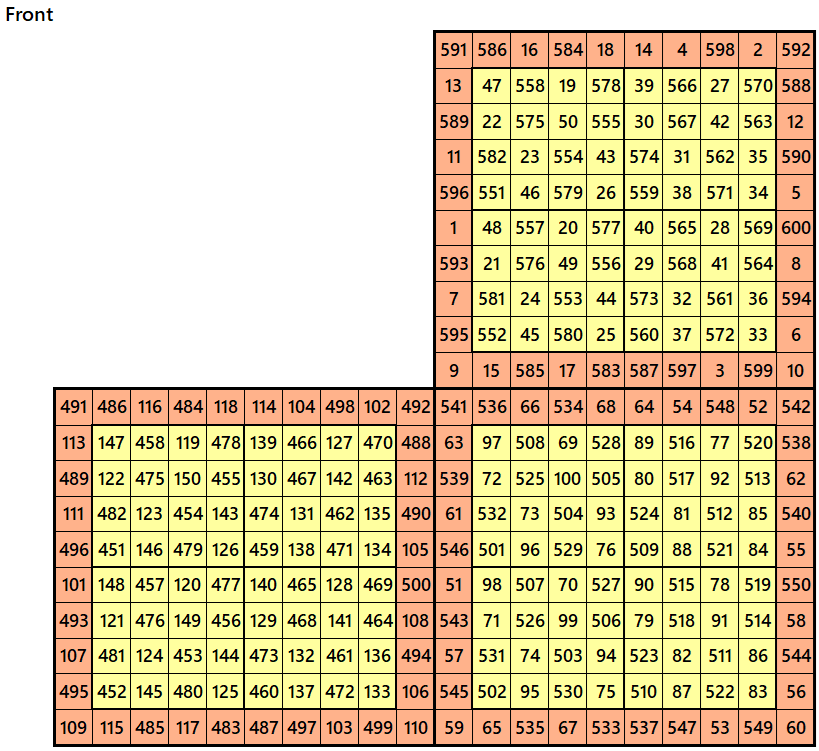
Example 4.
Let’s consider the following six magic squares of order 10
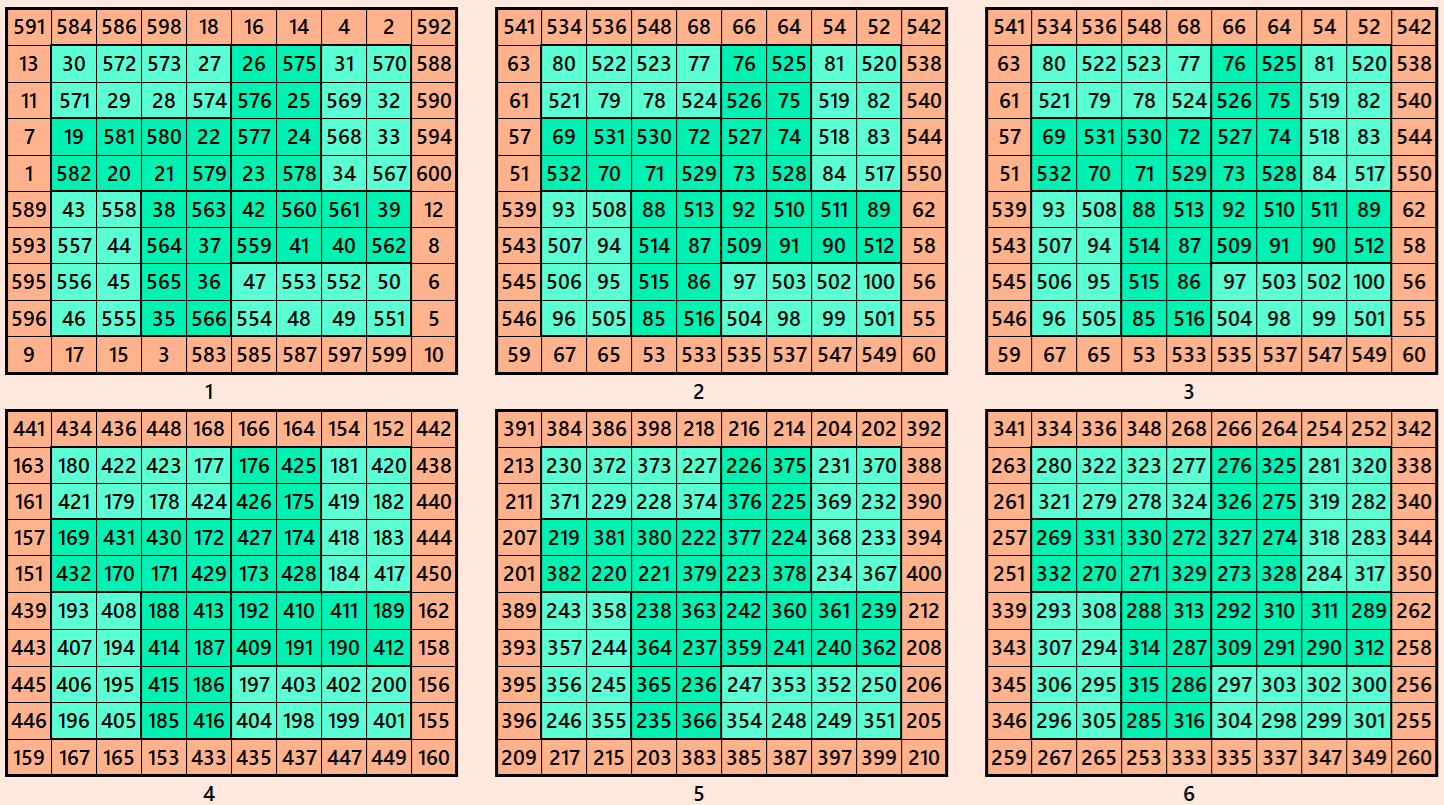
These magic squares are constructed using sequential numbres from 1 to 600. These are of equal magic sums, i.e,
S10×10(1)=S10×10(2)=S10×10(3)=S10×10(4)=S10×10(5)=S10×10(6):=3005.
These magic squares are also block-bordered magic squares. In this case, inner blocks of order 8 are striped magic squares of order 8. The stripes are magic rectangles of order 2×4.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
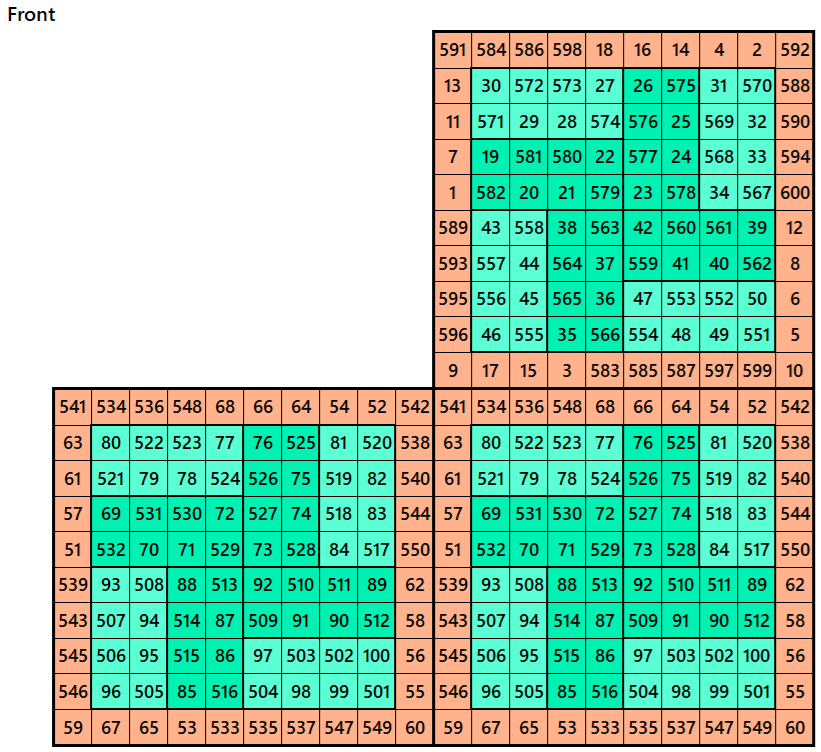
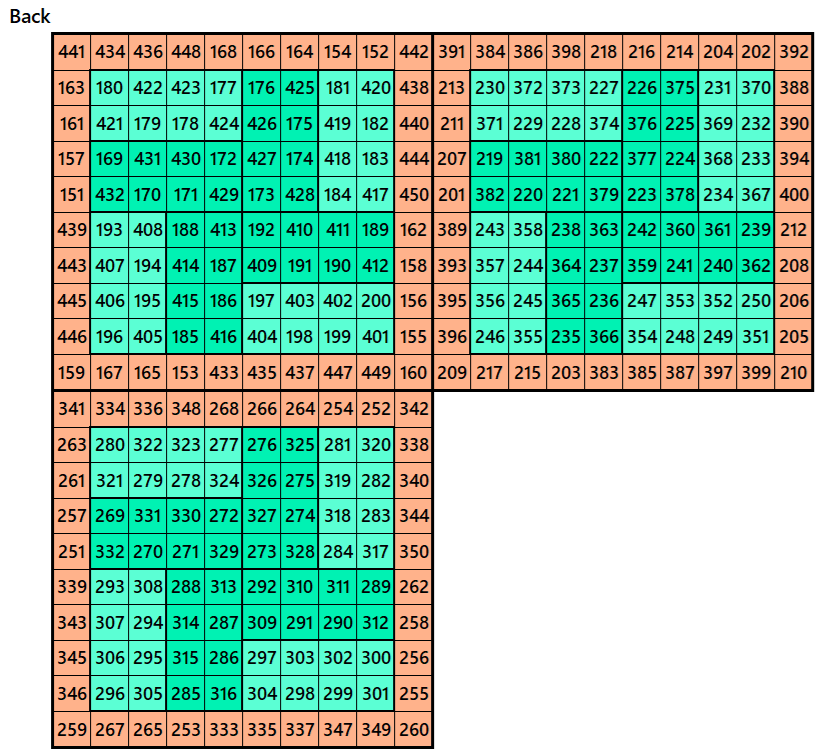
Example 5.
Let’s consider the following six magic squares of order 10
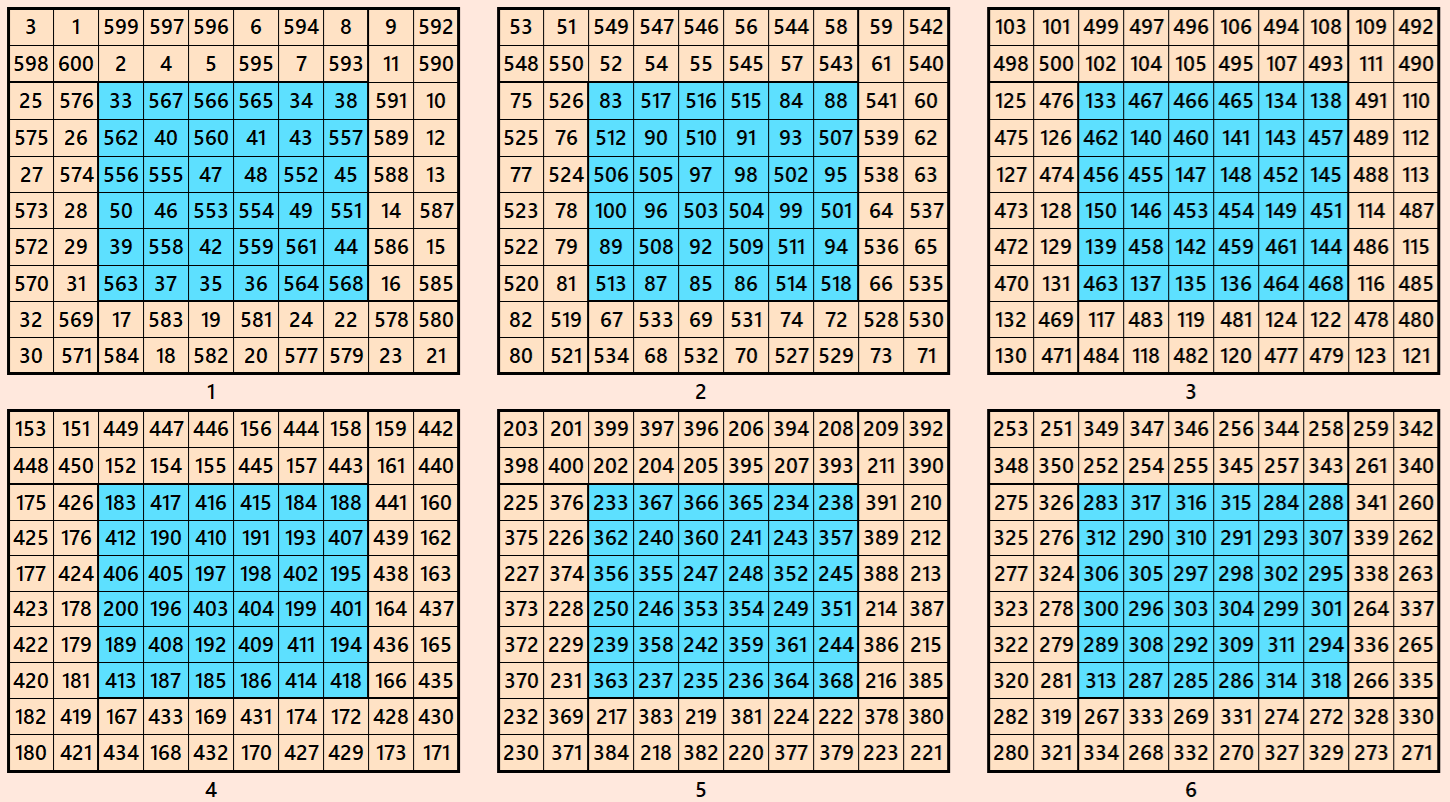
These magic squares are constructed using sequential numbres from 1 to 600. These are of equal magic sums, i.e,
S10×10(1)=S10×10(2)=S10×10(3)=S10×10(4)=S10×10(5)=S10×10(6):=3005.
These are double digit bordered magic squares. The inner blocks are magic squares of order 6.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
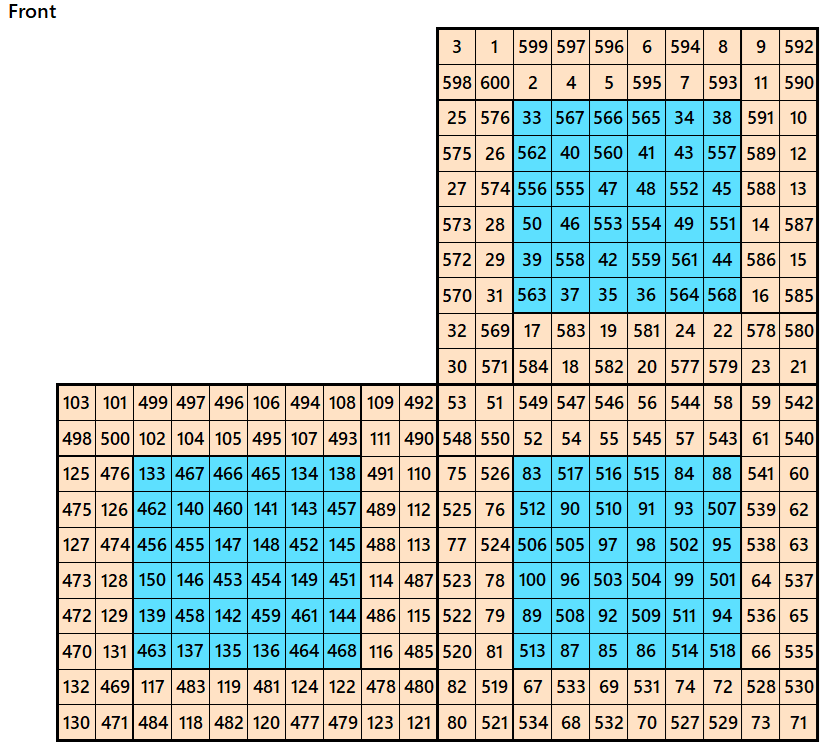
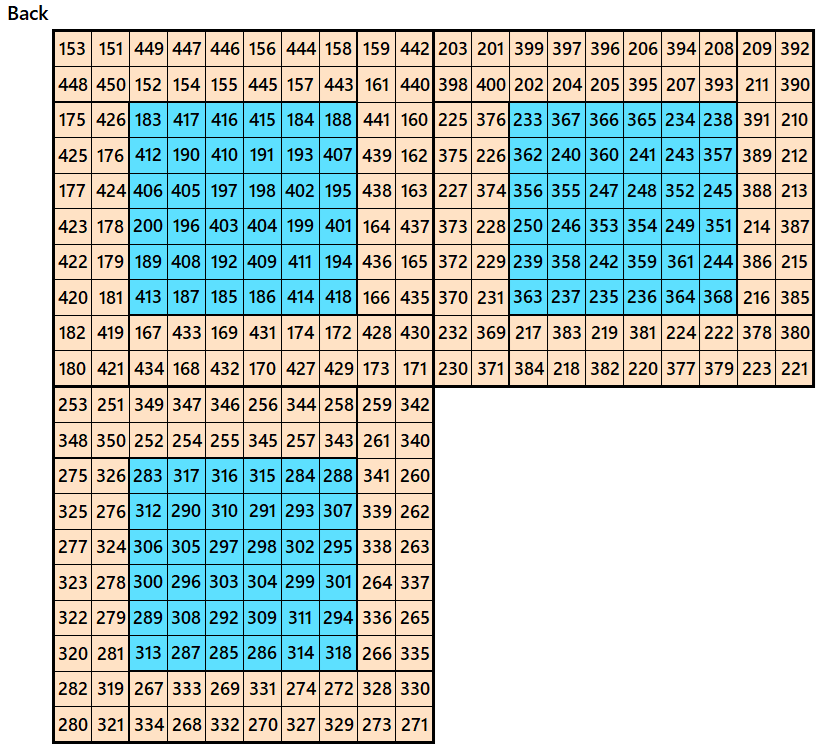
Example 6.
Let’s consider the following six magic squares of order 10
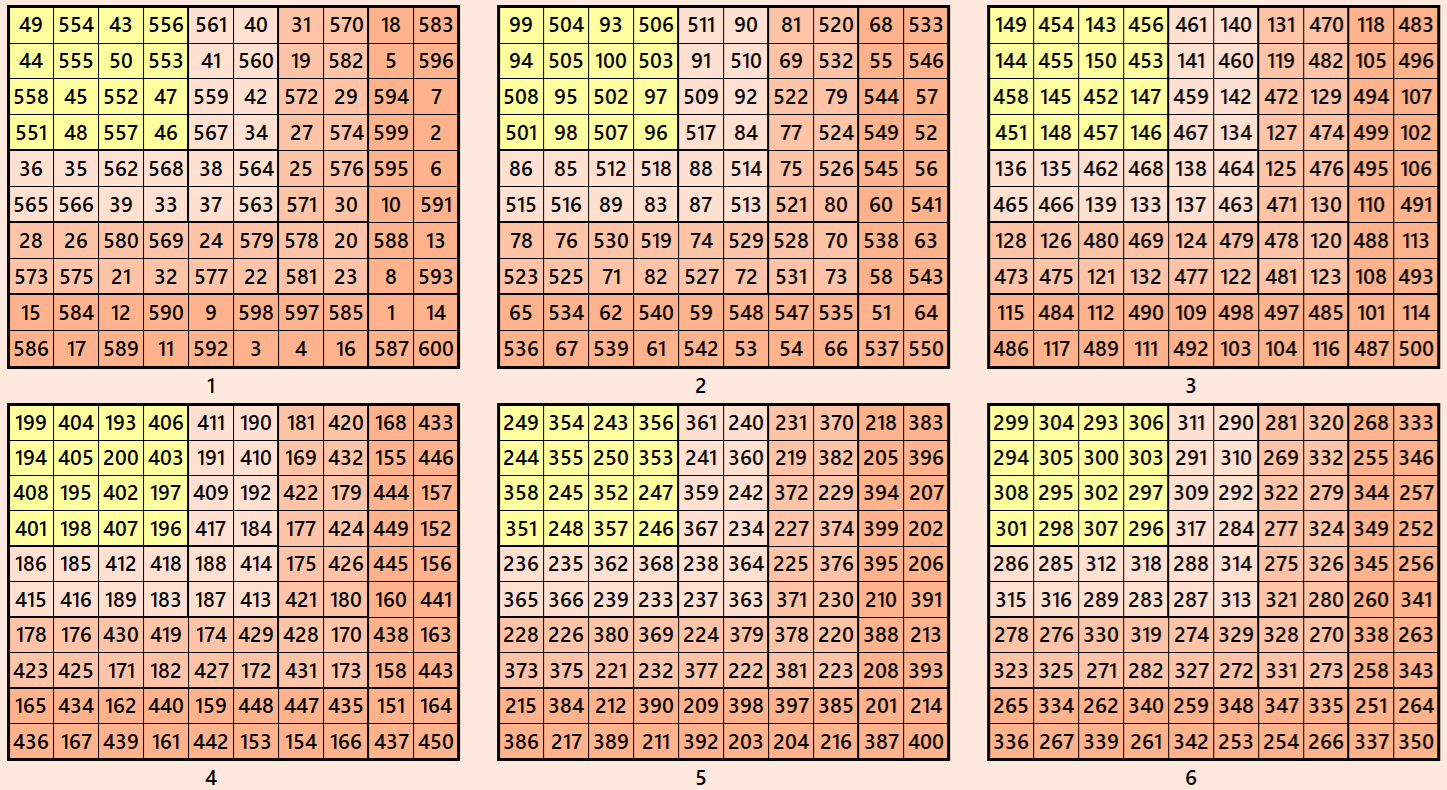
These magic squares are constructed using sequential numbres from 1 to 600. These are of equal magic sums, i.e,
S10×10(1)=S10×10(2)=S10×10(3)=S10×10(4)=S10×10(5)=S10×10(6):=3005.
These are cornered magic squares, the corneres are magic squares of order 8, 6 and 10.
Magic cube is composed with six magic squares representing front and back. ront and back. First three magic squares represent the front part and the last three represent the back part. See below:
References
- C. Boyer, Multimagic Squares, http://www.multimagie.com.
- B. Golunski, http://www.number-galaxy.eu/
- O.A. Dawood, A.M.S. Rahma and A. M.J. A.Hossen, Generalized Method for Constructing Magic Cube by Folded Magic Squares, I.J. Intelligent Systems and Applications, 2016, 1, 1-8, Published Online January 2016 in MECS (http://www.mecs-press.org/), DOI: 10.5815/ijisa.2016.01.01 – https://shorturl.at/pzqOP.
- W. Trump, Perfect Magic Cubes, https://shorturl.at/lyL3R.
- W. Trump, New Discoveries in the History of Magic Cubes, https://shorturl.at/qXwCh.
- W. Walkington, Magic Box Cubes, Rubik’s Cubes and Twisty Puzzles, https://shorturl.at/EaQRy
- H. White, Bordered Magic Squares – http://budshaw.ca/Download.html
- A. Winkel, The Magic Encyclopedia, http://magichypercubes.com/Encyclopedia/

