Universal and Upside-Down Magic Squares of Orders 7 to 10

There are many ways of representing magic squares with palindromic type entries. Also, we can write magic squares in the composite forms based on pair of Latin squares. This paper works with magic squares of order 3 to 6. By upside-down, we understand than by making 180^o it remains same. When the magic square is of both type, i.e., upside-down and mirror looking, we call it an universal magic square. By mirror looking we understand that putting in front of mirror, still we see the image as a magic square. In case of mirror looking, writing as digitais fonts, 2 becoms 5 and 5 as 2. In case of upside-down, 6 becomes 9 and 9 as 6.

The magic squares of order 9, we have considered in two different situations. One as bimagic and another as pandiagonal. In case of order 8, we considered the situations with pandiagonal and bimagic. For complete work for the orders 3 to 25, the readers can access the links given in the references at the end. This work can be accessed online at the following link:

• Inder J. Taneja, Universal and Upside-Down Magic Squares of Orders 7 to 10, Zenodo, November 05, 2024, pp. 1-120, https://doi.org/10.5281/zenodo.14041164

Magic Squares of Order 7

a) 2-Digits Cell Entries

Example 1. The Digits (0,1,2,5,6,8,9)

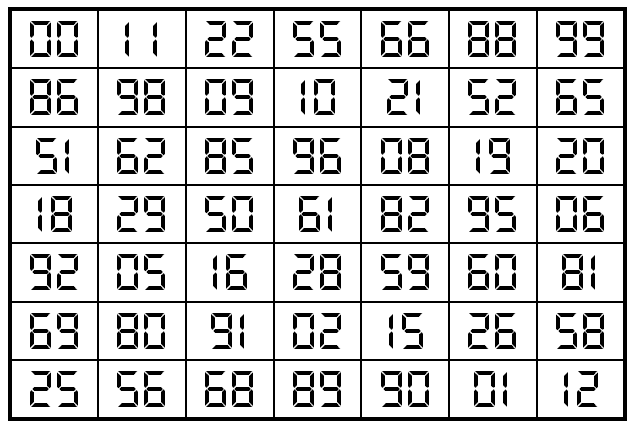
It is pandiagonal upside-down magic square with magic sum S_7×7(0,1,2,5,6,8, 9):=341.

b) 3-Digits Cell Entries

Example 2. The Digits (0,1,2,5,6,8,9)

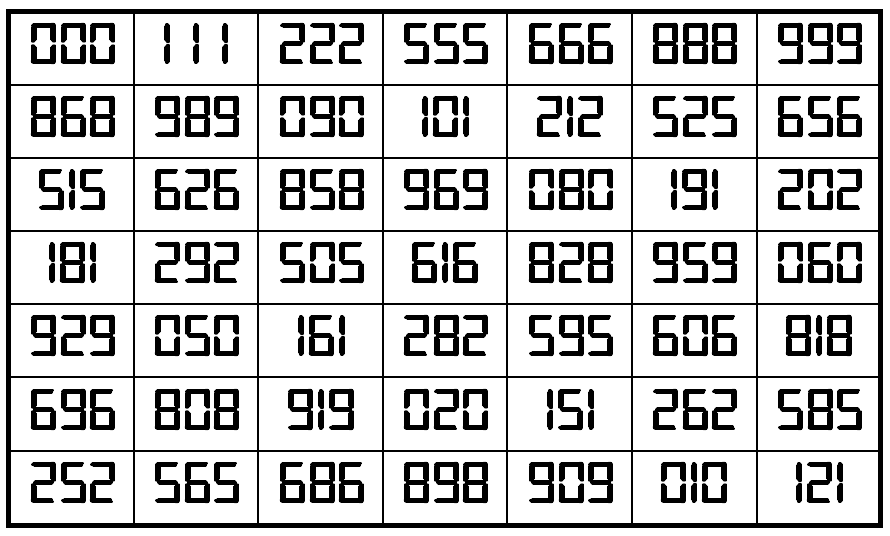
It is pandiagonal upside-down magic square with magic sum S_7×7(0,1,2,5,6,8, 9):=3441. In this case, the entries are palindromes.

c) 4-Digits Cell Entries

Example 3. The Digits (1,6,9)

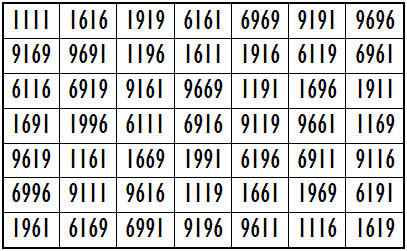
It is pandiagonal upside-down magic square with magic sum S_7×7(1,6,9):=36663.

Example 4. The Digits (2,5,8)

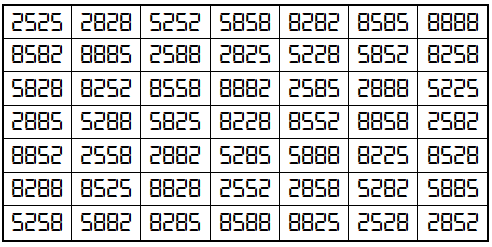
It is pandiagonal universal magic square with magic sum S_7×7(2,5,8):=42218.

c) 6-Digits Cell Entries

Example 5. The Digits (1,8)

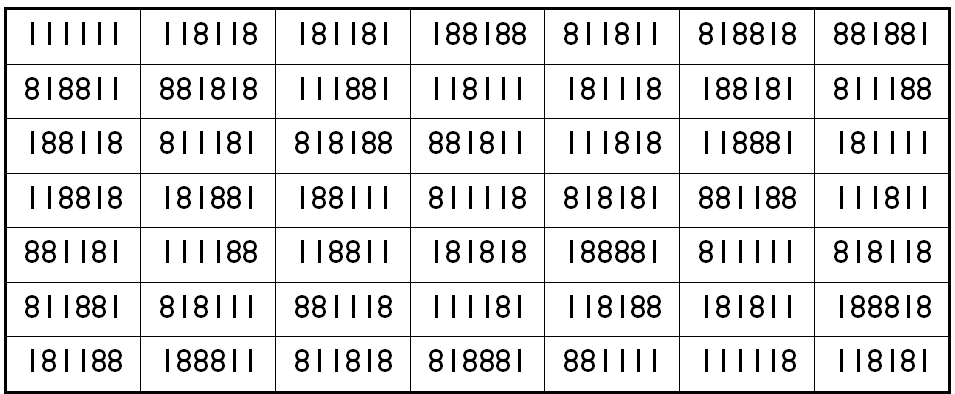
It is pandiagonal universal magic square of order 7 for 2-digits (1,8) with magic sum S_7×7(1,8):=3111108.

Example 6. The Digits (2,5)

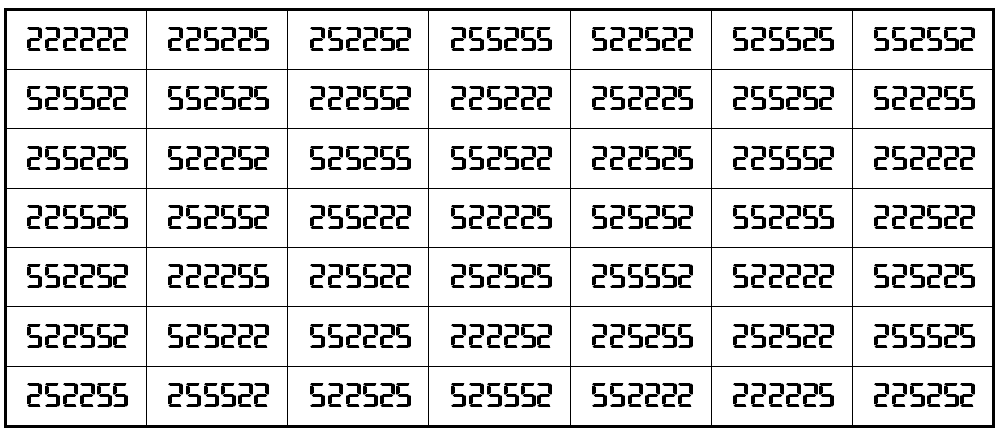
It is pandiagonal universal magic square of order 7 for 2-digits (2,5) with magic sum S_7×7(2,5):=2555553. For the mirror looking version, the sum is different S_7×7(2,5):=2888886.

Example 7. The Digits (6,9)

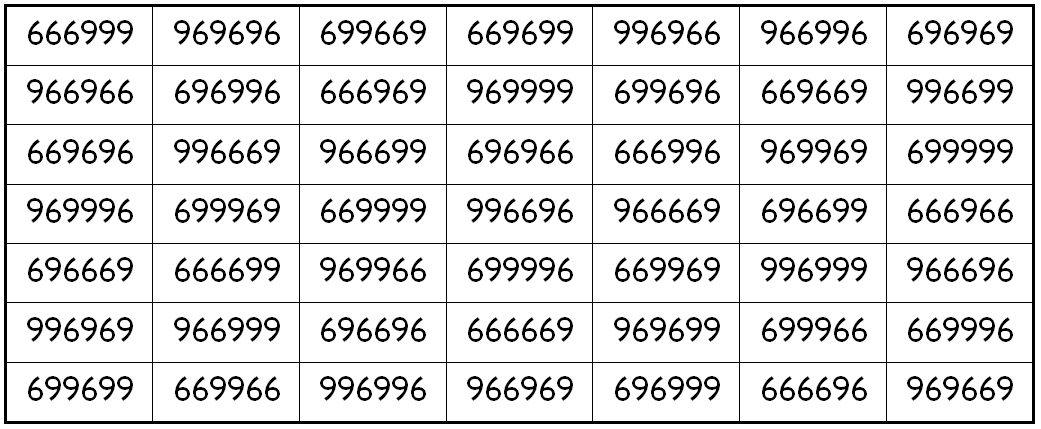
It is pandiagonal upside-down magic square of order 7 for 2-digits (1,8) with magic sum S_7×7(6,9):=5666994.

Magic Squares of Order 8

a) 4-Digits Cell Entries

Example 8. The Digits (1,6,9)

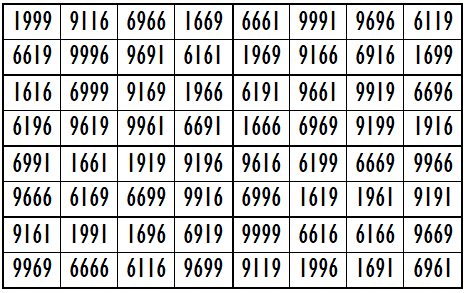
It is upside-down magic square with magic sum S_8×8(1,6,9):=52217.

Example 9. The Digits (2,5,8)

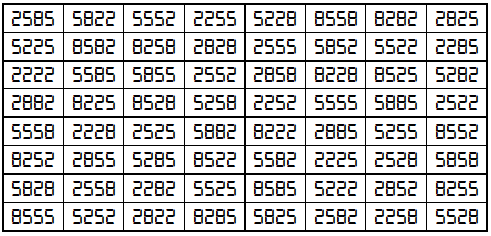
It is universal magic square with magic sum S_8×8(2,5,8):=41107.

b) 5-Digits Cell Entries

Example 10. The Digits (2,5,6,9)

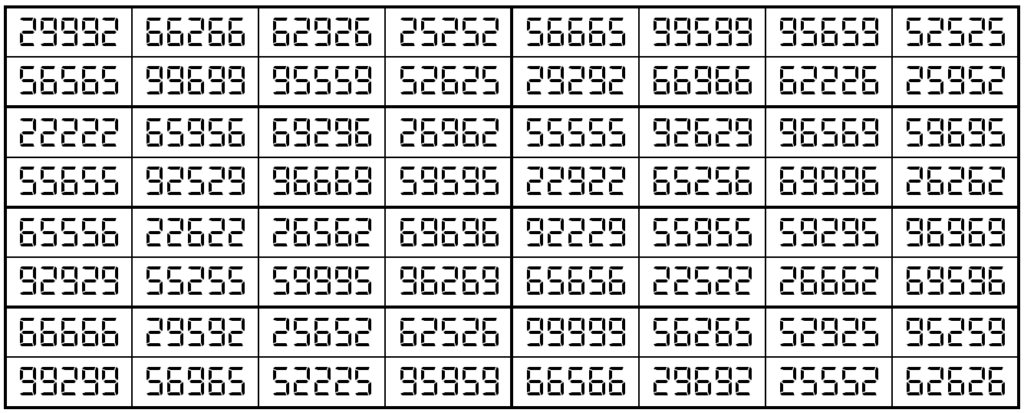
It is pandiagonal universal semi-bimagic square with magic sums S_8×8(2,5,6,9):=488884 and Sb_8×8(2,5,6,9):=34928450732.

Example 11. The Digits (0,2,5,8)

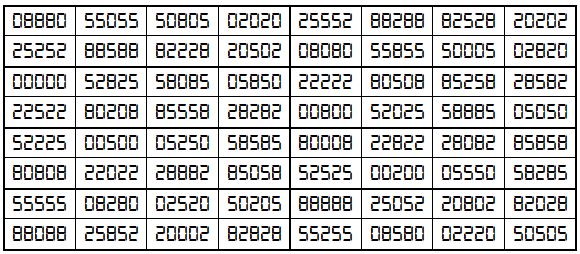
It is universal semi-magic square with semi-magic sum S_8×8(0,2,5,8):=333330.

c) 6-Digits Cell Entries:

Example 12. The Digits (1,8): Pandiagonal

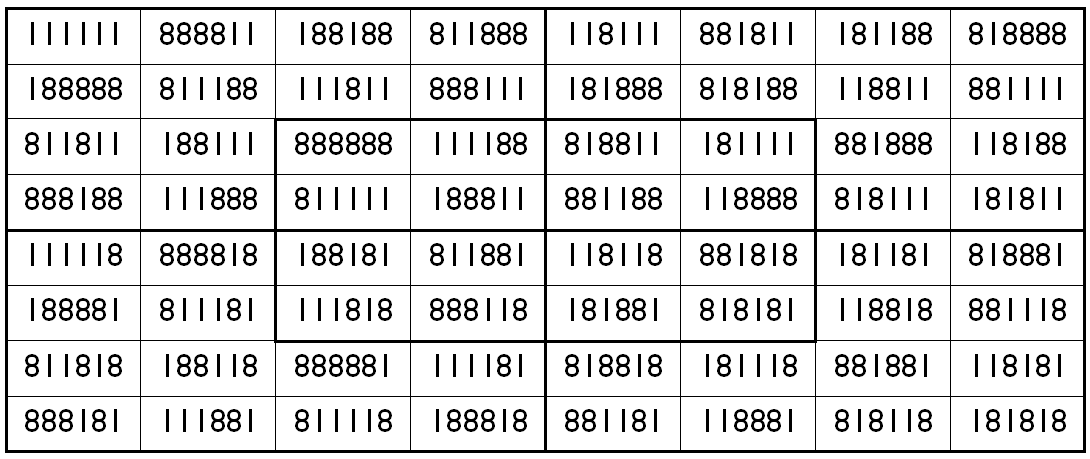
It is pandiagonal universal magic square of order 8 with magic sum S_8×8(1,8):=3999996. The blocks of order 4 are also pandiagonal with equal magic sums S_4×4(1,8):=1999998.

Example 13. The Digits (1,8): Pandiagonal and Bimagic

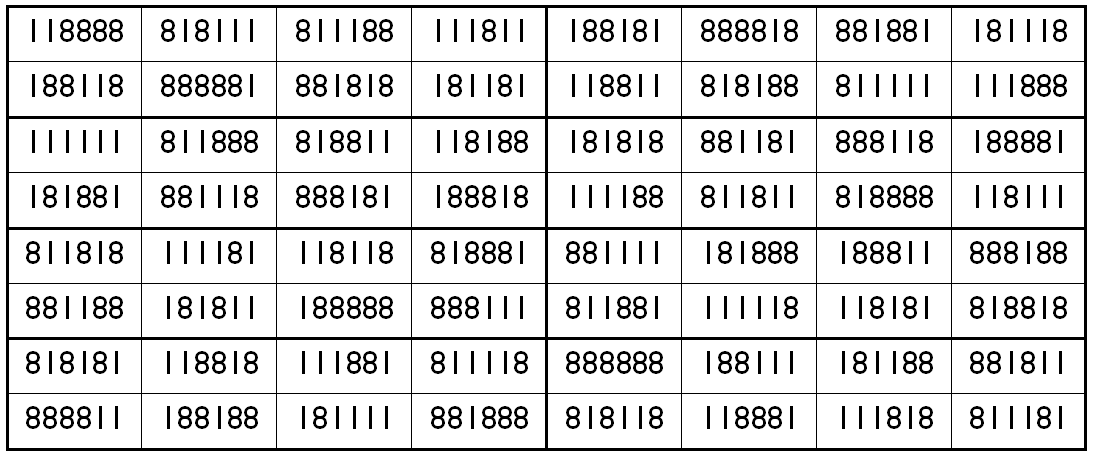
It is universal pandiagonal bimagic square of order 8 with magic sums S_8×8(1,8):=3999996 and Sb_8×8(1,8):=2989894989900.

Example 14. The Digits (2,5): Pandiagonal

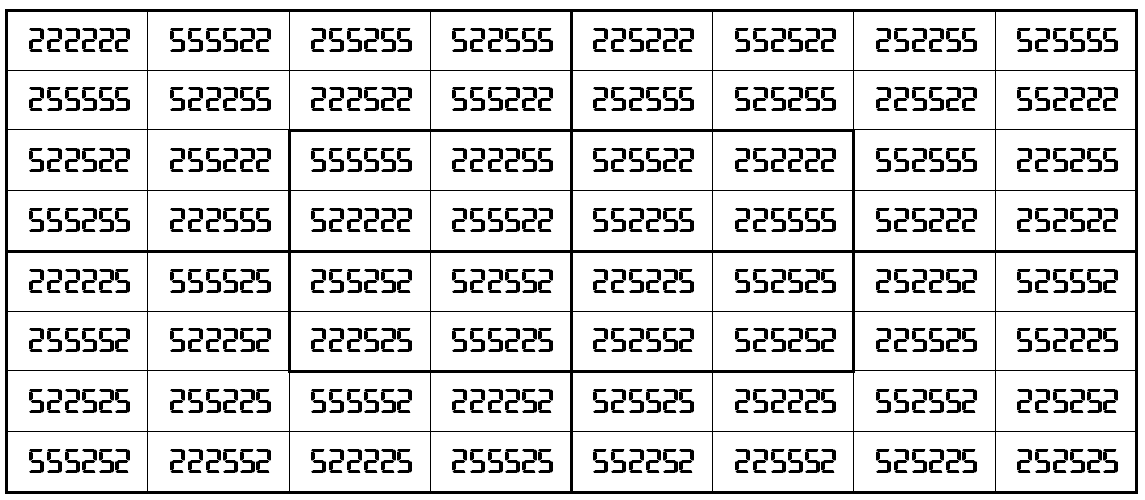
It is pandiagonal universal magic square of order 8 with magic sum S_8×8(2,5):=3999996. The blocks of order 4 are also pandiagonal with equal magic sums S_4×4(2,5):=1555554.

Example 15. The Digits (2,5): Pandiagonal and Bimagic

It is universal pandiagonal bimagic square of order 8 with magic sums S_8×8(2,5):=3999996 and Sb_8×8(2,5):=1391692305276

Example 16. The Digits (6,9): Pandiagonal

It is pandiagonal universal magic square of order 8 with magic sum S_8×8(6,9):=6666660. The blocks of order 4 are also pandiagonal with equal magic sums S_4×4(6,9):=3333330.

Example 17. The Digits (6,9): Pandiagonal and Bimagic

It is upside-down pandiagonal bimagic square of order 8 with magic sums S_8×8(6,9):=6666660 and Sb_8×8(6,9):=5737362626268.

b) 11-Digits Cell Entries

Example 18. The Digits (1,8)

It is pandiagonal universal bimagic magic square with magic sums S_8×8(1,8):=399999999996 and Sb_8×8(6,9):=29898989908389898989900.

Example 19. The Digits (2,5)

It is pandiagonal universal bimagic magic square with magic sums S_8×8(2,5):=311111111108 and Sb_8×8(6,9):=13916947251838608305276.

Example 20. The Digits (6,9)

It is pandiagonal upside-down bimagic magic square with magic sums S_8×8(6,9):=666666666660 and Sb_8×8(6,9):=57373737374426262626268.

Bimagic Squares of Order 9

a) 4-Digits Cell Entries

Example 21. The Digits (1,6,9)

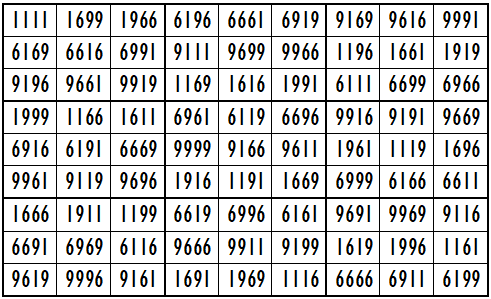
It is upside-down bimagic magic square with magic sums S_9×9(1,6,9):=53328 and Sb_9×9(1,6,9):=414976074.

Example 22. The Digits (2,5,8)

It is universal bimagic magic square with magic sums S_9×9(2,5,8):=49995 and Sb_9×9(2,5,8):=332267679.

b) 7-Digits Cell Entries

Example 23. The Digits (1,6,9)

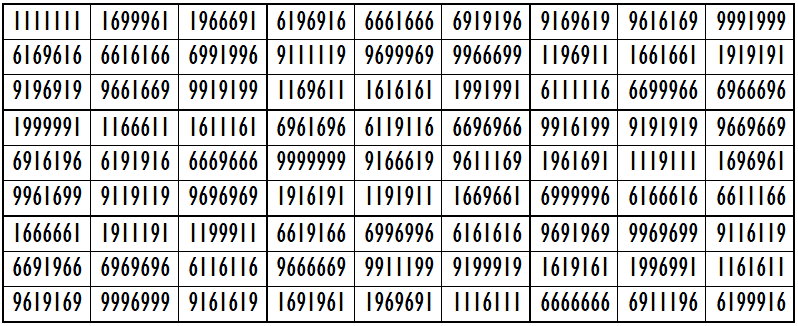
It is upside-down bimagic square of order 9 with 3-digits (1,6,9). The magic and bimagic sums are given by S_9×9(1,6,9):=53333328 and Sb_9×9(1,6,9):=415039806496074 respectively.

Example 24. The Digits (2,5,8)

It is universal bimagic square of order 9 with 3-digits (2,5,8). The magic and bimagic sums are given by S_9×9(2,5,8):=49999995 and Sb_9×9(1,6,9):=332323500767679 respectively.

c) 8-Digits Cell Entries

Example 25. The Digits (1,8): Bimagic

It is universal bimagic square with magic sums:

S_9×9(1,8):=333333330 and S_9×9(1,8):=333333330:=21264570654621018.

Moreover, the sums of nine entries in each blocks of order 3 are the same as of magic square.

Example 26. The Digits (2,5): Bimagic

It is universal bimagic square with magic and bimagic sums given by

S_9×9(2,5):=299999997 and Sb_9×9(2,5):=11638163616381639.

In the mirror looking case the magic and bimagic sums are given by

S_9×9(2,5):=399999996 and Sb_9×9(2,5):=19415941238603862.

The sum of 9 members of each block of order 3 are the same as of magic square.

Example 27. The Digits (6,9): Bimagic

It is universal bimagic square with magic sums:

S_9×9(6,9):=700009992 and S_9×9(6,9):=333333330:=56084162583030534.

Moreover, the sums of nine entries in each blocks of order 3 are the same as of magic square.

Pandiagonal magic Squares of Order 9

a) 4-Digits Cell Entries

Example 28. The Digits (6,8,9)

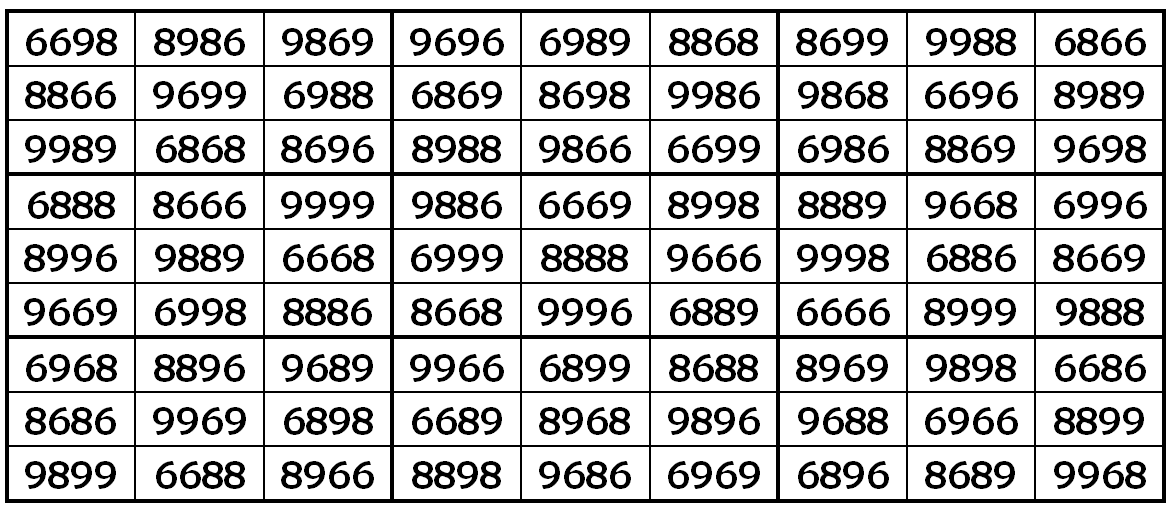
It is upside-down pandiagonal magic square of order 9 with 3-digits (6,8,9). The magic sum is given by S_9×9(6,8,9):=76659.

Example 29. The Digits (0,2,5)

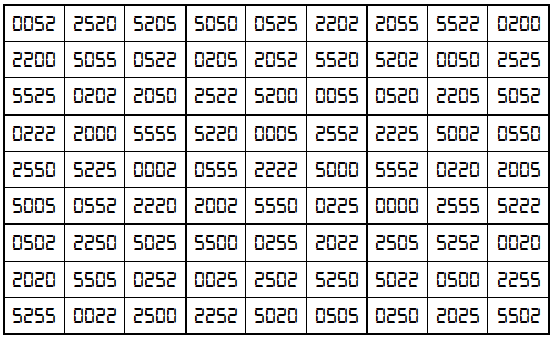
It is pandiagonal universal magic square of order 9 with 3-digits (0,2,5). The magic sum is given by S_9×9(0,2,5):=23331.

b) 7-Digits Cell Entries

Example 30. The Digits (6,8,9)

It is upside-down pandiagonal magic square of order 9 with 3-digits (6,8,9). The magic sum is given by S_9×9(6,8,9):=76666659.

Example 31. The Digits (2,5,8)

It is pandiagonal universal magic square of order 9 with 3-digits (0,2,5). The magic sum is given by S_9×9(2,5,8):=49999995.

c) 8-Digits Cell Entries

Example 32. The Digits (1,8): Pandiagonal

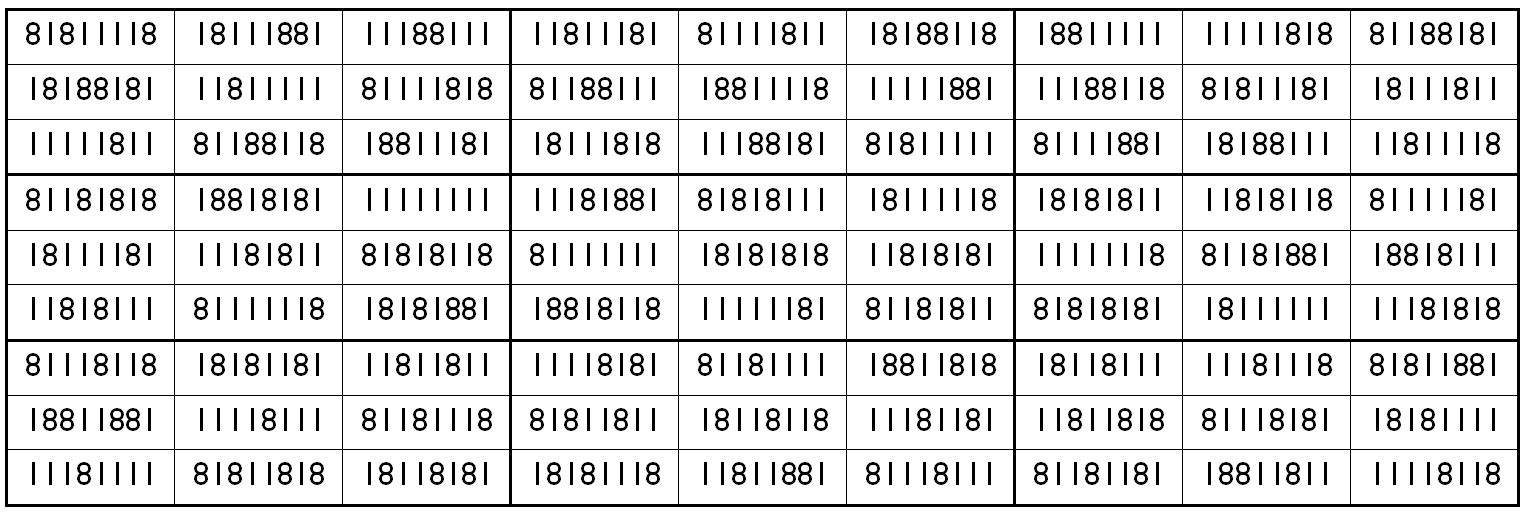
It is universal pandiagonal square with magic sum: S_9×9(1,8):=333333330. Moreover, the bocks of order 3 are semi-magic square with equal semi-magic sum, i.e., S_3×3 (1,8):=111111110.

Example 33. The Digits (2,5): Pandiagonal

It is universal pandiagonal magic square with magic sums: S_9×9(2,5):=299999997 and S_9×9(2,5):=399999996. The magic sum S_9×9(2,5):=399999996 refers to mirror looking version. The blocks of order 3 are semi-magic squares with equal semi-magic sums: S_3×3(2,5):=99999999 and S_3×3(2,5):=133333332.

Example 34. The Digits (6,9): Pandiagonal

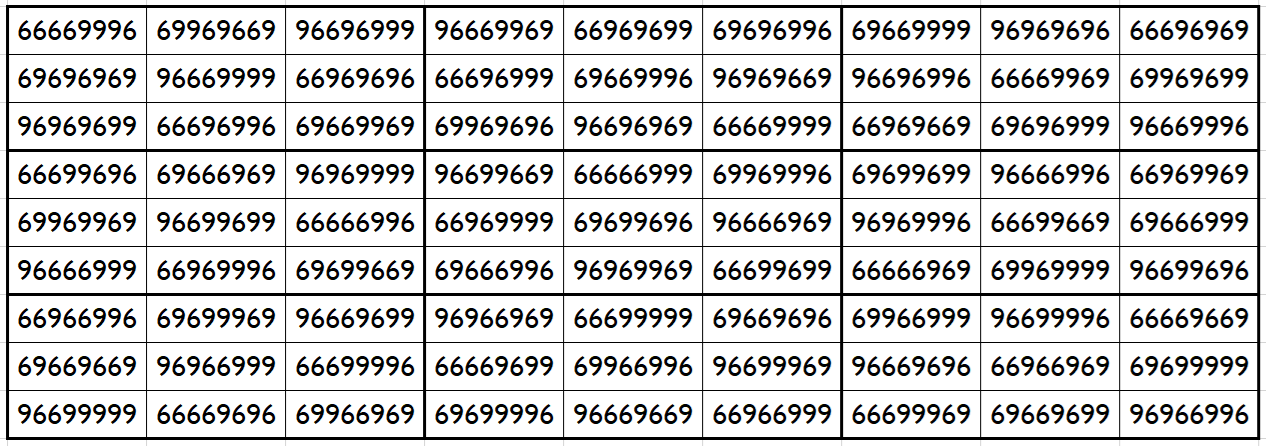
It is universal pandiagonal square with magic sum: S_9×9(6,9):=700009992. Moreover, the bocks of order 3 are semi-magic squares with equal semi-magic sums, i.e., S_3×3 (6,9):=233336664.

Magic Squares of Order 10

a) 4-Digits Cell Entries

Example 35. The Digits (1,6,9)

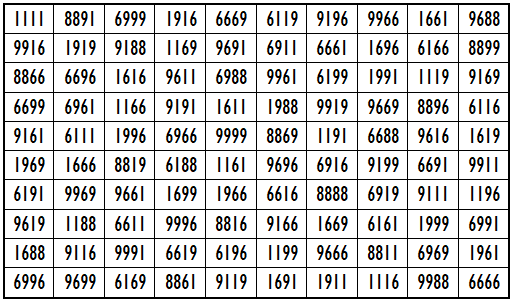
It is upside-down magic square of order 10 with 4-digits (1,6,8,9). The magic sum is given by S_10×10(1,6,8,9):=62216.

Example 36. The Digits (0,2,5,8)

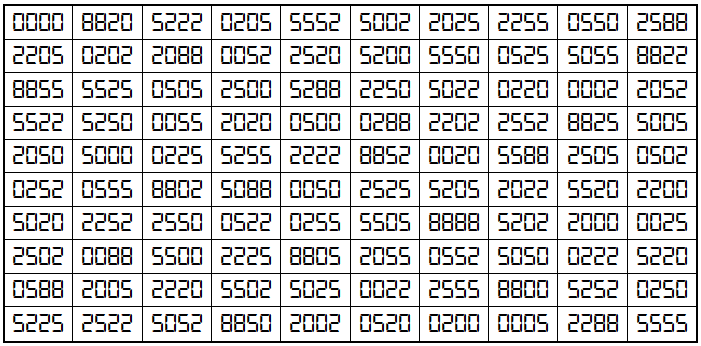
It is universal magic square of order 10 with 4-digits (0,2,5,8). The magic sum is given by S_10×10(0,2,5,8):=32219.

b) 6-Digits Cell Entries

Example 37. The Digits (1,6,9)

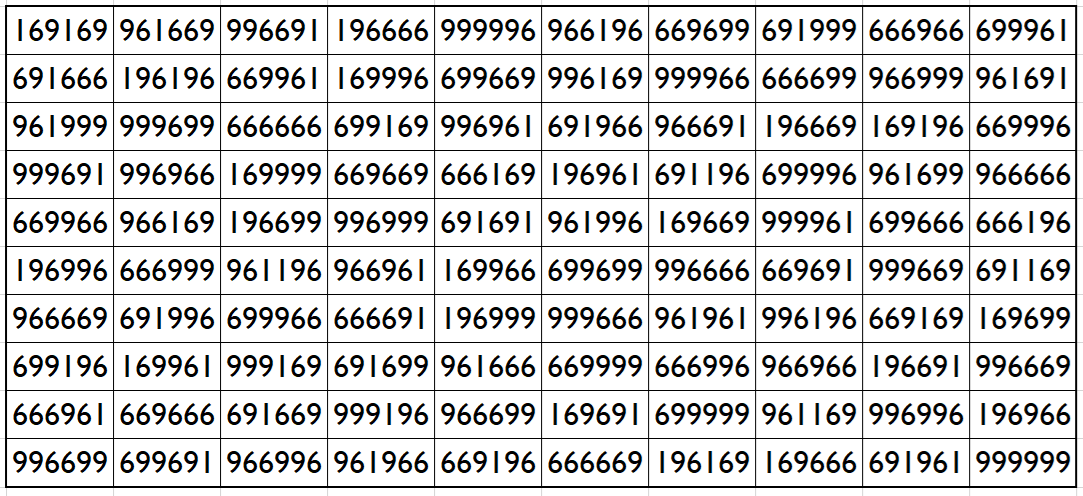
It is upside-down magic square of order 10 with 3-digits (1,6,9). The magic sum is given by S_10×10(1,6,9):=7019012.

Example 38. The Digits (2,5,8)

It is universal magic square of order 10 with 3-digits (2,5,8). The magic sum is given by S_10×10(1,6,9):=5708703.

c) 8-Digits Cell Entries

Example 39. The Digits (1,8)

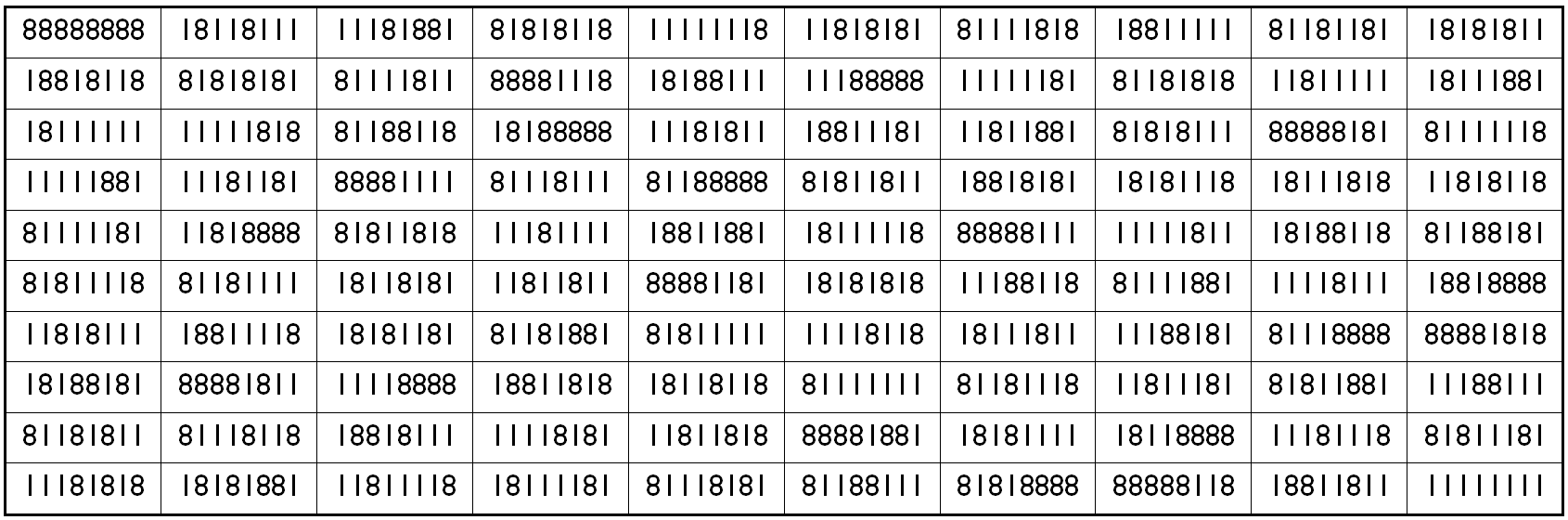
It is universal magic square of order 10 with magic sums S_10×10(1,8):=422222218.

Example 40. The Digits (2,5)

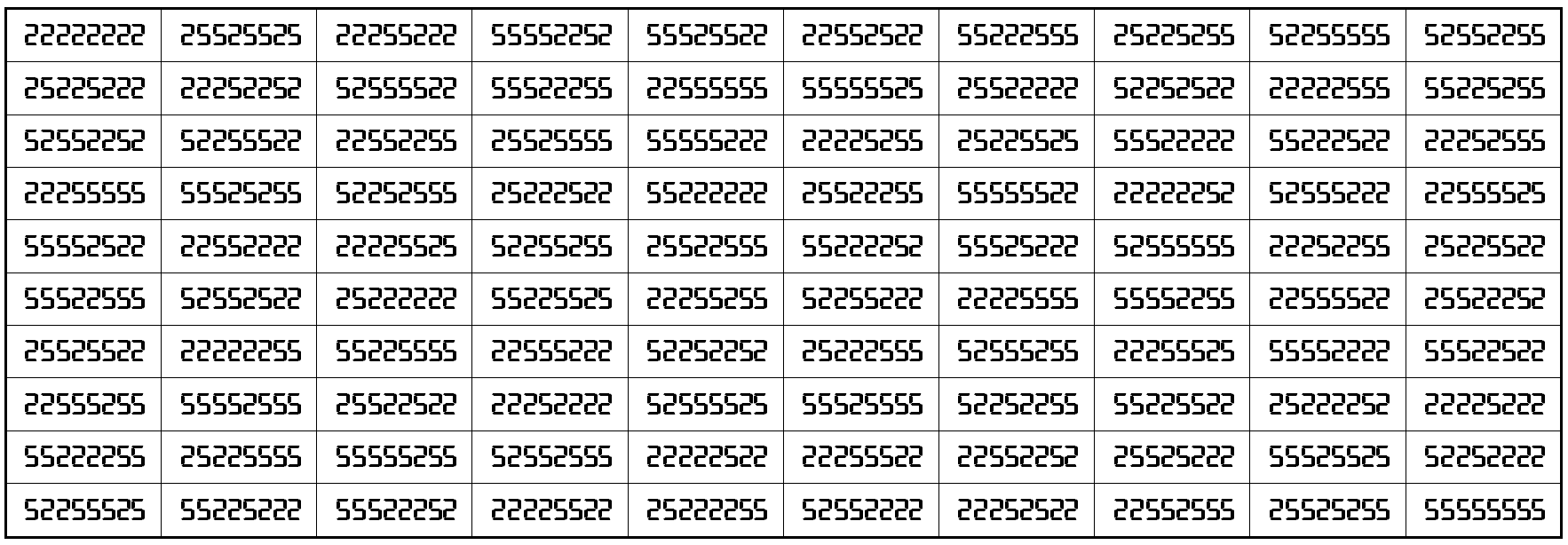
It is universal magic square of order 10 with magic sums S_10×10(2,5):=388888885.

Example 41. The Digits (6,9)

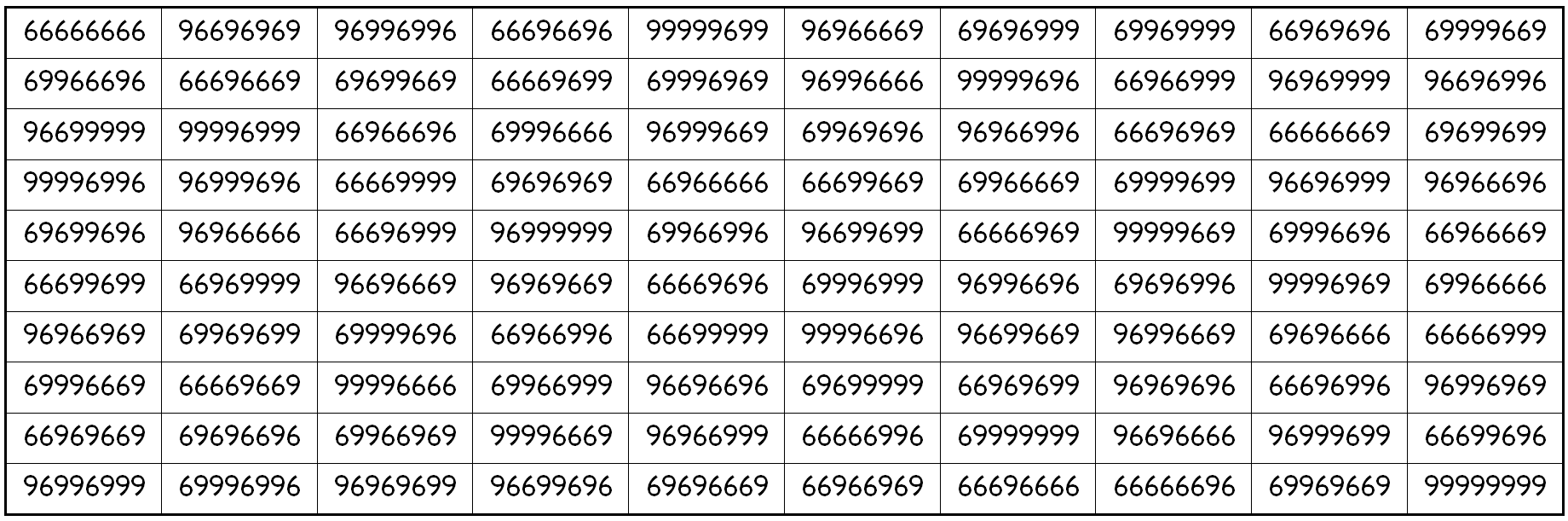
It is universal magic square of order 10 with magic sums S_10×10(6,9):=800660058.

References

1. Inder J. Taneja, Universal and Upside-Down Magic Squares of Orders 3 to 6, Zenodo, November 05, 2024, pp. 1-61, https://doi.org/10.5281/zenodo.14041149
   • Site link: Universal and Upside-Down Magic Squares of Order 3 to 6 (new site)
   • Site link: Universal and Upside-Down Magic Squares of Order 3 to 6 (old site)
2. Inder J. Taneja, Universal and Upside-Down Magic Squares of Orders 7 to 10, Zenodo, November 05, 2024, pp. 1-120, https://doi.org/10.5281/zenodo.14041164
   • Site link: Universal and Upside-Down Magic Squares of Orders 7 to 10 (new site)
   • Site link: Universal and Upside-Down Magic Squares of Orders 7 to 10 (old site)
3. Inder J. Taneja, Universal and Upside-Down Magic Squares of Orders 11 to 15, Zenodo, November 05, 2024, pp. 1-141, https://doi.org/10.5281/zenodo.14041168
   • Site link: Universal and Upside-Down Magic Squares of Orders 11 to 15 (new site)
   • Site link: Universal and Upside-Down Magic Squares of Orders 11 to 15 (old site)
4. Inder J. Taneja, Universal and Upside-Down Magic Squares of Order 16, Zenodo, October 16, 2024, pp. 1-28, https://doi.org/10.5281/zenodo.13942620
   • Site link: Universal and Upside-Down Magic and Bimagic Squares of Order 16 (new site)
   • Site link: Universal and Upside-Down Magic and Bimagic Squares of Order 16 (old site)
5. Inder J. Taneja, Universal and Upside-Down Magic Squares of Order 20, Zenodo, October 20, 2024, pp. 1-56, https://doi.org/10.5281/zenodo.13958700.
   • Site link: Universal and Upside-Down Magic Squares of Order 20 (new site)
   • Site link: Universal and Upside-Down Magic Squares of Order 20 (old site)
6. Inder J. Taneja, Universal and Upside-Down Magic Squares of Order 21, Zenodo, October 23, 2024, pp. 1-49, https://doi.org/10.5281/zenodo.13982859
   • Site link: Universal and Upside-Down Magic Squares of Order 21 (new site)
   • Site link: Universal and Upside-Down Magic Squares of Order 21 (old site)
7. Inder J. Taneja, Universal and Upside-Down Magic Squares of Order 24, Zenodo, October 29, 2024, pp. 1-82, https://doi.org/10.5281/zenodo.14004788
   • Site link: Universal and Upside-Down Magic Squares of Order 24 (new site).
   • Site link: Universal and Upside-Down Magic Squares of Order 24 (old site)
8. Inder J. Taneja, Universal and Upside-Down Magic and Bimagic Squares of Order 25, Zenodo, October 30, 2024, pp. 1-53, https://doi.org/10.5281/zenodo.14014851.
   • Site link: Universal and Upside-Down Magic and Bimagic Squares of Order 25 (new site)
   • Site link: Universal and Upside-Down Magic and Bimagic Squares of Order 25 (old site)