This work brings more concepts in magic squares. In past we studied a lot of upside-down and mirror looking magic squares. These are based some kind of digital/special fonts. To understand better let’s consider the following 10 digits from 0 to 9:

Upside-down (180 degrees rotation)
Let’s make 180 degrees rotation over the above 10 digits, we get

We observe that the numbers 0, 1, 2, 5, 6, 8 and 9 are still there. The difference is that 6 becomes 9.
Mirror Looking (Horizontal Flip)
Let’s see how these numbers can seen in mirror:

We observe that the numbers 0, 1, 2, 5 and 8 are still there. In this case the numbers 2 and 5 interchanges, i.e., 2 becomes 5 and 5 as 2.
In general there are two kinds of flips, i.e., horizontal flip and vertical filp. See the image below:

Source: https://www.mathsisfun.com/definitions/vertical-flip.html
Water Reflection (Vertical Flip)
Making vertical flip over the digits 0 to 9, we get

We observe the numbers 0, 1, 2, 3, 5 and 8 remains the same. The numebrs 0, 1, 2, 5 and 8 are already in mirror looking except the number. That’s why we call these numbers as universal numbers. Here also 2 becomes 5 and 5 as 2. Thus using vertical flip, we get an extra number as 3. Let’s call the operation as water reflection. This means that the numbers 0, 1, 2, 3, 5 and 8 are water reflexive.
The aim this work is write magic squares based on the numbers 0, 1, 2, 3, 5 and 8, where 3 is always there, i.e., making combinations of 3 with the numbers 0, 1, 2, 5 and 8. Below is an index of examples of this work
- Magic Squares of Order 7
- a) 4-Digits Cell Entries:
- Example 1. Magic Square with 3-Digits (0,1,3)
- Example 2. Magic Square with 3-Digits (0,3,8)
- Example 3. Magic Squares with 3-Digits (1,3,8)
- b) 6-Digits Cell Entries:
- Example 4. Magic Square with 2-Digits (3,8)
- Example 5. Magic Square with 2-Digits (1,3)
- Example 6. Magic Square with 2-Digits (0,3)
- a) 4-Digits Cell Entries:
- Magic Squares of Order 8
- a) 4-Digits Cell Entries:
- Example 7. Magic Square with 3-Digits (2,3,5)
- Example 8. Magic Square with 2-Digits (1,3,8)
- Example 9. Magic Square with 3-Digits (0,3,8)
- Example 10. Magic Square with 3-Digits (0,1,3)
- b) 6-Digits Cell Entries:
- Example 11. The Digits (3,8)
- Example 12. The Digits (1,3)
- Example 13. The Digits (0,3)
- a) 4-Digits Cell Entries:
- Magic Squares of Order 9
- a) 4-Digits Cell Entries
- Example 14. The Digits (2,3,5)
- Example 15. The Digits (1,3,8)
- Example 16. The Digits (0,3,8)
- Example 17. The Digits (0,1,3)
- b) 8-Digits Cell Entries
- Example 18. The Digits (3,8)
- Example 19. The Digits (1,3)
- Example 20. The Digits (0,3)
- a) 4-Digits Cell Entries
- Magic Squares of Order 9
- a) 4-Digits Cell Entries
- Example 21. The Digits (2,3,5)
- Example 22. The Digits (1,3,8)
- Example 23. The Digits (0,3,8)
- Example 24. The Digits (0,1,3)
- b) 8-Digits Cell Entries
- Example 25. The Digits (3,8)
- Example 26. The Digits (1,3)
- Example 27. The Digits (0,3)
- a) 4-Digits Cell Entries
- Magic Squares of Order 10
- a) 4-Digits Cell Entries:
- Example 28. The Digits (2,3,5,8)
- Example 29. The Digits (1,2,3,5)
- Example 30. The Digits (0,2,3,5)
- Example 31. The Digits (0,1,3,8)
- b) 6-Digits Cell Entries:
- Example 32. The Digits (2,3,5)
- Example 33. The Digits (1,3,8)
- Example 34. The Digits (0,3,8)
- Example 35. The Digits (0,1,3)
- c) 8-Digits Cell Entries:
- Example 36. The Digits (3,8)
- Example 37. The Digits (1,3)
- Example 38. The Digits (0,3)
- a) 4-Digits Cell Entries:
- References
Full work can be downloaded from the following link:
- Inder J. Taneja, Universal and Upside-Down Magic Squares of Orders 7 to 10, Zenodo, November 05, 2024, pp. 1-120, https://doi.org/10.5281/zenodo.14041164.
This work is for the orders 7 to 10. For the previous work on orders 3 to 6 and the further works refer the links below:
For the previous work on orders 3 to 13 refer the followig links:
- Inder J. Taneja, Water Reflection Magic Squares: Order 3 to 6.
- Inder J. Taneja, Water Reflection Magic Squares: Order 7 to 10.
- Inder J. Taneja, Water Reflection Magic Squares: Order 11 to 13.
- Inder J. Taneja, Water Reflection Magic Squares: Order 14 to 16
Magic Squares of Order 7
a) 4-Digits Cell Entries:
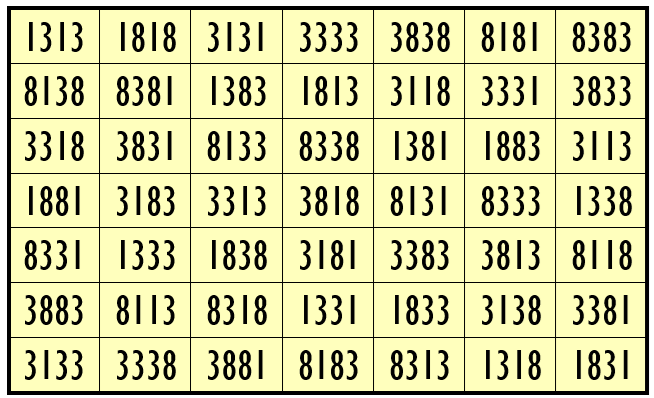
Example 1. Magic Square with 3-Digits (0, 1, 3)
Water Reflection Image
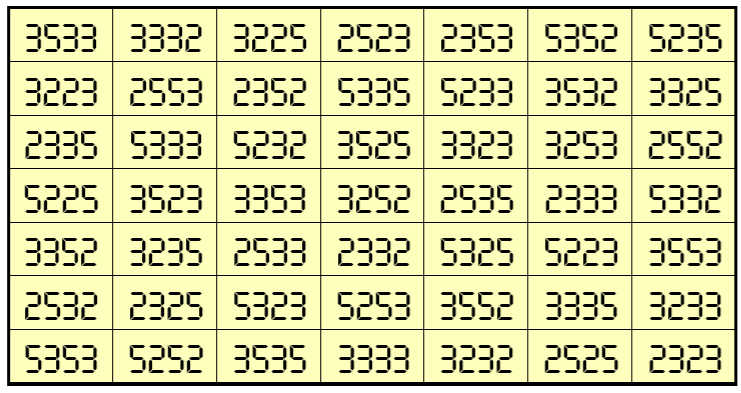
Example 2. Magic Square with 3-Digits (0, 3, 8)
Water Reflection Image

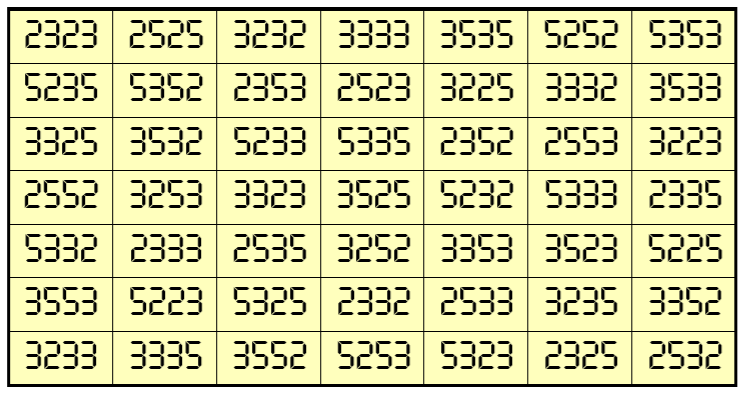
Example 3. Magic Squares with 3-Digits (1, 3, 8)
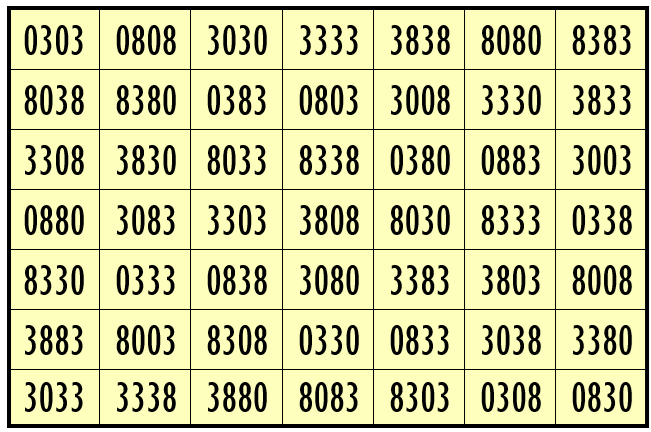
Water Reflection Image

Thus, we have four examples of water reflexive pandiagonal magic squares of order 7 having 4-digits cells entries with three number combinations (2,3,5), (1, 3, 8) and, (0,3,8).
b) 6-Digits Cell Entries:
Example 4. Magic Square with 2-Digits (3, 8)
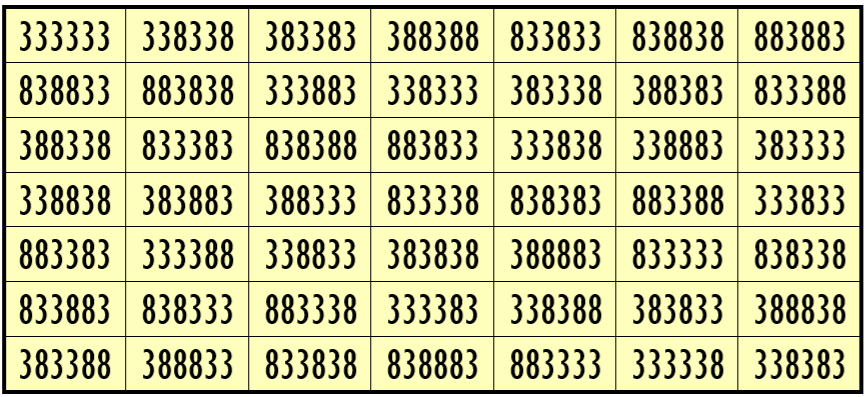
Water Reflection Image
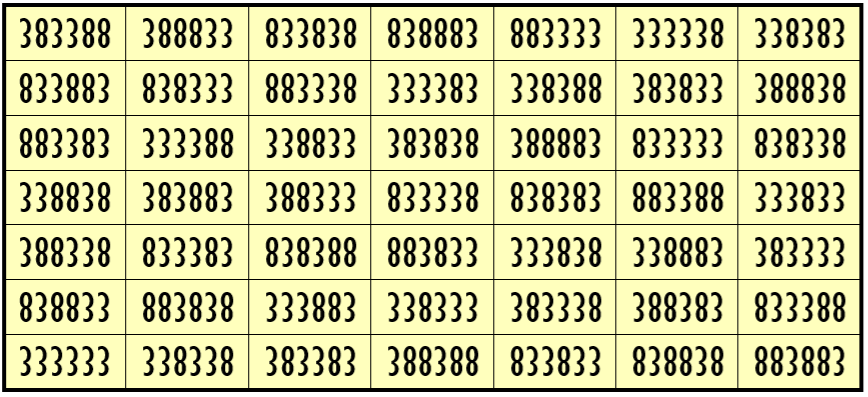
Example 5. Magic Square with 2-Digits (1, 3)

Water Reflection Image

Example 6. Magic Square with 2-Digits (0, 3)
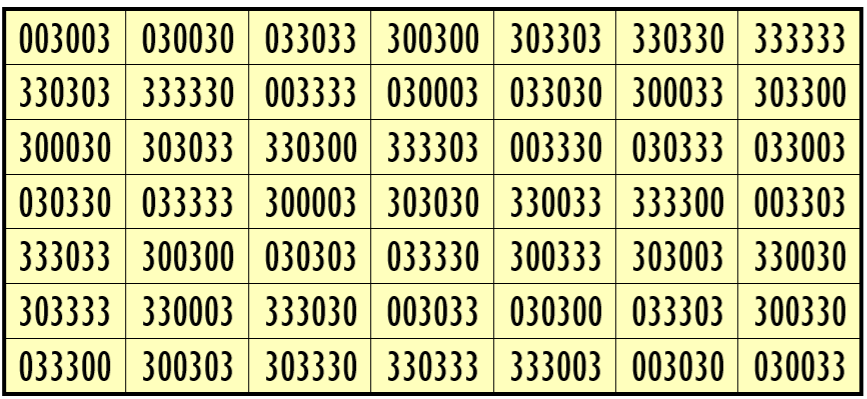
Water Reflection Image
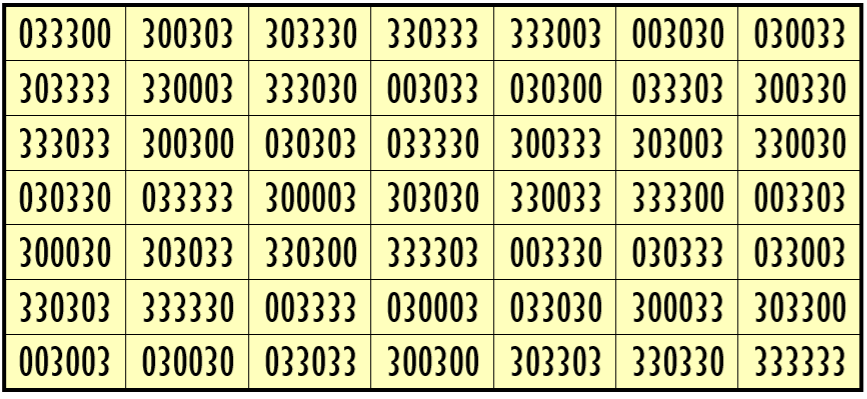
Thus, we have three examples of water reflexive pandiagonal magic squares of order 7 having 6-digits cells entries with two numbers combinations (3,8), (1,3) and, (0,3).
Magic Squares of Order 8
a) 4-Digits Cell Entries:
Example 7. Magic Square with 3-Digits (2, 3, 5)
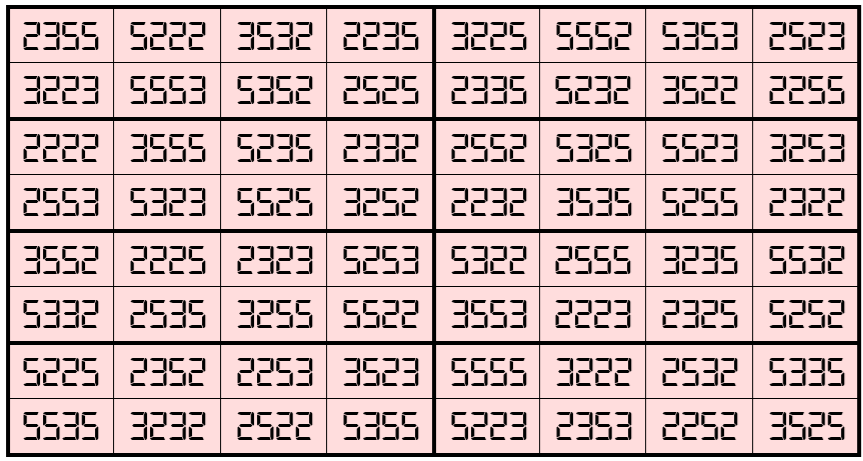
Water Reflection Image
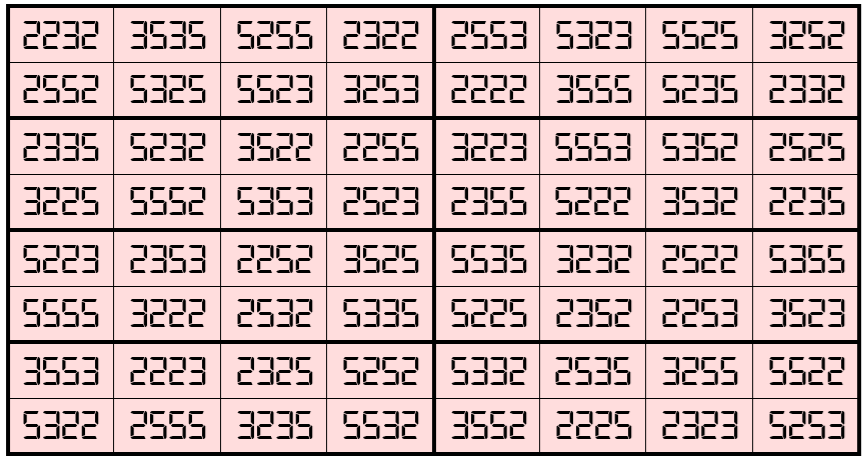
Example 8. Magic Square with 2-Digits (1,3,8)

Water Reflection Image
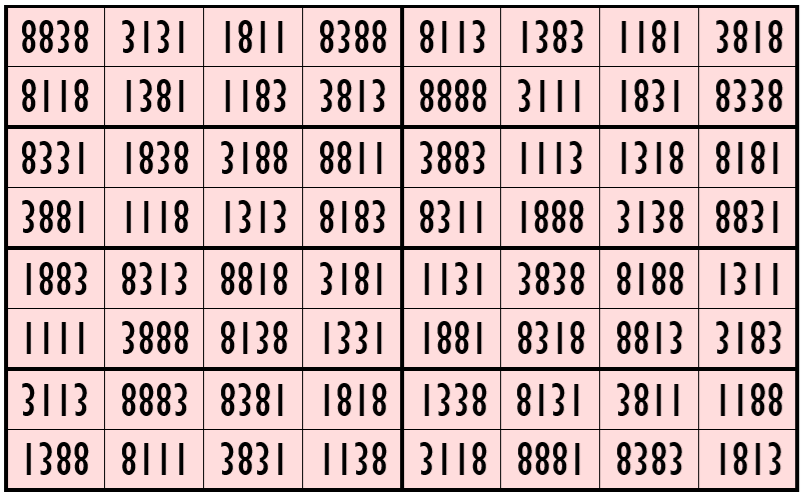
Example 9. Magic Square with 3-Digits (0, 3, 8)
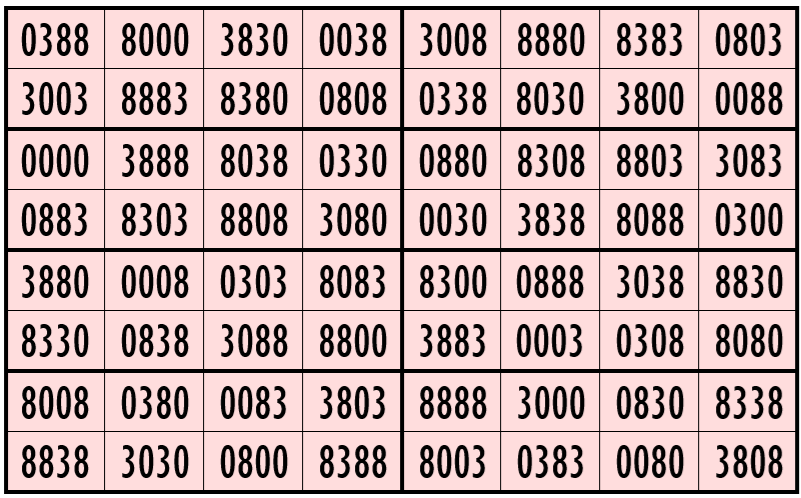
Water Reflection Image
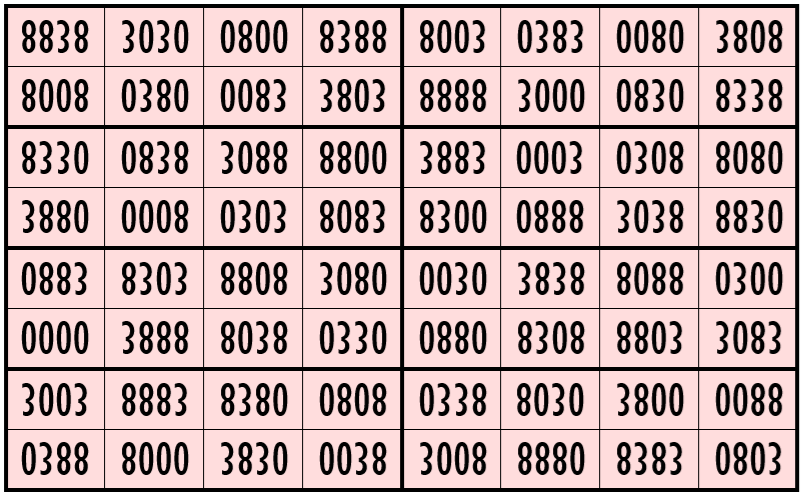
Example 10. Magic Square with 3-Digits (0, 1, 3)
Water Reflection Image
Thus, we have four examples of water reflexive magic squares of order 8 having 4-digits cells entries with three numbers combinations (2,3,5), (1,3,8), (0,3,8) and, (0,1,3). The blocks of order 2×4 are of equal sums as of magic square.
b) 6-Digits Cell Entries:
Example 11. The Digits (3, 8)
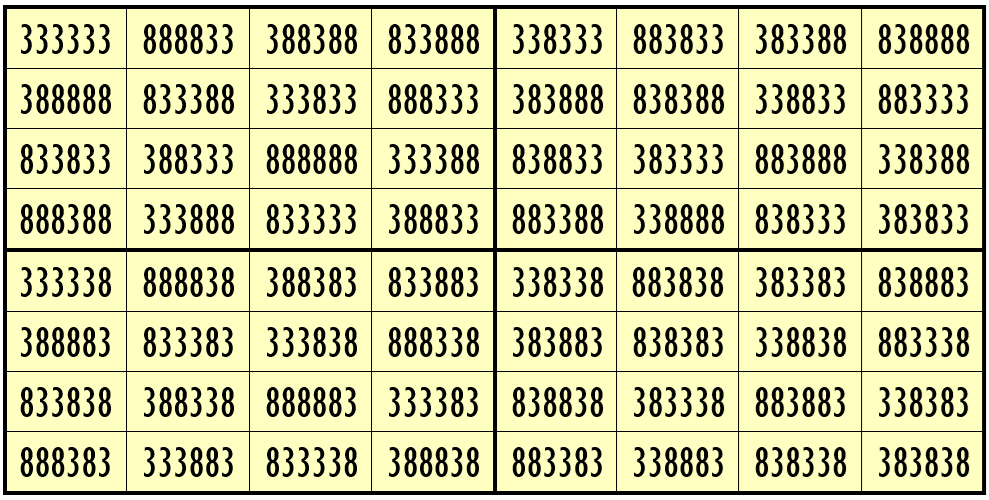
Water Reflection Image

Example 12. The Digits (1, 3)
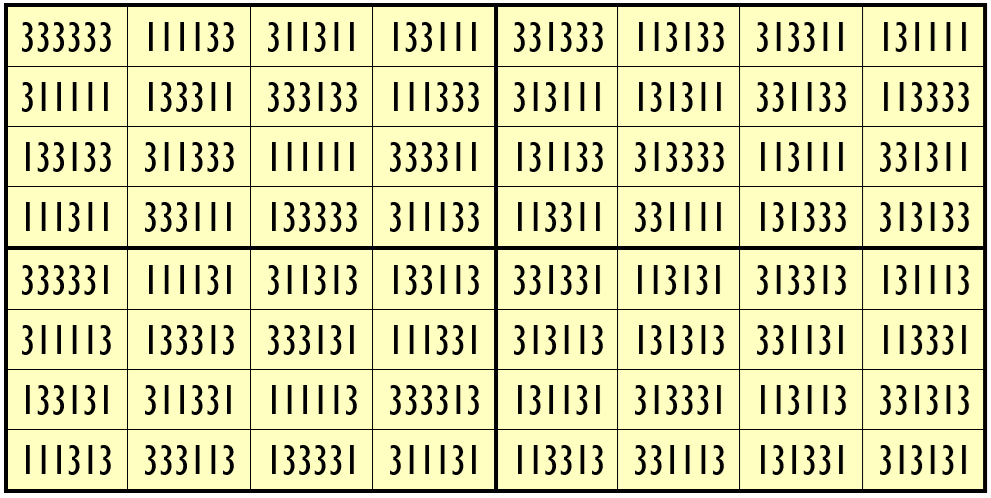
Water Reflection Image
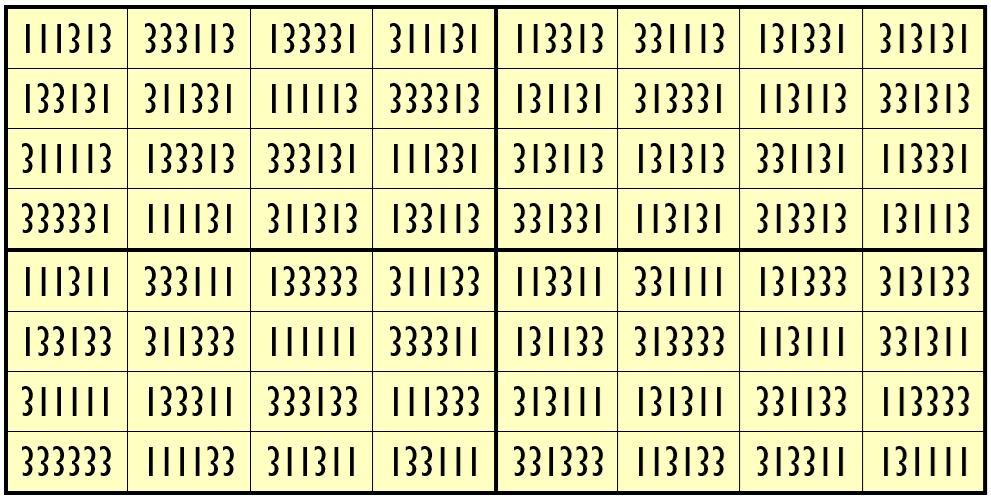
Example 13. The Digits (0, 3)
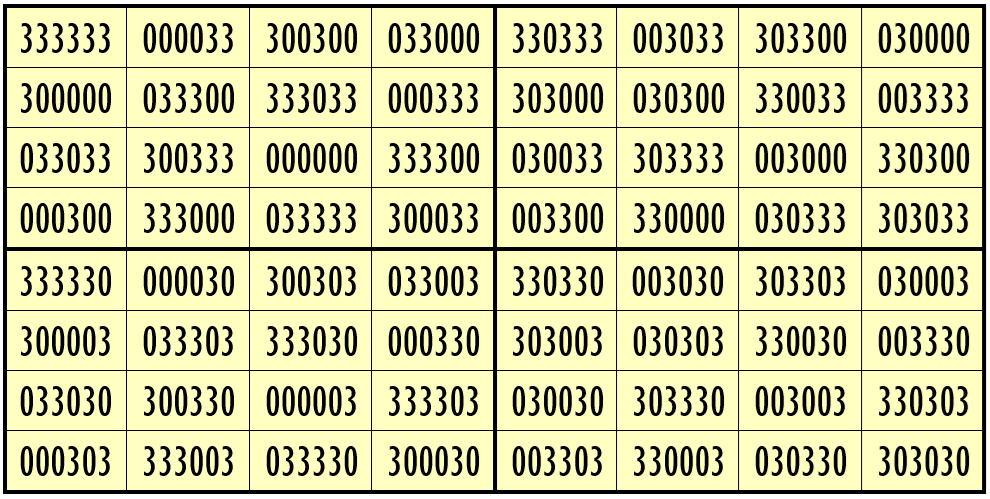
Water Reflection Image
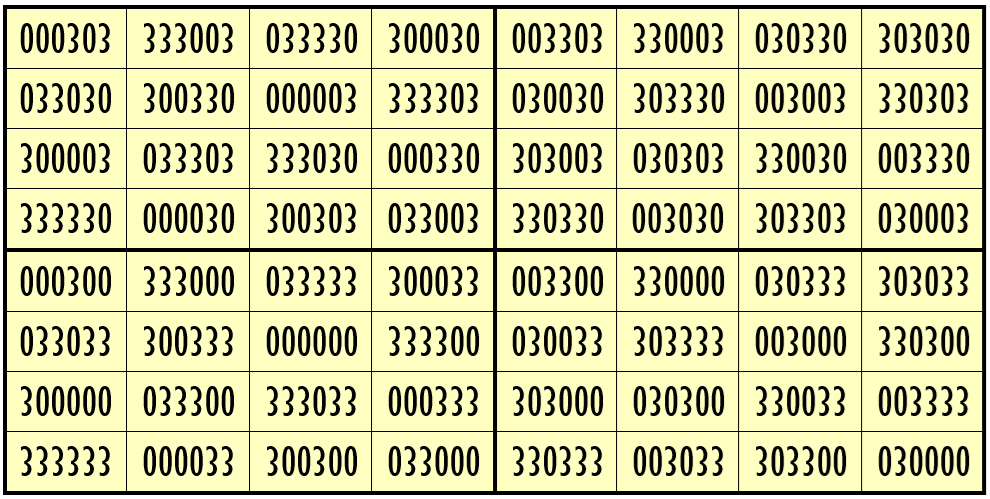
Thus, we have three examples of water reflexive pandiagonal magic squares of order 8 having 6-digits cells entries with two numbers combinations (3,8), (1,3) and (0,3). These magic squares are pandiagonal, where blocks of order 4 are equal sum pandiagonal magic squares.
Magic Squares of Order 9
a) 4-Digits Cell Entries
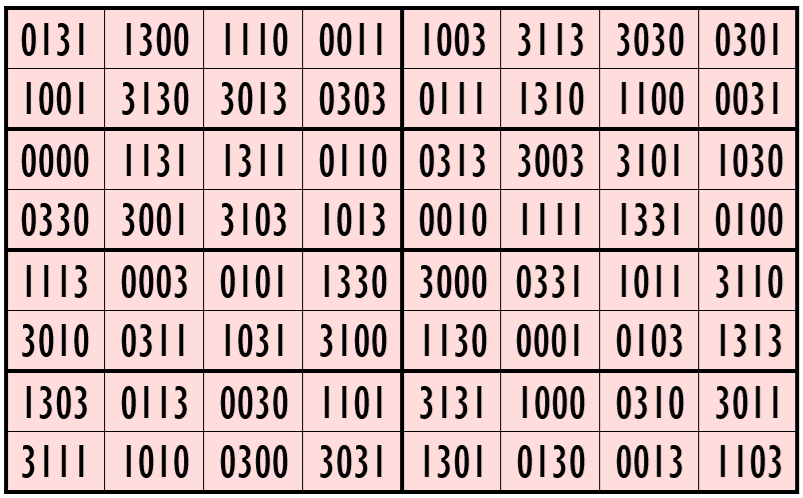
Example 14. The Digits (2, 3, 5)

Water Reflection Image

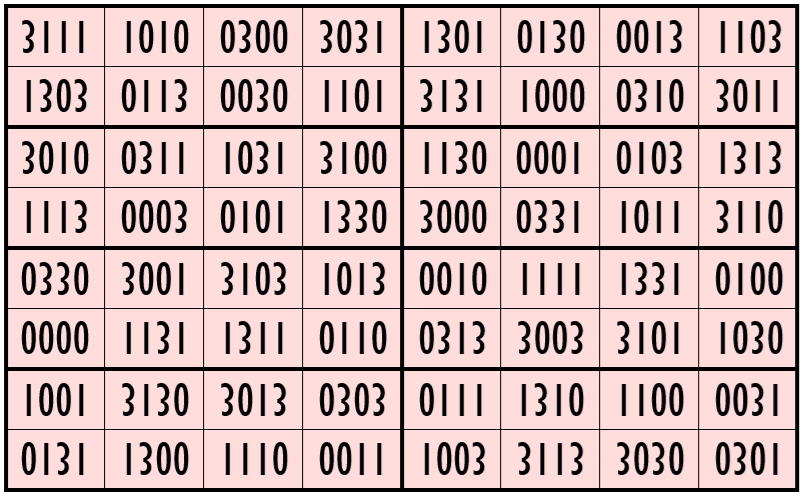
Example 15. The Digits (1, 3, 8)
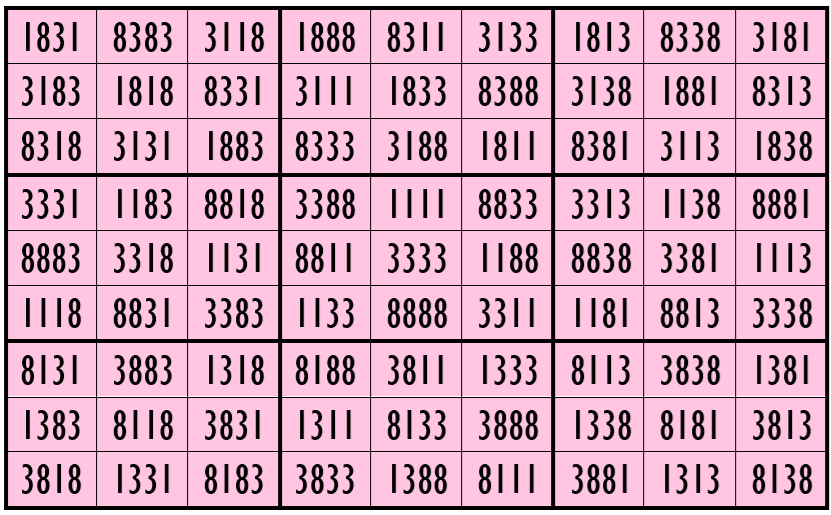
Water Reflection Image
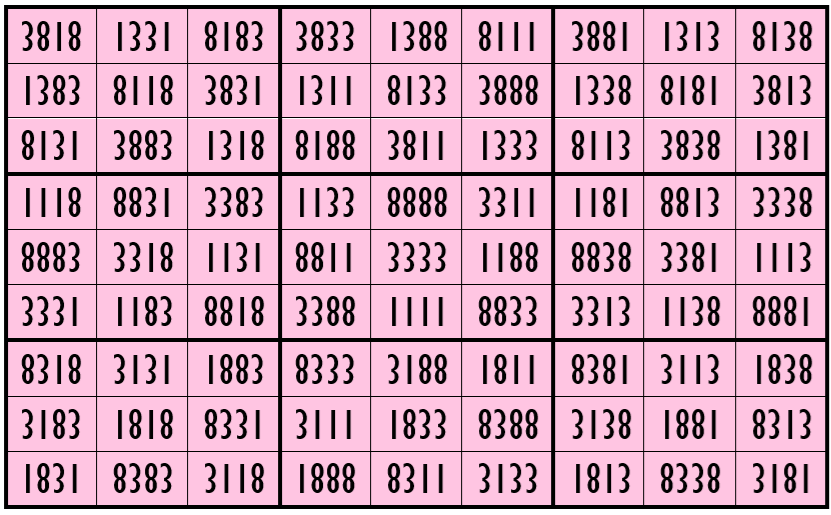
Example 16. The Digits (0, 3, 8)
Water Reflection Image
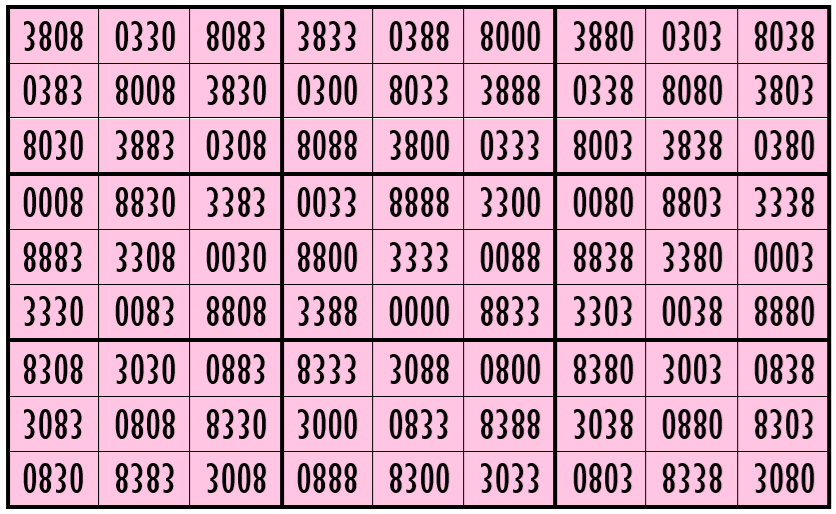
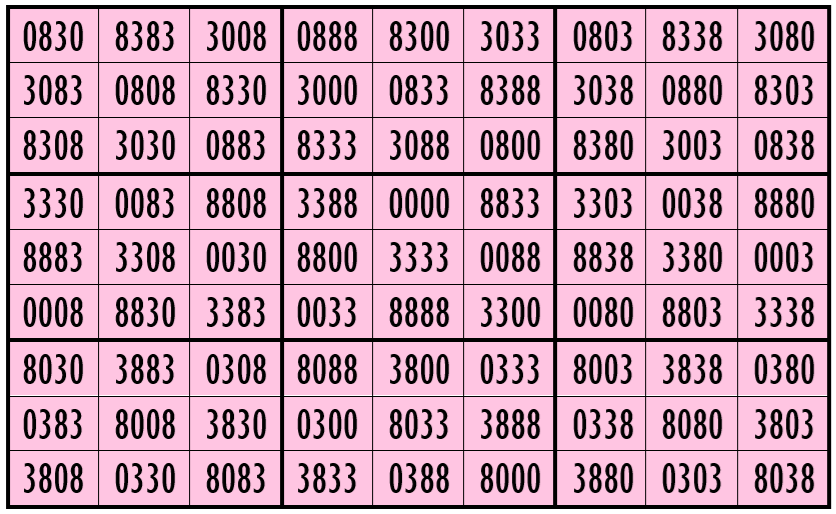
Example 17. The Digits (0, 1, 3)
Water Reflection Image
Thus, we have four examples of water reflexive pandiagonal magic squares of order 9 having 4-digits cells entries with 3 numbers combinations (2,3,5), (1,3,8) and (0,3,8) and (0,1,3).
b) 8-Digits Cell Entries
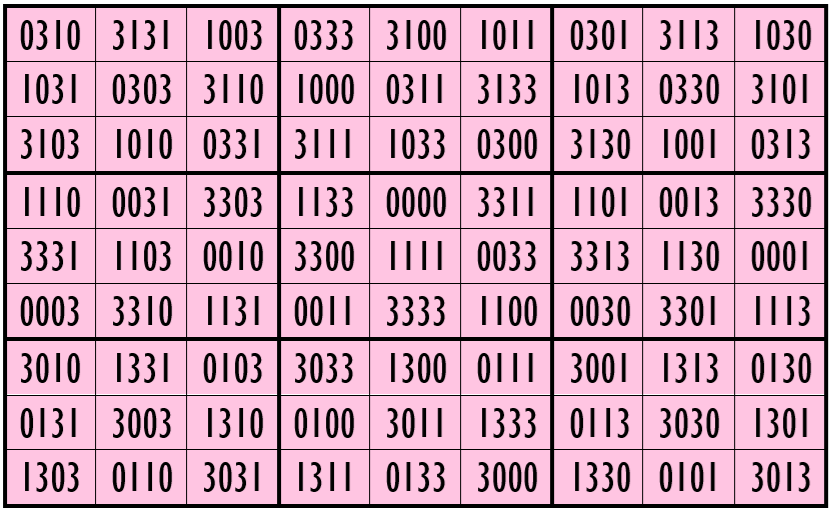
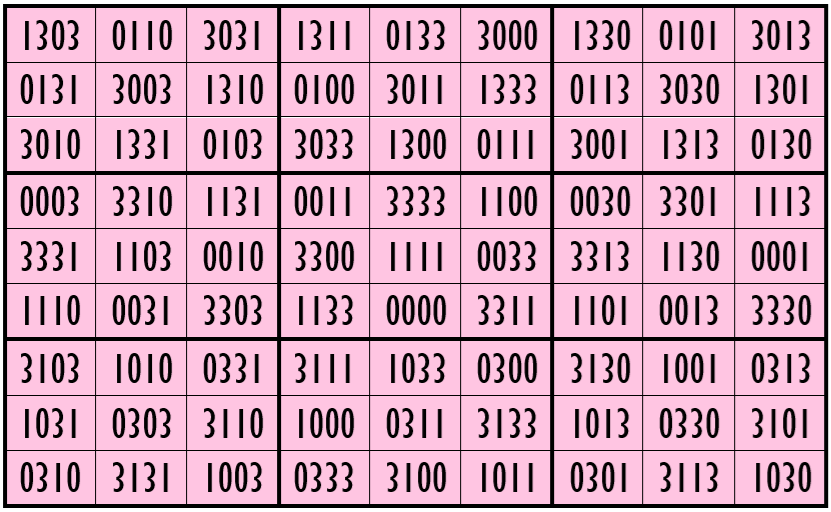
Example 18. The Digits (3, 8)
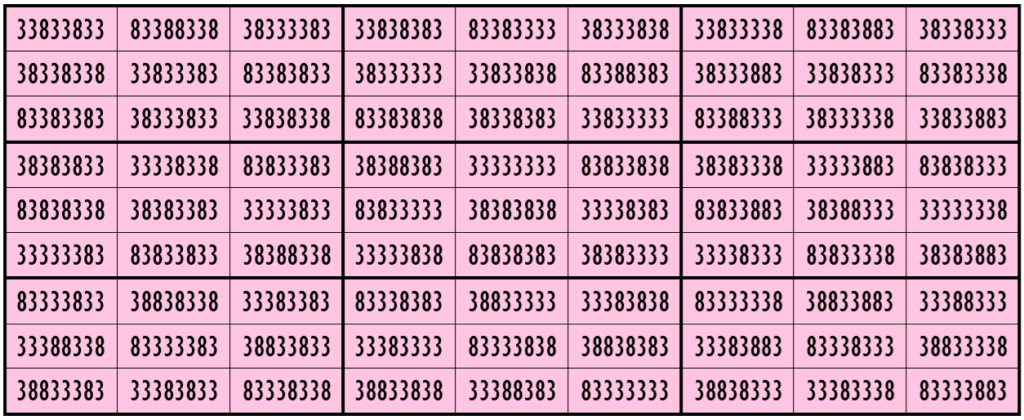
Water Reflection Image
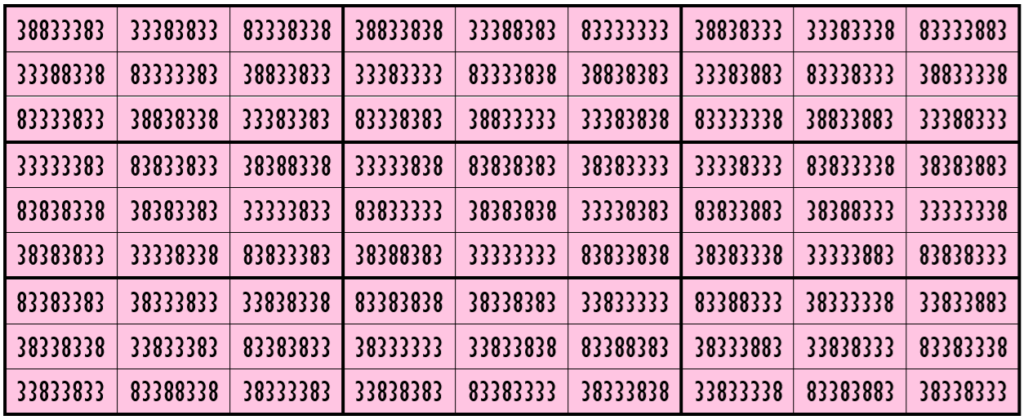
Example 19. The Digits (1, 3)
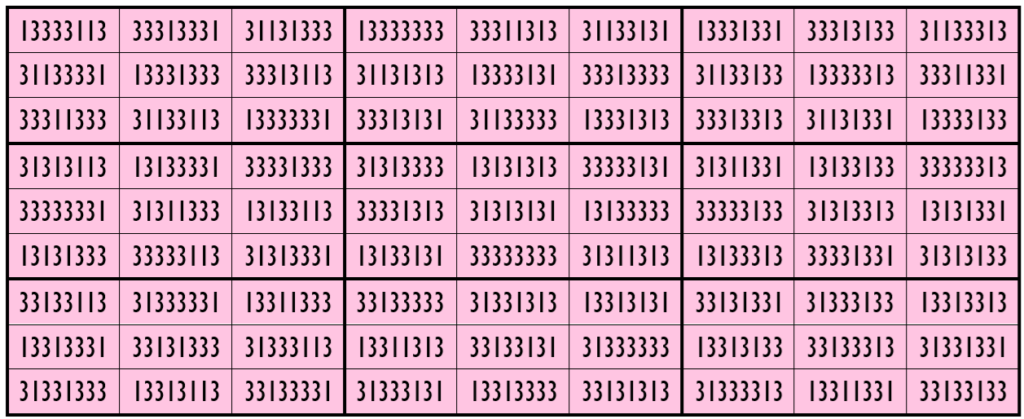
Water Reflection Image
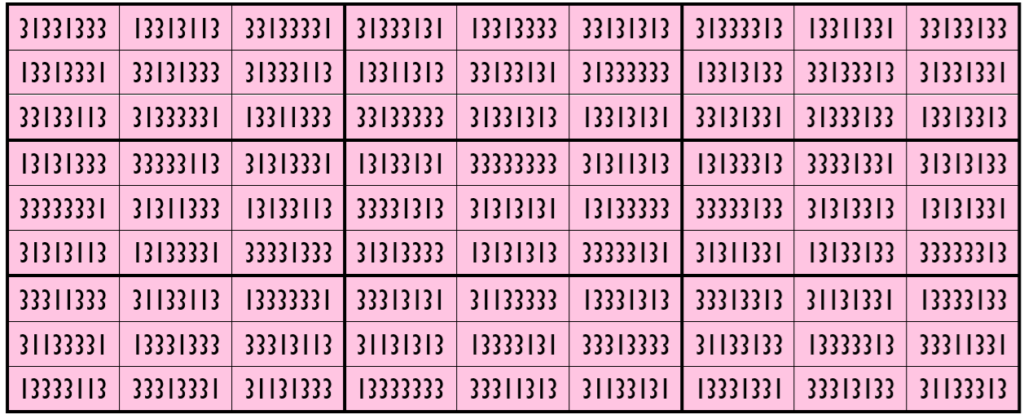
Example 20. The Digits (0, 3)
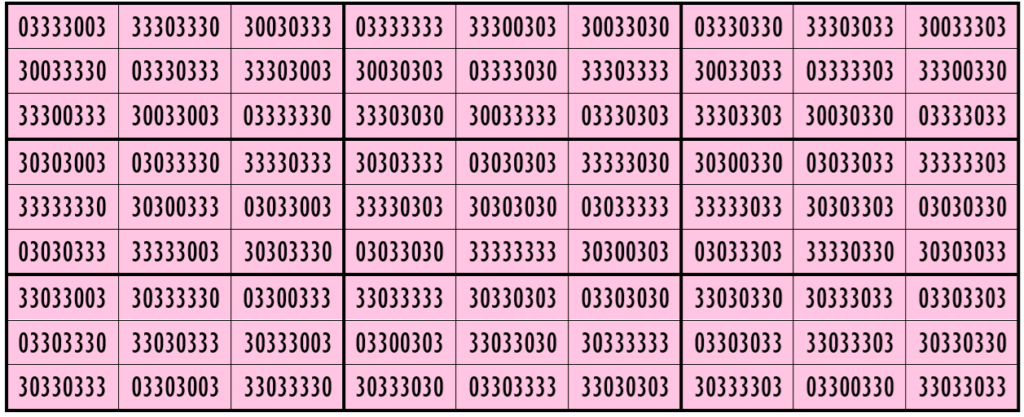
Water Reflection Image
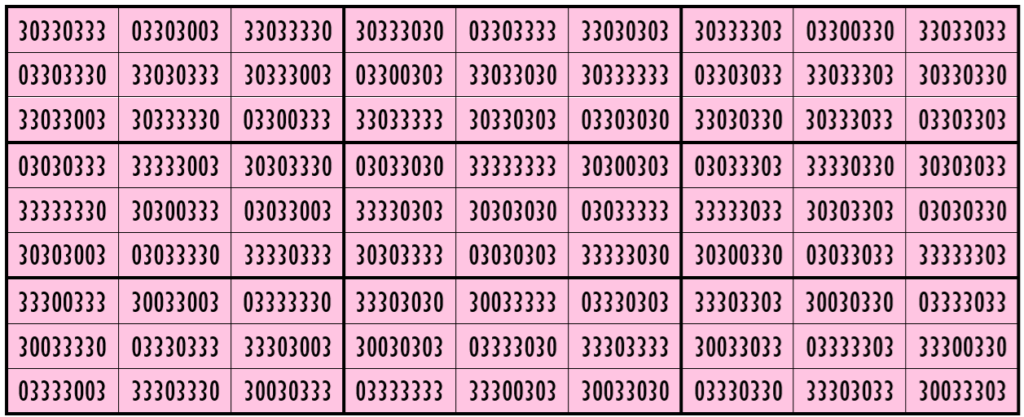
Thus, we have three examples of water reflexive pandiagonal magic squares of order 9 having 8-digits cells entries with 2 numbers combinations (3,8), (1,3) and (0,3).
Magic Squares of Order 9
a) 4-Digits Cell Entries
Example 21. The Digits (2, 3, 5)
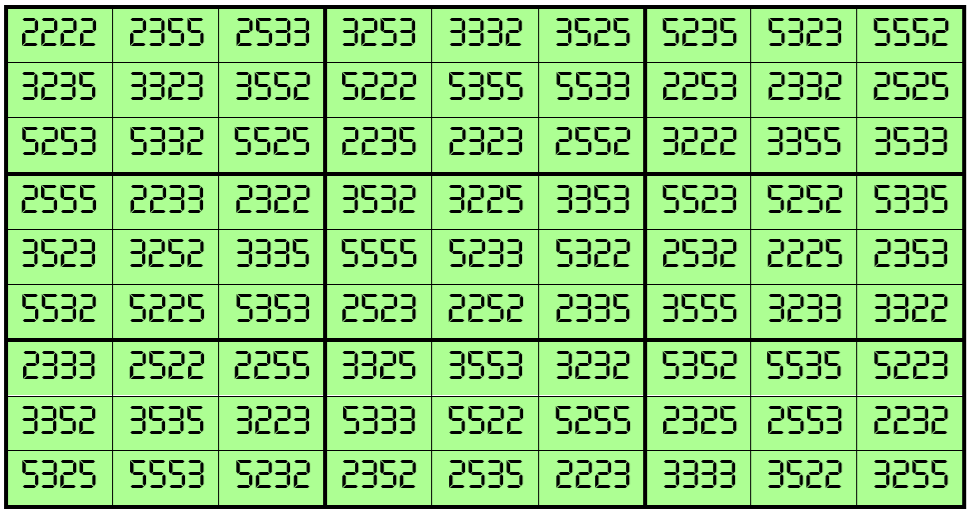
Water Reflection Image

Example 22. The Digits (1, 3, 8)
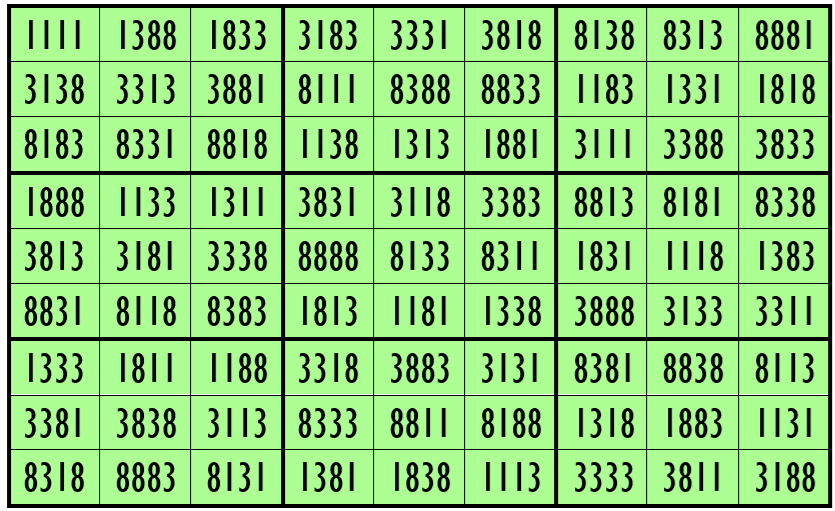
Water Reflection Image
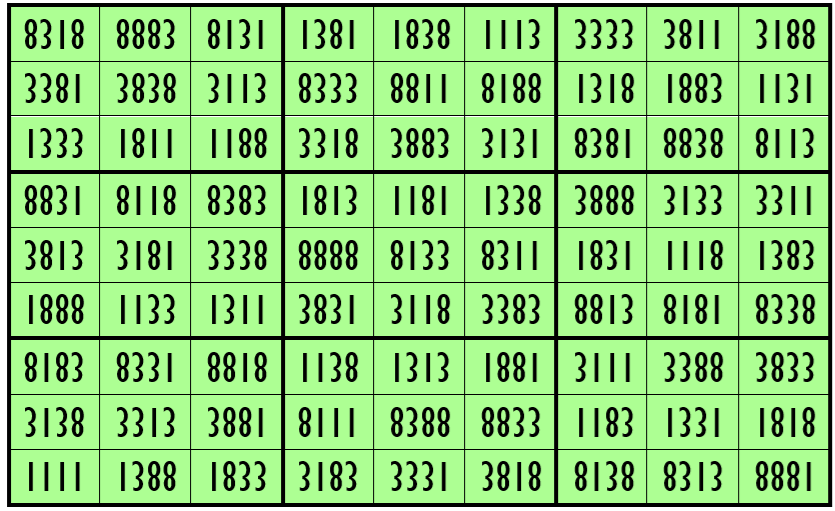
Example 23. The Digits (0, 3, 8)

Water Reflection Image

Example 24. The Digits (0, 1, 3)

Water Reflection Image

Thus, we have four examples of water reflexive bimagic squares of order 9 having 4-digits cells entries with 3 numbers combinations (2,3,5), (1,3,8) and (0,3,8) and (0,1,3). The magic and bimagic sums in each case be seen in an online complete work given above.
b) 8-Digits Cell Entries
Example 25. The Digits (3, 8)
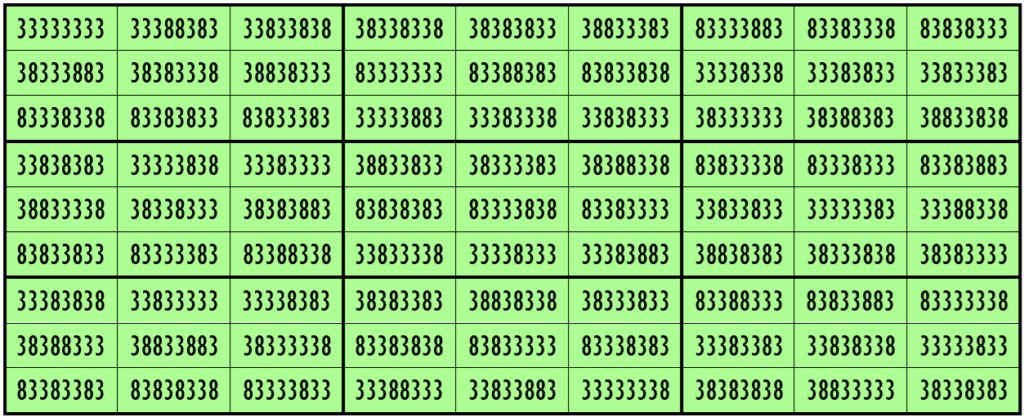
Water Reflection Image
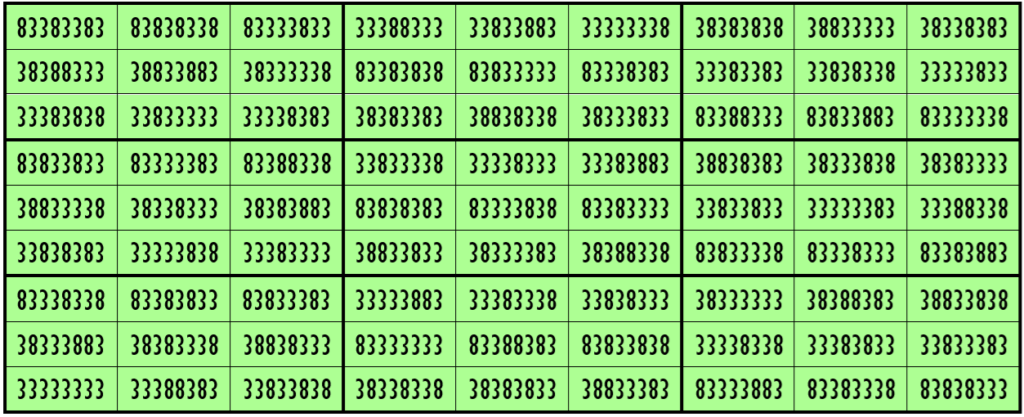
Example 26. The Digits (1, 3)

Water Reflection Image
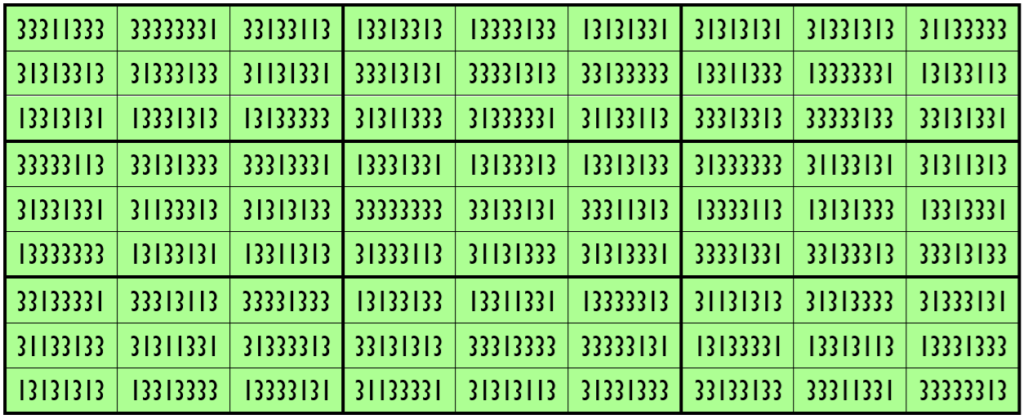
Example 27. The Digits (0, 3)
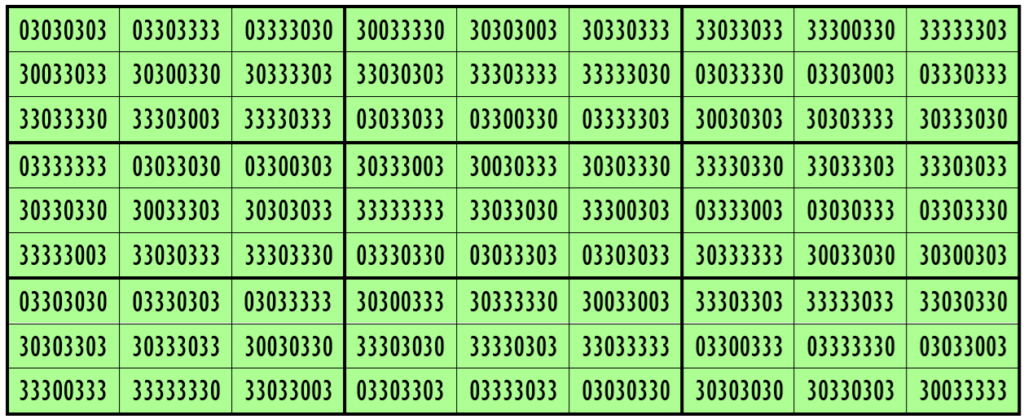
Water Reflection Image
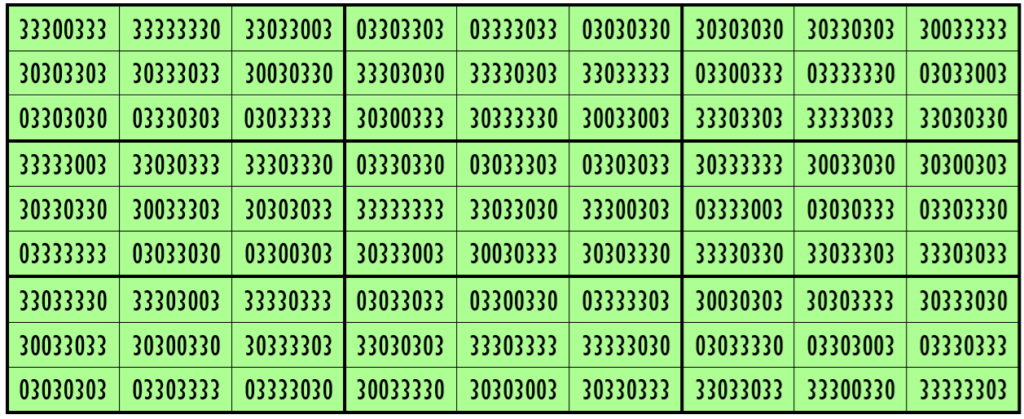
Thus, we have three examples of water reflexive bimagic squares of order 9 having 8-digits cells entries with 2 numbers combinations (3,8), (1,3) and (0,3). The magic and bimagic sums in each case be seen in an online complete work given above.
Magic Squares of Order 10
a) 4-Digits Cell Entries:
Example 28. The Digits (2, 3, 5, 8)
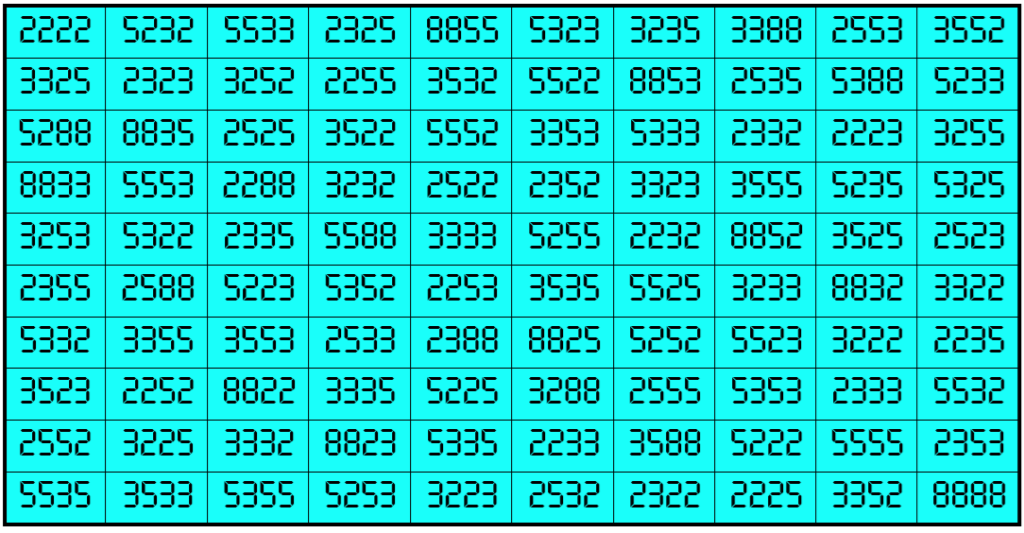
Water Reflection Image
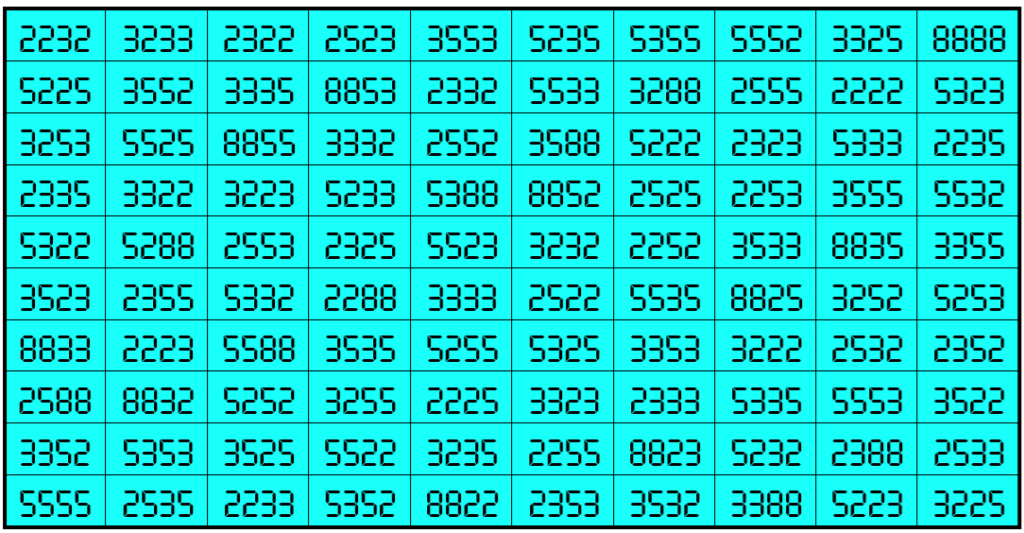
Example 29. The Digits (1, 2, 3, 5)
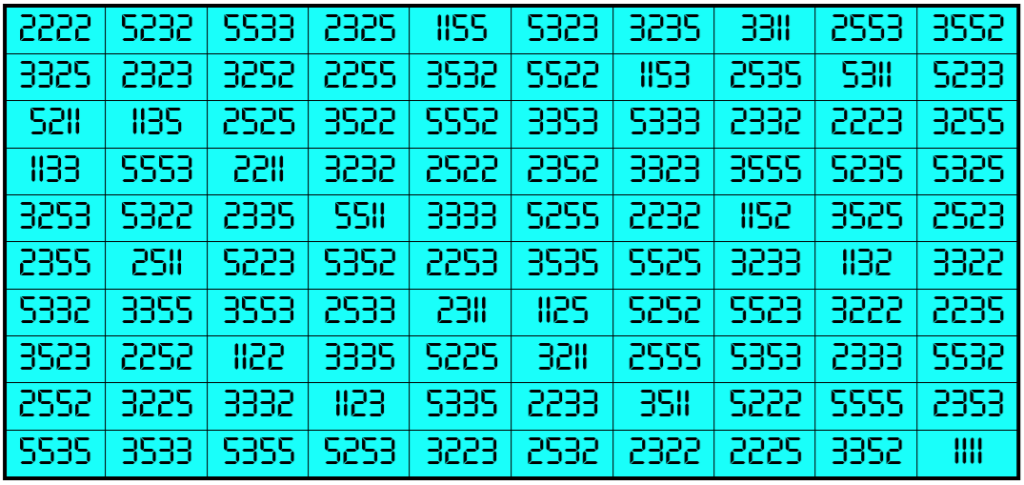
Water Reflection Image
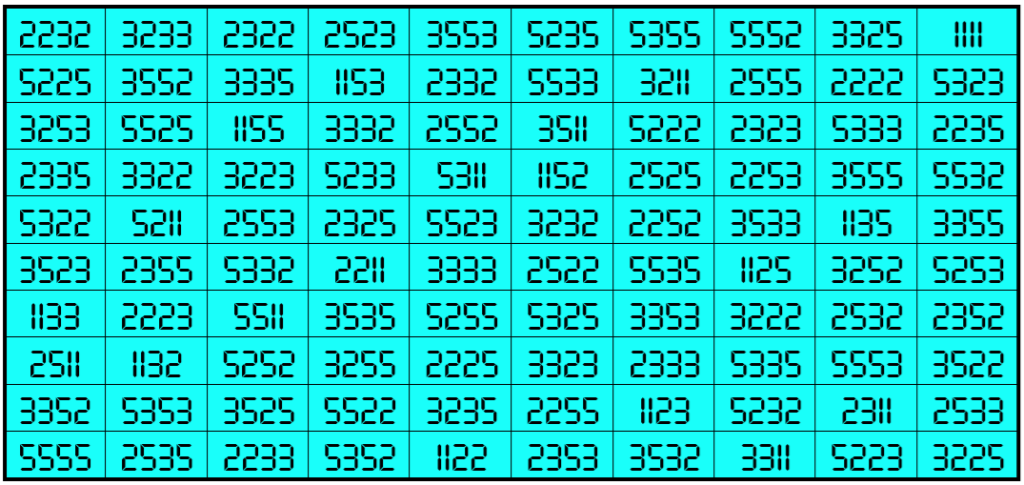
Example 30. The Digits (0, 2, 3, 5)
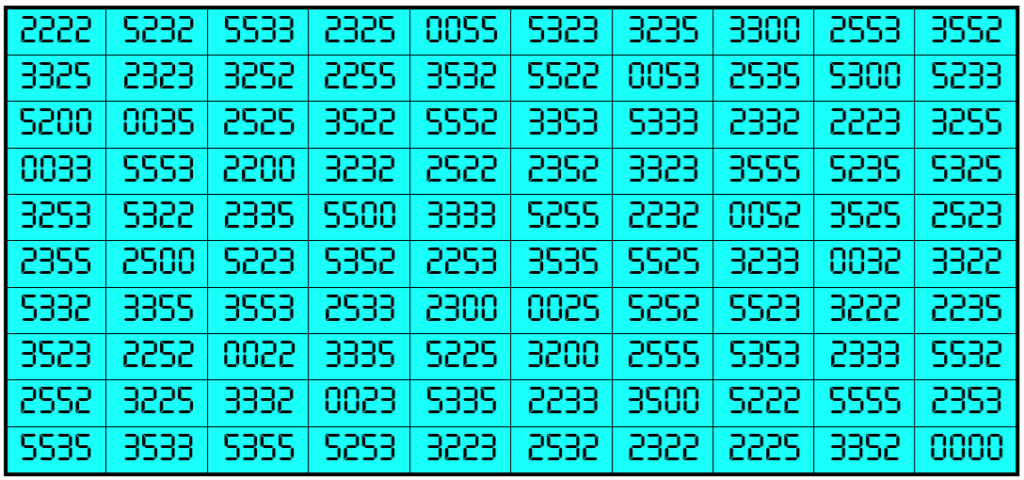
Water Reflection Image
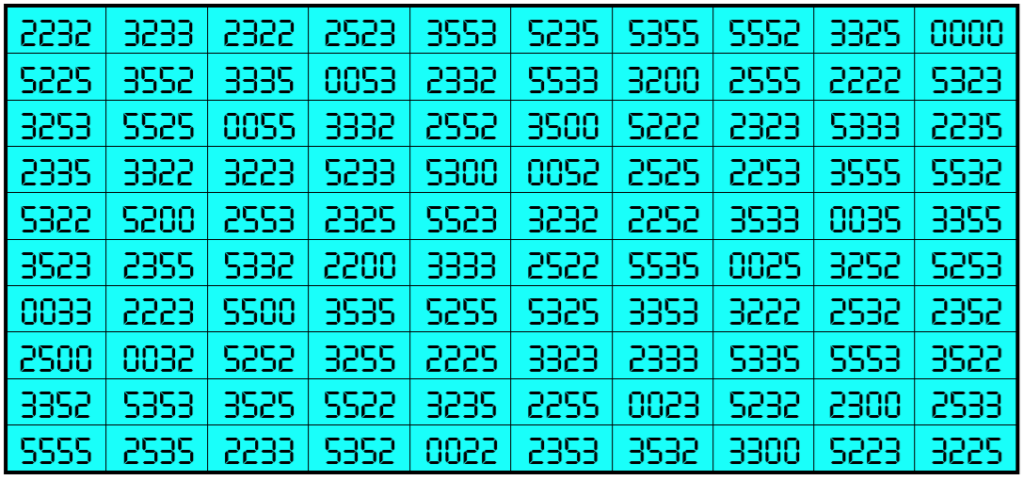
Example 31. The Digits (0, 1, 3, 8)
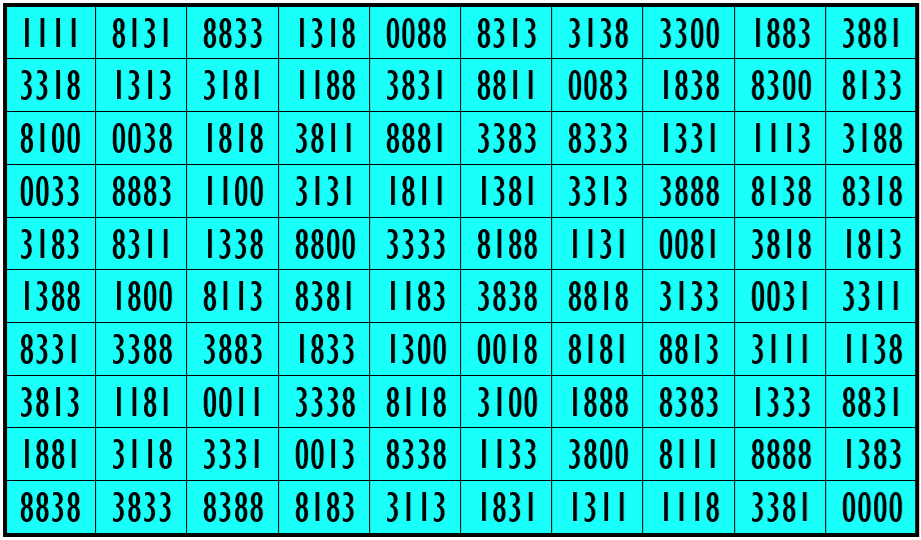
Water Reflection Image
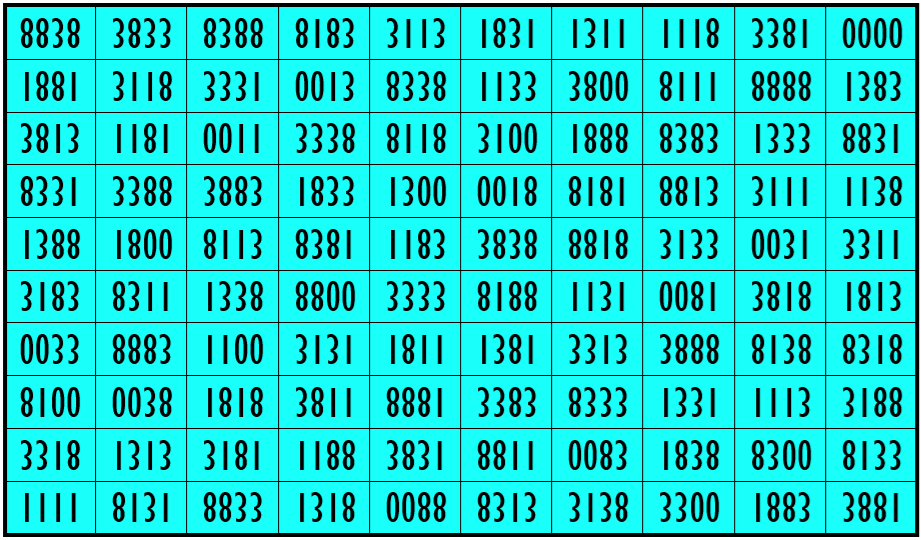
Thus, we have four examples of water reflexive magic squares of order 10 having 4-digits cells entries with four numbers combinations (2, 3, 5, 8), (1, 2, 3, 5), (0, 2, 3, 5) and (0,1, 3, 8).
b) 6-Digits Cell Entries:
Example 32. The Digits (2, 3, 5)
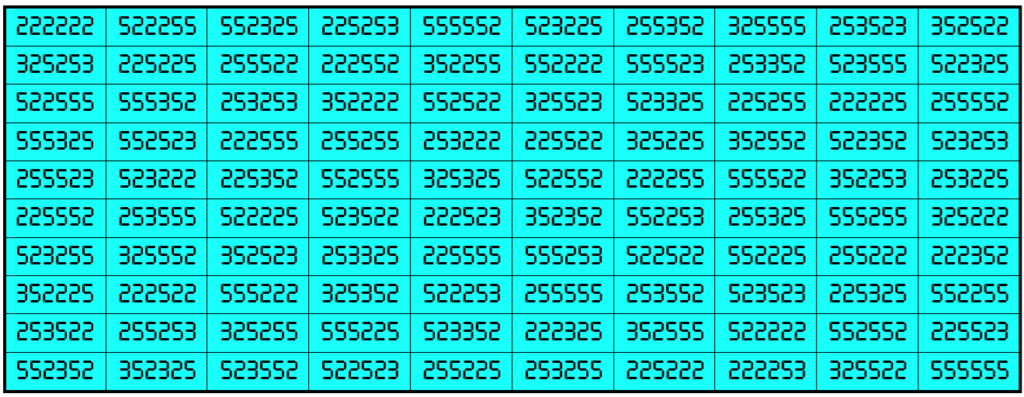
Water Reflection Image

Example 33. The Digits (1, 3, 8)
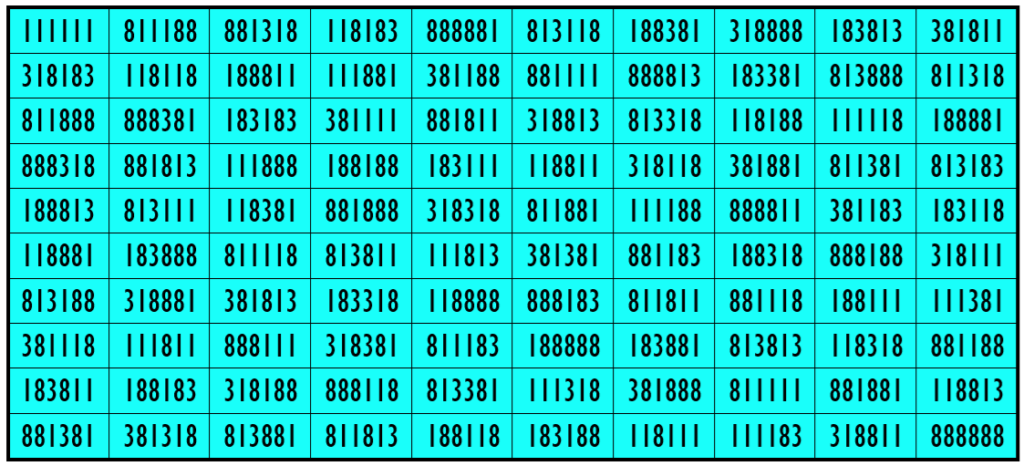
Water Reflection Image
Example 34. The Digits (0, 3, 8)
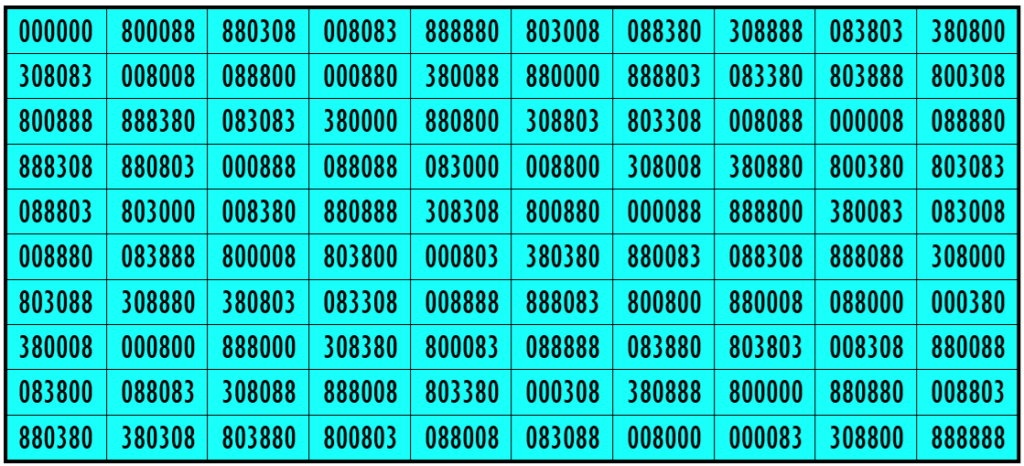
Water Reflection Image
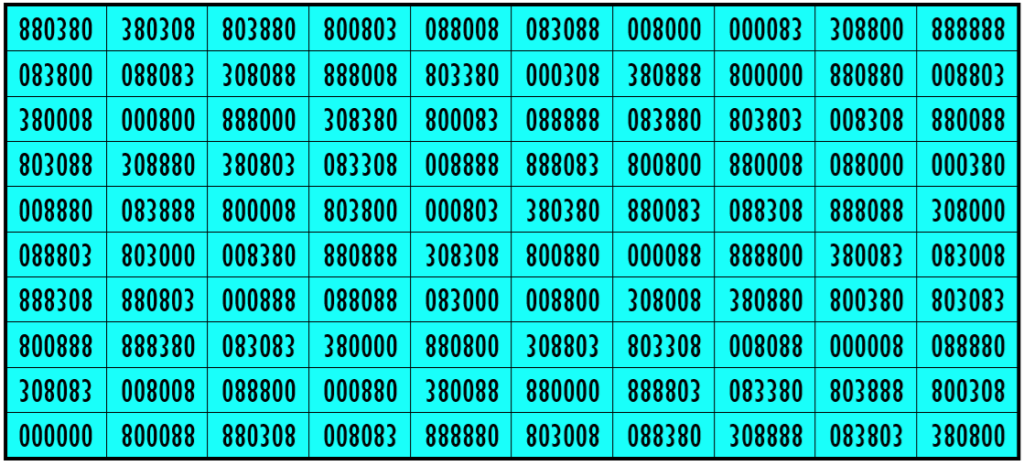
Example 35. The Digits (0, 1, 3)

Water Reflection Image

Thus, we have four examples of water reflexive magic squares of order 10 having 6-digits cells entries with 3 numbers combinations (2, 3, 5), (1, 3, 8), (0, 3, 8) and (0,1, 3).
c) 8-Digits Cell Entries:
Example 36. The Digits (3, 8)

Water Reflection Image
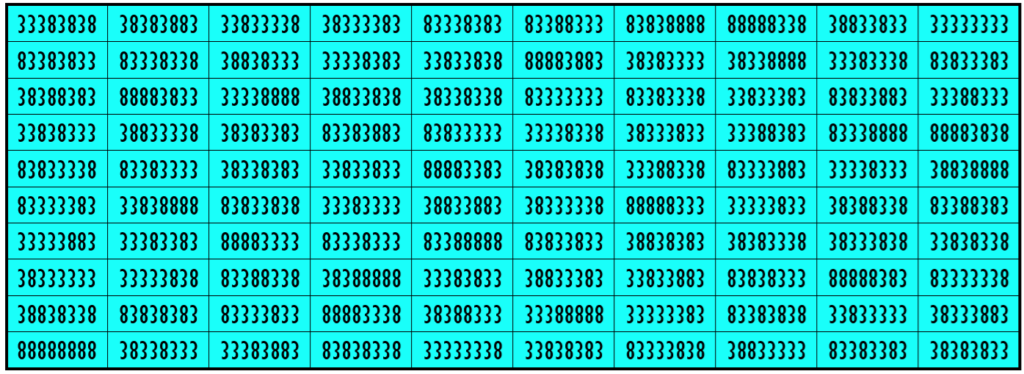
Example 37. The Digits (1, 3)

Water Reflection Image

Example 38. The Digits (0, 3)
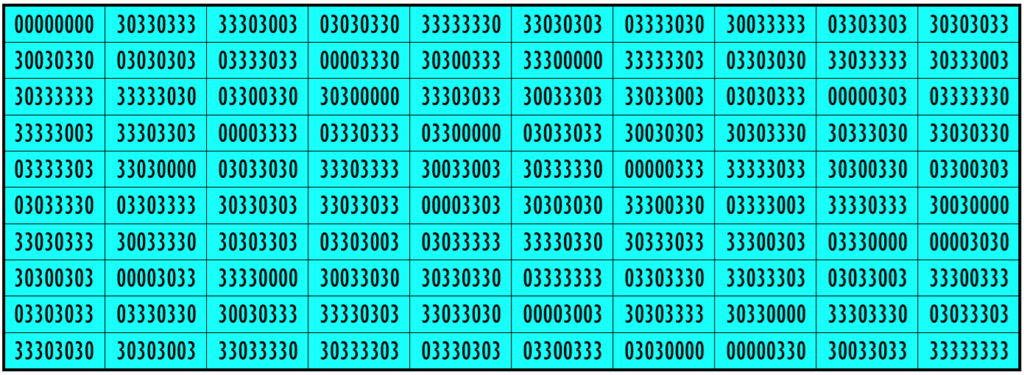
Water Reflection Image

Thus, we have three examples of water reflexive magic squares of order 10 having 8-digits cells entries with 2 numbers combinations (3, 8), (1, 3) and (0, 3).
References
Below are references of complete project in 8 parts for the orders 3 to 25. Mainly, it includes three things: Upside-down, Mirror Looking and Water Reflection properties of magic squares.
- Inder J. Taneja, Upside-Down, Mirror Looking and Water Reflection Magic Squares: Orders 3 to 6, Zenodo, January 07, 2025, pp. 1-93, https://doi.org/10.5281/zenodo.14607070.
- Inder J. Taneja, Upside-Down, Mirror Looking and Water Reflection Magic Squares: Orders 7 to 10, Zenodo, January 07, 2025, pp. 1-171, https://doi.org/10.5281/zenodo.14607071.
- Inder J. Taneja, Upside-Down, Mirror Looking and Water Reflection Magic Squares: Orders 11 to 13, Zenodo, January 15, 2025, pp. 1-146, https://doi.org/10.5281/zenodo.14649320.
- Site link: Universal and Upside-Down Magic Squares of Orders 11 to 15 (new site)
- Site link: Water Reflection Magic Squares: Order 11 to 13 (new site).
- Site link: Universal and Upside-Down Magic Squares of Orders 11 to 15 (old site)
- Site link: Water Reflection Magic Squares: Orders 11 to 13 (old site)
- Inder J. Taneja, Upside-Down, Mirror Looking and Water Reflection Magic Squares: Orders 14 to 16, Zenodo, January 15, 2024, pp. 1-140, https://doi.org/10.5281/zenodo.14649519.
- Site link: Universal and Upside-Down Magic and Bimagic Squares of Order 16 (new site)
- Site link: Water Reflection Magic Squares: Order 14 to 16 (new site).
- Site link: Universal and Upside-Down Magic and Bimagic Squares of Order 16 (old site)
- Site link: Water Reflection Magic Squares: Orders 14 to 16 (old site)
- Inder J. Taneja, Upside-Down, Mirror Looking and Water Reflection Magic Squares: Orders 17 to 20, Zenodo, January 17, 2025, pp. 1-86, https://doi.org/10.5281/zenodo.14676293.
- Inder J. Taneja, Upside-Down, Mirror Looking and Water Reflection Magic Squares: Orders 21 to 23, Zenodo, January 20, 2025, pp. 1-83, https://doi.org/10.5281/zenodo.14688709.
- Inder J. Taneja, Upside-Down, Mirror Looking and Water Reflection Magic Squares: Order 24, Zenodo, Janeiro 20, 2025, pp. 1-150, https://doi.org/10.5281/zenodo.14700325
- Inder J. Taneja, Upside-Down, Mirror Looking and Water Reflection Magic Squares: Order 25, Zenodo, January 21, 2025, pp. 1-79, https://doi.org/10.5281/zenodo.14715162.