This work brings striped magic squares of order 18. Before we proceed further below examples of 8 stripes used in whole the work.
Striped Magic Rectangles
Below are examples of magic rectangles used in this work. These are orders 2×4 to 2×18 used in this work. Since all these are of equal width, we call them stripes.

Whole the work on stripled magic squares of order 18 are always among above 8 types of magic rectangles, where the width is always same. The change is only in lenght. According to order of the stripes the entries are different but the sums are always same.
Below are few examples of striped magic squares of order 18. Due to high quantity of magic squares these are divided in 9 parts.
For online work click the following:
- Inder J. Taneja, Striped Magic Squares of 18, Zenodo, June 13, 2024, pp. 1-34, https://doi.org/10.5281/zenodo.11629567
Striped Magic Squares of Order 18
Part 1: Embedded with Striped Magic Squares of Order 14
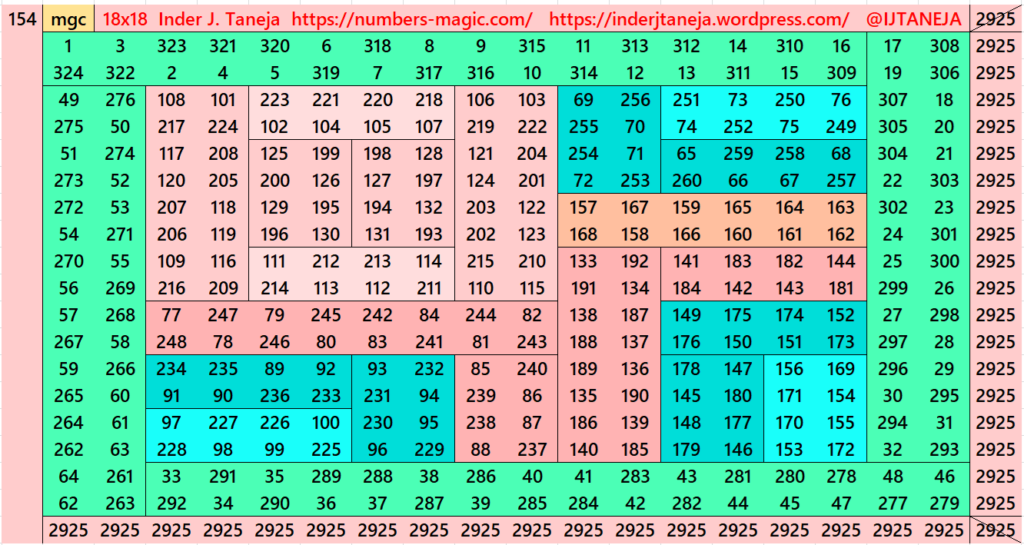
This part is with striped magic squares of order 18. In this part, we have embedded striped magic squares of order 14 studied before (Striped Magic Squares of Orders 4, 6, 8, 10, 12 and 14) . It already contains striped magic squares of order 10 and 6. Below are few examples. The complete work is given in pdf attached with this part.
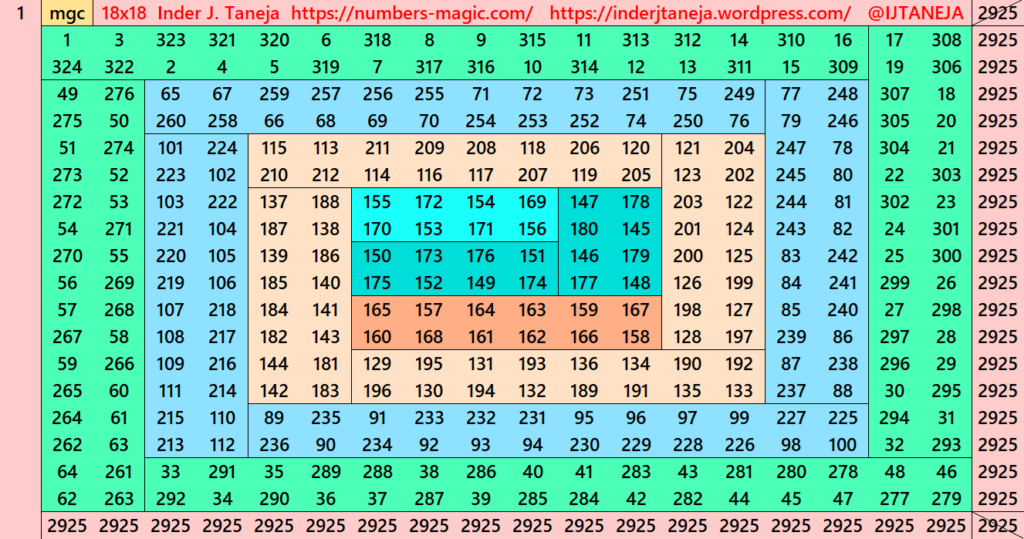
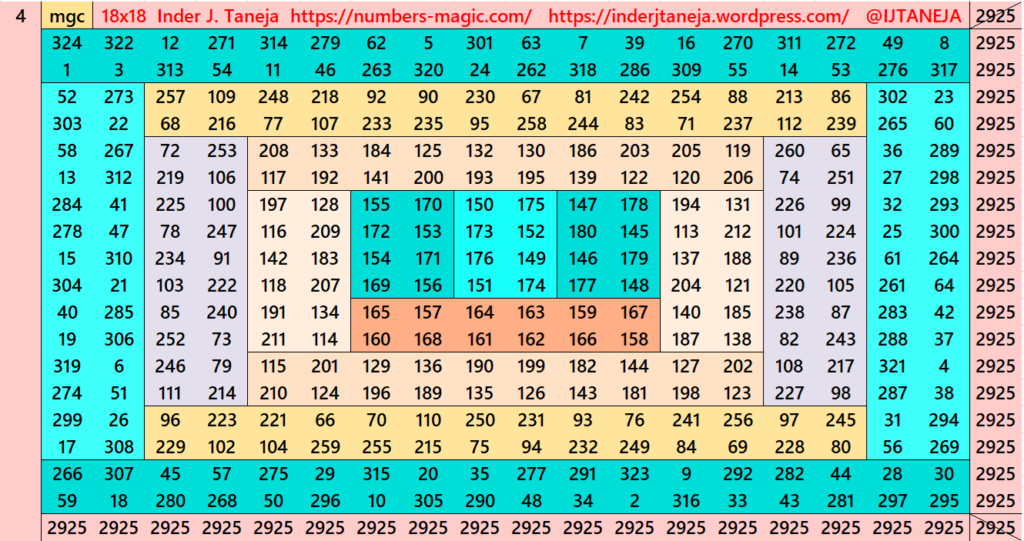
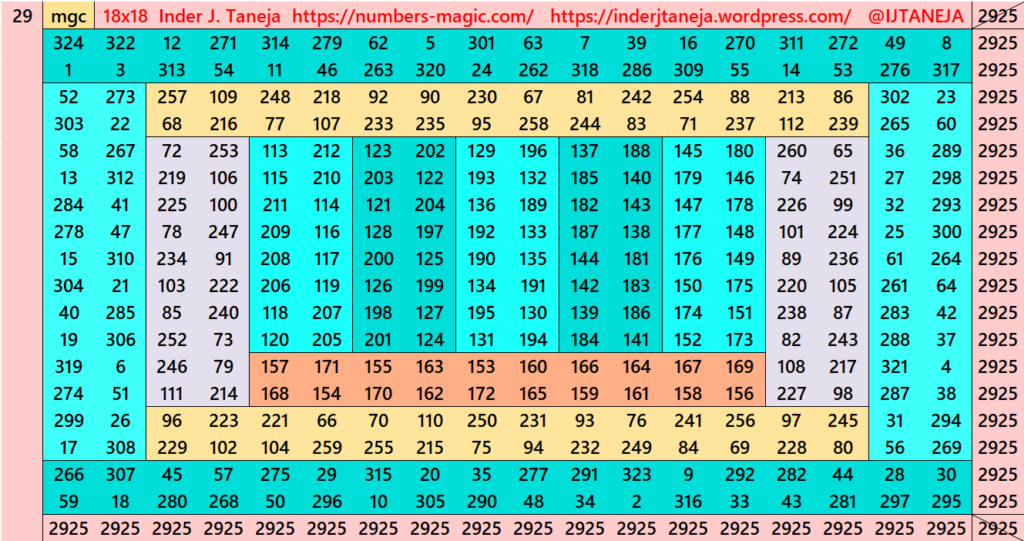
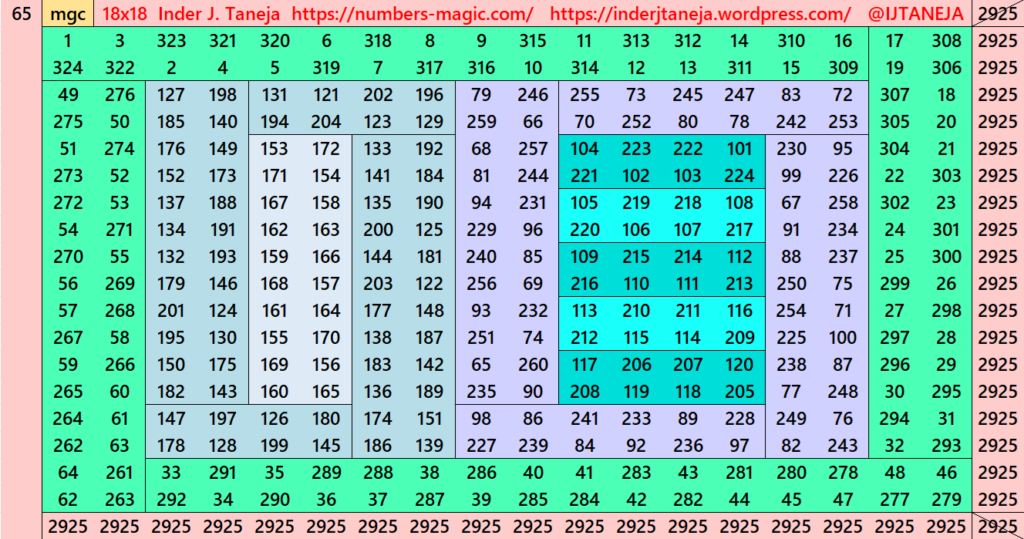
Pdf file of Part 1
There are total 289 striped magic squares in this part.
Part 2: Embedded with Symmetric Magic Rectangles
This part also contains embedded striped magic squares of order 6 and 10. The external part is different from the previous part. It contained symmetrical magic rectangles. See two examples below:
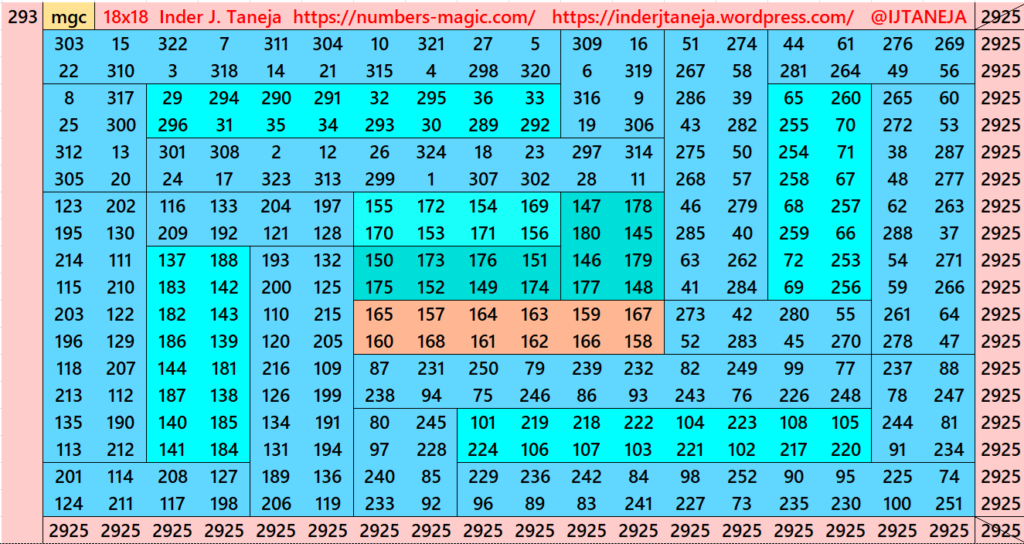
More examples are in Pdf file given below.
Pdf file of Part 2
There are total 72 striped magic squares in this part.
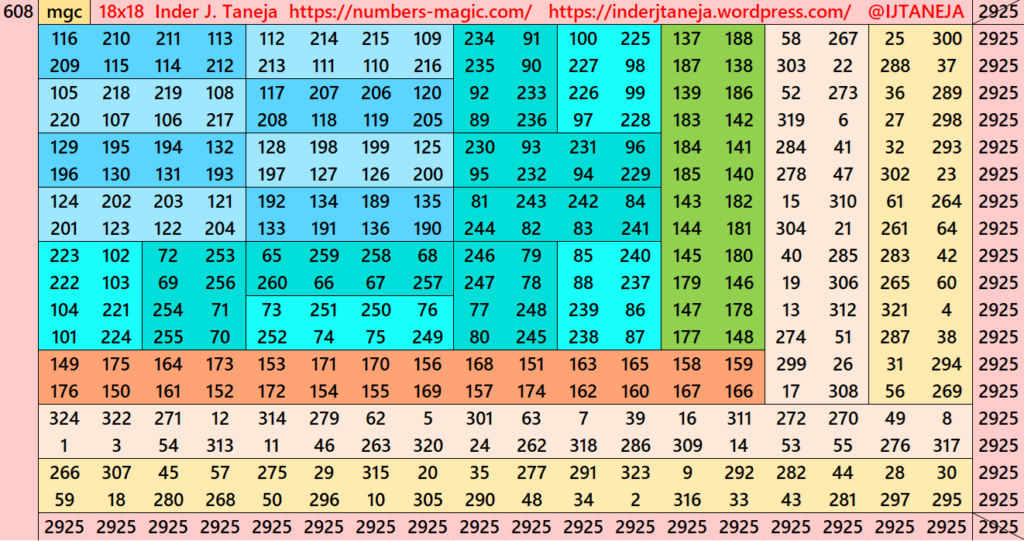
Part 3: Cornered with Striped Magic Squares of Order 14
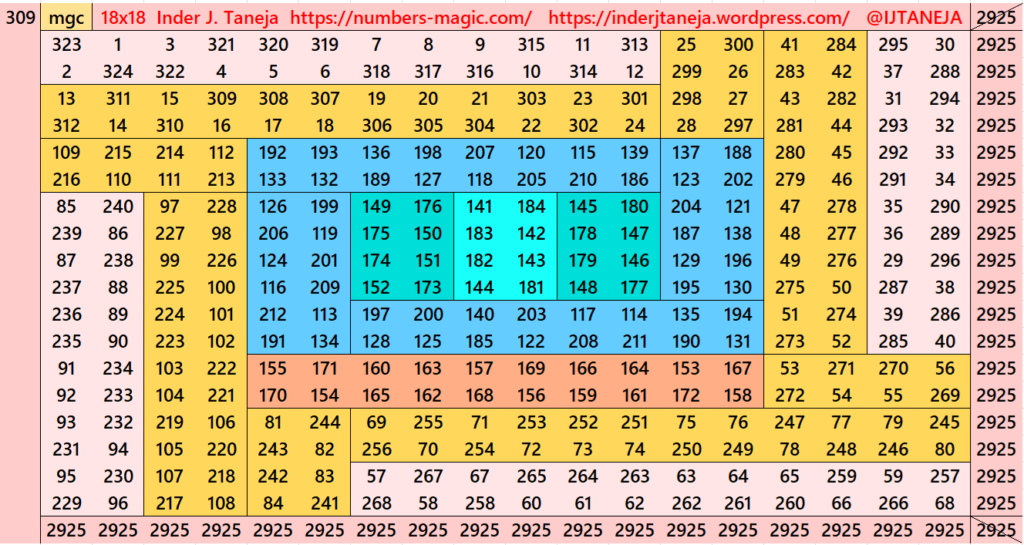
In the first part we have seen that the magic squares of order 14 are embedded in the magic squares of order 18. This section includes striped magic squares of order 18, with magic squares of order 14 positioned at the corners. See below few examples. The complete work of this section is given as pdf file at the end of this work.
Pdf file of Part 3
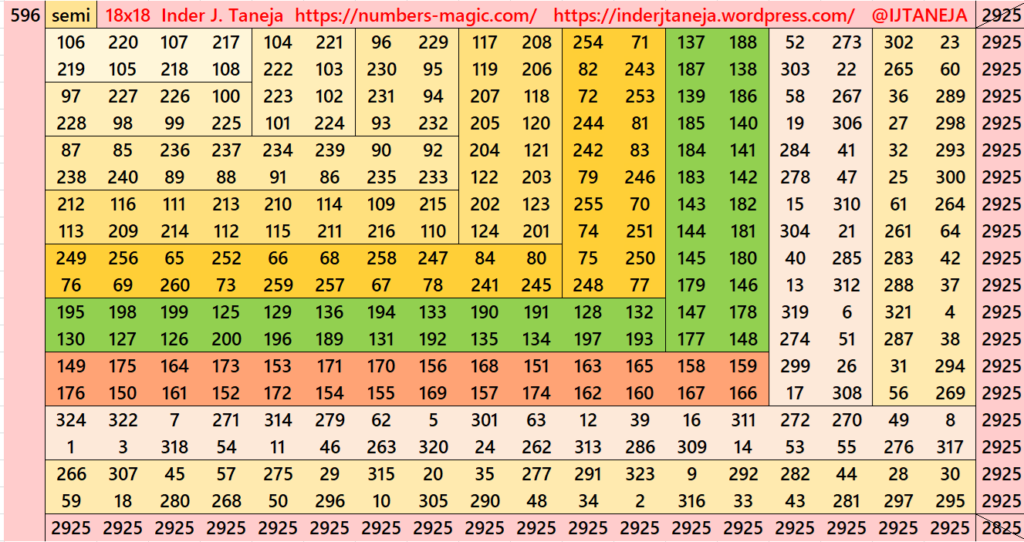
There are total 261 striped squares in this part out of them 100 are magic squares and 161 are semi- magic squares. Later on these semi-magic squares shall be converted in magic squares after some simplifications.
Part 4: Cornered with Striped Magic Squares of Order 12.
Using Algebraic Formula (a+b)^2=a^2+b^2+2ab
This part is very much simiar to part 3. The difference is that here we have striped magic squares of order 12 instead of order 14. The magic square of order 12 are already given in another work (Striped Magic Squares of Orders 4, 6, 8, 10, 12 and 14). The striped magic squares of order 12 are cornered in such a way that we apply the formula (a+b)^2=a^2+b^2+2ab. Here, the a=12 and b=6. The expressions ab or ba are considered in different ways. See below few examples. The whole work is given as pdf file in the end of this section.
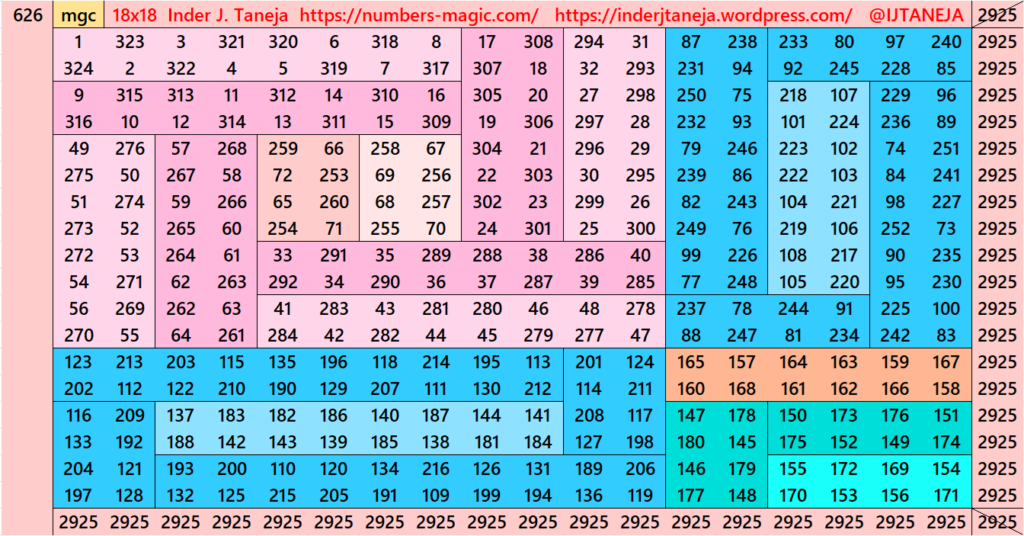
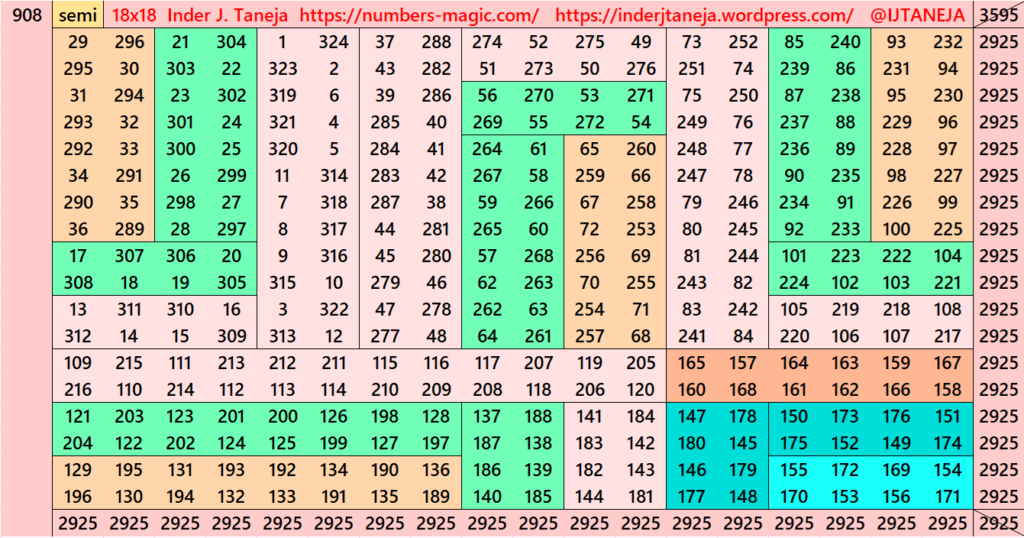
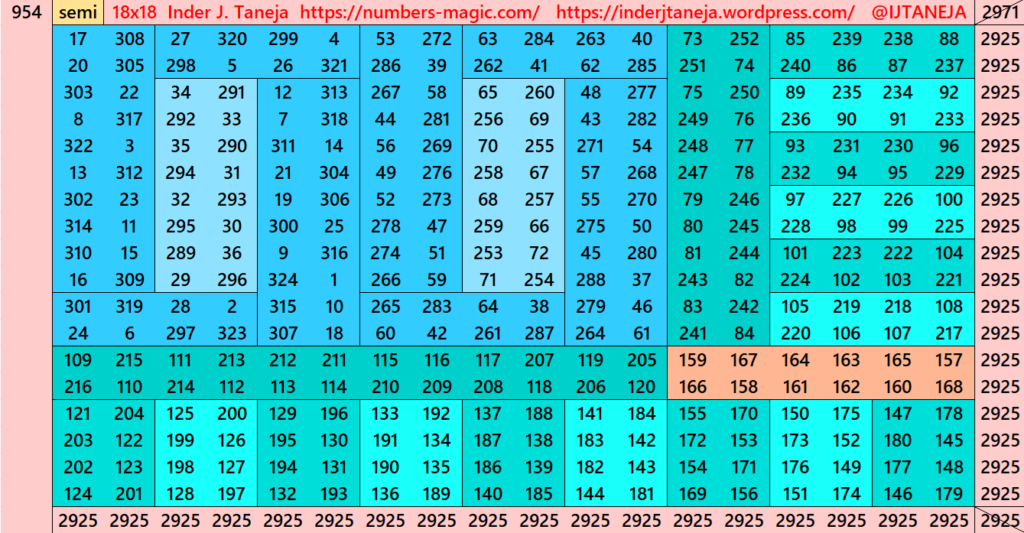
There are total 539 striped squares in this part. Out of them 259 are magic squares and 280 are semi- magic squares. Later on these semi-magic squares shall be converted in magic squares after some simplifications.
Pdf file of Part 4
Part 5: Cornered with Striped Magic Squares of Order 12
This section is very much similar to section 4. The difference is that here we havn’t divided the magic squares and/or magic rectangles in terms of the algebraic expressions (a+b)^2=a^2+b^2+2ab. The lower part we have just considered as magic rectangles of order 6×18. This we have taken different forms. The upper is with stripled magic squares of order 12 and magic rectangles of order 6×12 or better 12×6 (vertical order). See below few examples. The whole work is given as pdf file in the end of this section.
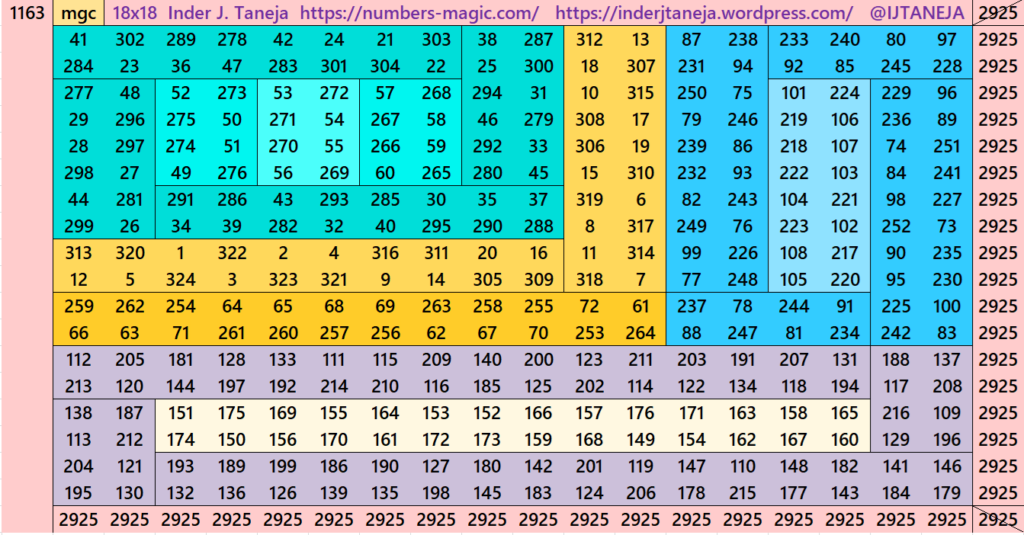
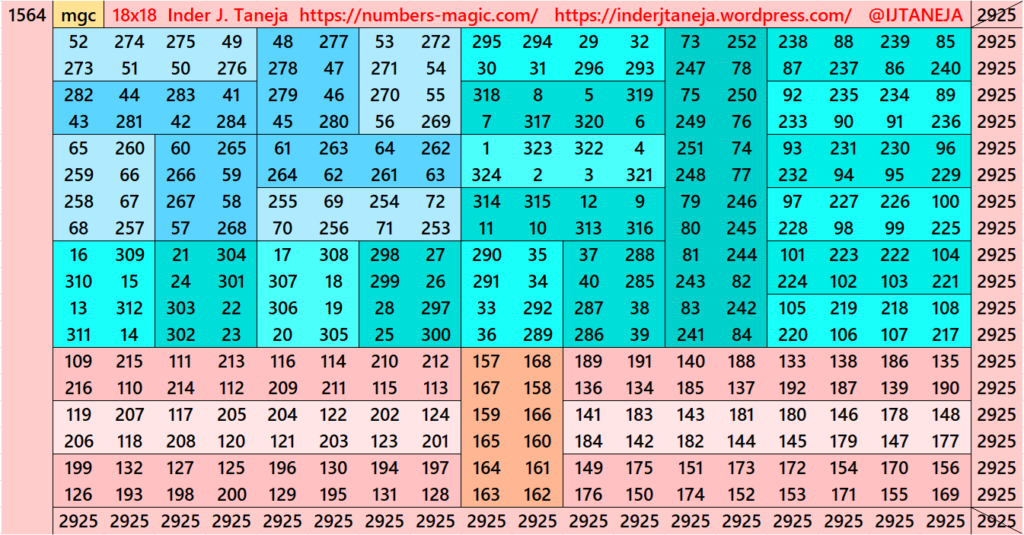
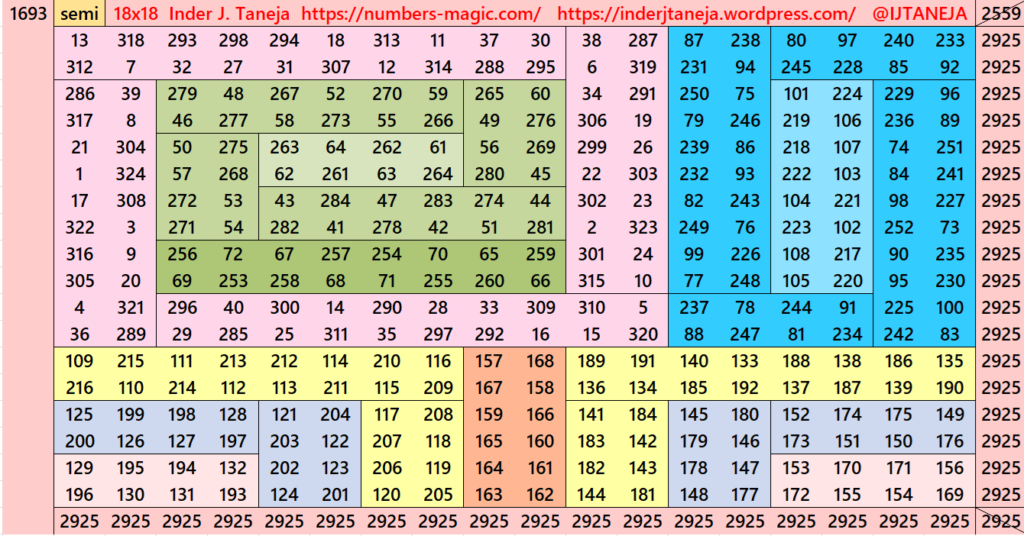
Pdf file of Part 5
There are total 798 striped squares in this part. Out of them 406 are magic squares and 392 are semi- magic squares. Later on these semi-magic squares shall be converted in magic squares after some simplifications.
Part 6: Cornered with Striped Magic Squares of Order 10.
Using Algebraic Formula (a+b)^2=a^2+b^2+2ab
This part is very much simiar to parts 3 and 4. The difference is that here we have striped magic squares of order 10 instead of orders 14 and 12. The magic squares of order 10 are already given in another work (Striped Magic Squares of Orders 4, 6, 8, 10, 12 and 14). The striped magic squares of order 10 are cornered in such a way that we apply the formula (a+b)^2=a^2+b^2+2ab. Here, the a=10 and b=8. The expressions ab or ba are considered in different ways. See below few examples. The whole work is given as pdf file in the end of this section.
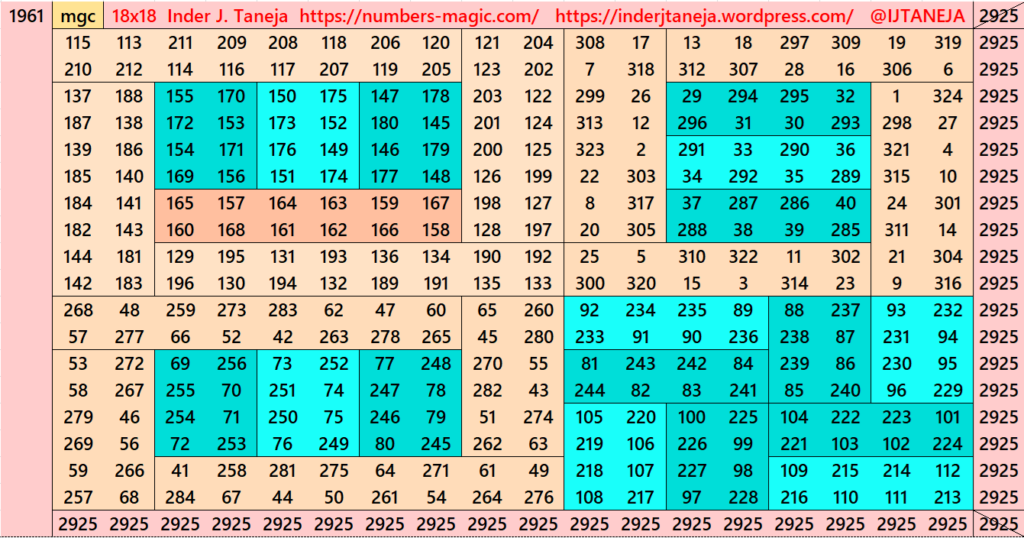
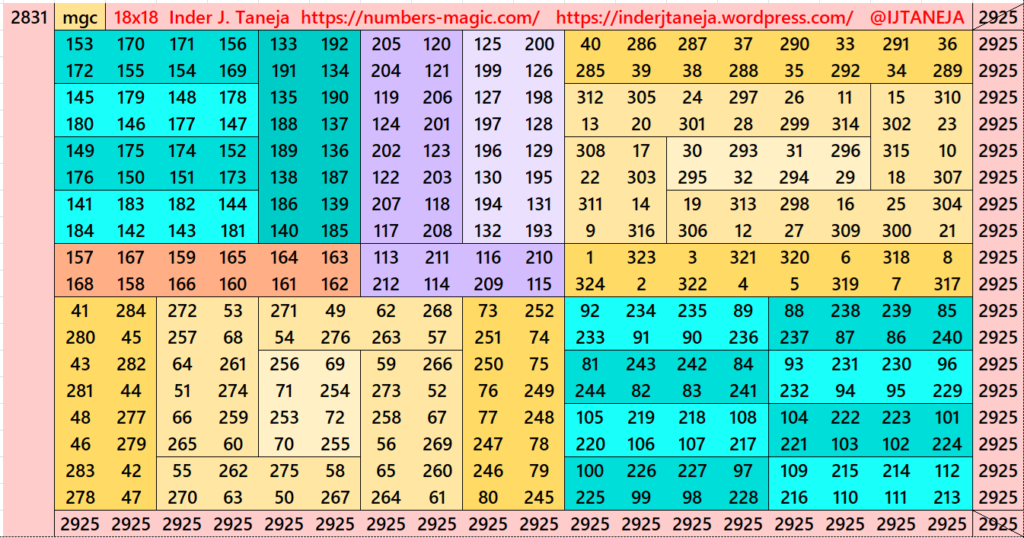
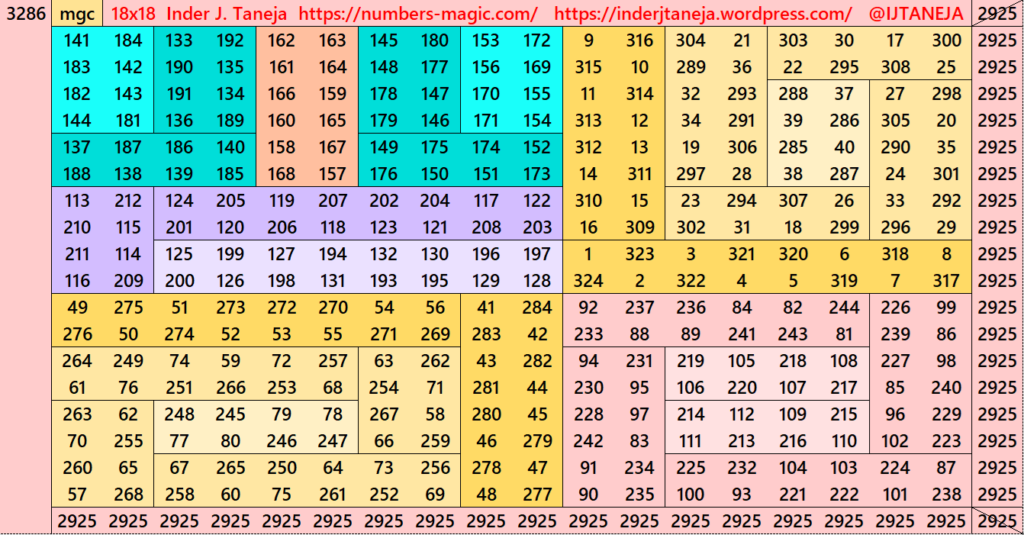
Pdf file of Part 6
There are total 1600 striped squares in this part. Out of them 1440 are magic squares and 160 are semi- magic squares. Later on these semi-magic squares shall be converted in magic squares after some simplifications.
Part 7: Embedded with Striped Magic Squares of Order 14
This section is very much similar to section 5. The difference is that here we havn’t divided the magic squares and/or magic rectangles in terms of the algebraic expressions (a+b)^2=a^2+b^2+2ab. The lower part we have just considered as magic rectangles of order 8x18. This we have taken different forms. The upper is with stripled magic squares of order 10 and magic rectangles of order 8×10 or better 10×8 (vertical order). See below few examples. The whole work is given as pdf file in the end of this section.
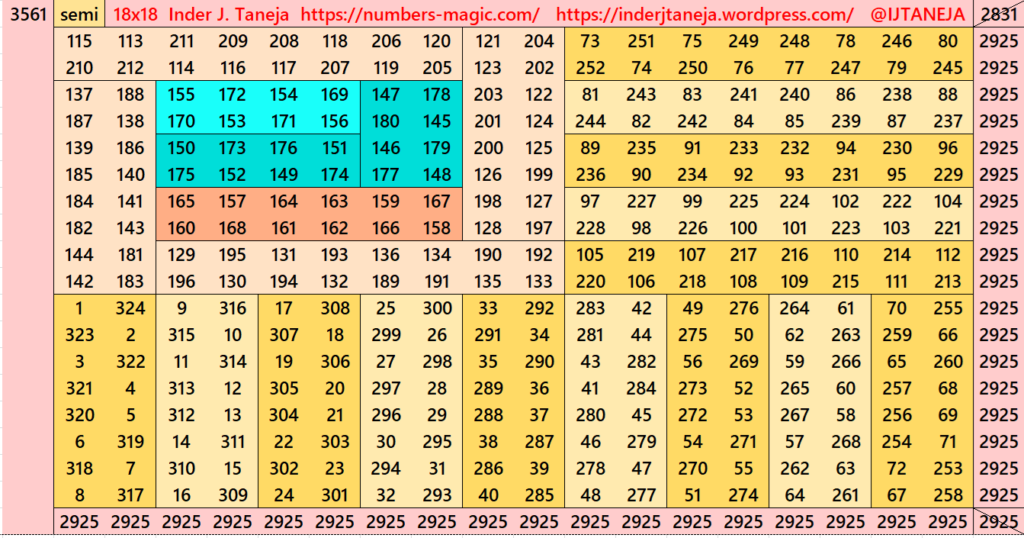
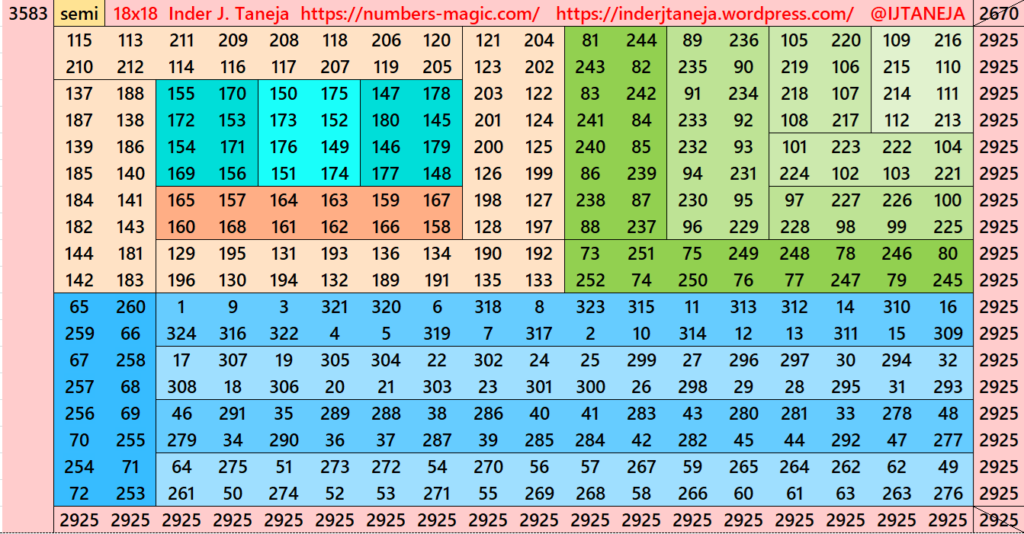
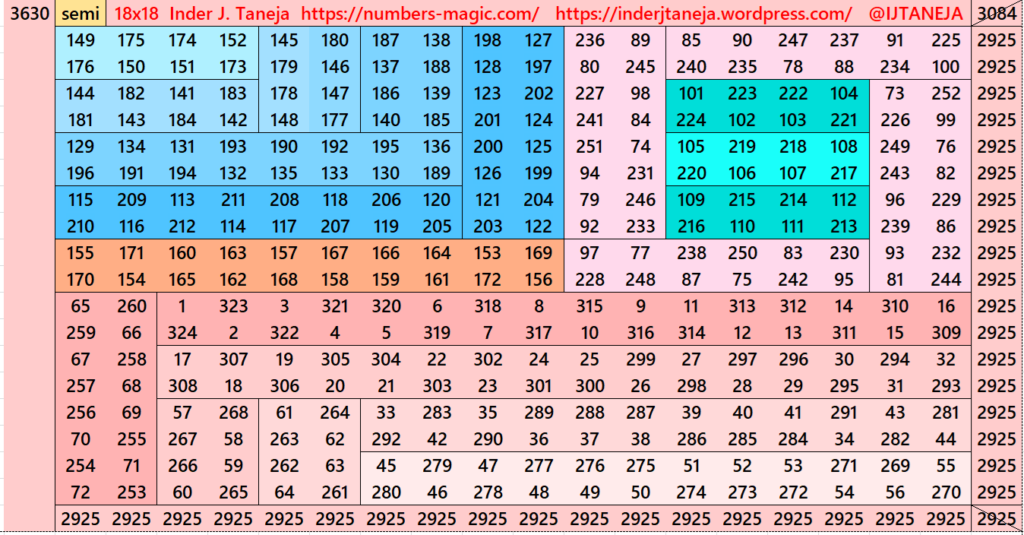
Pdf file of Part 7
There are total 480 striped squares in this part. All of them are semi-magic squares. Later all of on these semi-magic squares shall be converted in magic squares after some simplifications.
Part 8: Some Extra Magic Squares of Order 18
This part is not following any specific rule. These are just constructed based on some general idea. Any how all of them looks beautiful. See below few examples.
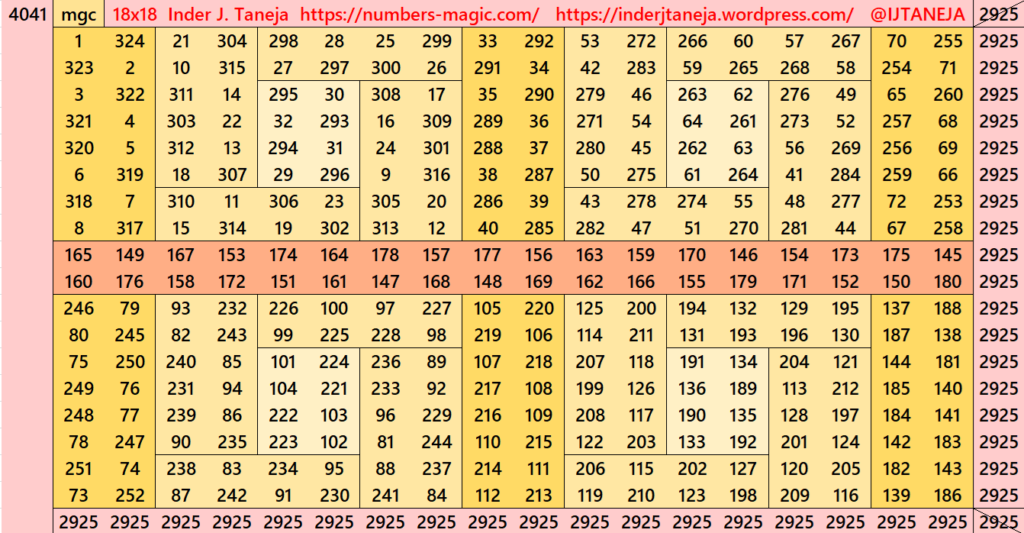
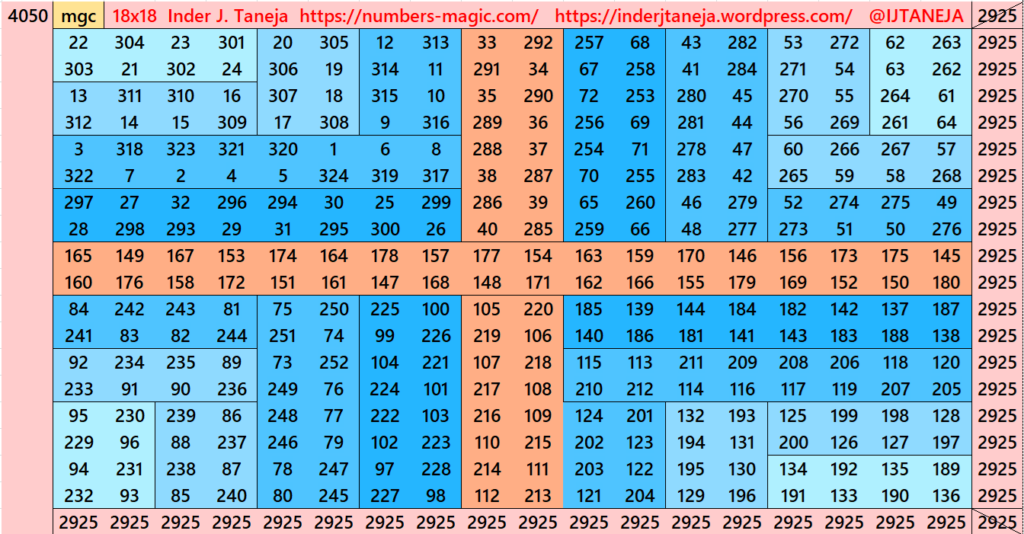
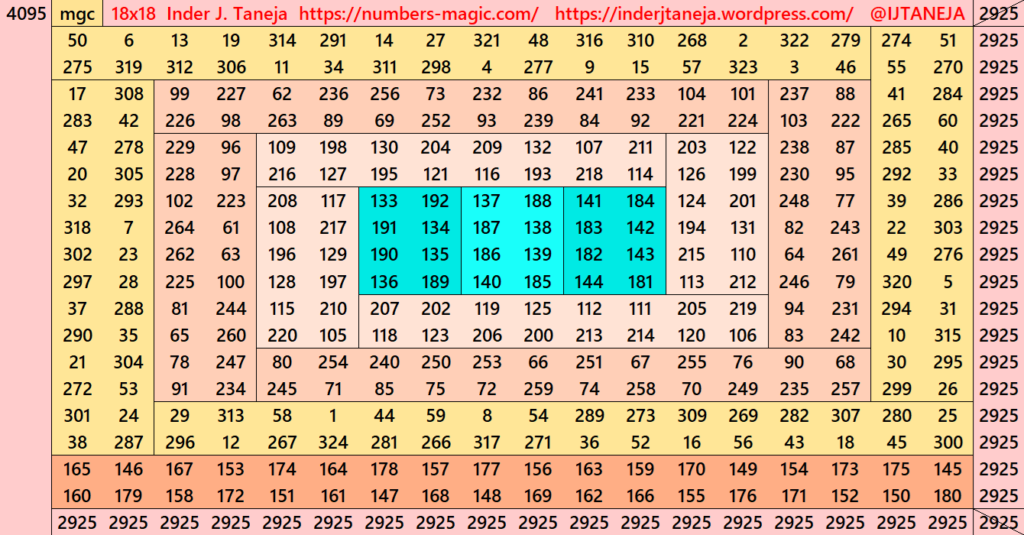
Pdf file of Part 8
There are total 58 striped squares in this part. All of them 39 are magic squares and 19 are semi-magic squares. Later all of on these semi-magic squares shall be converted in magic squares after some simplifications.
Part 9: Cornered with Striped Magic Squares of Order 16
This part is very much similar to part 3. He we have take striped magic squares of order 16 at the corner and then adjusted them in square of order 18. See below some examples:
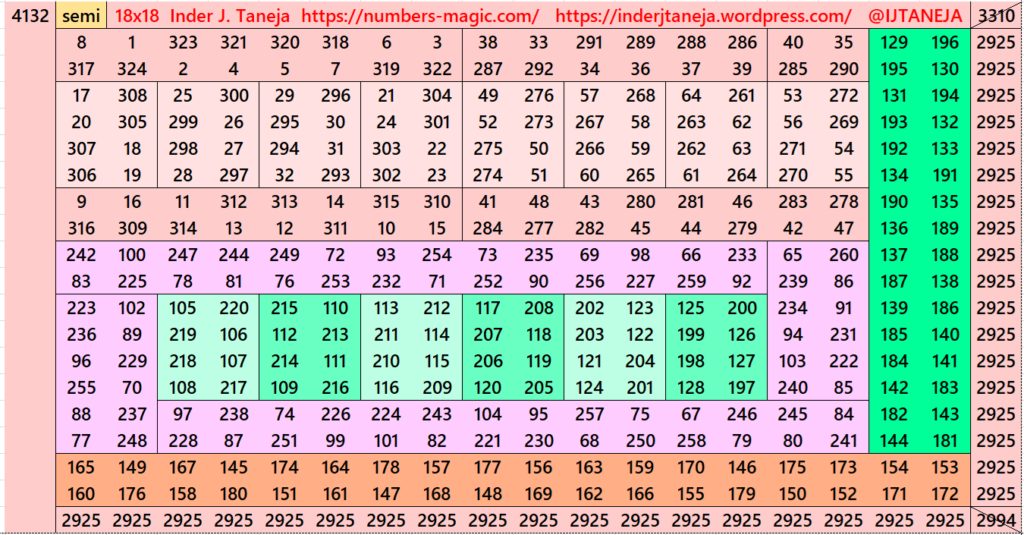
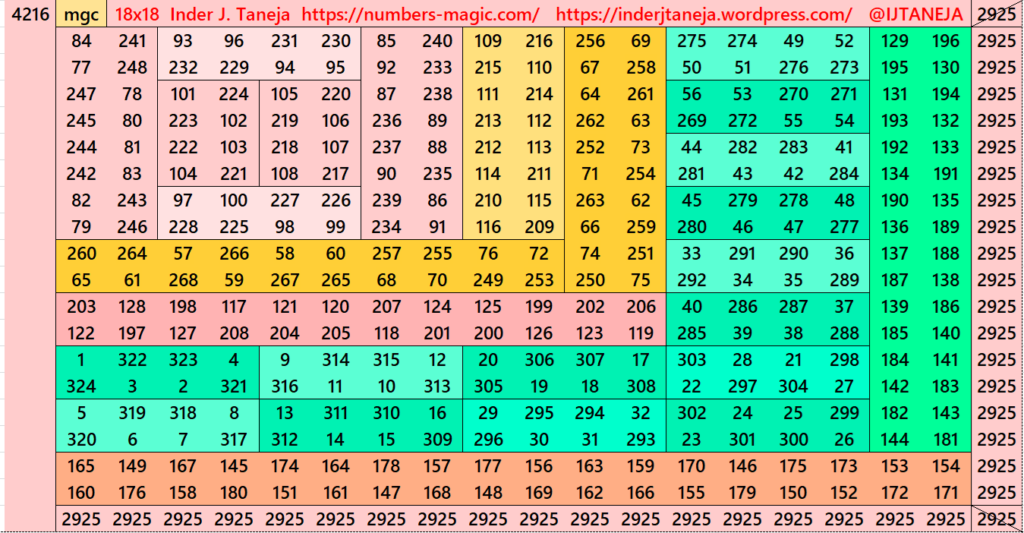
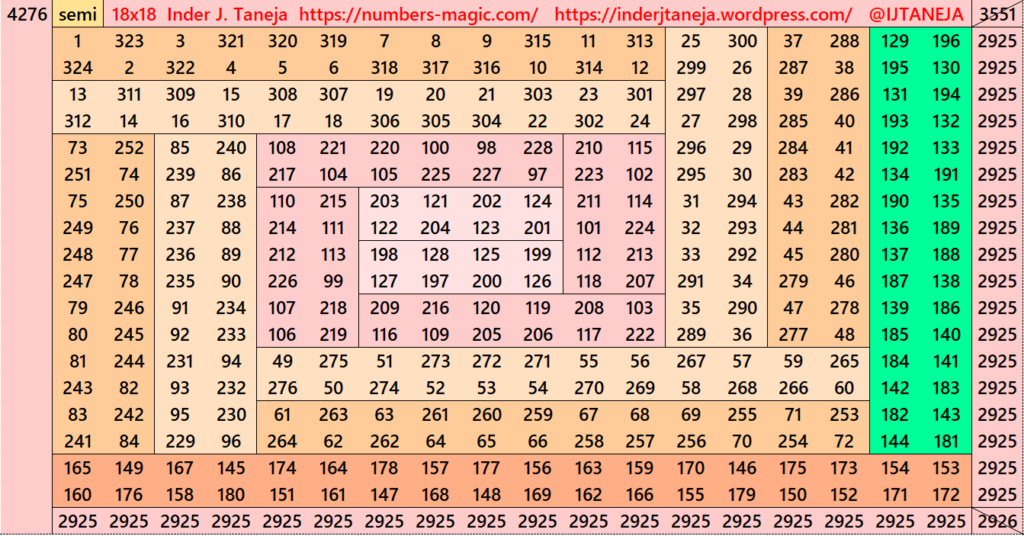
Pdf file of Part 9
In this section, there are a total of 266 striped squares. Among these, 57 are magic squares and 209 are semi-magic squares. These semi-magic squares will be transformed into magic squares following certain simplification
Pdf file of Complete Work
References
- Inder J. Taneja, Striped Magic Squares of Even Orders 6, 8, 10, 12 and 14, Zenodo, November 10, 2023, pp. 1-34, https://doi.org/10.5281/zenodo.10107355.
- Inder J. Taneja, Striped Magic Squares of 16, Zenodo, May 16, 2024, pp. 1-22, https://doi.org/10.5281/zenodo.11205510.
- Site Link: Striped Magic Squares of Order 16.
- Inder J. Taneja, Striped Magic Squares of 18, Zenodo, June 13, 2024, pp. 1-34, https://doi.org/10.5281/zenodo.11629567.
- Site Link: Striped Magic Squares of Order 18.

