Revised in December 06, 2023
838 Magic Squares of Order 12

This work brings magic squares of orders 12. It unifies most of the previous works. Different types of constructions are considered. These includes, bordered, magic rectangles, double digits bordered, cornered, etc. It is summarized as the following points:

Boarded magic squares.
Bordered magic rectangles.
Algebraic formula (a+b)².
Double digits bordered magic squares.
Cornered magic squares.
Striped Magic Squares

Just as an idea below are links of the works magic squares using the special aspects as double digits, corner, striped etc.

Inder J. Taneja, Double Digits Even and Odd Orders Bordered Magic Squares
Inder J. Taneja, Two Digits Bordered Magic Squares Multiples of 4: Orders 8 to 24.
Inder J. Taneja, New Concepts in Magic Squares: Double Digits Bordered Magic Squares of Orders 7 to 108.
Inder J. Taneja, New Concepts in Magic Squares: Cornered Magic Squares from Order 5 to 81
Inder j. Taneja, Cornered Magic Squares.
Inder J. Taneja, Even Orders Striped Magic Squares

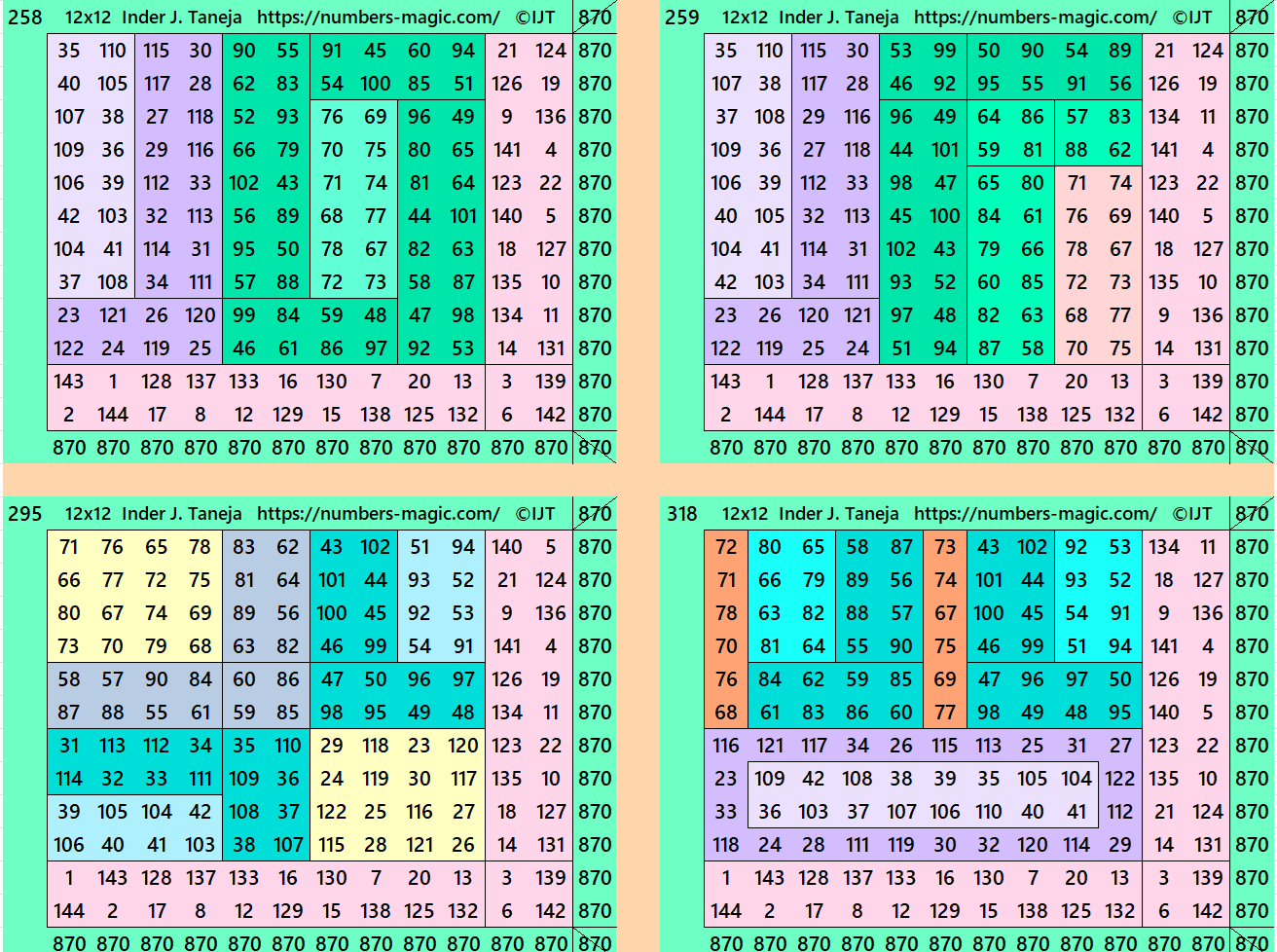
This work brings different types of magic squares of order 12. It is a revised version of the author’s previous work. Below are examples of magic squares of order 12. Total there are 838 examples, but only few are given below. In the end there is a pdf file for download of 838 magic squares of order 12. The work can also be seen online at the following link:
Inder J. Taneja, Different Types of Magic Squares of Orders 6, 8, 10 and 12, Zenodo, November 07, 2023, pp. 1-41, https://doi.org/10.5281/zenodo.10080859.