In 2013-2014, author (click here) wrote natural numbers in increasing and decreasing orders of 1 to 9 using only basic operations. See below some examples:

For more details and extension work by other see the following link:
- Inder J. Taneja, The Crazy Representations and 10958 Problem,
The above study include the natural numbers till 300000. In some case factorials and or square-roots are used. There are only four numbers where we used square-root. All other numbers are basic operation incluing factorials. See below these four numbers:

To see the whole work up to 300.000 numbers refer the following links:
- Inder J. Taneja, The Crazy Representations and 10958 Problem,
- Inder J. Taneja, Crazy Representations of Natural Numbers Using Factorial: From 20001-100000
- Inder J. Taneja, Crazy Representations of Natural Numbers Using Factorial: From 100001-200000
- Inder J. Taneja, Crazy Representations of Natural Numbers Using Factorial From 200001 to 300000
- Inder J. Taneja, Representation of Numbers from 1 to 20000 in Terms of Palindromic Digits 1357-9-7531
- Inder J. Taneja, Representation of Numbers from 1 to 10000 in Terms of Palindromic Digits 2022-2202,
- Inder J. Taneja, Multiple Choices for Crazy Representations of Natural Numbers
Crazy Representations: Extention to Half a Million Natural Numbers
Recently, the author extended the above work up to half-million, i.e., 500000 numbers in increasing and decreating orders of 1 to 9 and 9 to 1. Most of numbers are by use of factorials. There are only few numbers where the square-root is also applied. See below:
- Increasing Order

- Decreasing Order
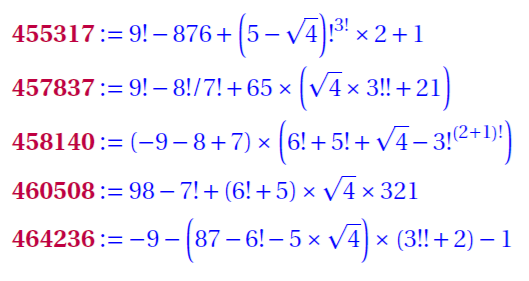
- Missing Numbers: Still there are 7 missing numbers. Out of them 4 are in the increasing case and 3 are in the decreasing case. See below these numbers:
- Increasing order missing: 469786, 469883, 474686, 499370
- Decreasing order missing: 431588, 464854, 468310.
These numbers can be writtern in terms of Triangular numbers:
- Increasing order
- 469786:=1-T(2+3)+T(4+5)T(6(7+8+9));
- 469883:=-1-T(2+T(T(T(3))))+(T(T(4))-T(T(T(5))))(T(T(6))-T(7+8+9));
- 474686:=(1+T(2+3))(T(T(4))-5+T(T(T(6))))+T(T(7+8+9));
- 499370:=-1+T(T(T(2+T(3))))+4(T(5)+T(T(6))T(7+8+9));
- Decreasing order
- 431588:=-9+T(T(T(8)+7)+6+5)-T(4)-T(T(T(3+2+1)));
- 464854:=-9+8-T(T(7))+6+T(T(54))T(3+2+1);
- 468310:=-9-T(T(8))+T(T(7))T(T(6))5+T(4+3+2+1);
Among 300.001 to 500.000 there are 200.000 numbers. The whole work we have divided in folloing five parts:
- Inder J. Taneja, Crazy Representations of Half a Million Natural Numbers: Part 1 – 300.001 to 340.000, Zenodo, December 05, 2024, pp. 1-1042, https://doi.org/10.5281/zenodo.14267963.
- Inder J. Taneja, Crazy Representations of Half a Million Natural Numbers: Part 2 – 340.001 to 380.000, Zenodo, December 05, 2024, pp. 1-1035, https://doi.org/10.5281/zenodo.14277644.
- Inder J. Taneja, Crazy Representations of Half a Million Natural Numbers: Part 3 – 380.001 to 420.000, Zenodo, December 05, 2024, pp. 1-1040, https://doi.org/10.5281/zenodo.14277646.
- Inder J. Taneja, Crazy Representations of Half a Million Natural Numbers: Part 4 – 420.001 to 460.000, Zenodo, December 05, 2024, pp. 1-1041, https://doi.org/10.5281/zenodo.14277648.
- Inder J. Taneja, Crazy Representations of Half a Million Natural Numbers: Part 5 – 460.001 to 500.000, Zenodo, December 05, 2024, pp. 1-1045, https://doi.org/10.5281/zenodo.14277650.