Block-Wise Construction of Bimagic Squares of Orders 49 and 343

Whole the work is done manually on excel sheets.

Below are bimagic squares written in blocks multiples of orders 7. These are orders 49 and 343. The work is done manually by author in 2011. It is summarized in the following link.

Inder J. Taneja, Bimagic Squares of Bimagic Squares and an Open Problem, Febuarary 11, 2011, 2011, pp. 1-14, (22.02.2011), https://doi.org/10.48550/arXiv.1102.3052.

Before proceeding further below are the basic formulas to check the sums of magic and bimagic squares

• Magic Sum

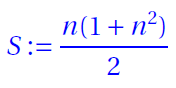
• Bimagic Sum

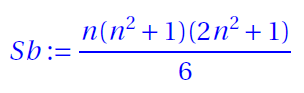
where n is the order the magic square.

Bimagic Square of Order 49

In this case, we have

S_49×49:=58849; Sb_49×49:= 94217249,

Blocks of order 7 are pandiagonal and of equal sums, S_7×7 :=8407. The magic squares of order 49 is also pandiagonal. See below the bimagic square of order 49.

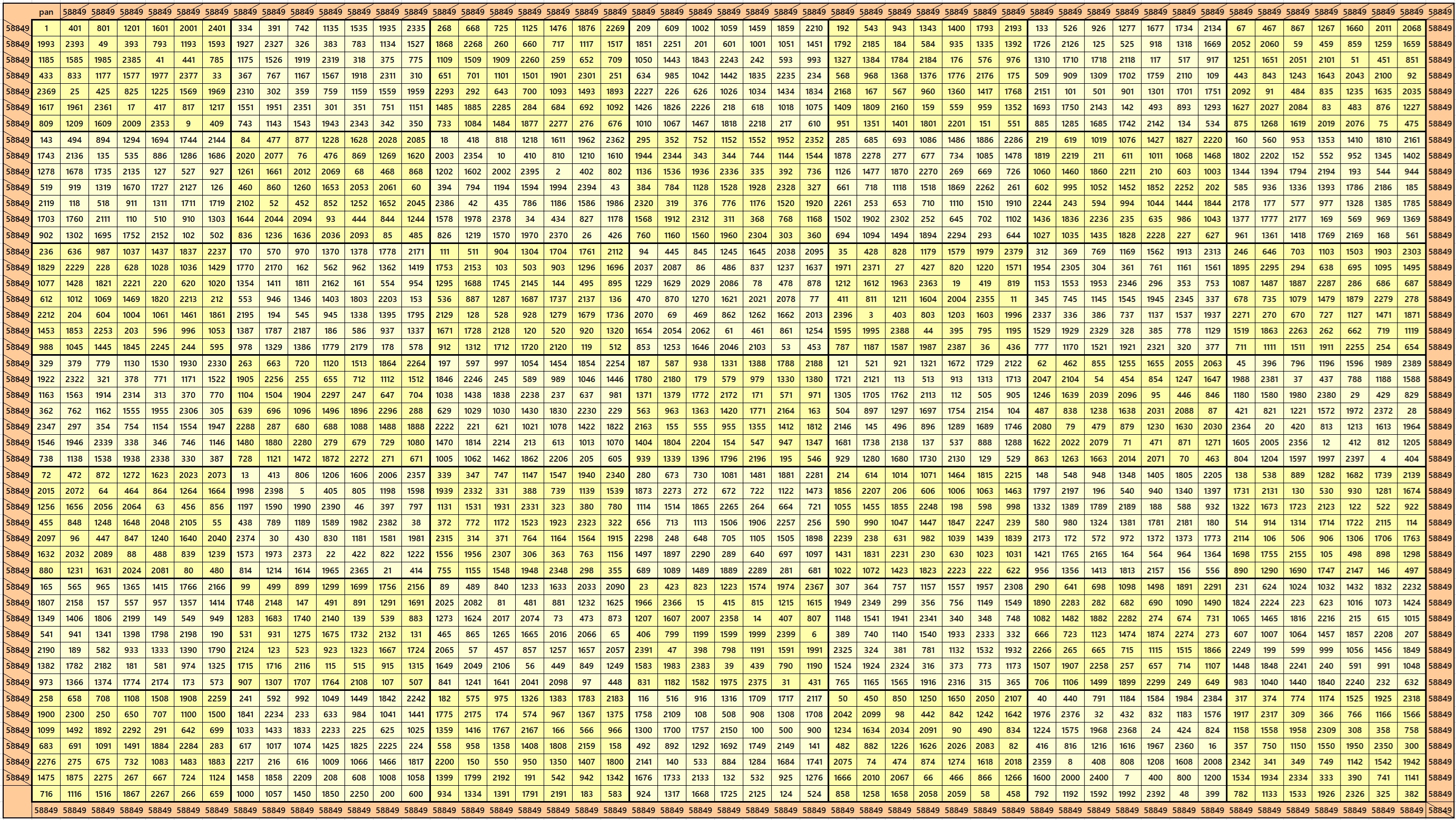
The work is similar to one studied by Gaston Terry in 1843.

Excel sheet of Bimagic Square of Order 49

Bimagic Square of Order 343: Blocks of Orders 7 and 49

Bimagic Square of order 343 with magic and bimagic sums

S_343×343:=20176975 and Sb_343×343:= 1582540680175

Block of order 49 are pandiagonal bimagic square with different bimagic sums, S_49×49:=2882425. Block of order 7 are also pandiagonal with equal sums S_7×7:=411775.

The magic square of order 343 is also pandiagonal. It is tested with software by H. White.

Excel sheet of Bimagic Square of Order 343