Different Types of Magic Rectangles in Construction of Even Orders Magic Squares

Never Seen Before.

This work brings magic squares in very different way. These are based on three different types of magic rectangles:
1. Bordered Magic Rectangles:
2. Double Digits Magic Rectangles:
3. Cornered magic rectangles.

First of let’s understand these magic rectangles one by one. Removing external borders in each case still we left with lower order magic rectangles. See below few examples in each case.

1. Bordered Magic Rectangles

Below are two examples of bordered magic rectangles

Example. Bordered Magic Rectangle of Order 12×18

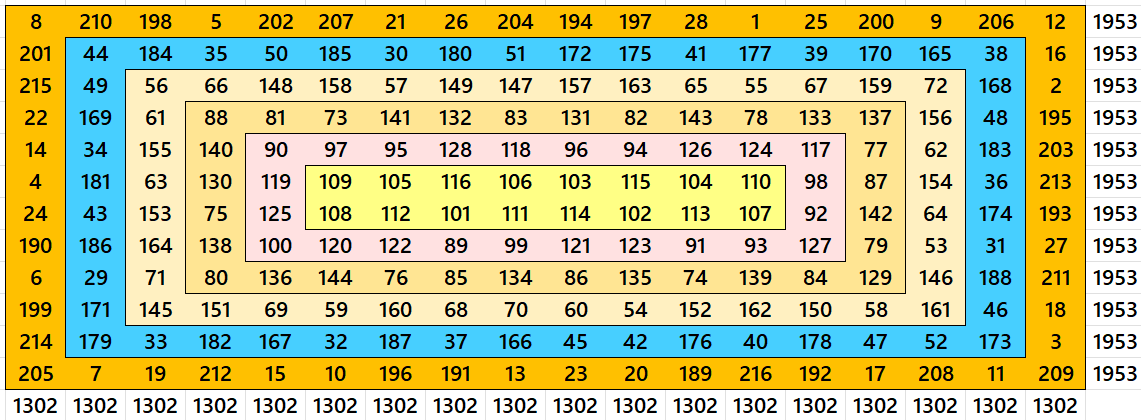
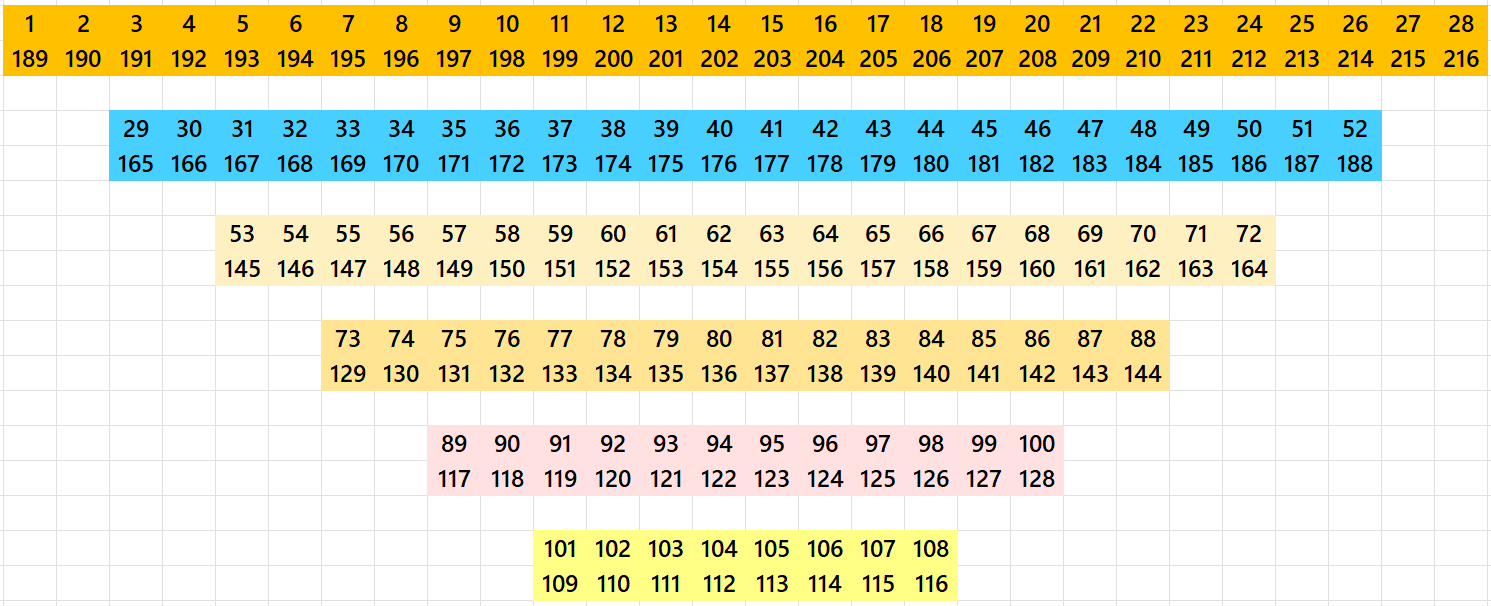
The entries according to colors are as follows:

More details are given in author’s recent work:

• Inder J. Taneja, Different Types of Magic Rectangles, Zenodo, September 04, 2023, pp. 1-26, https://doi.org/10.5281/zenodo.8316719.

2. Double Digits Magic Rectangles

Below are two examples of bordered magic rectangles

Example 1. Double Digits Magic Rectangle of Order 14×20

Except the corners, the entries entries sums are understood as

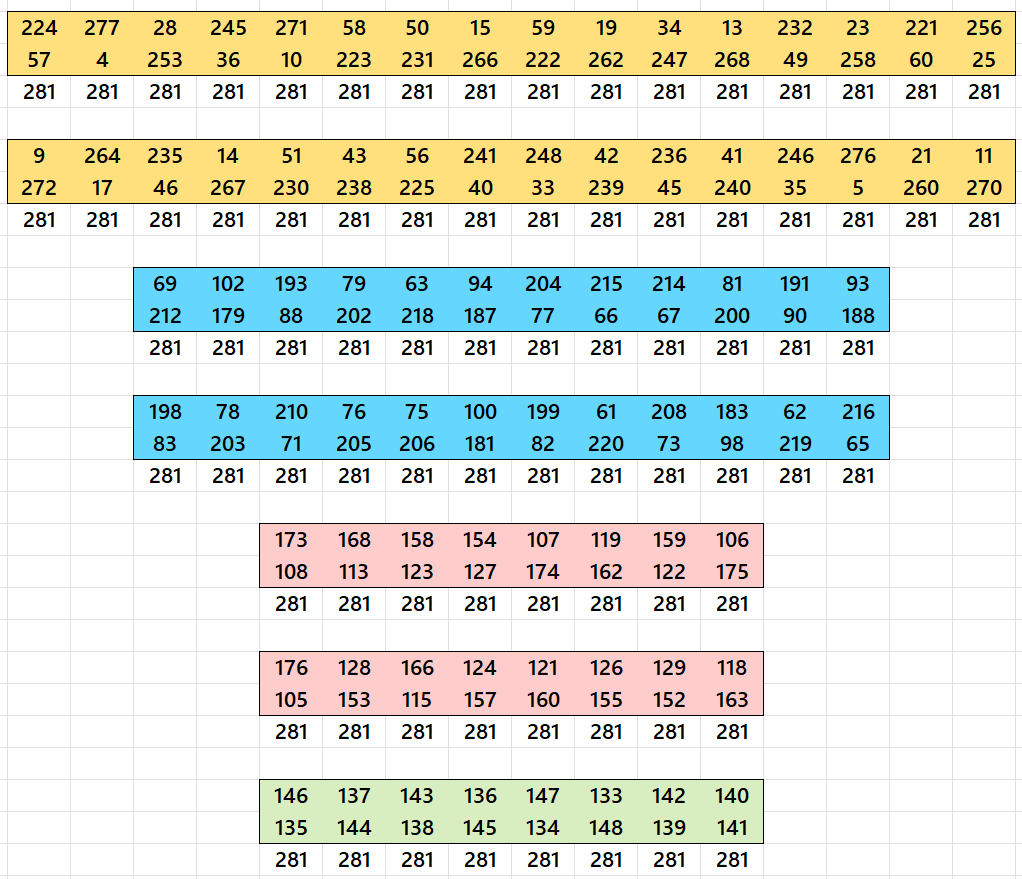
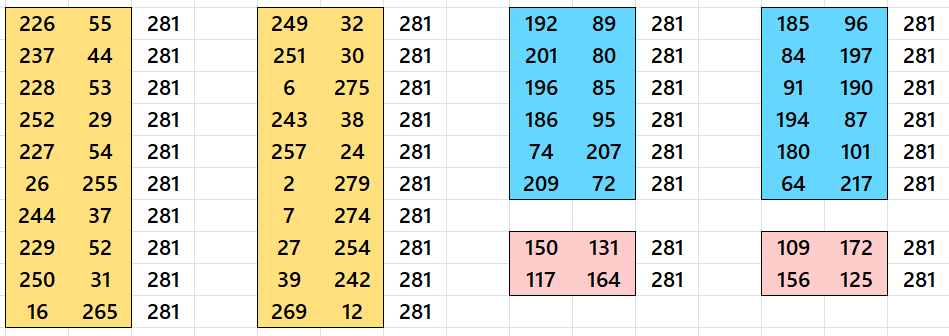
More details are given in author’s recent work:

• Inder J. Taneja, Different Types of Magic Rectangles, Zenodo, September 04, 2023, pp. 1-26, https://doi.org/10.5281/zenodo.8316719.

3. Cornered Magic Rectangles

Below is an example of cornered magic rectangles

Example. Cornered Magic Rectangle of Order 8×12

Let’s consider a cornered magic rectangle of order 10×24 formed by 240 sequencial entries, i.e., from 1 to 240:

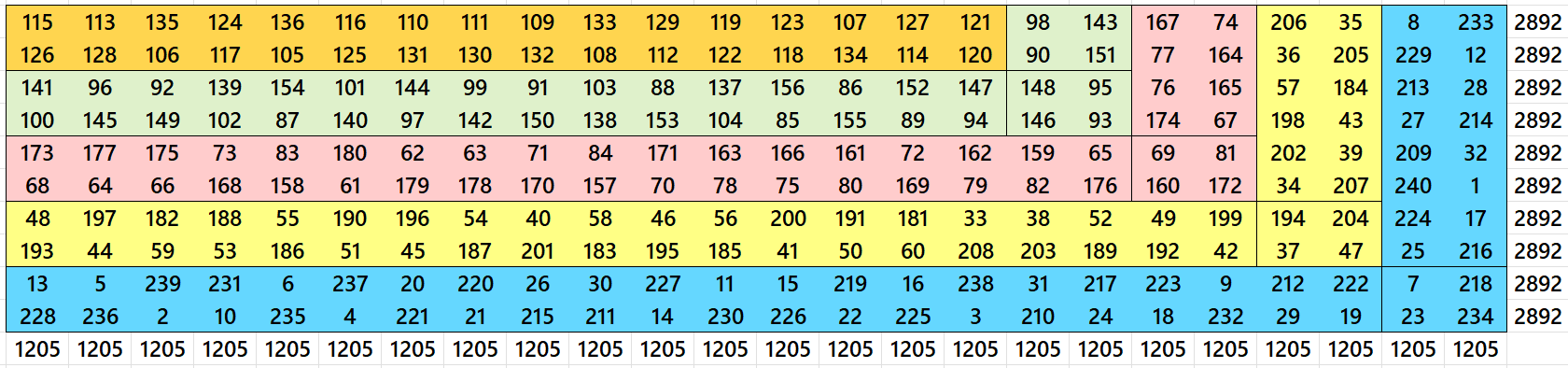
Distributions in colors is as follows:

More details are given in author’s recent work:

• Inder J. Taneja, Different Types of Magic Rectangles, Zenodo, September 04, 2023, pp. 1-26, https://doi.org/10.5281/zenodo.8316719.

Based on ideas given above, we shall construct magic squares of order 22. These are constructed with four magic rectangles. As explained above these are of are of equal sums. These are made with the help of script by H. White (Downloads (budshaw.ca) – NestedCornerRectangles)). These kinds of magic squares are never seen in the history. There are of different styles. All the three types of magic rectangles are used to bring magic squares of order 22. See below the summary.

SUMMARY: Even Orders Magic Squares from Orders 14 to 30:
Bordered, Double Digits and Cornered Magic Rectangles

1. Inder J. Taneja, Double Digits Even and Odd Orders Bordered Magic Squares.
   Also see: New Concepts in Magic Squares: Double Digits Bordered Magic Squares of Orders 7 to 108, pp. 1-30, August 09, 2023, Zenodo. https://doi.org/10.5281/zenodo.8230214.
   
2. Inder J. Taneja, Cornered Magic Squares.
   Also see: New Concepts in Magic Squares: Cornered Magic Squares of Orders 5 to 81, pp. 1-27, August 09, 2023, Zenodo. https://doi.org/10.5281/zenodo.8231157.
   
3. Inder J. Taneja, Different Types of Magic Rectangles, Zenodo, September 04, 2023, pp. 1-26, https://doi.org/10.5281/zenodo.8316719.
   
4. Inder J. Taneja, Different Types of Magic Rectangles in Construction of Magic Squares of Orders 14 and 18.
   Also see: Different Types of Magic Rectangles in Construction of Magic Squares of Orders 14 and 18, Zenodo, September 10, 2023, pp. 1-32, https://doi.org/10.5281/zenodo.8331709.
   
5. Inder J. Taneja, Different Types of Magic Rectangles in Construction of Magic Squares of Order 22.
   Also see: Different Types of Magic Rectangles in Construction of Magic Squares of Order 22, Zenodo, September 10, 2023, pp. 1-36, https://doi.org/10.5281/zenodo.8331743.
   
6. Inder J. Taneja, Different Types of Magic Rectangles in Construction of Magic Squares of Order 26.
   Also see: Different Types of Magic Rectangles in Construction of Magic Squares of Order 26, Zenodo, September 10, 2023, pp. 1-39, https://doi.org/10.5281/zenodo.8331750.
   
7. Inder J. Taneja, Different Types of Magic Rectangles in Construction of Magic Squares of Order 30. Also see: Different Types of Magic Rectangles in Construction of Magic Squares of Order 30, Zenodo, September 10, 2023, pp. 1-44, https://doi.org/10.5281/zenodo.8331755.
   
8. Inder J. Taneja, Different Types of Magic Rectangles in Construction of Magic Squares of Order 34. Also see: Different Types of Magic Rectangles in Construction of Magic Squares of Order 34, Zenodo, September 10, 2023, pp. 1-49, https://doi.org/10.5281/zenodo.8331759.
   
9. Inder J. Taneja, Cornered Magic Squares in Construction of Magic Squares of Orders 16, 20, 24 and 28
   Also see: Cornered Magic Squares in Construction of Magic Squares of Orders 16, 20, 24 and 28, Zenodo, September 10, 2023, pp. 1-35, https://doi.org/10.5281/zenodo.8332156.