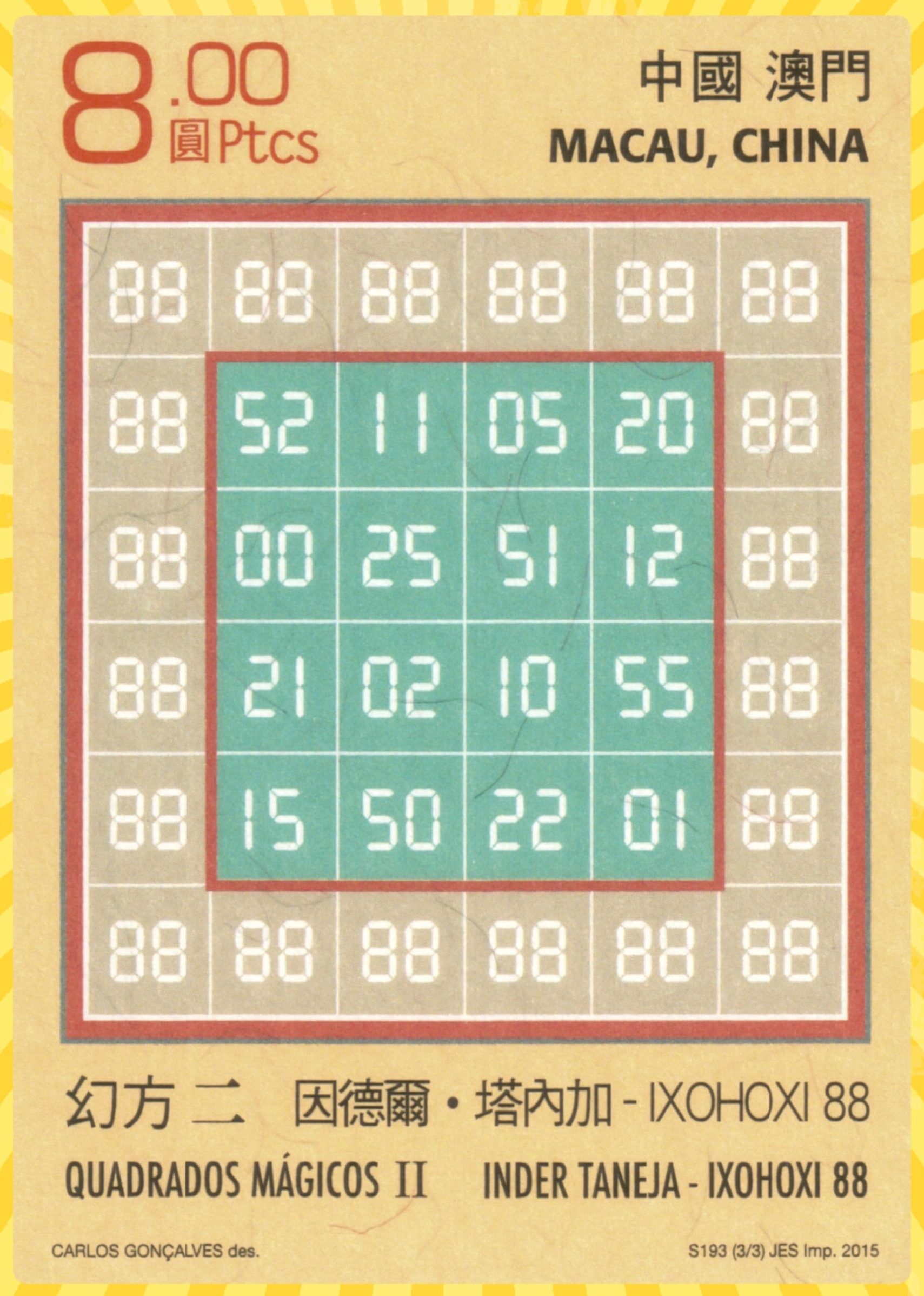
Never Seen Before
This work brings magic squares in very different way. These are based on three different types of magic rectangles:
1. Bordered Magic Rectangles:
2. Double Digits Magic Rectangles:
3. Cornered magic rectangles.
First of let’s understand these magic rectangles one by one. Removing external borders in each case still we left with lower order magic rectangles. See below few examples in each case.
1. Bordered Magic Rectangles
Below are two examples of bordered magic rectangles
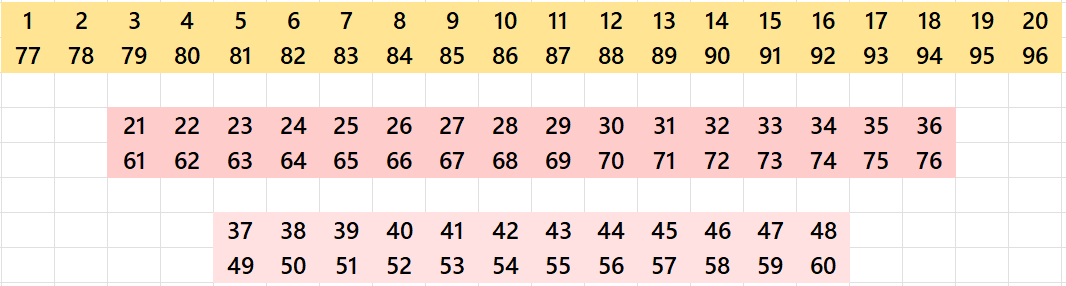
Example 1. Bordered Magic Rectangle of Order 12×18
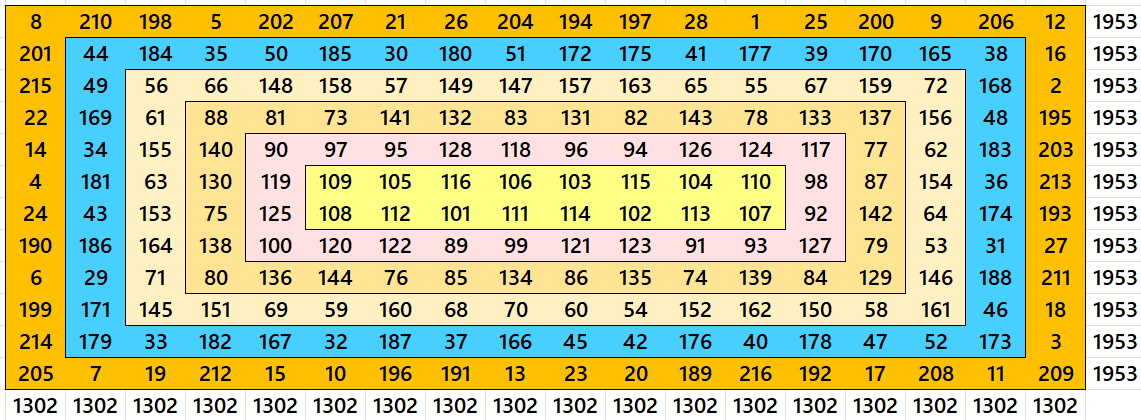
The entries according to colors are as follows:
Example 2. Bordered Magic Rectangle of Order 6×16
The entries according to colors are as follows:
More details are given in author’s recent work:
- Inder J. Taneja, Different Types of Magic Rectangles, Zenodo, September 04, 2023, pp. 1-26, https://doi.org/10.5281/zenodo.8316719.
2. Double Digits Magic Rectangles
Below are two examples of bordered magic rectangles
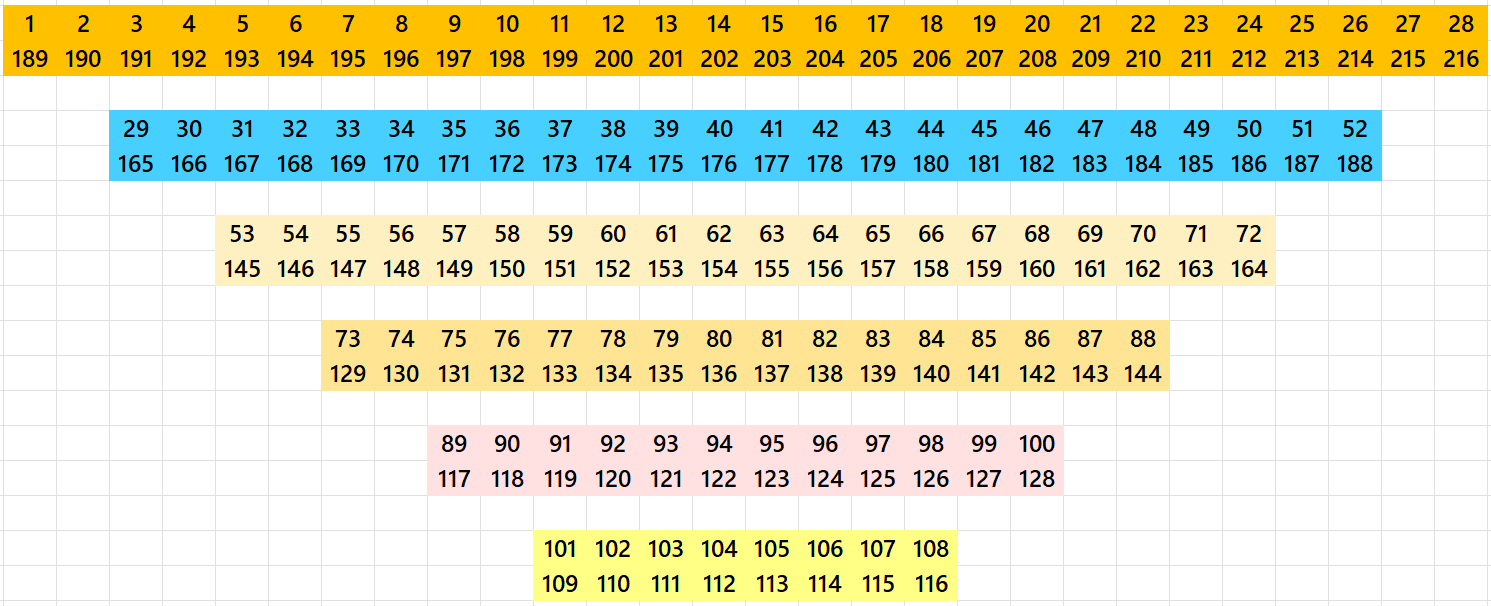
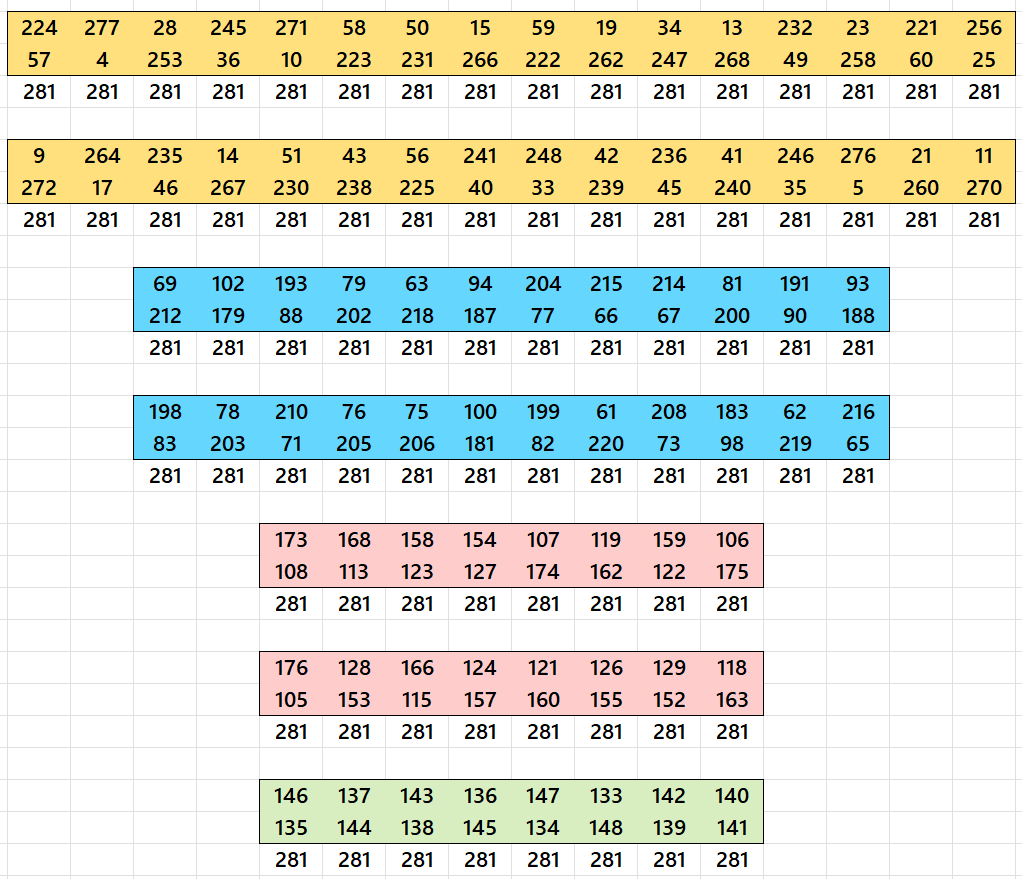
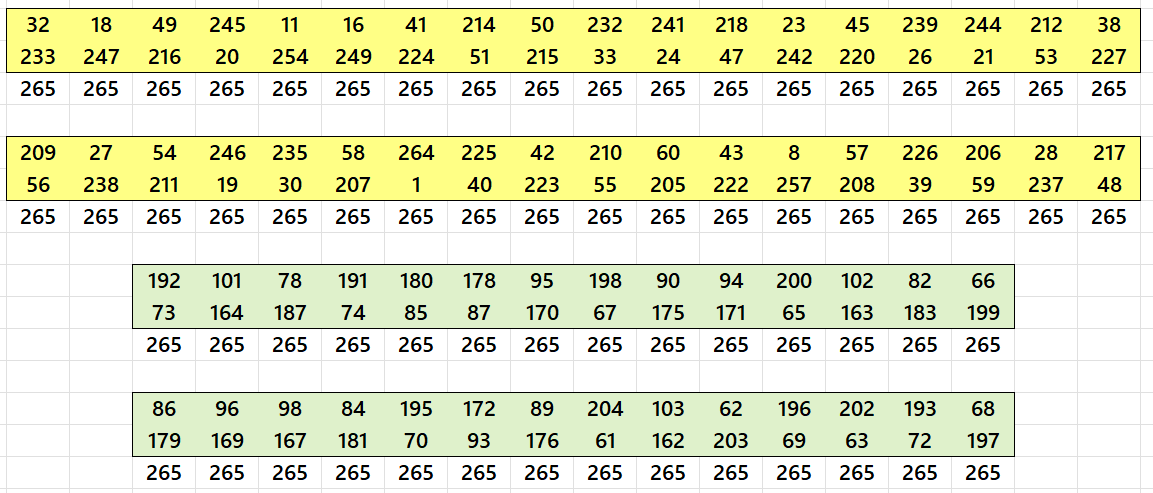
Example 1. Double Digits Magic Rectangle of Order 14×20

Except the corners, the entries entries sums are understood as
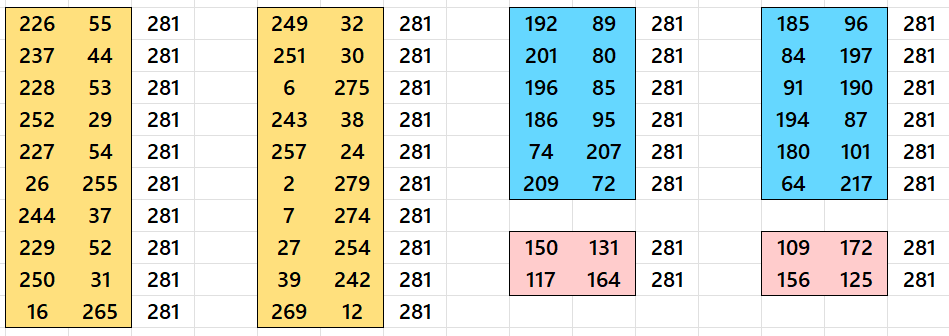
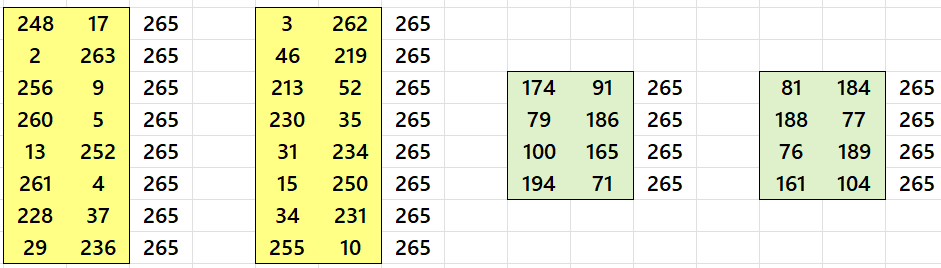
Example 2. Double Digits Magic Rectangle of Order 12×18
Except the corners, the entries entries sums are understood as

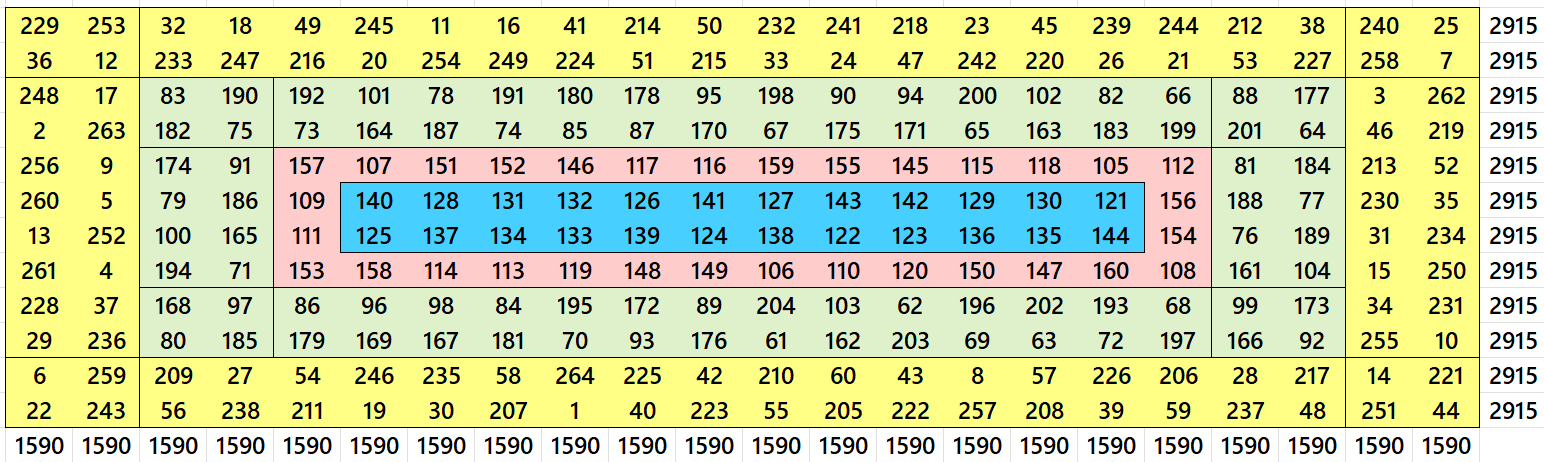
After reorganizing the internal magic rectangle of order 4×16, we have the following double digits magic rectangle:
More details are given in author’s recent work:
- Inder J. Taneja, Different Types of Magic Rectangles, Zenodo, September 04, 2023, pp. 1-26, https://doi.org/10.5281/zenodo.8316719.
3. Cornered Magic Rectangles
Below are two examples of cornered magic rectangles
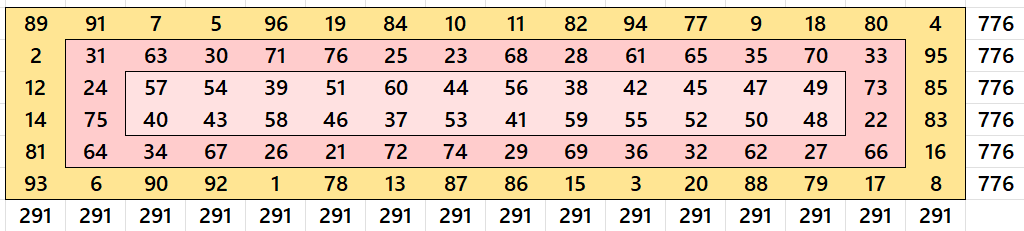
Example 1. Cornered Magic Rectangle of Order 8×12
Let’s consider a cornered magic rectangle of order 8×12 formed by 96 sequencial entries, i.e., from 1 to 96:
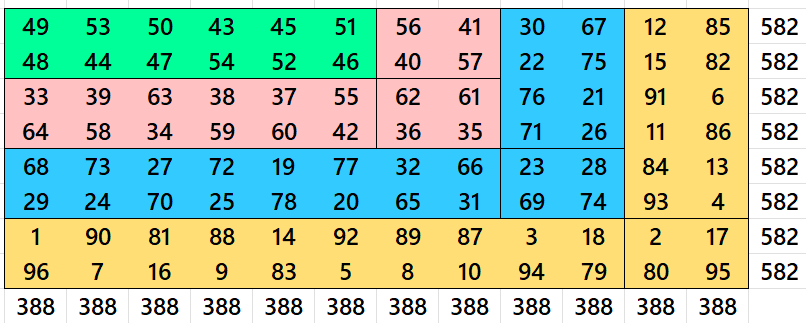
Distributions in colors as follows:

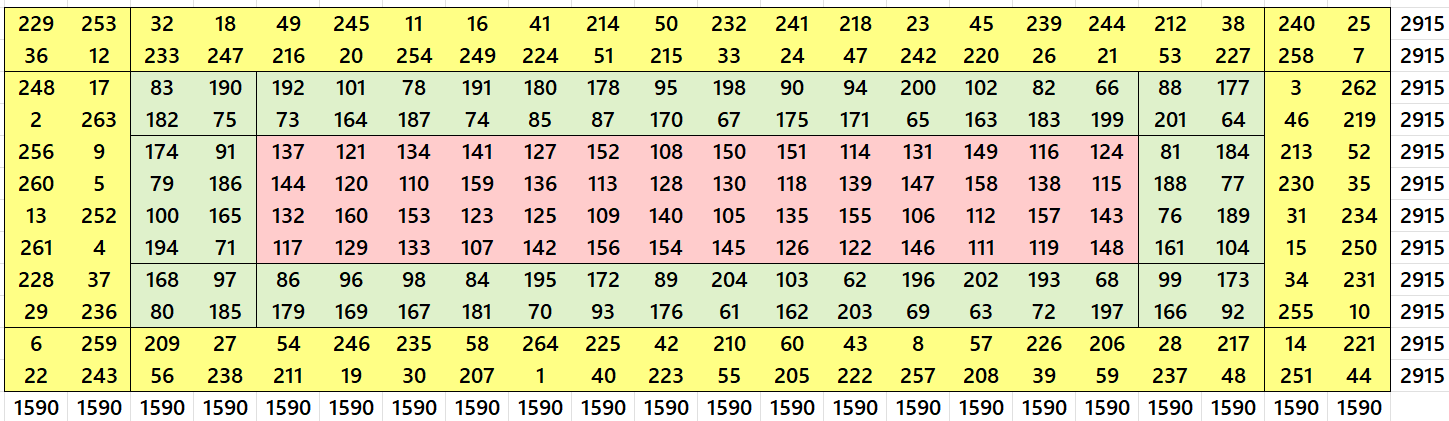
Example 2. Cornered Magic Rectangle of Order 8×12
Let’s consider a cornered magic rectangle of order 10×24 formed by 240 sequencial entries, i.e., from 1 to 240:
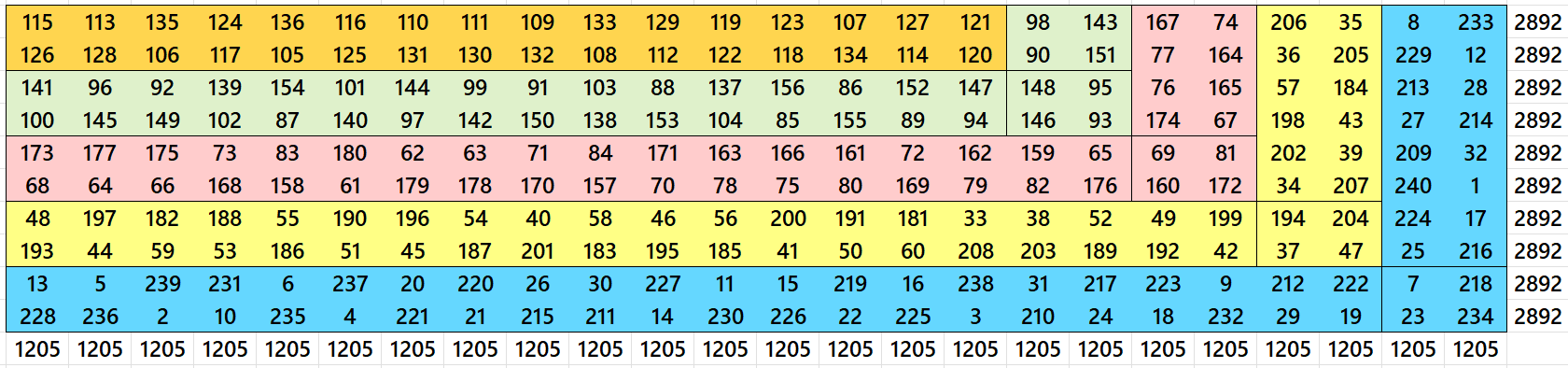
Distributions in colors as follows:

More details are given in author’s recent work:
- Inder J. Taneja, Different Types of Magic Rectangles, Zenodo, September 04, 2023, pp. 1-26, https://doi.org/10.5281/zenodo.8316719.
Based on ideas given above, we shall construct magic squares of order 22. These are constructed with four magic rectangles. As explained above these are of are of equal sums. These are made with the help of script by H. White (Downloads (budshaw.ca) – NestedCornerRectangles)). These kinds of magic squares are never seen in the history. There are of different styles. All the three types of magic rectangles are used to bring magic squares of order 22. See below:
Magic Squares of Order 22
Initially below are two double digits and cornered magic squares of order 22:

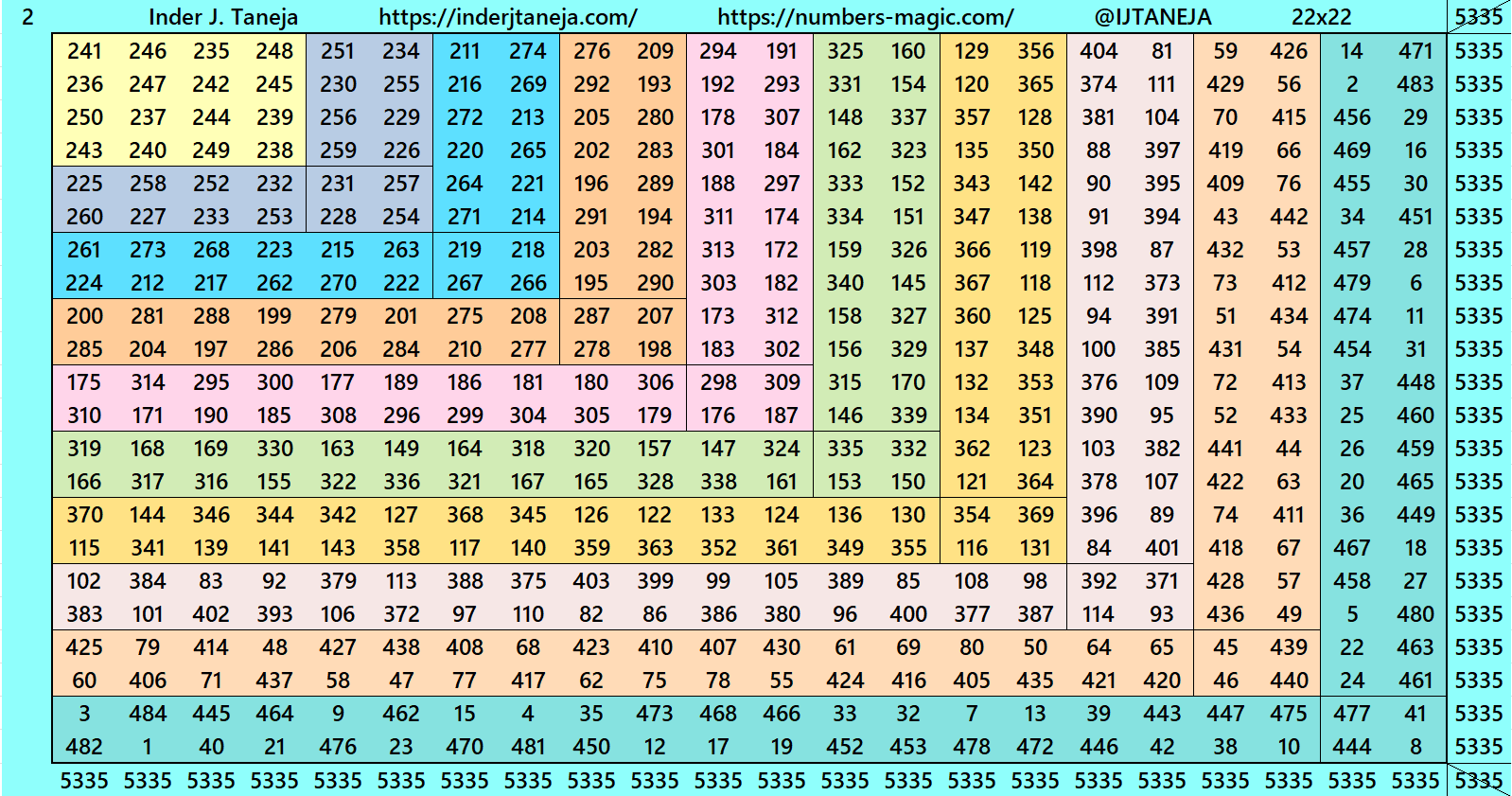
1. Bordered Magic Rectangles and
Magic Squares of Order 22
Below are examples of magic squares of order 22 centered in magic squares of order 6, 10 and 14 respectively. These are constructed with four equal sums bordered magic rectangles of orders 8×14, 6×16 and 4×18 respectively.
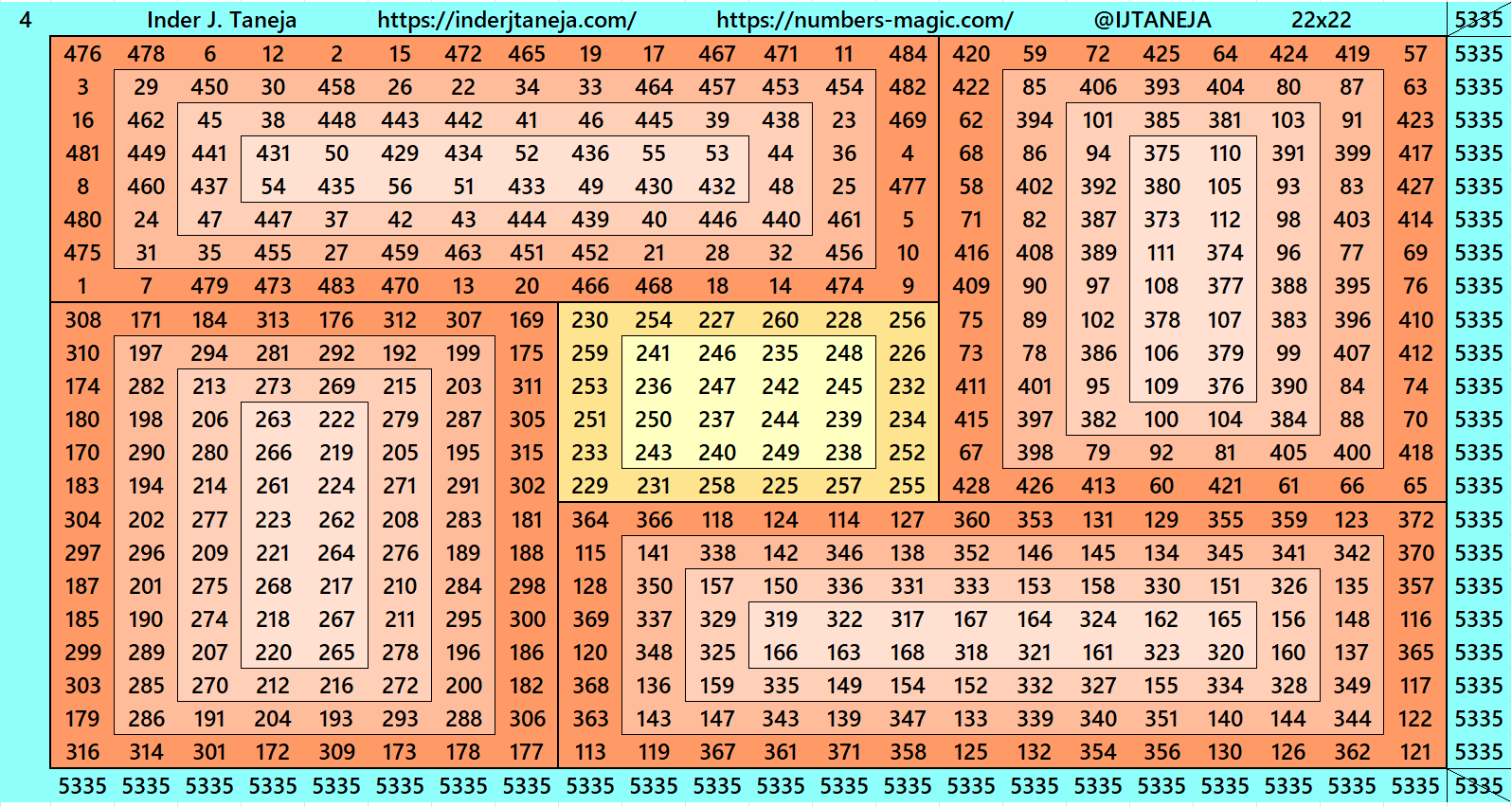
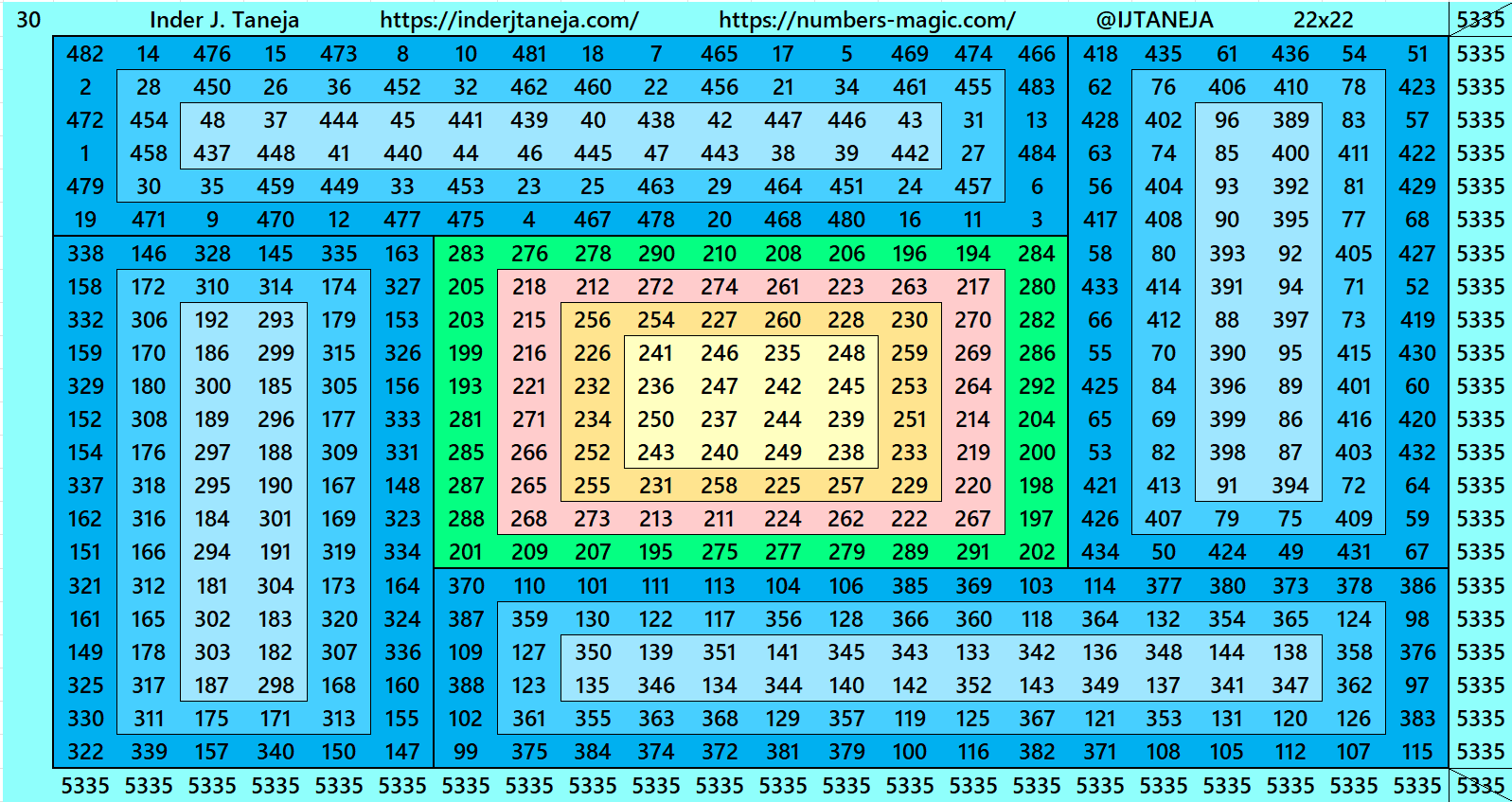
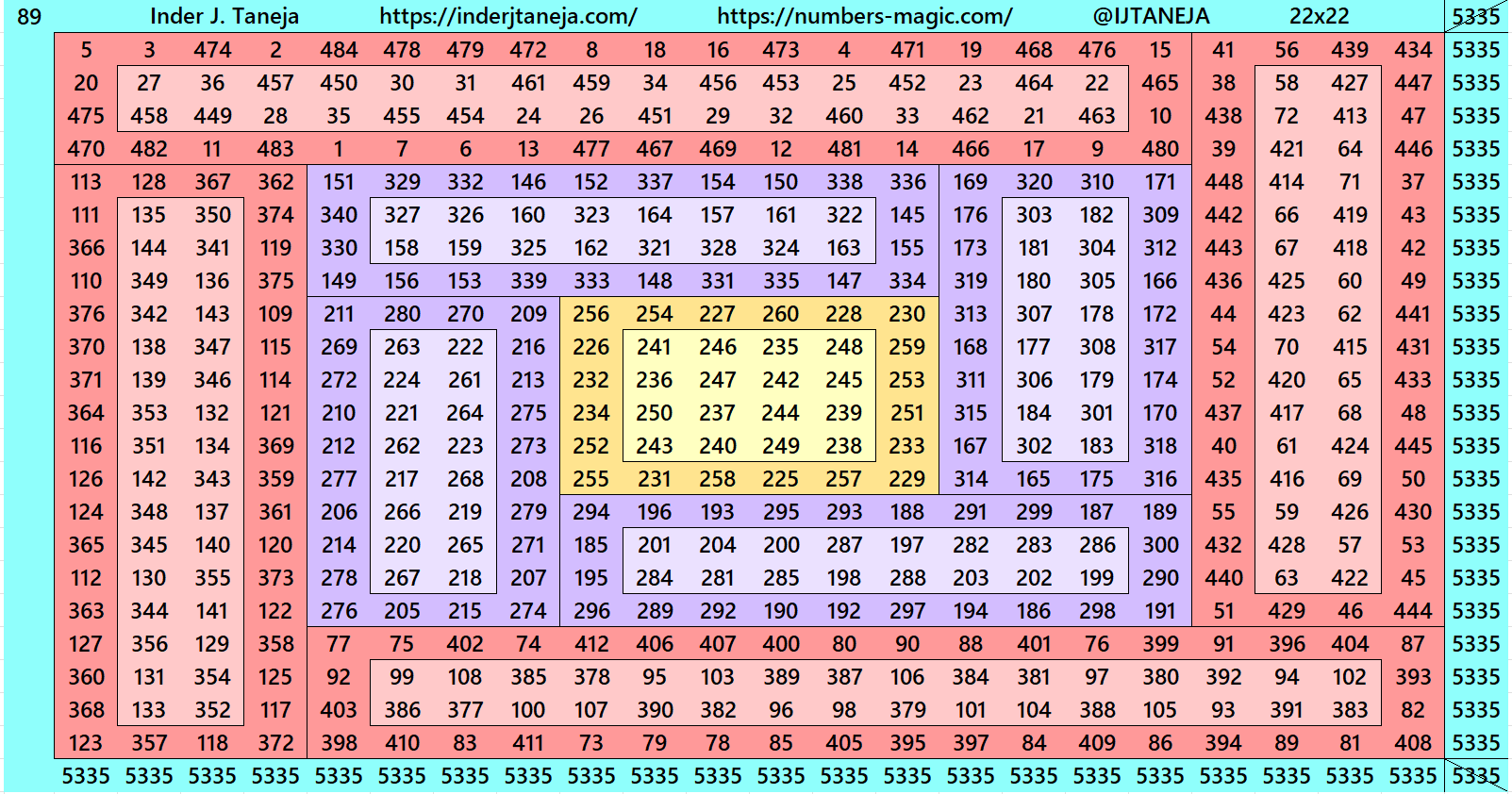
More examples are in pdf file attached at the end of work.
2. Double Digits Magic Rectangles and
Magic Squares of Order 22
Below are examples of magic squares of order 22 centered in magic squares of order 6 and 10 respectively. These are constructed with four equal sums double digits magic rectangles of orders 8×14 and 6×16 respectively.
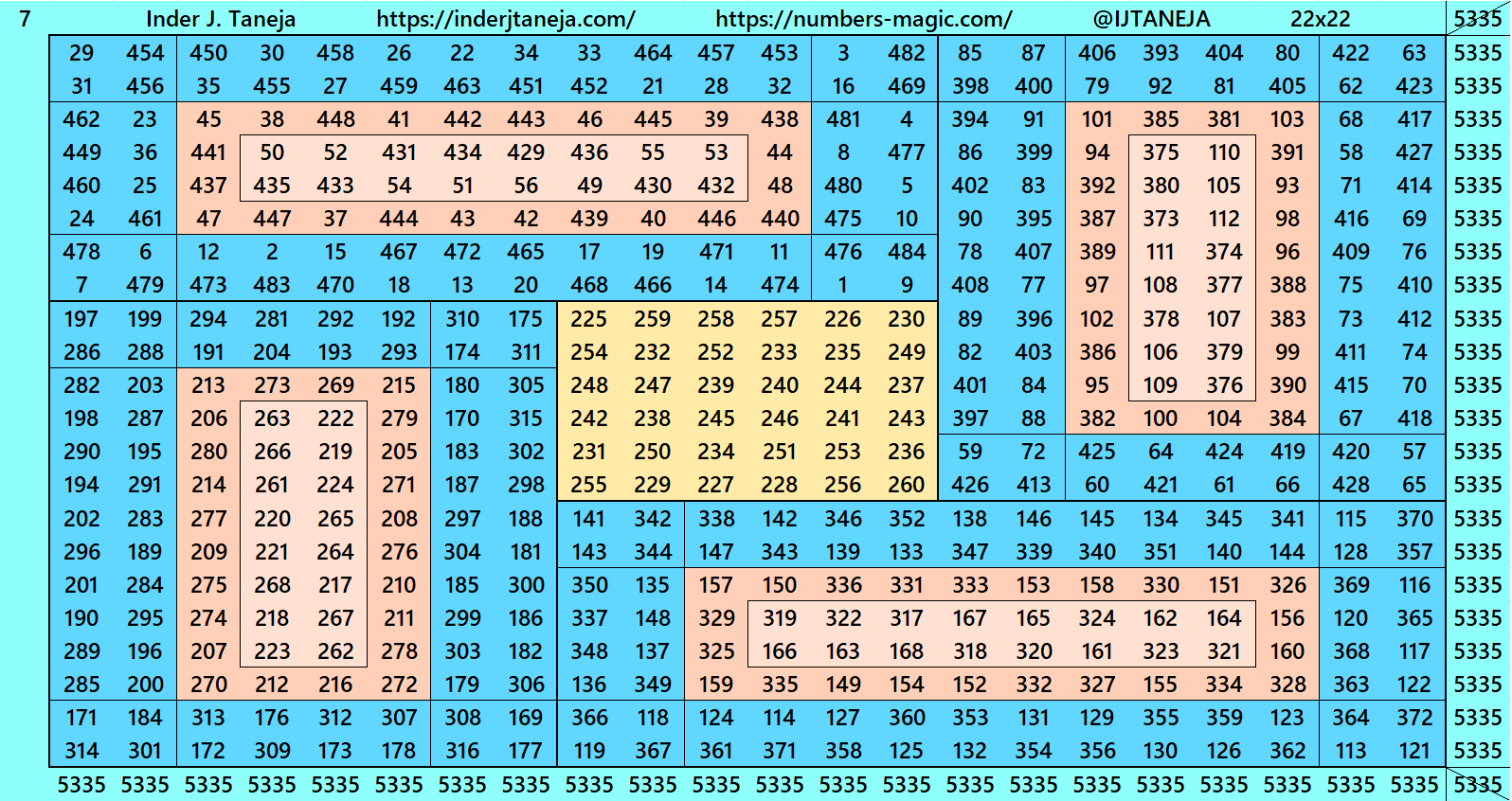
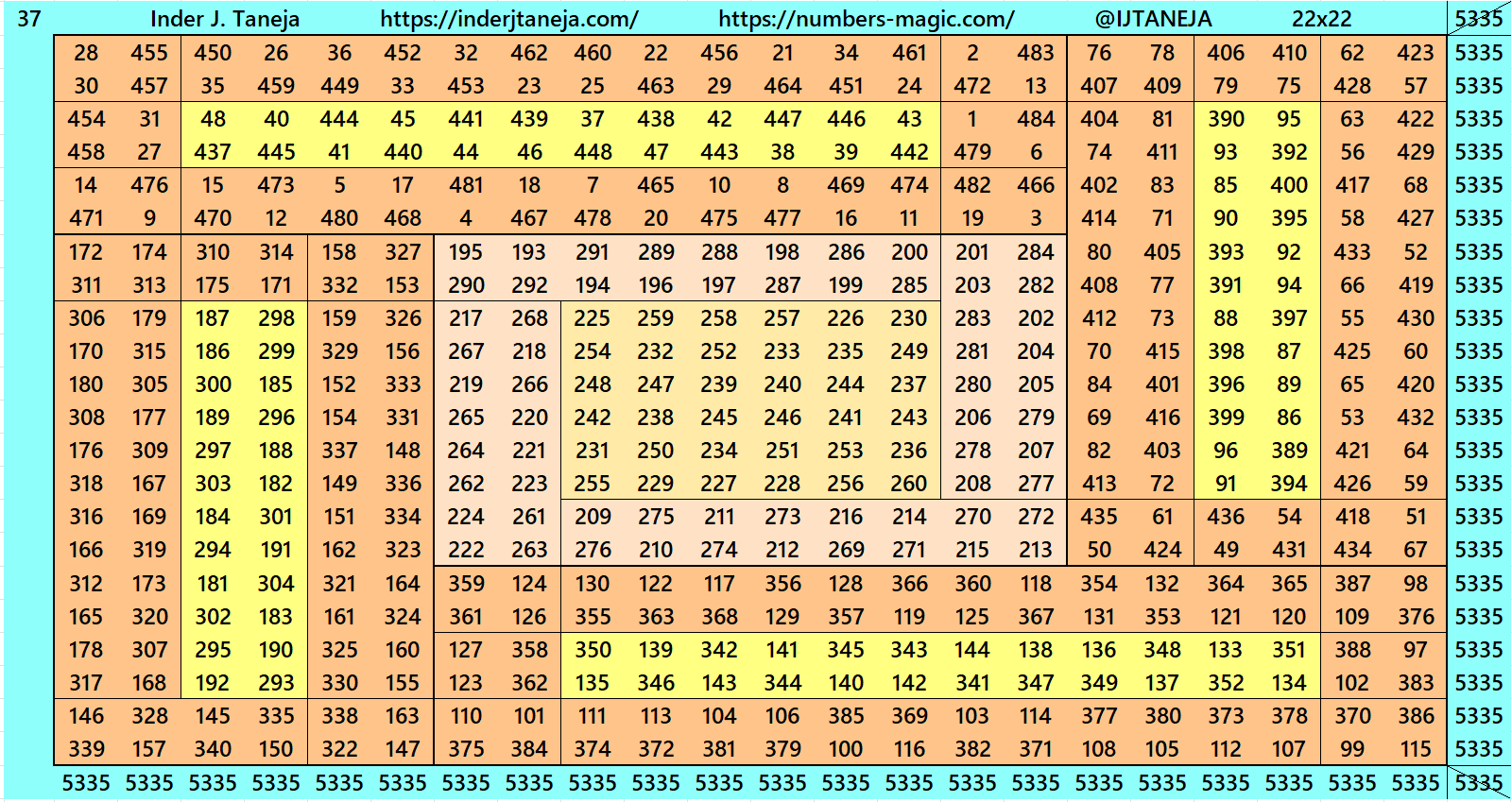
In this case we don’t have magic square of order 22 centered in magic square of order 14 having four equal sums double digits magic rectangles.
3. Cornered Magic Rectangles and
Magic Squares of Order 22: First Type
Below are examples of magic squares of order 22 centered in magic squares of order 6, 10 and 14 respectively. These are constructed with four equal sums cornered magic rectangles of orders 8×14, 6×16 and 4×18 respectively.
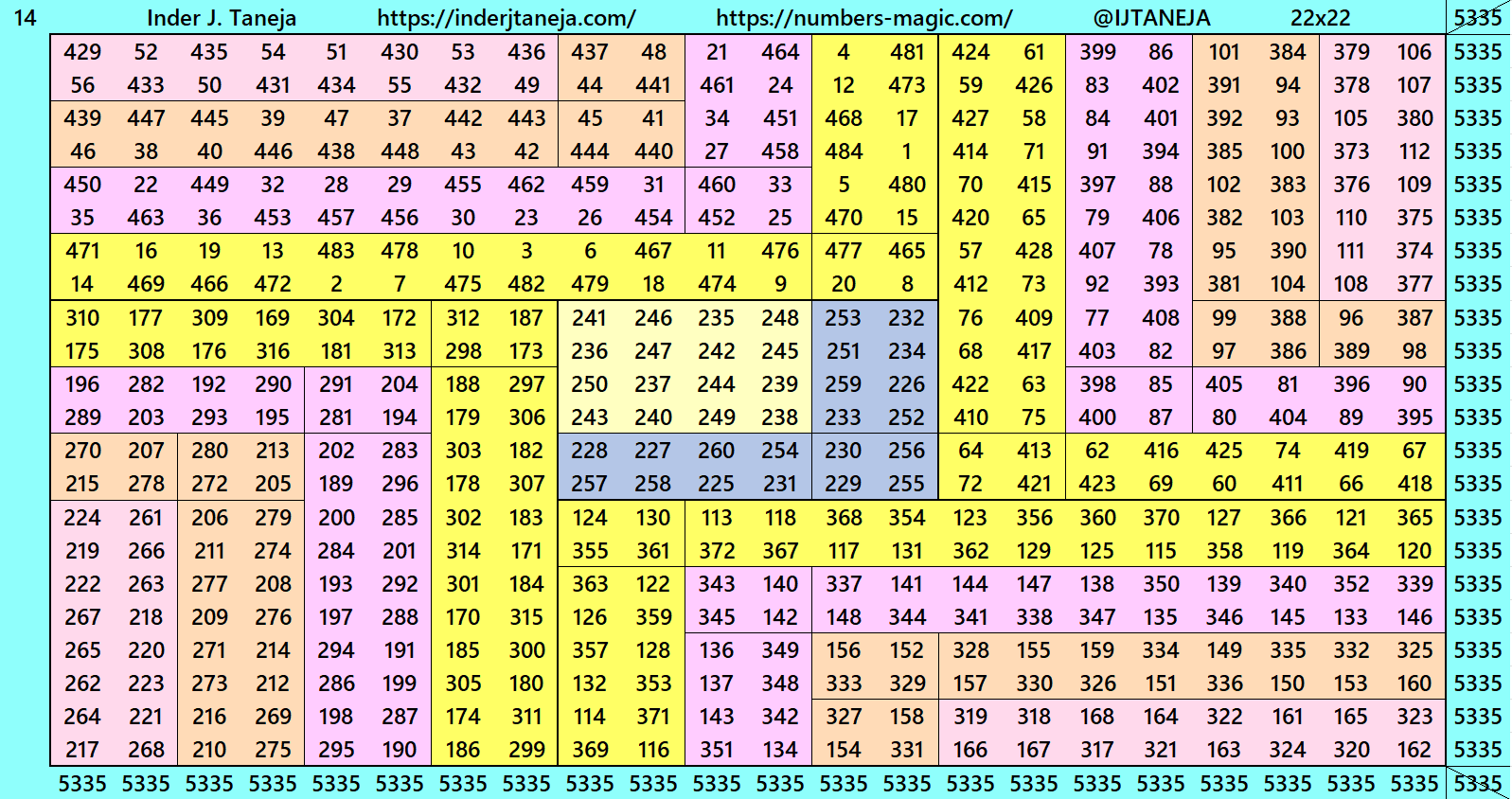
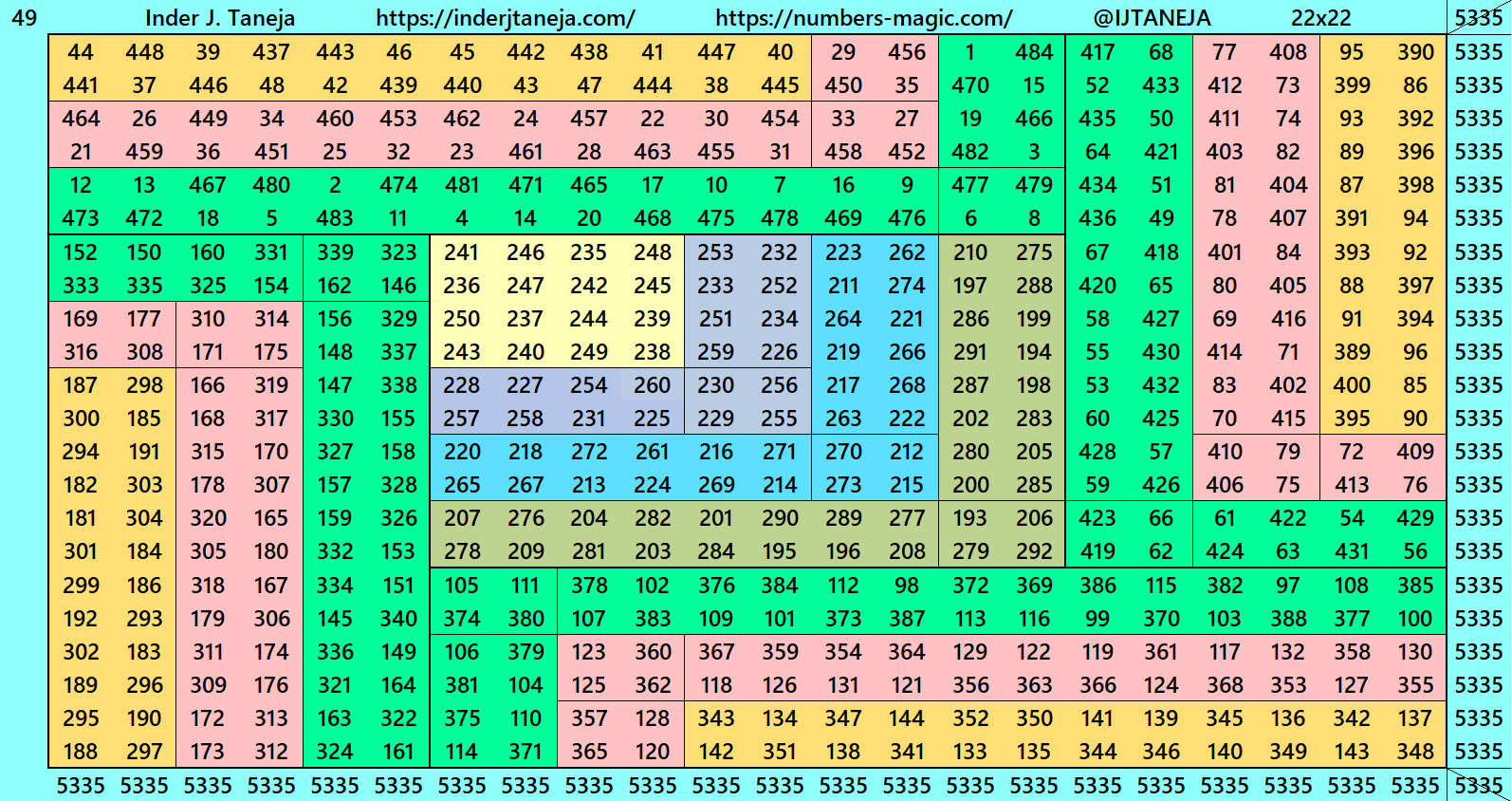
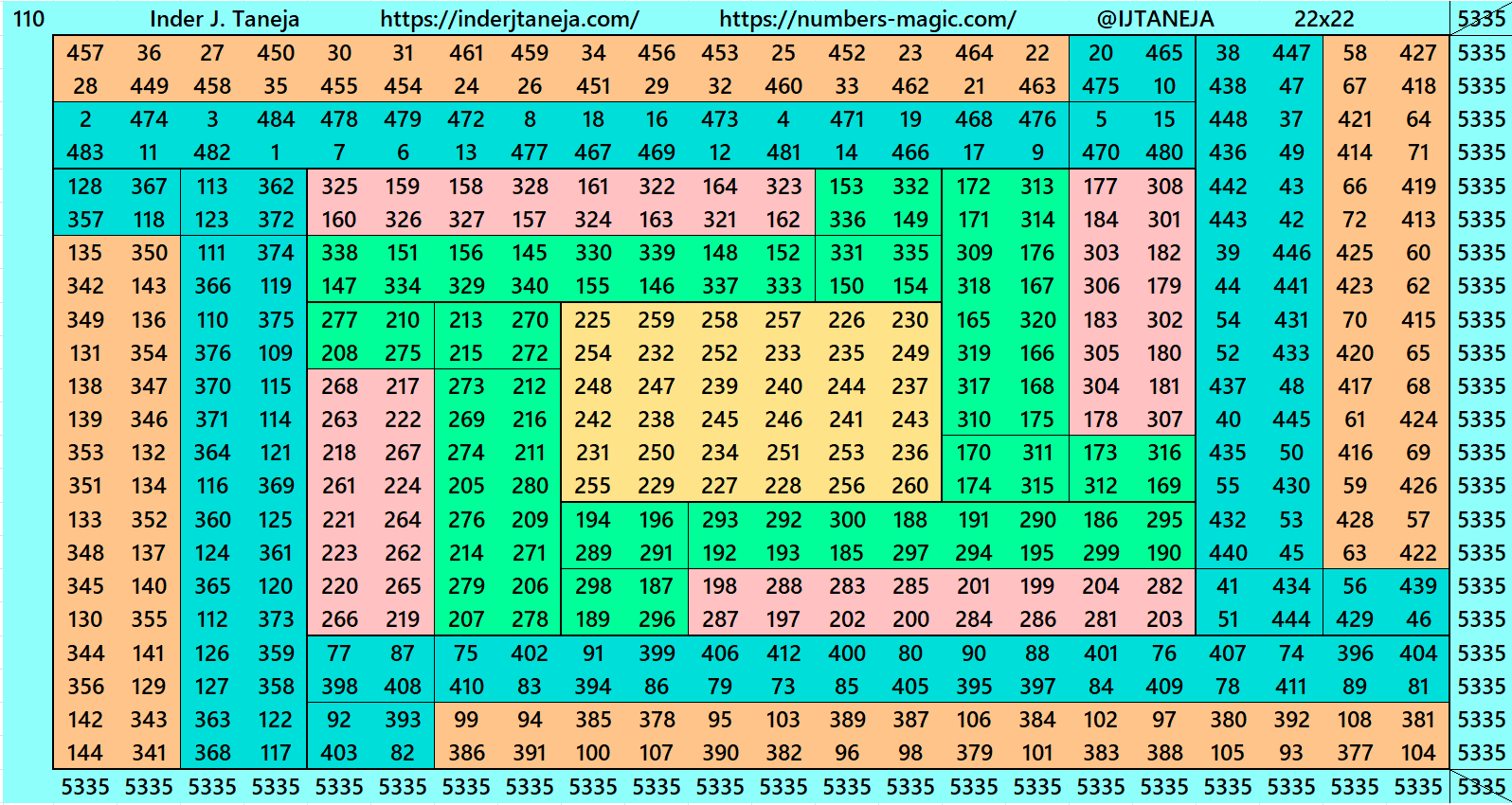
3. Cornered Magic Rectangles and
Magic Squares of Order 22: Second Type
Below are examples of magic squares of order 22 centered in magic squares of order 6 and 10 respectively. These are constructed with four equal sums cornered magic rectangles of orders 8×14 and 6×16 respectively.
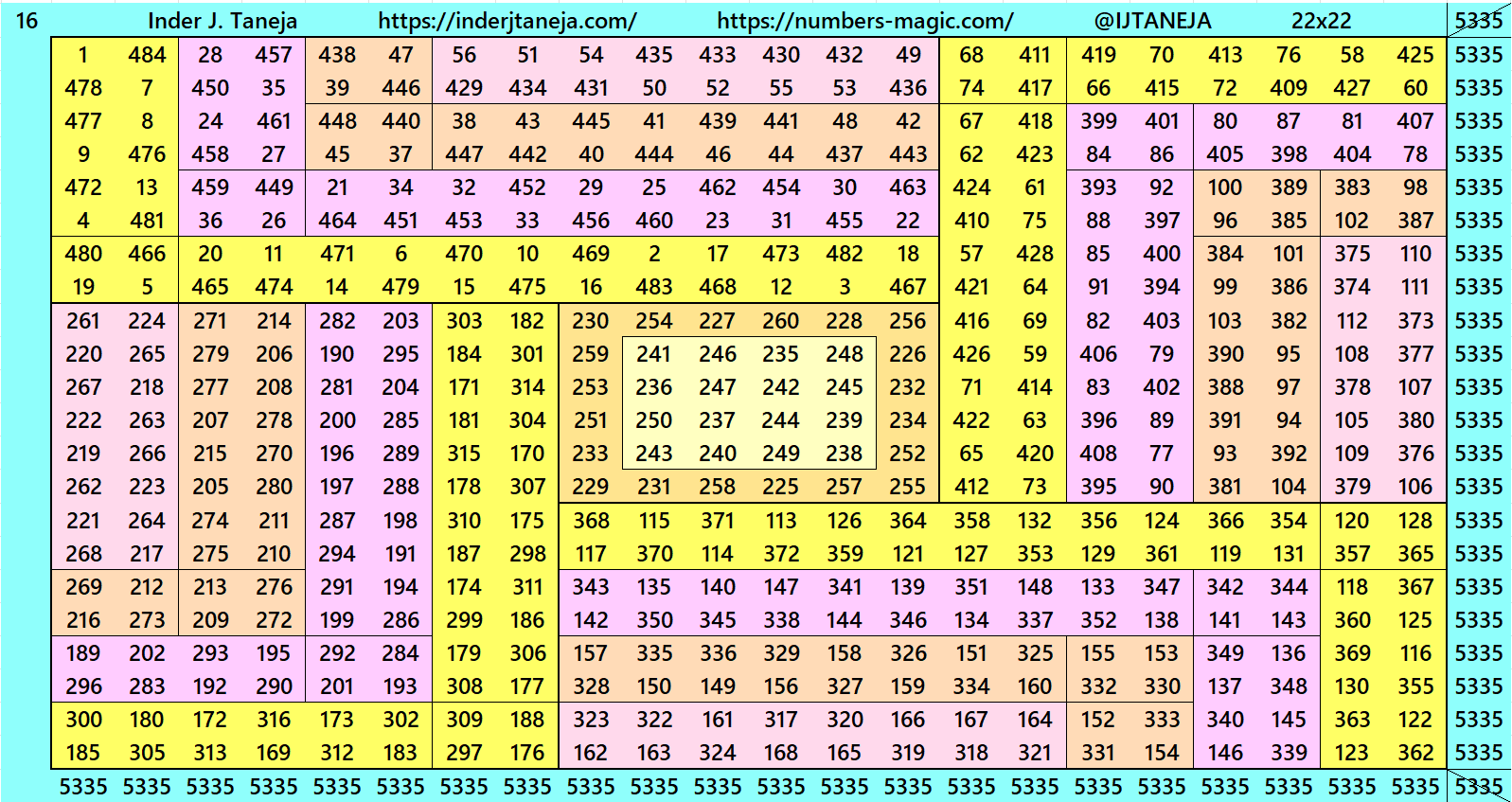

3. Cornered Magic Rectangles and
Magic Squares of Order 22: Third Type
Below are examples of magic squares of order 22 centered in magic squares of order 6, 10 and 14 respectively. These are constructed with four equal sums cornered magic rectangles of orders 8×14, 6×16 and 4×18 respectively.
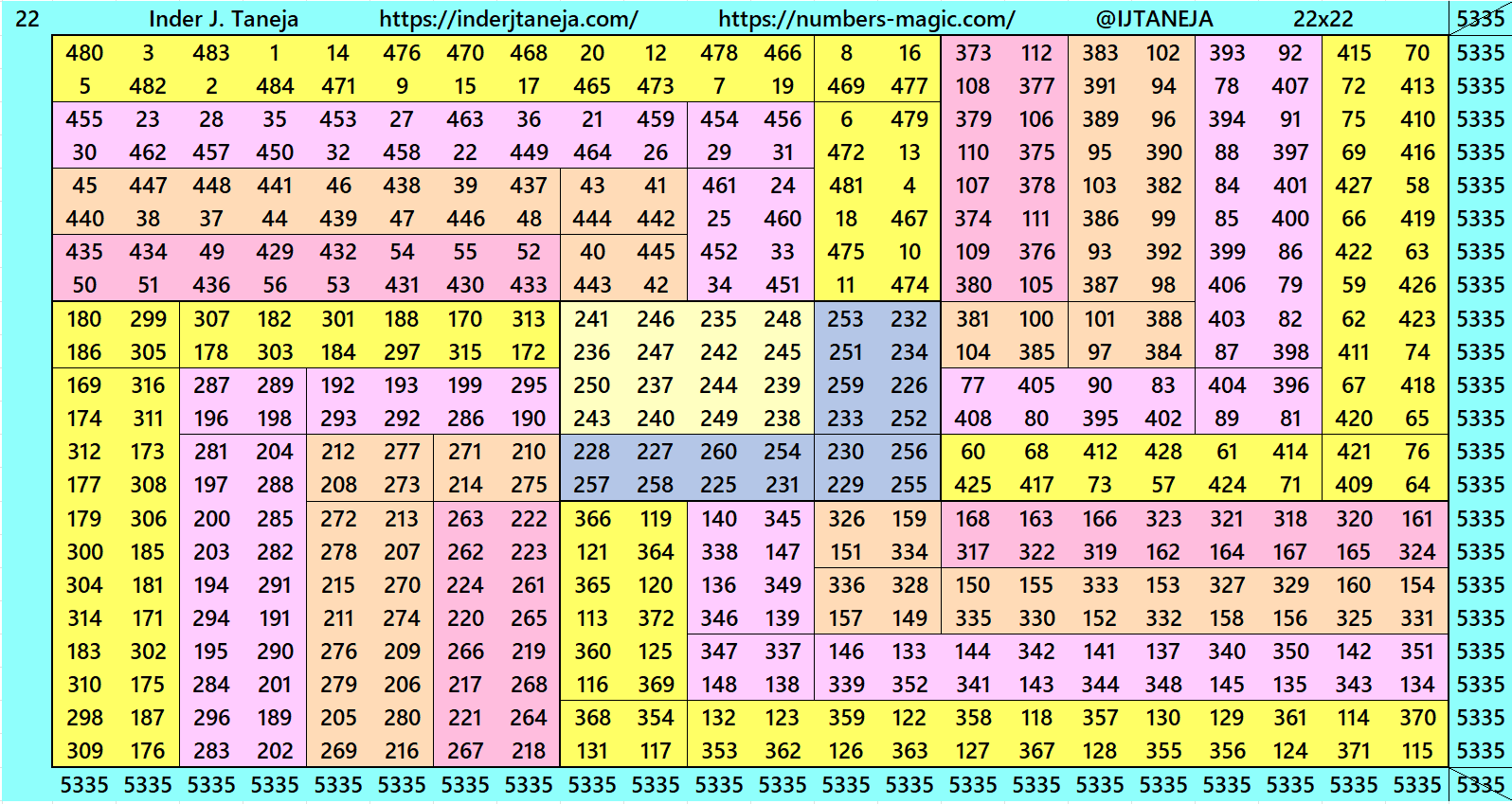
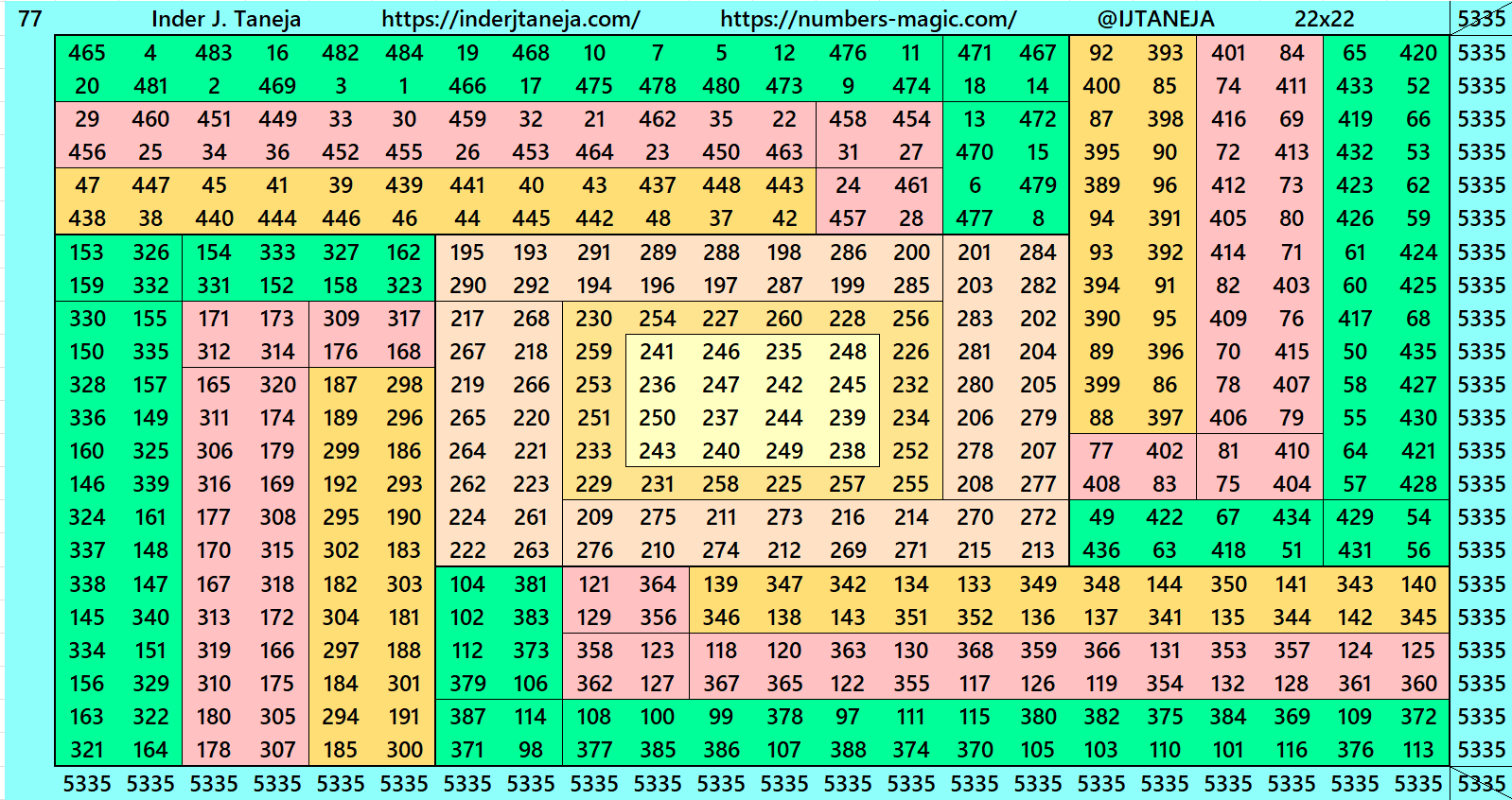
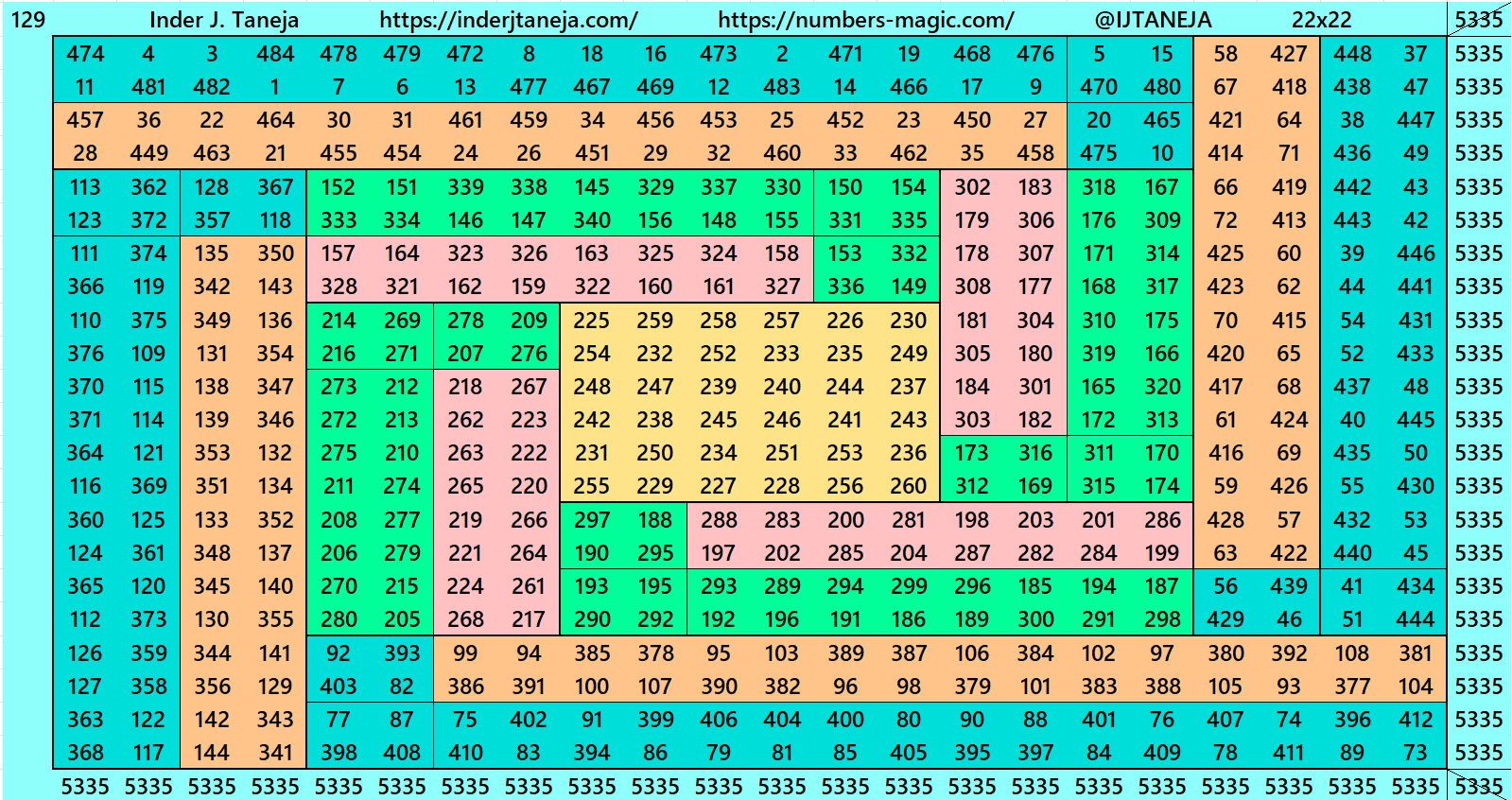
PDF File of Magic Squares of Order 22
Below is a pdf file of 132 magic squares of order 22 for download. These are constructed with 4 equal sums magic rectangles of three types as explained above. Magic squares number 1 and 2 are basic.
References
- Inder J. Taneja, Double Digits Even and Odd Orders Bordered Magic Squares.
Also see: New Concepts in Magic Squares: Double Digits Bordered Magic Squares of Orders 7 to 108, pp. 1-30, August 09, 2023, Zenodo. https://doi.org/10.5281/zenodo.8230214. - Inder J. Taneja, New Concepts in Magic Squares: Cornered Magic Squares of Orders 5 to 81, pp. 1-27, August 09, 2023, Zenodo. https://doi.org/10.5281/zenodo.8231157.
- Inder J. Taneja, Different Types of Magic Rectangles, Zenodo, September 04, 2023, pp. 1-26, https://doi.org/10.5281/zenodo.8316719.
- Inder J. Taneja, Different Types of Magic Rectangles in Construction of Magic Squares of Orders 14 and 18, Zenodo, September 10, 2023, pp. 1-32, https://doi.org/10.5281/zenodo.8331709.
- Inder J. Taneja, Different Types of Magic Rectangles in Construction of Magic Squares of Order 22, Zenodo, September 10, 2023, pp. 1-36, https://doi.org/10.5281/zenodo.8331743.
- Inder J. Taneja, Different Types of Magic Rectangles in Construction of Magic Squares of Order 26, Zenodo, September 10, 2023, pp. 1-39, https://doi.org/10.5281/zenodo.8331750.
- Inder J. Taneja, Different Types of Magic Rectangles in Construction of Magic Squares of Order 30, Zenodo, September 10, 2023, pp. 1-44, https://doi.org/10.5281/zenodo.8331755.
- Inder J. Taneja, Different Types of Magic Rectangles in Construction of Magic Squares of Order 34, Zenodo, September 10, 2023, pp. 1-49, https://doi.org/10.5281/zenodo.8331759.
- Inder J. Taneja, Cornered Magic Squares in Construction of Magic Squares of Orders 16, 20, 24 and 28, Zenodo, September 10, 2023, pp. 1-35, https://doi.org/10.5281/zenodo.8332156.