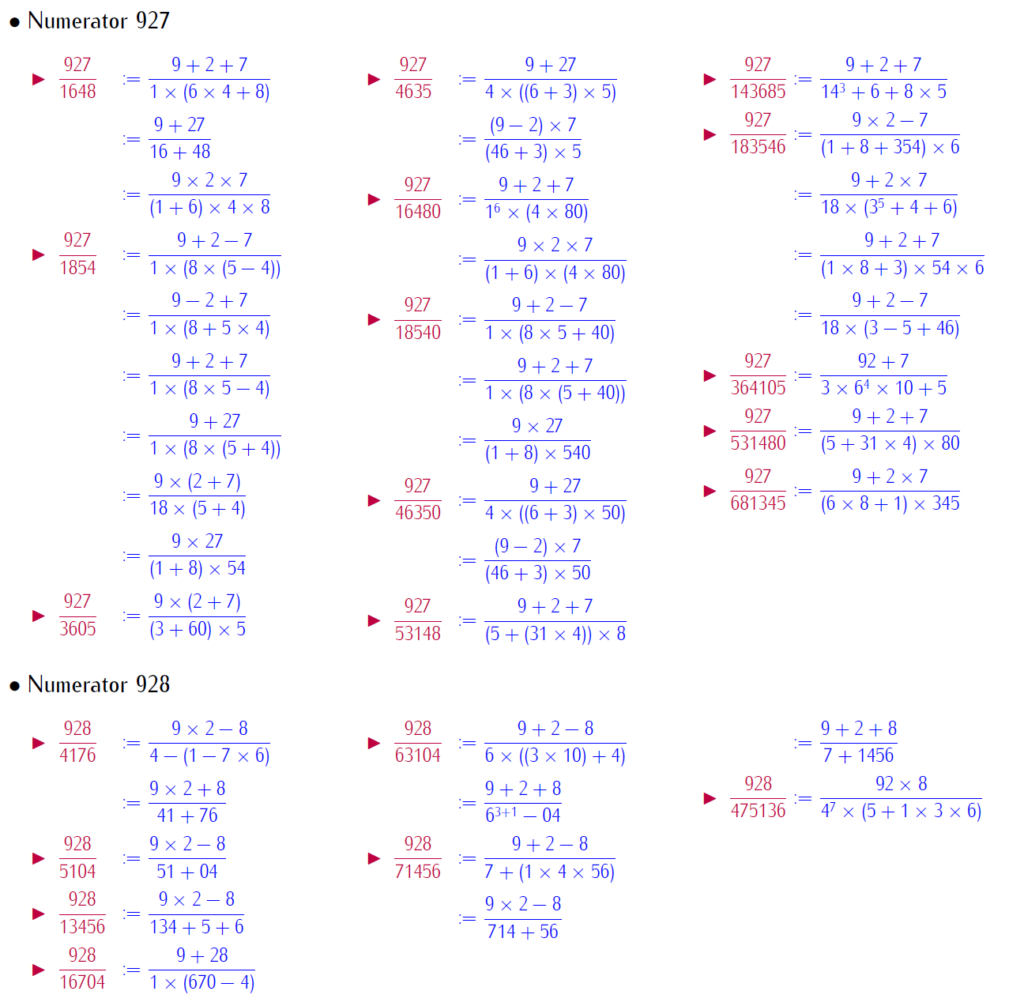
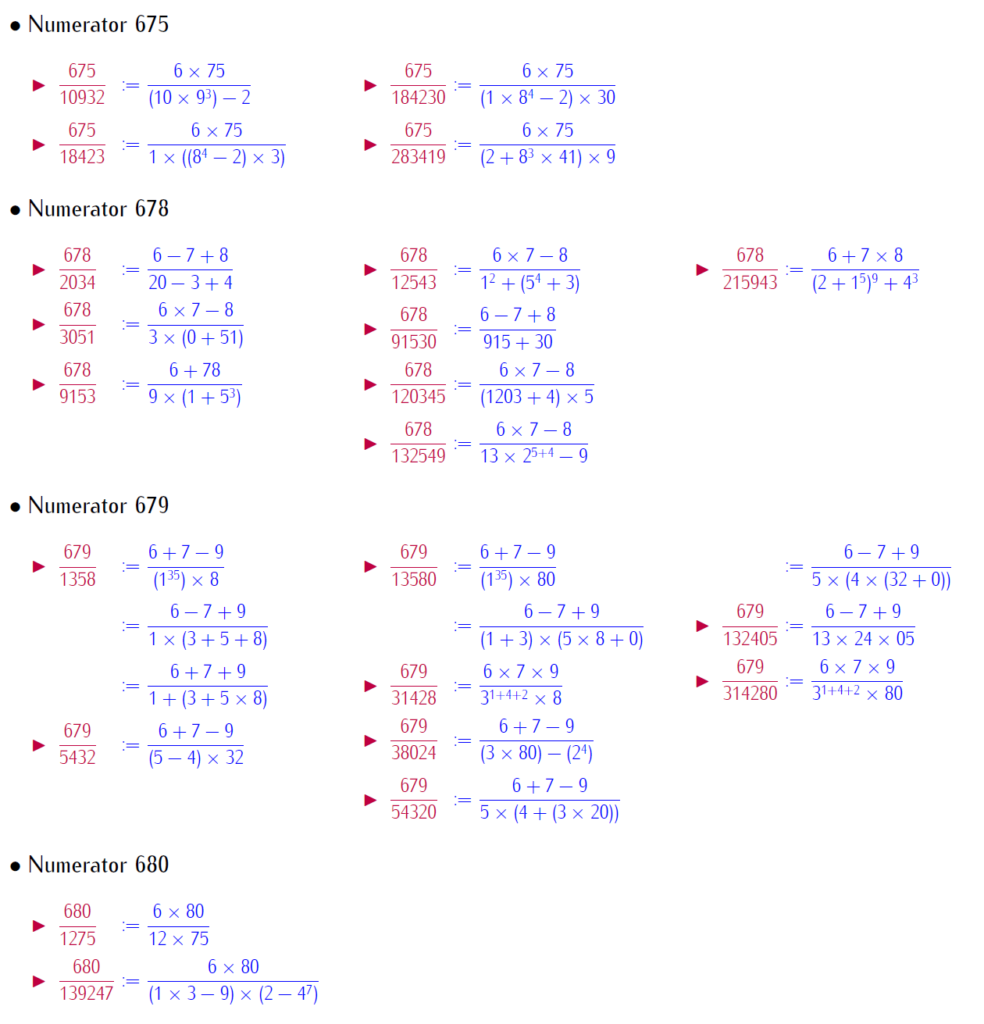
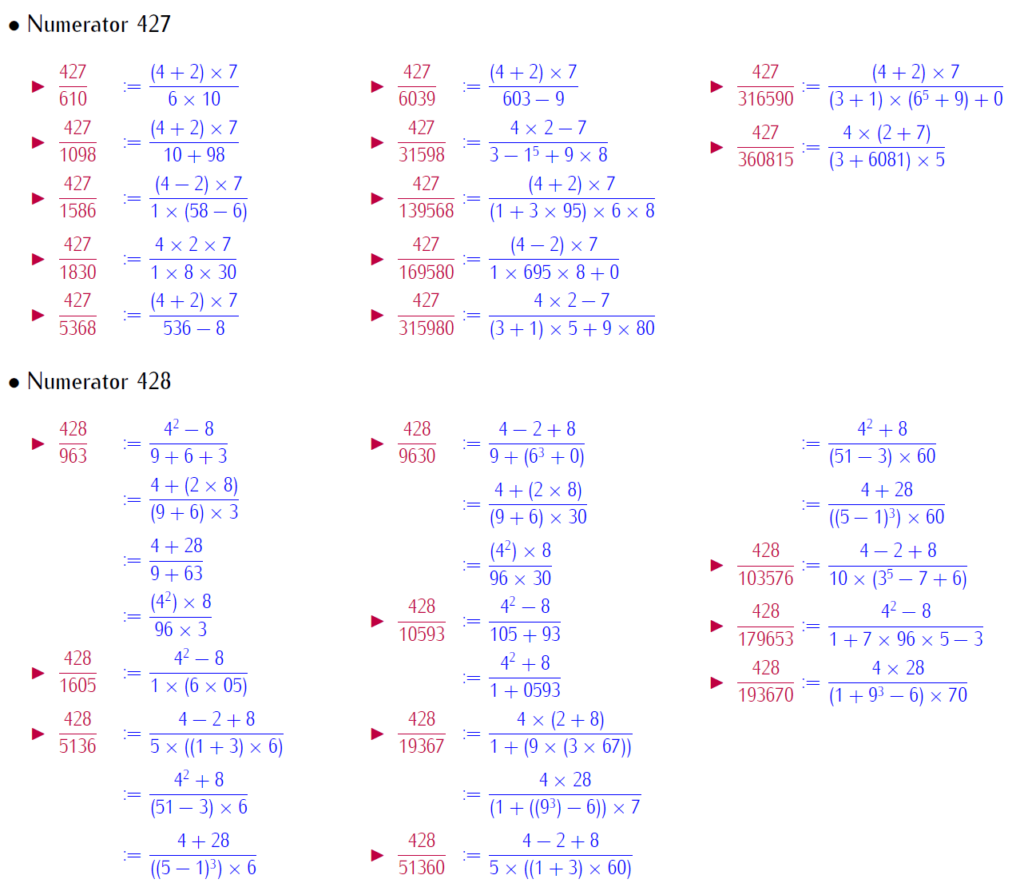
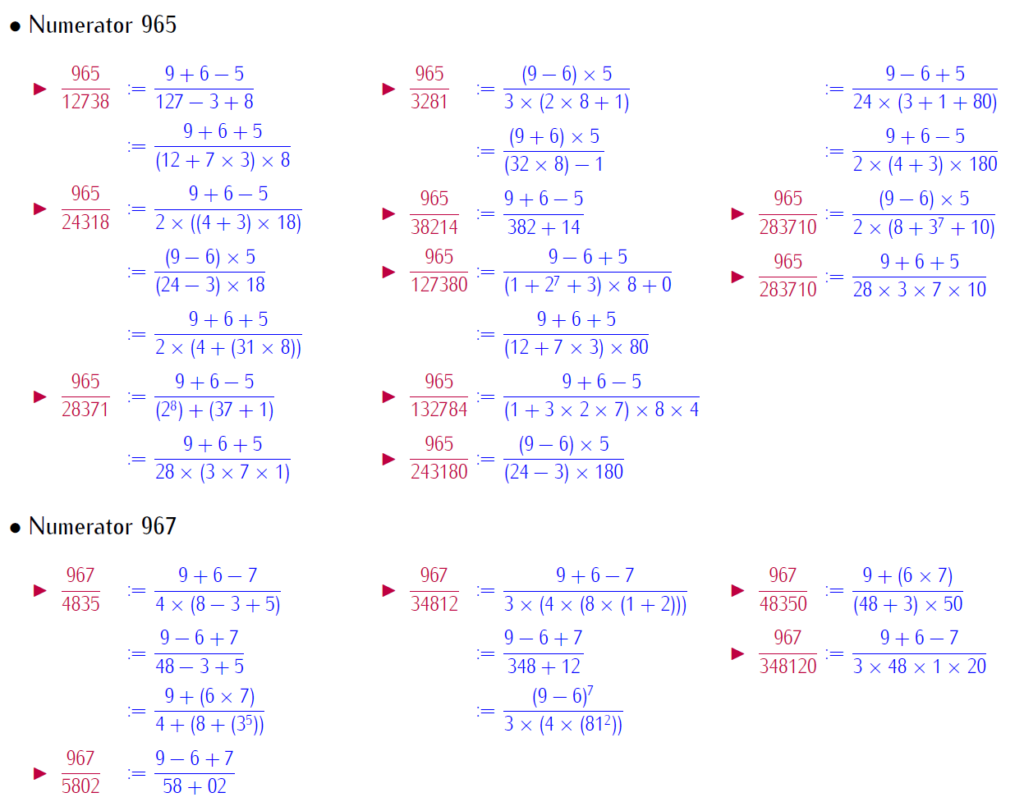
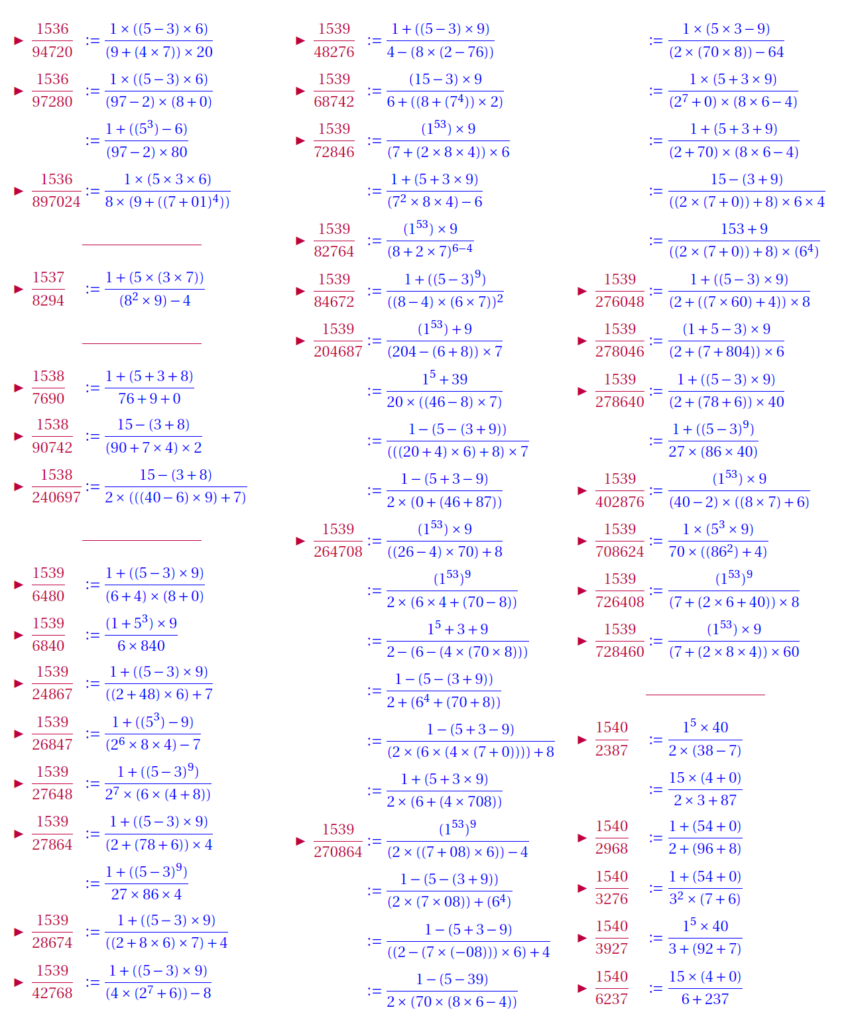
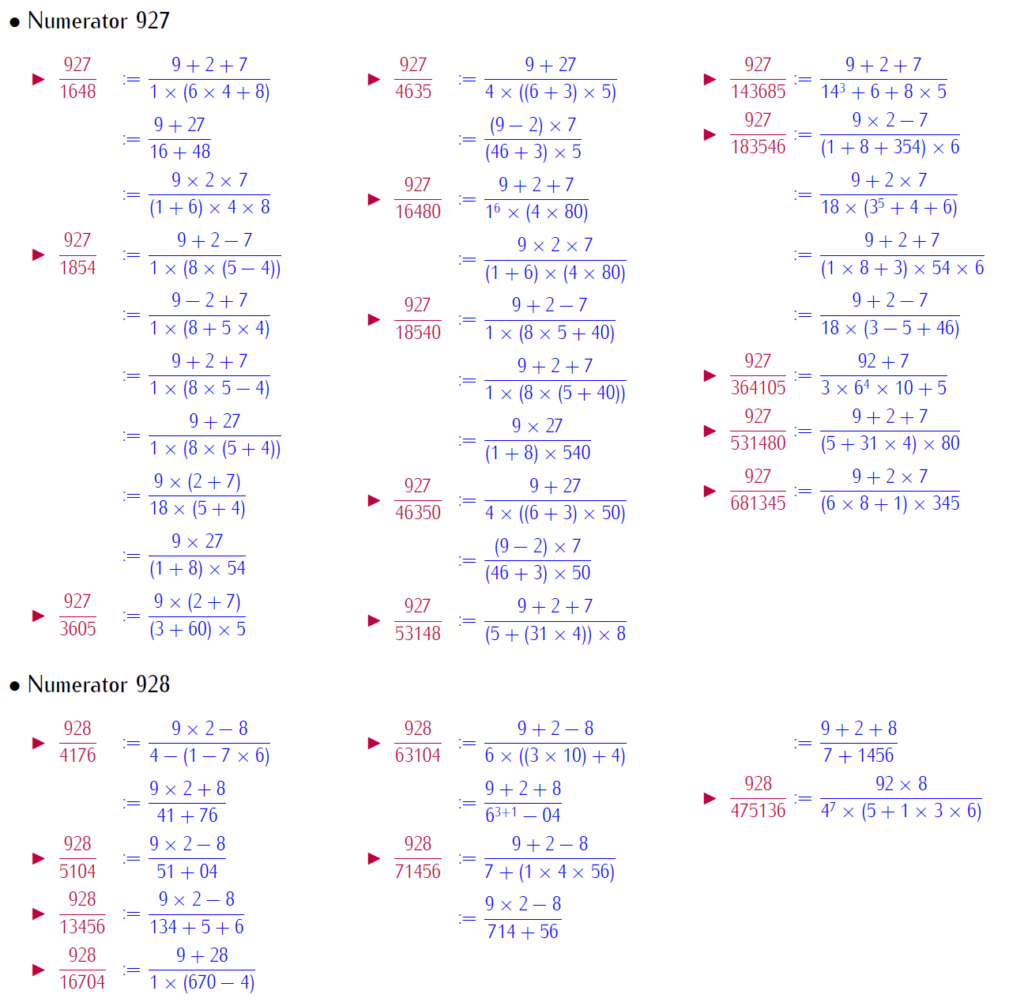
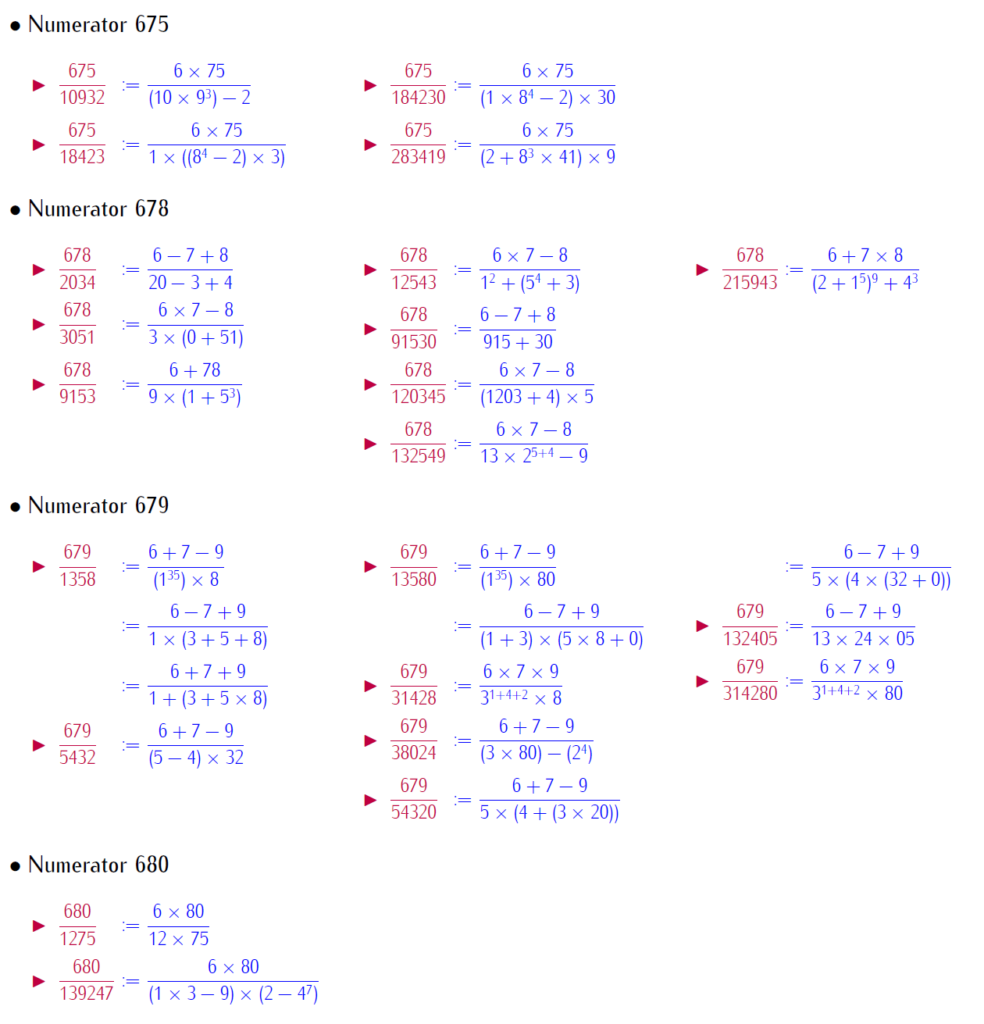
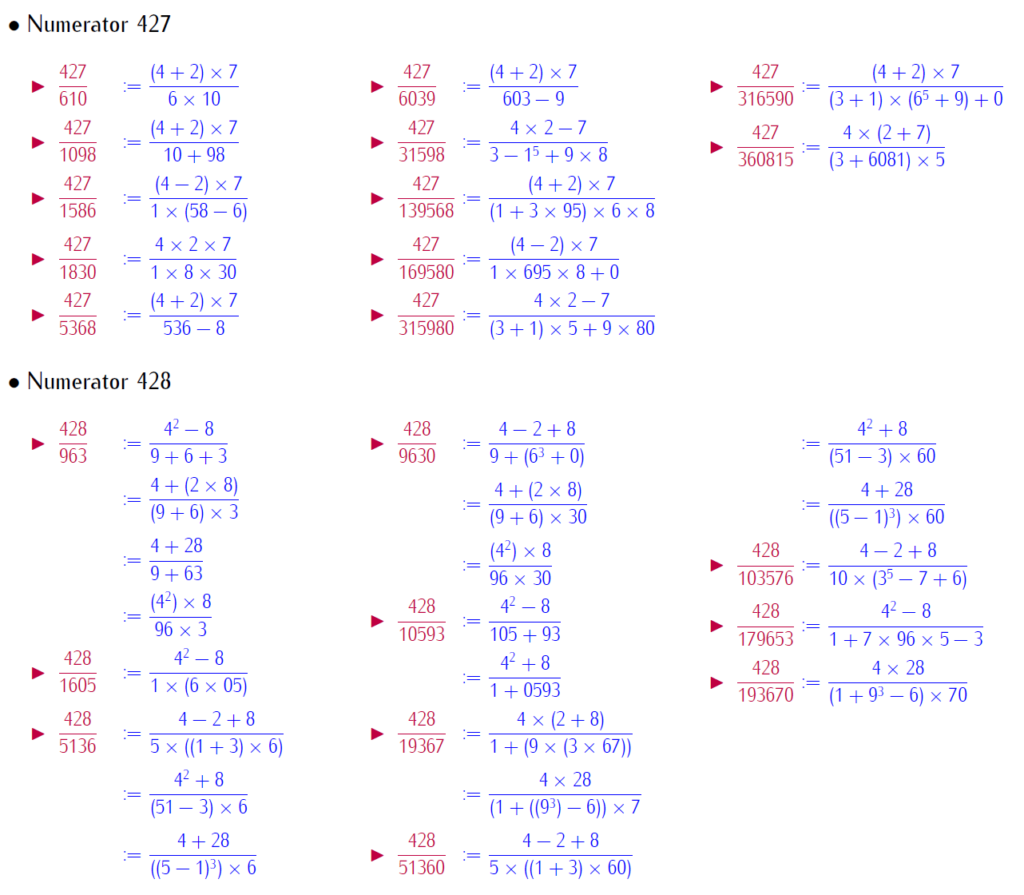
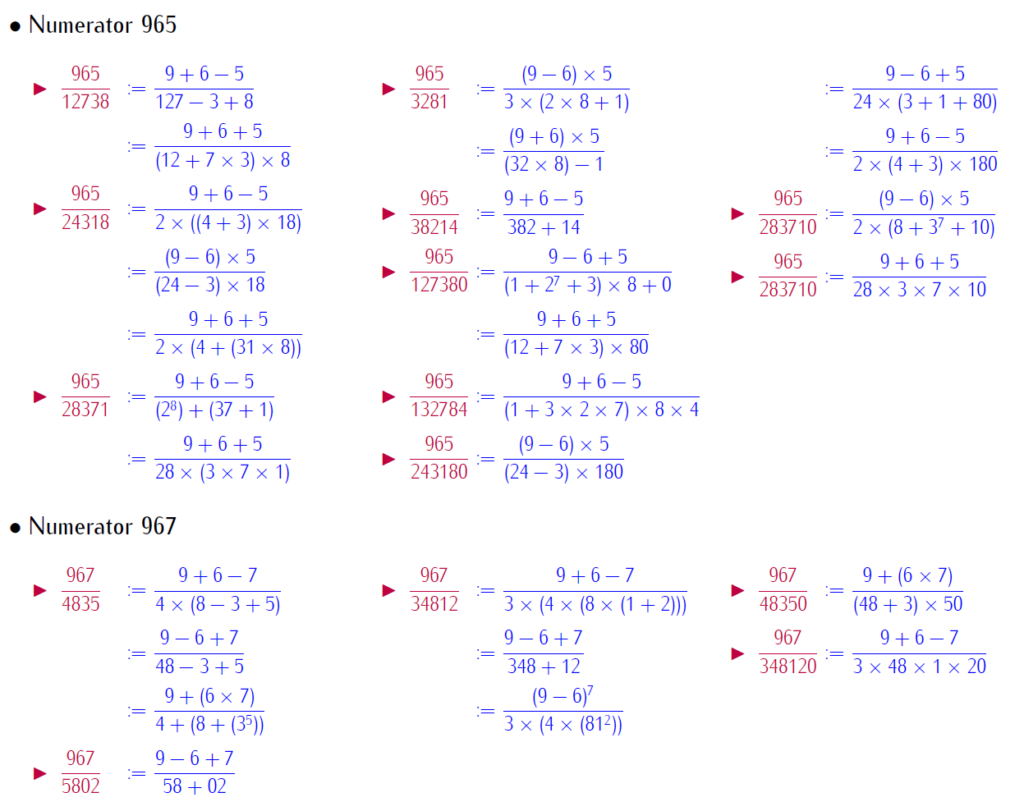
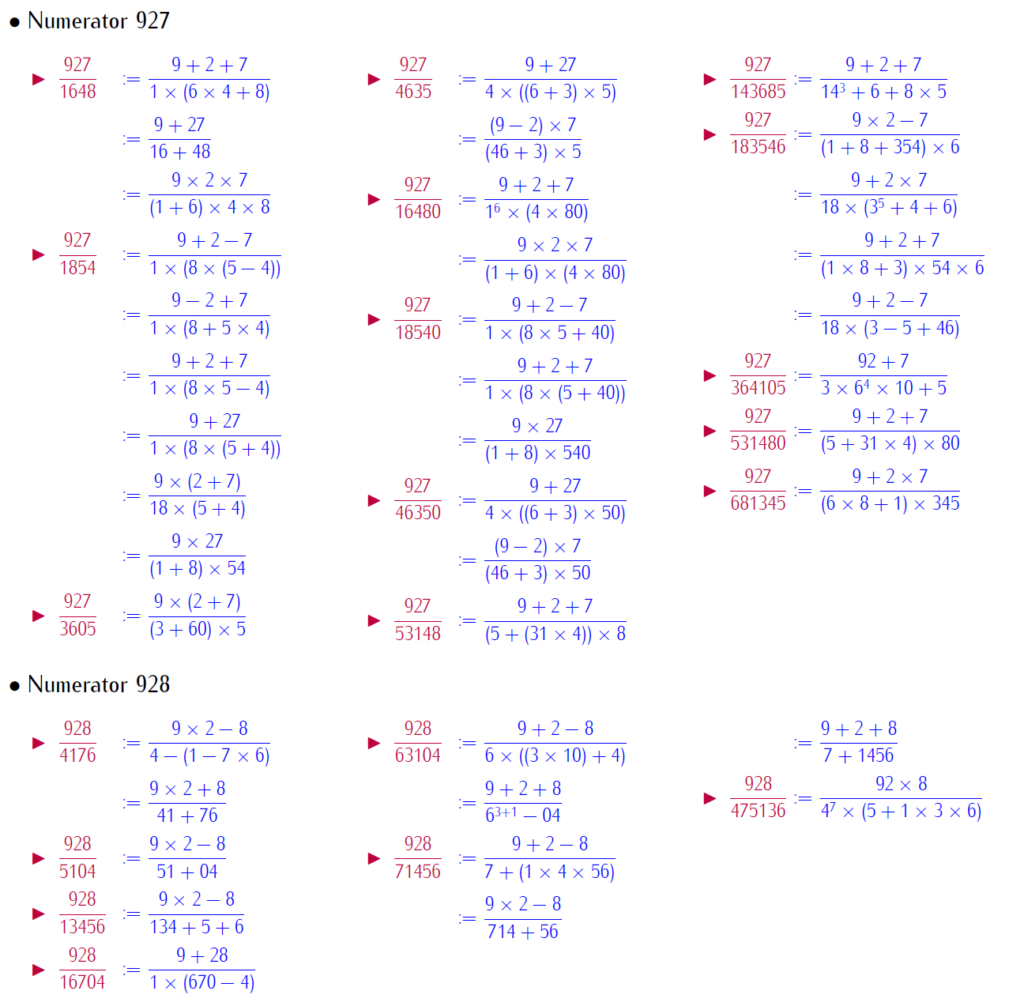
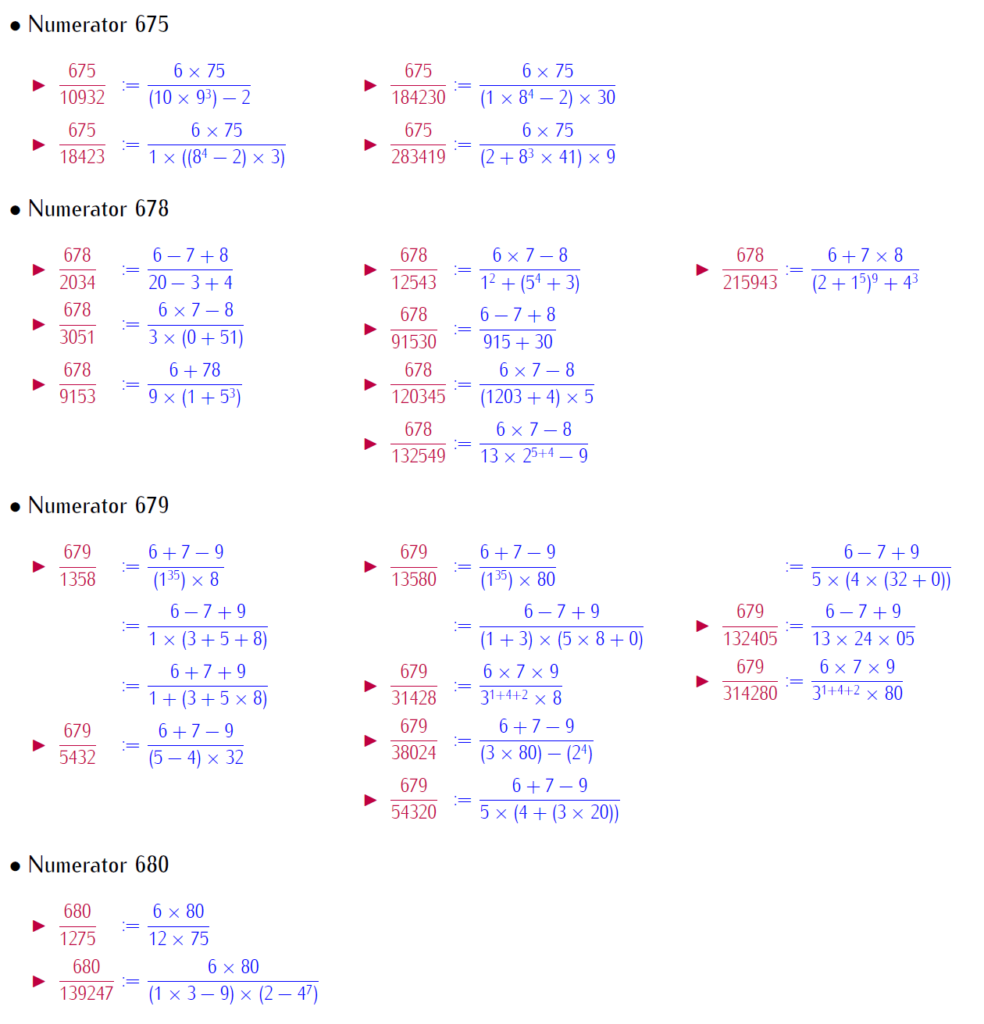
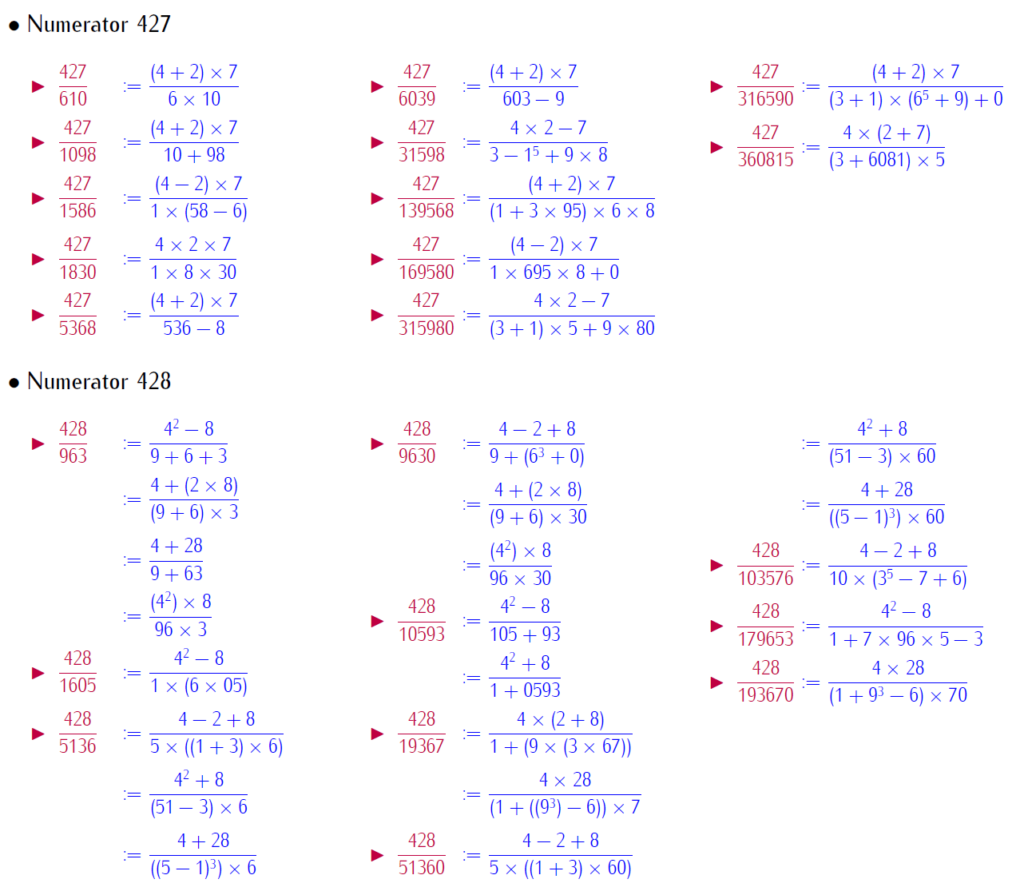
By selfie fractions, we understand that a fraction, where numerators and denominators are represented by same digits, with basic operation. This paper brings patterned selfie fractions. Patterned selfie fractions are understood as selfie fractions extendable in symmetric way. This work is with repeated digits. Below is a link for download the work:
- Inder J. Taneja, Patterned Selfie Fractions, Zenodo, October 27, 2019, pp. 1-267, http://doi.org/10.5281/zenodo.3520096
Below few slides of examples:
Below is a complete list of author’s work in this direction:
Selfie Fractions
- Inder J. Taneja, Selfie Fractions: Addable, Subtractable, Dottable and Potentiable, Zenodo, March 24, 2019, pp. 1-260, http://doi.org/10.5281/zenodo.2604531
- Inder J. Taneja, Pandigital Equivalent Selfie Fractions, Zenodo, April 02, 2019, pp. 1-392, http://doi.org/10.5281/zenodo.2622028
- Inder J. Taneja, Repeated Digits Selfie Fractions: Two and Three Digits Numerators, Zenodo, Septembr 12, 2019, pp. 1-1091, http://doi.org/10.5281/zenodo.3406655
- Inder J. Taneja, Different Digits Selfie Fractions: Two and Three Digits Numerators – Revised, Zenodo, September, 12, 2019, pp. 1-337, http://doi.org/10.5281/zenodo.3474091
- Inder J. Taneja, Different Digits Selfie Fractions: Four Digits Numerator, Zenodo, October 06, 2019, pp. 1-844, http://doi.org/10.5281/zenodo.3474267
- Inder J. Taneja, Different Digits Selfie Fractions: Five Digits Numerator – Pandigital, Zenodo, October 06, 2019, pp. 1-362, http://doi.org/10.5281/zenodo.3474379
- Inder J. Taneja, Patterned Selfie Fractions, Zenodo, October 27, 2019, pp. 1-267, http://doi.org/10.5281/zenodo.3520096