Creative Magic Squares: Singele Digit Representations

This work brings traditional magic squares of orders 3 to 10 in terms of single digit. In this case, the magic squares are written separately for each digit, i.e., for the digits 1 to 9. This has been done for all the orders 3 to 10. In case of orders 8 and 9 there are two possibilities, i.e, one as normal magic squares and another as bimagic squares. In case of magic square of order 10, two different ways are written. One as a general magic square without any block. Another as block-bordered magic squares with inner magic square of order 8. Again the inner magic square can be written in two ways, i.e., one just pandiagonal and another pandiagonal and bimagic. In case of single digit the representations of numbers are not uniform. Writing in terms of single letter “a”, we can get uniformity in representations of numbers. It is done in another work.

The whole work can be downloaded at the folloiwng link:

• Inder J. Taneja, Creative Magic Squares: Single Digit Representations, Zenodo, March 25, 2021, pp. 1-165, http://doi.org/10.5281/zenodo.4637121

Below are Examples of Magic Squares of Orders 3 to 10.

Magic Square of Order 3

Magic Square of Order 4

Magic Square of Order 5

Magic Square of Order 6

Magic Square of Order 7

Magic Square of Order 8: Pandiagonal

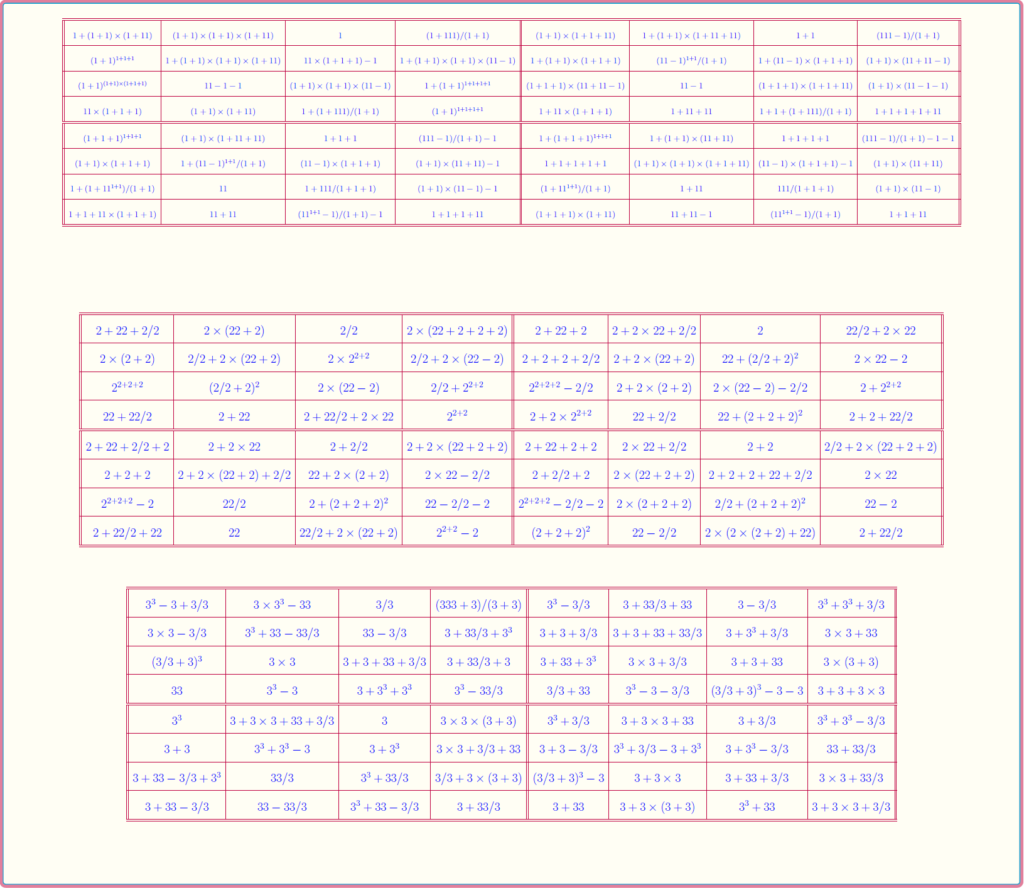
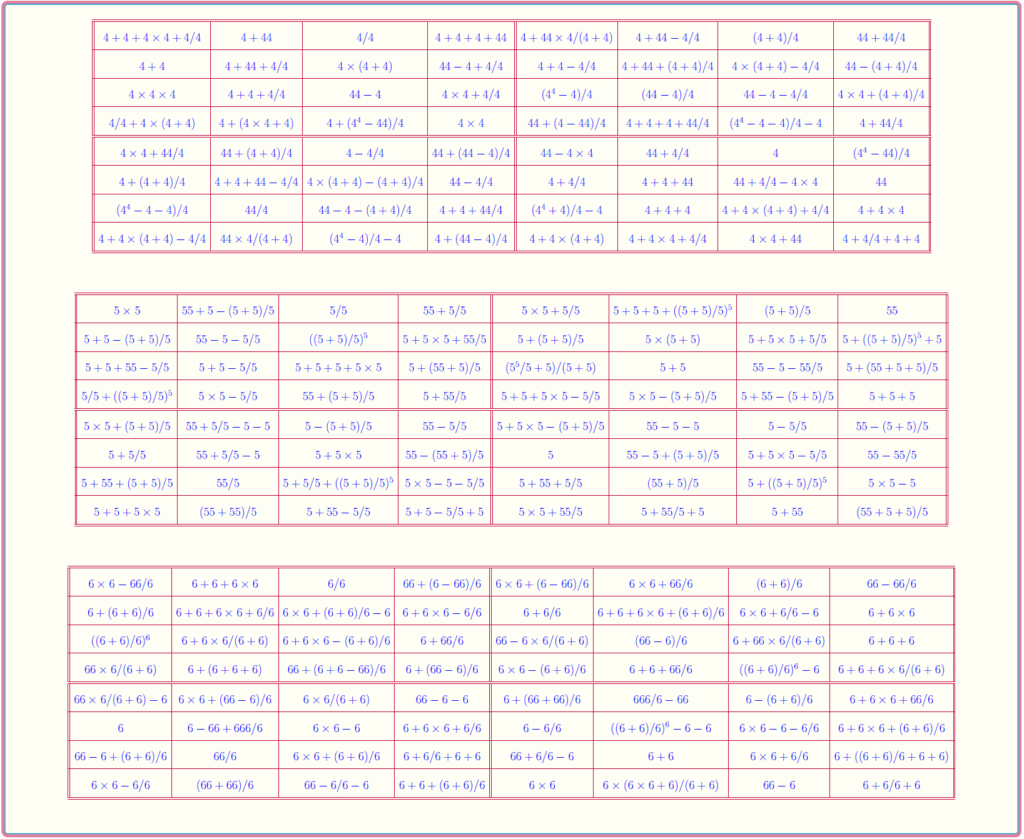
Magic Square of Order 8: Pandiagonal and Bimagic

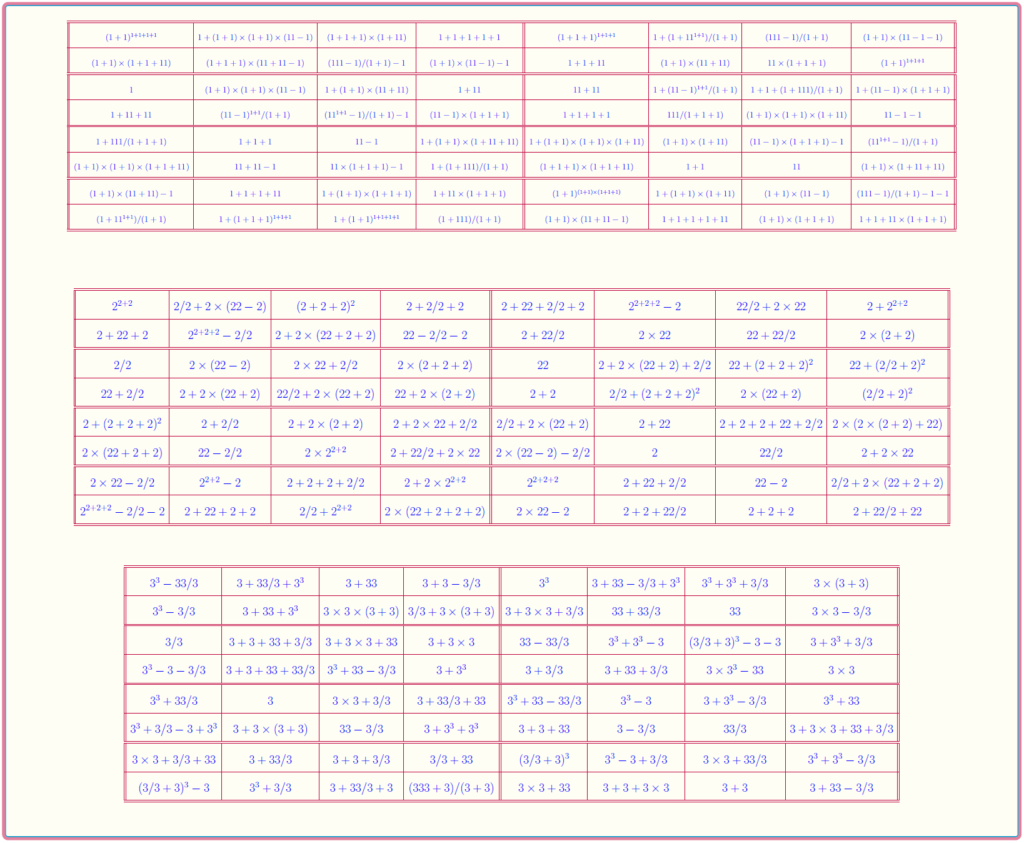
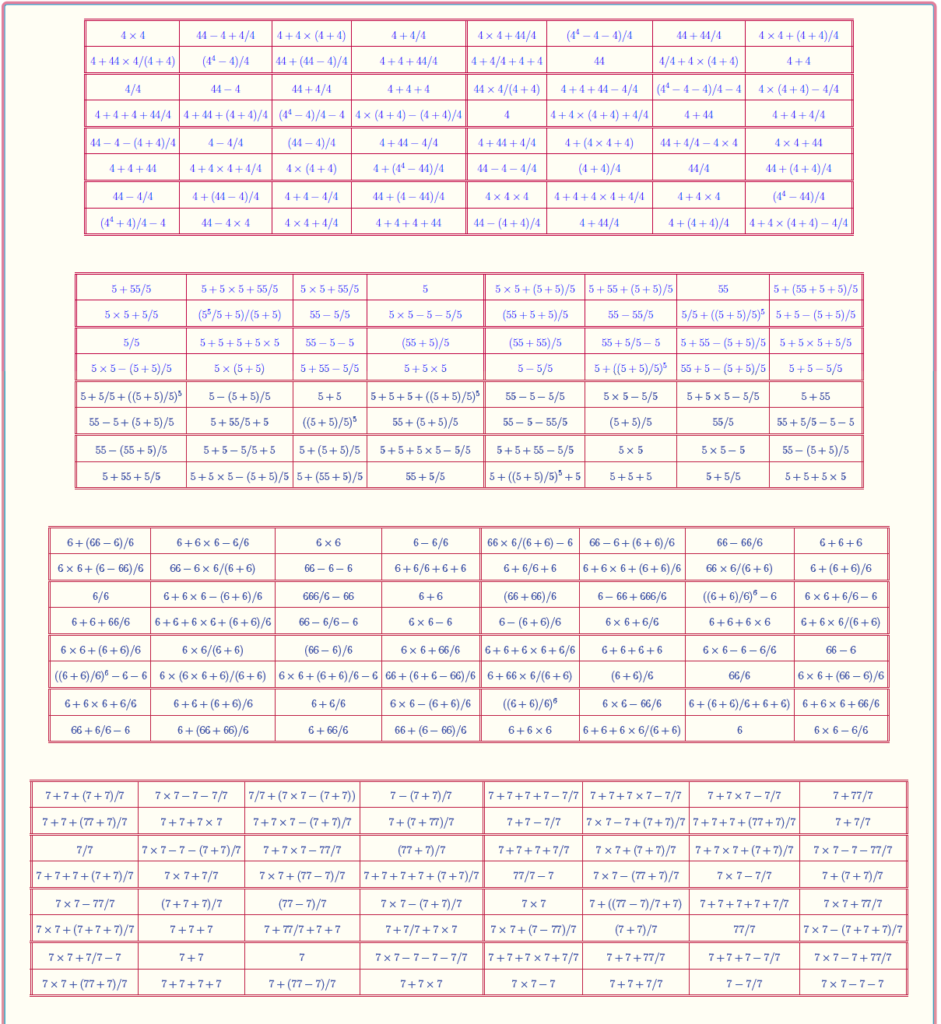
Magic Square of Order 9: Pandiagonal

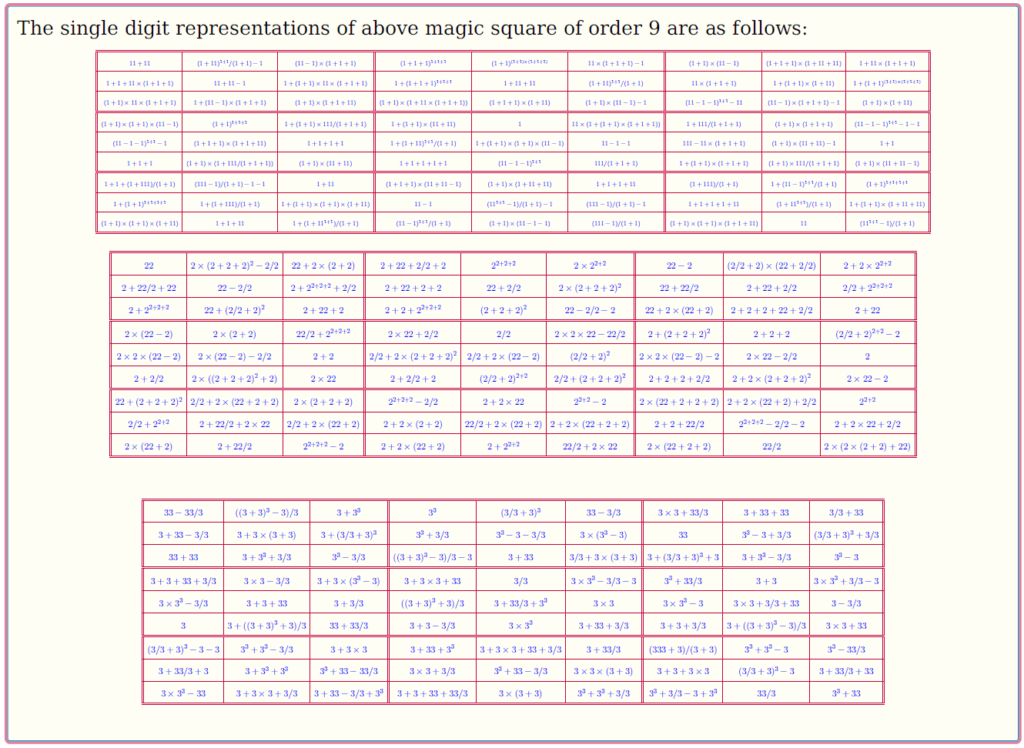
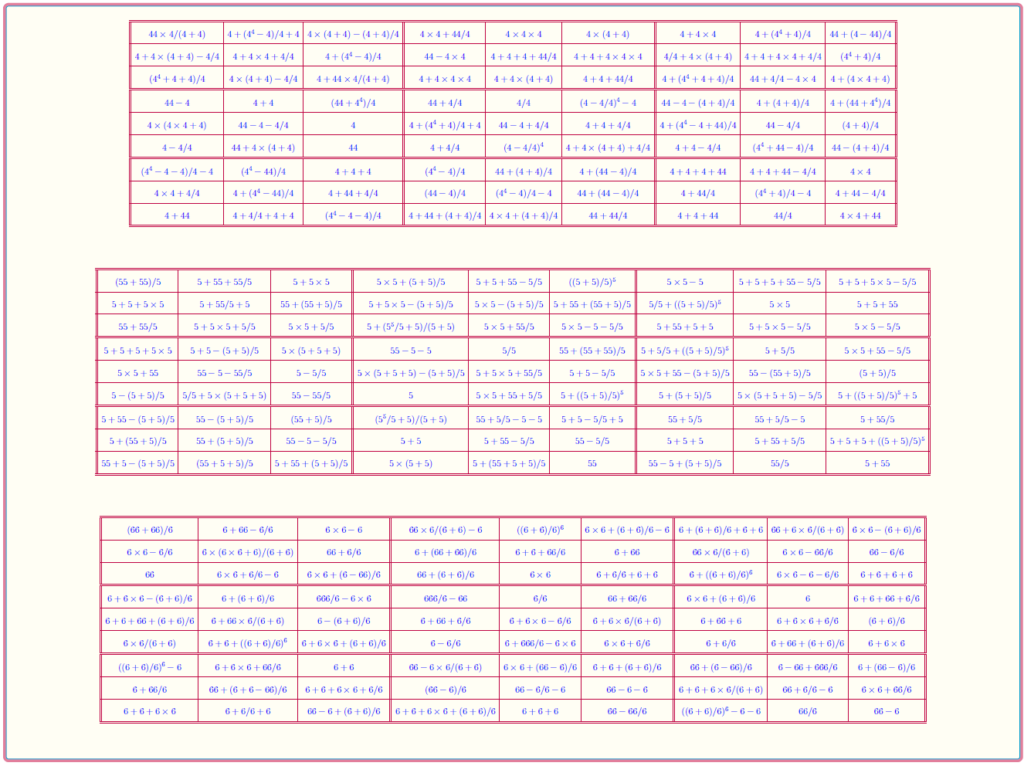
Magic Square of Order 9: Bimagic

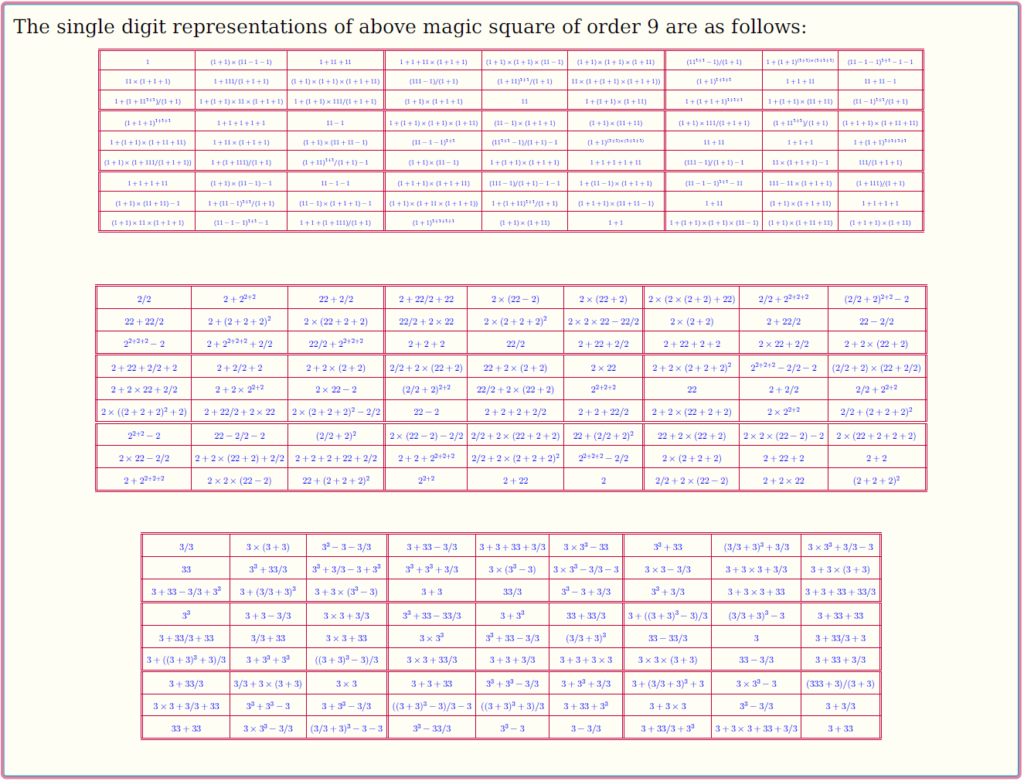
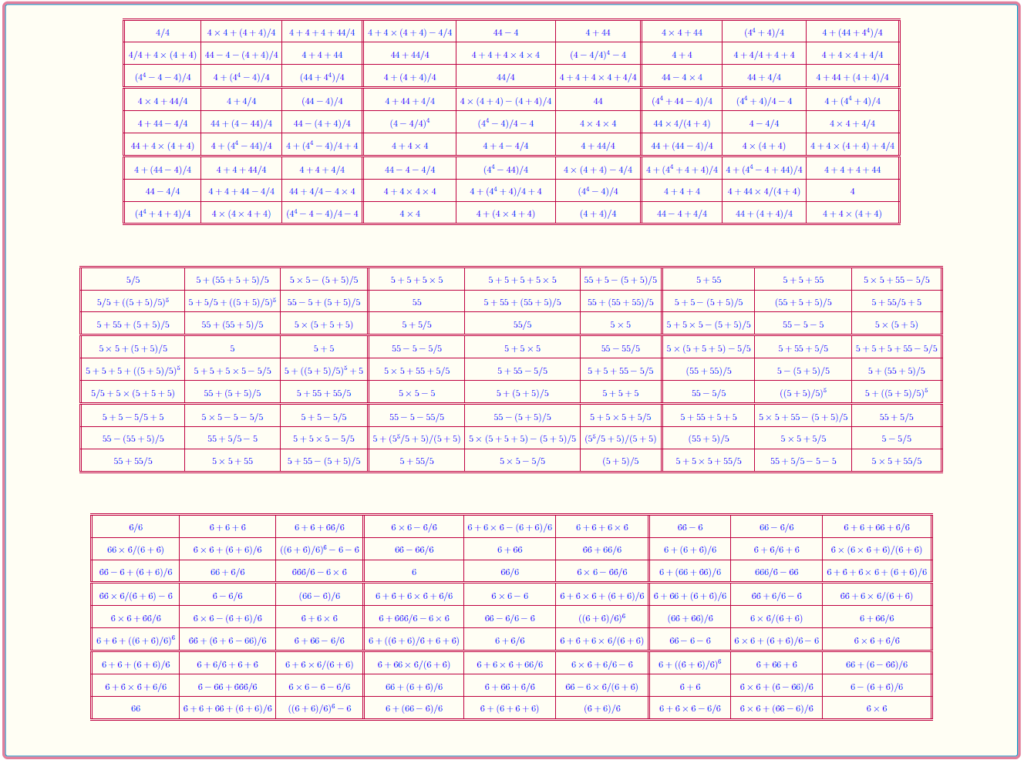
Magic Square of Order 10

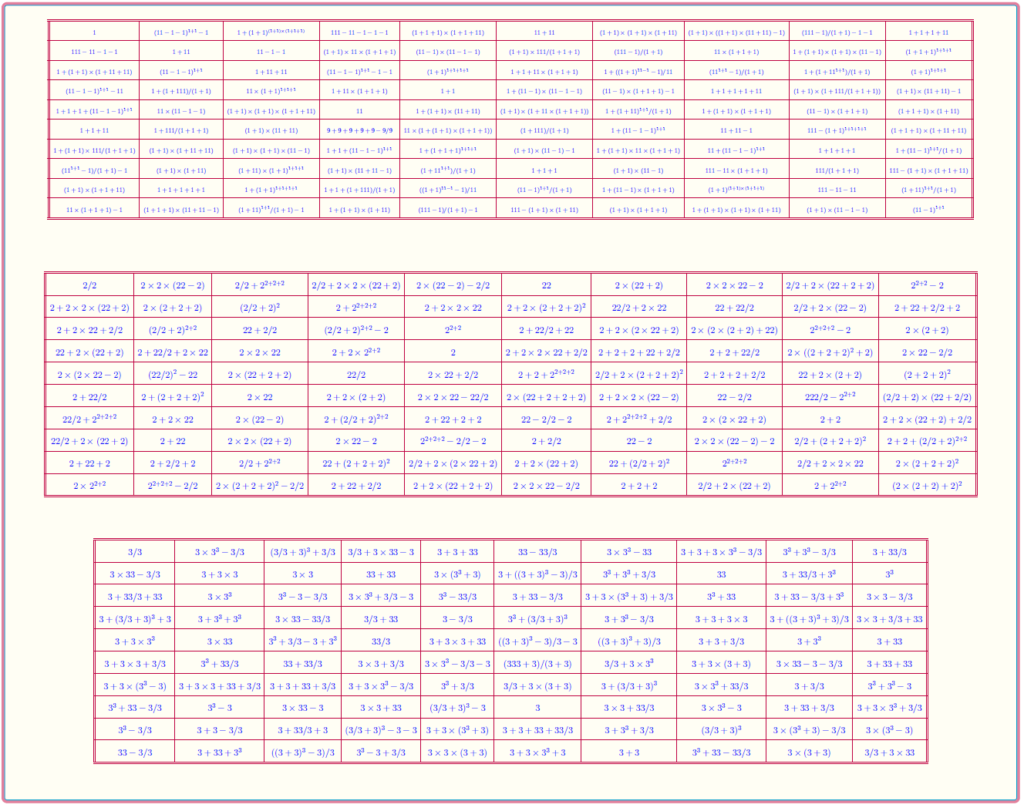
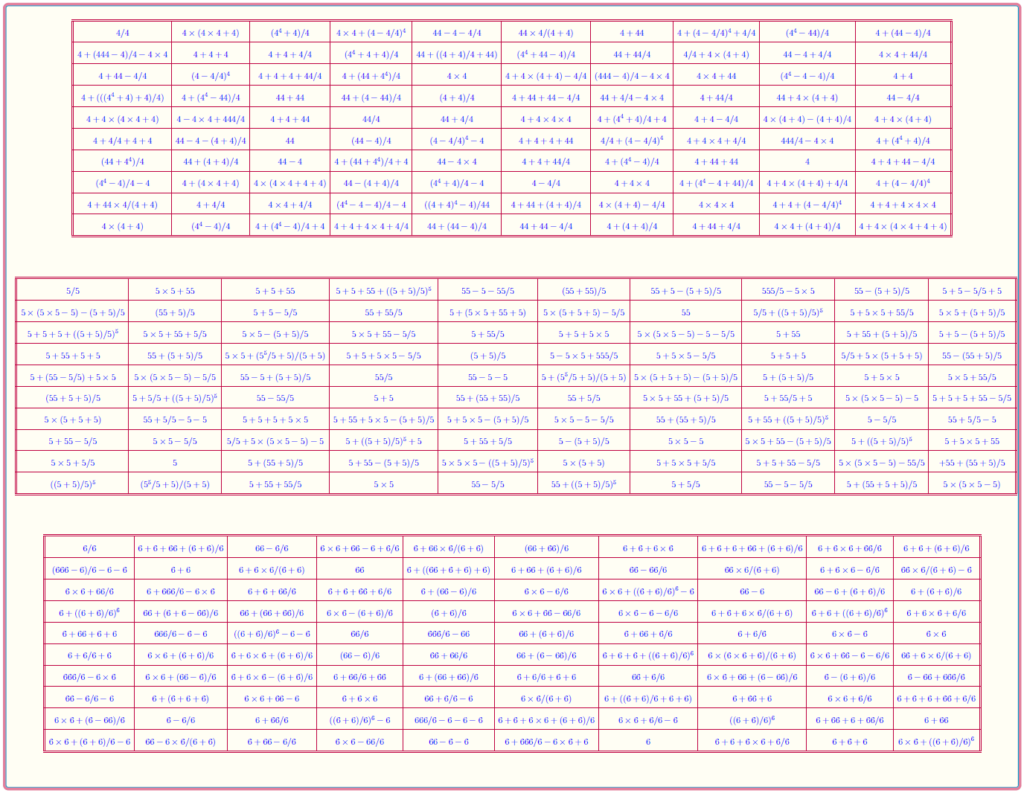
Bordered Magic Square of Order 10

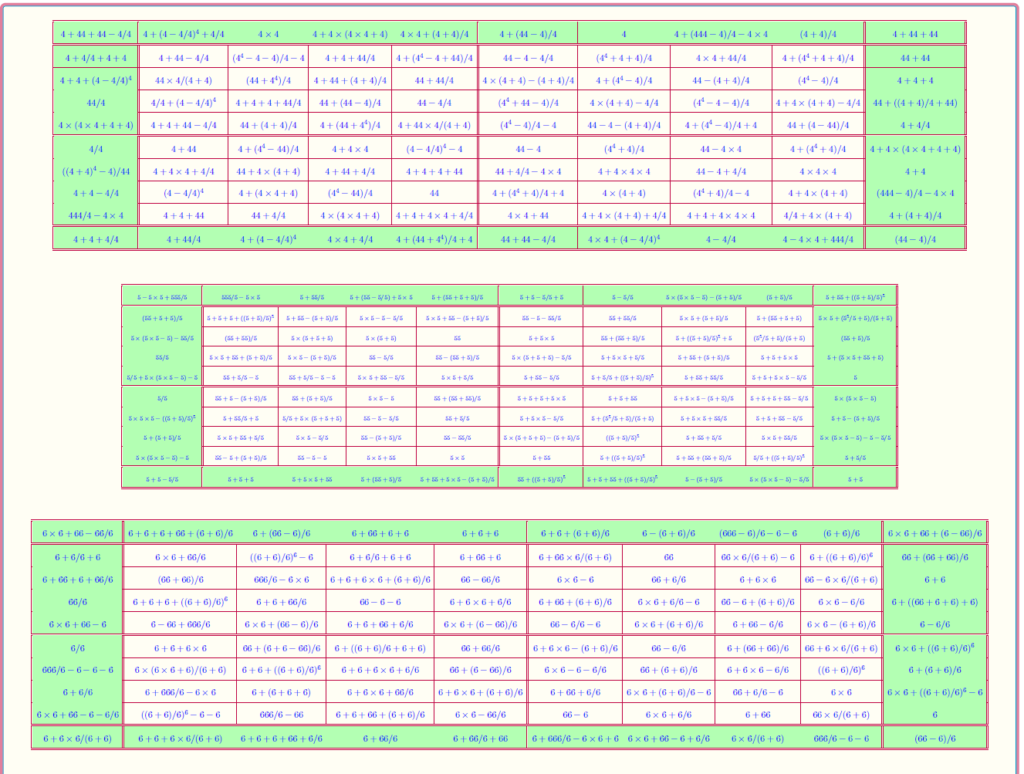
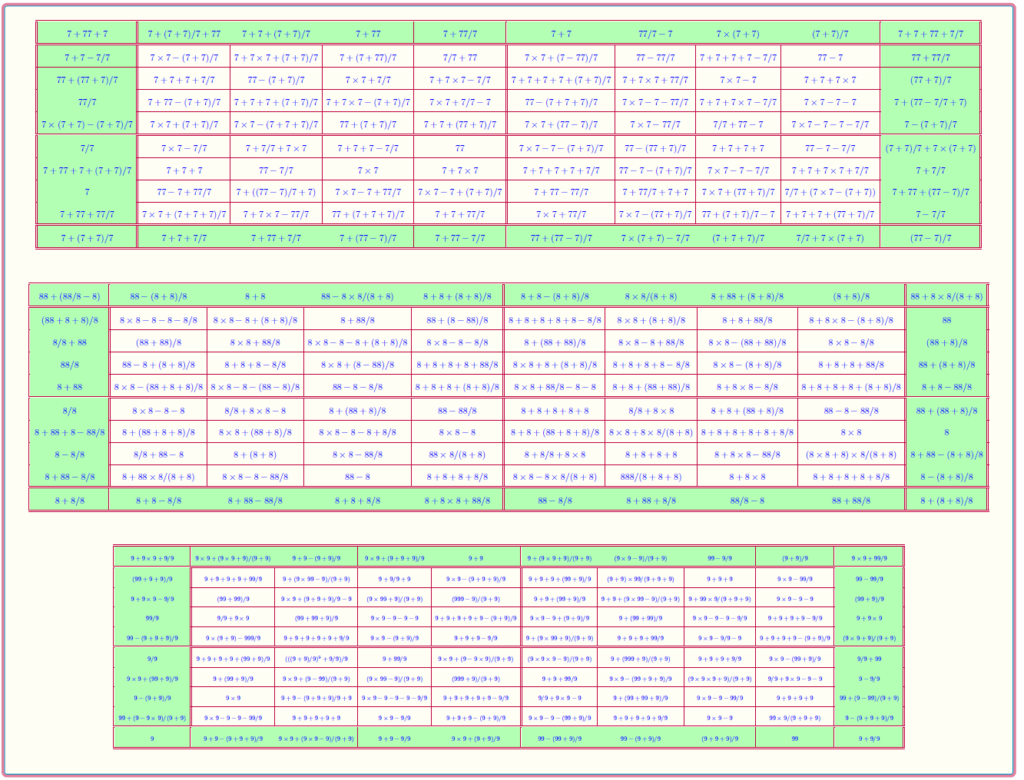
Author’s work on single digits for natural numbers can be seen at

• Inder J. Taneja, Single Digit Representation of Natural Numbers 1 to 10000
• Inder J. Taneja, Single Digits Representations of Natural Numbers from 1 to 20000,