8000+ Magic Squares of Order 22 in Different Styles, Models and Designs

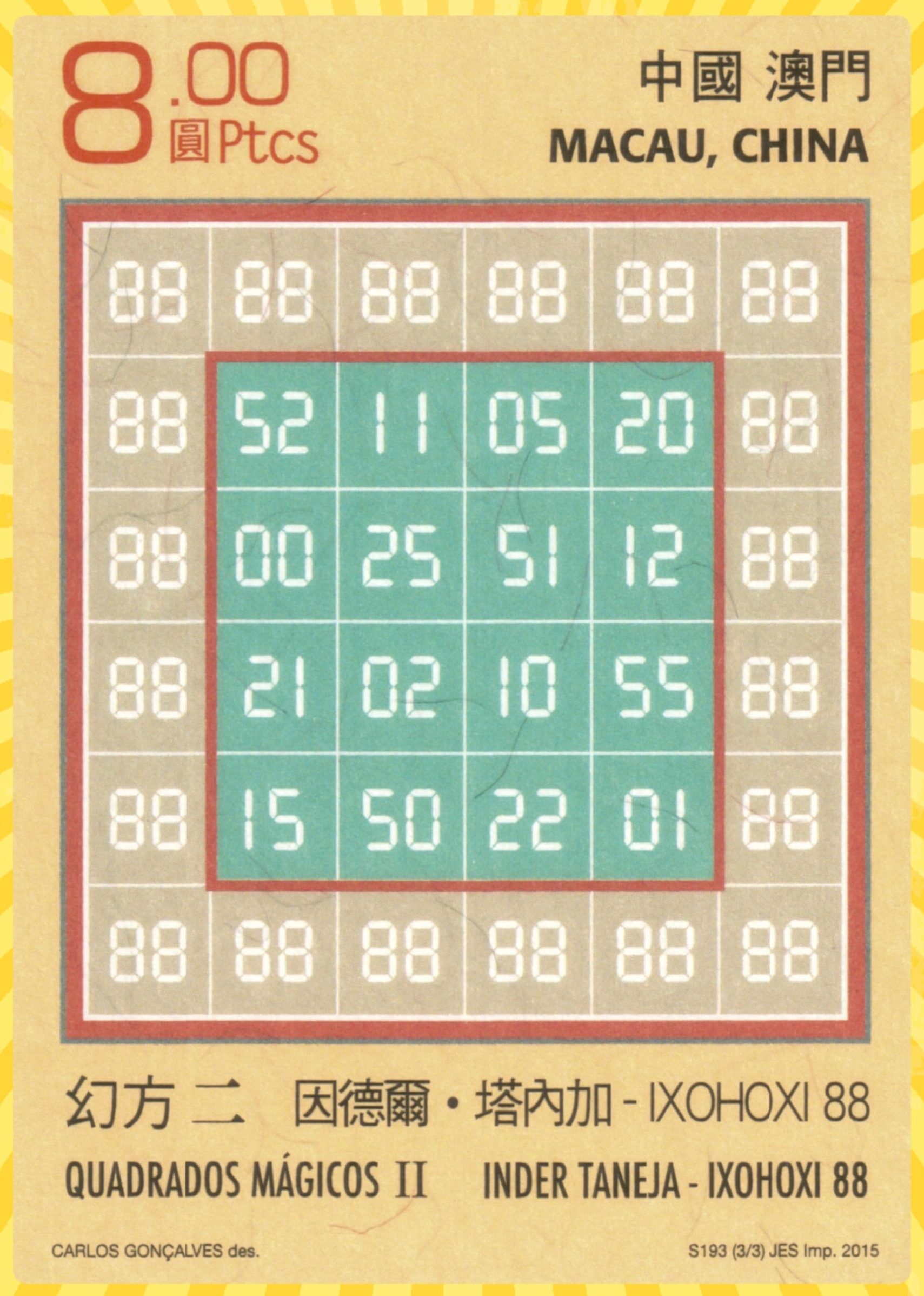
This work brings 8071 magic squares of order 22. Whole the work is based on small blocks of magic squares, bordered magic squares, bordered magic rectangles, etc. In order to construct these magic squares, the idea of possible combinations is considered. The main aspect lies in two facts as given below:

1. Using small blocks of bordered magic rectangles.
2. Using algebraic formula (a+b)².

Previous to it author constructed even order magic squares of orders 6 to 20 with different styles and designs. Below is the link of these works:

1. Inder J. Taneja, Different Styles of Magic Squares of Orders 6, 8, 10 and 12 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-26, https://doi.org/10.5281/zenodo.7319985.
2. Inder J. Taneja, Different Styles of Magic Squares of Order 14 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-40, https://doi.org/10.5281/zenodo.7319787.
3. Inder J. Taneja, Different Styles of Magic Squares of Order 16 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-63, https://doi.org/10.5281/zenodo.7320116.
4. Inder J. Taneja, Different Styles of Magic Squares of Order 18 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-85, https://doi.org/10.5281/zenodo.7320131.
5. Inder J. Taneja, Different Styles of Magic Squares of Order 20 Using Bordered Magic Rectangles, Zenodo, November 15, 2022, pp. 1-88, https://doi.org/10.5281/zenodo.7320877.

The author constructed in numbers the following orders of magic squares:
1. 1616 magic squares of order 20.
2. 810 magic squares of order 18.
3. 220 magic squares of order 16.
4. 125 magic squares of order 14.
5. 45 magic squares of order 12.
6. 16 magic squares of order 10.
7. 6 magic squares of order 8.
8. 3 magic squares of order 6.
These magic squares appear in the above links. Moreover, whole the work is up to order 42. These orders are with less possibilities. Whole the work can be seen at the link.

As written above this work brings 8071 magic squares of order 22 in different styles, models and designs. Whole the work is divided in different parts as given below. Only are few examples are given. The complete work is embedded as pdf files given at the end of each part.

This work can be acessed for download at the following link:
Inder J. Taneja, 8000+ Magic Squares of Order 22 in Different Styles, Models and Designs, Zenodo, pp. 1-135, 2023, https://doi.org/10.5281/zenodo.7809478.
As written above this work brings 8071 magic squares of order 22 in different styles, models and designs. Whole the work is divided in different parts as given below. Only are few examples are given. The complete work is embedded as pdf files given at the end of each part.

• Part 1. Bordered Square of Order 22
• Part 2. Cornered Magic Squares of Order 4
• Part 3. Closed Border of Order 4
• Part 4. Cornered Magic Squares of Order 6
• Part 5. Closed Border of Order 6
• Part 6. Cornered Magic Squares of Order 8
• Part 7. Closed Border of Order 8
• Part 8. (a+b)^2-Type, where a = 12 and b = 10
  • First Type
  • Second Type
  • Third Type
  • Forth Type
  • Fifth Type
  • Sixth Type
  • Seventh Type
  • Eight Type
• Part 9. (a+b)^2-Type, where a = 14 and b = 8
  • First Type
  • Second Type
  • Third Type
  • Forth Type
  • Fifth Type
  • Sixth Type
  • Seventh Type
  • Eight Type
  • Ninth Type
• Part 10. (a+b)^2-Type, where a = 16 and b = 6
  • First Type
  • Second Type
  • Third Type
  • Forth Type
  • Fifth Type
    • Open Corner With Magic Square of Order 4
    • Closed Corner
  • Sixth Type
    • Open Corner With Magic Square of Order 4
    • Closed Corner
• Part 11. (a+b)^2-Type, where a = 18 and b = 4: Open Corner With Magic Square of Order 4
  • First Type
  • Second Type
  • Third Type
  • Forth Type
  • Fifth Type
  • Sixth Type
  • Seventh Type
  • Eight Type
  • Ninth Type
• Part 12. (a+b)^2-Type, where a = 18 and b = 4: Closed Corner
  • First Type
  • Second Type
  • Third Type
  • Forth Type
  • Fifth Type
  • Sixth Type
  • Seventh Type
  • Eight Type
  • Ninth Type
• Part 13. a = 18 and b = 4, where a = 18 with c = 14 and d = 4

15 Pdf files are Embedded in the Work (8071 magic squares)

• 1-22×22-basic.
• 2-22×22-12x10a.
• 2-22×22-12x10b.
• 2-22×22-12x10c.
• 2-22×22-12x10d.
• 2-22×22-12x10e.
• 2-22×22-12x10f.
• 2-22×22-12x10g.
• 3-22×22-14x8a.
• 3-22×22-14x8b.
• 3-22×22-14x8c.
• 4-22×22-16x6a.
• 4-22×22-16x6b.
• 5-22×22-18x4a.
• 5-22×22-18x4b.

In the end there are 5 pdf files of complete work are given to summarize the above 15 files:

• 1-22×22-basic.
• 2-22×22-12×10.
• 3-22×22-14×8.
• 4-22×22-16×6.
• 5-22×22-18×4.

Part 1: Bordered Magic Square of Order 22

Part 2. Cornered Magic Squares of Order 4

Part 3. Closed Border of Order 4

Part 4. Cornered Magic Squares of Order 6

Part 5. Closed Border of Order 6

Part 2. Cornered Magic Squares of Order 8

Part 7. Closed Border of Order 8

Part 8. (a+b)^2-Type, where a = 12 and b = 10: First Type

Part 8. (a+b)^2-Type, where a = 12 and b = 10: Second Type

Part 8. (a+b)^2-Type, where a = 12 and b = 10: Third Type

Part 8. (a+b)^2-Type, where a = 12 and b = 10: Forth Type

Part 8. (a+b)^2-Type, where a = 12 and b = 10: Fifth Type

Part 8. (a+b)^2-Type, where a = 12 and b = 10: Sixth Type

Part 8. (a+b)^2-Type, where a = 12 and b = 10: Seventh Type

Part 8. (a+b)^2-Type, where a = 12 and b = 10: Eight Type

Part 9. (a+b)^2-Type, where a = 14 and b = 8: First Type

Part 9. (a+b)^2-Type, where a = 14 and b = 8: Second Type

Part 9. (a+b)^2-Type, where a = 14 and b = 8: Third Type

Part 9. (a+b)^2-Type, where a = 14 and b = 8: Forth Type

Part 9. (a+b)^2-Type, where a = 14 and b = 8: Fifth Type

Part 9. (a+b)^2-Type, where a = 14 and b = 8: Sixth Type

Part 9. (a+b)^2-Type, where a = 14 and b = 8: Seventh Type

Part 9. (a+b)^2-Type, where a = 14 and b = 8: Eight Type

Part 9. (a+b)^2-Type, where a = 14 and b = 8: Ninth Type

Part 10. (a+b)^2-Type, where a = 16 and b = 6: First Type

Part 10. (a+b)^2-Type, where a = 16 and b = 6: Second Type

Part 10. (a+b)^2-Type, where a = 16 and b = 6: Third Type

Part 10. (a+b)^2-Type, where a = 16 and b = 6: Forth Type

Part 10. (a+b)^2-Type, where a = 16 and b = 6:
Open Corner With Magic Square of Order 4: Fifth Type

Part 10. (a+b)^2-Type, where a = 16 and b = 6:
Closed Corner: Fifth Type

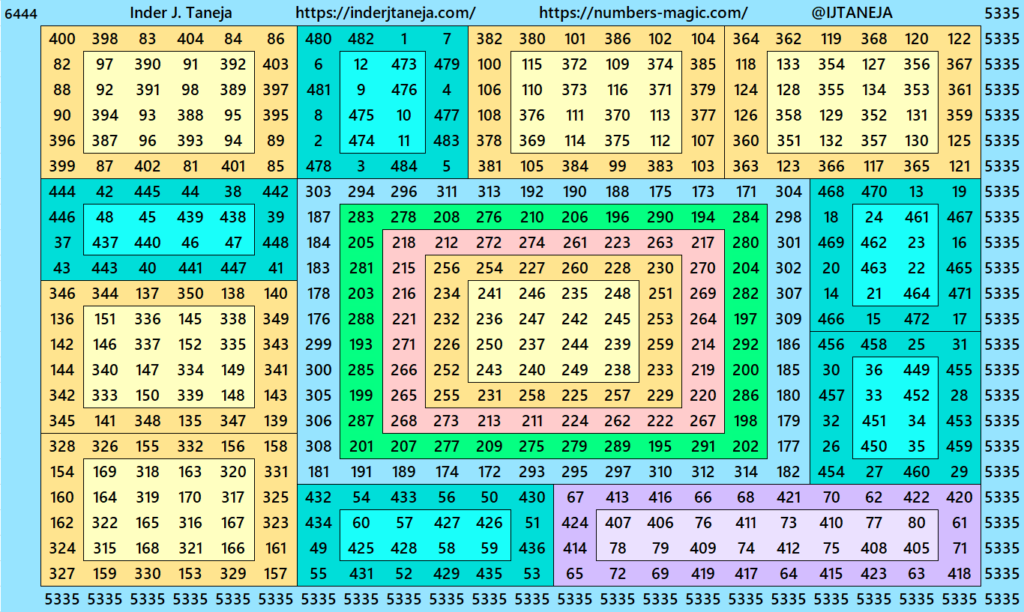
Part 10. (a+b)^2-Type, where a = 16 and b = 6:
Open Corner With Magic Square of Order 4: Sixth Type

Part 10. (a+b)^2-Type, where a = 16 and b = 6:
Closed Corner: Sixth Type

Part 11. (a+b)^2-Type, where a = 18 and b = 4:
Open Corner With Magic Square of Order 4 – First Type

Part 11. (a+b)^2-Type, where a = 18 and b = 4:
Open Corner With Magic Square of Order 4 – Second Type

Part 11. (a+b)^2-Type, where a = 18 and b = 4:
Open Corner With Magic Square of Order 4 – Third Type

Part 11. (a+b)^2-Type, where a = 18 and b = 4:
Open Corner With Magic Square of Order 4 – Forth Type

Part 11. (a+b)^2-Type, where a = 18 and b = 4:
Open Corner With Magic Square of Order 4 – Fifth Type

Part 11. (a+b)^2-Type, where a = 18 and b = 4:
Open Corner With Magic Square of Order 4 – Sixth Type

Part 11. (a+b)^2-Type, where a = 18 and b = 4:
Open Corner With Magic Square of Order 4 – Seventh Type

Part 11. (a+b)^2-Type, where a = 18 and b = 4:
Open Corner With Magic Square of Order 4 – Eight Type

Part 11. (a+b)^2-Type, where a = 18 and b = 4:
Open Corner With Magic Square of Order 4 – Ninth Type

Part 12. (a+b)^2-Type, where a = 18 and b = 4:
Closed Corner – First Type

Part 12. (a+b)^2-Type, where a = 18 and b = 4:
Closed Corner – Second Type

Part 12. (a+b)^2-Type, where a = 18 and b = 4:
Closed Corner – Third Type

Part 12. (a+b)^2-Type, where a = 18 and b = 4:
Closed Corner – Forth Type

Part 12. (a+b)^2-Type, where a = 18 and b = 4:
Closed Corner – Fifth Type

Part 12. (a+b)^2-Type, where a = 18 and b = 4:
Closed Corner – Sixth Type

Part 12. (a+b)^2-Type, where a = 18 and b = 4:
Closed Corner – Seventh Type

Part 12. (a+b)^2-Type, where a = 18 and b = 4:
Closed Corner – Eight Type

Part 12. (a+b)^2-Type, where a = 18 and b = 4:
Closed Corner – Ninth Type

Part 13. (a+b)^2-Type, where a = 18 and b = 4:
Again, a=18 is divided as c = 14 and d = 4.

It is already considered before in Part 9, where a = 14 and b = 8. It can be considered as b=8 divided in two parta of 4 each.

Five main pdf files of complete work are embedded for download:

First File: 1-22×22-basic

Second File: 2-22×22-12×10

Third File: 3-22×22-14×8

Forth File: 4-22×22-16×6

Fifth File: 5-22×22-18×4