Different Styles of Magic Squares of Order 18 Using Bordered Magic Rectangles

For the first time in this work, two new concepts in construction of magic square are considered. It is based on following two points:

1. Using small blocks of bordered magic rectangles.
2. Using algebraic formula (a+b)².

The whole work contains magic squares of even orders starting from order 6. This part is only for order 18. It is a revised version of the author’s previous work. For the complete work for the orders from 6 to 20 (even numbers) see the links below.

1. Inder J. Taneja, Different Styles of Magic Squares of Orders 6, 8, 10 and 12 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-26, https://doi.org/10.5281/zenodo.7319985.
2. Inder J. Taneja, Different Styles of Magic Squares of Order 14 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-40, https://doi.org/10.5281/zenodo.7319787.
3. Inder J. Taneja, Different Styles of Magic Squares of Order 16 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-63, https://doi.org/10.5281/zenodo.7320116.
4. Inder J. Taneja, Different Styles of Magic Squares of Order 18 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-85, https://doi.org/10.5281/zenodo.7320131.
5. Inder J. Taneja, Different Styles of Magic Squares of Order 20 Using Bordered Magic Rectangles, Zenodo, November 15, 2022, pp. 1-88, https://doi.org/10.5281/zenodo.7320877.

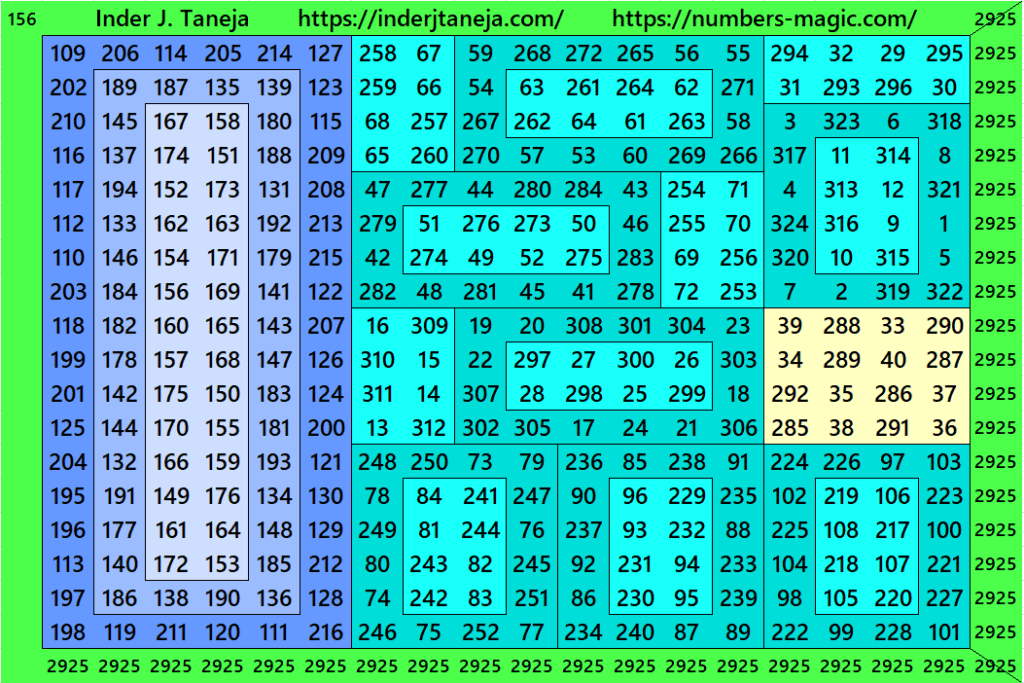
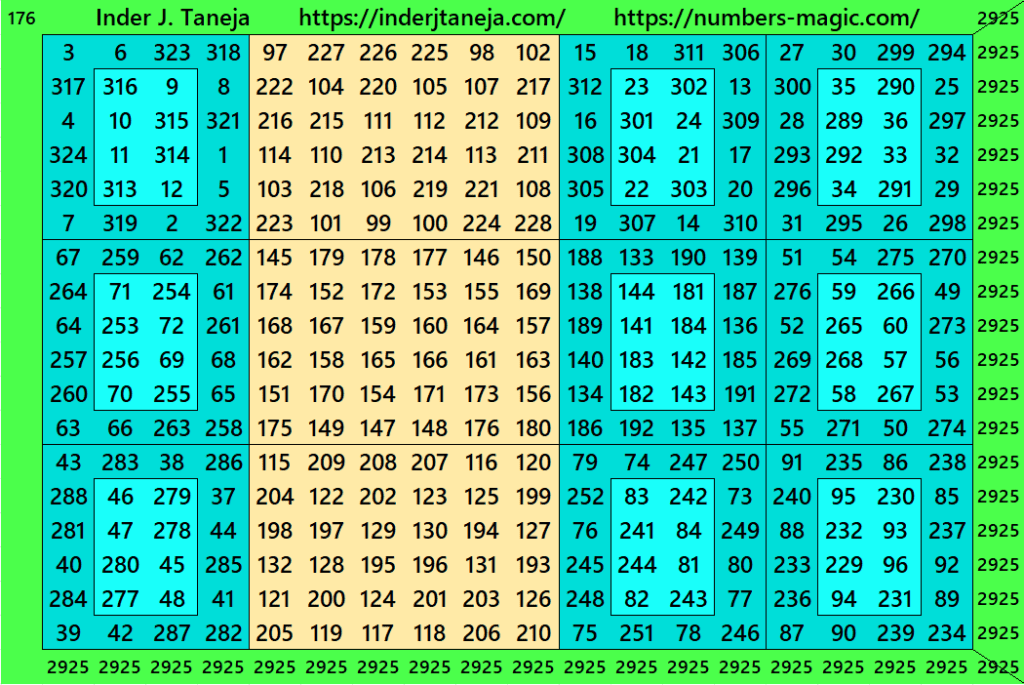
Total there are 810 magic squares of order 18 constructed by the author. Due to the high numbers below are few magic squares. The complete list can be downloaded as pdf files given at the end.

Magic Squares of Order 18

Two Pdf Files for Download