Different Styles of Magic Squares of Order 16 Using Bordered Magic Rectangles

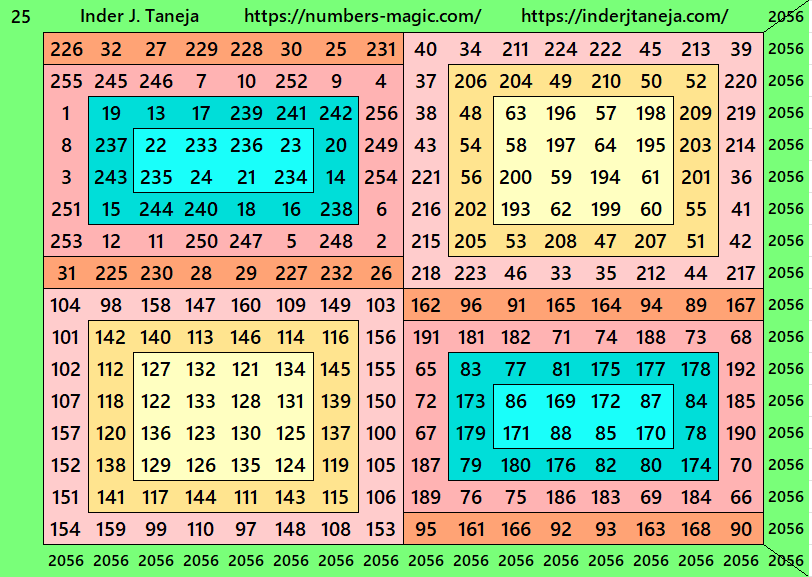
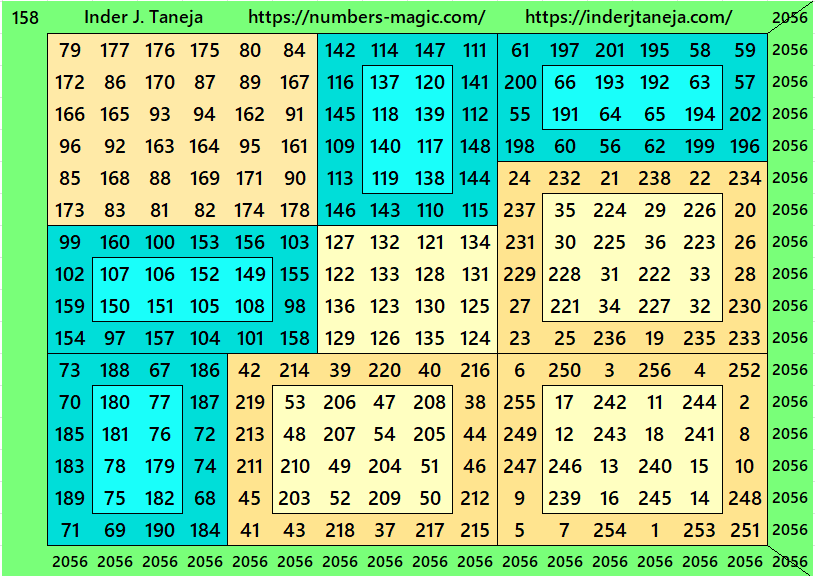
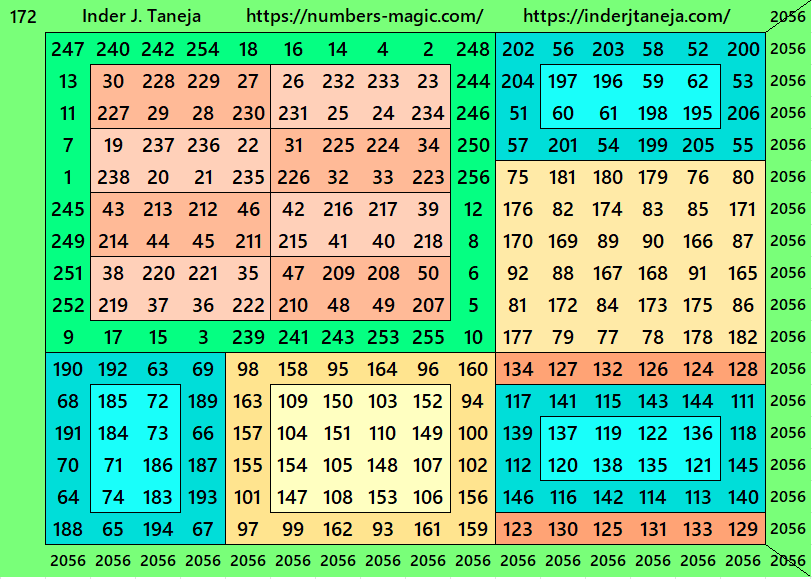
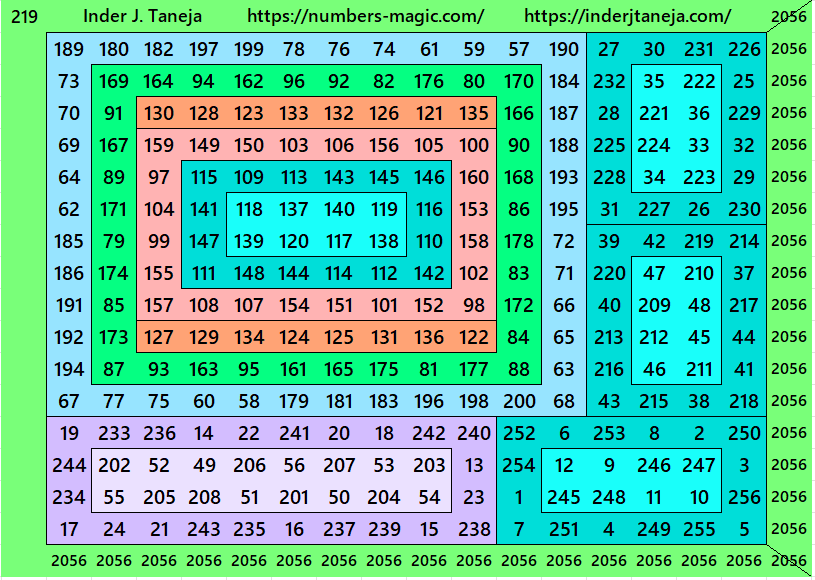
For the first time in this work, two new concepts in construction of magic square are considered. It is based on following two points:

1. Using small blocks of bordered magic rectangles.
2. Using algebraic formula (a+b)².

The whole work contains magic squares of even orders starting from order 6. This part is only for order 16. It is a revised version of the author’s previous work. For the complete work for the even orders from 6 to 20 see the links below.

1. Inder J. Taneja, Different Styles of Magic Squares of Orders 6, 8, 10 and 12 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-26, https://doi.org/10.5281/zenodo.7319985.
2. Inder J. Taneja, Different Styles of Magic Squares of Order 14 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-40, https://doi.org/10.5281/zenodo.7319787.
3. Inder J. Taneja, Different Styles of Magic Squares of Order 16 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-63, https://doi.org/10.5281/zenodo.7320116.
4. Inder J. Taneja, Different Styles of Magic Squares of Order 18 Using Bordered Magic Rectangles, Zenodo, November 14, 2022, pp. 1-85, https://doi.org/10.5281/zenodo.7320131.
5. Inder J. Taneja, Different Styles of Magic Squares of Order 20 Using Bordered Magic Rectangles, Zenodo, November 15, 2022, pp. 1-88, https://doi.org/10.5281/zenodo.7320877.

There is a total of 220 magic squares of order 16 given below. Also, a pdf is given at the end for download.

Magic Squares of Order 16

Pdf File for Download