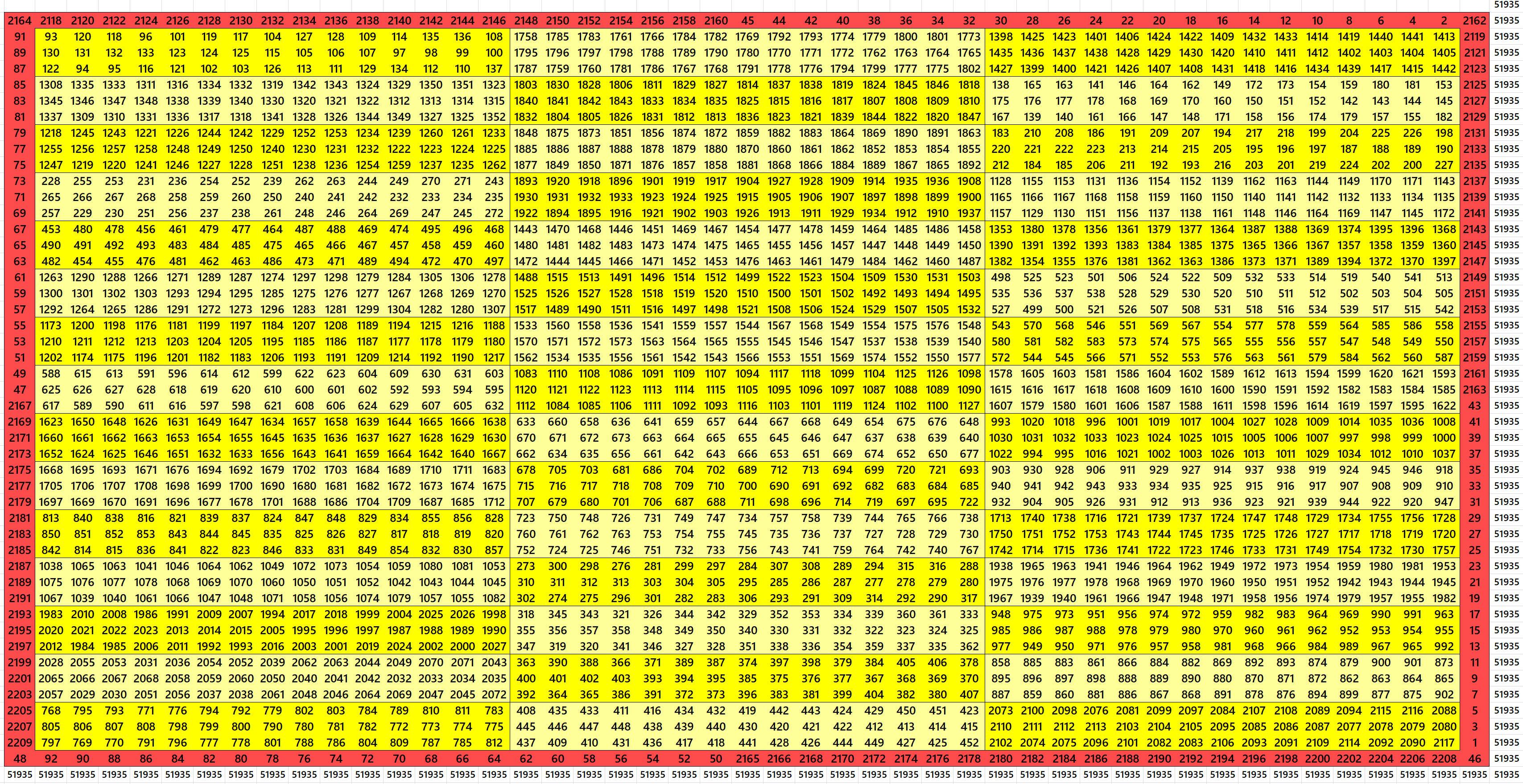
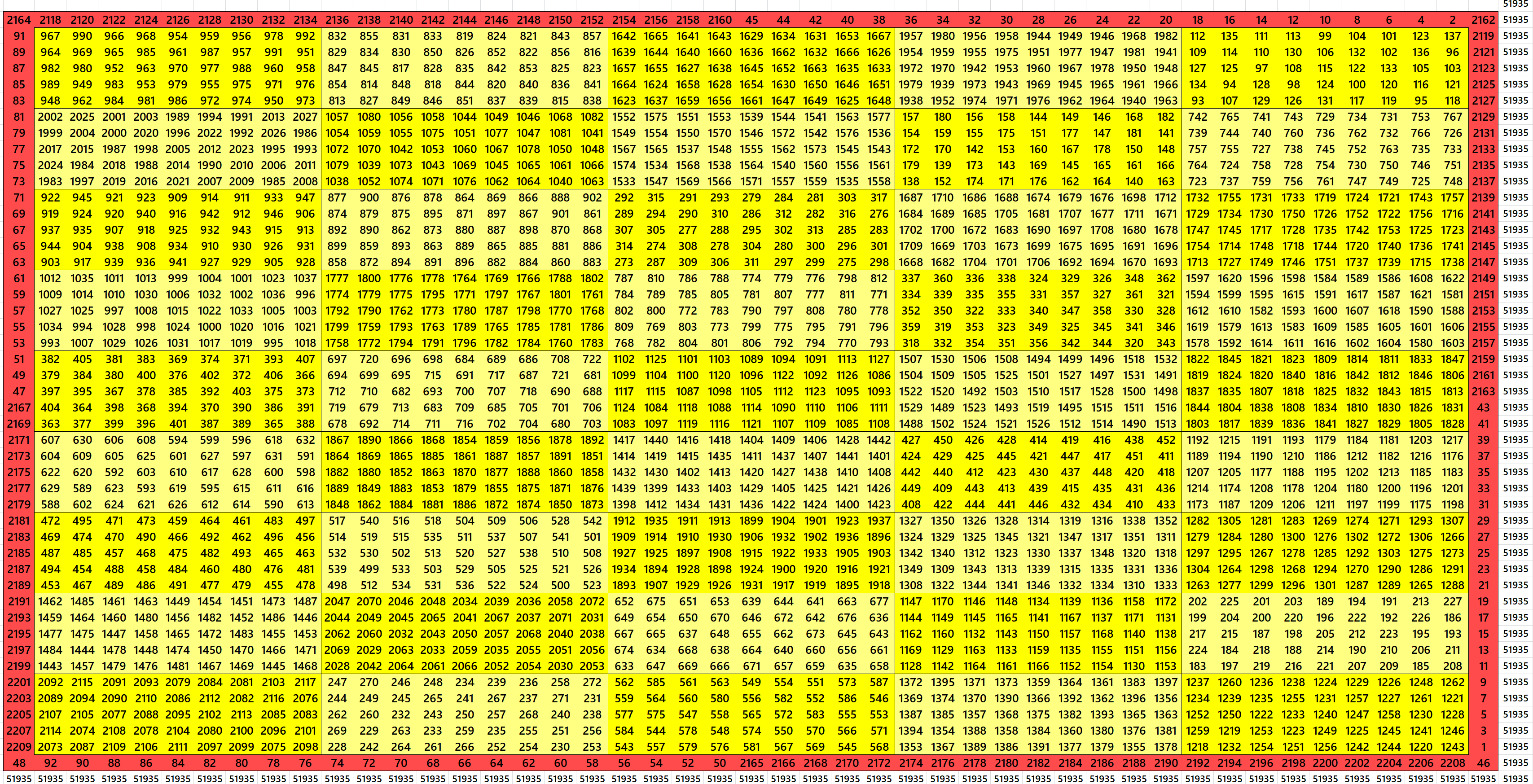
In this work, blocks of magic rectangles with equal and unequal sums are used to construct magic squares. The equal sum blocks magic rectangles lead us to even order magic squares, such as, of orders 8, 12, 16, 20, 24, 28, 32, 36, 40, 42, 44 and 48. These magic squares are constructed using magic rectangles of orders 2×4, 2×14, 4×6, 6×10, 6×14, etc. There is only one example of an even order magic square with different sums blocks of magic rectangles, i.e., of order eighteen. The odd order magic squares are with unequal sum blocks magic rectangles. These are of orders 15, 21, 27, 33, 39 and 45. These are constructed using magic rectangles of orders 3×5, 3×7, 3×9, 3×11, 3×13, 3×15, 5×7, etc. The magic squares of orders 12, 20, 24, 28, 42, 45 and 48 are written in two ways. These magic squares are used to bring block-bordered magic squares. These block-bordered are of orders 10, 14, 17, 19, 23, 26, 29, 31, 34, 37, 38, 41, 43, 46 and 47. Most of the magic squares from order 8 to 48 are studied in this work, except the orders 9, 11, 13 and 25. These are already studied by the author in another work
Link for downloading the work:
- Inder J. Taneja, Magic Rectangles in Construction of Magic and Block Bordered Magic Squares (Version 3), June 03, 2022, pp. 1-70, Zenodo, https://doi.org/10.5281/zenodo.6621071.
Below are examples of magic squares. These are written in three ways. The first two ways appear as Part 1. The third way is given below as Part 2.
- Part 1:
- Even Order Magic Squares: It includes magic squares of orders 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 44 and 48. – See the link: Magic Rectangles in Construction of Magic and Block Bordered Magic Squares: Part 1 – Even and Odd Order Magic Squares
- Odd Order Magic Squares: It includes magic squares of orders 15, 21, 27, 33, 39 and 45. See the link: Magic Rectangles in Construction of Magic and Block Bordered Magic Squares: Part 1 – Even and Odd Order Magic Squares
- Part 2:
- Block-Bordered Magic Squares: It includes magic squares of orders 10, 14, 17, 19, 22, 23, 26, 29, 31, 34, 37, 38, 41, 43, 46 and 47.
Block-Bordered Magic Square of Order 10

Block-Bordered Magic Square of Order 14
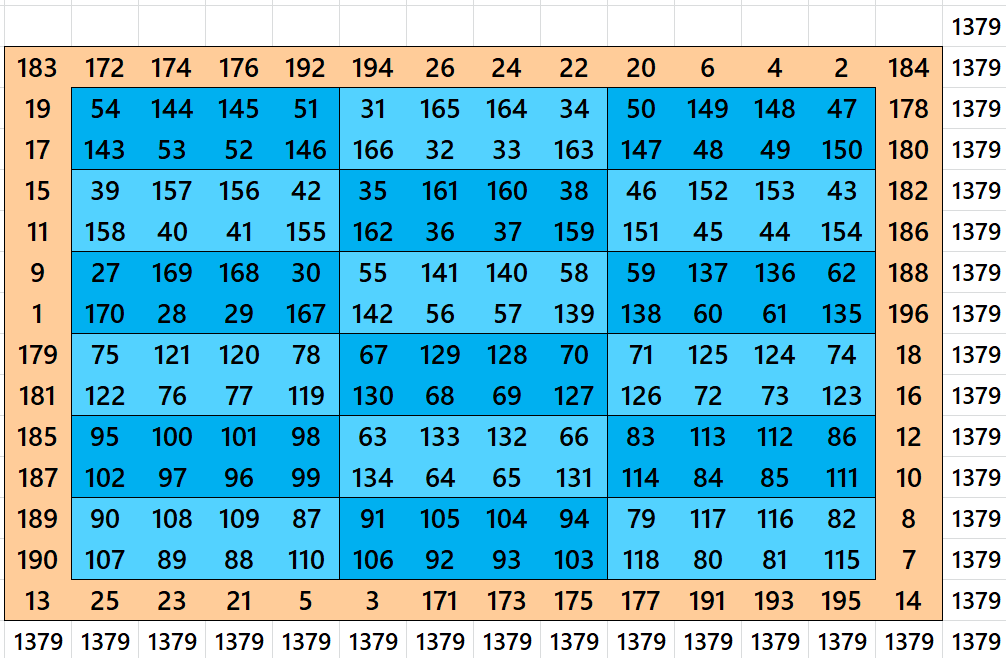
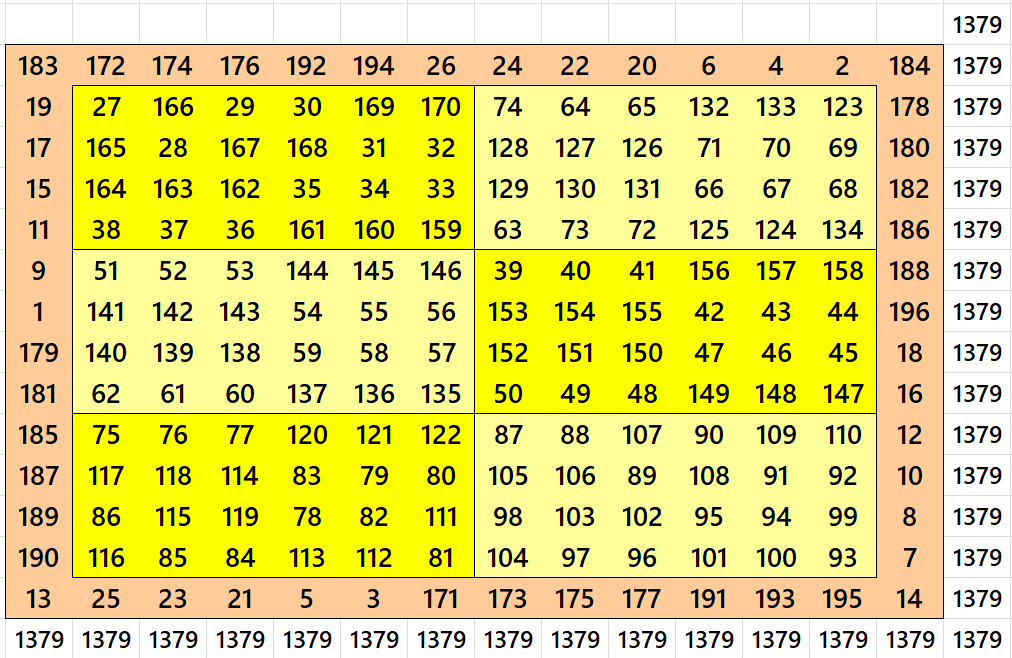
Block-Bordered Magic Square of Order 17

Block-Bordered Magic Square of Order 19
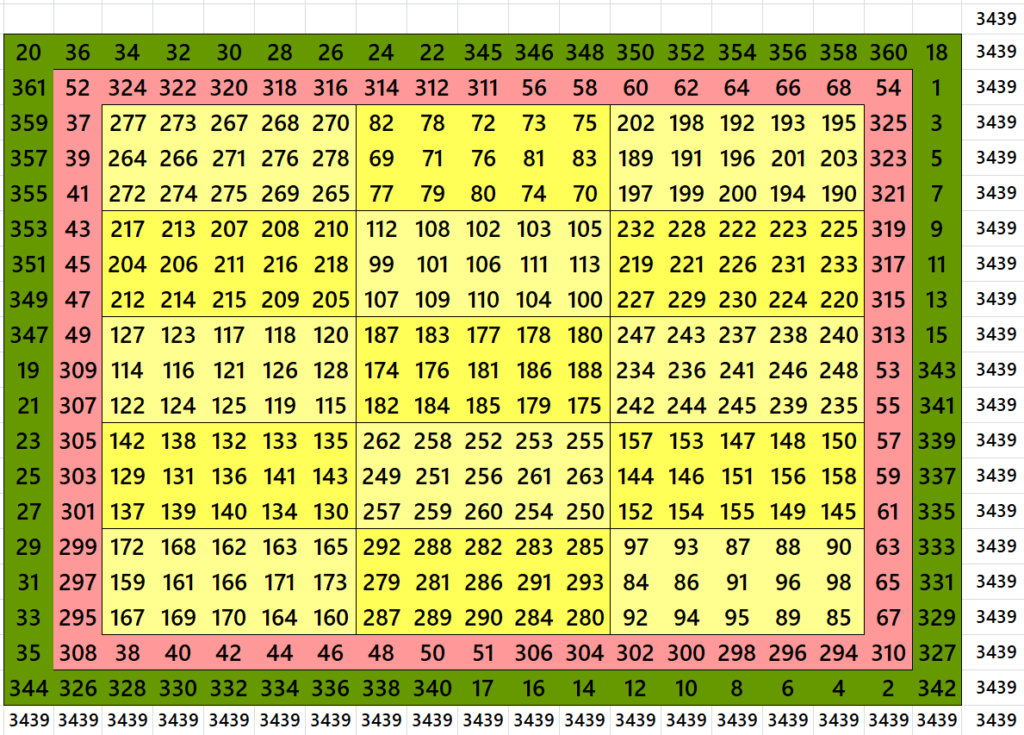
Block-Bordered Magic Square of Order 22
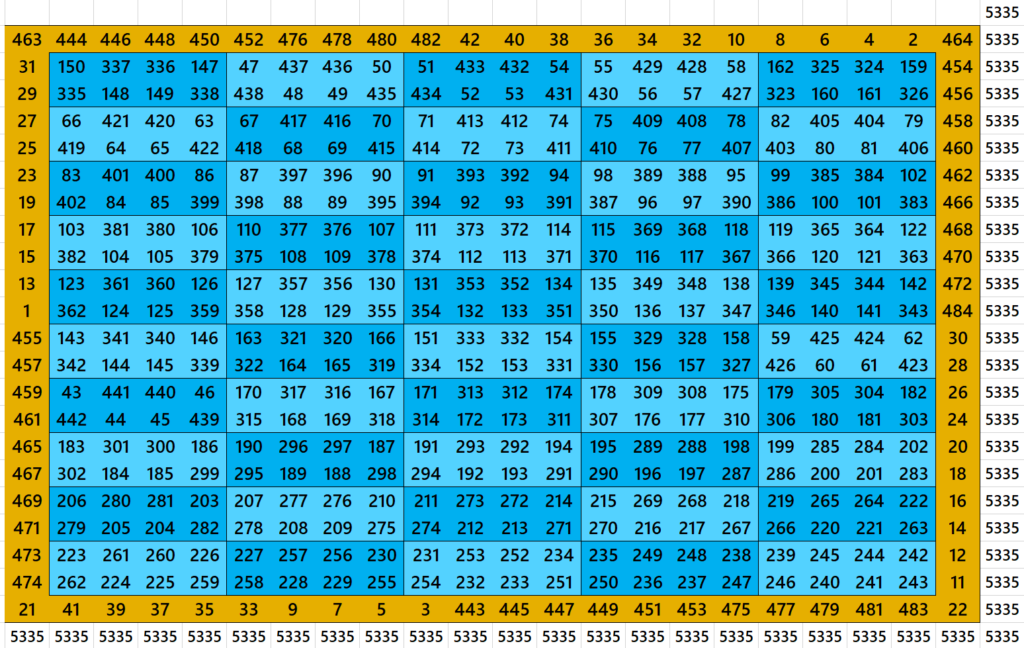
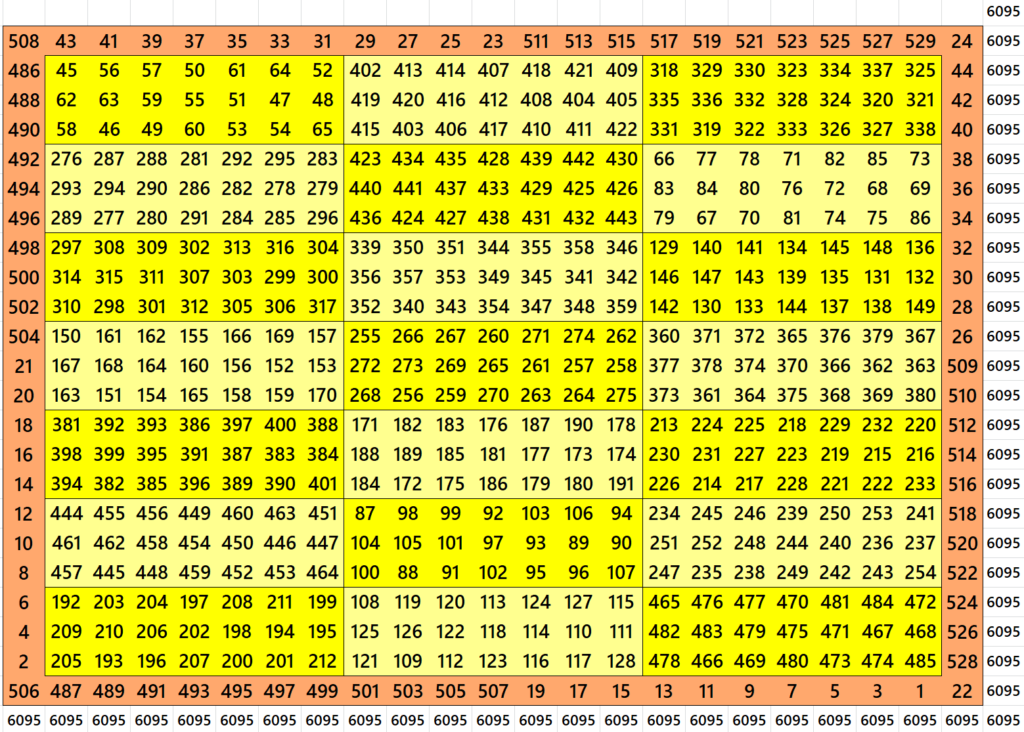
Block-Bordered Magic Square of Order 23
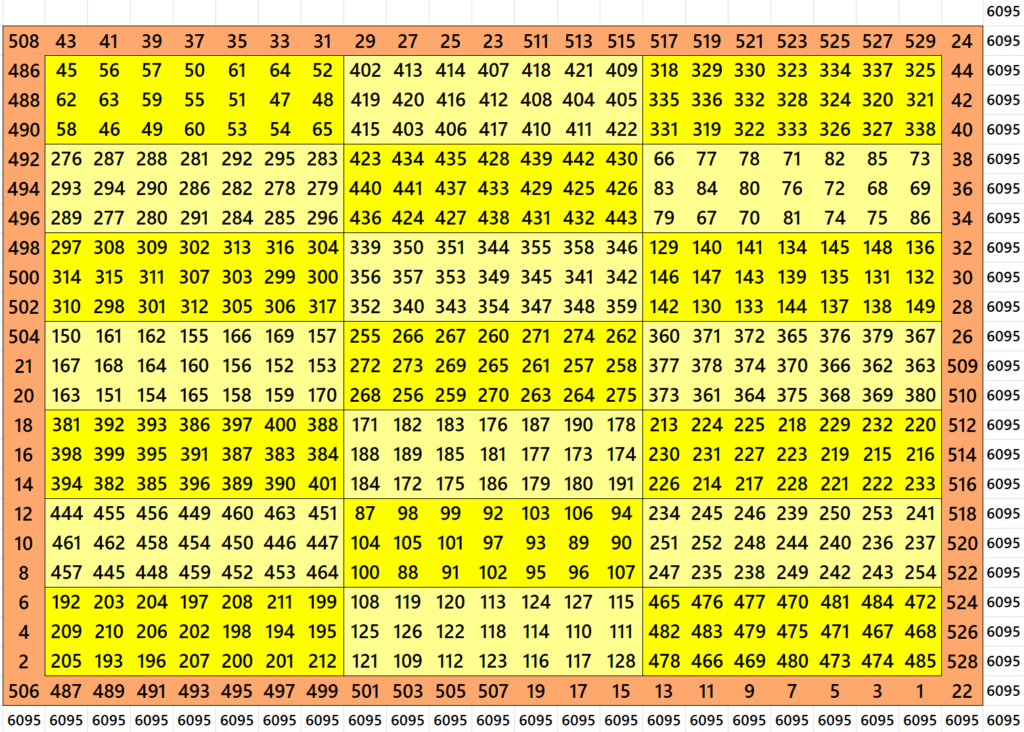
Block-Bordered Magic Square of Order 26
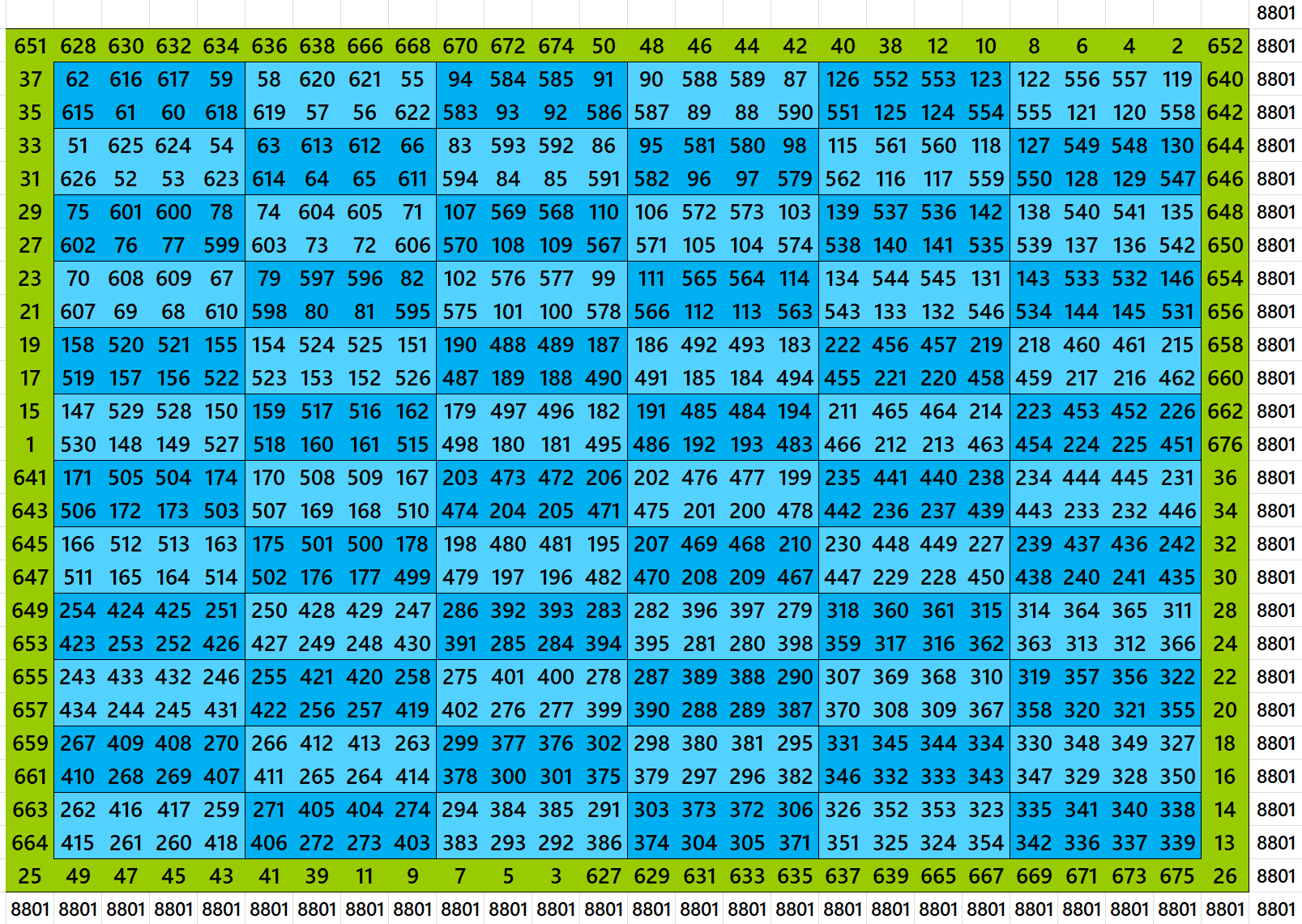
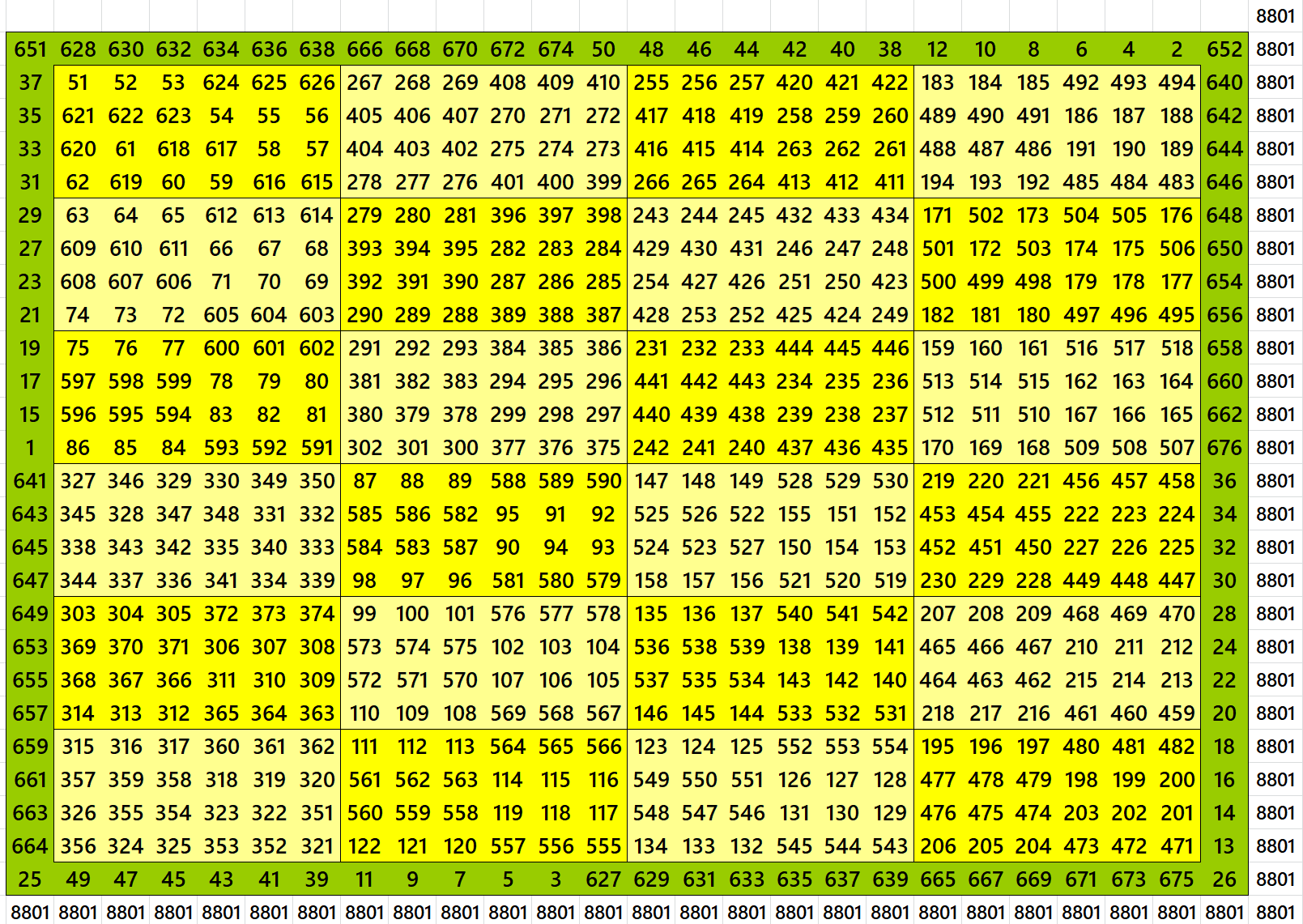
Block-Bordered Magic Square of Order 29
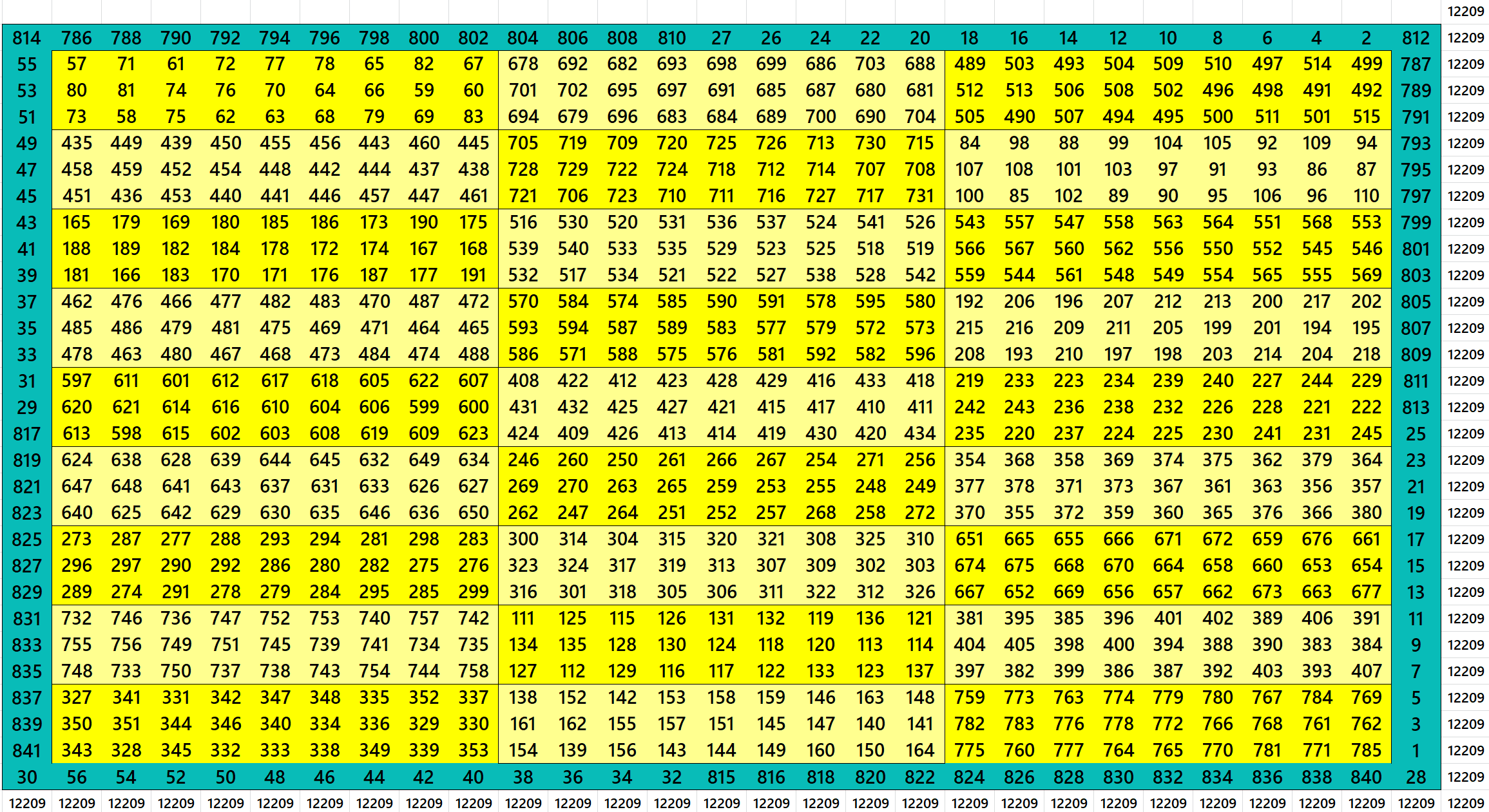
Block-Bordered Magic Square of Order 31
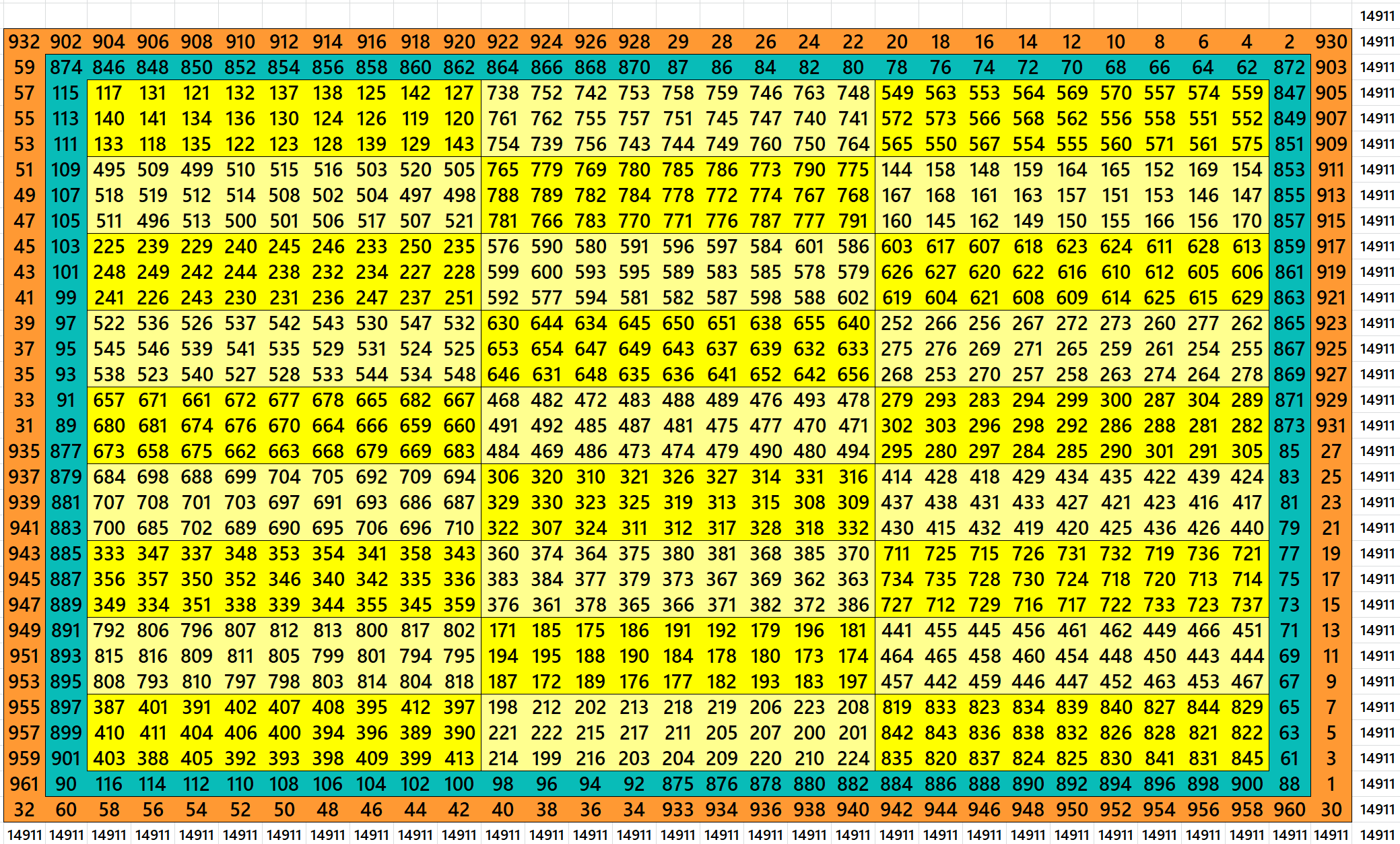
Block-Bordered Magic Square of Order 34
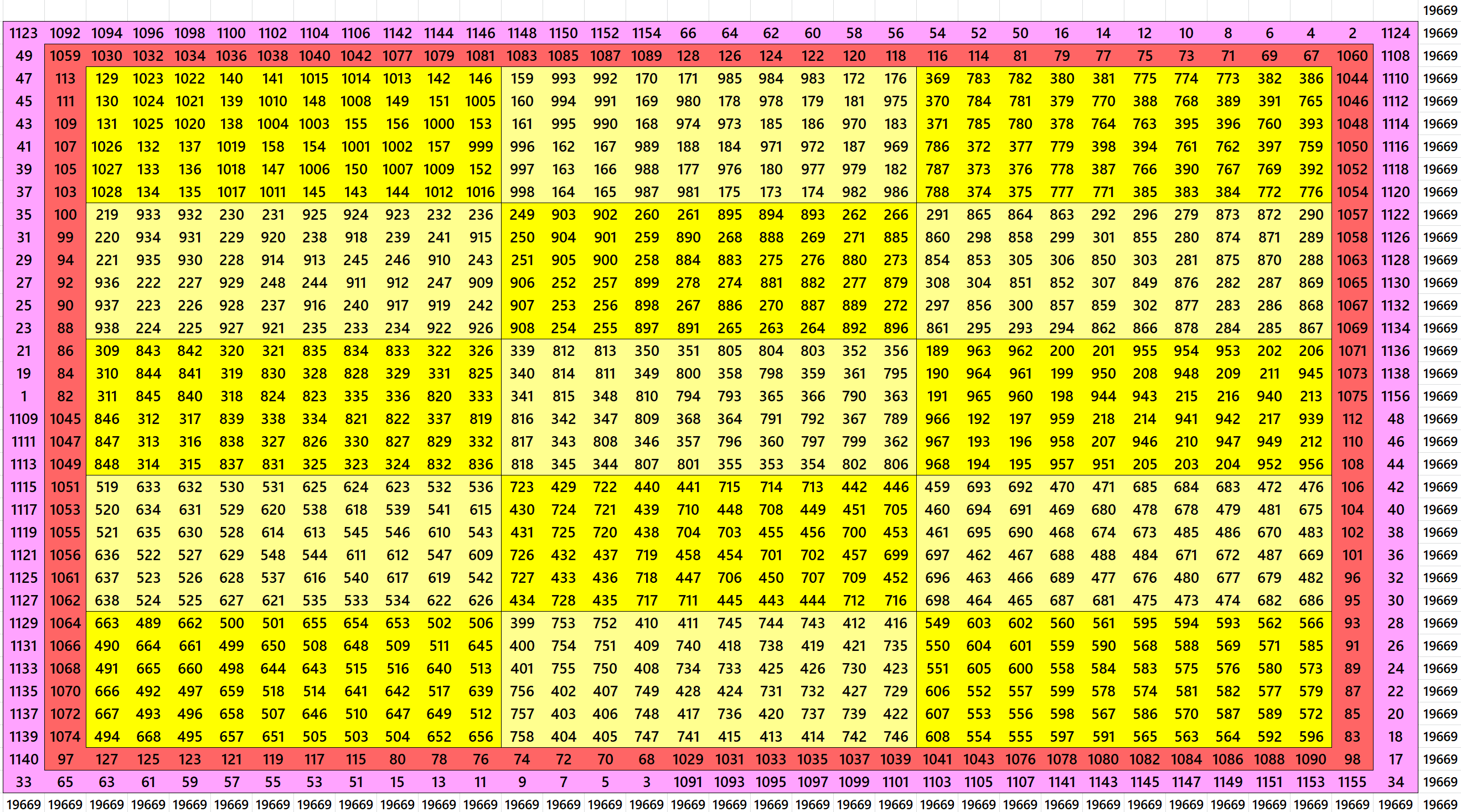
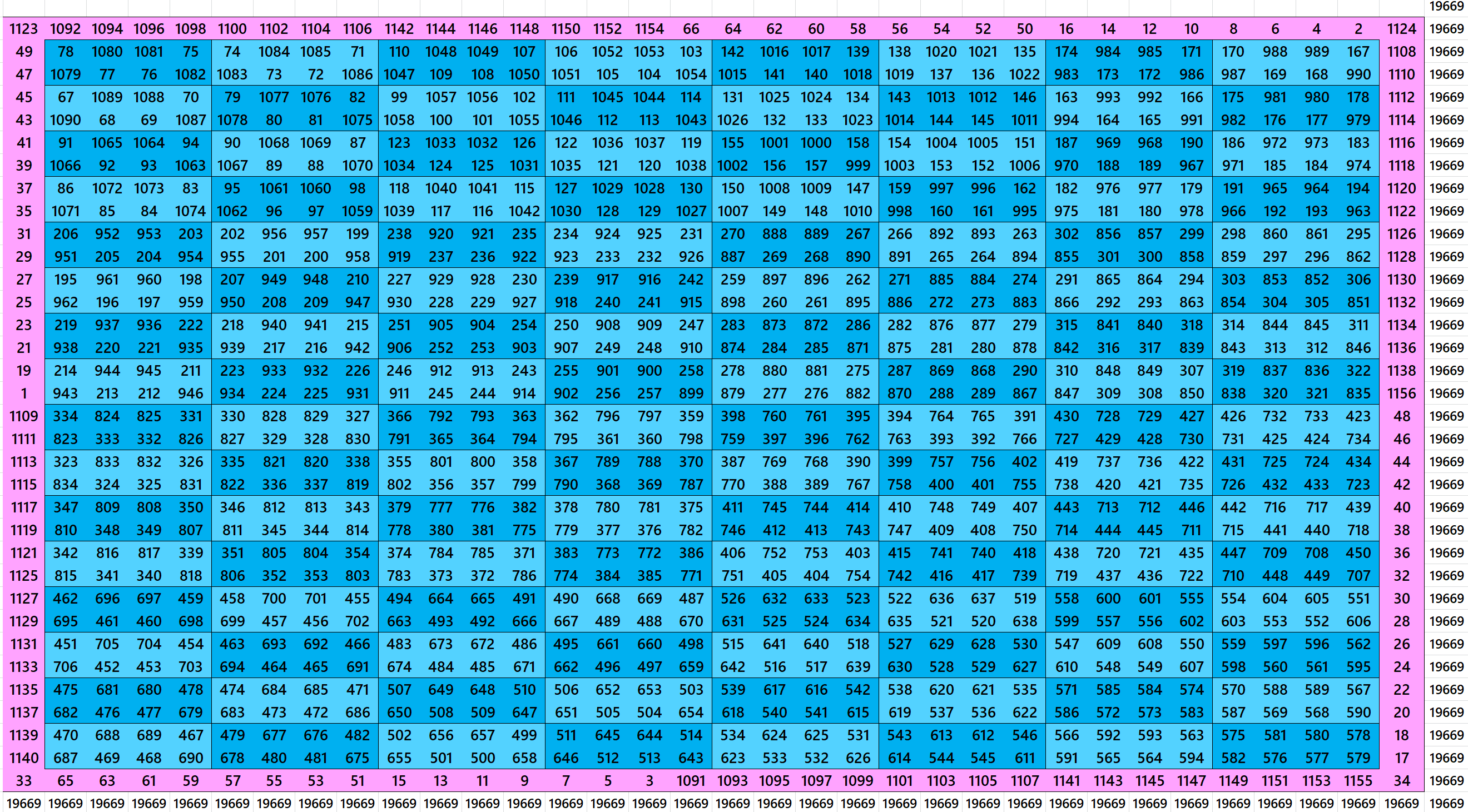
Block-Bordered Magic Square of Order 37
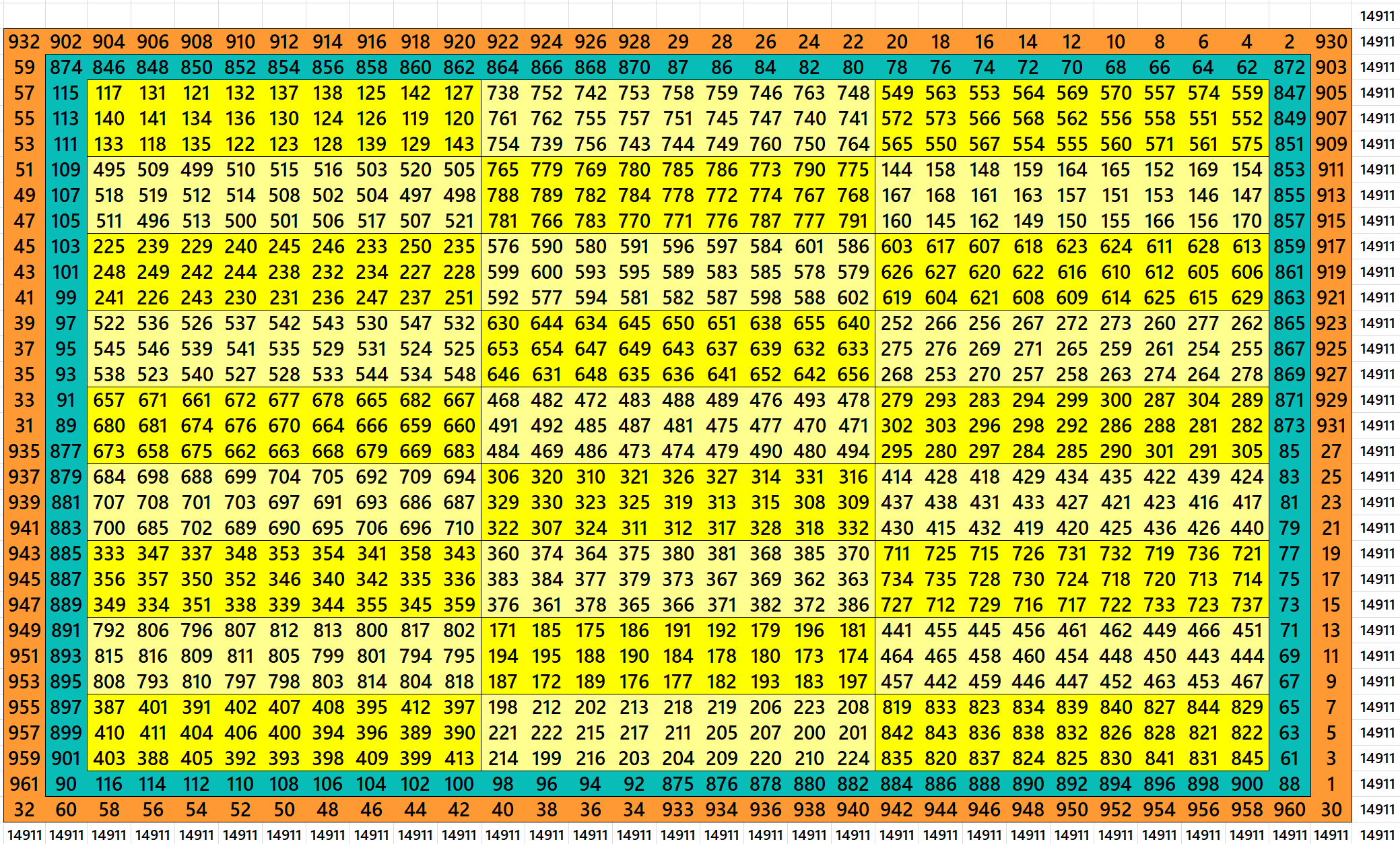
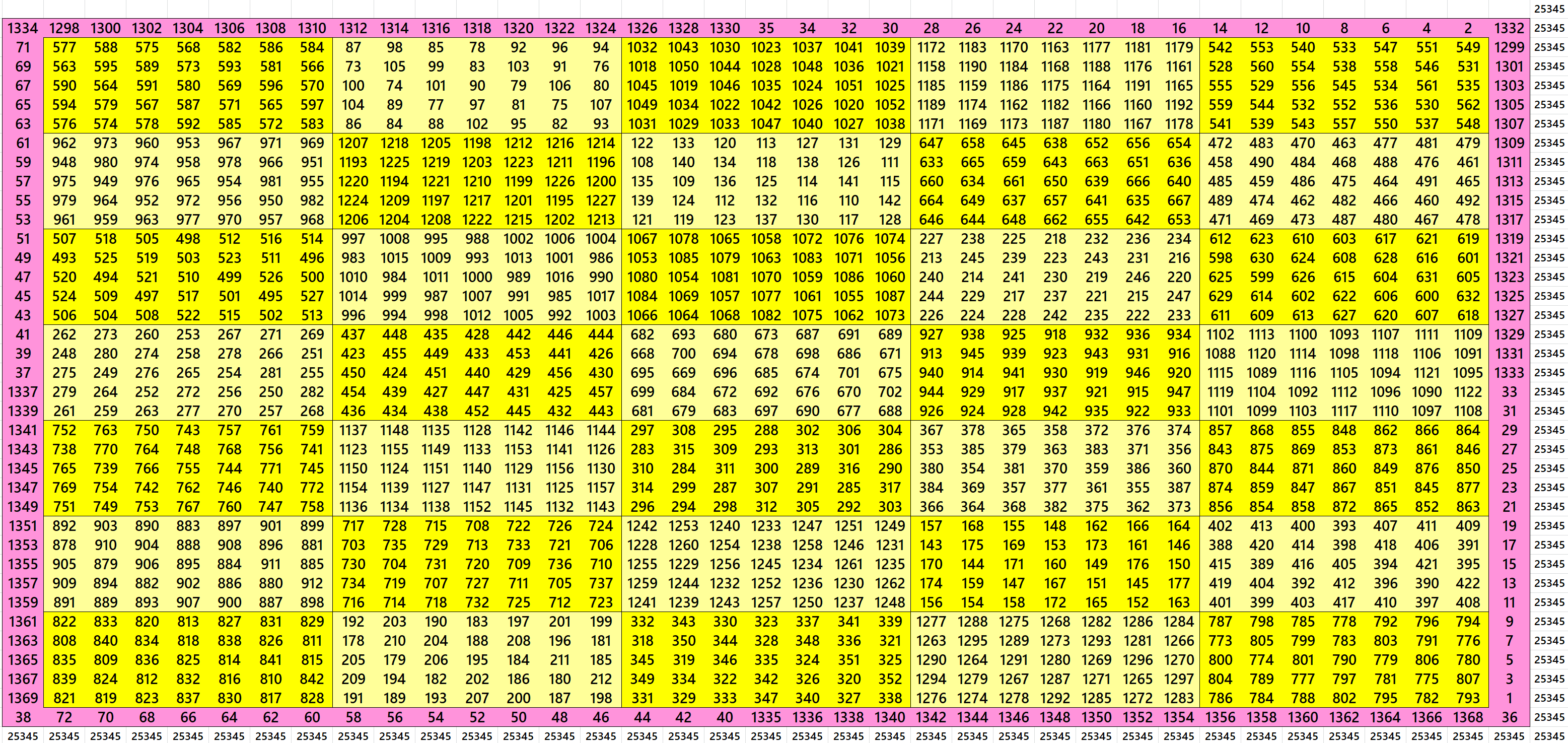
Block-Bordered Magic Square of Order 38

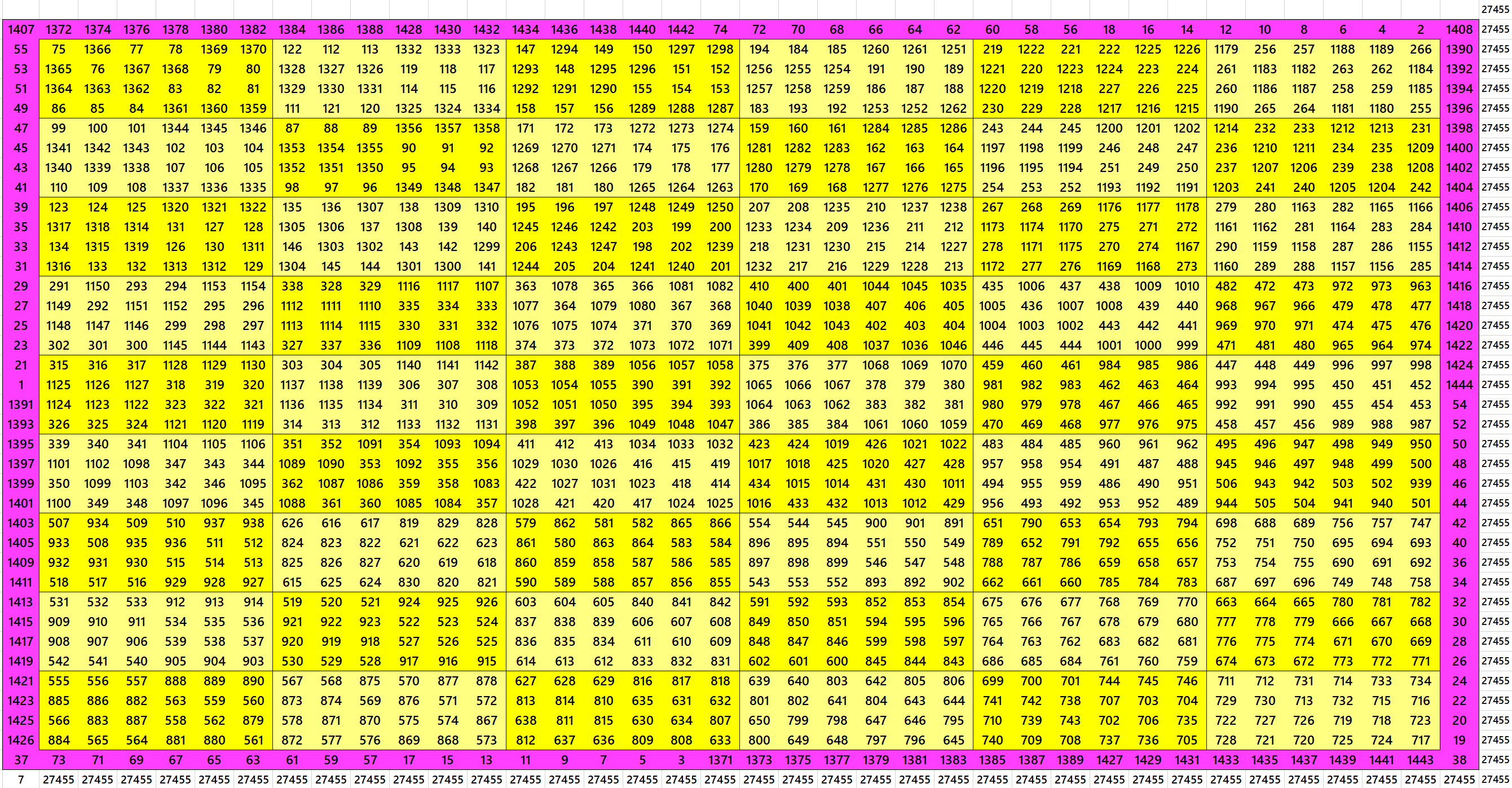
Block-Bordered Magic Square of Order 41
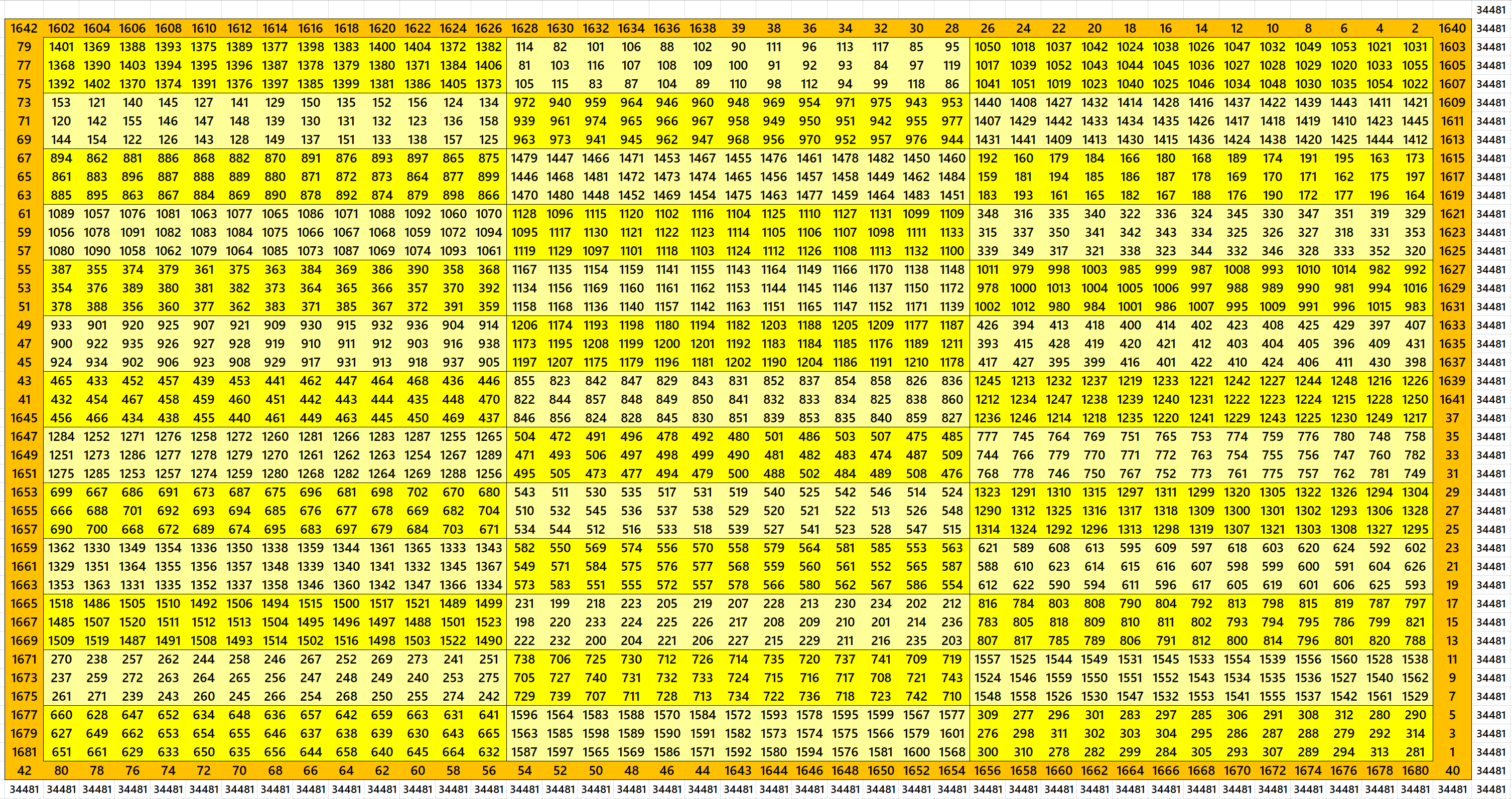
Block-Bordered Magic Square of Order 43
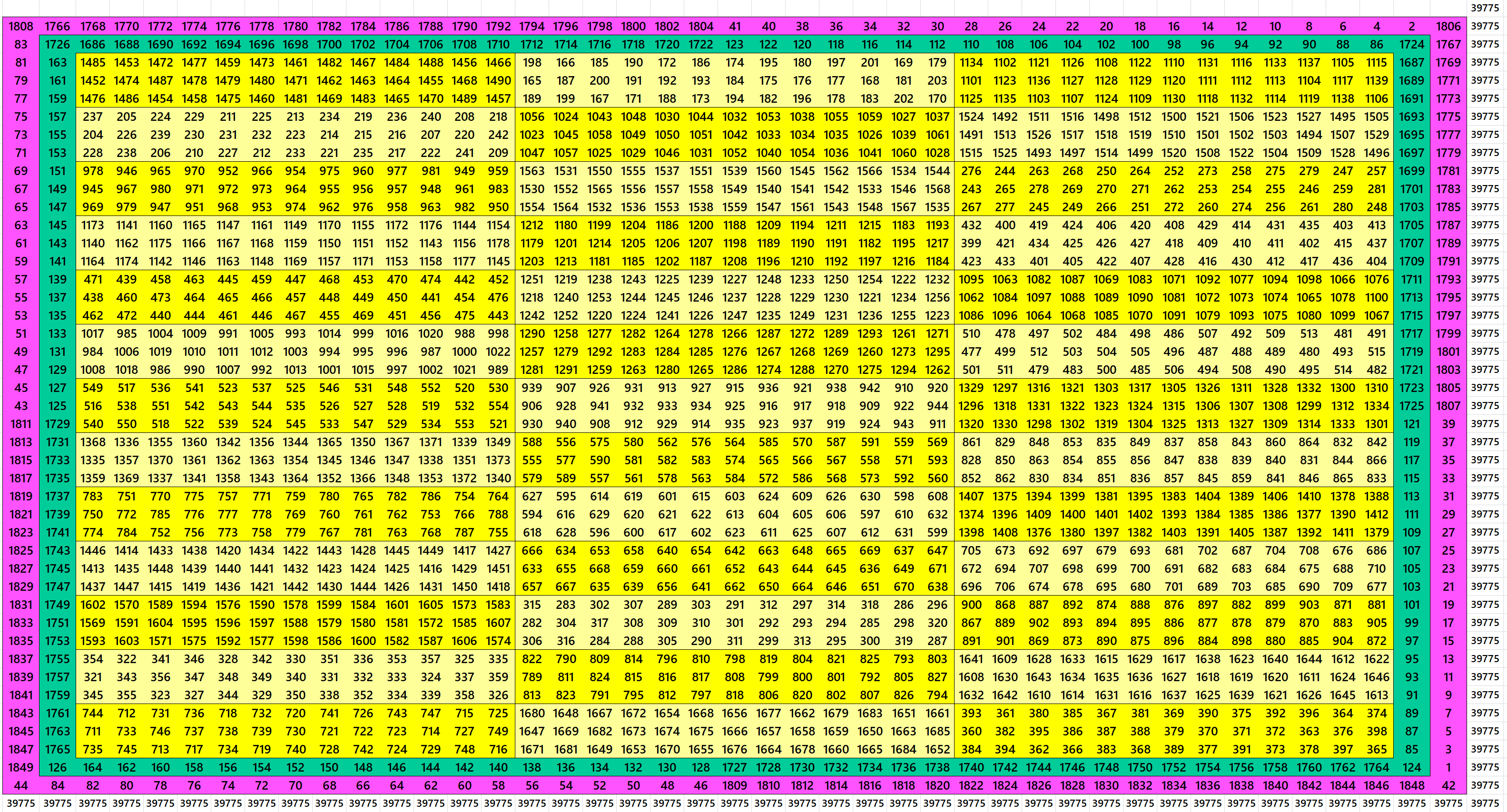
Block-Bordered Magic Square of Order 46
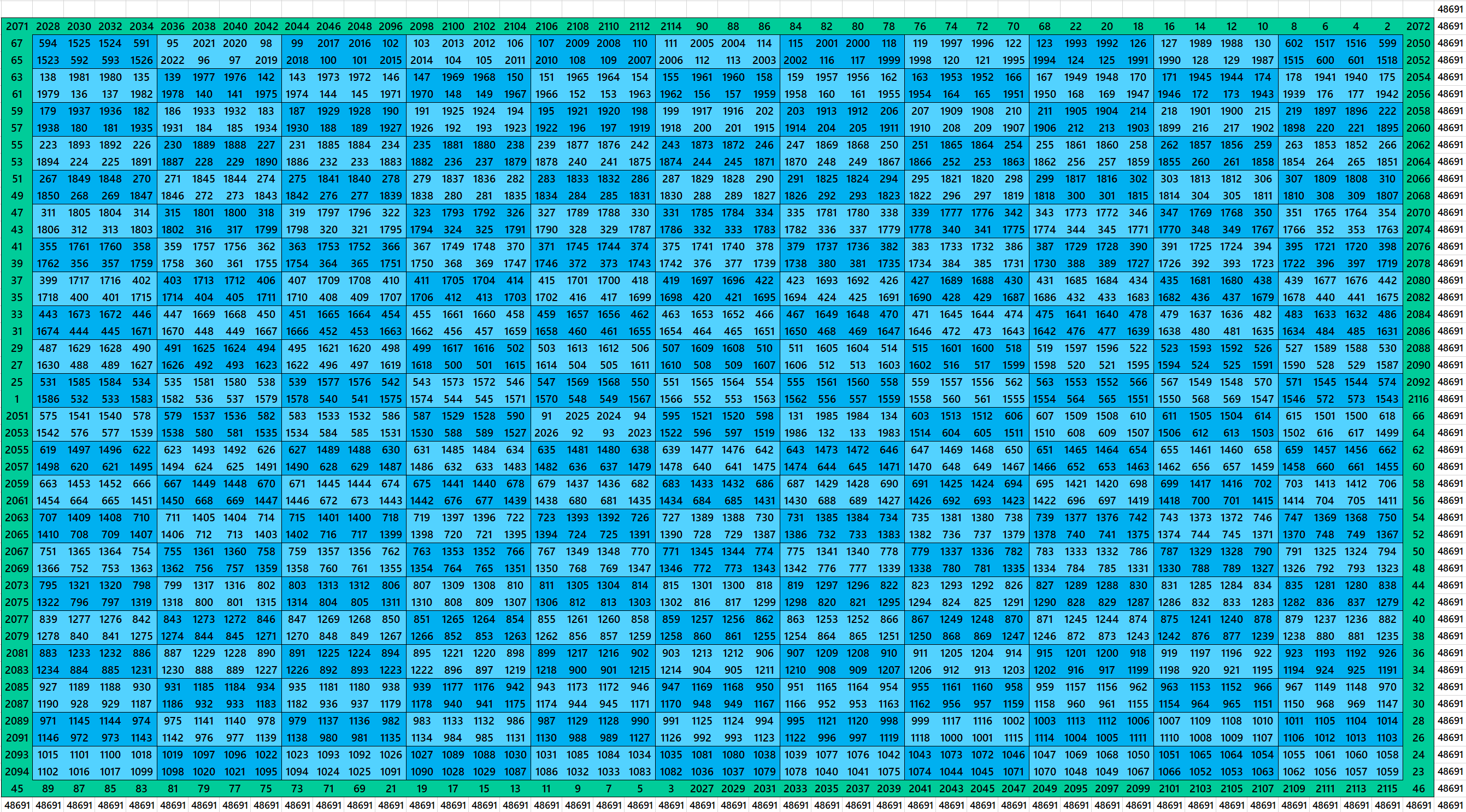
Block-Bordered Magic Square of Order 47