In this work, blocks of magic rectangles with equal and unequal sums are used to construct magic squares. The equal sum blocks magic rectangles lead us to even order magic squares, such as, of orders 8, 12, 16, 20, 24, 28, 32, 36, 40, 42, 44 and 48. These magic squares are constructed using magic rectangles of orders 2×4, 2×14, 4×6, 6×10, 6×14, etc. There is only one example of an even order magic square with different sums blocks of magic rectangles, i.e., of order eighteen. The odd order magic squares are with unequal sum blocks magic rectangles. These are of orders 15, 21, 27, 33, 39 and 45. These are constructed using magic rectangles of orders 3×5, 3×7, 3×9, 3×11, 3×13, 3×15, 5×7, etc. The magic squares of orders 12, 20, 24, 28, 42, 45 and 48 are written in two ways. These magic squares are used to bring block bordered magic squares. These block-bordered are of orders 10, 14, 17, 19, 22, 23, 26, 29, 31, 34, 37, 38, 41, 43, 46 and 47. Most of the magic squares from order 8 to 48 are studied in this work, except the orders 9, 11, 13 and 25. These are already studied by the author in another work
Link for downloading the work:
- Inder J. Taneja, Magic Rectangles in Construction of Magic and Block Bordered Magic Squares (Version 3), June 03, 2022, pp. 1-70, Zenodo, https://doi.org/10.5281/zenodo.6621071.
Below are examples of magic squares. These are written in three ways. The first two ways appear as Part 1. The third way is given in another link as Part 2.
- Part 1:
- Even Order Magic Squares: It includes magic squares of orders 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 44 and 48.
- Odd Order Magic Squares: It includes magic squares of orders 15, 21, 27, 33, 39 and 45.
- Part 2:
- Block-Bordered Magic Squares: It includes magic squares of orders 10, 14, 17, 19, 22, 23, 26, 29, 31, 34, 38, 41, 43, 46 and 47. See the link: Magic Rectangles in Construction of Magic and Block-Bordered Magic Squares: Part 2 – Block-Bordered Magic Squares
1. Even Order Magic Squares
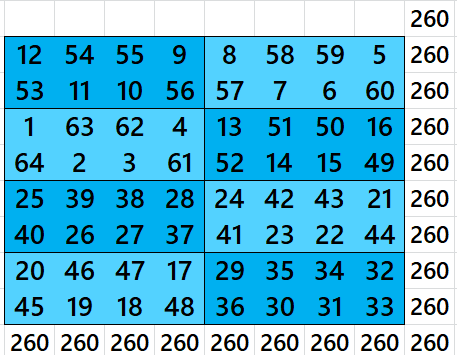
Magic Square of Order 8 with Equal Sum Blocks of Order 2×4
Magic Square of Order 12 with Equal Sum Blocks
First Way: Blocks of Order 2×4
Second Way: Blocks of Order 4×6

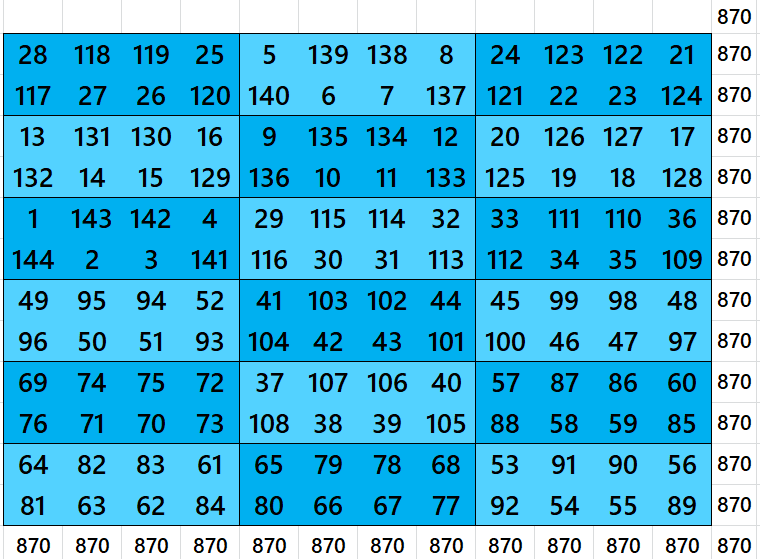
Magic Square of Order 16 with Equal Sum Blocks of Order 2×4
Magic Square of Order 18 with Different Sum Blocks of Order 2×6
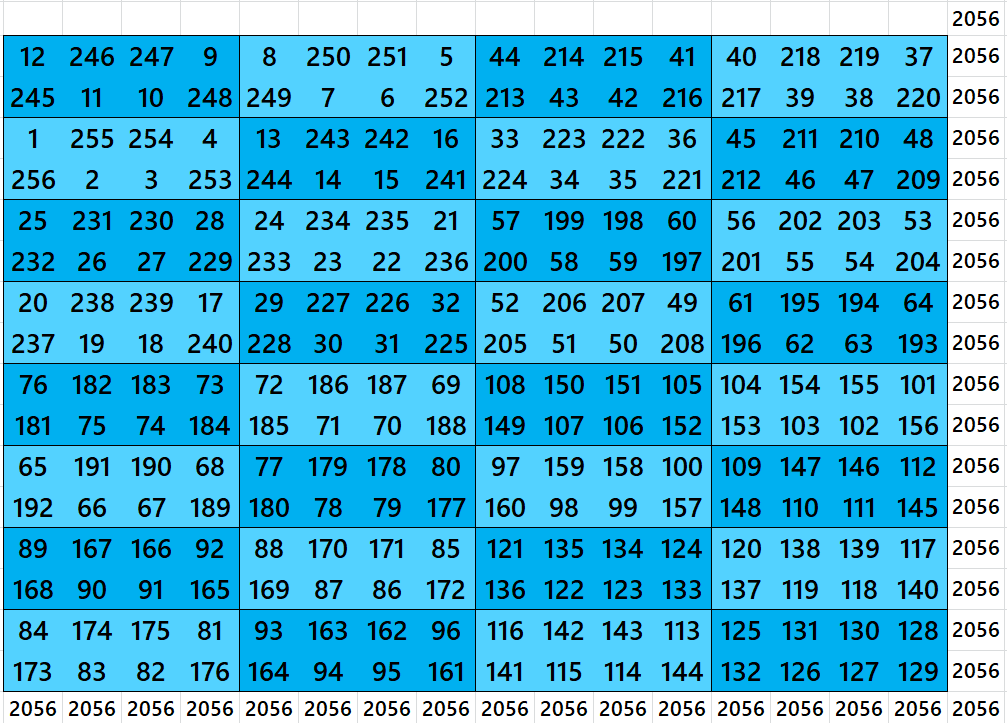
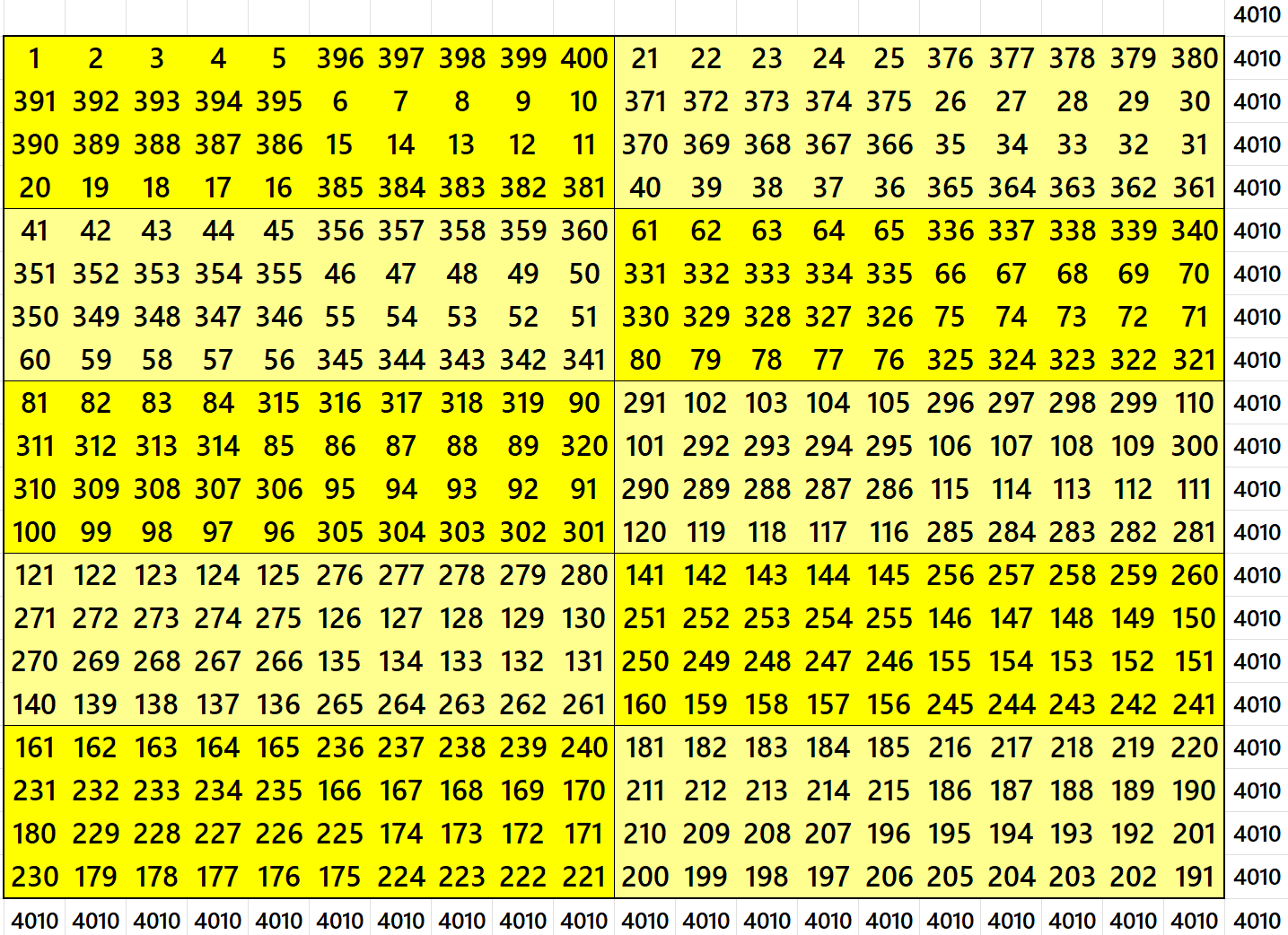
Magic Square of Order 20 with Equal Sum Blocks
First Way: Blocks of Order 2×4
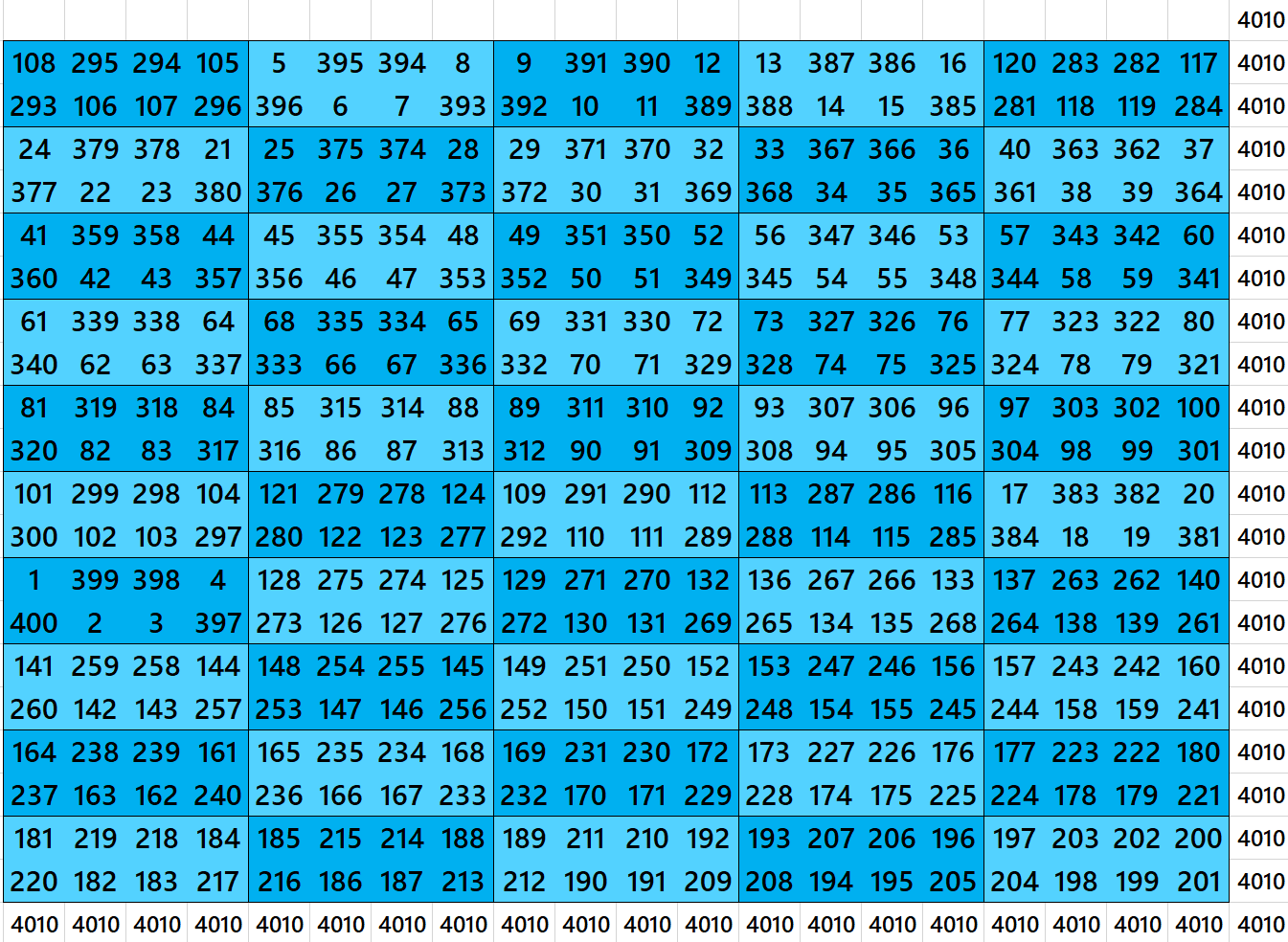
Second Way: Blocks of Order 4×10
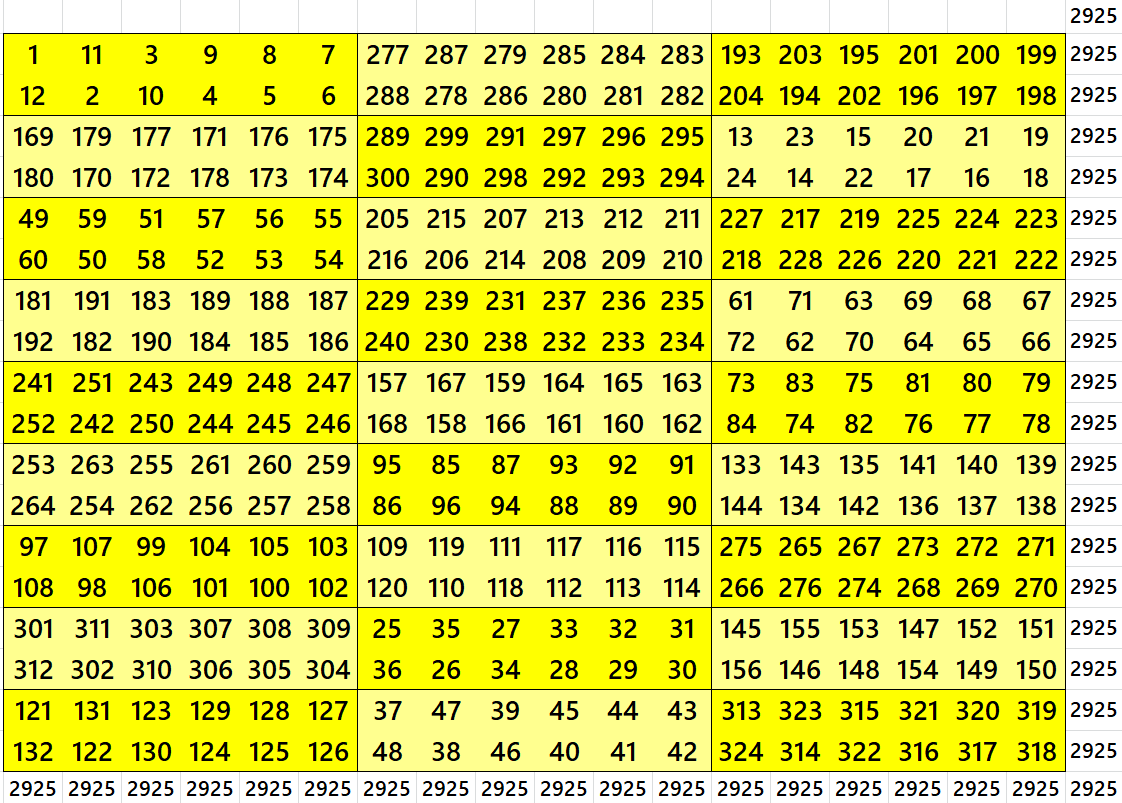
Magic Square of Order 24 with Equal Sum Blocks
First Way: Blocks of Order 2×4
Second Way: Blocks of Order 4×6

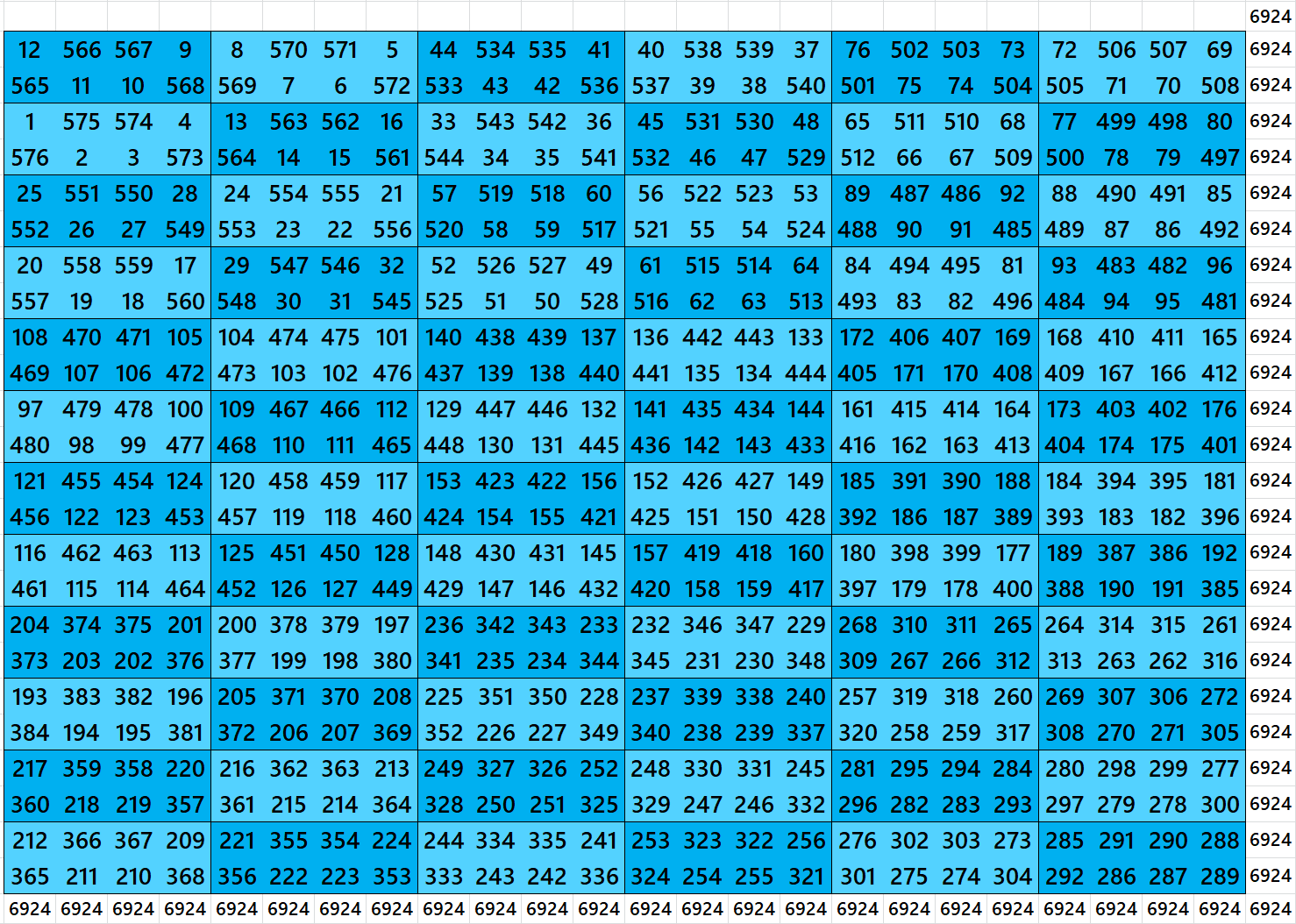
Magic Square of Order 28 with Equal Sum Blocks
First Way: Blocks of Order 2×4
Second Way: Blocks of Order 4×14
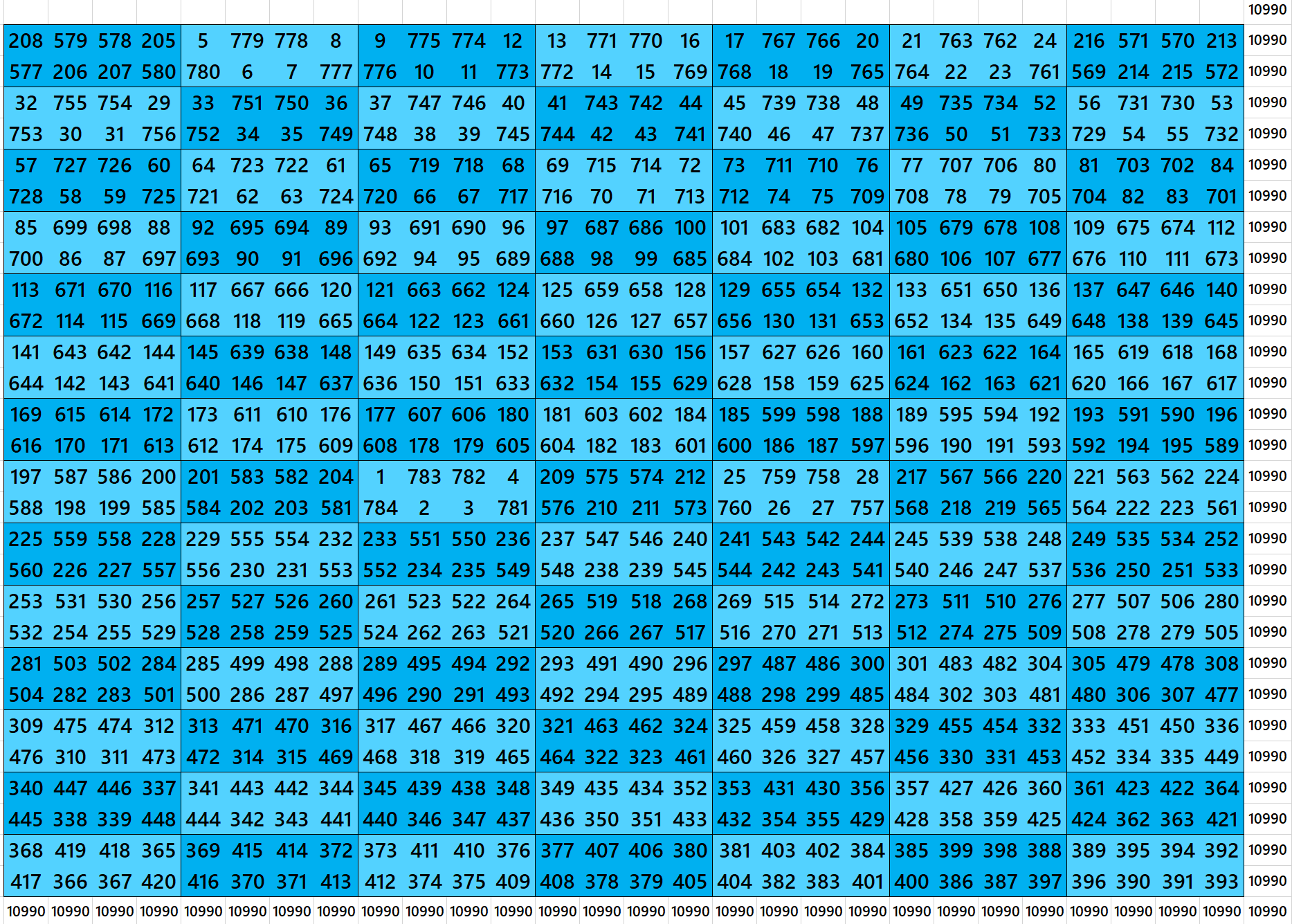
Magic Square of Order 30 With Equal Sum Blocks of Order 6×10
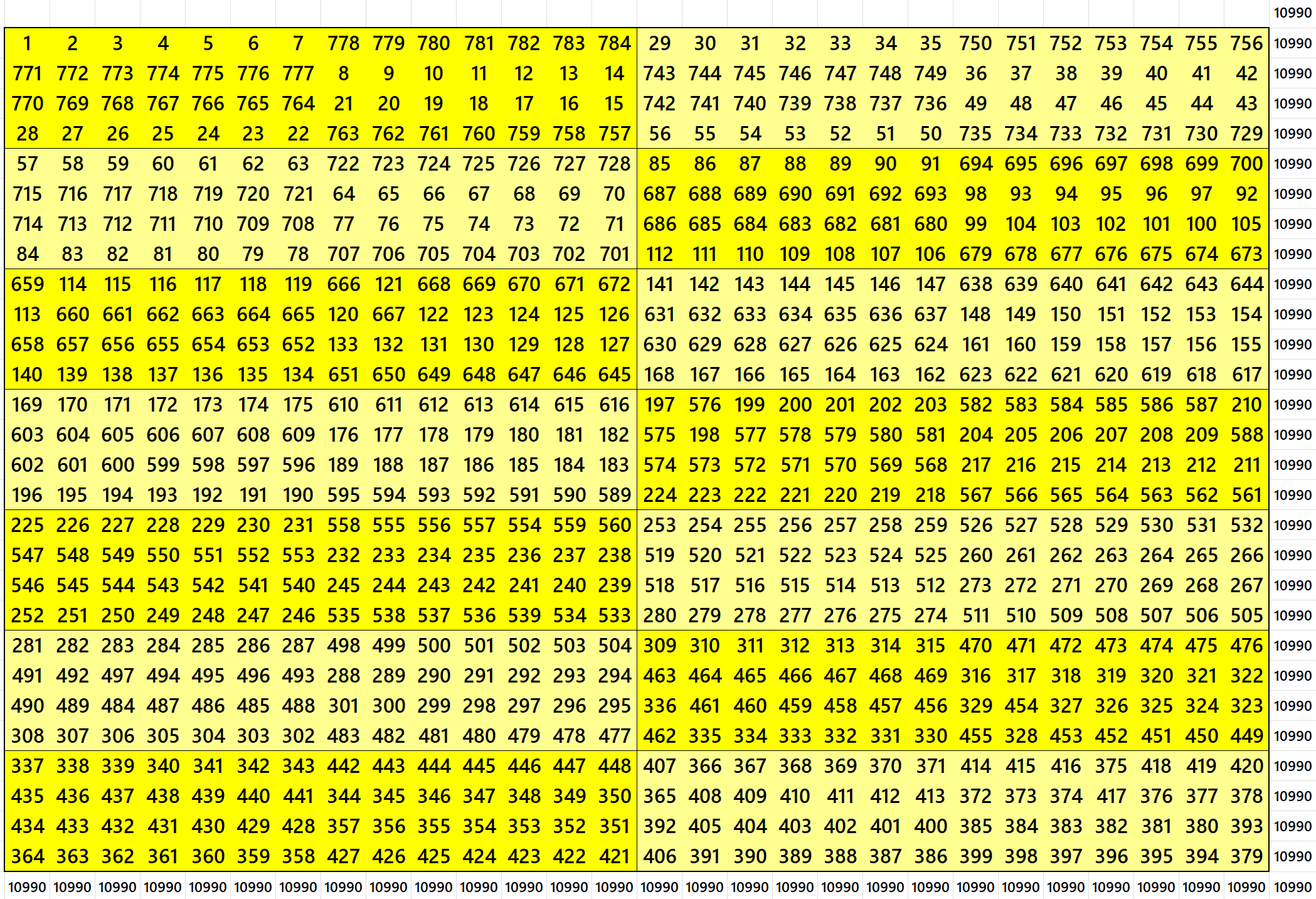
Magic Square of Order 32 With Equal Sum Blocks of Order 2×4
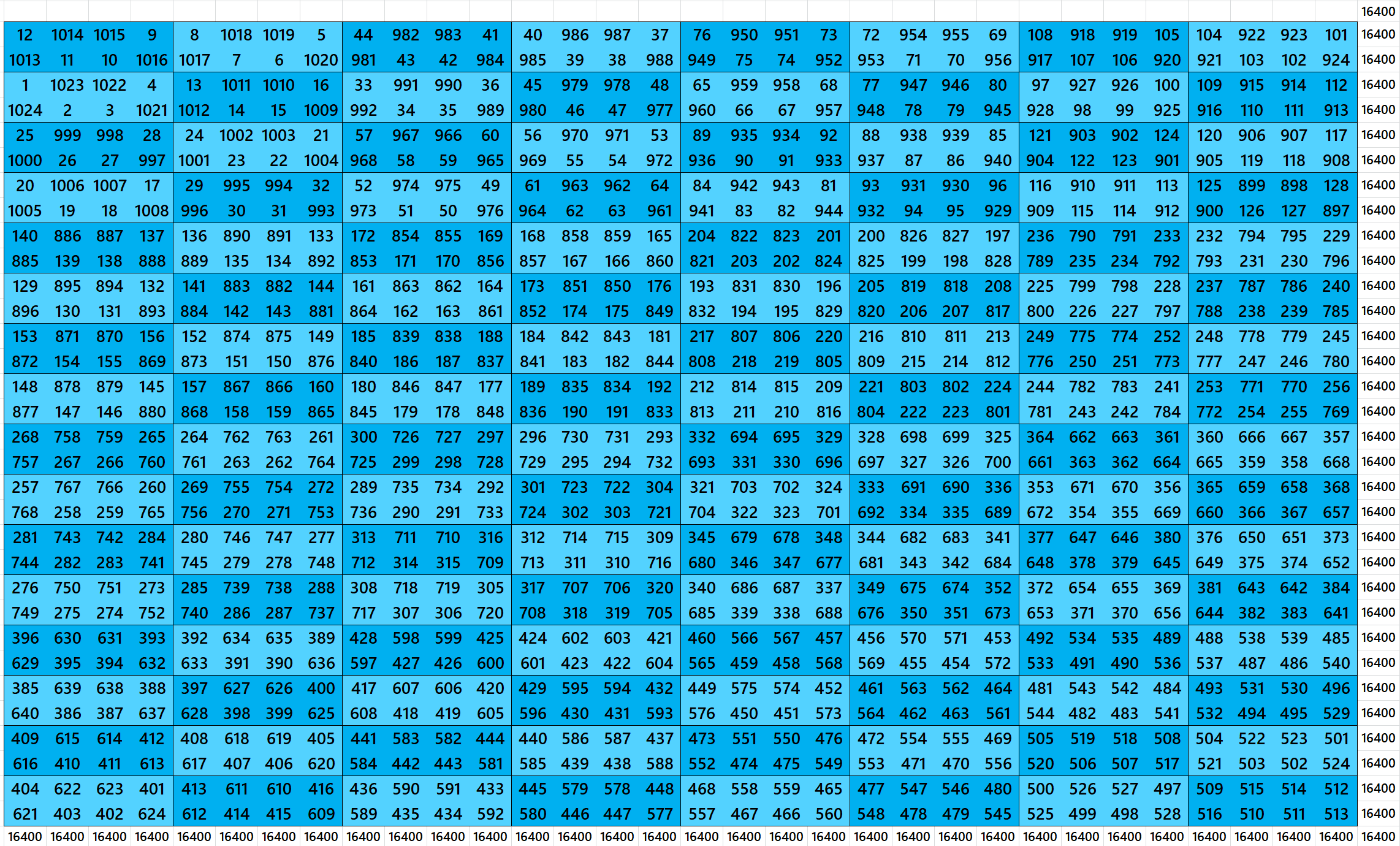
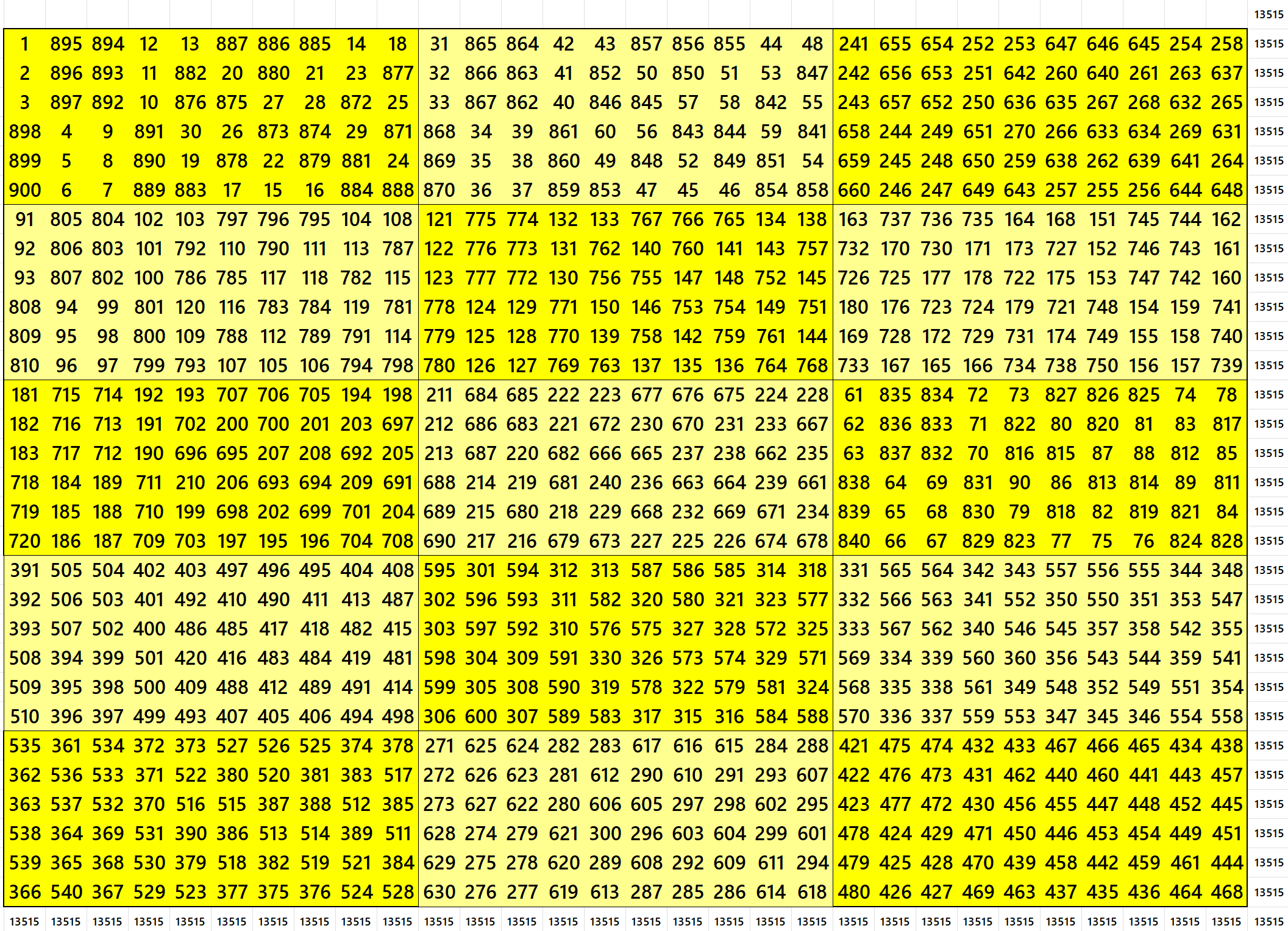
Magic Squares of Order 36 With Equal Sum Blocks
First Way: Blocks of Order 2×4

Second Way: Blocks of Order 4×6
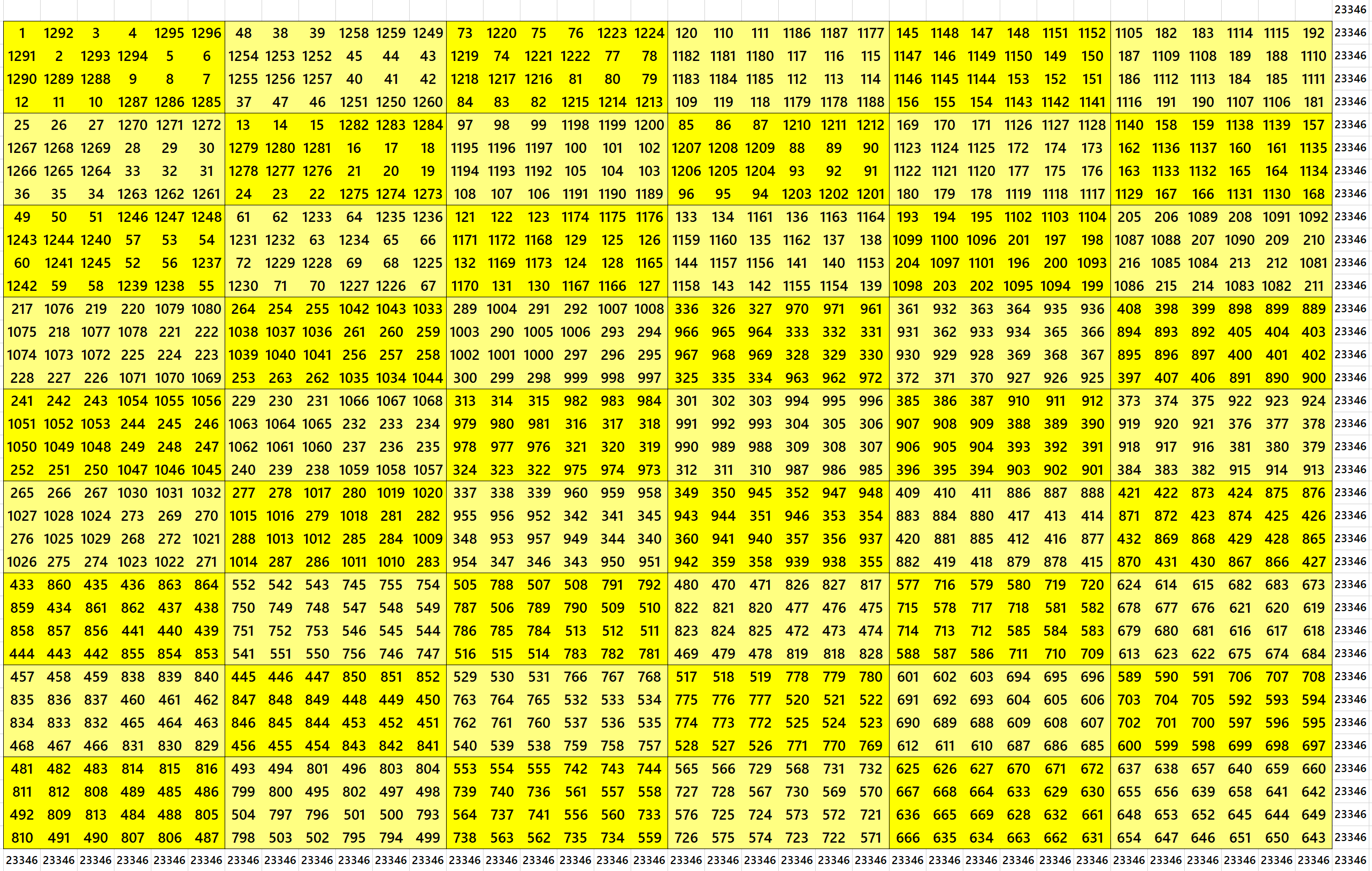
Magic Square of Order 40 With Equal Sum Blocks of Order 2×4

Magic Square of Order 42 With Equal and Unequal Sums Blocks
First Way: Unequal Sum Blocks of Order 2×4

Second Way: Equal Sum Blocks of Order 6×14
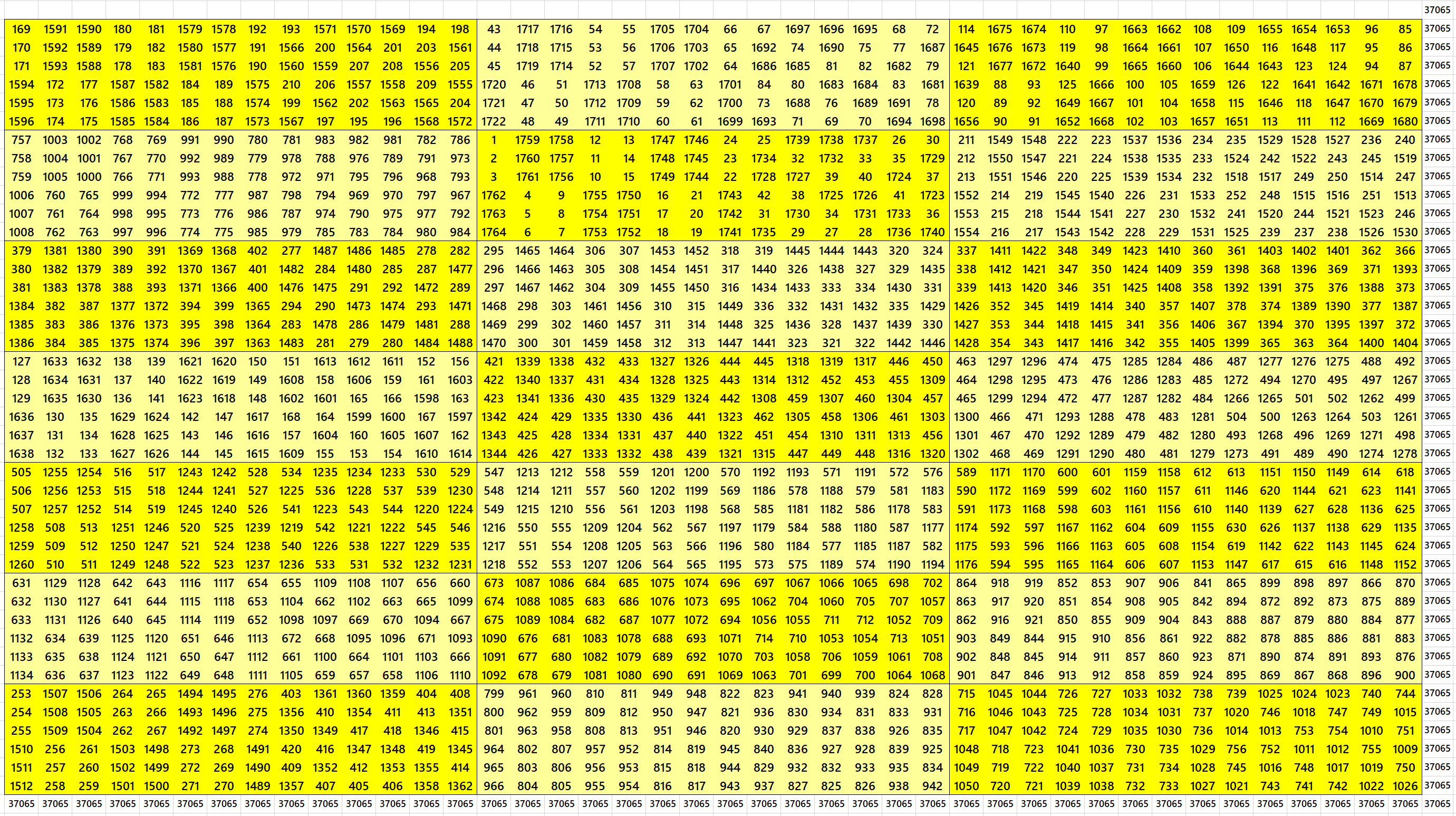
Magic Squares of Order 44 with Equal Sum Blocks of Order 2×4
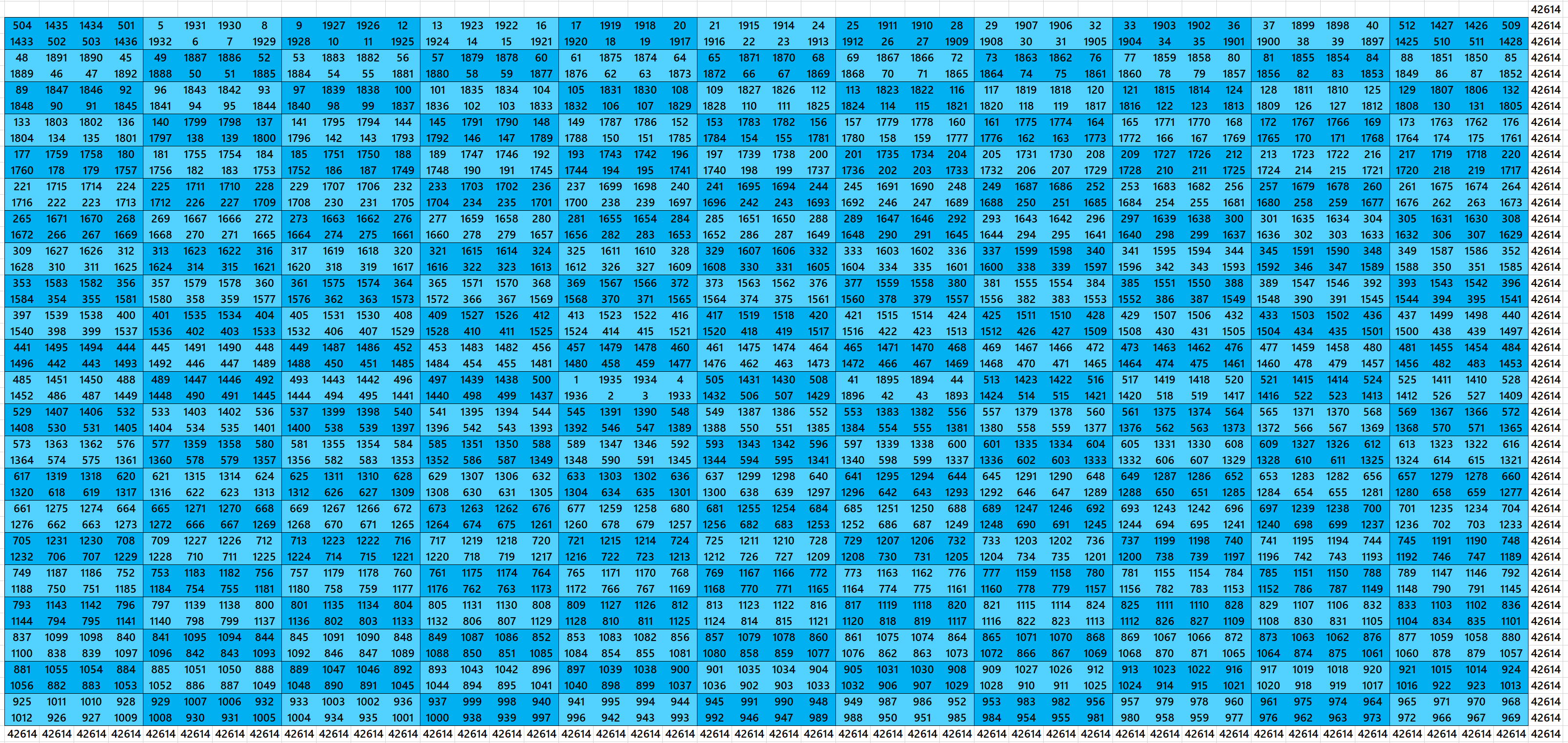
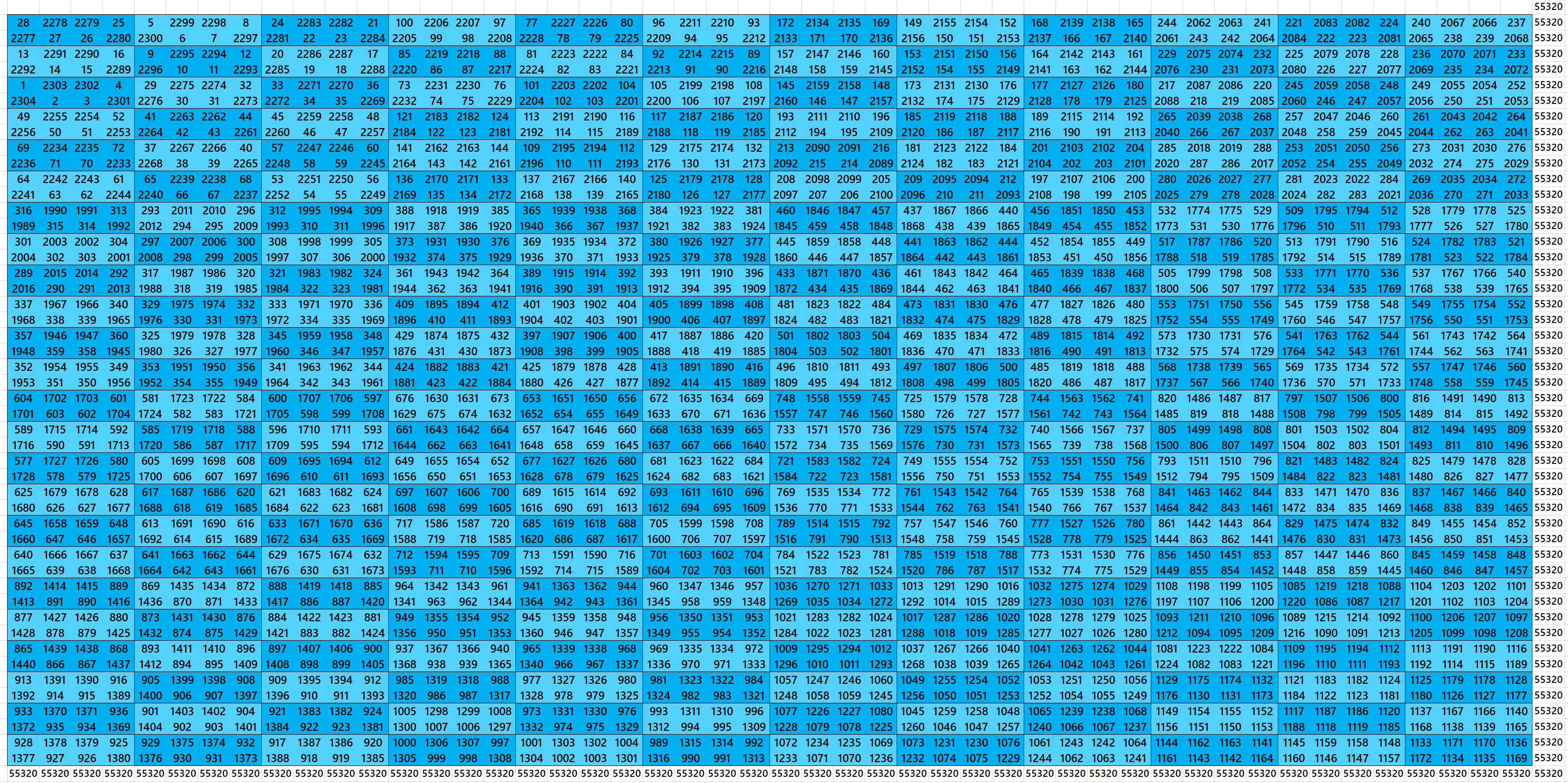
Magic Squares of Order 48 with Equal Sum Blocks
First Way: Blocks of Order 2×4
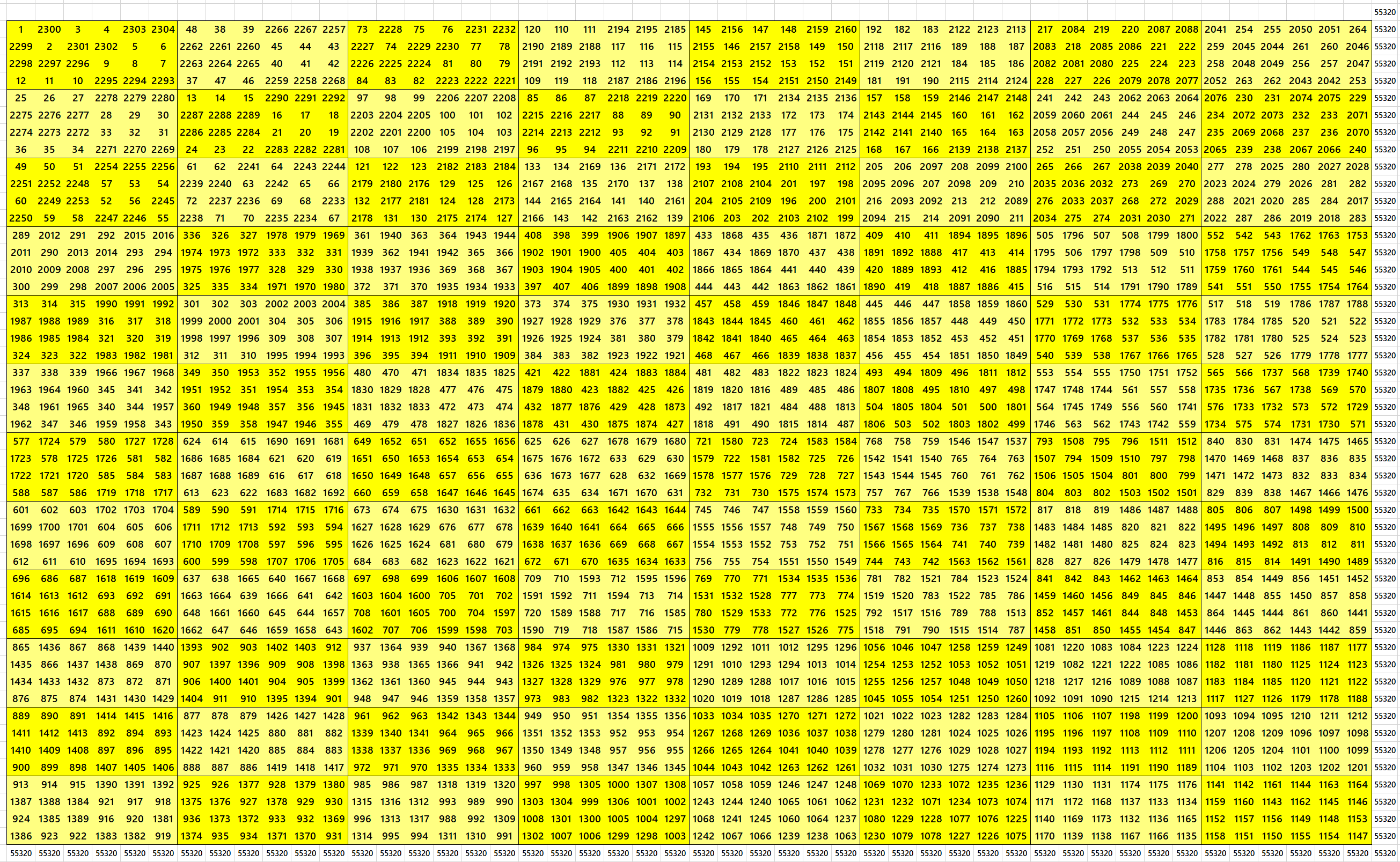
Second Way: Blocks of Order 4×6
2. Odd Order Magic Squares
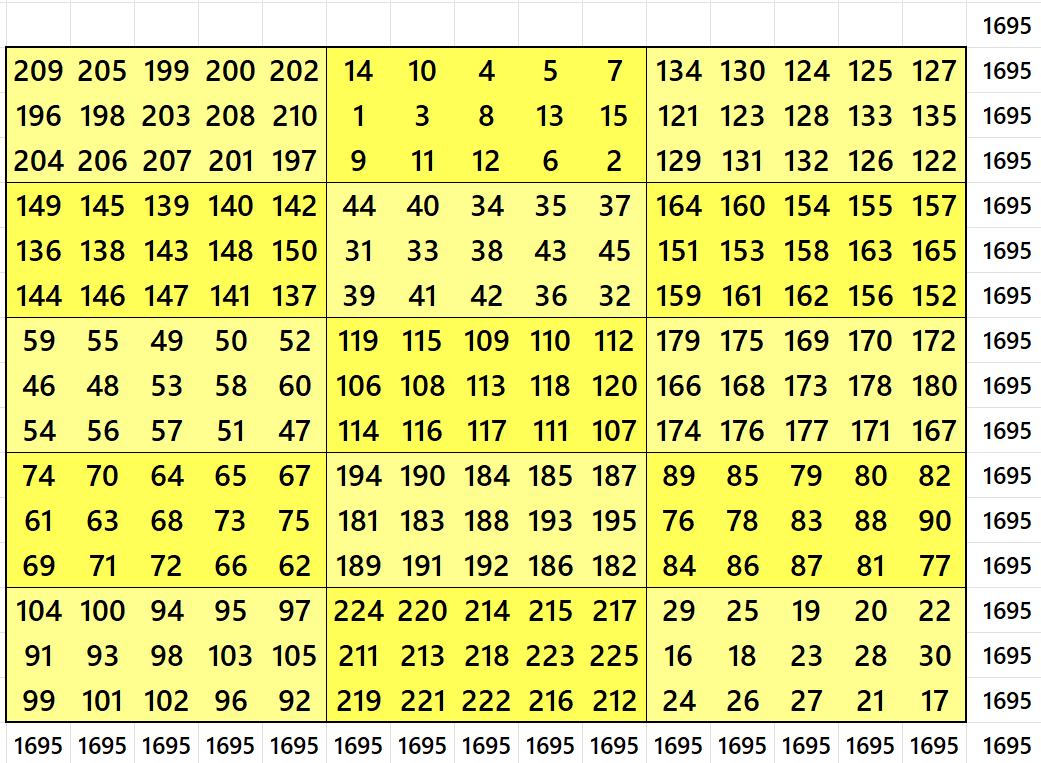
Magic Square of Order 15 with Unequal Sums Blocks of Order 3×5
Magic Square of Order 21 with Unequal Sums Blocks of Order 3×7

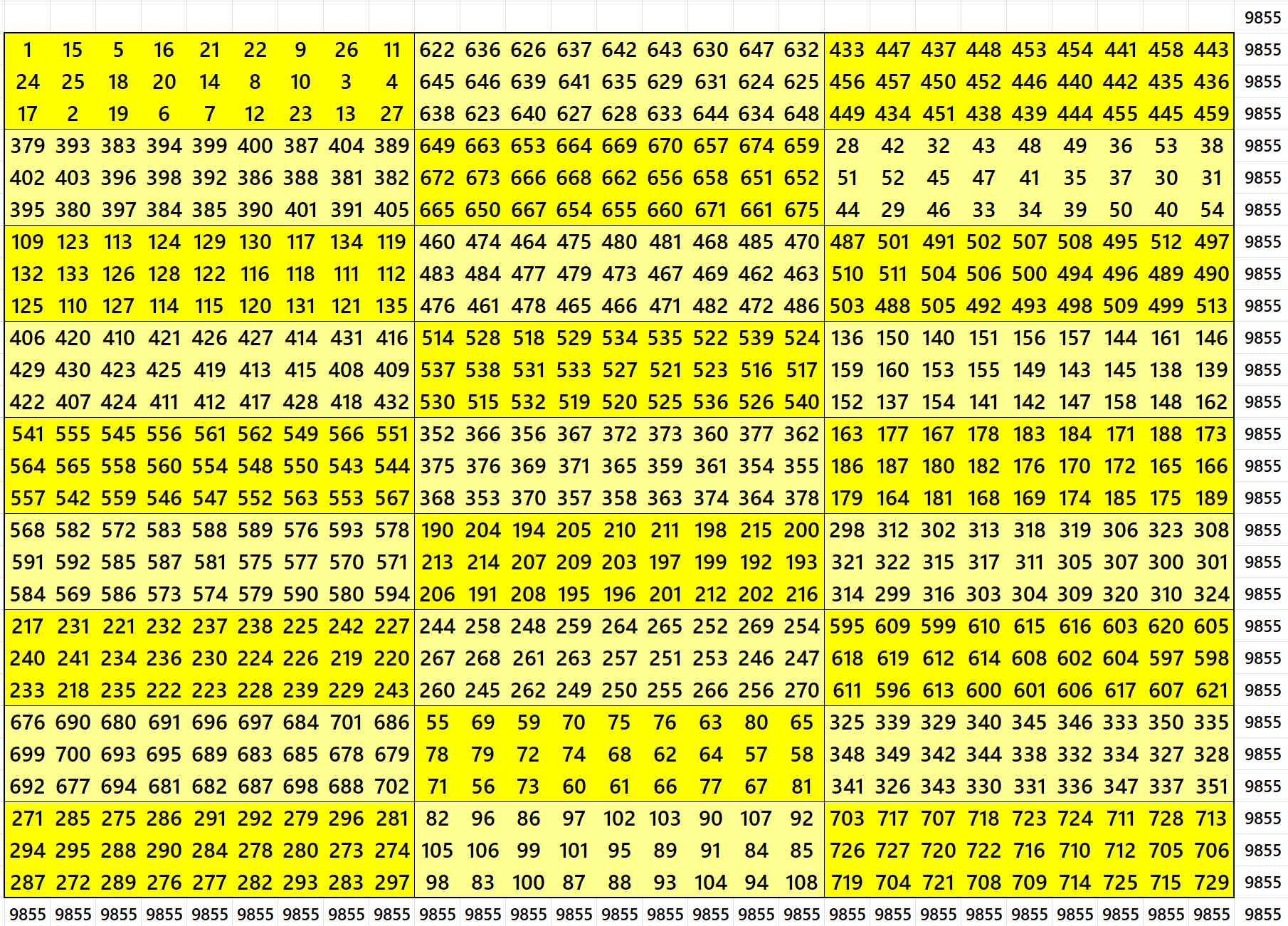
Magic Square of Order 27 with Unequal Sums Blocks of Order 3×9
Magic Square of Order 33 with Unequal Sums Blocks of Order 3×11

Magic Square of Order 35 with Unequal Sums Blocks of Order 5×7

Magic Square of Order 39 with Unequal Sums Blocks of Order 3×13
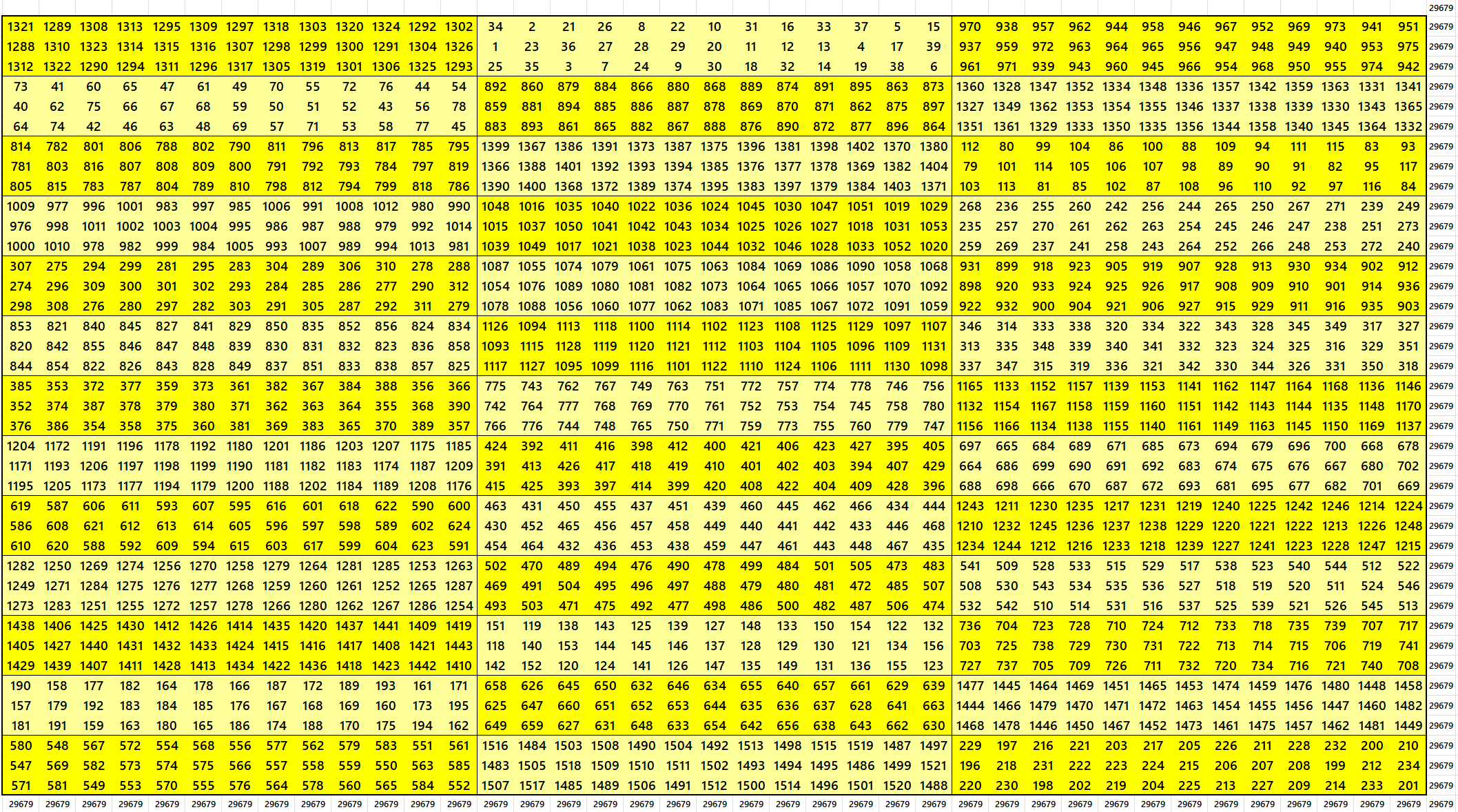
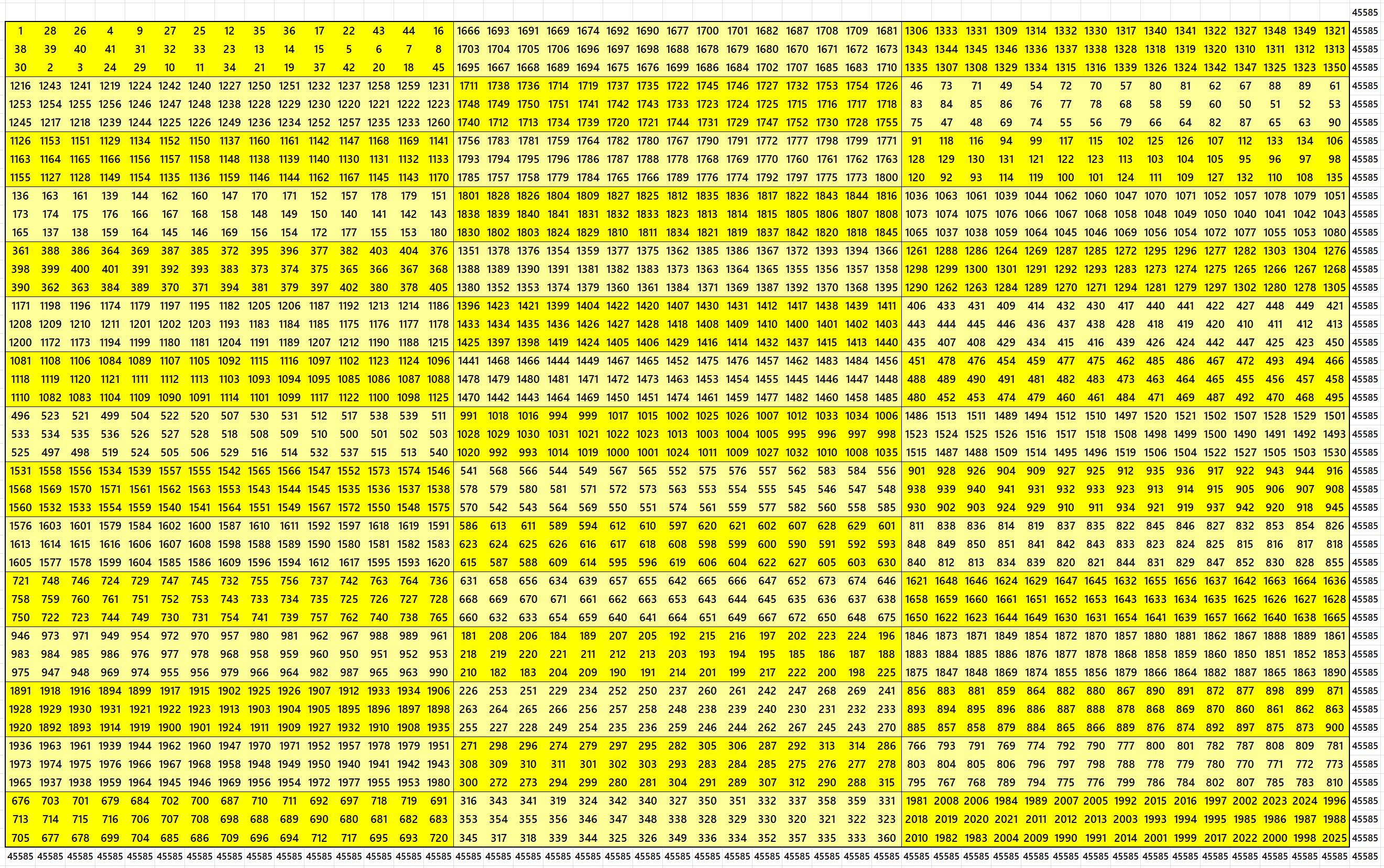
Magic Square of Order 45 with Unequal sum Blocks
First Way: Unequal Sum Blocks of Order 5×9
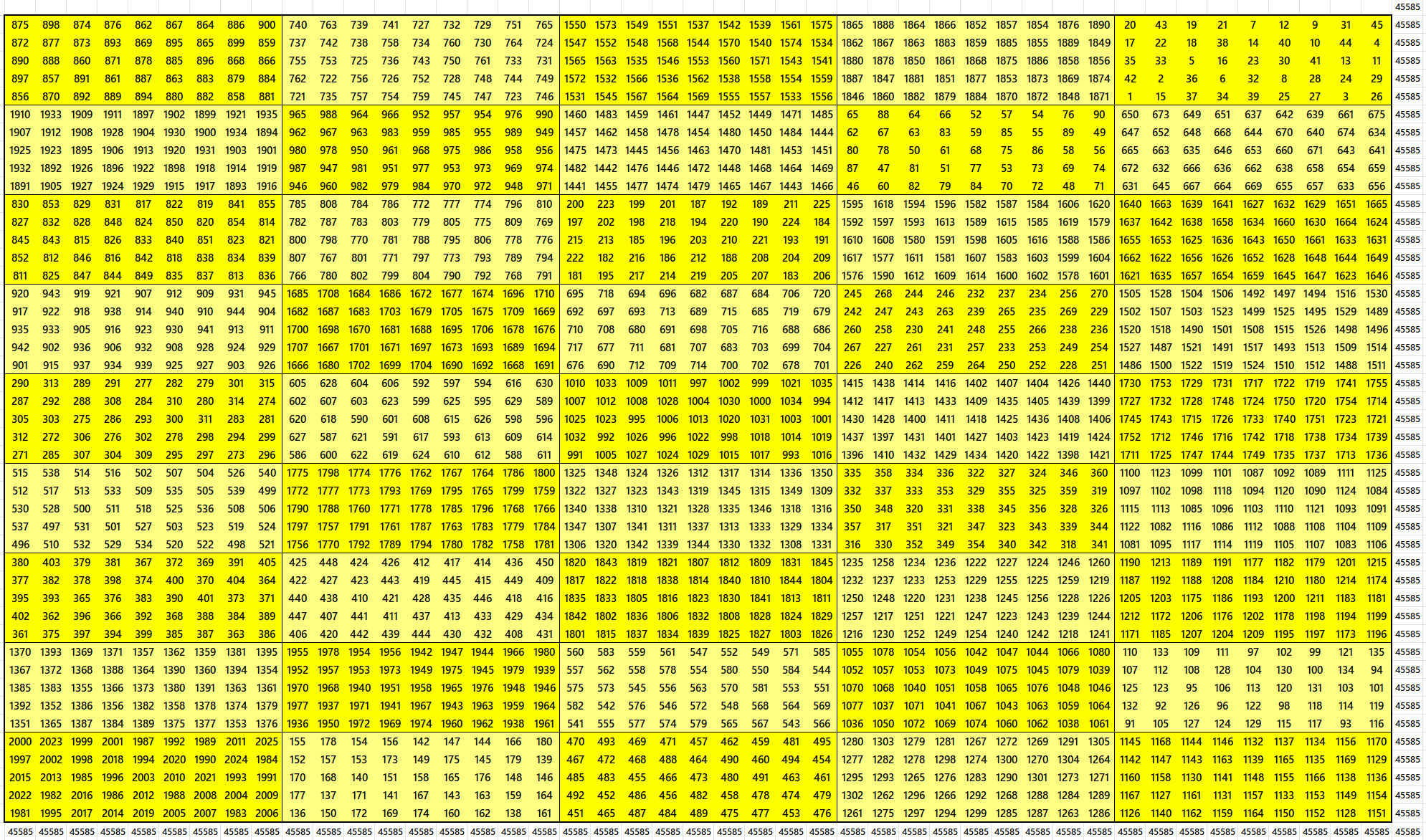
Second Way: Unequal Sum Blocks of Order 3×15