Figured Magic Squares of Orders 6, 8, 10, 12, 14 and 16: A Systematic Procedure

For the first time we are introducing the idea of magic squares by figures. This work brings magic squares of even orders from 6 to 16. For the orders 14 and 16 in some cases, the idea of construction is explained. It is based on external borders made by magic squares or bordered magic rectangles. Then inner blocks are previously known magic squares of smaller orders. The inicial work is up to order 30. Further orders shall be written in futures. The lack of numbers is due to the fact that readers can also try to complete them in their own ways. Otherwise, the readers can see the results in the author’s other works (click here). Below is a list of work of even order magic squares from orders 6 to 30. The readers can download the work from the links:

1. Inder J. Taneja, Figured Magic Squares of Orders 6, 10, 12, 14 and 16 Using Bordered Magic Rectangles, Zenodo, November 29, 2022, pp. 1-31, https://doi.org/10.5281/zenodo.7377674.
2. Inder J. Taneja, Figured Magic Squares of Orders 18 and 20 Using Bordered Magic Rectangles, Zenodo, November 29, 2022, pp. 1-87, https://doi.org/10.5281/zenodo.7377689.
3. Inder J. Taneja, Figured Magic Squares of Order 22 Using Bordered Magic Rectangles, Zenodo, November 29, 2022, pp. 1-61, https://doi.org/10.5281/zenodo.7377706.
4. Inder J. Taneja, Figured Magic Squares of Order 24 Using Bordered Magic Rectangles, Zenodo, November 29, 2022, pp. 1-104, https://doi.org/10.5281/zenodo.7377779.
5. Inder J. Taneja, Figured Magic Squares of Order 26 Using Bordered Magic Rectangles, Zenodo, November 29, 2022, pp. 1-88, https://doi.org/10.5281/zenodo.7377794.
6. Inder J. Taneja, Figured Magic Squares of Order 28 Using Bordered Magic Rectangles, Zenodo, December 02, 2022, pp. 1-179, https://doi.org/10.5281/zenodo.7390666.
7. Inder J. Taneja, Figured Magic Squares of Order 30 Using Bordered Magic Rectangles, Zenodo, December 02, 2022, pp. 1-179, https://doi.org/10.5281/zenodo.7390705.

Below are a few Examples of Figured Magic Squares of Orders 6, 8, 10, 12, 14 and 16. These are written in six parts. Orders 14 and 16 are written representing systematic procedure of construction.

• Part 1: Magic Squares of Order 6.
• Part 2: Magic Squares of Order 8.
• Part 3: Magic Squares of Order 10.
• Part 4: Magic Squares of Order 12.
• Part 5: Magic Squares of Order 14.
• Part 6: Magic Squares of Order 16.

Part 1: Magic Squares of Order 6

Part 2: Magic Squares of Order 8

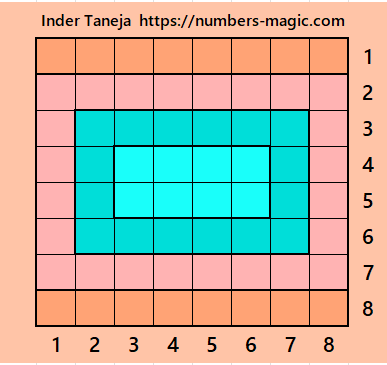
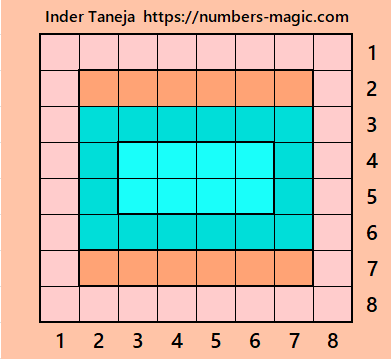
Part 3: Magic Squares of Order 10

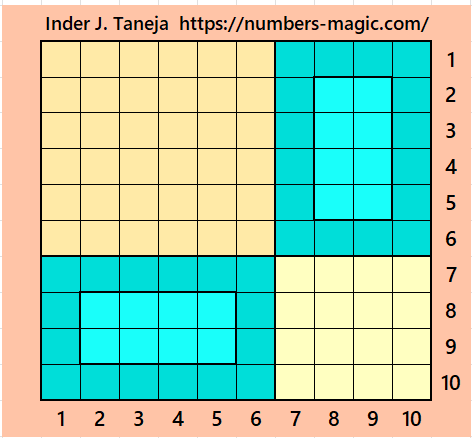
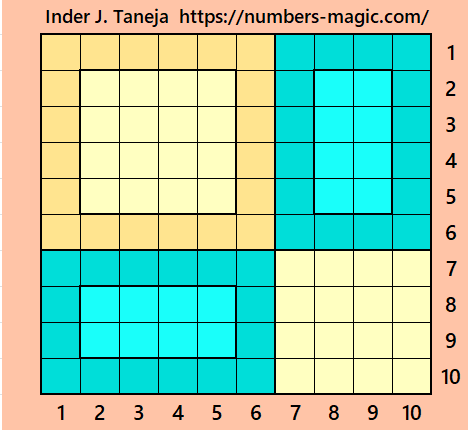
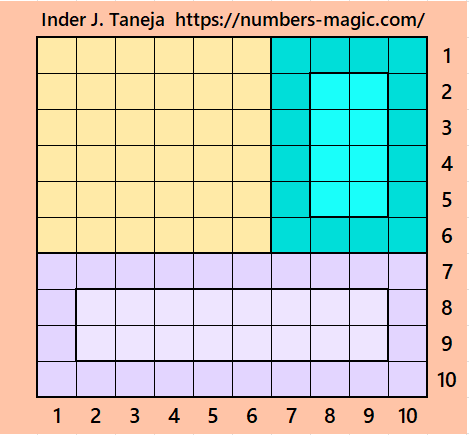
Part 3: Magic Squares of Order 12

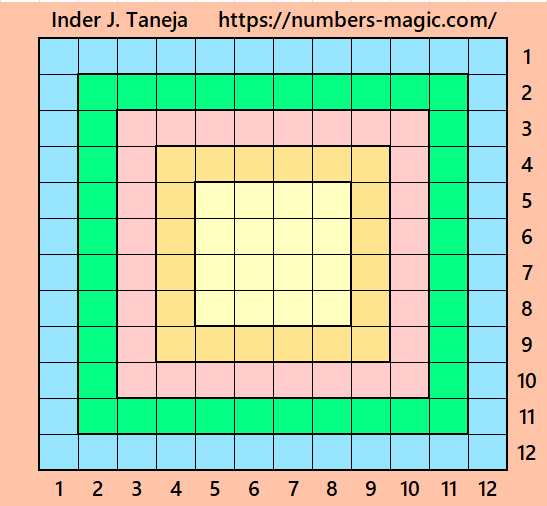
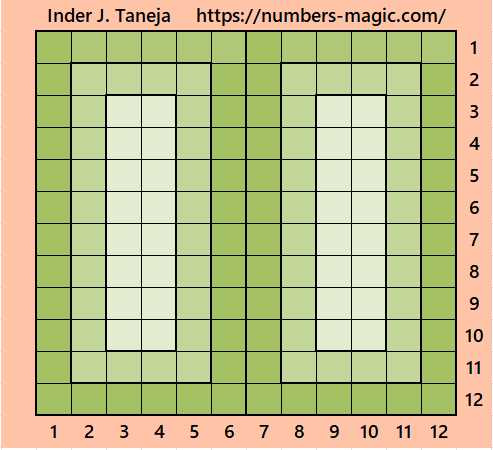
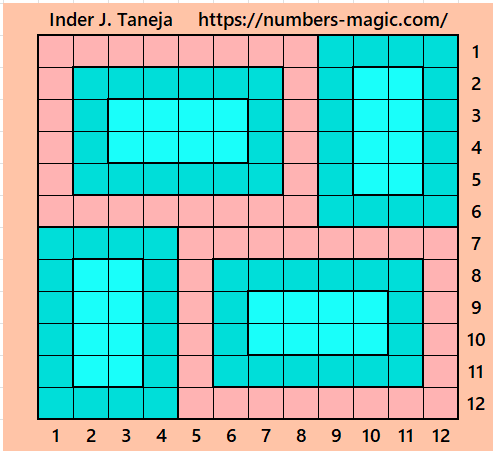
Part 4: Magic Squares of Order 14

In some cases, the idea of construction is explained. It is divided in four parts:

• Part 1: Bordered Magic Square of Order 14.
• Part 2: Cornered Magic Squares of Order 4.
• Part 3: Closed Border of Order 4 Bordered Magic Rectangles.
• Part 4: Magic Squares of Order 6 and 8 with BMRs of Order 6×8
• Part 5: Extra Examples.

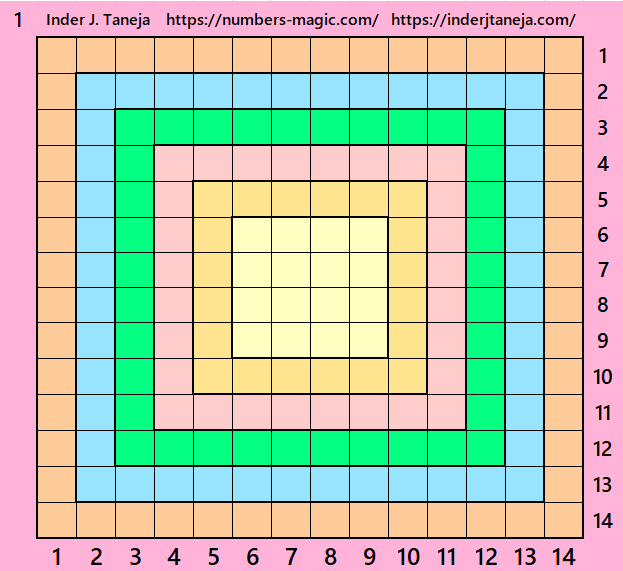
Part 1: Bordered Magic Square of Order 14

Part 2: Cornered Magic Squares of Order 4

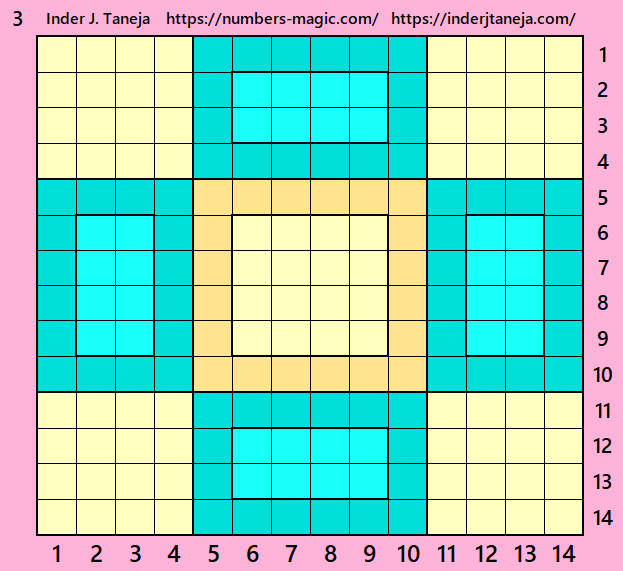
Part 3: Closed Border of Order 4 with Bordered Magic Rectangles

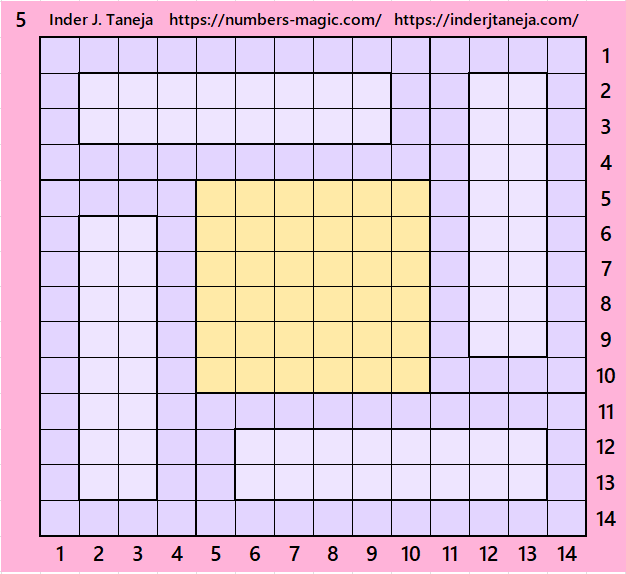
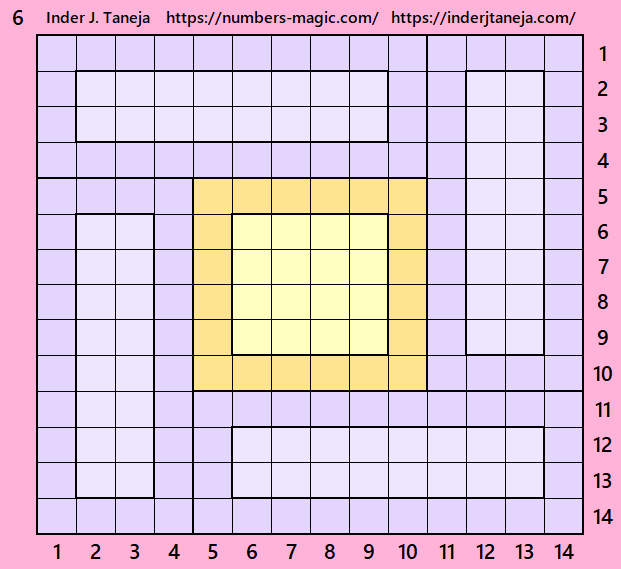
Part 4: Magic Squares of Order 6 and 8, and BMRs of Order 6×8

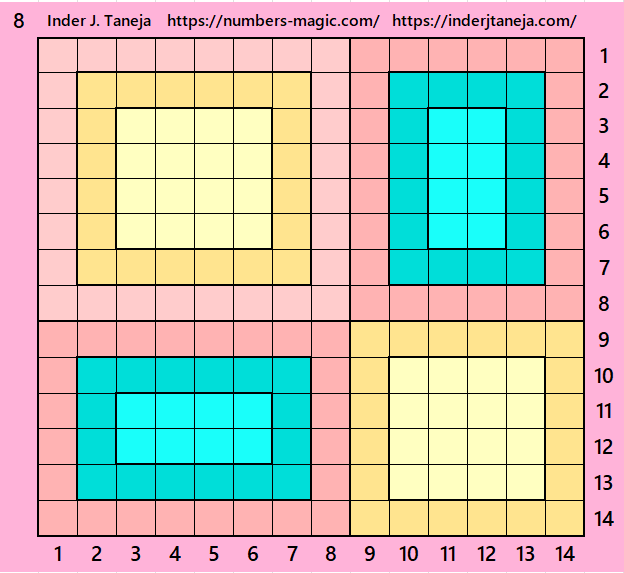
Part 5: Extra Examples

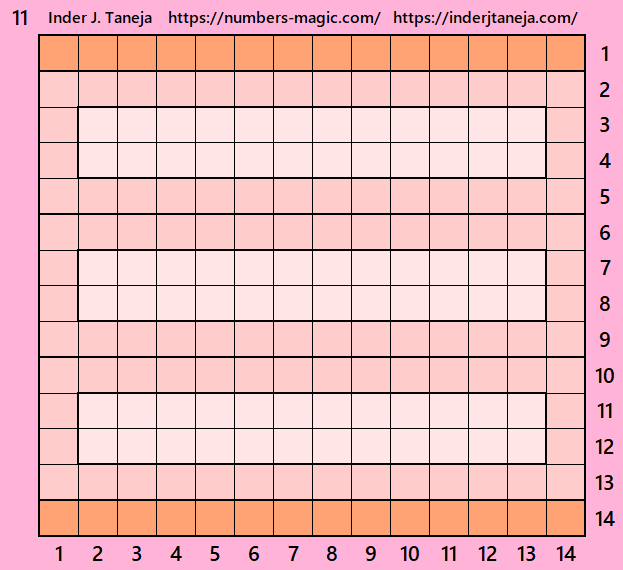
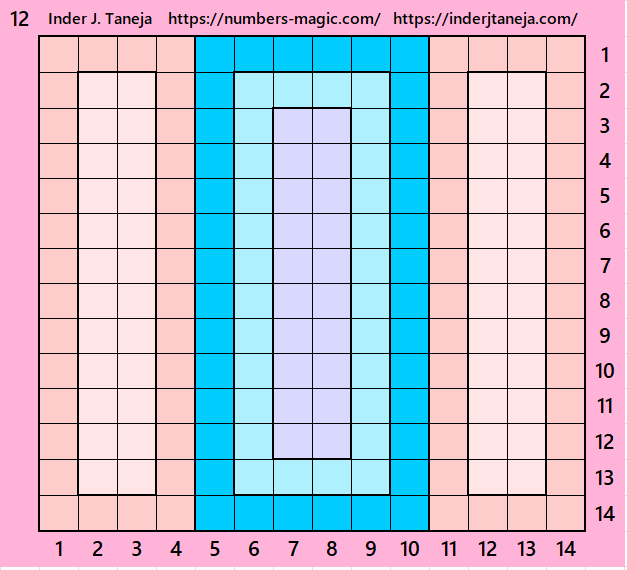
Magic Squares of Order 16

Below are a few examples of magic squares of order 16. In some cases, the idea of construction is explained. The examples are divided in following parts:

• Part 1: Bordered and Block-Wise Magic Squares of Order 16
• Part 2: Closed Border of Order 4
• Part 3: Corners with Magic Squares of Order 6
• Part 4: Closed Border of Order 6
• Part 5: Blocks of Order 8
• Part 6: Consecutive BMRs
• Part 7: Extra Examples.

Part 1: Bordered and Block-Wise Magic Squares of Order 16

Part 2: Closed Border of Order 4

Part 3: Corners with Magic Squares of Order 6

Part 4: Closed Border of Order 6

Part 5: Blocks of Order 8

Part 6: Consecutive BMRs of Orders 8×10 and 10×12

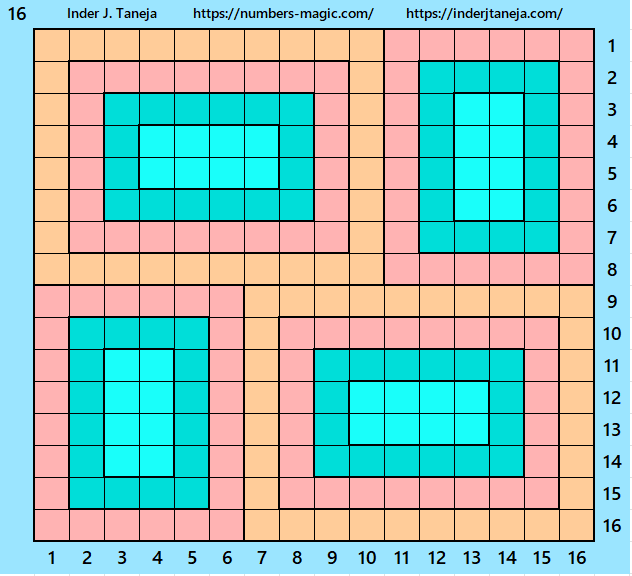
Part 7: Extra Examples